Творческая исследовательская работа "Тригонометрия вокруг нас"

 

 

 

 

 

 

 

 

Творческая исследовательская работа

 

Тригонометрия вокруг нас

 

 

 

 

 

 

 

 

Подготовили учащиеся  10 класса

Оганесян Арпине,

Чернова Вера

 

 

Руководитель: учитель математики

Пастухова Н.А.

 

 

 

 

 

Содержание:

 

1. Введение.     ________________________________________________________2

2. История возникновения и развития тригонометрии. ___________________3

 3. Применение тригонометрии в различных областях науки и

практической деятельности.

3.1 Тригонометрия в физике._____________________________________________5

3.2 Тригонометрия в навигации._________________________________________  9

3.3 Тригонометрия в архитектуре.________________________________________10

3.4 Тригонометрия в астрономии.________________________________________12

3.5 Тригонометрия в биологии и медицине._______________________________  13

3.6 Тригонометрия в геодезии.__________________________________________ 15

3.7 Тригонометрия в баллистике.________________________________________ 16

 

4. Заключение._______________________________________________________ 17

            5. Список литературы._______________________________________________  18

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1.      Введение

Изучая тригонометрию в 10 классе, мы задались вопросом: где в жизни используются понятия тригонометрии. Реальные процессы окружающего мира обычно связаны с большим количеством переменных и зависимостей между ними. Описать эти зависимости можно с помощью функций. Знание свойств функций позволяет понять суть происходящих процессов, предсказать ход их развития, управлять ими. В различных науках и областях человеческой деятельности возникают функциональные зависимости, которые могут касаться самых разнообразных явлений природы и окружающей среды.

В исследовательской работе рассматривается практическое применение понятий тригонометрии и тригонометрических функций.

Цель проекта: выявить связь тригонометрических функций с явлениями окружающего мира и практической деятельностью человека,  показать, что данные функции находит широкое применение в жизни.

Для достижения цели  необходимо было  решить  следующие задачи:

1. Изучить историю возникновения и развития тригонометрии.

2. Выяснить, какие законы природы выражаются тригонометрическими функциями.

3. Найти примеры применения тригонометрических функций в различных сферах деятельности человека.

Данная тема является актуальной.

     Восход и заход солнца, изменение фаз луны, чередование времен года, биение сердца, циклы в жизнедеятельности организма, вращение колеса, морские приливы и отливы - модели этих многообразных процессов описываются тригонометрическими функциями.

Тригонометрические вычисления применяются практически во всех сферах жизнедеятельности людей.

Для некоторых профессий знание тригонометрии  необходимо, т.к. позволяет измерять расстояния до недалёких звёзд в астрономии, контролировать системы навигации спутников. Принципы тригонометрии,  используются и в таких областях, как теория музыки, акустика, оптика, анализ финансовых рынков, электроника, теория вероятностей, статистика, биология, медицина (включая ультразвуковое исследование (УЗИ) и компьютерную томографию), сейсмология, метеорология, океанология, картография, многие разделы физики, топография и геодезия, архитектура, фонетика, экономика, электронная техника, машиностроение, компьютерная графика, кристаллография.

 

 

 

 

 

 

 

       

 

 

 

 

 

 

 

 

 

2. История возникновения и развития тригонометрии.

Как и всякая другая наука, тригонометрия возникла в результате человеческой практики в процессе решения конкретных практических задач. Термин «тригонометрия» происходит от греческих слов τρίγονον «тригонон» - треугольник  и μετρειν «метрио» - измерять, что означает измерять треугольник.  Задачи, в которых требуется измерять углы, появились так же давно, как и задачи, сводящиеся к измерению расстояний. Роль измерения углов оказывается особенно значительной в тех случаях, когда непосредственное измерение расстояний оказывается затруднительным или невозможным вследствие удаленности или недоступности предметов. Именно задача - решение треугольников, т.е. определение всех сторон и углов треугольника по трем  его известным, с древнейших времен составляла основу практических приложений тригонометрии.

Зачатки тригонометрии можно найти в математических рукописях Древнего Египта, Вавилона и Древнего Китая.   56-я задача из папируса Ринда (II тысячелетие до н. э.) предлагает найти наклон пирамиды, высота которой равна 250 локтей, а длина стороны основания — 360 локтей.

Одним из научных достижений древних египтян служит  метод определения высоты предмета по длине отбрасываемой им тени. Этот метод послужил основой гномоники –учения о солнечных часах (гномон – шест, вертикально установленный на горизонтальной площадке). Отношение длины тени к длине шеста, вычисляемое в течение солнечного дня позволяет определить высоту солнца над горизонтом. Деление линии, соединяющей концы положения тени шеста, на части дня дает часы. 

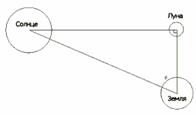
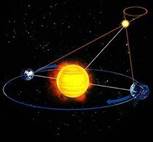
Дальнейшее развитие тригонометрии связано с именем астронома Аристарха Самосского (III век до н. э.). В его трактате «О величинах и расстояниях Солнца и Луны» ставилась задача об определении расстояний до небесных тел; эта задача требовала вычисления отношения сторон прямоугольного треугольника при известном значении одного из углов. Аристарх рассматривал прямоугольный треугольник, образованный Солнцем, Луной и Землёй во время квадратуры Ему требовалось вычислить величину гипотенузы (расстояние от Земли до Солнца) через катет (расстояние от Земли до Луны) при известном значении прилежащего угла (87°). 

 

Несколько десятилетий спустя  Клавдий Птоломей  в своих трудах «География», «Аналемма» и «Планисферий» даёт подробное изложение тригонометрических приложений к картографии, астрономии и механике. Составленные Гиппархом таблицы положений Солнца и Луны позволили предвычислять моменты наступления затмений (с ошибкой 1—2 ч). Гиппарх впервые стал использовать в астрономии методы сферической тригонометрии. Он повысил точность наблюдений, применив для наведения на светило крест нитей в угломерных инструментах — секстантах и квадрантах. Ученый составил огромный по тем временам каталог положений 850 звезд, разделив их по блеску на 6 степеней (звездных величин). Гиппарх ввел географические координаты — широту и долготу, и его можно считать основателем математической географии. (ок. 190 до н. э. — ок. 120 до н. э.)

 

В интересах практической астрономии и географических исследований были получены аналитические результаты для треугольников на сферических поверхностях. С тех пор плоская и сферическая тригонометрии развивались как неотъемлемые части единой науки.

Важный шаг вперед в период с V  по XII век был сделан индусами. Наряду  с  линией синуса индусы ввели в тригонометрию линию косинуса.  Им были известны также соотношения cosa =sin(90°- a)  и sin²a+cos²a = r² , а также формулы для синуса суммы и разности двух углов.

Следующий этап в развитии тригонометрии связан со странами Средней Азии, Ближнего Востока, Закавказья(VII-XV в.). Развиваясь в тесной связи с астрономией и географией,- среднеазиатская математика имела ярко выраженный «вычислительный характер» и была направлена на разрешение прикладных задач измерительной геометрии и тригонометрии. Из числа сделанных среднеазиатскими учеными важнейших успехов следует в первую очередь отметить введение всех шести тригонометрических линий: синуса, косинуса, тангенса, котангенса, секанса и косеканса, из которых лишь первые две были известны грекам и индусам.

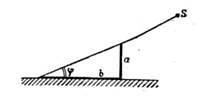Решая задачу об определении высоты  Солнца S  по тени b вертикально стоящего шеста a (см чертеж), сирийский астроном ал-Баттани (Хв.)пришел к выводу, что острый угол j в прямоугольном треугольнике определяется отношением одного катета к другому, и вычислил небольшую таблицу котангенсов через 1°. Точнее говоря, он вычислил длину тени b=a× =a×ctgj    шеста определенной длины (а=12) для j=1°,2°,3°…. В трудах среднеазиатских ученых тригонометрия превратилась из науки, обслуживающей астрономию, в особую математическую дисциплину, представляющую самостоятельный интерес.

 В Европе XII – XV вв., после того как были переведены с арабского и греческого языков на латинский некоторые классические математические и астрономические произведения, развитее тригонометрии продолжалось. Самым видным европейским представителем этой эпохи в области тригонометрии был Регимонтан. Он составил тригонометрические таблицы синусов через 1 секунду с точностью до 7-й значащей цифры. На пороге XVII в. развитие тригонометрии  получило новое направление – аналитическое.  Тригонометрия становится одной из глав математического анализа. Она находит широкое применение в механике, физике и технике, особенно при изучении колебательных движений и других периодических процессов. О свойствах периодичности тригонометрических функций знал еще Виет, первые математические исследования которого относились к тригонометрии. Швейцарский математик Иоганн Бернулли уже применял символы тригонометрических функций.

Развитию аналитической теории тригонометрических функций содействовали Исаак Ньютон и Леонард Эйлер. Эйлеру  принадлежит окончательное решение вопроса о знаках тригонометрических функций во всех четвертях круга, вывод формул приведения для общих случаев.

Дальнейшее развитие теории было продолжено в XIX в. Н.И. Лобачевским и другими учеными.

В наше время тригонометрия больше не рассматривается как самостоятельная ветвь математики. Важнейшая ее часть – учение о тригонометрических функциях является частью более общего, построенного с единой точки зрения учения о функциях, изучаемых в математическом анализе; другая же часть – решение треугольников – рассматривается как глава геометрии (плоской и сферической).

 

 

 

3. Применение тригонометрии в различных областях науки и практической деятельности.

3.1 Тригонометрия в физике.

В окружающем нас мире приходится сталкиваться с периодическими процессами, которые повторяются через одинаковые промежутки времени. Эти процессы называются колебательными. Колебательные явления различной физической природы подчиняются общим закономерностям и описываются одинаковыми уравнениями. Существуют разные виды колебательных явлений.

Гармоническое колебание — явление периодического изменения какой-либо величины, при котором зависимость от аргумента имеет характер функции синуса или косинуса.

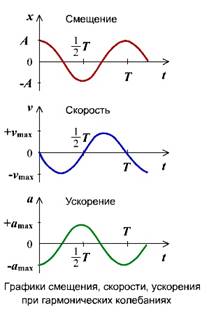
Механические колебания. Механическими колебаниями называют движения тел, повторяющиеся точно через одинаковые промежутки времени. Графическое изображение этой функции дает наглядное представление о протекании колебательного процесса во времени. Примерами простых механических колебательных систем могут служить груз на пружине или математический маятник.

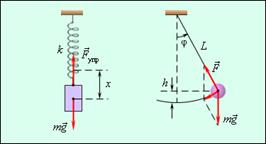
График гармонического колебания устанавливает зависимость смещения тела со временем. Если прикрепить к пружинному маятнику карандаш, за маятником уложить  бумажную ленту, которая равномерно перемещается, то маятник оставит след. На бумаге отобразится график движения.

 

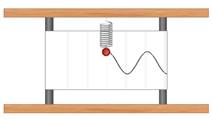
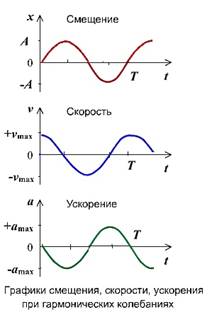
Графиком гармонического колебания является синусоида (или косинусоида). По графику колебаний можно определить все характеристики колебательного движения.

График косинуса в начальный момент имеет максимальное значение, а график синуса имеет в начальный момент нулевое значение. Если колебание начинаем исследовать из положения равновесия, то колебание будет повторять синусоиду. Если колебание начинаем рассматривать из положения максимального отклонения, то колебание опишет косинус. Или такое колебание можно описать формулой синуса с начальной фазой.

Уравнение гармонического колебания устанавливает зависимость координаты тела от времени.

x(t) = Asin(ωt + ), где х — значение изменяющейся величины, t - время, А - амплитуда колебаний, ω — циклическая частота колебаний, - полная фаза колебаний,   - начальная фаза колебаний.

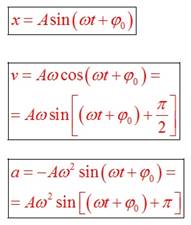
Математи́ческий ма́ятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки на конце невесомой нерастяжимой нити или лёгкого стержня и находящуюся в однородном поле сил тяготения[1]. Другой конец нити (стержня) обычно неподвижен. Математический маятник служит простейшей моделью физического тела, совершающего колебания: она не учитывает распределение массы. Однако реальный физический ма ятник при малых амплитудах колеблется так же, как математический с приведённой длиной.

 Если эти колебания малы, то угол отклонения маятника приближенно выражается формулой: j=j₀sin(t), где l-длина маятника, а j₀-начальный угол отклонения. Чем длиннее маятник, тем медленнее он качается. Измеряя период колебания маятника известной длины, можно вычислять ускорение земного тяготения g в различных точках земной поверхности.

Волны.  Волна – процесс распространения колебаний в упругой среде.

Механическая волна – механические возмущения, распространяющиеся в пространстве и несущие энергию. Виды механических волн:

1)      упругие волны – распространение упругих деформаций;

2)      волны на поверхности жидкости.

Характеристики волн:

1)      Скорость -  - расстояние, которое проходит волна за единицу времени (1 сек.). В однородной среде скорость постоянна. Скорость зависит от свойств среды – упругости и плотности (чем больше плотность и упругость среды, тем больше скорость волны). Скорость в твёрдых телах выше скорости в жидких средах, а в жидких средах – выше, чем в газах. Скорость волны – отношение длины волны к периоду: .

2)      Длина волны -  - расстояние, которое прошла волна за время, равное периоду колебаний – расстояние между 2 точками, фазы которых в один и тот же момент времени отличаются на 2. Единица измерения длины волны – метры.

3)      Фронт волны – геометрическое место точек, колеблющихся в одинаковой фазе.

4)      Уравнение волны – зависимость смещения колеблющейся точки, участвующей в волновом процессе, от координаты её равновесного положения и времени: .

 

     

        

 

 

 

 

 

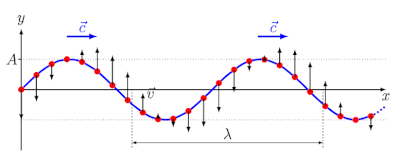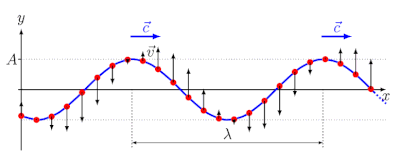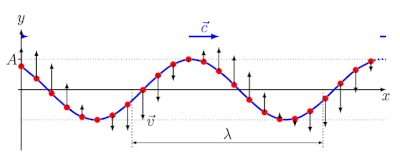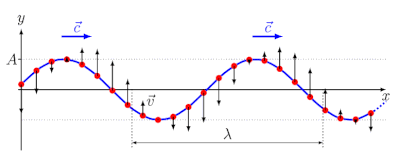
Графическое представление гармонического колебания и волны.

 

Звук – колебания и волны, которые действуют на ухо человека и вызывают слуховое ощущение. Звуковые колебания и волны – частный случай механических колебаний и волн.  

Волнова́я тео́рия све́та — одна из теорий, объясняющих природу света. Основное положение теории заключается в том, что свет имеет волновую природу, то есть ведёт себя как электромагнитная волна, от длины которой зависит цвет видимого нами света.
Теория подтверждается многими опытами (в частности, опытом Т. Юнга), и данное поведение света (в виде электромагнитной волны) наблюдается в таких физических явлениях, как дисперсия, дифракция и интерференция света. Теория берёт своё начало от Гюйгенса. Она рассматривает свет как совокупность поперечных монохроматических электромагнитных волн, а наблюдаемые оптические эффекты - как результат интерференции этих волн.

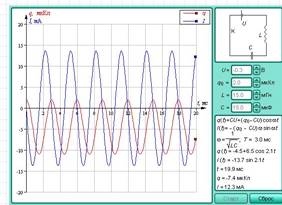Не только многие механические колебания происходят по синусоидальному закону. И в электрических цепях возникают синусоидальные колебания. Так в цепи, изображенной в правом верхнем углу модели, заряд на обкладках конденсатора изменяется по закону q = CU + (q₀ – CU) cos ωt ,где С- емкость конденсатора, U –напряжение на источнике тока, L –индуктивность катушки,   - угловая частота колебаний .

 Соответствующие графики q (t)и I(t).

 

 

 

 

 

 

 

 

В физике задача решения треугольника используется при решении многих физических задач: вычисление дальности полета снаряда, выпущенного под углом к горизонту, вычислении силы трения и других физических величин.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Многие природные явления объясняет физика при этом  используются формулы тригонометрии.

Например, радуга появляется из-за того, что солнечный свет испытывает преломление в капельках воды, взвешенных в воздухе, по закону преломления:

sin i₁ / sin i₂ = n₁ / n₂, где n₁ является показателем преломления первой среды; n₂ является показателем преломления второй среды; i₁-углом падения, i₂-углом преломления света. n₁=1, n₂≈1,33 – соответственно показатели преломления воздуха и воды, Впервые теория радуги была дана в 1637 году Рене Декартом.

 

 

 

 

 

 

 

 

Например, северное сияние  объясняется законами электродинамики. Попадание в верхние слои атмосферы планет заряженных элементов солнечного ветра обусловливается взаимодействием магнитного поля земли с солнечным ветром. 

Сила, действующая на перемещающуюся в магнитном поле заряженную частичку, именуется силой Лоренца. Она пропорциональна заряду частицы и векторному произведению поля и скорости перемещения частицы. Сила Лоренца вычисляется по формуле: , где  - заряд частицы, v- скорость частицы – B – вектор магнитной индукции,   - угол между

 

 

 

 

 

3.2 Тригонометрия в навигации.

Под навигацией понимается  наука, целью которой является изучение и создание наиболее удобных и полезных способов построения маршрута из одной точки в другую, его оценка и выбор лучшего варианта из всех предложенных. Данные маршруты необходимы мореплавателям, которые в течение своего путешествия сталкиваются с множеством трудностей, преград, вопросов по курсу движения.

На суднах в старые времена использовали для навигации квадранты и секстанты.  Секста́нт (от лат. sextans— шестой, шестая часть) — навигационный измерительный инструмент, используемый для определения высоты Солнца и других космических объектов над горизонтом с целью определения географических координат точки, в которой производится измерение. Например, измерив высоту Солнца в астрономический полдень, можно, зная дату измерения, вычислить широту места расположения прибора. Строго говоря, секстант позволяет точно измерять угол между двумя направлениями. Зная высоту маяка (с карты), можно узнать дистанцию до него, измерив угол между направлением на основание маяка и направлением на верхнюю часть и произведя несложный расчёт, используя тригонометрические значения угла.. Также можно измерять горизонтальный угол (то есть в плоскости горизонта) между направлениями на разные объекты. На современных арктических суднах применяется астро-компас.

 

 

 

 

 

 

 

 

Также навигация необходима: летчикам, которые управляют сложными высокотехничными самолетами, ориентируются, порой в очень экстремальных ситуациях С помощью тригонометрии, пилоты могли рассчитывать ветряные погрешности, для наиболее точного и безопасного ведения самолета. Для того, чтобы осуществить данные вычисления, используют треугольник скоростей. Данный треугольник образован вектором воздушной скорости (V), вектором ветра( W), вектором путевой скорости (Vп), где ПУ – путевой угол, УВ – угол ветра, КУВ – курсовой угол ветра

Для подсчета путевой скорости используют формулу: Vп =V cos УС + W cos УВ.

. 

 

 

 

 

 

 

3.3 Тригонометрия в архитектуре.

Широко используется тригонометрия в строительстве, а особенно в архитектуре. Большинство композиционных решений и построений рисунков проходило именно с помощью тригонометрии. Рассмотрим пример на построение одной скульптуры французского мастера Золотого века искусства.

Пропорциональное соотношение в построении статуи было идеально. Однако при поднятии статуи на высокий пьедестал, она смотрелась уродливой. Скульптором не было учтено, что в перспективе к горизонту уменьшаются многие детали и при взгляде снизу вверх уже не создается впечатления ее идеальности.

Чтобы добиться совершенства, пришлось провести следующие вычисления:  зная примерное расстояние от статуи до точки зрения, а именно от верха статуи до глаз человека и высоту статуи, можно рассчитать синус угла падения взгляда с помощью таблицы.  Когда  статую поднимают на высоту расстояния АС и НС увеличиваются, можно рассчитать значения косинуса угла С, по таблице найдем угол падения взгляда, затем вычислить АН, а также синус угла С. Сравнив измерения АН в первом и во втором случаи нашли коэффициент пропорциональности, который помог получить чертеж, а потом скульптуру, при поднятии которой зрительно фигура была приближена к идеалу.

 

 

 

 

 

 

 

 

 

 

 

 

 

Культовые здания во всем мире были спроектированы благодаря математике, которая может считаться гением архитектуры. Некоторые известные примеры таких зданий:Детская школа Гауди в Барселоне, Ресторан в Лос-Манантиалесе в Аргентине, мост в Сингапуре. При проектировании этих зданий не обошлось без тригонометрии.

 

 

 

 

 

 

 

 

 

 

 

 

 

3.4 Тригонометрия в астрономии.

Тригонометрические понятия используются в астрономии при определении расстояний до космических объектов.

Расстояния до звезд, галактик и других объектов Вселенной слишком велики, и, если выражать их в метрах, то получим цифры со многими нулями, но так как это неудобно для записи вычислений, то для определения расстояний в астрономии применяют другие единицы измерения: в пределах Солнечной системы принято пользоваться такой единицей измерения, как астрономическая единица (а. е.) — среднее расстояние от Земли до Солнца: 1 а.е. = 149597870,5 км.

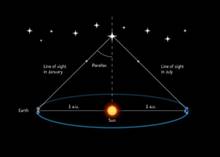
Используя астрономическую единицу, можно находить годичные параллаксы звезд, т.е. углы, под которыми виден со звезд средний радиус земной орбиты. Так как Земля вращается вокруг Солнца, то положение звезд на небе должно изменяться. Если мы измерим параллакс какой-то звезды, то расстояние до нее находится по формуле: ,

где R — расстояние до звезды; р — годичный параллакс.

 

 

 

 

Измерения показали, что самые близкие к Солнцу звезды имеют годичный параллакс меньше 1" (одной секунды дуги). Поэтому

При бесконечно малым р, можно заменить sinр на р и тогда формула  примет вид:

Громадные расстояния до звезд выражать в астрономических единицах так же неудобно, как и в километрах. Для этого используется такая внесистемная единица измерения, как парсек (пк). Эту единицу измерения предложил в 1912 г. Г. Тернер. Один парсек — это расстояние, с которого средний радиус земной орбиты виден под углом одна секунда.

Из формулы следует, что 1 пк = 206 265 а. е.

Из тригонометрии известно, что предмет бывает виден под углом, равным одной секунде дуги, если он удален от наблюдателя на расстояние, в 206 265 раз превышающее его линейные размеры или его диаметр. Следовательно, расстояние Земля  - Солнце примерно в 11 500 раз больше диаметра Земли.

 

 

 

 

 

 

 

3.5 Тригонометрия в биологии и медицине.

Одно из фундаментальных свойств живой природы - это цикличность большинства происходящих в ней процессов..Биоритмы - периодически повторяющиеся изменения характера и интенсивности биологических процессов и явлений. Они свойственны живой материи на всех уровнях ее организации— от молекулярных до биосферы. Одни биологические ритмы относительно самостоятельны (частота сокращений сердца, дыхания), другие связаны с приспособлением организмов к геофизическим циклам — суточным (колебания интенсивности деления клеток, обмена веществ). Способность к таким изменениям жизнедеятельности передается по наследству и обнаружена практически у всех живых организмов. Их можно наблюдать в отдельных клетках, тканях и органах, целых организмах и популяциях. Биоритмы подразделяют на физиологические, имеющие периоды от долей секунды до нескольких минут и экологические, по длительности совпадающие с каким либо ритмом окружающей среды. К ним относят суточные, сезонные, годовые, приливные и лунные ритмы. Основной земной ритм – суточный, обусловлен вращением Земли вокруг своей оси, поэтому практически все процессы в живом организме обладают суточной периодичностью.

Множество экологических факторов на нашей планете, в первую очередь световой режим, температура, давление и влажность воздуха, атмосферное и электромагнитное поле, морские приливы и отливы, под влиянием этого вращения закономерно изменяются.

Человек со дня рождения находится в трех, биоритмах: физическом, эмоциональном и интеллектуальном.

Физический цикл равен 23 дням.Он определяет энергию человека, его силу, выносливость, координацию движения.

Эмоциональный цикл (28 дня) обусловливает состояние нервной системы и настроение.

Интеллектуальный цикл (33 дня) определяет творческую способность личности.

Любой из циклов состоит из двух полупериодов, положительного и отрицательного.

В течение первой половины физического цикла человек энергичен и достигает лучших результатов в своей деятельности; во второй половине цикла энергичность уступает лености.

В первой половине эмоционального цикла человек весел, агрессивен, оптимистичен, переоценивает свои возможности, во второй половине - раздражителен, легко возбудим, недооценивает свои возможности, пессимистичен, все критически анализирует.

Первая половина интеллектуального цикла характеризуется творческой активностью, во второй половине происходит творческий спад.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Тригонометрия играет важную роль в медицине. С ее помощью иранские ученые открыли формулу сердца - комплексное алгебраически-тригонометрическое равенство, состоящее из 8 выражений, 32 коэффициентов и 33 основных параметров, включая несколько дополнительных для расчетов в случаях аритмии.

В медицине используются приборы, основанные на записи колебательных процессов, происходящих в органах человека. Например, Фонокардиография – графическая регистрация фонов и шумов сердца.

Примененный в практических целях в 70-х годах 19 века англичанином А.Уоллером аппарат, записывающий электрическую активность сердца, продолжает служить человеку и по сей день. Электрокардиограф позволяет выявить явные отклонения от нормального ритма сердца, такие как Инфаркт миокарда, Ишемическая болезнь сердца, синусовая брадикардия, тахекардия,аритмия, синдром слабости синусового узла. На рис. представлены три вида кардиограммы. Первая кардиограмма здорового человека, вторая, того же человека, только с синусовой тахикардией, после физической нагрузки, а третья кардиограмма больного человека с синусовой аритмией.

 

 

 

 

 

 

 

 

 

 

 

 

 

Аппараты ЭКГ снимают кардиограмму у людей, фиксируя удары сердца. При чтении графиков врач-кардиолог учитывает количество интервалов и зубцов, максимум и минимум скачков, протяженность периодов: все это играет важную роль в определении диагноза и правильности лечения.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3.6 Тригонометрия в геодезии.

Процесс возведения строений, путей, мостов и иных зданий наступает с изыскательских и проектных работ. Все без исключения измерения на стройке ведутся с поддержкой геодезических приборов, таких как тахеометр и тригонометрический нивелир. При тригонометрическом нивелировании устанавливают разность высот между несколькими точками земной поверхности.

 

                                                                                              нивелир

Тригонометрическое нивелирование — метод определения превышений по измеренному углу наклона и длине наклонной линии или её проекции на горизонтальную плоскость.^. Зная S — наклонное расстояние и горизонтальный угол α, можно вычислить превышение между точками по упрощенной формуле h. = S · sinα.

С помощью приборов, таких как астролябия, измеряющих углы, и тригонометрических таблиц  можно проводить измерительные работы на местности.

 

 

 

 

 

 

 

 

 

 

 

 

 

Например, измерение высоты предмета.

Предположим, что требуется определить высоту АН какого – то предмета. Для этого отметим точку В на определённом расстоянии а от основания Н предмета и измерим угол АВН. По этим данным из прямоугольного треугольника АНВ находим высоту предмета: АН = НВ tgАВН.

Если основание предмета недоступно, то можно поступить так: на прямой, проходящей через основание Н предмета, отметим две точки В и С на определенном расстоянии ВС = а друг от друга и измерим углы АВН и АСВ: угол АВН = α, угол АСВ = β, угол ВАС = α – β. Эти данные позволяют определить все элементы треугольника АВС; по теореме синусов находим АВ:

Из прямоугольного треугольника АВН находим высоту АН предмета:

АН = АВ sin α.

 

 

3.7 Тригонометрия в баллистике.

Баллистика– наука о движении тел в поле тяжести Земли. Она изучает в первую очередь принципы движения всевозможных объектов, в частности пуль и снарядов, а также законы природы, влияющие на это движение и способность тела преодолевать возникшие на его пути преграды.

При расчетах и изучении баллистического движения любого тела, стоит обратить внимание на огромное количество факторов – массу, скорость и обтекаемость тела, атмосферные условия и многое-многое другое. Но даже при учете этого, в баллистике есть свои основные формулы, применяемые в исследованиях.

 Формулы баллистического движения.

 На брошенное под углом к горизонту тело в полете действует по меньшей мере – сила тяжести и сопротивление воздуха. Если исключить из этого силу сопротивления, то, согласно 2-го закону Ньютона, тело движется с ускорением, равным ускорению свободного падения; проекции ускорения на координатные оси равны: а_х = 0, а_у = -g. Проекции скорости тела, следовательно, изменяются со временем следующим образом: Vx = Vx₀ = V₀ · cos α; Vy = Vy₀ – g· t = V₀ ·sin α – g · t, где V₀ - начальная скорость, α – угол бросания. Координаты тела, следовательно, изменяются так: x = x₀ + V₀ ·t · cos α;       y = y₀ + V₀ · t · sin α – 0,5 · g · t². Если за точку отсчета берутся координаты х = у = 0, то:

x = V₀ ·t · cos α; y = V₀ · t ·sin α – 0,5 · g · t². Дальнейшие расчеты производятся при введении таких переменных как дальность полета и время, в итоге же получается финальное уравнение траектории движения. Выглядит оно следующим образом:

 y = x · tg α – g · x² / 2 · V₀² · cos²α.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4. Заключение.

Связь математики с окружающим миром позволяет «материализовать» знания. Это помогает нам лучше понять жизненную необходимость знаний, приобретаемых в школе. Мы убедились, что знания тригонометрии используются во многих областях науки и профессиональной деятельности человека. Тригонометрия применяется в таких областях науки как: астрономия, физика, баллистика, медицина, компьютерная графика и многих других. Без знания тригонометрии нельзя провести многие расчеты, используемые в строительстве, в архитектуре. Многие достижения в медицине связаны с применением свойств тригонометрических функций. Многие явления природы описываются с помощью физических законов и формул, использующих тригонометрические понятия.

Мы думаем, что тригонометрия нашла отражение в окружающем мире, и сферы деятельности человека, в которых она  играет важную роль, будут только расширяться.

 

 

h = S ⋅ sin ⁡ α . {\displaystyle h=S\cdot \sin \alpha .}

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5. Список литературы.

 

1.      .Атанасов П.Т., Атанасов Н.П. Сборник математических задач с практическим содержанием: Книга для учителя.-М.:Просвещение,1987-110с.

2.      .Виленкин Н.Я. Функции в природе и технике: Кн. для внеклассного чтения IX-X кл.-М.:Просвещение,1985-148-165с(Мир знаний).

3.      Глейзер Г.И. История математики в школе, IX-X классы.-М.:Просвещение,1983-55-58с

4.      Рыбников К.А.Возникновение и развитие математической науки: Книга для учителя.- М.:Просвещение,1987-107-119с

5.      Детская энциклопедия «Я познаю мир. Физика». –М.: издательство «АСТ», 1997.

6. Мордкович А.Г., Семенов П.В. Алгебра и начала математического анализа. 10 класс. В 2 ч.  Ч. 1. Учебник для учащихся общеобразовательных учреждений (профильный  уровень)  - М.: Мнемозина, 2010.

7.      Перышкин А.В. Физика. 10кл.: Учебник для учащихся общеобразовательных учреждений - М.: Дрофа, 2018.

8.      https://nauka.club/fizika/ballisticheskoe-dvizhenie.html

9.     https://ru.wikipedia.org/wiki

 

 

Скачано с www.znanio.ru