Творческая исследовательская работа "Вписанные и описанные мнгогранники"

 

 

 

 

 

 

 

Творческая исследовательская работа

 

ВПИСАННЫЕ И ОПИСАННЫЕ МНОГОГРАННИКИ.

 

 

 

 

 

 

 

 

Подготовила ученица 11А класса

Стекольникова Мария

 

Руководитель: учитель математики

Пастухова Н.А.

 

 

 

 

 

 

 

 

 

 

 

ОГЛАВЛЕНИЕ

Введение.

Основная часть.

Часть 1. История комбинации  многогранников и сферы.

Часть 2. Вписанные и описанные многоугольники и их свойства.

Часть 3. Призма, описанная около сферы

Часть 4. Пирамида, описанная около сферы.

Часть 5. Призма, вписанная в сферу.

Часть 6. Пирамида, вписанная в сферу.

Часть 7. Практическое применение комбинации многогранников и сферы.

Заключение.

Используемые литература и источники.

Приложение.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ВВЕДЕНИЕ

Математика - прикладная наука. Такие профессии, как; архитектор, дизайнер, художник, дизайнер рекламы, промышленный дизайнер предполагают знание основ геометрии, развитого пространственного воображения, навыков грамотного рисования, изображения пространственных тел и их комбинаций. Заключительная тема изучения стереометрии в общеобразовательной школе «Комбинация геометрических тел» является развитием системы всех знаний, умений и навыков курсов планиметрии и стереометрии; она углубляет и расширяет курс геометрии и показывает практическое применение геометрических знаний в реальной жизни. Одним из самых важных достижений при изучении геометрии является формирование и развитие пространственных представлений, а также способности и умения производить операции над пространственными объектами. Эти умения формируются также при решении разнообразных задач на комбинации фигур. Аналогичные задачи встречаются и на ЕГЭ по математике, для их успешного решения и проведена данная исследовательская работа.

Данная работа представляет собой теоретическое исследование, где предметом исследования являются комбинации сферы и многогранников.

 Целью исследования стал вопрос, как определить положение центра сферы относительно многогранника, входящего в данную комбинацию, как построить данную конфигурации тел и установить метрическую зависимость между радиусом сферы и элементами многогранника, входящего в комбинацию.

В ходе исследования решались задачи:

·                     знакомство с  историей комбинации  многогранников и сферы;

·                     установление аналогии между вписанными и описанными многоугольниками и вписанными и описанными многогранниками;

·                    решение теоретических  задач по теме  «Комбинация многогранника и сферы».

·                    Знакомство с практическим применением комбинации призмы и пирамиды со сферой.

 

Часть 1. История комбинации  многогранников и сферы.

Комбинация (лат. combinatio) – сочетание, соединение в правильном порядке; план; замысел. Комбинировать – соединять, сочетать, придумывать комбинации.

Частым случаем комбинации многогранников и тел вращения являют вписанные в многогранники сферы и описанные около многогранников сферы.

История многогранников уходит в глубокую древность и связана с именами таких ученых как Пифагор, Евклид, Архимед, Платон и Кеплер. Одной из первых и самых известных школ была Пифагорейская. Пифагорейцев поражала красота, совершенство и гармония правильных многоугольников. Позже учение пифагорейцев о правильных многогранниках изложил в своих трудах другой древнегреческий ученый, философ – идеалист Платон. С тех пор правильные многогранники (тетраэдр, куб, октаэдр, икосаэдр и додекаэдр) стали называться Платоновыми телами. Среди ученых, исследовавших многогранники, особое место принадлежит Иоганну Кеплеру (1571-1630). Вера в гармонию, красоту и математически закономерное устройство мироздания привела его к мысли о том, что пяти правильным многогранникам соответствуют только шесть (как казалось тогда) планет Солнечной системы: Меркурий, Венера, Земля, Марс, Юпитер, Сатурн. Поскольку для каждого правильного многогранника центры вписанной и описанной сфер совпадают, то вся модель имела единый центр – Солнце. Вокруг сферы Меркурия описан октаэдр. Этот октаэдр вписан в сферу Венеры, вокруг которой описан икосаэдр. Вокруг икосаэдра описана сфера Земли, а вокруг этой сферы - додекаэдр. Додекаэдр вписан в сферу Марса, вокруг которой описан тетраэдр. Вокруг тетраэдра описана сфера Юпитера, вписанная в куб. Наконец, вокруг куба описана сфера Сатурна.

 

 

 

 

Часть 2. Вписанные и описанные многоугольники и их свойства.

Вписанный многоугольник.

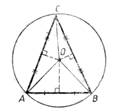Определение: Если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника, а многоугольник – вписанным в окружность.

Теорема. Около любого треугольника можно описать окружность и притом только одну.

В отличие от треугольника около четырехугольника не всегда можно описать окружность. Например: ромб.

Теорема. В любом вписанном четырехугольнике сумма противоположных углов равна 180⁰.

Если сумма противоположных углов четырехугольника равна 180⁰, то около него можно описать окружность.

Для того чтобы четырехугольник АВСD был вписанным, необходимо и достаточно, выполнения любого из следующих условий:

·                   ABCD выпуклый четырехугольник и ∠ABD=∠ACD;

·                   Сумма двух противоположных углов четырехугольника равна 180⁰.

Центр окружности равноудален от каждой из его вершин и поэтому совпадает с точкой пересечения серединных перпендикуляров к сторонам многоугольника, а радиус равен расстоянию от центра до вершин.

Для треугольника:   

Для правильного многоугольника: ;                                                                  

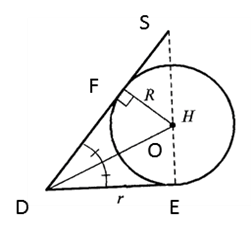
Описанный многоугольник.

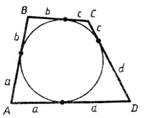Определение: Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник – описанным около этой окружности.

 

 

 

 

 

Теорема. В любой треугольник можно вписать окружность и притом только одну.

Не во всякий четырехугольник можно вписать окружность. Например: прямоугольник, не являющийся квадратом.

Теорема. В любом описанном четырехугольнике суммы длин противоположных сторон равны.

Если суммы длин противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.

Для того чтобы выпуклый четырехугольник ABCD являлся описанным, необходимо и достаточно, чтобы выполнялось условие AB+DC=BC+AD (суммы  длин противоположных сторон равны).

Центр окружности равноудален от сторон многоугольника, значит, совпадает с точкой пересечения биссектрис углов многоугольника (свойство биссектрисы угла). Радиус равен расстоянию от центра окружности до сторон многоугольника.

Для треугольника: 

 

 

 

 Для правильного     многоугольника:     

 

 

Часть 3. Призма, описанная около сферы

Сфера называется вписанной в призму, если она касается оснований призмы и всех ее боковых граней, при этом призма называется описанной около сферы.

В правильную призму можно вписать сферу тогда и только тогда, когда её высота равна диаметру окружности, вписанной в основание. Рассмотрим определение положения центра шара, вписанного в многогранник на примере задачи.

Задача 1

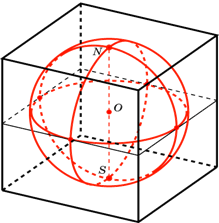
Вокруг сферы радиуса R описана правильная шестиугольная призма. Найдите её объем.  (рис. 1)

Решение.

Центр вписанной в призму сферы лежит в точке пересечения двух плоскостей, делящих двугранные углы при основании пополам, как точка, одинаково удаленная от граней этих углов, и является вершиной двух пирамид, основаниями которых служат основания призмы. Двугранные углы при основании рассматриваемых пирамид равны как половины прямых двугранных углов при основании призмы, поэтому высоты пирамид проходят через центры окружностей, вписанных в основание призмы, и равны радиусам этих окружностей, так как линейные углы двухгранных углов при основании содержат по 45^о. Высоты пирамид лежат на одной прямой, так как основания пирамид параллельны друг другу как основания призмы. Следовательно, центр вписанной сферы должен лежать на высоте прямой призмы, соединяющей центры её оснований в точке, делящей высоту пополам, одинаково удаленной от основания призмы.
Радиус сферы равен радиусу окружности, вписанной в основание призмы.
Объем призмы V = 3R2R = 4R³.

Ответ: 4R³.

 

Задача 2

Радиус сферы равен R. Найдите площадь полной поверхности описанного около сферы многогранника, если этот многогранник является кубом. (рис. 2)

Решение.

В кубе центр вписанной сферы совпадает с центром куба. Пусть a - ребро куба. S_п = 6S_o = 6a² . Так как сфера вписана в куб, то 2R = h = a. S_п = 6a² = 6 (2R)² = 24R².

Ответ: 24R².

 

Если в многогранник (в данном случае в призму) можно вписать сферу радиусом r, то объем этого многогранника  , где  - площадь полной поверхности многогранника.

Докажем это. Представим многогранник как объединение пирамид, вершинами которых является центр сферы, а основаниями – грани многогранника. Обозначим площади граней многогранника S₁, S₂, …, S_n, по условию S= S₁+ S₂+ …+ S_n. Радиус, проведенный в точку касания какой-нибудь грани со сферой, является высотой пирамиды, для которой эта грань служит основанием. Объем многогранника равен сумме объемов всех таких пирамид: .

 

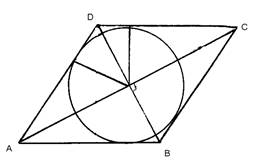
Задача 3

Около сферы описан прямой параллелепипед, у которого диагонали основания равны a и b. Найдите полную поверхность параллелепипеда.
Решение.

Способ 1. (рис.3а)

Пусть радиус сферы OK=R. Тогда, проведя через центр сферы плоскость, параллельную основанию параллелепипеда, в сечении получим параллелограмм A₂B₂C₂D₂ описанный около окружности радиуса R. Так как суммы противоположных сторон такого описанного параллелограмма равны, он представляет собой ромб. Пусть сторона ромба равна m, тогда полная поверхность параллелепипеда S=2S_o+S_б=2m2R+4m2R=6S_о. Но S_o=0,5ab. Получим S_o =60,5ab = 3ab.

Способ 2. (рис. 3б)

Воспользуемся формулой:

V = rS; S =, V = 2r = abr, S = = 3ab.
Ответ: 3ab

 

Задача 4

В основании правильной треугольной призмы лежит правильный треугольник со стороной 6. Найдите объем этой призмы, если известно, что в нее можно вписать сферу. (рис. 4)

Решение.

Так как в призму можно вписать сферу, то радиус сферы R равен половине высоты призмы, то есть h=2R. L – точка касания шара с гранью BB₁C₁C и OL = O₁K. Задача сводится к нахождению O₁K.
O₁K = AK. Из треугольника ABC находим АК = 6 = . ОК = , R = , h = 2. V(ABCA₁ B₁C₁) = S_o  h =2 = 54.

Ответ: 54

 

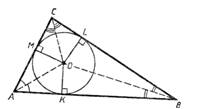
Часть 4. Пирамида, описанная около сферы.

Сфера называется вписанной в пирамиду, если она касается основания пирамиды и её боковых граней. В этом случае пирамида называется описанной около сферы.

Центр сферы, касающейся двух пересекающихся плоскостей, лежит в плоскости, которая делит на два равных угла двухгранный угол, образованный этими плоскостями. Такая плоскость называется биссектральной плоскостью двугранного угла. Аналогия с центром окружности, вписанной в многоугольник, который лежит на пересечении биссектрис углов многоугольника. Итак, центром вписанной в пирамиду сферы является точка пересечения высоты пирамиды и биссектрисы линейного угла двугранного угла при основании, лежащего в плоскости, которая проходим через высоту пирамиды.

Сферу можно вписать в любую треугольную пирамиду; в правильную пирамиду и в пирамиду, у которой двугранные углы при сторонах основания равны.

Центр сферы лежит на высоте пирамиды и совпадает с центром окружности, вписанной в равнобедренный треугольник, боковой стороной которого является апофема, а высотой – высота пирамиды. Радиус сферы равен радиусу этой окружности. Если основание высоты пирамиды совпадает с центром вписанной в основание окружности, то радиус сферы R, высота H, радиус окружности r, вписанной в основание пирамиды, связаны соотношением   =.  (рис. 5).

При решении задач на сферу, вписанную в правильный тетраэдр, полезно знать, что если все плоские углы трёхгранного угла равны 60^о, то расстояние от вершины угла до центра вписанного в этот угол шара радиуса R равно 3R, а расстояние от центра этого шара до ребра тетраэдра равно R. Все высоты правильного тетраэдра проходят через центр вписанной в него сферы и делятся этим центром в отношении 3 : 1, считая от вершины.

 

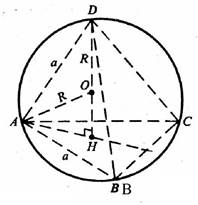
Задача 5

В правильный тетраэдр с ребром а вписана сфера. Найдите: а) радиус сферы; б) расстояние от центра сферы до вершины, грани и ребра тетраэдра. 

(рис. 6)

Решение.

Пусть в правильный тетраэдр SABC вписана сфера с центром O и радиусом r. Если точка E – центр грани ABC, D – середина ВС, то
EА = , SE =  = .
Так все четыре отрезка, соединяющие вершины правильного тетраэдра с центром его противоположных граней, равны, перпендикулярны соответствующим граням, пересекаются в одной точке и делятся ею в отношении 3 : 1, считая от вершины, то эта точка является центром O сферы, вписанной в тетраэдр. Значит, r = . Тогда OE =  – расстояние от центра O до грани  тетраэдра (плоскость АВС перпендикулярна радиусу ОE сферы, проведенному в точку E касания сферы и грани AВС). Далее, АO = SO =  – расстояние от центра О до вершины А тетраэдра. Расстояние от центра O сферы до ребра АS равно длине медианы OM (M равнобедренного треугольника АSO,   значит это OM =  = =.

Ответ: а) r = ;  б) ; ; .

 

2 способ (а)

Из подобия треугольников SOF и SDE следует  ,  ,  

 , , , , .

 

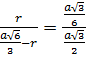Задача 7

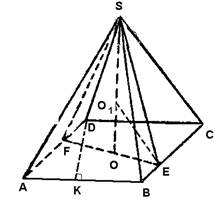
Сфера радиуса 4 вписана в пирамиду, в основании которой лежит ромб с острым углом 60^о. Боковые грани пирамиды наклонены к плоскости основания под углом 60^о. Найдите объем пирамиды. (рис. 7)

Решение.

Основание высоты пирамиды – центр вписанного в ромб круга. FE – высота  ромба. По теореме о трёх перпендикулярах SE перпендикулярна ВС, SF перпендикулярна AD. Точки касания поверхности сферы с боковыми гранями лежат на апофемах этих граней.
V_n = _oSO = . OF = OO₁ctg30^o = 4, EF = 24,
Из треугольника ADK имеем: AD = . Следовательно,     _o = ADEF =    = 384. V = .

 

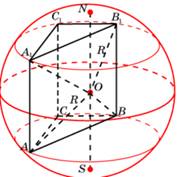
Часть 5. Призма, вписанная в сферу.

 Призма называется вписанной в сферу, если все её вершины принадлежат поверхности сферы. В этом случае сфера называется описанной около призмы. Чтобы около призмы можно было описать сферу, необходимо и достаточно, чтобы призма была прямой, и около основания призмы можно было описать окружность. При этом центр шара будет лежать на середине высоты, соединяющей центры окружностей, описанных около основания призмы. Перпендикуляр, опущенный из центра описанной около многогранника сферы на ребро многогранника, будет делить это ребро как хорду сферы пополам. Кроме того, центр сферы будет проецироваться в центр боковой грани, являющейся прямоугольником.

 

Задача 8

Докажите, что около призмы можно описать сферу тогда и только тогда, когда призма прямая и около многоугольника основания можно описать окружность. (рис. 8)

Действительно, если многоугольника основания призмы можно описать окружность, то центр сферы, описанной около призмы, будет лежать на высоте призмы, проходящей через центр окружности, описанной около основания. Так как призма прямая, то её высота, проходящая через центр окружности, описанной около одного основания, проходит через центр окружности, описанной около другого основания. Центр сферы, описанной около призмы, должен так же лежать на плоскости, перпендикулярной боковому ребру и проходящей через его середину, так как поверхность сферы проходит через вершины призмы, лежащие на концах этого ребра. Так как данная призма прямая, то эта плоскость пройдёт через середину высоты. Середина высоты и будет центром сферы, описанной около призмы, так как одинаково удалена от всех вершин. Необходимость приведенных условий вытекает из следующих рассуждений. Так как сечением поверхности сферы плоскостью служит окружность, то вершины основания призмы должны лежать на окружности, то есть в сновании призмы должен лежать многоугольник, около которого можно описать окружность. То же можно сказать о боковых гранях, поэтому боковые грани должны быть прямоугольниками, то есть призма должна быть прямой.

 Радиус шара R, радиус окружности r, описанной около основания призмы, и высота H призмы связаны зависимостью .

Например, если a – длина стороны основания, то для правильной треугольной призмы r =  и ; для правильной четырёхугольной призмы r =  и ; для правильной шестиугольной призмы r = a и . Если сфера описана около куба,  то центр сферы совпадает с центром куба ( центр куба удалён от каждой его вершины на расстояние , где а – длина ребра куба), а радиус этой сферы равен .

 

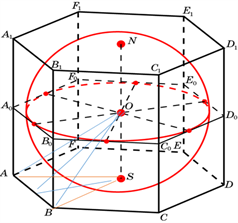
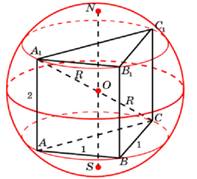
Задача 9

В шар радиусом 2 вписана правильная треугольная призма ABCA₁B₁C₁. Прямая ВА₁ образует с плоскостью ВСC₁ угол 30^о. Найдите объём призмы.(рис. 9)

Решение.

Пусть D₁ – середина ребра B₁C₁. Так как призма правильная, то A₁D₁ перпендикулярно B₁C₁ и СС₁ перпендикулярно A₁D₁, B₁C₁ ∩ СС₁ = С₁, значит A₁D₁ перпендикулярно ВCC₁ по признаку перпендикулярности прямой и плоскости. Угол A₁BD₁ = 30^o как угол между прямой A₁B и плоскостью BCC₁.
Пусть AB = a. Тогда A₁D₁ = . Но треугольник A₁BD₁ прямоугольный и A₁BD₁ = 30^o. Следовательно, BA₁ = . Из треугольника ABA₁ по теореме Пифагора имеем: AA₁ = . Отрезок

MB = , OM = . Поэтому из прямоугольного треугольника OMA имеем , откуда a = 2. Объем призмы V_(ABCA1B1C1) = S_ABCAA₁. V_(ABCA1B1C1) = S_ABCAA₁.  Но S_ABC = ,

AA₁ = , a = 2,  значит V = .

Ответ: 72.

 

Задача 10

При каком соотношении между сторонами основания прямой треугольной призмы центр сферы, описанной около призмы, лежит: а) на боковой грани призмы; б) внутри призмы; в) вне призмы? (рис. 10 а, б, в)

Так как центр шара должен лежать на перпендикуляре к плоскости основания призмы, проходящем через центр окружности, описанной около многоугольника основания, то в случае: а) когда центр описанной окружности лежит внутри многоугольника основания, центр сферы лежит внутри призмы; б) когда центр описанной окружности лежит на стороне многоугольника основания, центр сферы лежит на боковой грани призмы; в) когда центр описанной окружности лежит вне многоугольника основания, центр сферы лежит вне призмы. Для треугольной призмы указанные случаи положения центра сферы будут иметь место при следующем соотношении между сторонами треугольника основания: а)квадрат большей стороны меньше суммы квадратов двух других сторон; б)равен сумм квадратов двух других сторон; в) больше суммы квадратов двух других сторон.

Задача 11

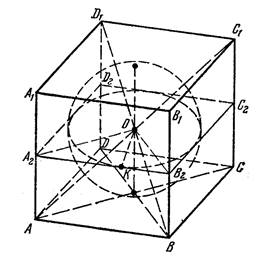
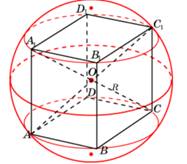
Радиус сферы равен R. Найдите площадь полной поверхности вписанного в сферу куба. (рис. 11)

Решение.

Центр сферы совпадает с центром куба — точкой пересечения диагоналей куба.

Пусть ребро куба равно х. Тогда диагональ куба d = . С другой стороны, d = 2R; 2R= , x= . Площадь поверхности одной грани равна х², а полная поверхность куба равна 6х².  6.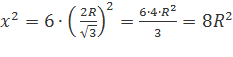

Ответ:

 

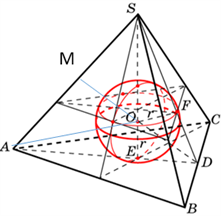
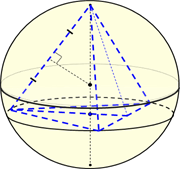
Часть 6. Пирамида, вписанная в сферу.

Пирамида называется вписанной в сферу, если все её вершины принадлежат поверхности сферы; тогда сферу называют описанной около пирамиды. Чтобы около пирамиды можно было описать сферу, необходимо и достаточно, чтобы около её основания можно было описать окружность. Центр описанной сферы лежит на прямой, содержащей высоту пирамиды, и совпадает с центром окружности, описанной около равнобедренного треугольника, боковой стороной которого является боковое ребро пирамиды, а высотой – высота пирамиды. Радиус сферы равен радиусу этой окружности.

Если около пирамиды описана сфера, то ее центр является точкой пересечения всех плоскостей, проведенных через середины ребер пирамиды перпендикулярно этим ребрам. ( рис. 12) Аналогия с центром описанной около треугольника окружности, который совпадает с точкой пересечения серединных перпендикуляров к сторонам треугольника.

Радиус сферы R, высота пирамиды H и радиус окружности r, описанной около основания пирамиды, связаны соотношением: (рис. 13)

R² = (H – R)² + r².

Сферу можно описать около любой треугольной пирамиды, около правильной пирамиды. Центр сферы проецируется на апофемы боковых граней правильной пирамиды и лежит на ее высоте.

 

Задача 12

В правильной пирамиде высота H, радиус круга, описанного около основания, - r. При каком соотношении между высотами и радиусом основания центр описанной сферы лежит: а) на основании, б) внутри пирамиды, в) вне пирамиды? (рис. 14 а, б, в)

Решение.

В первом случае, высота пирамиды и радиус основания равны радиусу шара. OT = OC = R; OT = H; OC = r; H = r.

Во втором случае, высота пирамиды больше радиуса шара, а радиус основания пирамиды меньше радиуса шара. H > R; R > r; H > r.

В третьем случае, высота пирамиды меньше радиуса основания. H < r.

 

При решении задач на сферу, описанную около правильного тетраэдра, полезно знать, что все плоские углы трёхгранного угла равны 60^о, все высоты правильного тетраэдра проходят через центр описанной около него сферы.

 

Задача 13

В сферу радиуса R вписана правильная четырёхугольная пирамида. Определите объем это пирамиды, если радиус окружности, описанной около её основания, равен r. (рис. 15)

Решение.

Задача сводится к нахождению высоты пирамиды.
Пусть OO₁ = x, тогда MO₁ = R + x, O₁N = R – x, по теореме о пропорциональности отрезков хорд в круге имеем AO₁  O₁C = MO₁  O₁N или , отсюда , высота MO₁ = R + или MO₁ = R -  (зависит от расположения плоскости основания пирамиды).
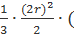V(пирамиды) = S_o  h =  R ±  ) =  R ±  ).

Ответ:  R ±  ).

 

Задача 14

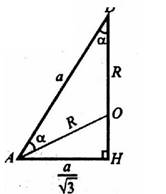
Радиус сферы равен R. Найдите площадь полной поверхности вписанного правильного тетраэдра. (рис. 16 а, б)

Решение.

Пусть ребро тетраэдра равно a. Центр описанной сферы лежит на высоте DH, точка Н — центр ΔАВС, поэтому HA = . Из прямоугольного ΔАDH:  , ∠ADH = α, . Из ΔАОD по теореме косинусов:

            
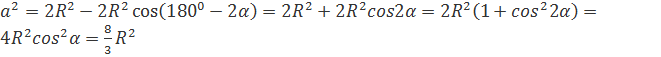
Площадь грани тетраэдра равна , все грани равны и их 4, значит

           Ответ:    .

 

Часть 7. Практическое применение комбинации многогранников и сферы.

Для развития пространственного  воображения у детей младшего возраста используют  игрушки, имеющие геометрическую форму. А также упаковки комплектов игрушек часто имеют геометрическую форму.

Комплект «Лего» в форме шара упакован в коробку  кубической формы.

Для расчета размеров используемого для упаковки материала требуется учет метрической зависимости между радиусом шара и элементами куба, входящего в комбинацию.

 

 

 

 

 

 

 

 

Елочный стеклянный шар выдувают такого размера, чтобы он был описан около  правильного тетраэдра.

 

 

 

 

 

 

 

Некоторые детали механизмов представляют собой комбинацию многогранников и сферы. Например, автомобильное импульсное зарядное устройство.

 

 

 

 

 

 

 

 

 

Для вытачивания на токарном станке комбинаций многогранников, вписанных в сферу, необходимы расчеты, связанные с метрическим соотношением размеров их элементов.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Часто в архитектурном сооружении сочетаются различные геометрические фигуры, что позволяет создавать разнообразные архитектурные сооружения, непохожие друг на друга. Эти  пространственные геометрические фигуры служат основой сооружения в целом или отдельных его частей.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Центральный парк Манхэттен. Шар вписан в куб.

 

 

 

 

ЗАКЛЮЧЕНИЕ.

Наука геометрия  возникла из практических задач, ее предложения выражают реальные факты и находят многочисленные применения. В конечном счете, в основе всей техники, так или иначе, лежит геометрия, потому что она появляется всюду, где нужна хотя бы малейшая точность в определении формы и размеров.

И технику, и инженеру, и квалифицированному рабочему, и людям искусства геометрическое воображение необходимо, как геометру или архитектору. Математика, в частности геометрия, представляет собой могущественный инструмент познания природы, создания техники и преобразования мира.

Мое исследование показало, что проблема исследования многогранников была насущной всегда.  Правильные многогранники имеют красивые формы. Они являются удивительным символом симметрии, привлекавшим внимание выдающихся мыслителей. Этим объясняется непрекращающийся интерес человека к многогранникам.

Геометрия  предлагает ряд общих правил организации частей в целое, которые помогают расположить эти части в пространстве, так, что в них проявляется порядок.

История изучения и изображения многогранников, их комбинаций со сферой являет собой яркий пример взаимопроникновения различных областей знания, неразрывности понятий «наука» и «искусство» как различных способов познания мира, двух основных составляющих единого целого — культуры, главного наследия человеческой цивилизации. 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Используемые литература и источники.

1.     Геометрия. 10-11 классы: учебник для общеобразовательных учреждений: базовый и профильный уровни/ Атанасян Л.С., Бутузов В.Ф, Кадамцева С.Б. и др.  – М. Просвещение, 2010.

2. Практическая геометрия. Комбинация геометрических тел. 10-11 классы: методическое пособие/Сагателова Л.С., Студенецкая В.Н. – М. «Глобус», 2010.

3. Дидактические материалы по геометрии. 11 класс/ Зив Б.Г. – М. Просвещение, 2014.

4. Задачи по готовым чертежам. Стереометрия, в 2 частях/Орехова А.И. – Мозырь. «Белый Ветер», 2012.

5. Готовимся к ЕГЭ. ( Геометрия): вписанные и описанные фигуры в пространстве/ Смирнова И.М., Смирнов В.А. – М. Мнемозина, 2008.

6. Электронное приложение к УМК Смирнова В.А.

7.https://yandex.ru/images/search?text=%D0%A1%D1%84%D0%B5%D1%80%D0%B0%20%D0%B8%20%D0%BA%D1%83%D0%B1.%20%D0%9F%D0%B0%D1%80%D0%BA%20%D0%B2%20%D0%9C%D0%B0%D0%BD%D1%85%D1%8D%D1%82%D1%82%D0%B5%D0%BD%D0%B5&lr=1948

8.https://yandex.ru/images/search?p=31&text=%D0%98%D0%B3%D1%80%D1%83%D1%88%D0%BA%D0%B8.%20%D1%81%D1%84%D0%B5%D1%80%D0%B0%20%D0%B2%D0%BF%D0%B8%D1%81%D0%B0%D0%BD%D0%BD%D0%B0%D1%8F%20%D0%B2%20%D0%BA%D1%83%D0%B1&lr=194

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ПРИЛОЖЕНИЕ

Чертежи к задачам.

Задача 1 (рис. 1)                                        Задача 2 (рис. 2)

                                                  

 

 

 

 

 

 

 

 

 

 

 

 

Задача 3 (рис. 3а)                                        Задача 3  (рис. 3б)

                                                   

 

 

 

 

 

 

 

 

 

 

 

 

 

 

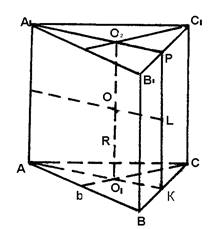    Задача 4 (рис.4)                                             (рис. 5)

 

 

 

 

 

 

 

 

 

 

 

Задача 5. (рис. 6)                                          Задача 7 (рис. 7)

 

 

 

 

 

 

 

 

 

 

 

 

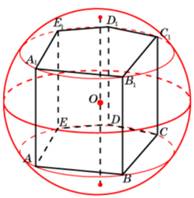Задача 8. (рис. 8)                                          Задача 9. (рис. 9)

 

 

 

 

 

 

 

 

 

 

 

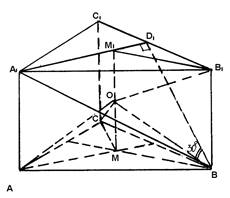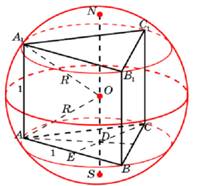Задача 10 (рис. 10а)            (рис. 10б)                       (рис. 10в)  

 

 

 

 

 

 

 

 

 

 

 

 Задача 11. (рис. 11)            (рис. 12)                                    (рис. 13)

 

 

 

 

 

 

 

 

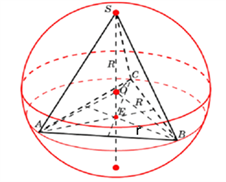
Задача 12 (рис. 14а)                (рис. 14б)                      (рис. 14в)

 

 

 

 

 

 

 

 

 

 

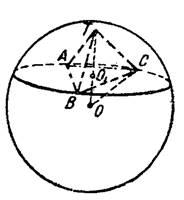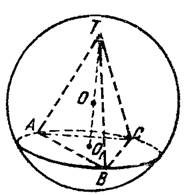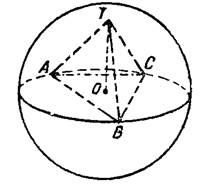Задача 13 (рис. 15)               Задача 14 (рис. 16а)            (рис. 16б)

 

 

 

 

 

 

 

 

 

 

 

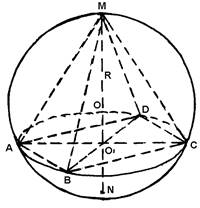Скачано с www.znanio.ru