Творческие лабораторные работы по физике

Л/р № 1. Стрельба из баллистического пистолета по мишени.

Цель работы: установив мишень (кольцо на штативе) на расчетном расстоянии от места выстрела и на расчетной высоте, продемонстрировать попадание в мишень (пролет снаряда через кольцо) при выстреле под выбранным углом из баллистического пистолета – проверить тем самым формулы расчета тела, брошенного под углом к горизонту.

Оборудование: баллистический     пистолет;     лабораторный     штатив;      штатив      с      кольцом; измерительная лента или рулетка.

Введение

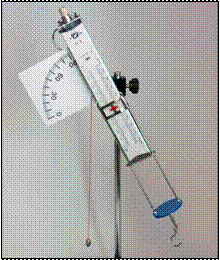
1.  Пистолет баллистический. В основе конструкции прибор имеет двухстороннюю пружину, которая связана с проволочной продольной рамкой с подвижным стрелочным указателем. На нижних концах рамки закреплена круглая площадка с двумя штырями. На них размещается шарик так, что его центр тяжести совпадает с центром площадки. В сжатом состоянии пружина удерживается проволочным крючком, один конец которого закреплен на корпусе прибора, а второй - заводится в специальное отверстие боковой поверхности площадки. Прибор оснащен транспортирной шкалой с отвесом и стержнем - для закрепления в муфте штатива. Прибор позволяет ставить следующие лабораторные работы: зависимость силы упругости от удлинения пружины, определение коэффициента жесткости пружины, исследование зависимости дальности полета снаряда от угла его вылета, определение дальности полета снаряда при горизонтальной стрельбе, сравнение импульса силы упругости пружины с

изменением импульса снаряда, сравнение работы силы упругости с изменением кинетической энергии, тела.

2.  Теория вопроса.

Итак, целью работы является попадание в кольцо-мишень при стрельбе из баллистического пистолета под углом к горизонту. Как узнать, где должна находиться эта мишень (на какой высоте и на каком расстоянии)?

Полет тела, брошенного под углом к горизонту (в нашем случае снаряда, выпущенного из баллистического пистолета), описывается следующими двумя уравнениями, позволяющими вычислить положение тела в любой момент времени t:

по горизонтали (вдоль стола): x = v₀t·Cosα;

по вертикали (по высоте): y = v₀t·Sinα - gt²/2. Это позволяет нам рассчитать:

-  время полета при выстреле под углом α = 45^о (из второго уравнения, если в момент падения

y = 0, то t_пол = v₀·Sinα/g),

-  дальность полета снаряда (x_max = v₀²/g)

- 

Чтобы воспользоваться этими формулами, надо только придумать, как измерить начальную скорость v₀ (скорость вылета снаряда из баллистического пистолета).

Скорость вылета снаряда можно узнать, если выстрелить вертикально вверх и заметить высоту, на которую поднимется снаряд, ибо Н = v₀²/2g.

Ход работы.

Много лучше ход работы разработать самим, если вы поняли, как узнать начальную скорость снаряда, как рассчитать, на каком расстоянии и на какой высоте нужно установить кольцо- мишень. Или см. описание далее.

1.   Закрепите в нижней лапке штатива баллистический пистолет для стрельбы вертикально вверх под углом 90° к горизонту(см. рис. справа).

Произведите предварительный выстрел из пистолета и заметьте, на какую приблизительно высоту поднимется снаряд.

Расположите     на      этом      уровне      свои     глаза      и передвиньте    на     этот    уровень    верхнее    кольцо. Повторив выстрел, кольцо передвигают по вертикали так,             чтобы     выпущенный     из     пистолета     снаряд достигал ровно края кольца.

Измерив рулеткой или лентой расстояние от верхнего конца заряженного в пистолет снаряда до кольца, мы определим высоту подъема снаряда Н при стрельбе. Повторите опыт 2—3 раза, каждый раз определяя высоту максимального подъема снаряда, и найдите ее среднее значение Н_ср.

2.  По формуле высоты максимального подъема (Н_ср = v₀²/2g) определите квадрат начальной скорости вылета снаряда v₀² = 2gН_ср.

3.  Закрепите в штативе баллистический пистолет у основания стола и установите его для стрельбы под углом 45^о. По формуле дальности полета

(x_max = v₀²/g) определите место для установки штатива с кольцом, а по формуле высоты полета (y_max = v₀²/4g) определите, на какой высоте нужно установить кольцо-мишень, чтобы при выстреле снаряд пролетел точно через кольцо (см. рис. ниже).

Как видим, кольцо устанавливается на высоте y_max и на расстоянии x_max/2 (на половине пути пролета снаряда). Запишите аккуратно эти расчеты в свой отчет. Установите свободный штатив на расчетном расстоянии от баллистического пистолета, закрепив на этом штативе кольцо- мишень на нужной высоте, используя измерительную ленту (рулетку).

4.  Произвести 3—4 выстрела в направлении кольца под углом 45^о (см. рис. внизу).

5.  Пролетает ли снаряд в кольцо? Если нет, проверьте свои расчеты и правильность установки штатива с кольцом и угла стрельбы. Покажите свои расчеты и результат стрельбы учителю. Сделайте вывод, подтверждаются ли формулы расчета движения тела, брошенного под углом к горизонту. Ответьте на контрольные вопросы.

Контрольные вопросы:

1.  Как, используя приведенное выше уравнение вертикальной координаты полета тела

y = v₀t·Sinα - gt²/2, получить формулу расчета времени полета t_пол?

2.  Как получить формулу расчета высоты полета при выстреле под углом 45о, используя уравнение координаты y = v₀t·Sinα - gt²/2 и времени полета t_пол = v₀·Sinα/g?

3.  Как получить формулу дальности полета тела при выстреле под углом 45о, используя

уравнение координаты x = v₀t·Cosα и времени полета t_пол = v₀·Sinα/g?

4.  Где можно использовать знания, полученные в ходе работы?