Учбурчак ички бурчаклар йиғиндиси ҳақида теорема

Sana:

Sinf: 7-“B”

Mavzu: Uchburchak ichki burchaklarining yig`indisi haqida teorema.

Dars shiori: Matematika- aql gimanastikasi.

Darsning maqsadi:

a) Ta`limiy: O`quvchilarda uchburchak burchaklarining 180⁰ ga tengligini isbotlash ko`nikmasini hosil qilish, to`g`ri burchakli, teng yonli, teng tomonli uchburchaklarning burchaklari haqida ma`lumotlar berish. Masalalar yechish orqali uchburchak burchaklari haqida olgan bilimlarini mustahkamlash;

b) Tarbiyaviy: O`quvchilarga axloqiy, aqliy va estetik tarbiya berish. Vatanga mehr, milliylik ro`hida tarbiyalash.

s) Rivojlantiruvchi: O`quvchilarni tafakkuri, xotirasi va geometriya faniga bo`lgan qiziqishini rivojlantirish, muomala madaniyatiga o`rgatish;

Dars tipi: Yangi bilimlarni o`zlashtirish darsi.

Dars uslubi: Og`zaki, ko`rgazmali-amaliy, yozma.

Dars jihozi: 7-sinf darsligi, ko`rgazma qurollar, plakatlar va texnika vositasi.

Dars bosqichlari vaqt taqsimoti:

1. Tashkiliy qism	3 daqiqa
2. Yangi mavzuni yoritish a) Yangi mavzuni yoritishga tayyorgarlik b) Yangi mavzuni yoritish	15 daqiqa
3. Yangi mavzuni mustahkamlash a) Masalalar yechish b) Yakka tartibdagi mustaqil ish d) Xulosa	17 daqiqa
4. Darsga yakun yasash va baholash	3 daqiqa
5. Uyga vazifa	2 daqiqa

Darsning borishi:

I. Tashkiliy qism: Salomlashish, davomatni tekshirish, zarur ko`rgazmali qurollarni darsga hozirlash.

II. O`tilgan mavzuni takrorlash va uyga vazifani og`zaki usulda tekshirish va yangi mavzuga hozirlik ko`rish.

O`tilgan mavzuni so`rash. (Savol –javob viktorinasi orqali so`raldi)

1.Uchburchaklar tengligining birinchi alomatini ayting?

2. Uchburchaklar tengligining ikkinchi alomatini ayting? 3.Uchburchaklar tengligining uchinchi alomatini ayting?

4. uchburchak balandligi deb nimaga aytiladi?

5. Mos burchaklar teng bo`lsa, bir tomonli burchaklar yig`indisi…?

6. Ko`pburchak deb nimaga aytiladi?

7. Teng yonli uchburchakning xossalarini ayting?

8. Kesma o`rta perpendikularining xossasini ayting?

9. Uchburchak medianasi deb nimaga aytiladi?

10. Uchburchak bissektrisasi deb nimaga aytiladi?

11. Qanday uchburchak o`tmas burchakli uchburchak deyiladi?

12. Qanday uchburchak o`tkir burchakli uchburchak deyiladi?

13. Qanday uchburchak o`tkir burchakli uchburchak bo`ladi?

14. Qanday uchburchak teng yonli uchburchak bo`ladi?

15. Qanday uchburchak teng tomonli uchburchak bo`ladi?

16. Vertikal burchaklar deb qanday burchaklarga aytiladi?

17. Ikki to`g`ri chiziqni kesuvchi bilan kesganda hosil bo`lgan almashinuvchi burchaklar xossasini ayting?

18. Qo`shni burchaklar deb qanday burchaklarga aytiladi?

19. Parallel to`g`ri chiziqlar deb nimaga aytiladi?

20. Qaysi burchaklar yig`indisi 180⁰ ga teng bo`ladi?

21. Perpendikular to`g`ri chiziqlar kesishganda …. hosil bo`ladi.

22. Ikki to`g`ri chiziqning parallellik alomatlarini ayting?

(Bu savollarga javob olingandan keyin 2017-yil “Xalq bilan muloqot va inson manfaatlari” yili yozuvi hosil bo`ladi)

Chizma Berilgan Yechish

ABC- P=AB+BC+AC

teng tomonli P=178+178+178=

AB=178 mm =534 mm

BC=178 mm

AC=178 mm Javob: 534 mm

P=?

(Natijada Zahiriddin Muhammad Boburning 534 yosh tavalludi kuni sanasi kelib chiqadi)

O`quvchi: Zahiriddin Muhammad Bobur 1483-yilda 14-fevralda Farg`ona viloyatining poytaxti Andijonda tug`ilgan. 12 yoshli shahzoda otasi vafotidan so`ng Andijon taxtiga o`tiradi. Bobur lirikasining asosiy janrlari g`azal, ruboiy va tuyuq bo`lib, shoir qit`a, fard kabi janrlarda ham ijod qilgan. Shoir she`rlarida Vatan ishqi mavzusi yetakchilik qiladi. Bobur 20 yoshida “Xatti Boburiy” yozuvini kashf etgan. Boburiylar sulolasi 1483-1858- yillar mobaynida hukm surgan. Kishilik tarixida Boburchalik shaxsiy imkon, iqtidor va fazilatlari beqiyos kishilar juda kam uchraydi.

Bobur buyuk podshoh, mumtoz shoir, nazariyotchi, adabiyotshunos, faqih, tilshunos, san`atshunos, etnograf, hayvonot va nabotot olamining bilimdoni sifatida ko`p qirrali faoliyat va ijod sohibi. Birgina “Boburnoma” uning yugirmadan ortiq sohalarda qiziqqanligiga yaqqol misoldir. Bobur, birinchi navbatda , shoh, boburiylar sulolasining asoschisidir.

Chizma Berilgan Yechish

ABC- P=AB+BC+AC

teng yonli P=201+201+174=

AB=201 mm = 576 mm

BC=201 mm

AC=174 mm Javob: 576 mm

P=?

(Natijada g`azal mulkining sultoni Alisher Navoiy bobomizning 576 yosh tavalludi kuni sanasi kelib chiqadi)

O`quvchi: XV asr jahon ma`naviyatining buyuk siymasi Alisher Navoiy o`zbek she`riyatining sultoni, Movarounnahr va Xurosonning ma`naviyati, madaniyati taraqqiyotiga juda katta ta`sir ko`rsatgan shoir. “Majolis un-nafois”, “Badoye` ul-bidoya”, “Lison ut-tayr”, “Muhokamat ul-lug`atayn”, “Mahbub ul-qulub”, ayniqsa, 50 ming misradan oshiq she`riy merosni o`z ichiga olgan “Xamsa” asari bilan o`zbek adabiyotini boyitgan.

“Agar bu ulug’ zotni avliyo desak,u avliyolarning avliyosi,

mutafakkir desak ,mutafakkirlarning mutafakkiri,shoir desak shoirlarning sultonidir”

Islom Karimov.
“Yuksak ma’naviyat-yengilmas kuch".

Chizma Berilgan Yechish

ABC- P=AB+BC+AC

to`g`ri burchakli P=301+159+221=

AB= 301 mm = 681 mm

BC= 159 mm

AC= 221 mm Javob: 681 mm

P=?

(Natijada buyuk sarkarda, sohibqiron bobomiz Amir Temurning 681 yosh tavalludi kuni sanasi kelib chiqadi)

O`quvchi: Kesh (hozirgi Shahrisabz) shahri yaqinidagi Xoja Ilg‘or qishlog‘ida tug‘ilgan. O‘rta asrning yirik davlat arbobi, buyuk sarkarda, kuchli, markazlashgan davlat asoschisi. Amir Temur ilm-fan va madaniyat homiysi bo‘lgan. Sohibqironning bunyodkorlik sohasidagi tarixiy xizmatlari beqiyos. Saltanati tarkibidagi ko‘plab shaharlarda turli me’moriy obidalar — madrasalar, maqbaralar, masjidlar qurdirgan.

O‘zbekiston Respublikasida „Amir Temur“ ordeni ta’sis etilgan. Bu orden bilan davlatchilikni mustahkamlashdagi ulkan xizmatlari uchun, me’morchilikni, ilm-fan, adabiyot va san’atni, shu jumladan, harbiy mahoratni rivojlantirishga ulkan hissa qo‘shgan fuqarolar mukofotlanadilar.

Yangi mavzu bayoni.

Teorema: Uchburchak ichki burchaklarining yig`indisi 180⁰ ga teng.

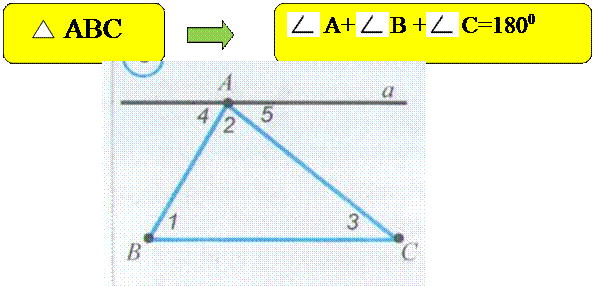
Isbot. A uchdan BC tomonga parallel a to`g`ri chiziq o`tkazamiz.

1= 4, chunki bu burchaklar, a va BC parallel to`g`ri chiqizlarni AB kesuvchi bilan kesganda hosil bo`lgan almashinuvchi burchaklardir.

3= 5, chunki bu burchaklar, a va BC parallel to`g`ri chiziqlarni AC kesuvchi bilan kesganda hosil bo`lgan almashinuvchi burchaklardir.

4+ 2+ 5=180⁰, chunki bu burchaklar umumiy uchga ega va yoyiq burchakni tashkil qiladi. Hosil bo`lgan bu uchta tenglikdan,

1+ 2+ 3=180⁰, ya`ni A+ B+ C=180⁰

Ekanligini hosil qilamiz. Teorema isbotlandi.

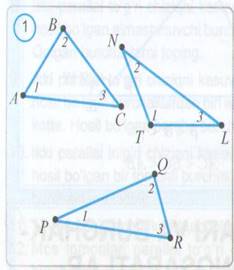
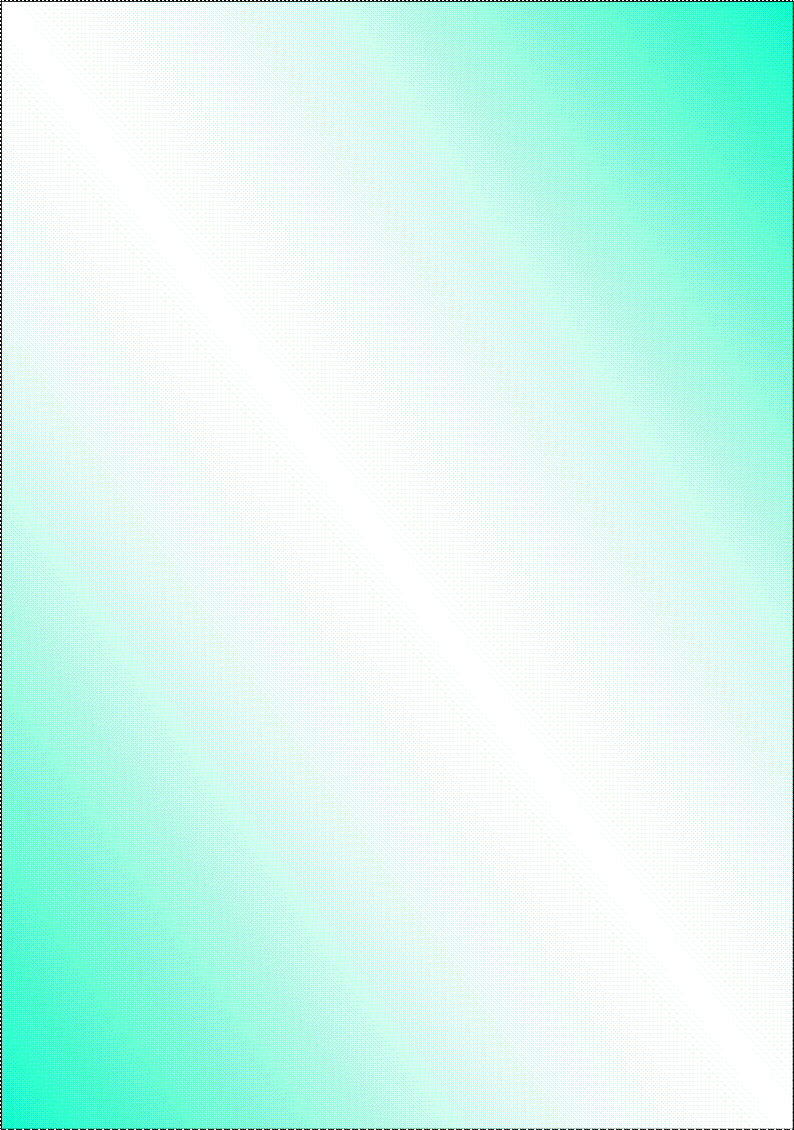
1.Quyidagi rasmda tasvirlangan

ABC uchburchakning uchala

burchaklarini transporter yo`rdamida

o`lchang va ularning yig`indisini

hosoblang. Xuddi shu ishni MNL va

PQR uchburchaklar uchun ham

bajaring. Natijalar asosida jadvalni

to`ldiring. Qanday xossani

aniqladingiz? Uni bitta jumla bilan

ifodalang.

Uchburchaklar	1	2	3	1+ 2+ 3
ABC	60⁰	60⁰	60⁰	180⁰
ТLN	120⁰	25⁰	35⁰	180⁰
PQR	45⁰	65⁰	70⁰	180⁰

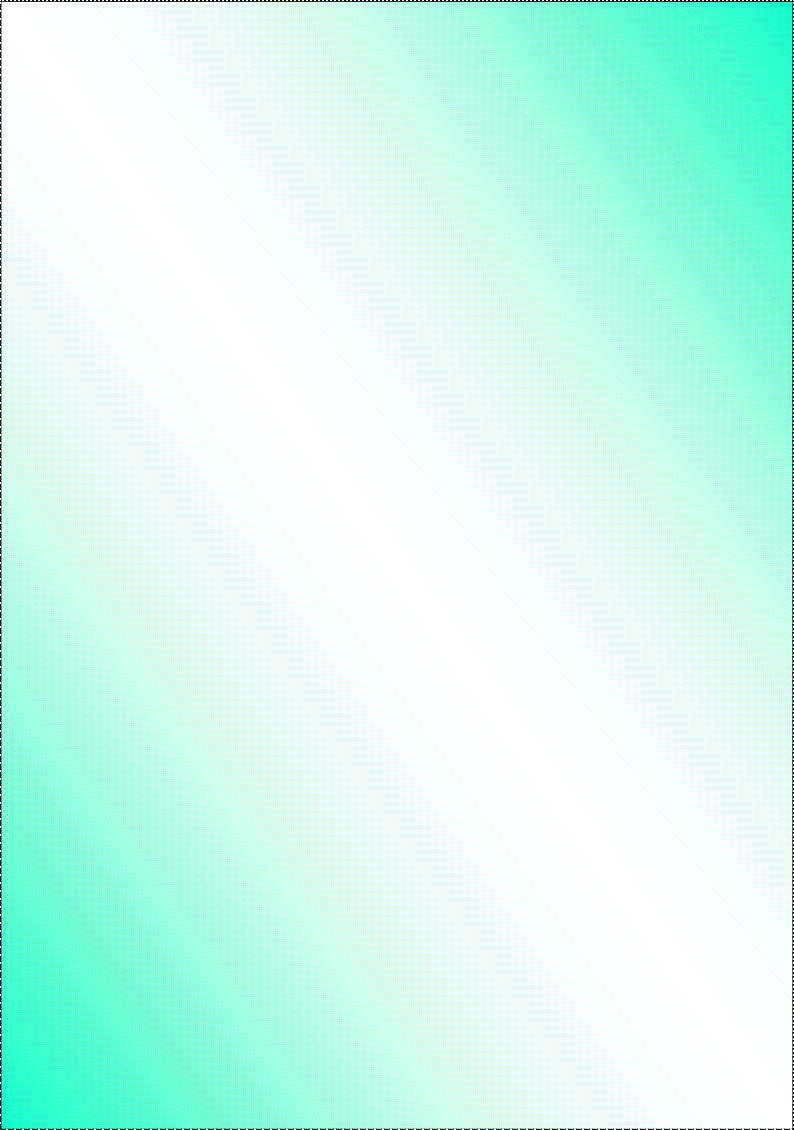Demak shunday xulosaga kelamizki ixtiyoriy har qanday uchburchakning yig`indisi 180⁰ ga tengligini isbotladik.

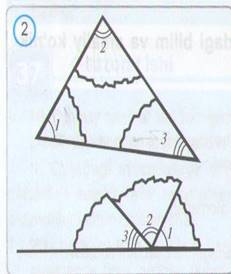2.Bir varaq qog'ozga ixtiyoriy ABC

uchbui chakni chizing va burchaklarini

1, 2 va 3 raqamlar bilan belgilang.

Uning burchaklarini 2-rasmda

ko'rsatilgandek qilib yirtib oling

va yonma-yon qo'ying. Bundan

qanday xulosa chiqarish mumkin?

Mavzuni mustahkamlash.

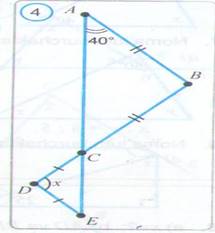
1-masala. Rasmda berilgan

ma`lumotlardan foydalanib

noma`lum burchak x ni toping.

Yechilishi: ABC-teng yonli

uchburchak bo`lgani uchun,

ACB= A=40⁰. Vertikal burchaklar

xossasiga ko`ra,

DCE= ACB=40⁰. Shartga ko`ra

CED ham teng yonli. Shu bois, DCE= DEC=40⁰.

Demak, uchburchak burchaklarining yig`indisi haqidagi teoremaga ko`ra, CDE da: 40⁰ +40⁰+x=180⁰ yoki x=100⁰

Javob: 100⁰

2-masala. Uchburchak ichki burchaklari 2:3:7 kabi nisbatda bo`lsa, ularning gradus o`lchovini toping.

Yechilishi: Shartga ko`ra, uchburchak ichki burchaklarini 2x, 3x va 7x deb belgilaymiz. U holda uchburchak ichki burchaklari yig`indisi haqidagi teoremaga ko`ra 2x+3x+7x=180⁰ tenglikka ega bo`lamiz. Undan x=15⁰ekanligini topamiz.

Demak, uchburchak burchaklarining gradus o`lchovi 30⁰, 45⁰ va 105⁰ ga teng ekan.

Javob: 30⁰,45⁰,105⁰.

3-masala: Uchburchakning nechta burchagi to`g`ri bo`lishi mumkin.

Javob: To`g`ri burchakli uchburchaklarimizni

bitta burchagi va faqat bitta burchagigina

to`g`ri burchak bo`lishi mumkin.

B 90⁰ C

4-masala: Uchburchakning nechta burchagi o`tmas bo`lishi mumkin.

N Javob: O`tmas burchakli uchburchaklarimizni

bitta burchagi va faqat bitta burchagigina

o`tmas burchak bo`lishi mumkin.

M K

5-masala: Burchaklar: a) 5⁰, 55⁰, 120⁰,; b) 46⁰, 150⁰, 4⁰; c) 100⁰, 20⁰, 50⁰ bo`lgan uchburchak mavjudmi?

a) Berilgan Yechish

A=50⁰ A+ B+ C=180⁰

B=55⁰ 5⁰+55⁰+120⁰=180⁰

C=120⁰180⁰= 180⁰

ABC=? Javob: Ha. Sababi berilgan ichki burchaklarimizni yig`indisi 180⁰ ga teng.

b) Berilgan Yechish

A=46⁰ A+ B+ C=180⁰

B=150⁰ 150⁰+46⁰+4⁰=180⁰

C=4⁰150⁰+50= 180⁰

200⁰≠180⁰

ABC=?

Javob: Yo`q. Sababi berilgan ichki burchaklarimizni yig`indisi 180⁰ dan katta.

c) Berilgan Yechish

A=100⁰ A+ B+ C=180⁰

B=20⁰ 100⁰+20⁰+50⁰=180⁰

C=50⁰170⁰≠ 180⁰

ABC=?

Javob: Yo`q. Sababi berilgan ichki burchaklarimizni yig`indisi 180⁰ dan kichik.

6-masala: Agar uchburchakning ikkita burchagi: a) 60⁰va 40⁰; b) 70⁰va 85⁰; c) 90⁰va 45⁰; d) 105⁰va 30⁰ bo`lsa, uning uchunchi burchagini toping.

a) Berilgan Chizma

ABC

40⁰

A=60⁰

B=40⁰ C x 60⁰ A

C=?

Yechish.

A+ B+ C=180⁰

60⁰+40⁰+X=180⁰

100⁰+X=180⁰

X=180⁰-100 Javob: C=80⁰

X=80⁰

b)Berilgan Chizma

MNK M

70⁰

M=70⁰

N=85⁰

85⁰ x

N K

K=?

Yechish.

M+ N+ K=180⁰

70⁰+85⁰+X=180⁰

155⁰+X=180⁰

X=180⁰-155⁰ Javob: K=25⁰

X=25⁰

c)Berilgan Chizma

QPR P

45⁰

Q=90⁰

P=45⁰

90⁰ x

Q R

R=?

Yechish.

P+ Q+ R=180⁰

90⁰+45⁰+X=180⁰

135⁰+X=180⁰

X=180⁰-135⁰ Javob: R=45⁰

X=45⁰

d)Berilgan Chizma

ABC

30⁰

A=105⁰

B=30⁰ A 105⁰ x C

C=?

Yechish.

A+ B+ C=180⁰

105⁰+30⁰+X=180⁰

135⁰+X=180⁰

X=180⁰-135⁰ Javob: C=45⁰

X=45⁰

Darsda faol ishtirok etgan o`quvchilar baholanib, baholari kundalik daftar va jurnalga tushirildi.

Uyga vazifa: 6-7 masalalar

Zarafshon shahar

8-umumiy o`rta ta`lim maktabining

MATEMATIKA fani o`qituvchisi

Abdullayeva Marhabo Mahmudovnaning

“Uchburchak ichki burchaklarining yig`indisi haqida teorema”

mavzisida o`tgan bir soatlik

dars ishlanmasi

Zarafshon 2017

Учбурчак ички бурчаклар йиғиндиси ҳақида теорема

Материалы на данной страницы взяты из открытых истончиков либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

06.01.2020