Поделиться
Публикация является частью публикации:
Физика. 7кл. Учебник_Перышкин А.В_2006 -192с.pdf
А.В,Перышкин
сновная единица длины в СИ етр (1 м) 
м -0,01 м
 |
=
0,001 м Эталон метра
сновная единица объема в СИ убический метр (1 м з)
= 1 000 000 000 м з
0,001 мз ке = 0,000001 мз 
1 0.001
мз
Основная единица площади в СИ квадратный метр (1 м 2)
1 км2 1 000 000 м?
1 дм2 = 0,01 ма 1 см2 =0,0001 м2
0,000001 м2
Основная единица скорости в СИ
метр в секунду
(1 
с
0,28
1 см 1 . 0,01 м = 0,01
м 1 3600 км с 1000 •
3600 1000 ч
А. В . Перышкин
класс
учрежденийРекомендовано Министерством образования
Российской Федерации
10-е издание, дополненное
Москва • 2006
удк 373.167.1:53 
ББК 22.зя72
П27
Учебник подготовлен к изданию Н. В. Филонович
Перыщкин
П27 Физика. 7 кл. : учеб, для общеобразоват. учреждений / А. В, Перышкин. — 10-е изд., доп. — М. : Дрофа, 2006. — 192 с, : ил.
1,SBN 5-358-00257-Х
Настоящая книга является
переработанным вариантом учебника А. В. Перышкина •Фиаика. 7 кл... В нем
сохранены структура и методология изложения материала.
В соответствии с требованиями государственного стандарта общего образования внесены изменения в отдельные главы и параграфы учебника.
Достоинством книги являются ясность, краткость и доступность изложенин. Все главы учебника содержат богатый иллюстративный материал.
удк 373.167.1:53
ББК 22.зя72
Учебное изДание
Перышкин Александр Васильевич
ФИЗИКА
7 класс
Учебник для общеобразовательных учреждений
Ответственный
редактор Е. Н. Тихонова
Оформление И. Д. АнДреев
Художники Н. А. Николаева, З.А. Флоринсказ
Художественный редактор А. А- Шувалова
Технический редактор М. В. БиДенко
Компьютерная верстка Д. А. Дачевский, Т. В. Рыбина
Корректоры Е. Е. Никулина. Г. И. Мосякина
Санитарно-зпндемиологичеекое заключение № 77.99.ОЗ.95З.Д.ОО4992.О8.О5 от 16.08.2005.
'“стцписаяо к печатн 17.11.05. Формат 
Бумага офсетная. Гарнитура
Печать»офсетуая. Усл. леи. л. 14,04. Тираж 109 ООО экз. Заказ 6908.
ООО •Дрофа». 127018, Москва, Сущевский
ввл, 49 
редлоз«енмя и замечания по содержанию оформлению книги просум .паправлять
•в редакцию- общего образования издательства «Дрофа»:
127018; Москва, аул 79. Тел.: (495) 795-05-41. Femai1: chief@drofa.ru
По вопроеам—ЈрцЬбретення продукции издательства «Дрофа• обращаться по адресу: 327018, Москва, Сущевский нвл. 49. Тел.: (495) 795-05-50. 795-05-51. Факс: (495) 795-05-52.
Торговый дом • Школьник.. 109172, Моекнн. Малые Каменщики.
д. 6. стр. ША. Тел.: (495) 911-70-24, 912-15-16, 912-45-76,
Сеть магазинов • Переплетные птицы», Тел.; (495) 91? 45-76.
Отпечатано с готовых
диапозитишља е ОАО «Московские учебннкм юртолитография • . 
[25252, Моеквд. ул. Зорге, 15.
е ООО «Дрофа», 1999
5-358-00257-Х ООО
•Дрофа•. 2006, с изменениями
ВВЕДЕНИЕ 
Ребята, вы приступаете к изучению нового ля вас предмета, который называется «Физика» .
Слово «физика» происходит от греческого слова «фюзис», что
означает природа. Оно впервые п•оявилось в сочинениях одного из ве
ЛИЧаЙШИХ мыслителей древности —
Аристотеля, жившего в IV в. до нашей эры.
В русский язык слово «физика» было введено Михаилом Васильевичем Ломоносовым, когда он издал в России первый учебник физики в переводе с немецкого языка.
Физика — одна из основных наук о природе.
Если внимательно приглядеться к происходящему в окружающем нас мире, то можно заметить, что в нем происходят разнообразные изменения, или явления.
Изменения, происходящие с телами и веществами в окружаю-
тах, например, кусочек льда, внесенный в теплую комнату, начнет таять. Вода в чайнике, поставленном на огонь, закипит. Если по проволоке пропустить электрический ток, то она нагреется может даже аскалиться докрасна (как в электрической лампочке).
Таяние льда, кипение воды, падение камня, нагревание проволоки током, ветер, гром —- все это различные явления.
в физике изучают: механические, электрические, магнит 
ные, тепловые, звуковые и световые
явления. Все эти явления называют физическими.
Любые превращения или проявления свойств вещества, которые происходят без изменения его состава, называют физическими явлениями.
з
Может ли одна такая наука, как физика, изучить множество явлений?
Физика обладает необыкновенной особенностью. Изучая самые простые явления, можно вывести общие законы.
Например, изучАя свободное падение шариков, имеющих разный
размер, с различной высоты, можно установить законы, которые будут ВЫПОЛнятьСя
при падении других тел
Задача физики состоит в том, чтобы
открывать и изучать законы, которые связывают между собой различные физические
явления, ПРОИСХОДЯЩИе в 
природе.
Например, выяснено, что причиной падения на Землю различных тел является их притяжение Землей. Смена дня и ночи объясняется тем, что Земля движется вокруг своей оси (рис. 1). Одна из причин возникновения ветра — неравномерное нагревание воздуха и т. д.
Изучением природы занимаются и другие науки: биология,
химия, география, астрономия. Все эти науки применяют законы физики. Например,
в географии они необходимы для объяснения окли
мата, течения рек,
образования ветров и других явлений, В астрономии законы физики используют при
изучении строения [1 развития небесных тел.
Из этой книги вы узнаете о многих важнейших открытиях, благодаря которым развивалась физика, изучите различные физические явления, поймете, как они связаны между собой, узнаете имена учеНьТХ, ОТКРЫВШИХ важнейшие законы.
1. Что такое физика? 2. Что изучает физика? З. Приведите
примеры физических явлений. 4. Почему физику считают одной из основных наук 
о природе?
В физике, кроме обычных слов, используют специа.'|ьньје слова, или термины, обозначающие физические понятия. Некоторые из таких слов постепенно вошли. в нашу разговорную речь. Например, такие, как «электричество», «энергия», «сила» и др.
Рис.
В физике каждое из окружающих нас тел (песчинку, камень,
Луну) принято называть физическим телом или просто телом.
Физические тела показаны на рисунке 2— это ручка, листок, капля воды, теннисный мяч,
Всякое тело имеет форму и объем. На рисунке З изображены тела разной формы, но одинакового объема — кусок пластилина и слон, вылепленный из такого же куска пластилина. На рисунке 4 — тела разного объема, но одинаковой формы — две ложки.
Все то, из чего состоят физические тела, называют веществом. Железо, медь, резина, воздух, вода все это различные вещества.
Вода вещество, капля воды — физическое тело, алюминий 
вещество,
алюминиевая ложка — физическое тело.
Вещество — это один из видов материи. А словом «материя.
в науке называют все, что есть во Вселенной.
Материя — это все то, что существует во Вселенной независимо от нашего сознания (небесные тела, растения, животные н др.).
Примерами другого вида материи являются свет, радиоволнь . Нам известно, что радиоволны реально существуют, несмотря на то что мы их не видим.
В этом параграфе вы познакомились с новыми для вас терминами: физи ческое тело, вещество, материя,
Изучая физику, вы будете постоянно расширять свои знания, узнавать новые термины и тем самым постигать язык этой интересноЙ науки.
Введение
1. что в физике понимают под термином «физическое тело»? 2, Что называют веществом? Приведите примеры физических тел и веществ. З. В чем сходство и различие тещ изображенных на рисунках З, 4?
Многие знанпя получены людьми из собственных наблюдений.
Для изучения какого-либо явления необходимо прежде всего
наблюдать его и по возможности не один раз. Чтобы изучить такое явленце, как
падение тел на Землю, недостаточно один раз увидеть, как падает то или иное
тело. Следует выяснить, будет ли разница в 
падении тела легкого и
тяжелого. Одинаково ли падают тела различных размеров с разной
высоты? Это можно узнать, если много раз наблюдать различные случаи падения
тел.
Конечно, ждать, пока какое-либо тело упадет само, не стоит. Для этого берут разные тела и заставляют их падать. Тем самым вызывакот явление падения тел, иными СЛОВАМИ, проводят опыт. Во время опытов обычно выполняют измерения.
Опыты отличаются от наблюдений тем, что их проводят с
определенной целью, по заранее обдуманному плану. Для составления такого плана
лучше всего иметь предварительные догадки о том, как протекает явление, т. е. выдвинуть
гипотезУ.
Выдвигая ту или иную
гипотезу, ученые с помощью физического эксперимента находят подтверждение
физиче
скоЙ теории или ее опровержение.
Чтобы
получить научные знания об окружающем нас мире, необходимо обдумать и объяснить
результаты проведенных опытов, найти причины наблюдаемых
явлений, сделать выводы .
Известна легенда об итальянском ученом Г, Галилее, Для того
чтобы 
чить, как происходит падение тел. Гали
лей ронял разные шары наклон ной башв г. Пизе (рис. 5),
Проделав такие опьт• ты, ученый получил подтверждение своеи гипотезы и откры.п закон падения
тел.
ВееленјП
Таким образом, источниками физических знаний являются наблюДения и опыты.
Вопросы
Как мы получаем знания о явлениях
природы? 2. Чем отличаются 
наблюдения от опытов? З- Достаточно ли одних опытов. для того чтобы по
лучить научные знания?
S 4. Физические величины.
В быту, технике, при изучении физических явлений часто
приходится выполнять различные измерения, Так, например, изучая падение тела,
необходимо измерить высоту, с которой падает тело, массу 
тела, его скорость,
время падения, Высота, масса, скорость, время и т. д. являются физическими
величинами. Физическую величину можно измерить.
Измерить какую-нибудь величину — это значит сравнить ее с однородной величиной, принятой за единицу.
Так, например, измерить длину стола — значит сравнить ее с
другой длиной, которая принята за единицу длины, например с метром 
Для каждой физической величины приняты
свои единицы.
Для удобства все страны мира стремятся пользоваться
одинаковыми единицами физических величин. С 1903 г. в России и других странах
применяется Международная система единиц СИ (систе
ма интернациональная).
в этой системе основной единицей длины является метр (1 м), единицей времени
секунДа (1 с), единицей массы — килограмм (1 кг).
Часто применяют единицы, которые в 10, 100, 1000 и т. д.
раз больше принятых единиц (кратные). Эти единицы получили наименования с
соответствующими приставками, взятыми из греческог0 языка. «Дека» 10, «гекто•
100, «кило» 1000 и др.
Если используются единицы, которые в 10, 100 и 1000 и т, д. Раз меньше принятых единиц (Дольные), то применяют приставки, взятые из латинского языка. «Деци» 0,1, «санти» — 0,01, «милли» 0,001 идР.
Приставки к названиям единиц
— гекто (100 или 10 ) деци
(0,1 или 10—1 )
— кило (1000 или 10 ) санти
(0,01 или 10 2)
М --— мега (1 ООО ООО или 10 ) МИЛЛИ (0,001 или 10 З )
 |
Пример.
Длина теннисной ракетки 60 см. Выразите ее длину в метрах (м).
60 см 0,6 м или 6 , 10
Для проведения опытов
необходимы приборы. Одни из них очень просты и предназначены для простых измерений.
К таким приборам можно отнести: измерительную линейку, рулетку (рис. 6),
измерительный цилиндр (рис. 7) и др.
По мере развития физики приборы
усложнялись и совершенствовались. Появились амперметры (рис. 8), вольтметры
(рис. 9), секундомеры (рис. 10), термометры (рис. 11, 12). 23 5 Измерительные
приборы, как правило, имеют шкалу. Это значит, что на при- 20 10 боре нанесены
штриховые деления, а рядом написаны значения величин, соответ- 15 ствующие
делениям. Расстояния между двумя штрихами, возле которых написа-
Рио. З О
ны значения
физической величины, могут быть дополнительно разделены еще на несколько
делений. Эти деления иногда не обозначены числами,
Определить, какому значению величины соответствует каждое самое малое деление, нетрудно. Так, например, на ри-ас сунке 6, а изображена измерительная ли-40 нейка. Цифрами 1, 2, З, 4 и т. д. обозначены расстояния между штрихами, которыезо 30 разделены на 10 одинаковых делений. Следовательно, каждое деление (расстояние между ближайшими штрихами) соответст-10вует 1 мм. Эта величина называется ценой деления шкалы прибора.
перед тем как приступить к измерению физической величины, следует определить цену деления шкалы используемого прибора.
Для того чтобы определить цену деления, необходимо:
Рис. 12 шкалы. возле которых написаны
значения величины;—- вычесть из большего значения меньшее и получен нос чиело разДелить на число Делений, находящихся «не.ж:Ду ними.
Определим цену деления термометра, изображенного на рисув ке 12.
Воеде.ые
Возьмем два штриха, около которых нанесены значения измеряемой величины (температуры).
Например, штрихи с обозначениями 10 ос и 20 ос. Расстояния между этими штрихами разделены на 10 делений. Следовательно, цена каждого деления будет равна:
20 о с, 10 о с
1 ос,
10
Следовательно, термометр показывает 24 ос.
1 . Что значит измерить какую-либо величину? 2. Каковы единицы длины, времени, массы в СИ? З. Как определяется цена деления шкалы измеригельного прибора?
1, Определите цену деления секундомера
(см, рис. 10).
2. По рисункам 8 и 9 определите цену
деления амперметра и вольтметра.
Всякое измерение может быть выполнено с бодьщей или меньшей точностью.
В качестве примера рассмотрим измерение длины оруска демонст ационным метром с сантиметровыми делениями (рис. 13).
Рис. 13
Вначале определим цену деления линейки. Она будет равна 1 см.
Если левый конец линейки совместить с
нулевым штрихом, то 
правый будет находиться между 11 и 12
штрихами, но ближе к 11.
Какое же из этих двух значений следует
принять за длину брус
ка? Очевидно, то, которое ближе к
истинному значению, т. е. 11 см.
Считая, что длина бруска 11 см, мы допустили неточность, так как брусок
чуть длиннее 11 r•
В физике допускаемую при измерении неточность называют
погрешностью
измерений, Погрешность измерения не может быть больше цены Деления
измерительного прибора.
В пашем случае погрешность измерения бруска не превышает 1 см. Если такая точность измерений нас не удовлетворяет, то можно произвести измерения с большеи точностью. Но тогда придется ВЗЯТь масштабную линейку с миллиметровыми делениями, т. е. с ценой деления 1 мм.
В этом случае длина бруска окажется равной 11,4 см.
Из этого примера видно, что точность измерений зависит от цены деления тка,ЛЬ1 прибора,
Чем меньше цена деления, тем больше точность измерения.
Точность измерения зависит также от правильного применения измерительного прибора, расположения глаза при отсчете по прибору.
Вследствие несовершенства измерительных приборов и наших
органов чувств при любом измерении получаются лишь приближенные значения,
несколько ббльшие или меньшие истинного значения измеряемой величины.
Во время выполнения лабораторных работ ИЛи просто измерений следует считать, что:
погрешность измерений равна половине цены Деления шкалы измерительного прибора.
Так, если длина шариковой ручки 14 см, а цена деления линейки Т мм, то погрешность измерения будет равна 0,5 мм, или 0,05 см.
Следовательно, длину ручки можно записать
в следующем виде:
где — длина ручки.
Истинное значение длины ручки находится в интервале от 13,95 см до 14,00 см.
При записи величин, с учетом погрешности, следует пользовать
формулой:
где А — измеряемая величина, а — результат
измерений, Ла 
грешность измерений (А -— греч. буква
«дельта»).
Как понимать выражение «измерить длину
с точностью до 1 мм»? 2, Можно ли линейкой, имеющей сантиметровые деления,
измерить длину сточностью до 1 мм? З. Какова связь точности измерений с ценой
деления шкалы прибора? 4. Какой формулой необходимо пользоваться при
определении физических величин с учетом погрешности?
1.Измерьте линейкой с миллиметровыми делениями длину и ширину
вашего учебника. Запишите результаты с учетом погрешности измерения.
2. Пользуясь рисунком 11, определите погрешность измерения градусника.
Развитие физики сопровождалось изменением представлений 
людей
об окружающем мире. Отказ от привычных взглядов, возникновение новых теорий,
изучение физических явлений характерно для физики с момента зарождения этой
науки до наших дней.
Рис 14
Рис. 15
Важное значение имеют открытия в области физики для развития
техники. Так, например, двигатель внутреннего сгорания, приводящий в движение
автомобили, тепловозы, речные и морские суда (рис. 14), был создан на основе
изучения тепловых явлений.
С развитием науки в технике за последние десятилетия произошли
грандиозные изменения.
То, что раньше считалось научной фантастикой, сейчас является реальностью. Сегодня трудно представить нашу жизнь без видеомагнитофона, компьютера, мобильной и интернет-связи.
Современное кино, телевидение, радио, магнитная запись (рис. 15) — все это возникло после того, как были изучены многие звуковые, световые и электрические явления.
Введение
Ньютон Исаак
1727) Отрыл основные законы движевия теп закон тяготении. изучил вахные
свойства свела. разработал важнейшие разделы мдтем;тт
Максвелл Джеймс
(1831—1879). Создал 
СОРИН) электромагнитного поля.
предсказал существование в свободном пространстве апекгромагнитного изпучения и
его распространенве сп скоро. ст ыо слета
В свою очередь, развитие техники влияет на развитие науки. Так, например, усовершенствованные машины, компьютеры, точные измерительные и другие приборы используются учеными при исследовании физических явлений. После того как были созданы современные приборы и ракеты, стало возможным глубже изучить космическое пространство.
Подобных примеров можно привести множество. Открытия, сделанные в науке, есть результат упорного труда многих ученых разных стран.
Рассмотрим некоторые этапы развития физики.
Возникновение физической теории связано с именем выдающегося английского физика и математика Исаака Ньютона. Обобщив результаты наблюдений и опытов своих предшественников (И. Кеплера, Г. Галилея), Ньютон создал огромный труд «Математические начала натуральнои философии», В этой работе ученый изложил важнейшие законы механики, которые были названы его именем. Законы Ньютона привели к бурному развитию представлений о механическом движении.
Дальнейшее развитие физики определилось
изучением тепловых и электромагнитных явлений. Стремление ученых проникнуть в
глубь тепловых процессов привело к 
зарождению идей о молекулярном строении
вещества.
Исследования электромагнитных явлений коренным образом изменило научную картину мира. Оказалось, что нас окружают физические тела и поля. Общую теорию электромагнитных явл ений создал Джеймс Максвелл.
Теория Максвелла объяснила природу света и помогла разработке новых технических приборов и устройств, основанных на явлениях электромагнетизма.
новый этап бурного развития физики начался в ХХ в. Возникли и
стали развиваться новые направления: ядерная физика, физика элементарных
частиц, физика твердого тела и 
др. Возросла роль физики и ее влияние на
технический и социальный прогресс. Свой вклад в развитие современной физики
внесли видные 
ученые России: М. Г. Басов, П. П. Капица 
Л, Б.
Ландау Л. И. Мандельштам, А. М. Прохоров и др.
Ярким подтверждением связи науки и техники явился огромный прорыв в области изучения космоса, Так, 4 октября 1957 г. в нашей стране был запущен первый в мире искусственный спутник Земли, а 12 апреля
1961 г. Юрий Алексеевич Гагарин стал первым
космонавтом, облетевшим земной шар за 1 ч 48 мин. 21 июля 1969 г. впервые была
осуществлена посадка на Луну американского космического корабля с астронавтами 
на
борту: Нейлом Армстронгом и Эдвином Олдрином. Большой вклад, в научную и техническую
разработку космических полетов сделал Сергей Павлович Королев.
|
Здесь названы лишь основные этапы развития физики и перечислены
немногие из выдающихся людей науки, сделавших важные
открытия, благодаря которым развивалась эта наука.
1 . Какое значение имеет физика для техники? Покажите это на примерах. 2. Каких ученых вы знаете? Какие открытия ими были сделаны?
Королев Сергей Павлович ( 1907— 1966) Конструктор. под руко
водством которого были построены
первые пипозируемые косми
ческие корабли, отработана аппаратура для выхола 
в космос
Гагарин Юрии Алексеевич 1934— 
Переши в мире летчик -КОСМИН,АВТ
ПЕРВОНАЧАЛЬНЫЕ СВЕДЕНИЯ
О СТРОЕНИИ ВЕЩЕСТВА
S 7. Строение вещества
Еще в глубокой древности, 2500 лет назад, некоторые ученые
высказывали предположение о строении вещества. Греческий ученый демокрит
(460—370 до н. э.) считал, что все вещества состоят из мельчайших частичек. В
научную теорию эта идея превратилась только в XVIII в, и получила дальнейшее
развитие в XlX в. ВОЗНИКновение представлений о строении вещества позволило не
только объяснить многие явления, но и предсказать
как они будут протекать в тех или иных условиях. Появилась
возможность влиять на прохождение явлений,
Многие опыты подтверждают представления о строении вещества- Рассмотрим некоторые из них.
Попытаемся сжать теннисный мячик. При этом объем воздуха, который заполняет мяч, уменьшится. Можно уменьшить и объем надувного шарика, и кусочка воска, если приложить некоторое усилие.
Объем тела изменяется также при его нагревании и охлаждении.
Проделаем опыт. Возьмем медвый или
латунный шарик, который 
в ненагретом состоянии проходит сквозь
кольцо (рис. 16), Если шарик нагреть, то, расширившись, он
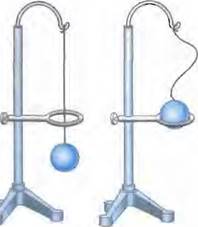(4уже сквозь кольцо
не пройдет (рпс„ 17), Через некоторое время шарик, остыв,
уменьшится в объ-
кольцо, нагревшись от шарика, расширится,
и шарик вновь пройдет сквозь кольцо.
С помощью опыта определим, как меняется объем жидкости при 
нагревании.
 |
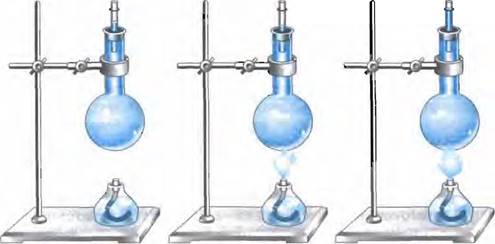
Следовательно, при нагревании объем тела
увеличивается, а при ох.аажДении уменьшается.
Попытаемся объяснить, почему происходит изменение объема тела.
По-видимому, все вещества состоят из отдельных частичек,
между которыми 
промежутки. Если частицы удаляются друг от
друга, то объем тела увеличивается, И наоборот, когда частицы сблиЖаются, объем
тела уменьшается.
Тогда возникает вопрос: если все тела
состоят из мельчайших частиц, почему они кажутся нам сплошными (например, железо,
вода,
стекло, дерево)?
Современная наука доказала, что частицы вещества так малы, что мы иХ не видим.
Для того чтобы убедиться в том, что
частицы вещества малы, проделаем опыт .
В сосуде с водой растворим маленькую крупинку синей гуаши.
Через некоторое время вода в нем станет синей. отольем немного окрашенной воды в
другой сосуд и дольем в него чистую воду. Раствор во втором сосуде будет
окрашен слабее, чем в первом. Потом из второго рис , 19 сосуда снова отольем
раствор уже в третий сосуд и дольем его вновь чистой водой. В этом сосуде вода будет окрашена еще слабее, чем
во втором (рис. 19).
Поскольку в воде растворили очень маленькую крупинку гуаши и только часть ее попала в третий сосуд, то можно предположить, что крупинка состояла из большого числа мельчайших час,тлц.
 |
1 Из чего состоят вещества? 2. Какие опыты подтверждают, что
вещества состоят из мельчайших частиц? З. Как меняется объем тела при изменении
расстояния между частицами? 4. Какой опыт показывает, что части ды вещества
очень малы?
все вещества состоят из отдельных частиц это предположение было доказано современной наукой. Эти ЧАСТИЦЫ были названы молекула.ми (в переводе с латинского «маленькая масса»).
Молекула вещества л— это мельчайшая частица
данного вещества
Например, самая маленькая частица воды молекула воды. Наименьшей частицей сахара является молекула сахара.
Попытаемся представить себе, каковы размеры молекул.
Если бы можно было
уложить в один ряд „вплотную друг к другу 10 ООО ООО (или 10 7 )
молекул воды, то получилась бы ниточка длиной всего в 2 мм. Малый размер
молекул позволяет получить тонкие пленки различных веществ, Капля масла,
например, может растекаться по воде слоем толщиной всего в 0,000002 м (или 2 •
10 -6 м).
Даже небольшие тела состоят из огромного числа молекул.
Так, Рис. 20 например, в крупинке сахара содержится очень большое число
молекул, Подсчитано, что в 1 смз воздуха находится около 27 • 10 18 молекул.
Чтобы понять, насколь 
ко велико это число, представим следующее.
Через маленькое отверстие пропускают по миллиону молекул в секунду, тогда
указанное количество молекул пройдет через отверстие за 840 000 лет.
И: -за очень малых размеров молекулы невидимы невооруженным глазом или в обычные микроскопы. Но при помощи специального прибора — электронного микроскопа удалось сфотографировать наиболее крупные из них. На рисунке 20 показано расположение молекул белка.
Окружающие нас тела, даже похожие на первый взгляд, будут различны. В природе вы не встретите двух совершенно одинаковых снежинок или песчинок, людей, животных и лР.
Ученые с помощью опытов доказали, что молекулы разных ве
ЩеСТВ отличаются друг от друга, а молекулы одного и того же вещества одинаковы». Например, воду, полученную из сока или молока, нельзя отличить от воды, полученной путем перегонки из морской воды. Молекулы воды одинаковы. Из таких молекул не может состоять никакое другое вещество.
Молекулы, в свою очередь, состоят из еще более мелких
частиц — атомов.
Например, наименьшая частица воды это молекула воды
Она состоит из трех атомов: двух атомов водорода и одного атома
кислорода. Из курса химии вы узнаете, что
воду обозначают 1-120. Н атом водорода, О атом кислорода.
Молекулы принято изображать схематически, т, е. с помощью моделей молекул. Две молекулы воды показаны на рисунке 21. Если разделить две молекулы воды, то образуется два атома кислорода и четыре атома водорода, На рисунке 22 показано, что каждые два атома водорода могут соединиться в молекулу водорођа, а атомы кислорода — в молекулу кислорода.
Рис. 2' 22
|
томы
тоже состоят из еще более мелких частиц, но об этом вы узнаете в курсе химии 8
класса.
Вопросы
го такое молекула? 2. Что вы знаете о
размерах молекул? З, Из каких частиц состоит молекула воды? 4. Как изображается
схематически молекула воды?
Всем хорошо известно, что если в комнату ВН(ЭСТИ какое-либо пахучее вещество, например духи или нафталин, то запах вскоре будет чувствоваться во всей комнате. Распространение запахов происходит из-за того, что молекулы духов (или нафталина) Движутся.
Возникает вопрос, почему же запах в комнате распространяется не мгновенно, а спустя некоторое время.
Дело в том, что движению молекул пахучего вещества в определенном направлении мешает движение молекул воздуха. Молекулы духов (или нафталина) на своем пути сталкиваются с молекулами газов, которые входят в состав воздуха. Они постоянно меняют направление движения и, беспорядочно перемещаясь, разлетаются по комнате.
Проделаем опыт, который можно объяснить только тем, что тела состоят из молекул, которые находятся в непрерывном движении.
23
 |
ды (рис. 23).
Вначале между водой и медным купоросом будет видна резкая граница,
которая через несколько дней станет не такой резкой. Граница, отделяющая одну
жидкость от другой, исчезнет через 2—3 недели. В сосуде образуется однородная
жидкость бледно-голубого цвета. Это значит, что жидкости перемешались.
Наблюдаемое явление объясняется тем, что молекулы воды и
медного купороса, которые расположены возле границы раздела этих жидкостей,
поменялись местами (рис. 24), Граница раздела стала расплывчатой. Молекулы
медного купороса оказались в нижнем слое воды, а молекулы воды
переместились в верхний слой медного купороса.
Если дать мензурке постоять 2—3 недели, то граница раздела
будет еще более расплывчатой и постепенно совсем исчезнет. Вся вода 
окрасится
в голубой цвет. Это происходит потому, что молекулы, двигаясь непрерывно и
беспорядочно, распространяются по всему объему. Жидкость в сосуде становится
однородной.
Рис, 24
Явление, при котором происходит взаимное проникновение молекул одного вещества между молекулами другого, называют диффузией.
в твердых телах также происходит
диффузия, но только еще медленнее.
Например, очень гладко отшлифованные пластинки свинца и золо-
та
кладут одна на другую
и ставят на них некоторый груз. (Пластинку золота, как более тяжелую,
располагают вни 
ЗУ.) При комнатной температуре (20 ос)
за
лет золото и свинец взаимно
проникают друг в друга на расстояние около 1 мм (рис. 25). Во всех приведенных
опытах мы наблюдаем взаимное проникновение молекул веществ, т.
Диффузию.
Процесс диффузии ускоряется е повышением температуры. Это происходит потому,
Рис 25 что с повышением температуры увеличивается скорость движения молекул.
Явление диффузии играет большую роль в природе. Так, например, благодаря ДИФфузиъг поддерживается однородный состав атмосферного воздуха вблизи поверхности Земли. Диффузия растворов различных солей в почве способствует нормальному питанию растений и т. д.
1 . Что такое
шите опыт. З. ПРиведите диффузия? примеры 2. Как диффузии протекает диффузия в окружающем в жидкостях? мире. Опи-
1. Налейте в один стакан холодной воды, в другой теплой. Опустите в каждый из них несколько кристалликов марганцовки. Объясните наблюдаемое явление.
2. Пользуясь рисунком 23, объясните процесс протекамИЯ диффузии в жидкостях.
Если все тела состоят из мельчайших частиц (молекул или атомов), почему же твердые тела и жидкости не распадаются на отдельные молекулы или атомы? Что заставляет их держаться вместе, ведь молекулы разделены между собой промежутками и находятся в непрерывном беспорядочном движении?
Дело в том, что между молекулами существует взаимное притяжение. Каждая молекула притягивает к себе все соседние молекулы и сама притягивается ими.
 |
Заметить притяжение между двумя молекулами совершенно невозможно. Когда же притягиваются многие миллионы таких частиц, взаимное притяжение становится значительным. Поэтому трудно разорвать руками веревку или стальную проволоку.
Притяжение между молекулами в разных веществах неодинаково. Этим объясняется различная прочность тел, Например, стальная проволока прочнее медной. Это значит, что частицы стали притягиваются сильнее друг к другу, чем частицы меди.
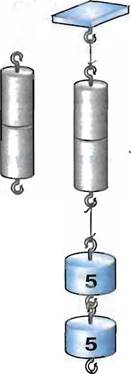
Притяжение между молекулами становится заметным только тогда, когда они находятся очень близко
друг к другу. На расстоянии, превышающем размеры самих молекул, притяжение
ослабевает. Две капли воды сливаются в одну, если они соприкасаются. Два
свинцовых цилиндра сцегтяются вместе, если их вплотную прижать друг к другу
ровными, только что срезанными поверхностями. При этом сцепление может быть
настолько прочным, что цилиндры не удается оторвать друг от друга даже при
большой нагрузке (рис. 26).
Однако осколки стекла
нельзя срастить, даже плотно прижимая их. Из-за неровностей не удается их
сблизить на то расстояние, на котором частицы могут притянуться друг к другу.
Но если размягчить стекло путем нагрева, то различные части можно сблизить и
стекло в этом случае спаивается,
Это значит, что частицЫ стекла оказались на таком расстоянии, когда действует притяжение между ними.
Соединение кусков металла при сварке или паике, а также
склеивание основано на притяжении молекул друг к другу.
Следовательно, между молекулами (атомами) существует взаимное притяжение, которое заметно только на расстояниях, сравнимых с размерами самих молекул (атомов).
 |
метнее проявляется притяжение, а 
при Дальнеиијем сближении отРис, 26
талњивание.
Многие наблюдаемые явления подтверждают существование отталкивания между молекулами.
Так, например, сжатое тело распрямляется. Это происходит из-за того, что при сжатии молекулы оказываются на таком расстоянии друг от друга, когда начинает проявляться отталкивание.
Некоторые явления, происходящие в природе, можно объяснить притяжением молекул друг к другу, например смачивание твердого тела жидкостью.
К пружине подвешивают на нитке стеклянную пластинку так, чтобы ее нижняя поверхность была расположена горизонтально (рис. 27). Эту пластинку подносят к сосуду с водой так, чтобы она легла на поверхность воды (рис. 27, а). При отрывании пластинки от воды пружина заметно растянется (рис. 27, б). Это доказывает существование притяжения между молекулами. По растяжению пруэкины можно судить о том, насколько оно велико. Оторвав пластинку, можно увидеть, что на ней остается тонкии слой воды, т. е. плас-
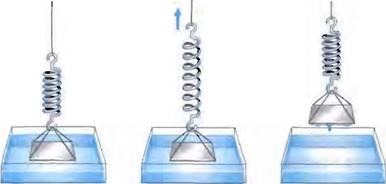
а) 6) в) Рис 27
тина смочена водой (рис. 27, в).
Значит, при отрывании пластины мы преодолевали притяжение между молекулами
воды. Разрыв произошед не там, где соприкасаются молекулы воды с частицами
стекла, а там, где молекулы воды соприкасаются друг с другом
Вода смачивает не только стекло, но и кожу, дерево и другие вещества.
Во многих случаях вода может и не смачивать тела, Например, если опустить в воду кусочек воска или парафина, а затем вынуть, то он окажется сухим. Всем хорошо известно, что вода не смачивает и жирные поверхности тел.
 |
Если жидкость смачивает твердое тело, то это значит, что молекулы жидкости притягиваются друг к другу слабее, чем к молекулам тела.
Когда наблюдается несмачиваемость, то это означает, что молекульт жидкости притягиваются сильнее друг к друђу, чем к молекулам твердого тела.
В быту мы часто сталкиваемся с явлениями смачивания и несмачивания.
Так, например, благодаря явлению смачивания мы можем писать, вытирать мокрые предметы и т. д.
Как взаимодействуют между собой
молекулы? 2. Когда заметнее проявляется отталкивание, а когда притяжение между
молекулами? З. Какое явление, наблюдаемое в природе, основано на притяжении молекул твердого
тела и жидкости? 4. Какие примеры смачивания и несмачивания твердых тел
жидкостью можно привести?
1. Смочите два листочка бумаги: один водой, другой растительным маслом. Слипнутся ли они? Ответ обоснуйте,
2. У водоплавающих
птиц перья и пух остаются сухими. Какое явление здесь наблюдается?
В природе вещества встречаются в трех состояниях: в твердом, ЖИДКОМ и газообразном. Например, вода может находиться в твердом (лед), в жидком (вода) и газообразном (водяной пар) состояниях. В хорошо знакомом вам градуснике ртуть — это жидкость. Над поверхностью ртути находятся ее пары, а при температуре —39 а с, ртуть превращается в твердое тело.
 |
В обычных условиях трудно сжать или растянуть твердое тело.
Для придания твердым телам нужной формы и объема на заводах и фабриках их обрабатывают на специальных станках: токарных, строгальных, шлифовальных.
Твердое тело имеет собственную форму и объем.
В отличие от твердых тел жидкости легко меняют свою форму. Они принимают форму сосуда, в котором находятся.
Например, молоко, наполняющее бутылку, имеет форму бутылки. Налитое же в стакан, оно принимает форму стакана (рис. 28). Но, изменяя форму, жидкость сохраняет свой объем.
В обычных условиях только маленькие Кале-ЛЬКИ жидкости имеют свою форму — форму шара. Это, например, капли дождя или капли, на которые разбивается струя жидкости.
На свойстве жидкости легко изменять свою форму основано изготовление предметов из расплавленного стекла (рис. 29).
Глава 1. Первоначальные сведения о ветцеслвл
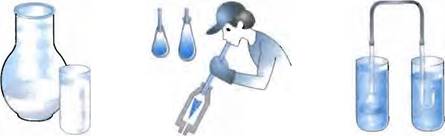
Рис. 28 Рис. 29 Рис. ЗО
Жидкости легко меняют свою форму, но сохраняют объем.
Воздух, которым мы дышим, является газообразным веществом, или газом. Поскольку большинство газов бесцветны и прозрачны, то они невидимы.
Присутствие воздуха можно почувствовать, стоя у открытого
окна движущегося поезда. Его наличие в окружающем пространстве можно ощутить,
если в комнате возникнет сквозняк, а также доказать е помощью простых опытов,
Если стакан перевернуть вверх дном и попытаться опустить его в воду, то вода в стакан не войдет, поскольку он заполнен воздухом. Теперь опустим в воду воронку, которая соединена резиновым Ш.Д&Нгом со стеклянной трубочкой (рис. 30). Воздух из воронки начнет выходить через эту трубочку.
Эти и многие другие примеры и опыты подтверждают, что в окрулающем пространстве имеется воздух,
Газы в отличие от жидкостей легко изменяют свой объем. Когда мы сжимаем теннисный мяйик, то тем самым меняем объем воздуха, наполняющего мяч. Газ, помещенный в закрытый сосуд, занимает весь его целиком. Нельзя газом заполнить половину бутылки так, как это можно сделать жидкостью.
Газы не имеют собственной формы и постоянного объема. Они принимают форму сосуда и полностью заполняют предоставленныл им объем.
1 . Какие три состояния вещества вам известньР 2. Перечислите свойства твердых тел. З. Назовите свойства жидкостей, 4. Какими свойствами обладают газы?
В предыдущем параграфе вы изучали свойства твердых тел, жидкостей и газов.
Объяснить свойства веществ можно, если знать их молекулярное строение,
Одно и то же вещество может находиться в различных состояниях.
Так, например, вода, замерзая, становится твердым телом (лед), а при кипении обраЩается в газообразное состояние (пар). Это три состояния одного и того же вещества (воды), т. е, жидкое, твердое и гавообразное, А если все три состояния воды ---- это состояния одного и того же вещества, значит, и молекулы его не отличаются друг от друга. Отсюда можно сделать вывод, что различные свойства вещества во всех состояниях определяются тем, что его молекулы расположены иначе и движутся по-разному,
Если газ сжимается и объем его уменьшается, следовательно, в
газах расстояние межДу молекулами намного больше размеров самих молекул,
Поскольку в среднем расстояния между молекулами в десятки раз больше размера
молекул, то они слабо притягиваются друг к другу
Молекулы газа, двигаясь во всех направлениях, почти не притятиваются
друг к другу и заполняют весь сосуд. Газы не имеют собственной формы и
постоянного объема.
Молекулы жидкости расположены близко друг к другу.
Расстояния между каждыми двумя молекулами меньше размеров молекул, поэтому
притяжение между ними становится значительным.
Молекулы жидкости не расходятся на большие расстояния, и жидкость в обычных условиях сохраняет свой объем, но не сохраняет форму.
Поскольку притяжение между молекулами жидкости не так велико, то они могут скачками менять свое положение. Жидкость не сохраняет свою форму и принимает форму сосуда. Они текучи, их легко перелить из одного сосуда в другой .
Жидкость трудно сжимается, так как при этом молекулы
сближаются на расстояние, когда заметно проявляется отталкивание.
В твердых телах притяжение между молекулами (атомами) еще больше, чем- у жидкостей. Поэтому в обычных условиях твердые тела сохраняют свою форму и объем.
В твердых телах молекулы (атомы) расположены в определенном порядке. Это лед, соль, металлы и др. Такие тела называются кристаллами.
Молекулы или атомы твердых тел колеблются около определенной точки и не могут далеко переместиться от нее. Твердое тело поэтому сохраняет не только объем, но и форму.
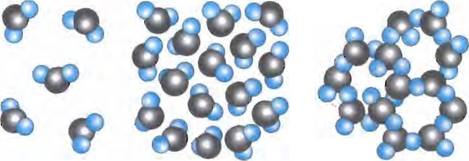
Рис. 31
Расположение молекул воды в трех разных состояниях показано на рисунке 31: газообразном водяной пар (рис. 31, а), жидком — вода (рис. 31, б) и твердом• лед (рис. 31, в).
Вопросы1 . Каково расположение молекул газа? 2. Чем объясняется способность жидкостей сохранять свой объем? З. Как расположены частицы в твердых телах?
Налейте в пластмассовую бутылочку воды и закройте крышкой.
Попытайтесь сжать в ней воду. Затем вылейте воду, снова закройте бутылочку.
Теперь попробуйте сжать воздух. Объясните результаты опыта.
ВЗАИМОДЕИСТВИЕТЕЛ
Если вдали на дороге виден автомобиль, то определить, движется он или нет, трудно. Для того чтобы узнать, движется автомобиль или нет, проследим, как меняется его положение относительно других тел. Например, полотна дороги, домов, деревьев. Если положение автомобиля меняется относительно этих тел, то говорят, что он движется относительно этих тел.
Подобным образом мы определяем, движется или нет поезд, самолет, человек и др.
Итак, чтобы судить о движении тела, надо узнать, меняется ли положение этого тела среди окружающих его тел.
Если положение автомобиля меняется относительно домов или
деревьев, то говорят, что он движется относительно этих тел. Если 
же положение
движущегося автомобиля не меняется относительно, например, движущегося поезда,
то относительно Друг Друга они не движутся, а находятся в состоянии покоя.
Изменение с течением времени положения тела относительно других тел называется механическим движением.
Сидя в поезде, мы движемся относительно полотна железной
дороги,
но относительно вагона находимся в покое. Поэтому, говоря о движении тела,
обязательно указывают, относительно каких тел происходит это движение.
Наиболее часто мы будем рассматривать движение тел относительно Земли- При этом надо помнить, что и сама Земля вращается
Глава П ездимодеъ,Асу вне тел
как вокруг своей оси, так и вокруг
Солнца. Солнце, в свою очередь, движется относительно многочисленных звезд.
Движение относительно Земли
человека, автомобиля, самолета (рис. 32), колебаниа маятника, течение воды,
перемеРис. 32 щение воздуха (ветер) все это примеры механического движения.
Перемещение отдельной молекулы, даже о т дельного атома также является
механическим движением
Изменяя свое положение в пространстве, переходя из одного
места в другое, тело движется по некоторой линии, которую назы
ВтОТ траекторией движения тела.
Траектория может быть вид мой, как, например, светящийся след метеора в ночном
небе (рис. 33).
Траектория движения молекулы газа — ломаная линия (рис.
34 
Длина этой траектории — сумма длин всех отрезков.
Траектория движения лыжника, прыгающего с трамплина, кривая линия (рис. 35). Ее
длина измеряется от точки отрыва О до точки приземления Л, но не по прямой, А
следуя всем изгнбарае
Длина траектории, по которой движется тело в течение некоторого промежутка времени, называется путем.
так, длина траектории ОА — это путь, проЙденныЙ 
за
время спуска с горы (см. рис. 35). Путь обозначают буквой s.
путь это физическая величина, которую можно измерить. Часто это сделать непросто, например в случае движения молекулы.
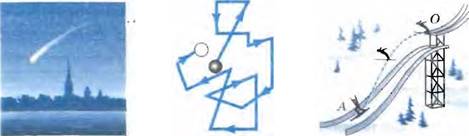
33 рис, 34 Рис.
35
Глава П.Взаимодействие ген
Основной единицей пути в Международной системе (СИ)
является метр (м). Используются и другие единицы длины: миллиметр (мм),
сантиметр (см), Дециметр (дм) и километр (км)
1 мм 0,001 м; 1 дм —0,1 м;
1 см 0,01 м;
1 км 1000 м.
Вопросы
Что называется механическим
движением? 2. Почему указывают, относительно каких тел Движется тело? З. Что
называют путем, пройденным телом? 4. Какова единица пути в СИ?
1. Приведите примеры тел, движущихся относительно Земли; неподвижных относительно Земли.
2. Почему во время снежной метели трудно указать, движется поезд или нет?
З. Какую траекторию оставляет в небе реактивный самолет?
Измерьте среднюю длину своего шага. Пользуясь этой мерой, определите путь, который вы проходите от своего дома до ближайшей остановки автобуса,
Рассмотрим движение автомобиля. Например, если автомобиль за каждую четверть часа (15 мин) проходит 20 км, за каждые полчаса (30 мин) — 40 км, за каждый час (60 мин) 80 км и т. д., то говорят, что он движется равномерно.
Если тело за любые равные промежутки временн проходит равные
пути, то его движение называют равномерным.
авномерное движение
встречается очень редко. Почти равномерно вижется Земля вокруг Солнца, проходя
приблизительно равные пути за одинаковое время, — за каждый год она делает
ровно один оборот.
Практически никогда водителю автомобиля не удается поддерживать равномерность движения по разным причинам приходится то ускорять, то замедлять езду. Движение стрелок часов (минутной и часовой) только кажется равномерным, в чем легко убедиться, наблюдая за движением секундной стрелки. Она то движется, то останавливается. Точно так же движутся и две остальные стрелки, тоЛЬКО медленно, и поэтому их рывков не видно. Молекулы газов, ударяясь друг о друга, на какое-то мгновение останавливаются, затем снова разгоняются. При следующих столкновениях, уже с другими молекулами, они снова замедляют свое движение в пространстве.
Все это примеры неравномерного движения. Так движется
поезд, отходя от станции, проходя за оДинаковьье промежут«и времени все большие
и большие пути. Лыжник или конькобежец проходят на соревнованиях равные пути за
различное время. Так движутся взлетающий самолет, открываемая дверь, падающая
снежинка.
Если тело за равные промежутки времени проходит разные пути, то
его движение называют неравномерным. •
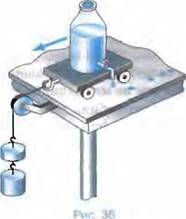
Неравномерное движение можно наблюдать на опыте. На рисунке 36 изображена. тележка с капельницеи, из которой через одинаковые промежутки времени падают катти. При движении тележки под действием привязанного к ней груза мы видим, что расстояния между следами от капель неодинаковы. А это и означает, что за одинаковые промежутки времени тележка проходит разные пути.
Какое движение называют равномерным?
2. Какое движение называют неравномерным? З. Приведите примеры неравномерного
движения.
для 7 хп»сга
Глава П.
Мы часто говорим, что одни тела движутся быстрее, другие медленнее. Например, по шоссе шагает турист, мчится автомобиль, в воздухе летит самолет. Допустим, что все они движутся равномерно, тем не менее движение этих тел будет отличаться.
Автомобиль движется быстрее пешехода, а самолет быстрее автомобиля. В физике величиной, характеризующей 6bicTpoTY движения тел, является скорость.
Предположим, что турист за 1 ч проходит 5 км, автомобиль 90 км, а самолет пролетает 850 км. Тогда говорят, что скорость туриста 5 км в час, скорость автомобиля 90 км в час, а скорость самолета 850 км в час.
Скорость при равномерном Движении тела показывает, какой путь прошло тело в еДиницу времени.
Таким образом, используя понятие скорости, мы можем теперь сказать, что турист, автомобиль и самолет движутся с различными скоростями.
При равномерном движении скорость тела остается постоянной.
Если велосипедист проезжает в течение 5 с путь, равный 25 м, то
25 м м
его скорость будет равна (5 метров в секунду).
с
Чтобы опреДелить скорость при равномерном Движении, наДо путь, пройденный телом за какой-то промежуток времени, разДелить на этот промежуток времени:
путь скорость =
время
Скорость обозначают буквой и, путь — s, время — t.
Формула для нахождения скорости будет иметь вид:
Скорость тела при равномерном движении это величина, равная отношению пути ко времени, за которое этот путь пройден.
Глава П. Взаимодействие теп
В Международной системе (СИ) скорость измеряют в
метрах на секунДу
Это значит, что за еДиницу скорости принимается скорость такого равномерного Движения, при котором за 1 секунДу тело проходит путь, равный 1 метру.
Скорость тела можно измерять также в километрах в час 
километрах
в секунДу ксм); сантиметрах в секуњДу е
Пример. Поезд, двигаясь равномерно, за 2 ч проходит путь, равный 108 км. Вычислите скорость движения поезда. Запишем условие задачи и решим ее.
|
Дано: S = 108 км |
|
|
Решение:
108 км км
Выразим скорость поезда в единицах СИ, т. е. километры переведем в метры, а часы в секунды:
км 54 000 м
54
3600 б с
Ответ: = 54 км, или 15 ! .
с
Таким образом, числовое значение скорости зависит от выбранной единицы.
Скорость, кроме числового значения, имеет и направление.
Если требуется узнать, где будет находиться через 2 ч самолет, вылетевший из Владивостока, то необходимо знать не только значение его скорости, но и ее направление.
Величины, которые, кроме числового значения (модуля), имеют
еще и направление, называют векторными.
Скорость — это векторная физическая величина.
Все векторные величины обозначают соответствующими буквами со стрелочкой. Например, скорость обозначается буквой со стрелочкой, а модуль скорости той же буквой, но без стрелочки и.
7.
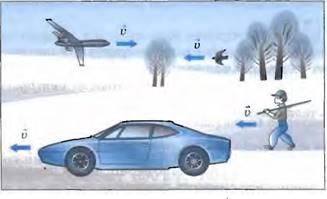
Рис. 37
На рисунках стрелка показывает направление скорости, т. е. направление движения тела (рис. 37).
Некоторые физические величины не имеют направления. Они характеризуются только числовым значением. Это путь, время, объем, длина и др. Они являются скалярными.
Если при движении тела его скорость изменяется от одного
участка
пути к другому, то такое движение является неравномерным.
Для характеристики неравномерного движения тела вводят понятие среднеи скорости.
Например, поезд от Москвы до Санкт-Петербурга идет со скоро-
км
СТЬЮ 80 Какую скорость имеют в виду? Ведь скорость поезда на
остановках равна нулю, после остановки — увеличивается, а перед следующей остановкой — уменьшается.
В данном случае поезд движется неравномерно, а значит, ско-
км
рость, равная 80 -— — это средняя скорость движения поезда.
Она определяется почти так же, как и скорость при равномерном движении .
Чтобы опреДелипгь среДнюю скорость тела
дри неравно 
мерном Движении, наДо весь пройденныи путь
разДелить на все время движенил:
S 
ср 
Следует напомнить, что только при равномерном движении отнощение ! за любой промежуток времени будет постоянно.
При неравномерном движении тела средняя скорость характеризует
движение тела за весь промежуток времени. Она не поясняет, как двигалось тело в
различные моменты времени ЭТОГО промежутка. В таблице 1 приводятся средние
скорости движения некоторых тел.
Таблица 1
Средние скорости движения некоторых тел, скорость звука, радиоволн и света, м/с
Что показывает скорость тела при
равномерном движении? 2. По какой формуле определяют скорость тела, если
известен его путь и время, за которое он пройден? З. Какова единица измерения
скорости в СИ? 4. Чем, кроме числового значения, характеризуется скорость тела?
5. Как определяют среднюю скорость при неравномерном движении?
ДОН
П.
Упражнение 4
км км м 1. Выразите скорости тел: 54 — и 36
с
км м 2. Поезд идет со скоростью 72 — Выразите его скорость в
—
с
З. Гоночный автомобиль за 10 мин проезжает путь, равный 109,2 км. Определите его среднюю скорость.
4. Лучшие конькобежцы дистанцию 1500 м пробегают за 1 мин 52,5 с. С какой средней скоростью они проходят эту дистанцию?
5. Лыжник, спускаясь с горы, проходит 50 м за 5 с. Спустившись с горы и продолжая двигаться, он до полной остановки проходит еще 30 м за 15 с. Найдите среднюю скорость лыжника за все время движения.
Если известны скорость тела и время при равномерном движении, то можно найти пройденный им путь.
Поскольку - , то путь определяют по формуле s = vt.
Чтобы опреДелить путь, пройденный телом при равномерном Движении, наДо скорость тела умножить на время его Движения.
Теперь, зная, что s = vt, можно найти время, в течение которого двигалось тело, т. е.
Чтобы опреДелить время при равномерном Движении, надо путь, пройденный телом, разделить на скорость его Движения.
Если тело движется неравномерно, то, зная его среднюю скорость движения и время, за которое происходит это движение, находят путь: S = vcpt.
Пользуясь этой формулой, можно определить время при неравномерном движении тела:
гл ва П. Взаимодействие тел
Вопросы1 . Как определить путь: а) при равномерном движении тела; б) при неравномерном движении тела? 2. Как определить время: а) при равномерном движении тела; б) при неравномерном движении тела?
Упражнение 5
1. Пользуясь таблицей 1, найдите скорости страуса, автомобиля, искусственного спутника Земли. Определите пути, пройденные ими за 5 с.
2. На велосипеде можно без особого напряжения ехать со скоростью З . На какое расстояние можно уехать за 1,5 ч?
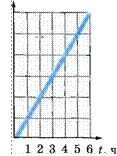
З. На рисунке 38 показан график зависимости пути
равномерного движения тела от времени (s — ось пройденных путей, t — ось
времени). По этому графику найдите, чему равен путь, пройденный телом за 2 ч.
Затем рассчитайте скорость тела.
4. График зависимости скорости равномерного движения тела от времени представлен на рисунке 39. По этому графику определите скорость движения тела. Рассчитайте путь, который пройдет тело за
5. По графикам зависимости путей от времени (рис. 40) двух тел, движущихся равномерно, определите скорости этих тел. Скорость какого тела больше?
S , км
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ппппгт |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с
50010
8
4008
6
зоо' 6
4
2004
10022
1 2 3 4 5 6 t, c 1 2 3 4 5 6 t, c
Рис, за Рис, 39
И. Взаимодпйсяпие
S 17. Инерция
Наблюдения опыты показывают, что скоросТЬ
тела сама по себе измениться не может.
Футбольный мяч лежит на поле. Ударом ноги футболист приводит его в движение. Но сам мяч не изменит свою скорость и не начнет двитаться, пока на него не подействуют другие тела. Пуля, влоэкенная в ружье, не вылетит до тех пор, пока ее не вытолкпут пороховые газы,
Таким образом, и мяч, и пуля не меняют свою скорость, пока на них не подействуют другие тела.
Футбольный мяч, катящийся по земле, останавливается из-за трения о землю.
Пуля, прошедшая сквозь фанерную мишень, уменьшает свою скорость, так как на нее подействовала мишень.
Тело уменьшает свою скорость и останавливается не само по себе, а под действием других тел.
Галилей Галилео
переыь« 
на существоо;зние яв-: пения инерции и применип 
дня 
грономическиу нс
следований Открыл 
и Юпитера . солнечнее
Под действием другого тела происходит также изменение направления скорости.
теннисный мяч меняет направление движения после удара о ракетку. Шайба ПОСЛе удара о клюшку хоккеиста также изменяет направление движения. Направление движения молекулы газа меняется при соударении ее с другой молекулой или со стенками сосуда.
Значит, изменение скорости тела (величины и направления) происходит в результате действия на него другого тела.
Проделаем опыт. Установим наклонно на столе доску. Насыплем на стол, на небольшом расстоянии от конца доски, горку песка. Помести.м на наклонную доску тележку. Тележка, скатившись с доски на стол и попав в песок, быстро останавливается (рис. 41, а). На своем пути тележка встречает препятствие в виде горки песка. Скорость тележки уменьшается
очень быстро. Ее движение неравномерно
Выровняем песок и вновь отпустим тележку с прежней высоты. Теперь тележка пройдет большее расстояние по столу, прежде чем остаНОВИТСЯ (рис. 41, б).
а) 
Рис„ 41
Ее скорость изменяется медленнее, а движение становится ближе кравномерному.
Если совсем убрать песок с пути тележки, то препятствием ее движению будет только трение о стол. Тележка до остановки пройдет еще большее расстояние (рис. 41, в). В этом случае ее скорость уменьшается еще медленнее, а движение становится еще ближе к равномерному.
Итак, чем меньше деиствие другого тела на тележку, тем дольше сохраняется скорость ее движения и тем ближе оно к равномерному.
Как же будет двигаться тело, если на него совеем не будут
действовать другие тела? Можно ли это установить на опыте? Тщательные опыты
по изучению движения тел были впервые проведены Г. Галилеем. Они позволили
установить, что если на тело не действуют другие тела 
то оно находится или в покое, или
движется прямолинейно и равномерно отнеюительно Земли.
Явление сохранеиия скорости тела при отсутствии действия ва него других тел называют инерцией.
(Инерция от лат. инерциа — неподвижность, бездеятельность.)
Таким образом, движение тела при отсутствии действия на него
других тел называют движением по инерции.
Например, пуля, вылетевшая из ружья, продолжала бы двигатьсл, сохраняя свою скорость, если бы на нее не действовало другое
П. Взаимодействие
тело — воздух. Вследствие этого скорость пули уменьшается. Велосипедист,
перестав работать педалями, продолжает двигаться. Он смог бы сохранить скорость
своего движения, если бы на велосипед не действовало трение. Следовательно,
скорость его уменьшается и он 
танавливается.
Итак, если на тело не действуют другие тела, то оно движется с постоянной скоростью.
Вопросы1. В результате чего меняется скорость тела? Приведите
примеры. 2. Какои опыт показывает, что изменение скорости тела происходит при
уменьшении препятствий? З, Что называется инерцией 7 4. Как движется
тело, если на него не действуют другие тела? 
Вам уже известно, что при неравномерном движении скорость
тела меняется с течением времени. Изменение скорости тела происходит под
действием другого тела.
Проделаем опыт. К тележке прикрепим упругую пластинку. Затем изогнем ее и свяжем нитью. Тележка относительно стола находится в покое (рис. 42, а). Станет ли двигаться тележка, если упругая пластинка выпрямится?
Для этого пережж м нить. Пластинка выпрямится. Тележка же остается на прежнем месте (рис. 42, б).
Затем вплотную к согнутой пластинке поставим еще одну такую же тележку (рис. 43, а). Вновь пережжем нить. После этого обе те-
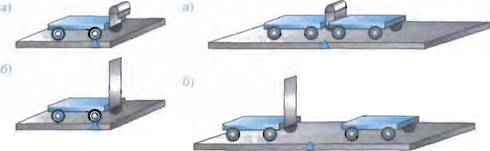
Рис. 42 Рис. аз
П. теп
лежки приходят в движение относительно стола. Они разъезжаются в разные стороны (рис. 43, б).
Чтобы изменить скорость тележки, понадобилось второе тело. Опыт показал, что скорость тела меняется только в результате действия на него другого тела (второй тележки). В нашем опыте мы наблюдали, что в движение пришла и вторая тележка. Обе стали двигаться относительно стола.
Тележки Действуют друг на Друга, т. е. они взаимоДействуют. Значит, действие одного тела на другое не может быть односторонним, оба тела действуют друг на друга, т. е. взаимодействуют.
Мы рассмотрели самый простой случай взаимодействия двух тел. Оба тела (тележки) до взаимодействия находились в покое относительно стола и относительно друг друга.
Например, пуля также находилась в покое относительно ружья перед выстрелом. При взаимодействии (во время выстрела)
пуля и ружье движутся в разные стороны. Происходит явление отДачи.
Если человек, сидящий в лодке, отталкивает от себя другую лодку, то происходит взаимодействие. Обе лодки приходят в движение (рис. 44).
Если же человек прыгает с лодки на берег, то лодка отходит в сторону, противоположную прыжку (рис. 45). Человек подействовал на лодку. В свою очередь, и лодка действует на человека. Он приобретает скорость, которая направлена к берегу.
Итак, в результате взаимодействия оба тела могут изменить свою скорость.
1 . Какие опыты показывают, что тела приходят в движение при
взаимодействии с другими телами? 2. Какие примеры показывают, что при
взаимодействил меняются скорости обоик тел? З. Опишите явление взаимодействия
тел на примере выстрела из ружья (винтовки).
S 19. Масса тела. Единицы массы
при взаимодействии двух тел скорости первого и второго тела всегда меняютея.
Одно тело после взаимодействия приобретает скорость, которая может значительно отличаться от скорости другого тела. Например, после выстрела из лука скорость стрелы гораздо больше скорости, котогууо приобретает тетива лука после взаимодействия.
рис,
Почему так происходит? Проведем опыт, описанный в S 18.
Только теперь возьмем разные тележки (рис. 46, а). После того Как нить
пережгли, тележки начинают разъезжаться с различными скоростями (рис. 46, б),
Про тележку, которая после взаимодействия приобрела меньшую скорость, говорят,
что она массивнее другой тележки. 
нее больше масса. Тележка, которая после
взаимодействия движется с большей скоростью, имеет меньшую массу. Значит,
тележки имеют разные массы.
Скорости, которые приобрели тележки в результате
взаимодействия, можно измерить. По этим скоростям сравнивают массы взаимодействующих
тележек.
П, тел
приемер. Скорости тележек до взаимодействия равны нулю. Пос-
м
ле взаимодействия скорость одной тележки стала равна 10 , а ско-
с
Рость другой 20 — . Поскольку скорость, которую приобрела вторая тележка, в 2 раза больше скорости первой, по и ее масса в 2 раза меньше массы первой тележки.
Если после взаимодействия скорости изначально покоившихся
тележек одинаковы, то и их массы одинаковы. Так, в опыте, изображенном на
рисунке 42, после взаимодействия тележки разъезжаются с равными скоростями.
Следовательно, их массы были одинаковы. Если после взаимодействия тела
приобрели разные CkOpocти, то их массы различны.
Во сколько раз скорость первого тела больше (меньше) скорости второго тела, во столько раз масса первого тела меньше (больше) массы второго.
Чем меньше меняется скорость тела при взаимодействии, тем 66.тьшую массу оно имеет. Такое тело называют более инертным.
Чем больше меняется скоросгь тела при взаимодействии, тем
меньшую массу оно имеет. Это тело мепее инертно.
Это значит, что для всех тел характерно свойство по-разному менять свою скорость при взаимодействии. Это свойство тела называют инертностью.
масса тела это физическая величина, которая характеризует его инертность.
Следует знать, что любое тело: Земля, человек, книга и. т.
д. 
обладает массой.
Массу обозначают буквой т.
За единицу массы в СИ принят килограмм (1 кг). 
Килограмм
— это масса эталона, Эталон изготов.лен из сплава двух металлов: платины и
иридия. Международный эталон килограмма хранится в г. Севре (близ Парижа) (рис.
47). С международного эталона сделано более 40 точнейших копий, разосланных в
разные страны. Одна из копий междунаРодного эталона килограмма имеется в нашей
стране, в Институте метрологии им, Д. И. Менделеева в Санкт-Петербурге 47
Взаимодействие тел
На практике используют и другие единицы массы: тонна (т), грамм (г), миллиграмм (мг).
1 т — 1000 кг (10 3 кг); 1 г — 0,001 кг (10 З кг);
1 кг 1000 г (10 3 г); 1 мг = 0,001 г (10—3 г);
1 кг 1 ООО ООО мг (10 6 мг); 1 мг = 0,000001 кг (10-6 кг).
В дальнейшем при изучении физики понятие массы будет раскрыто глубже.
Вопросы 
1. Как проводился опыт с двумя взаимодействующими тележками? 2. Каким образом можно установить, что масса одной из тележек больше, а другой меньше? З. Какова единица массы в СИ? 4. Какие единицы массы также используют на практике?
Упражнение 6
1.Выразите в килограммах массы тел: З т; 0,25 т; ЗОО г; 150 г; 10 мг.
2.Из неподвижной лодки, масса которой 80 кг, прыгает на берег мальчик. Масса мальчика 40 кг, скорость его при прыжке 2 — . Какую скорость приобрела лодка?
З. Из винтовки вылетает пуля со скоростью 700 — . Винтовка при
отдаче приобретает скорость 1,6 . Определите массу винтовки, если масса пули 10 г.
Для того чтобы измерить массу тела, можно использовать метод, описанный в S 19.
Сравнивая скорости, приобретенные телами при взаимодействин, определяют, во сколько раз масса одного тела больше (или меньше) массы другого. Измерить массу тела этим способом можно, если масса одного из взаимодействующих тел известна. Таким способом определяют в науке массы небесных тел, а также молекул и атомов.
П. геп
На практике массу тела можно узнать с помощью весов. Весы бывают 2 различного типа: учебные, медицин- 1 ские, аналитические, аптекарские, электронные и др.
На рисунке 48 изображены учебные весы. Главной частью таких весов является коромысло (1). К середине коромысла прикреплена стрелка — указа- з тель (2), которая движется вправо или влево. К концам коромысла подвешены чашки (З). При каком условии весы будут находиться в равновесии?
|
Поместим на чашки весов тележки, |
|
|
которые применялись в опыте (см. S 18). |
Рис, 48 |
Поскольку при взаимодействии тележки
приобрели одинаковые скорости, то мы выяснили, что их массы одинаковы. Следовательно, весы будут находиться в равновесии. Это значит, что массы тел, лежащих на чашках весов, равны друг другу.
Теперь на одну чашку весов поместим тело, массу которого необходимо узнать. На другую будем ставить гири, массы которых известны, до тех пор, пока весы не окажутся в равновесии.
Следовательно, масса взвешиваемого тела будет равна общей мас-
се гирь.
При взвешивании используется специальный набор гирь (рис. 49).
Вниепдвиствие теп
Различные весы предназначены для взвешивания разных тел, как очень тяжелых, так и очень легких, Так, например, с помощью вагонных весов можно определить массу вагона от 50 до 150 т. Массу комага, равную 1 мг, можно узнать с помощью аналитических весов.
Вопросы
Как определить массу тела по
взаимодействию его с другим телом известной массы? 2. Каково условие равновесия
учебных весов? 3. Как можно определить массу тела при помощи весов?
S 21. Плотность вещества
Тела, окружающие нас, состоят из различных веществ: дерева, железа, резины п т. д.
Масса любого тела зависит не только от его размеров, но и от того, из какого вещества это тело состоит. При этом тела, имеющие равные оббемы, но изготовленные из разных веществ, имеют
разные массы.
Взвесим два цилиндра
равного объема, но изготовленные из разных веществ. Например, один цилиндр
алюминиевый, а другой — свинцовый, Опыт показывает, что масса алюминиевого цилиндра
почти в 4 раза меньше массы свинцового (рис. 50).
В то же время тела с равными массами, изготовленные из разных веществ, имеют разные оббемы.
Так, железный брус массой 1 т занимает объем 0,13 мз лед массой объем Риг 50 1 Д м з . Объем льда почти в 9 раз больше объема железного бруса (рис. 51).
Это объясняется тем, что разные вещества могут иметь
разную плотность.
Отсюда следует, что тела объемом 1 м каждое, изготовленные из
разных веществ, имеют розные массы. Так, алюминий объемом 1 м з имеет
массу 2700 кг, свинец такого же объема (1 м ) имеет массу 11 ЗОО кг.
 |
плотность показывает, чему равна
масса вещества, взятого в объеме 1 мз (или 1 смЗ).
Сак эке можно найти плотность данного вещества?
пример. Мраморная плита имеет объем 2 мз , а ее масса равна 5400 кг. Определите плотность мрамора.
Известно,
что мрамор объемом 2 мз имеет массу 5400 к г. Следо
вате.льно, 1 м з мрамора будет иметь массу в 2 раза меньшую, т. е. 5400 : 2 = 2700 кг. Таким образом, плотность мрамора будет равна
2700 кг на 1 м з .
и,гак, если известна масса тела и его объем, можно определить плотность.
 |
пл[ОТНОСТЬ — это
физическая величина, которая равна отношенито массы тела к его объему:
масса плотность
 |
Обозначим величины, входящие в это выражение, буквами: плотность вещества р (греч. буква «ро»), масса тела — т, его объем У.
тогда
получим формулу для вычисления плотности:
Р
Единицей плотности
вещества в СИ является килограмм на КУ
кг биш?ский
метр 1
м лотность вещества выражают очень часто и в граммах на ку-
г
бическ,ий
сантиметр 1 (рис. 52).
З
см
 |
 |
 |
 |
113,6 д— 7,80,0013
з СМ см см см
ВОДИ Ртуть Железо Воздух
Рис 52
Глава П. Взаимолеиствие теп
кг
Если плотность вещества выражена в —-j , то ее можно перевести
м в следующим образом.
см
кг
Пример. Плотность серебра 10
500 Выразите ее в
м см
Вначале переведем килограммы в граммы, а затем кубические метры в кубические сантиметры.
10 500 кг 10 500 ООО г (или 10,5 • 10 6 г), 1 м з = 1 ООО ООО см З (или 10 6 см 3 ).
кг 10,5 • 10 6 г
Тогда р 10 500 мЗ 106 см
= 10,5 см
Следует помнить, что плотность одного и того же вещества в твердом, жидком и газообразном состояниях различна.
кг кг
Так, плотность льда равна 900 з, воды 1000 з , водяного пара
м м кг
0,590
м
Ниже приведены таблицы плотностей некоторых твердых тел, жидкостей и газов.
Плотности некоторых твердых тел
(при норм. атм. давл., t = 20 ос)
П. теп
Окончание табл. 2
|
Твердое тело |
р, кг/м з |
г/смЗ |
Твердое тело |
р, кг;мз |
р. г/смЗ |
|
Олово |
7300 |
|
Парафин |
900 |
0,90 |
|
Цинк |
7100 |
7,1 |
лед |
900 |
0,90 |
|
Чугун |
7000 |
|
Дуб (сухой) |
700 |
о, то |
|
Корунд |
4000 |
|
Сосна (сухая) |
400 |
0,40 |
|
Алюминий |
2700 |
|
Пробка |
240 |
О 24 |
Плотности некоторых жидкостей (при норм. атм. давл ., t = 20 ОС)
Плотности некоторых газов (при норм. атм. давл., t = 20 ос)
Вопросы
Как можно найти плотность вещества? 2.
Какой буквой обозначают плотность? З. Какова единица плотности в СИ? 4. Какие
еще единицы плотности вам известны?
Упражнение 7
таблице 2 дана плотность редкого металла
осмия, равная
кг
22 600 . Что это означает? м
2. Пользуясь таблицами плотностей (табл. 2, З), определите, плотность какого вещества больше: цинка или •серебра; бетона или мрамора; бензина или спирта,
|
2,5 см |
еме 100 смЗ . Определите плотность древе- |
|
Рис. 53 |
см м |
З. Три кубика -— из
мрамора, льда и латуни -— имеют одинаковый объем. Какой из них имеет ббльшую
массу, а какой — 1 см меньшую?
4. Самое легкое дерево бальза. Масса древесины этого дерева равна 12 г при объ0,5 см
5. Кусочек сахара имеет размеры: а 2,5 см, Ь = 1 см, с 0,5 см (рис. 53). Его масса равна 0,32 г. Определите плотность сахара. Проверьте полученный результат по таблице 4.
Знать плотность веществ очень важно для различных практических целей. Инженер, создавая машину, заранее по плотности и объему материала может рассчитать массу будущей машины. Строитель может определить, какова будет масса строящегося здания.
Следовательно, зная плотность вещества и объем тела, всегда можно определить его массу.
Поскольку плотность любого вещества определяют по формуле
р Г , то отсюда можно найти массу, т
П, теп
плотность,
наДо плотность умножить на объем,
Пример. Определите массу стальной детали объемом 120смЗ.
По таблице 2 находим, что плотность стали равна 7,8 Запи-
см шем условие задачи и решим
|
Дано: 120 см р- 7,8—з см |
|
|
Решение:
= 120 см з • 7,8 з 936 г.
см
Ответ: т = 936
 |
Чтобы выч.цслцть оббем тела, если известна его масса и плотность, наДо массу разДелить на плотность.
Пример. Масса подсолнечного масла, заполняющего бутылку, равна 930 г. Определите объем бутылки.
По таблице З находим, что плотность
подсолнечного масла равна
0,93 —
см
Запишем условие задачи и решим ее.
|
Дано: р = 0,93 см т |
|
|
Решение:
р
930
0,93 смз 1000 см
Ответ: л.
Глава П. тел
Для определения объема пользуются формулой, как правило, в тех случаях, когда объем сложно найти с помощью простых измерений.
1. Как вычисляется масса тела по его плотности и объему? 2. По какой формуле можно определить объем тела?
Упражнение В
1. Какова масса 0,5 л спирта, молока, ртути?
2. Определите объем льдинки, масса котороЙ 108 г.
З. Сколько килограммов керосина входит в пятилитровую бутыль?
4. Грузоподъемность лифта З т. Сколько листов железа можно погрузить в лифт, если длина каждого листа З м, ширина 60 см и толщина 4 мм?
Возьмите баночку из-под меда. Рассмотрите внимательно этикетку. Найдите на ней, какова масса меда и объем баночки. Затем рассчитайте плотность меда. Полученный результат проверьте по таблице З.
Каждый из нас постоянно встречается с различными случаями
действия тел друг на друга. В результате взаимодействия скорость движения
какого-либо тела меняется. Вам уже известно, что скорость тела меняется тем
больше, чем меньше его масса.
Рассмотрим некоторые примеры, подтверждающие это.
Толкая руками вагонетку, мы можем привести ее в движение (рис. 54). Скорость вагонетки меняется под действием руки человека.
П, тел
Кусочек железа, лежащий на пробке, опущенной в воду, притягивается магнитом (рис. 55). Кусочек железа и пробка изменяют свою скорость под действием магнита.
Действуя на пружину рукой, можно ее сжать. Сначала в движение приходит конец пружины. Затем движение передается осталь-
|
ным ее частям. Сжатая пружина, распрямляясь, может, например, привести в движение шарик (рис. 56). |
Рис. 55 |
При сжатии пружины
действующим телом была рука человека. Когда пружина распрямляется, действующим
телом является сама пружина. Она приводит в движение шарик.
Ракеткой или рукой
можно остановить или изменить направление движения летящего мячика (рис. 57).
Во всех приведенных примерах тело под
|
действием другого тела приходит в движение, останавливается или изменяет направление своего движения. |
|
Таким образом,
скорость тела меняется при взаимодействии его с другими телами.
Часто не указывают, какое тело и как действовало на данное тело. Просто говорят, что на тело Действует сила или к нему приложена сила. Под действием силы тело меняет свою скорость.
Сила, действующая на тело, может не только изменить скорость всего тела, но и от-
Рис.“, 57
дельных его частей.
Например,
если надавить пальцами на ластик, то он сожмется, изменит свою форму (рис. 58).
В таких случаях говорят, что тело Деформируется.
Деформацией называется любое изменение формы и размера тела.
зава тел
Приведем другой пример. Доска, лежащая на опорах, прогибается, если на нее садится человек (рис. 59). Серединадоски перемещается на большее расстояние, чем края.
Под действием силы скорость различных тел за одно и то же время может изменяться одинаково. Для этого необходимо к этим телам приложить разные силы.
Так, чтобы привести в движение грузовую машину, необходима
ббльшая сила, чем 
Рис. 59 для легкового автомобиля.
Следовательно, числовое значение силы может быть различным: ббльшим или
меньшим. Что же такое сила?
Сила является мерой взаимоделствия тел.
Сила — физическая величина, значит, ее можно измерить.
Сила, каж и скорость, является векторнои величиной, Она характеризуется не только числовым значением, но и направлением. Сила обозначается буквой со стрелочкой, а ее модуль той же буквой Е, но без стрелочки.
Когда говорят о силе, важно указывать, к какой точке тела приложена действующая на него сила.
На чертеже силу изображают в виде отрезка прямой со стрелкой на конце (рис. 60). Начало отрезка —- точка А есть точка приложения силы. Длина отрезка условно обозначает в определенном масштабе модуль силы.
Итак, результат действия силы на тело зависит от ее модуля,
направления и точки приложения.
1 . В результате чего может меняться скорость тела? Приведите
при 
меры. 2. Что такое сила? З. От чего зависит результат действия силы на 
тело? 4. Как изображают силу на
чертеже?
Выпустим камень из рук — он упадет на землю (рис. 61). То
эке самое произойдет и с любым другим телом. Белл мяч бросить в горизонтальном
направлении, то он не летит прямолинейно и равномерно. Его траекторией будет
кривая линия (рис. 62).
Искусственный спутник, запущенный с Земли, так же летит не по прямой. а движется вокруг Земли (рис, 63).
В чем же причина наблюдаемых явлений? На эти тела действует сила — это сила притяжения к Земле. Вследствие притяжения к Земле падают тела, поднятые над Землей, а потом отпущенные.
Листья деревьев опускаются на Землю, пото
му что Земля
притягивает их. Благодаря притя- 
жению к Земле течет вода в реках. Рис.
Рис. 62
Земля притягивает к
себе все тела: дома, людей, Луну, Солнце, воду в морях и океанах и т, д. В свою
очередь, и Земля притягивается к этим телам.
Притяжение существует не только между Землей и телами, находящимися на ней. Все тела притягиваются друг к другу. Притягиваются между собой Луна лт Земля. Притяжение Земли к Луне вызывает приливы и отливы воды. Огромные массы воды поднимаются в океанах и морях дважды в сутки на много метров. Вам Рис, 63
Глаза П. теп
хорошо известно, что Земля и другие планеты движутся вокруг Солнца, притягиваясь к нему и друг к другу.
Притяжение всех тел Вселенной друг к другу называется всемирным тяготением.
Английский ученый Исаак Ньютон первым доказал и установил закон всемирного тяготения.
Согласно этому закону, силы притяжения межДу телами тем больше, чем больше массы этих тел. Силы притяжения межДу телами уменьшаются, если увеличивается расстояние межДу ними.
Для всех живущих на Земле особенно важное значение имеет сила притяжения тел к Земле.
Сила, с которой Земля притягивает к себе тело, называется силой тяжести.
Сила тяжести обозначается буквой F с индексом: Етяж. Она всегда направлена вертикально вниз.
Земной шар немного сплюснут у полюсов, поэтому тела,
находящиеся около полюсов, расположены немного ближе к центру Земли. В связи с
этим сила тяжести на полюсе немного больше, чем на экваторе или на других
широтах. Сила тяжести на вершине горы несколько меньше, чем у ее подножия. 
Сила тяжести пряло пропорциональна массе этого тела.
Если сравнивать два тела с разной массой, то про тело с большей массой говорят: оно тяжелее. Тело с меньшей массой будет легче.
Во сколько раз масса одного тела больше массы другого тела, во столько же раз и сила тяжести, действующая на первое тело, больше силы тяжести, действующей на второе. Когда массы тел одинаковы, то одинаковы и действующие на них силы тяжести.
Вопросы1. Почему тела, брошенные горизонтально, падают на землю? 2. Какую силу называют силой тяжести? Как ее обозначают? З. Почему сила тяжести на полюсах Земли несколько больше, чем на экваторе и других широтах? 4. Как зависит сила тяжести от массы? 5. Как направлена сила тяжести?
Вам уже известно, что на все тела, находящиеся на Земле, действует сила тяжести. В результате действия силы тяжести на Землю падает подброшенный камень, выпущенная из лука стрела, снежинки, листья, оторвавшиеся от веток, и др.
На книгу, лежащую на столе, также действует сила тяжести, но книга не проваливается сквозь стол, а находится в покое. Подвесим тело на нити. Оно падать не будет.
Почему же покоятся тела, лежащие на опоре или подвешенные на нити? По-видимому, сила тяжести уравновешивается какой-то другой силой. Что же это за сила и как она возникает?
Проведем опыт. На середину горизонтально расположенной до-
ски поставим
гирю (рис. 64). Под действием силы тяжести гиря начнет двигаться вниз и прогнет
доску, т. е. доска деформируется. При этом возникает сила, с которой опора
(доска) действует на тело, расположенное на ней. Из этого опыта можно сделать
вывод, что на гирю, кроме силы тяжести, направленной вертикально вниз,
действует другая сила. Эта сила направлена вертикально вверх. Она и уравно-
|
весила силу тяжести. Эту силу называют силой |
рис. 64 |
|
упругости. Итак, сила, возникающая в теле в ре- |
|
зультате его
деформации и стремящаяся вержуть тело в исходное положение, называется силой
упругости.
Силу упругости обозначают буквой F с индексом: Fупр•
Чем сильнее прогибается опора (доска), тем больше сила упругости. Если сила упругости становится равной силе тяжести, действующей наупр тело, то опора и тело останавливаются.
Теперь подвесим тело на нити. Нить (подвес) растягивается (рис. 65). В нити (подвесе), такжетяж как и в опоре, возникает сила упругости. При растяжении подвеса сила упругости увеличивается. Если сила упругости будет равна силе тя- Рис. 05
жести, то растяжение прекращается. Сила упругости возникает только при деформации тел. Если исчезает деформация тела, то исчезает и сила упругости.
Деформации бывают разных видов: растяжения, сжатия, сдвига, изгиба, кручения.
С двумя видами деформации вы уже познакомились — сжатия (см. рис. 56) и изгиба (см. рис. 64). Более подробно эти и другие виды деформации вы изучите в старших классах.
Теперь попытаемся выяснить, от чего зависит сила упругости.
Английский ученый Роберт Гук, современник Ньютона, установил, как зависит сила упругости от деформации.
 |
Если к свободному
концу шнура подвесить чашку с гирькой, то шнуР удлинится. Его длина станет
равной L. Удлинение шнура Al (Д — гре 
буква «дельта») можно найти так:
Если менять гирьки на чашке, то будет меняться и длина шнура, а значит, его удлинение (деформация) М.
Опыт показал, что моДуль силы упругости при растяжении (или сжатии) тела прямо пропорционален изменению длины тело.
В этом и заключается закон Гука. Записывается закон Гука следующим образом:
р = КМ,
где — удлинение тела (изменение его длины), Ь — коэффициент пропорциональности, который называется жесткостью.
Жесткость тела зависит от формы и размеров, а также от материала, из которого оно изготовлено.
Закон Гука справедлив только для упругой деформации. Если после прекращения действия сил, деформирующих тело, оно возвращается в исходщое положение, то деформация является упругой.
Более подробно закон Гука и виды деформаций вы изучите в старших классах.
Вопросы1. Когда возникает сила упругости? 2. Что называют деформацией тела? З. Какие виды деформаций вы знаете? 4. Как формулируетсязакон Гука? 5. Как записывается закон Гука?
В повседневной жизни очень часто используется понятие «вес» . Попытаемся выяснить, что же это за величина. В опытах, когда тело ставили наопору, сжималась не только опора, но и тело, притягиваемое Землей.
Деформированное, сжатое тело давит на опору с силой, которую
называют весом тела.
Если тело подвешено на нити (подвесе), то растянута не только нить (подвес), но исамо тело.
Вес тела это сила, с которой тело вследствие притяженля к Земле действует на опору илл подвес.
Вес тела — ато векторная физическая вели-
|
чина и обозначается буквой Р. Однако следует помнить, что сила тяжесптц |
ТЯЗ< |
|
|
|
|
|
|
Р |
|
приложена к тепу, а вес приложен к опоре или поДвесџ (рис. 67, а, б).
кли тело и опора
неподвижны или движутся равномерно и прямолинейно, то вес тела по своему
числовому значению равен силе тяжести, т. е.
тяж•
Следует помнить, что сила тяжести возникает вследствие взаимодействия тела и Земли. Рис (57
Глава П. Взаимодействие тел
Вес тела возникает в результате взаимодействия тела и опоры (подвеса). Опора (подвес) и тело при этом деформируются, что приводит к появлению силы упругости.
Вопросы1. Что называют весом тела? 2. Чем отличается вес тела от силы тяжести?
S 27. Единицы силы.
Вам уже известно, что сила — это физическая величина. Она кроме числового значения (модуля) имеет направление, т. е. это векторная величина.
Силу, как и любую физическую величину, можно измерить, т. е. сравнить с силой, принятой за единицу.
Единицы физических величин всегда выбирают условно. Так, за единицу силы можно было принять любую силу. Например, можно выбрать в качестве единицы силы силу упругости какой-либо пружины, растянутой до определенной длины. За единицу силы можно принять и силу тяжести, действующую на какое-нибудь тело.
Вы знаете, что сила является причиной изменения скорости тела. Именно поэтому за еДиницу силы принята сила, которая за
м время 1 с изменяет скорость тела массой 1 кг на 1 
с
В честь английского физика И. Ньютона эта единица названа ньютоном (1 Н).
Часто применяют и другие единицы — килоньютон (кН), миллиньютон (мН):
1 кн = 1000 н, 1 н- 0,001 кн.
Попытаемся определить величину силы в 1 Н. Установлено, что
1 Н приблизительно равен силе тяжести, которая действует на тело
массой кг, или более точно кг (т. е. около 102 г).
10 9,8
Необходимо помнить, что сила тяжести, действующая на тело, зависит от географической широты, на которой находится тело. Сила тяжести меняется и при изменении высоты над поверхностью Земли.
Глава П. Взаимодеиствие теп
Если единицей силы является 1 Н, то как рассчитать силу тяжести, которая действует на тело любой массы?
Известно, что, во сколько раз масса одного тела больше массы другого тела, во столько же раз сила тяжести, действующей на первое тело, больше силы тяжести, действующей на второе тело. Таким
1 образом, если на тело массой кг действует сила тяжести, равная
9,8
2
1 Н, то на тело кг будет действовать сила тяжести, равная 2 Н. 9,8
5 5,5
На тело массой кг —- сила тяжести, равная 5 Н, кг 5,5 н
9,8 9,8
9,8 и т. д. На тело массой кг будет действовать сила, равная 9,8 Н.
9,8 9,8
Поскольку кг = 1 кг, то на тело массой 1 кг Действует 9,8 сила тяжести, равная 9,8 Н. Значение силы тяжести, действуюн
 |
кг
Значит, если на тело массой 1 кг действует сила, равная 9,8 Н, то на тело массой 2 кг действует сила, в 2 раза ббльшая. Она равна 19,6 Н. На тело массой З кг в З раза ббльшая и равная 29,4 Н ит. д.
Таким образом, чтобы определить силу тяжести, действующую
на тело любой массы, необходимо 9,8 — умножить на массу этого кг
тела.
Массу тела выражают в килограммах. Тогда получим, что
н
= 9,8 — 
кг
н
Величину 9,8 обозначают буквой g, и формула для силы тякг жести будет иметь вид:
тяж = gm,
где т — масса тела, g — называют ускорением свободного паДения.. (Понятие ускорения свободного падения будет вами изучено в 9 классе.)
При решении задач, когда не требуется
большой н точности, g 9,8 округляют до g = 10 
кг вам уже известно, что Р тяже если
тело и опора неподвижны или движутся равномерно и прямолинейно. Следовательно,
вес тела можно определить по формуле:
тяж Р
= gm.
|
Дано: т = 1,5 кг н 10— кг |
|
Р тяж |
Пример, На
столе стоит чайник с водой массой 1,5 кг. Определите сильт тяжести и
вес чайника. Покажите эти силы на рисунке68.
Решение:
ТЯЖ STlT7,
Р gm, н тяж - Р = 10 • кг— 15 Н
кг
Ответ:
15 Н.
Теперь изобразим силы графически. Выберем масштаб. Пусть З Н будет равен отрезку длиной 0,3 см, Тогда силу в 15 Н необходимо начертить отрезком длиной 1,5 см.
Следует учитывать, что сила тяжести действует на тело, а значит, приложена к самому телу. Вес действует на опору или подвес,
е. приложен к опоре, в нашем случае к
столу.
Вопросы
1 Что значит измерить какую-либо силу? 2. Что принято за единицу си
З. Как рассчитать силу тяжести, действующую на тело любой массы?
4. ю какой формуле можно определить вес тела?
Упражнение 9
1. Определите силу тяжести, действующую на тело массой 3,5 кг;
400 г: т;
60 г
2. Найдите вес тела, масса которого 5 кг, ЗОО г.
З. Вес человека 700 Н. Определите его массу, Сделайте рисунок и покажите вес тела.
Глава П. Взаимодеистеие теп
4. Выразите в ньютонах следующие силы: 240 кН, 25 кН, 5 кН, 0,2 кн.
5.
На столе стоит телевизор массой 5 кг. Определите силу тяжести и
вес телевизора. Изобразите ати силы на рисунке.
S 28. Динамометр
На практике часто приходится измерять силу, с которой одно тело действует на другое. Для измерения силы используется прибор, который называется динамометр (от греч. Динамис — сила, метрео измеряю).
Динамометры бывают различного устройства. Основная их часть стальная пружина, которой придают разную форму в зависимости от назначения прибора. Устройство простейшего динамометра основывается на сравнении любой силы с силой упругости пружины.
Простейший динамометр можно изготовить из пружины
с двумя 
крючками, укрепленной на дощечке (рис, 69,
а). К нижнему концу пружины прикрепляют указатель, а на доску наклеивают
полоску
белой бумаги.
Отметим на бумаге черточкой положение указателя при
нерастянутой пружине. Эта 
отметка будет нулевой отметкой (см. рис.
69, а),
Затем к крючку будем подвешивать груз
1 массой кг, т. е. 102 г. На этот груз будет 9,8 действовать сила тяжести, равная 1 Н. Под действием этой силы (1 Н) пружина растянется, указатель опустится вниз. Его новое положение отмечаем на бумаге и ставим цифру 1 (рис. 69, б). После чего подвешиваем груз массой 204 г и ставим цифру 2. Это означает, что в таком положении сила упругости пружины равна 2 Н. Подвесив груз массой 306 г, наносим метку З ит. д.
Для того чтобы измерить десятые доли ньютона, нужно нанести деления — 0,1; 0,2; Рис. 60
З Физии. Учееемк для 7 «пасся
Глава П. Взаимоде•јствие теп
0,3; 0,4 и т. д. Для этого расстояния
между отметками О и 1; 1 и 2; 2 и З; З и 4 и далее делят на десять равных
частей. Так можно сделать, учитывая, что сила упругости пружины F увеличивается
во столько раз, во сколько увеличивается ее удлинение М. Это следует из закона
Гука: Fуп . р КМ, т. е. сила упругости тела при растяжении прямо
пропорциональна изменению длины тела.
Проградуированная пружина и буРис. 70 дет простейшим динамометром.
С помощью динамометра измеряют не только силу тяжести, но и другие силы (сила упругости, сила трения и т. д.). Так, например, для измерения силы различных мышечных групп человека используют медицинские динамометры. Для измерения мускульной силы руки при сжатии кисти в кулак применяют ручной динамометр силомер (рис. 70).
Применяют также ртутные, гидравлические, электрические и другие динамометры.
В последнее время тцироко применяются электрические динамометры. Они состоят из датчика, который преобразует деформацию в электрический сигнал.
Для измерения больших сил, таких, например, как тяговые усилия тракторов, тягачей, локомотивов, морских и речных буксиров, используют специальные тяговые динамометры (рис. 71). Ими можно
Рис. 71
Глдеа П. ВЗАИМОЛР'АСТНИП мен
Вопросы
1 . Как называют прибор для измерения силы? 2. Как изготовить простейший динамометр? З. Как нанести на шкалу динамометра деления, соответствующие 0,1 Н? 4. Какие типы динамометров вам ИЗВеСТНЬР
Упражнение 10
1. Определите цену деления каждого прибора и силу тяжести, действующую на каждый груз (рис. 72).
2. Чему равен вес каждого груза (см. рис. 72)? Укажите точку его приложения?
З. По рисунку 73 определите, с какой силой растягивается каждая пружина под действием подвешенного к ней груза (масса одного
груза 102 г).
Рис. 72 Рис. 73
з-
S 29. Сложение двух сил, направленных по одной прямой.
Равнодействующая сил
В большинстве случаев, с которыми мы встречаемся в жизни, на тело действует не одна, а сразу несколько сил. Так, например, на парашютиста, спускающегося на землю, действуют сила тяжести и сила сопротивления воздуха. На тело, висящее на пружине, действуют две силы: сила тяжести и сила упругости пружины, вкаждом подобном случае можно заменить несколько сил, в дейСтвИТеЛЬНОСТИ приложенных к телу, одной силой, равноценной по своему Действию этим сЦл0М.
Сила, которая производит на тело такое же действие, как не
сколько
одновременно действующих сил, называется равнодействующей этих сил.
найдем равнодействующую двух сил, действующих на тело по одной прямой в одну сторону.
Обратимся к опыту. К
пружине один под другим подвесим два груза массой 102 и 204 г, т. е. весом 1 и
2 Н (рис, 74, а), Отметим 
ину, на которую растянулась пружина.
Снимем эти грузы, заме-
Рис, 74 75
Глава П. ВЗаимодвйСтние теп
ним одним грузом, который растягивает пружину на такую же длину (рис. 74, б). Вес этого груза оказывается равным З Н.
Из опыта следует, что: равнодействующая сил, направленных 
по
одной прямой в одну сторону, направлена в ту же сторону, а ее модуль равен сумме
модулей составляющих сил.
На рисунке 75 равнодействующая сил, действующих на тело, обозначена буквой R, а слагаемые силы буквами и 172. В этом случае
Выясним теперь, как найти равнодействующую двух сил, дейст
вующих на тело по одной прямой в
разные стороны. Тело — столик динамометра. ПОСТ&ВИМ на столик гирю весом 5
Н, т. е. подействуем на него силой 5 Н, направленной вниз (рис. 76, а).
Привяжем к столику нить и подействуем на него с силой, равной 2 Н (рис. 76, б),
направ
ленной вверх. Тогда динамометр покаэкет силу З Н. Эта сила есть
равнодействующая двух сил.• 5 ни 2 н.
Итак, равнодействующая двух сил, направленных по одной прямой в противоположные стороны, направлена в сторону большей по модулю силы, а ее м дуль равен разности модулей составляющих сил(рис. 77):
Если к телу приложены две равные и направленные противоположно силы, то равнодействующая этих сил равна нулю. Например,
а) 0)
Рис. 76 ряс, 7Т
Глава П. Влавиодевс:твьзе теп
если в нашем опыте за конец нити потянуть силой 5 Н, то стрелка динамаометра установится на нулевом делении. Равнодействующая двух сил в этом случае равна нулю:
Тело под действием двух равных и противоположно направленных сил будет находиться в покое или двигаться равномерно и прямолинейно.
Например, в покое находится тело, изображенное на рисунке 74.
1 . Приведите примеры действия на тело
нескольких сил. 2. Какую силу называют равнодействующей нескольких сил? З.
Опишите опыт, в котором определяют равнодействующую двух сил, направленных по
одной прямой в одну сторону. Чему равна эта равнодействующая? 4. Чему равна
равнодействующая двух сил, направленных по одной прямой в противоположные
стороны? 5. Как будет двигаться тело под действием двух равных противоположно
направленных сил?
Упражнение 1 1
1. Человек, масса которого 70 кг, держит на плечах ящик массой 20 кг. С какой силой человек давит на землю?
2. В игре по перетягиванию
каната участвуют четыре человека. Два из них тянут канат в одну сторону с
силами 330 Н и 380 Н, два 
в противоположную сторону с силами ЗОО Н и
400 Н. В каком направлении будет двигаться канат и чему равна равнодействующая
этих сил? Сделайте чертеж.
З. Человек спускается на парашюте, двигаясь равномерно. Сила тяжести парашютиста вместе с парашютом 700 Н. Чему равна сила сопротивления воздуха?
Санки, скатившись с горы, движутся по горизонтальному пути неравномерно, скорость их постепенно уменьшается, и через некоторое время они останавливаются. Мальчик, разбежавшись, скользит на коньках по льду, но, как бы ни был гладок лед, мальчик все-таки останавливается. Останавливается и велосипед, когда велосипедист прекращает вращать педали. Мы знаем, что причиной всякого изме-
нения скорости движения (в данном случае уменьшения) является сила. Значит, и в рассмотренных примерах на каждое движущееся тело действовала сила.
При соприкосновении одного тела с другим возникает взаимодействие, препятствующее их относительному движению, которое называют трением. А силу, характеризующую это взаимодействие,
называют силои трения. Она обозначается буквой F с индексом: (рис. 78).
|
прикасающихся тел. Даже гладкие на вид по- |
тр |
|
верхности тел имеют неровности, бугорки и царапины. На рисунке 79, а неровности изображены в увеличенном виде. Когда одно тело скользит или катится по поверхности другого, эти неровности цепляются друг за Друга, |
Рис. 78 |
Сила трения это еще
один вид силы, отличающийся от рассмотренных ранее силы тяжести и силы
упругости.
Одной из причин возникновения силы трения является шероховатость поверхностей со-
что создает некоторую
силу, задерживающую движение.
Другая причина трения взаимное притяжение молекул соприкасающихся тел.
Возникновение силы
трения обусловлено главным образом первой причиной, когда поверхности тел
шероховаты. Но если поверхности тел хорошо отполированы, при соприкосновении
часть их молекул располагается очень близко друг к другу. В этом случае
начинает заметно проявляться притяжение между молекулами ёбприкасающихся тел.
Силу трения можно уменьшить во много раз, если ввести между трущимися поверхностями смазку. Слой смазки (рис. 79, б) разъединяет поверхности трущихся тел. В этом случае соприкасаются не поверхности тел, а слои смазки. Смазка же в большинстве случаев
|
жидкая, а трение слоев жидкости меньше, чем твердых поверхностей. Например, на коньках |
б) |
|
малое трение при скольжении по льду объяс- |
Рис. 79 |
Глава П. Взаимодействие тел
няется также действием смазки. Между коньками и льдом образуется тонкий слой воды. В технике в качестве смазки широко применяют различные маслб.
При скольэ,тении одного тела по поверхности другого
возникает трение, которое называют трением скольжения. Например, такое трение
возникает при движении саней и лыж по снегу.
Если же одно тело не скользит, а катится по поверхности другогот то трение, возникающее при этом, называют тренйём качения. Так, при движении колес вагона, автомобиля, при перекатывании 6ревен или бочек по земле проявляется трение качения.
Рис. ВО
Силу трения можно измерить. Например, чтобы измерить силу
трения скольжения деревянного бруска по доске или по столу, надо прикрепить
нему динамометр (рис. 80, а). Затем равномерно двигать брусок по доске, держа
динамометр горизонтально. Что при 
этом покажет динамометр? На брусок в
горизонтальном направлении действуют две силы. Одна сила — сила упругости
пружины динамометра, нап авленная в сторону движения. Вторая сила это сила
трения, направленная против движения. Так как брусок движется равномерно, то это
значит, что равнодействующая этих двух сил равна нулю. Следовательно, эти силы
равны по модулю, но противоположны по направлению. Динамометр показывает силу
упругости (силу тяги), равную по модулю силе трения.
Таким образом, измеряя силу, с которой динамометр действует на тело при его равномерном движении, мы измеряем с ту трения,
Если на брусок положить груз, например гирю, и измерить по описанному выше способу силу трения, то она окажется больше силы трения, измеренной без груза.
Чем больше сила, прижимающая тело к поверхности, тем больше возникающая при этом сила трения.
Положив деревянный брусок на круглые палочки, можно измерить силу трения качения (рис. 80, б), Она оказывается меньше силы трения скольжения.
Таким образом, при равных нагрузках сила трения качения всегда меньше силы трения скольжения. Именно поэтому люди еще в древности применяли катки для перетаскивания больших грузов, а позднее стали широко использовать колесо.
Вопросы1 . Какие известные вам наблюдения и опыты показывают, что
существует сила трения? 2. Какую силу называют силой трения? З. В чем
заключаются причины трения? 4. Объясните, как смазка влияет на силу трения, 
5. Какие виды трения вы знаете? 6, Как
можно измерить силу трения? 7. Как показать, что сила трения зависит от силы,
прижимающей тело к поверхности? 8. Как показать на опытах, что при равных
нагрузках сила трения скольжения больше силы трения качения? Как это
используется в технике?
Мы ознакомились с силой трения, возникающей при движении одного тела по поверхности другого. Но можно ли говорить о силе трения между соприкасающимися твердыми телами, если они находятся в покое?
Когда тело находится в покое на наклонной плоскости, оно удерживается на ней силой трения. Действительно, если бы не было трения, то тело под действием силы тяжести соскользнуло бы вниз по наклонной плоскости. Рассмотрим случай, когда тело находится в покое на горизонтальной плоскости. Пусть, например, на полу стоит шкаф. Попробуем его передвинуть. Если на шкаф нажать слабо, то он не тронется с места. Почему? Действующая сила в этом случае уравновешивается силой трения между полом -и ножками шкафа.
Так как эта сила существует между покоящимися друг относительно друга телами, то эту силу принято называть силой трения покоя.
На рисунке 81 изображен транспортер, с помощью которого поднимают тюки с хлопком. Тюки удерживаются на ленте транспортера силой трения покоя.
81
Сила трения покоя удерживает гвоздь, вбитый в доску, не дает развязаться банту на ленте, удерживает нитку, которой сшиты два куска ткани, и т. п.
Вопросы1. Какая сила удерживает тела на наклонной плоскости? 2. Почему шкаф сдвигается с места под действием только определенной силы? Приведите примеры практического использования силы трения покоя.
В природе и технике трение имеет большое значение. Трение может быть полезным и вредным. Когда оно полезно, его стараются увеличить, когда вредно — уменьшить.
Без трения покоя ни люди, ни животные не могли бы ходить по земле, так как при ходьбе мы отталкиваемся ногами от земли. Когда трение между подошвой обуви и землей (или льдом) малб, например в гололедицу, то отталкиваться от земли очень трудно, ноги при этом скользят. Чтобы ноги не скользили, тротуары посыпают песком. Это увеличивает силу трения между подошвой обуви и льдом. Не будь трения, предметы выскальзывали бы из рук.
Глава П. Взаимојнмствие тел
Сила трения
останавливает автомобиль при торможении, но без трения покоя он не смог бы и
начать движение. Колеса, вращаясь, проскальзывали бы, а автомобиль продолжал бы
стоять на месте, буксовал. Чтобы увеличить трение, поверхность шин у автомобиля
делают с ребристыми выступами (рис. 82). Зимой, когда дорога бывает особенно
скользкая, ее посыпают песком, очищают ото льда.
У многих растений и животных имеются различные органы, служащие для хватания (усики растений, хобот слона, цепкие хвосты лазающих животных). Все они име-
|
ют шероховатую поверхность для увеличения трения. |
Рис. 82 |
Вам уже известно, что во многих случаях трение вредно и с
ним приходится бороться. Например, во всех машинах из-за трения нагреваются и
изнашиваются движущиеся части. Для уменьшения трения соприкасающиеся
поверхности делают гладкими, между ними вводят смазку. Чтобы уменьшить трение
вращающихся валов Рис. 83 машин и станков (рис. 83), их опирают на подшипники.
Деталь подшипника, непосредственно соприкасающуюся с валом, называют вкладышем.
Вкладыши делают из твердых материалов — бронзы, чугуна или стали. Внутреннюю
поверхность их покрывают особыми материалами, чаще всего баббитом (это сплав
свинца или олова с другими металлами), и смазывают. Подшипники, в которых вал
при вращении скользит по поверхности вкладыша, называют подшипниками
скольжения.
Мы знаем, что сила трения качения при одинаковой нагрузке значительно меньше силы трения скольжения. На этом явлении основано применение шариковых и роликовых подшипников. В таких подшипниках вращающийся вал не скользит по неподвижному вкладышу подшипника, а катится по нему на стальных шариках или роликах.
Устройство простейших
шарикового и роликового подшипников изображено на рисунке 84. Внутреннее кольцо
подшипнпка, изготовленное из твердой стали, насажено на вал. Наружное же кольцо
закреплено в корпусе машины. При вращении вала внутреннее кольцо катится на
шариках или роликах, находящихся между кольцами.
Замена в машинах подшипников скольжения шариковыми или роликовыми подшипниками позволяет уменьшать силу трения в 20—30раз,
Шариковые и роликовые подшипники используют в разнообразных машинах: автомобилях, токарных станках, электрических двигателях, велосипедах т д, Без подшипников невозможно представить современнуко промышленность и транспорт.
Вопросы1 . Приведите примеры, показывающие. что трение может бь1ТЬ полезным. Каково значение трения на транспорте? 2. Приведите примеры, когда трение может быть вредным. З. Какие способы увеличения и уменьшения трения вы знаете? 4. для какой цели используют в машинах ПОДШИПник? 5. Как устроен подшипник скольжения? шариковый подшипник? Какой из них заметнее уменьшает трение?
ДАВЛЕНИЕ ТВЕРДЫХ ТЕЛ, жидкостей И ГАЗОВ
По рыхлому снегу человек идет с большим трудом, глубоко
проваливаясь при каждом шаге, Но, надев лыжи, он может идти, почти не
проваливаясь в него рис. 85), Почему? На лыжах или без лыж человек действует на
снег с одной и той же силой, равной своему весу. Однако действие этой силы в
обоих случаях различно, потому что различна площадь поверхности, на которую
давит человек с лыжами и без лыж. Площадь поверхности лыжи почти в 20 раз
больше площади подошвы. Поэтому, стоя на лыжах, человек действует на каждый квадратный
сантиметр площади поверхности снега с силой, в 20 раз меньшей, чем стоя на
снегу без
лыж.
Ученик, прикалывая кнопками газету к доске, действует на
каждую кнопку с одинаковой силой. Однако кнопка, имеющая более острый конец,
легче входит в дерево.
Значит, резу.ћьтат действия силы зависит не только от ее модуля, направления и точки приложения, но и от площади той поверхности, перпендикулярно которой она действует.
Этот вывод подтверждают
опыты. Рис. В5
В углы небольшой доски вбивают гвозди. Сначала гвозди, вбитые
в доску, устанавливают на песке остриями
вверх и кладут на доску гирю (рис. 86, а). В этом случае шляпки гвоздей только
незна 
чительно вдавливаются в песок. Затем доску
переворачивают и ставят гвозди на острие (рис. 86, б). В этом случае площадь
опоры меньше, и под действием той же силы гвозди значительно углубляются в
песок.
0)
Рис. Вб
От того, какая сила действует на каждую единицу площади поверхности, зависит результат действия этой силы.
В рассмотренных примерах силы действовали перпендикулярно поверхности тела. Вес человека был перпендикулярен поверхности снега; сила, действовавшая на кнопку, перпендикулярна поверхности доски.
Величина, равная отношению силы, действующей перпендикулярно поверхности, к площади этой поверхности, называется давлением.
Чтобы опреДелить Давление, надо силу, Действующую перпендикулярно поверхности, разДелить на площаДь поверхности:
сила давление =
площадь
Обозначим величины, входящие в это выражение: давление Р, сила, деиствующая на поверхность, — F' и площадь поверхности —s.
Тогда получим формулу:
Понятно, что ббльшая по значению сила, действующая на ту же площадь, будет производить большее давление.
За еДиницу Давления принимается такое Давление, которое произвоДит сила в 1 Н, Действующая на поверхность площаДью 1 м 2 перпенДикулярно этой поверхности.
Единица давления ньютон на њваДратный метр 1 4).
В честь французского ученого Блеза Паскаля она называется паскалем (Па). Таким образом,
н
1 Па = 1 — 
м
Используются также другие единицы давления: гектопаскаль (ГПа) и килопаскаль (кПа).
 |
1 гПа = 100 Па 1 Па 0,01 гПа
Пример. Рассчитать давление, производјамое на пол
мальчиком, масса которого 45 кг, а площадь подошв его ботинок, соприкасаю-
2
щихся с полом, равна ЗОО см 
Запишем условие задачи и решим ее.
|
Дано: т 45 кг S ЗОО см2 |
|
|
сиР gm,
н
• 45 кг 450 н, кг
450 
н
15 000 Па 15
кПа.
0,03 м 2
Ответ: р = 15 кПа.
Вопросы
Приведите примеры, показывающие, что
действие силы зависит от ПЛОЩЕЏДИ опоры, на которую действует эта сила. 2.
Почему человек, идуидий на лыжахг не проваливается в снег? З. Почему острая
кнопка легче входит в дерево, чем тупая? 4. На каком опыте можно показать, что
действие силы зависит от площади опоры? 5. Что называют давлением? 6. Как
определяют давление? 7. Какие вы знаете единицы давления?
Упражнение 12
н
1.Выразите в паскалях давление: 5 гпа; 0,02 кпа;
Н
10Выразите в
гектопаскалях и килопаскалях давление•
см2
10 000 па; 5800 Па.
 |
Теловек нажимает на лопату силой 600 Н.
Какое давление ока
зывает лопата на почву, если ширина ее
лезвия 20 см, а толщина ре 
жущего края 0,5 мм? Зачем лопаты остро
затачивают?
4. Мальчик массой 45 кг стоит на лыжах. Длина каждой лыжи
1,5 м, ширина 10 см. Какое давление оказывает мальчик на снег? Сравните его с
давлением, которое производит мальчик, стоящий без лыж
тяжелый гусеничный трактор производит на почву давление 40—50 кПа? т. е. всего в 2—3 раза больше, чем давление мальчика массой 45 кг. Это объясняется тем, что вес трактора распределяется на ббльшую площадь. А мы установили, что чем больше площадь опоры, тем меньше давление, производимое одной и тои же силой на эту опору.
В
зависимости от того, хотят ли получить малое или бОЛЬШОе давление, площадь
опоры увеличивают или уменьшают. Например, для того чтобы грунт мог выдержать
давление возводимого здания, увели
площгщь нижней части фундамента.
Шины грузовых автомобилей и шасси самолетов делают значительно шире, чем легковых (рис, 87). Особенно широкими де 87 лают шины у автомобилей, предназначенных для передвижения в пустынях.
Тяжелые машины, такие, как трактор, танк или болотоход, имея большую опорную площадь гусениц, проходят ло бОЛОТИСТОЙ местности, по которой не пройдет человек.
 |
большой силой создать
большое давление. Например, вдавливая 
кнопку в доску, мы действуем на нее с
силой около 50 Н. Так как площадь острия кнопки примерно 1 мм? , то давление,
производимое ею, равно:
50 н
Р 
0,000001 м2 50 000 000 Па 50 000 кПа.
Это давление в 1000 раз больше давления, производимого гусеничным трактором на почву.
Лезвие режущих и острие колющих инструментов (ножен,
ножниц, резцов, пил, игл и др.) остро оттачивают, Острое лезвие имеет маленькую
площадь, поэтому при помощи даже малой силы создает
ся большое давление, и
таким инструментом легко работать.
Режущие и колющие приспособления встречаются и в живой природе: это зубы, когти, клювы, шипы и др. — все они из твердого материала, гладкие и очень острые.
1 , Приведите примеры использования больших площадей опоры для
уменьшения давления. 2. Зачем у сельскохозяйственных машин делают колеса с
широкими ободами? З. Почему режущие и колющие инструменты оказывают на тела
очень большое давление?
Упражнение 13
1. Рассмотрите устройство плоскогубцев и клещей (рис. 88). При помощи какого инструмента можно произвести большее давление на зажатое тело, действуя одинаковой силой?
Рис. ВВ
2. Зачем при бброновании плотных почв на бороны кладут тяжелые предметы?
1. Зная свою массу и площадь ботинка, вычислите, какое давление вы производите при ходьбе и стоя на месте.
 |
Указание. Площадь опоры ботинка определите следующим образом.
Поставьте ногу на лист клетчатой бумаги и обведите контур той части подошвы, на
которую опирается нога (рис. 89). Сосчитайте число полных квадратиков, попавших
внутрь контура, и прибавьте к нему половину числа неполных 
Рис. 89
квадратиков, через которые прошла линия контура. Полученное число умножьте на
ПЛОЩщдЬ одного квадратика площадь квадратика на листе, взятом из школьной
тетради, равна -- см2) и найдите площадь подошвы.
2. Рассмотрите на рисунке 87 колеса двух автомашин. Подготовьте небольшое сообщение о способах уменьшения и увеличения давления.
S 35. Давление газа
Мы уже знаем, что газы, в отличие от твердых тел и жидкостей, заполняют весь сосуд, в котором они находятся. Например, стальной баллон для хранения газов, камера автомобильной шины или волей-
больный мяч. При этом газ оказывает давление на стенки, дно и крышку баллона, камеры или любого другого тела, в котором он находится. Давление газа обусловлено иными причинами, чем давление твердого тела на опору.
б)
Рис. 90 Рис. 9)
 |
Итак, давление газа на стенки сосуда (и на помещенное в газ тело) вызывается ударами молекул газа.
Рассмотрим следующий опыт. Под колокол воздушного насоса помещают завя5АнныЙ резиновый шарик. Он содержит небольшое количество воздуха (рис. 91, а) и имеет неправильную форму. Затем насосом откачивают воздух из-под колокола. Оболочка шарика, вокруг которой воздух становится все более разреженным, постепенно раздувается и принимает форму шара (рис. 91, б).
Как объяснить этот опыт?
В нашем опыте
движущиеся молекулы газа непрерывно ударяют о стенки шарика внутри и снаружи.
При откачивании воздуха число молекул в колоколе вокруг оболочки шарика
уменьшается. Но внутри завязанного шарика их число не изменяется. Поэтому число
ударов молекул о внешние стенки оболочки становится меньше, чем число ударов о
внутренние стенки. Шарик раздувается до тех пор, пока сила упругости его
резиновои• оболочки не станет равной силе давления газа. Оболочка шарика
принимает форму шара. Это показывает, что газ Давит на ее стенки по всем
направлениям оДинањово. Иначе говоря, число ударов молекул, приходящихся на
каждый квадратный сантиметр площади поверхности, по всем направлениям
одинаково. Одинаковое давление по всем направлениям 
характерно для газа и
является следствием 
беспорядочного движения огромного числа
молекул.
 |
чит, что в каждом кубическом сантиметре
газа молекул станет больше, плотность газа увеличится. Тогда число ударов
молекул о стенки сосуда возрастет, т. е. возрастет давление газа. Это можно
подтвердить опытом.
На рисунке 92, а изображена стеклянная трубка, один конец которой закрыт тонкой резиновой пленкой, В трубку вставлен поршень. При вдвигании поршня объем воздуха в трубке уменьшается, т, е. газ сжимается (рис. 92, б). Резиновая пленка при этом выгибается наружу, указывая на то, что давление воздуха в трубке увеличилось.
Наоборот, при увеличении объема этой же массы газа число
мо
лекул
в каждом кубическом сантиметре уменьшится. От этого 
уменьшится число
ударов о стенки сосуда — давление газа станет меньше. Действительно, при
вытягивании поршня из трубки объем воздуха увеличивается, пленка прогибается
внутрь сосуда (рис. 92, в) 
Это указывает на уменьшение давления
воздуха в трубке. Такие же явления наблюдались бы, если бы вместо воздуха в
трубке находился. любой другой газ.
Итак, при уменьшении объема газа его давление увеличивается, а При увеличении объема давление уменьшается при условии, что масса и температура газа остаются неизменными.
А как изменится
давление газа, если нагреть его при постоянном объеме? Известно, что скорость
движения молекул газа при нагревании увеличивается. Двигаясь быстрее, молекулы
будут ударять о стенки сосуда чаще. Кроме того, каждый удар молекулы о стенку
сосуда станет сильнее. Вследствие этого стенки сосуда будут испытывать большее
давление.
Следовательно, Давление газа в закрытом сосуДе тем больше, чем выше температџра газа, при условии, что масса газа и объем не изменяются,
Из этих опытов можно сделать общий вывод, что давление газа тем больше, чем чаще Риг, 93 и сильнее молекулы ударяют о стенки сосуда. Для хранения и перевозки газов их сильно
 |
Вопросы
1. Какие свойства газов отличают их от твердых тел и жидкостей? 2. Как
объясняют давление газа на основе учения о движении молекул? з. Как можно на
опыте показать, что газ производит давление на стенки сосуда, в котором он
находится? 4. Из чего можно заключить, что газ производит одинаковое давление
по всем направлениям? 5. Почему давление газа увеличивается при сжатии и
уменьшается при расширении? б. В каком состоянии газ производит большее
давление: в холодном или нагретом? Объясните почему. 7. Почему сжатые газы
содержат в специальных 
баллонах?
S 36. Передача давления жидкостями и газами. Закон Паскаля
В отличие от твердых тел отдельные слои и мелкие частицы жидкости и газа
могут свободно перемещаться относительно друг друга по 
всем направлениям, Достаточно, например,
слегка подуть на поверх-
ность воды в
стакане, чтобы вызвать движение воды. На реке или озере при малейшем ветер
ке
появляется рябь.
Подвижностью частиц газа и жидкости объясняется, что Давление, производимое на них, передается не только в направлении Действия силы, а в кажДую точку жидкости или газа. Рассмотрим это явление подробнее.
На рисунке 94, а изображен сосуд, в котором содержится газ (или жидкость). Частицы
|
Паскаль Блез |
газа равномерно распределены по всему сосуду. |
|
(1623—1662). |
Сосуд закрыт поршнем, который может переме- |
|
Открыв и исследэеал |
|
|
ряд важных свойств |
Прилагая некоторую силу, заставим пор- |
|
жидкостен и газов. |
шень немного войти в и сжать газ, находя- |
|
Опытами подтвердил |
щийся непосредственно под ним. Тогда частицы |
|
существование атмосферного давления |
расположатся в этом месте более плотно, чем прежде (рис. 94, б). Благодаря подвижности частицы газа будут перемещаться по всем направле- |
 |
рве. 94
Вб
Давление, производимое на жидкость или газ, передается в любую точку одинаково во всех направлениях.
Это утверждение называют законом Паскаля.
На основе закона Паскаля легко объяснить следующие опыты.
 |
На рисунке 95 изображен полый шар, имеющий в различных местах узкие
отверстия. К шару присоединена трубка, в которую вставлен поршень. Если набрать
воды в шар и вдвинуть в трубку поршень, то вода польется из всех отверстий
шара. В этом опыте поршень давит на поверхность воды в трубке. Частицы воды,
находящиеся под поршнем, уплотняясь, передают его давление другим слоям,
лежащим глубже. Таким образом, давление поршня передается в каждую точку
жидкости, заполняющей шар. В результате часть воды выталкивается из шара в виде
рисе 95 Рис 96 одинаковых струек, вытекающих из всех отверстий.
Если шар заполнить дымом, то при вдвигании поршня в трубку из всех отверстий шара начнут выходить одинаковые струйки дыма (рис. 96). Это подтверждает, что и газы переДают произвоДимое на них Давление во все стороны оДинаково.
Вопросы
1 . Как передают давление жидкости и газы? 2. Пользуясь рисунком 94, объясните, почему жидкости и газы передают давление во все стороны одинаково. З. Как читается закон Паскаля? 4. На каком опыте можно показать особенность передачи давления жидкостями и газами?
Упражнение 14
1. По рисунку 97 объясните передачу давления твердым, сыпучим телами и жидкостью. Изобразите стрелками, как передается давление.
2. При изготовлении бутылок через трубку вдувают воздух и расплавленное стекло принимает нужную форму (см. рис. 28). Какое физическое явление здесь используют?
 |
а) в) 
Рис.
97 рис л
з.Автомашину заполнили грузом. Изменилось ли давление в камерах колес автомашины? Одинаково ли оно в верхней и нижней частях камеры?
4. Объясните явление, показанное на рисунке 98. Как изменится наблюдаемое явление, если увеличить сжатие?
Из пластмассовой бутылочки с завинчивающейся пробкой изготовьте прибор для демонстрации закона Паскаля (придумайте сами, как это сделать, опробуйте прибор).
S 37. Давление в жидкости и газе
На жидкости, как и на все тела на Земле, действует сила
тяжести. Поэтому каждый слой жидкости, налитой в сосуд, своим весом создает
давление на другие слои, которое по закону Паскаля переда 
ется по всем
направлениям. Следовательно, внутри ЖИДКОСТИ су 
ществует давление. В
этом можно убедиться на опыте.
В стеклянную трубку, нижнее отверстие которой закрыто тонкой резиновой пленкой, на.льем воду, Под действием веса жидкости дно трубки прогнется (рис, 99).
Опыт показывает, что, чем выше столб воды над резиновой плен 
кой, тем больше она про гиб ается
(рис. 100). Но всякий раз после того,
 |
а) а)
Рис. 93 Рис, 100 Рис. 101 Рис. 102
как резиновое дно прогнулось, вода в трубке приходит в равновесие (останавливается), так как, кроме силы тяжести, на воду действует сила упругости растянутой резиновой пленки.
Опустим трубку с резиновым дном, в которую налита вода, в другой, более широкий сосуд с водой (рис, 101, а). Мы увидим, что по мере опускания трубки резиновая пленка постепенно выпрямляется. Полное выпрямление пленки показывает, что силы, действующие на нее сверху и снизу, равны (рис. 101, б). Наступает полное выпрямление пленки тогда, когда уровни воды в трубке и сосуде совпадают.
Такой же опыт можно провести с трубкой, в которой резиновая
пленка закрывает боковое отверстие, как это показано на рисунке 102, а..
Погрузим эту трубку с водой в другой сосуд с водой, как это изображено на
рисунке 102, б. Мы заметим, что пленка снова выпрямится, как только уровни воды
в трубке и в сосуде сравняются. Это означает, что силы, действующие на
резиновую пленку, одинаковы с обеих сторон.
Возьмем сосуд, дно которого может отпадать. Опустим его в банку с водой (рис. 103, а). Дно при этом окажется плотно прижатым к
краю сосуда и не
отпадет. Его прижимает сила давления воды, направленная снизу вверх.
Будем осторожно наливать воду в сосуд и следить за его дном. Как только уровень воды в сосуде совпадет с уровнем воды в банке, дно отпадет от сосуда (рис. 103, б).
В момент отрыва на дно давит сверху вниз столб жидкости в сосуде, а снизу вверх на дно передается давление такого же, по высоте столба жидкости, но находящеЙся в банке. Оба эти давления одинаковы, дно же отходит от цилиндра вследствие действия на него силы тяжести.
Рис. 103 Выще были описаны опыты с водой, но если взять вместо воды другую жид-
кость, то результаты опыта будут те же.
Итак, опыты показывают, что внутри жидкости существует давление и на одном и том же уровне оно одинаково по всем направлениям. С глубиной давление увеличивается.
Газы в этом отношении не отличаются от жидкостей, ведь они тоже имеют вес. Но надо помнить, что плотность газа в сотни раз меньше плотности жидкости. Вес газа, находящегося в сосуде, мал, и его «весовое» давление во многих случаях можно не учитывать.
Вопросы
1. Как на опытах показать, что давление внутри жидкости на разных уровнях разное, а на одном и том же уровне во всех направлениях одинаково? 2. Почему во многих случаях не принимают во внимание давление газа, созданное его весом?
S 38. Расчет давления жидкости на дно и стенки сосуда
Рассмотрим, как можно рассчитать давление жидкости на дно и стенки сосуда. Решим сначала задачу для сосуда, имеющего форму прямоугольного параллелепипеда (рис. 104).
Сила Е, с которой жидкость, налитая в этот сосуд, давит на его дно, равна весу Р жидкости, находящейся в сосуде. Вес жидкости можно определить, зная ее массу т. Массу, как известно, можно вы-
«вдвостее газов
числить по формуле: т
pV. Объем жидкости, налитой в выбранный нами сосуд, легко рассчитать. Если
высоту столба жидкости, находящейся в сосуде, обозначить буквой Ь, а площадь
дна сосуда S, то V = Sh.
Масса жидкости т = pV, или т pSh.
Вес этой жидкости Р = gm, или Р = gpSh.
Рис,
Так как вес столба жидкости равен силе, с которой жидкость давит на дно ссхуда, то, разделив вес Р на площадь S, получим давление жидкости р:
gpSh р , или р — Р = gph.
Мы получили формулу для расчета
давления жидкости на дно сосуда. Из этой формулы видно, что Давление жиДкости
на дно сосџДа зависит только от плотности и высоты столба жиД• кости.
Следовательно, по выведенной формуле можно рассчитывать давление жидкости, налитой в сосуд любой формы. Кроме того, по ней можно вычислить и давление на стенки сосуда. Давление внутри жидкости, в том числе давление снизу вверх, также рассчитывается по этой формуле, так как давление на одной и той же глубине одинаково по всем направлениям,
При расчете давления по формуле р gph надо плотность р выра-
жать в килограммах на кубический метр , а высоту столба жид-
н кости — в метрах (м), g 9,8 , тогда давление будет выражено в
кг паскалях (Па).
Пример. Определите давление нефти на дно цистерны, если вы-
кг сота столба нефти 10 м, а плотность ее 800 3' м
Запишем условие задачи и решим ее.
|
Дано: К = 10 м кг р = 800 —МЗ |
|
|
Решение: р = gph,
н кг 
— •800 — • 10 м 80
000 Па 80 кпа. кг МЗ
Ответ: р = 80 кПа.
Вопросы
1 . Выведите формулу для расчета давления жидкости на дно сосуда, имеющего форму прямоугольного параллелепипеда. 2. От каких величин и как зависит давление жидкости на дно сосуда? З. По какой формуле рассчитывают давление жидкости на стенки сосуда, давление внутри жидкости? В каких единицах надо выражать величины, входящие в эту формулу?
Упражнение 15
1.Определите давление
на глубине 0,6 м в воде, керосине, ртути. 2. Вычислите давление воды на дно
одной из глубочайших морских впадин, глубина которой
кг
10 900 м. Плотность морской воды 1030
З. На рисунке 105 изображена футбольная камера, соединенная с вертикально расположенной стеклянной трубкой, В камере и трубке находится вода. На камеру положена дощечка, а. на нее — гиря. массой 5 кг. Высота столба воды в трубке 1 м. Определите площадь соприкосновения дощечки с камерой.
1. 
Возьмите
высокий сосуд. В боковой поверхности его на разной высоте от дна сделайте три
небольших отверстия. Закройте отверстия спичками и наполните сосуд водой.
Откройте отверстия и проследите за струйками вытекающей воды (рис. 106). Почему
вода вытекает из отверстий? Из чего следует, что давление увеличивается с
глубиной?
2. Налейте в стеклянный сосуд (стакан или банку) произвольное количество воды. Сделайте необходимые измерения и рассчитайте дав-
Рис. ление воды на дно сосуда.
S 39. Сообщающиеся сосуды
На рисунке 107 изображены два сосуда, соединенные между
собой резиновой трубкой. Такие сосуды называют сообщающи 
МИСЯ. Лейка, чайник,
кофейник примеры сообщающихся сосудов (рис. 108). Из опыта мы знаем, что вода,
налитая, например, 
лейку, стоит всегда в резервуаре лейки и в
боковой трубке на одном 
ровне.
 |
опыт. В начале опыта (рис. 107, а) резиновую трубку в середине за-
|
д) Рис, 107 ЖИМаЮТ и в одну из трубок наливают |
в) |
воду, Затем зажим открывают, и вода
начинает перетекать в другую трубку до тех пор, пока поверхности воды в обеих
трубках не установятся на одном уровне (рис. 107, б). Можно закрепить одну из
трубок в штативе, а другую поднимать, опускать или наклонять в стороны. И в
этом случае, как только жидкость успокоится, ее уровни в обеих трубках будут
одинаковыми (рис, 107, в). Рис. ТОН
В сообщающихся сосудах любой формы и сечения поверхности однородной жидкости устанавливаются на одном уровне (при условии, что давление воздуха над жидкостью одинаково) (рис. 109).
Рис.
109 Рис,
 |
Если в один из сообщающихся сосудов налить жидкость одной плотности, а во второй — другой, то при равновесии уровни этих жидкостей не будут одинаковыми. И это понятно. Мы ведь знаем, что давление жидкости на дно сосуда прямо пропорционально высоте столба и плотности жидкости. А в этом случае плотности жидкостей различны, поэтому высоты столбов этих жидкостей будут различны.
При равенстве давлений высота столба жидкости с большей плотностью будет меньше высоты столба жидкости с меньшей плотностью (рис. 110).
Вопросы
1 . Какие примеры сообщающихся сосудов вы можете привести?
2. Как располагаются поверхности однородной жидкости в сообщающихся
сосудах? З. Как располагаются поверхности разнородных жидкостей в сообщающихся сосудах?
Упражнение 16
1. На рисунке 111 показано водомерное стекло парового котла, где 1 — паровой котел, 2 — краны, З — водомерное стекло. Объясните действие этого прибора.
пар
22
з
ВоДа1
 |
2. На рисунке 112 изображен артезианский колодец. Слой земли
2 состоит из песка или другого материала, легко пропускающего воДУ. Слои 1 и З, наоборот, водонепроницаемы. Объясните действие та-
кого колодца.
З. Докажите, что в сообщающихся сосудах высоты столбов над уровнем разделА двух разнородных жидкостей (см. рис. 110) обратно пропорциональны плотностям жидкостей.
Указание. Используйте формулу для расчета давления жидкости.
4. Изменится ли расположение жидкости (см. рис. 107), если 
правый
сосуд будет шире левого? уже левого? если сосуды будут иметь разную форму?
1. Подумайте, как можно было бы наиболее простыми средствами устроить фонтан где-нибудь в парке или во дворе. Начертите схему такого устройства и объясните принцип его действия. Изготовьте модель фонтана.
2.
На рисунке 113, а дана схема устройства шлюза. а на
рисунке 113, б — схема ШЛIОЗОВп1[ИЯ судов. Рассмотрите рисунки и объясните
принцип действия шлюзов. Какое явление использув работе шЛЮЗОВ?
З. В два сосуда налита вода (рис. 114). В ка
ком сосуде
давление воды на дно больше и на сколько, если h1 40 см, а ТО см В каком
направлении и до каких пор будет переливаться вода, если открыть кран? (Ответ:
в „Левом сосу 
де 2,94 кПа.)
S 40. Вес воздуха. Атмосферное давление
На воздух, как и на всякое тело, находящееся на Земле, действует силатяжести, и, следовательно, воздух обладает весом. Вес воздуха легко вычислить, зная его массу.
На опыте покажем, как определить массу воздуха. Для этого 
можно
взять прочный стеклянный шар с пробкой и резиновой трубкой с зажимом (рис.
115), Выкачаем насосом из него воздух, зажмем 
трубку зажимом и
уравновесим на весах. Затем, открыв зажим на резиновой трубке, впустим в шар
воздух. Равновесие весов при этом на
рушится. Для его восстановления придется
положить на другую чашку весов гири, масса которых и будет равна массе воздуха
в объ-
еме шара.
Опытами установлено,
что при температуре О ФС и нормальном атмосферном давлении масса
воздуха объемом 1 м з равна 1,29 кг. Вес этого воздуха легко
вычислить:
Н
— • 1,29 кг- 13 н. кг
 |
тмосфера, как показали наблюдения за
полетом искусственных спутников Земли, простирается на высоту нескольких тысяч
километров.
Вследствие действия силы тяжести верхние слои воздуха,
подобно воде океана, сжимают нижние слои. Воздушный слой, прилегающий непосредственно
к Земле, сжат больше всего и, согласно закону Паскаля, передает производимое на
него давление по всем направлениям.
В результате этого земная поверхность и тел5, находящиеся на ней. испытывают давление всей толщи воздуха, или, как обычно говорят, испытывают атмосферное давление.
Существованием атмосферного давления могут быть объяснены многие явления, с которыми мы встречаемся в жизни. Рассмотрим некоторые из них.
На рисунке 116 изображена стеклянная трубка, внутри которой
находится поршень, плотно приле-
Рис 136
гающий к стенкам
трубки. Конец трубки опущен в воду. Если поднимать поршень, то за ним будет
подниматься и вода. Происходит это потому, что при подъеме поршня между ним и
водой образуется безвоздушное пространство. В это пространство под 
давлением
наружного воздуха и поднимается вслед за поршнем вода.
Это явление используется в водяных насосах и некоторых других устройствах.
На рисунке 117 показан цилиндрический со
суд.
Сосуд закрыт пробкой, в которую вставлена трубкА с краном. Из сосуда насосом
откачивают Рис 1 17 воздух. Затем конец трубки погружают в воду. Если теперь
открыть кран, то вода фонтаном брызнет внутрь сосуда. Вода поступает в сосуд
потому, что атмосферное давление больше давления разреженного воздуха в сосуде.
Вопросы
 |
4. Опишите опыты, подтверждающие существование атмосферного давления.
Упражнение 17
1. Как для объяснения явлений, изображенных на рисунках 116 и 117, используется закон Паскаля?
2. Какое физическое явление мы используем, набирая лекарства пипеткой?
1. Измерьте объем комнаты в вашей квартире и вычислите массу
кг и вес воздуха в ней, считая,
что его плотность равна 1,29
2. Объясните действие шприца.
З. Автоматическая поилка для птиц (рис. 118) состоит из
бутылки, наполненной водой и опрокинутой в корытце так, что горлышко находится
немного ниже уровня воды в корытце. Почему вода не выливается из бутылки? Если
уровень воды в корытце понизится и горлышко бутылки выйдет из воды, часть воды
из бутылки выльется. Почему?
Изготовьте такой прибор и проделайте с ним указанные опыты.
4. На рисунке 119 изображен прибор ливер, служащий для взятия проб различных жидкостей. Ливер опускают в жидкость, затем закрывают пальцем верхнее отверстие и вынимают из жидкости. Когда верхнее отверстие открывают, из ливера начинает вытекать жидкость. Проделайте опыт и объясните действие этого прибора.
S 41 . Почему существует воздушная оболочка Земли
 |
Но почему же тогда
все они не упадут на поверхность Земли? Каким образом сохраняется воздушная
оболочка Земли, ее атмосфера? Чтобы понять это, надо учеств, что молекулы
газов, составляющих атмосферу, находятся в непре рывном и беспорядочном
движении. Но тогда возникает другой вопрос: почему эти молекулы не улетают в
мировое пространство?
Для того чтобьТсовсем покинуть Землю, молекула, как и космический корабль или ракета, должна иметь очень большую скорость не меньше 11,2 ксм). Это так называемая вторая
КОСМИЊсСКОЯ скорость. Скорость большинства молекул воздушной
оболочки Земли значительно меньше этой космической скорости. Поэтому
большинство их и «привязано» к Земле Рис
силой тяжести, лишь ничтожно малое число молекул улетает в космическое пространство, покидает Землю.
Беспорядочное движение молекул и действие на них силы тя
жести
приводят в результате к тому, что молекулы газов «парят» в пространстве около
Земли, образуя воздушную оболочку, или ат 
мосферу.
Измерения показывают, что плотность воздуха быстро уменьщается с высотой. Так, на высоте 5,5 км над Землей плотность воздуха в 2 раза меньше его плотности у поверхности Земли, на высоте 11 км — в 4 раза меньше и т. д. Чем выше, тем воздух разреженнее. И наконец, в самАх верхних слоях (сотни и тысячи километров над Землей) атмосфера постепенно переходит в. безвоздушное пространство. Четкой границы воздушная оболочка, окружающая Землю, не имеет.
 |
Однако это различие в плотности и давлении газа, содержащегося в сосуде, столь мало, что его можно во многих случаях совсем не учитывать, Но для атмосферы, простирающейся на несколько тысяч километров, различие это существенно.
Вопросы
1 . Почему молекулы газов, входящих в состав атмосферы, не
падают на Землю под действием силы тяжести? 2. Почему молекулы газов, входящих
в состав атмосферы, двигаясь во все стороны, не покидают Землю? 
З. Как изменяется плотность атмосферы
с увеличением высоты?
Упражнение 18
1. Предполагают, что Луна когда-то была окружена атмосферой, но постепенно потеряла ее. Чем это можно объяснить?
2. Чтобы вдохнуть воздух, человек при помощи мышц расширяет грудную клетку. Почему воздух входит при этом в легкие? Как происходит выдох?
S 42. Измерение атмосферного давления. Опыт Торричелли
Рассчитать
атмосферное давление по формуле для вычисления давления столба жидкости (S 38)
нельзя. Для такого расчета надо знать высоту атмосферы и плотность воздуха. Но
определенной границы у атмосферы нет, а плотность воздуха на разной высоте
различна. Однако измерить атмосферное давление можно с помощью опыта,
предложенного в XVII в. итальянским ученым Эванджелиста Торричелли, учеником
Галилея.
Опыт Торричелли состоит в следующем;
|
стеклянную трубку длиной около 1 м, запаян- |
|
|
ную с одного конца, наполняют ртутью. Затем, |
Торричелли Эванджелиста ( 1603— 1647). |
|
плотно закрыв другой конец трубки, ее пере- |
Измерил атмосферное |
|
ворачивают, опускают в чашку с ртутью и под |
даыпоние рдољСвотал |
|
ртутью открывают конец трубки (рис. 120). |
ряд вопросов а физике |
|
Часть ртути при этом выливается в чашку, а |
и математике |
 |
в трубке воздуха нет, там безвоздушное
пространство.
|
а |
|
|
|
|
|
|
Торричелли, предложивший описанный выше опыт, дал и его
объяснение. Атмосфера давит на поверхность ртути в чашке. Ртуть находится в
равновесии. Значит, давление в трубке на уровне (см, рис, 120) равно ат
мосферному
давлению. Если бы оно было больше атмосферного, то ртуть выливалась бы из
трубки в чашку, а если меньше, то поднималась бы в трубке вверх.
Давление в трубке на уровне аат создается весом столба
ртуги в трубке, так как в верхней части трубки над 
ртутью воздуха нет.
Отсюда следует, что атмосферное давление равно давлению столба ртути в трубке,
т. е.:
Ратм Рртути•
Измерив высоту столба ртути, можно рассчитать дав
ление, которое производит ртуть. Оно и
будет равно атмосферному давлению. Если атмосферное давление уменьшится, то
столб ртути в трубке Торричелли понизится . Рис, 120
4' Фи.зи«а. ГГ
Чем больше атмосферное давление, тем вьице столб ртути в опыте Торричелли. Поэтому на практике атмосферное давление можно измерять высотои ртутного столба (в миллиметрах или сантиметрах). Если, например, атмосферное давление равно 780 мм РТ. ст., то это значит, что воздух производит такое же давление, какое производит вертикальный столб ртути высотой 780 мм.
Следовательно, в этом случае за единицу атмосферного давления 
принимают 1 миллиметр ртутного столба
(1 мм ст..). Найдем соотношение между этой единицей и известной нам единицей
давления 
паскалем (Па).
Давление столба ртути рртути высотой 1 мм равно:
н р р— 9,8 — • 13 600 0,001 м 133,3 Па. кг м
Итак, 1 мм РТ. ст. 133,3 Па.
в настоящее время атмосферное давление принято измерять и в гектопаскалях. Например, в сводках погоды может быть объявлено, что давление равно 1013 ГПа, это то же самое, что 760 мм РТ. ст,
 |
ление непостоянно, оно
может увеличиваться й уменьшаться. Торри
челли заметил также,
что изменения атмосферного давления связаны с изменением погоды.
Если к трубке с ртутью, использовавшейся в опыте Торричелли,
прикрепить вертикальную шкалу, то получится простейший при
бор ртутный
барометр (от греч. барос — тяжесть, метрео -— измеряю). Он служит для измерения
атмосферного давления.
орВопросы
Почему нельзя рассчитывать давление
воздуха так же, как рассчиТЫВЕ\ЮТ давление жидкости на дно или стенки сосуда?
2. Объясните, как с помощью трубки Торричелли можно измерить атмосферное
давление.
. Что означает запись: «Атмосферное
давление равно 780 мм РТ. ст.»? 4. Как называют прибор для измерения
атмосферного давления? Как он устроен? 5. Скольким гектопаскалям равно давление
ртутного столба вы
сотой 1 мм?
Упражнение 19
1. На рисунке 121 изображен водяной барометр, созданный Паскалем в 1646 г. Какой высоты был столб воды в этом барометре при атмосферном давлении, равном 760 ММ РТ. СТ.?
2.
 |
Рис 121
з, Из трубки длиной 1 м, запаянной е одного конца и с краном на другом конце, выкачали воздух. Поместив конец с краном в ртуть, открыли кран. Заполнит ли ртуть всю трубку? Если вместо ртути взять воду, заполнит ли она всю трубку?
4. Выразите в гектопаскалях давление, равное: 740 мм РТ. ст,;
780 ММ РТ. СТ.
5, Рассмотрите рисунок 120, Ответьте на вопросы:
а) Почему для уравновешивания давления атмосферы, высота которой достигает десятков тысяч километров, достаточно столба ртути высотой около 760 мм?
б) Сила атмосферного давления действует на ртуть, находящуюся в чашечке, сверху вниз. Почему же атмосферное давление удерживает столб ртути в трубке?
в) Как повлияло бы наличие воздуха в трубке над ртутью на показания ртутного барометра?
г) Изменится ли показание барометра, если трубку наклонить? опустить глубже в чашку со ртутью?
 |
1. Погрузите стакан в воду, переверните его под водой вверх дном и затем медленно вытаскивайте из воды. Почему, пока края стакана находятся под водой, вода остается в стакане (не выливается)?
2. Налейте в стакан воды, закройте листом бумаги и, поддерживая лист рукой, переверните стакан вверх дном. Если теперь от-
пять руку от бумаги
(рис. 123), то вода из стакана не выльется. Бумага остается как бы 
приклеенной
к краю стакана. Почему? Ответ обоснуйте.
З. Положите на стол длинную деревянную линейку так, чтобы ее конец выходил за край стола. Сверху застелите стол газетой, разгладьте газету руками, чтобы она плотно лежала на столе и линейке. Резко ударьте по свободному концу линейки — газета не поднимется, а прорвется. Объясните наблюдае-
Рис. 123 мые явления.
S 43.
Барометр-анероид
В практике для измерения атмосферного давления используют металлический барометр, называемый анероидом (в переводе с греческого «безжидкостный» . Так барометр называют потому, что он не содержит ртути).
 |
поверхностью (рис,
125). Из этой коробочки выкачан воздух, а 
чтобы атмосферное
давление не раздавило коробочку, ее кры 
пружиной 2 оттягивают
вверх. При увеличении атмосферного дав
ления крышка прогибается вниз и натягивает
пружину. П 
уменьшении давления пружина выпрямляет
крышку. К пружине с помощью передаточного механизма З прикреплена
стрелка-указатель 4, которая передвигается вправо или влево при изменении
давления. Под стрелкой укреплена шкала, деления которой нане
сены по
показаниям ртутного барометра. Так, число 750, против которого стоит стрелка
анероида (см. рис, 124), показывает, что в данный момент в ртутном барометре
высота ртутного столба 750 мм.
Следовательно, атмосферное давление
равно 750 мм РТ. СТ., ИЛИ 
1000 гПа.
Знание атмосферного давления весьма важно для предсказывания цОТОДЫ на ближайшие дни, так как изменение атмосферного давления связано с изменением погоды. Барометр „-— необходимый прибор при метеорологических наблюдениях. •
Рис, 124 Рис. 125
Вопросы
1 . Как устроен барометр-анероид? 2. Как градуируют шкалу барометра-анероида? З. для чего необходимо систематически и в разных местах земного шара измерять атмосферное давление? Какое значение это имеет в метеорологии?
Упражнение 20
ассмотрите рисунок 124 и ответьте на
вопросы:
а) Как называется изображенный на рисунке прибор?
б) В каких едийицах проградуированы его внешняя и внутренняя шкала?
в) Вычислите цену деления каждой шкалы.
г) Запишите показания прибора по каждой шкале.
S 44. Атмосферное давление на различных высотак
 |
Сложнее обстоит дело с газами. Газы сильно
сжимаемы.
сильнее газ сжат, тем больше его плотность и тем большее давление он производит. Ведь давление газа создается ударами его молекул о поверхность тела.
Слои воздуха у поверхности Земли сжаты всеми вышележащими слоями воздуха, находящимися над ними. Но чем выше от поверхности слой воздуха, тем слабее он сжат, тем меньше его плотность, Следовательно, тем меньшее давление он производит. Если, например, воздушный шар поднимается над поверхностью Земли, то давление воздуха на шар становится меньше. Это происходит не только дотому, что высота столба воздуха над ним уменьшается, но еще и потому, что уменьшается плотность воздуха. Вверху она меньше, чем внизу. Поэтому зависимость давления воздуха от высоты сложнее, чем жидкости.
наблюдения показывают, что атмосферное давление в местностях,лежащих на уровне моря, в среднем равно 760 мм РТ. ст.
Атмосферное давление, равное давлению столба ртути
высотой 760 мм при температуре О о с, называется нормальным атмосфер
ным
давлением.
Нормальное атмосферное Давление равно 101 ЗОО Па 1013 гПа.
Чем больше высота над уровнем моря, тем давление меньше.
При небольших подъемах в среднем на каждые 12 м подъема
давление уменьшается на 1 мм РТ, ст. (или на 1,33 ГПа)
Зная зависимость давления от высоты, можно по изменению по
казаний
барометра определить высоту над уровнем моря. Анероиды, 
имеющие шкалу, по
которой непосредственно можно отсчитать высоту, называют высотомерами. Их
применяют в авиации и дри подъемах на горы.
Вопросы
 |
Как объяснить, что атмосферное давление уменьшается по мере 
увеличения высоты подъема над уровнем
Земли? 2. Какое атмосферное давление называют нормальным? З. Как называют
прибор для измерения ВЫСОТЫ по атмосферному давлению? Что он собой
представляет? Отличается ли его устройство от устройства барометра?
Упражнение 21
1. Почему
воздушный шарик, наполненный водородом, при 
подъеме над Землей
увеличивается в объеме?
2. У подножия горы
барометр показывает 760 мм рта ст., а на вер
шине 722 мм РТ. ст.
Какова примерно высота горы?
З. Выразите нормальное атмосферное давление в гектопаскалях
4. При массе. 60 кг и росте 1,6 м площадь поверхности тела человека равна примерно 1,65 м2 . Рассчитайте силу, с которой атмосфера давит на человека (при нормальном атмосферном давлении).
С помощью барометра-анероида измерьте атмосферное давление на первом и последнем этажах здания школы. Определите по полученным данным расстояние между этажами.
S 4,3. Манометры
мыуже знаем, что для измерения атмосферного давления применяют барометры. Для измерения давлений, ббльших или меньших атмосферного, используют манометры (от греч. мОНос редкий, неплотный, метрео измеряю). Манометры бывают жиДкостные и металлические,
Рассмотрим сначала устройство и действие открытого жидкостного манометра. Он состоит из двухколенной стеклянной трубки, в которую наливают какую-нибудь жидкость. Жидкость устанавливается в обоих коленах на одном уровне, так как на ее поверхность в коленах сосуда действует только атмосферное давление.
Рис- 126 Рис. 127
Чтобы понять, как работает такой манометр, его можно
соединить резиновой трубкой с круглой плоской коробкой, одна сторона которой
затянута резиновой пленкой (рис. 126). Если слегка нада
вить пальцем на
пленку, то уровень жидкости в колене манометра, 
соединенном с
коробкой, понизится, в другом колене повысится. Чем это объясняется?
При надавливании на пленку увеличивается давление воздуха в коробке. По закону Паскаля это увеличение давления передается и жидкости в том колене манометра, которое присоединено к коробке. Поэтому давление на жидкость в этом колене будет больше, чем
108
Слава Ш, Давление твердых тел, вмдкостей и газоа
вдругом, где на жидкость действует атмосферное давление. Под действием силы этого избыточного давления жидкость начнет перемещаться. В колене со сжатым воздухом жидкость опустится, в другом — поднимется. Жидкость придет в равновесие (остановится), когда избыточное давление сжатого воздуха уравновесится давлением, которое производит избыточный столб жидкости в другом колене манометра.
Чем сильнее давить на пленку, тем выше избыточный столб жидкости, тем больше его давление. Следовательно, об изменении давления можно суДить по высоте этого избыточного столба,
На рисунке 127 показано, как таким манометром можно измерять давление внутри жидкости. Чем глубже погружают в жидкость коробочку, пьем больше становится разность высот столбов жиДкости в коленах манометра, тем, следовательно, и большее Давление произвоДит жиДкость.
Если установить коробочку прибора на какой-нибудь глубине внутри жидкости и поворачивать ее пленкой вверх, вбок и вниз, то показания манометра при этом не будут меняться, Т. ак и должно быть, ведь на одном и том же уровне внутри жиДњости давление по всем направлениям оДинањово.
На рисунке 128 изображен металлический манометр, Основная часть такого манометра— согнутая в дугу металлическая трубка 1 (рис. 129), один конец которой закрыт. Другой конец трубки с помощью крана 4 сообщается с сосудом, в котором измеряют давление. При увеличении давления трубка разгибается. Движение закрытого конца ее при помощи рычага 5 и зубчатки З передается стрелке 2,
2
5
128 129
движущейся около ШКаЛЫ прибора. При уменьшении давления трубка благодаря своей упругости возвращается в прежнее положение, а стрелка -— к нулевому делению шкалы.
Вопросы
Как называют приборы для измерения
давлений, больших или меньших атмосферного? 2. Как устроен и действует открытый
жидкостный манометр? З. Почему в открытом манометре уровни однородной жидкости
в обоих коленах одинаковые? 4. Что доказывает опыт, изображенный на рисунке 1279
5. Как показать, что давление в жидкости на одной и той же глубине
одинаково по всем направлениям? 6. Как устроен и действует металлический
манометр?
S 46. Поршневой жидкостный насос
В опыте, рассмотренном нами ранее, было установлено, что вода в стеклянной трубке под действием атмосферного давления поднималась за поршнем. На этом основано действие поршневых насосов.
 |
Насос схематически изображен на рисунке 130. Он состоит из цилиндра,
внутри которого ходит вверх и вниз плотно прилегающий к стенкам поршень 1 . В
нижней части цилиндра и в самом поршне установлены клапаны 2, открывающиеся
только вверх. При движении поршня вверх вода под действием атмосферного
давлепия входит в трубу, поднимает нижний клапан и движется за поршнем.
При 
ПОРШНЯ вниз вода, находящаяся под
поршнем, давит на нижний клапан, и он закрывается, Одновременно под давл 
нием
воды открывается клапан внутри поршня, и вода переходит в пространство над
поршнем, При последующем движении поршня вверх вместе с ним поднимается и
находящаяся над 
ним вода, которая и выливается в отводящую
трубу. Одновременно за поршнем поднимается новая порция воды, которая при
последующем
Рис. 130 опускании поршня окажется над ним, и т. д.
Вопросы
1 . Какое явление используют в устройстве поршневого водяного насоса? 2. Как устроен и действует такой насос?
Упражнение 22
1. На какую предельную высоту можно поднять воду поршневым насосом (см, рис. 130)при нормальном атмосферном давлении?
2. На
какую наибольшую высоту можно поднять спирт, ртуть поршневым насосом (см. рис.
130) при нормальном атмосферном давлеНИИ?
З. Объясните работу поршневого насоса с воздушной камерой (рис. 131), где 1 поршень,
— всасывающий клапан, З —
нагнетательный клапану 4 — воздушная камера, 5 — рукоятка.
 |
S 47. Гидравлический пресс
Закон Паскаля позволяет объяснить действие гидравлическои
машины (от грей. гиДравликос — водяной). Это машины, действие 
которых
основано на законах движения п равновесия жидкостей.
Основной частью гидравлическои машины
с ужат два цилиндра разного диаметра, снабженные п о ршня
соедине трубкой (рис. 132).
Пространство под поршнями и трубку заполняют жидкостью (обычно минеральньгм
маслом). ВЫСоТЫ столбов жидкости в обоих цилиндрах одинаковы, пока на поршни не
действуют силы.
Допустим теперь, что Fl и — силы, действующие на поршни, St и S2 площади поршней, Давление под первым
1
(малым) поршнем равно Р! S а под вторым (большим)по закону Паскаля давление покоящейся жидкостью во все стороны
передается
одинаково, т. е, рт или 
, откуда:
Следовательно, сила во СтоЛЬко раз больше силы РТ, во сколько раз площаЭь большого поршня больше площаДи малого. Например, если площадь большого поршня 500 см 2 , а малого 5 см? и на малый поршень действует сила 100 Н, то на больший поршень будет действовать сила, в 100 раз большая, т. е. 10 ООО Н.
Таким образом, с помощью гидравлической машины можно ма„той силой уравновесить большую силу.
огношение показывает выигрыш в силе. Например, в приве-
10 000 н денном
примере выигрыш в силе равен100.
100 н
Гидравлическую машину, служащую для прессования (сдавливания), называют гидравлическим прессом.
Гидравлические прессы применяются там, где требуется
большая сила. Например, для выжимания масла из семян на маслобойных заводах,
для прессования фанеры, картона, сена. На металлургических заводах
гидравлические прессы используют при изготовлении стальных валов машин,
железнодорожных колес и многих других изделий. Современные гидравлические
прессы могут развивать силу в десятки и сотни миллионов ньютонов.
Устройство гидравлического
пресса схематически показано на Рис, 133 рисунке 133. Прессуемое тело 1
кладут на платформу, соединенную с
большим поршнем 2. При помощи малого ПОРШНЯ З создается большое давление на
жидкость. Это давление без изменения передается в каждую точку жидкости,
заполняющей цилиндры (закон Паскаля). Поэтому такое же давление действует и на
поршень 2. По так как площадь поршня 2 больше 
площади поршня 3, то и
сила, действующая на него, будет больше силы, действующей на поршень З. Под
действием этой силы портень 2 будет подниматься. При подъеме портня 2 тело
упирается в неподвижную верхнюю платформу и сжимается. Манометр 4, при помощи
которого измеряют давление жидкости, 5 предохранительныЙ клапан, автоматически
открывахсщийся, когда давление превышает „допустимое значение,
Из малого цилиндра в большой жидкость перекачивается повторными движениями малого поршня З. Это осуществляется так. При подъеме малого поршня клапан 6 открывается, и в пространство, находящееся под поршнем, засасывается жидкость. При опускании малого поршня под действием давления ЖИДКОСТИ клапан 6 закрывается, а клапан 7 открывается, жидкость переходит в большой сосуд.
Вопросы
1. Какой закон используют в устройстве гидравлических машин?
2. Какой выигрыш в силе дает гидравлический пресс (при отсутствии трения)?
Упражнение 23
1. На рисунке 134
изображена упрощенная схема гидравлического подъемника (гидравлического
домкрата), где поднимаемое тело. 2 — малый поршень, З --- клапаны, 4 — клапан
для опускания груза, 5 — большой поршень. Груз какой массы можно поднять такой
машиной, если известно, что площадь малого поршня см?. большого — 1440 ем 2
, а сила, действующая на малый поршень, может достигать 1000 Н? Трение не
учитывать.
2, В гидравлическом прессе площадь малого поршня 5 см2 , шлощадь большого — 500 см2 . Сила, действующая на малый поршень, 400 Н, на
Рис- 135
большой — 36 кН. Какой выигрыш в силе дает этот пресс? Почему пресс не дает максимального (наибольшего) выигрыша в силе? Какой выигрыш в силе должен был бы давать этот пресс при отсутствии силы трения между поршнем и стенками пресса?
з.Можно ли создать машину, подобную гидравлической, исполь
зуя
вместо воды воздух? Ответ обоснуйте.
На рисунке 135 изображена схема автомобильного
гидравлического тормоза, где 1 — тормозная педаль, 2 — цилиндр с поршнем, 
тормозной
цилиндр, 4 тормозные колодки, 5 пружина, 6 — тормозной барабан. Цилиндры и
трубки заполнены специальной ЖИДКОСТЬЮ. Расскажите по эгои схеме, как действует
тормоз.
S 48, Действие жидкости и газа на погруженное в них тело
Под водой мы можем легко поднять камень, который с трудом поднимаем Б воздухе, Если погрузить пробку под воду и выпустить ее из рук, то она всплывет. Как можно объяснить эти явления?
Мы знаем (S 38), что жидкость давит на дно и стенки сосуда,
а ес
ли внутрь ее поместить какое-нибудь
твердое тело, то оно также будет подвергаться давлению.
Глава III. Давление твердых теп, жидкостей и Г1ЗOВ
Рассмотрим силы,
которые действуют со стороны жидкости на погруженное в нее тело. Чтобы легче
было рассуждать, выберем тело, которое имеет форму параллелепипеда с
основаниями, параллельными поверхности жидкости (рис. 136). Силы, действующие
на боковые грани тела, попарно равны и уравновешивают друг друга. Под действием
этих сил тело только сжимается. А вот силы, действую-
Рис. 136
щие на верхнюю и нижнюю грани тела,
неодинаковы. На верхнюю грань давит сверху с силой Е 1 столб жидкости высотой
h1. На уровне нижней 
грани тела давление производит столб
жидкости высотой 122. Это давление, как мы знаем (S 37), передается внутри
жидкости во все стороны. Следовательно, на нижнюю грань тела снизу вверх с
силои F2 давит столб жидкости высотой h2. Но h2 больше h1, следовательно, и
модуль силы F2 больше модуля силы Е 1. Поэтому тело выталкивается из жидкости с
силой Fвыр равной разности сил
Рассчитаем эту выталкивающую силу. Силы F1 и F2, действующие на верхнюю и нижнюю грани параллелепипеда, можно вычислить, зная их площади (Sl и S2) и давление жидкости на уровнях этих граней (Р1 и Р2). Отсюда получаем:
F1 = P1S1, а F2 P2S2, так как рт 
Р2 p.,kg1l2, а S1 S2 
S,
где S — площадь основания параллелепипеда.
Тогда Евыт — F1 py,gh2S — pxgh1
px,gSh, где h —
высята параллелепипеда.
Но Sil = Г, где У — объем параллелепипеда, а ржу = т — масса
.идкости в объеме параллелепипеда.
Следовательно, 
= grn,« Рж,
т. е. выталкивающая сила равна весу жиДкоспти в объеме погруженного в нее тела.
Существование силы, выталкивающей тело из жидкости, легко обнаружить на опыте.
На рисунке 137, а изображено тело, подвешенное к
пружине со стрелкой указателем на конце. Растяжение пружины отмечает на 
штативе
стрелка. При опускании тела в воду пружина сокращается (рис. 137, б) Такое же
сокращение пружины получится, если дейст
вовать на тело снизу
вверх с некоторой силой, например нажать ру
кой.
Следовательно, опыт подтверждает, что на тело,
находящееся в .жиДњости, Деиствџет сила, выталкивающал. вто тело из 
усиДкости
К газам, как мы знаем, также применим закон Паскаля.
Поэтому 
и на тела, нахоДящиеся в газе, Действует
сила, выталкивающая их из газа. Под действием этой силы воздушные шары
поднимаются вверх, Существование силы, выталкивающеи тело из 
газа, можно
также наблюдать на опыте.
К укороченной чашке весов подвешивают стеклянный шар или
большую колбу, закрытую пробкой. Весы уравновешивают. Затем под колбу (или шар)
ставят широкий сосуд так, чтобы он окружал всю колбу. Сосуд наполняют
углекислым газом, плотность которого больше плотности воздуха. При этом
равновесие весов нарушается 
Чашка с подвешенной колбой поднимается
вверх (рис. 138). На 
колбу, погруженную в углекислый газ,
действует ббльшая вытал 
кивающая сила по сравнению с той, которая
действует на не 
воздухе.
137 Рис,
138
Сила, выталкивающая тело из жидкости или газа, направлена противоположно силе тяжести, приложенной к этому телу.
Поэтому если какое-либо тело взвесить в жидкости или газе, то его вес окажется меньше веса в вакууме (пустоте). Именно этим объясняется, что в воде мы иногда легко поднимаем тела, которые с трудом удерживаем в воздухе.
Вопросы
Какие известные вам из жизни явления
указывают на существование выталкивающей силы? 2. Как доказать, основываясь на
законе 
Паскаля, существование выталкивающей силы, действующей на тело,
погруженное в жидкость? З. Как показать на опыте, что на тело, находящееся в
жидкости, действует выталкивающая сила? 4. Как на опыте показать, что на тело,
находящееся в газе, действует выталкивающая сила?
S 49- Архимедова сила
Силу, с которой тело, находящееся в жидкости, выталкивается ею, можно рассчитать, как это сделано в S 48. А можно определить ее значение на опыте, используя для этого прибор, изображенный на рисунке 139.
Рис. 139
К пружине подвешивают небольшое ведерко и тело
цилиндрической формы. Растяжение пружины отмечает стрелка на штативе 
(рис.
139, а), Она показывает вес тела в воздухе. Приподняв тело, под него
подставляют отливной сосуд, наполненный жидкостью до уровня отливной трубки.
После чего тело погружают целиком в жидкость (рис. 139, б). При этом часть
жиДкости, объем кото
рой равен объему тела, выливается из
отливного сосуда в стакан. Указатель пружины поднимается вверх, пружина
сокращается, показывая уменьшение веса тела в жидкости. В данном случае на
тело, кроме силы тяжести, действует еще и сила, выталкивающая его из жидкости.
Если в ведерко вылить жидкость из стакана (т. е. ту, которую вытеснило тело),
то указатель пружины возвратится к своему начальному положению (рис. 139, в).
На основании этого опыта можно заключить, что сила, выталкивающая целиком погруженное в жидкость тело, равна весу жидкости в объеме этого тела. Такой же вывод мы получили и В S 48.
Если бы подобный опыт проделать с телом, погруженным в какой-либо газ, то он показал бы, что сила, выталкивающая тело из газа, также равна весу газа, взятого в объеме тела.
Силу, выталкивающую тело из жидкости или
газа, называют ар
химеДовои силой в честь древнегреческого
ученого Архимеда, который впервые указал на ее существование и рассчитал ее
значение.
Архимед (287-—212 до
н. э, Установил правило рычага,
открыл закон г ищхх;татики 
Итак, опыт подтвердил, что архимедова (или выталкивающая)
сила равна весу жидкости в объеме тела, т. е. ЕА Рж gi71)k. Массу жидкости тж,
вытесняемую телом, можно выразить через ее плотность (р ) и объем тела 
(Гт),
погруженного в жидкость (так как 
объем вытесненной телом ЖидкОстИ равен Ут
— объему тела, погруженного в жидкость), т. е. тж ржут. Тогда получим:
Следовательно, архимедова сила зависит от плотности жидкости,
в которую погружено тело, и от объема этого тела. Но она не зависит, например,
от плотности вещества тела, погружаемого в ЖИдКостЬ, так как эта вели
чина
не входит в полученную формулу.
Определим теперь вес тела, погруженного в жидкость (или в газ), т'ак как две силы, действующие на тело в этом случае, направлены в противоположные стороны (сила тяжести вниз, а архимедова сила вверх), то вес тела в жидкости Р1 будет меньше веса тела в вакууме Р — gm (т масса тела) на архимедову силу FA = (т — масса жидкости (или газа), вытесненной телом), т. е.
р 1 — Р РА, или Р1 gm — щпж.
1. аким образом, если тело погружено в жиДњоспть (или газ , то оно теряет в своем весе столько, сколько весит вытесненная им жиДкость (или газ).
|
Дано: т = 1,6 МЗ кг 1030 н
|
|
|
пр„мер. Определить выталкивающую силу, действующую на
камень объемом 1,6 м з в морской воде. Запишем условие задачи и
решим ее. Решение:
н кг
9,8 •
1030
16 480 н
кг
 |
16,5 кн.
Ответ: 16,5 кн.
Вопросы
1 . как можно на опыте определить с какои силой тело, погруженное целиком
в жидкость, выталкивается из жидкости? 2. Чему равна эта сила? З. Как называют
силу, которая выталкивает тела, погруженные в жидкости и газы? 4. Как
подсчитать архимедову силу? 5. От каких величин зависит 
архимедова сила? От каких величин она
не зависит?
Упражнение 24
1. К
коромыслу весов подвешены два цилиндра одинаковой массы: свинцовый и
алюминиевый. Весы находятся н равновесии. Нару
щится ли равновесие
весов, если оба цилиндра одновременно погрузить в воду? спирт? Ответ обоснуйте.
Проверьте его на опыте. Как зависит выталкивающая сила от объема тела?
2. К коромыслу весов подвешены два алюминиевых цилиндра одинакового объема. Нарушится ли равновесие весов, если один цилиндр погрузить в воду, другой — в спирт? Ответ обоснуйте. Зависит ли выталкивающая сила от плотности жидкости?
З. Объем куска железа 0,1 дмз . Какая
выталкивающая сила б 
дет на него действовать при полном его
погружении в воду? в керосин?
4. Бетонная плита объемом 2 м з погружена в Ходу. Какую силу необходимо приложить, чтобы удержать ее в воде? в воздухе?
Задание 14Предположив, что золотая корона царя Гиерона в воздухе весит 20 Н, а в воде 18,75 Н, вычислите плотность вещества короны.
Полагая, что к золоту было подмешано только серебро, определите, сколько в короне было золота и сколько серебра.
При решении задачи плотность золота считайте равной
КГ кг
 |
S 50. Плавание тел
На тело, находящееся внутри жидкости,
действуют две силы: сила тяжести, направленная вертикально вниз, и архимедова
сила, направденная вертикально вверх, Рассмотрим, что будет происходить с телом
под действием этих сил, если вначале оно было неподвижно, 
При этом
возможны три случая:
1) если сила тяжести
Ртяж больше архимеДовой силы FA 
то тело буДет опускаться на дно, тонуть,
т. е. если тяж
РА, то тело тонет;
2) если сила тяжести
равна архимеДовой силе А, то 
тело может нахоДиться в равновесии в любом
месте жидкос
тц, т. е. если тяж — то тело плавает;
З) если сила тяжести РТяж меньше архилеДовой силы РА, то тело
буДет поДниматься из .жиДкости, всплывать. т. е. если 
FA, то тело всплывает.
Рассмотрим последний случай подробнее.
Когда всплывающее тело достигнет поверхности жидкости,
то при дальнейшем его движении вверх архимедова сила будет уменьшаться, Почему?
Да потому, что будет уменьшаться объем части тела, погруженной в жидкость, а
архимедова сила равна весу жидкос
ти в объеме погруженной в нее части тела.
Когда архимедова сила станет равной силе тяжести, тело остановится и будет плавать на поверхности жидкости, частично погрузившись в нее.
Полученный вывод легко проверить на опыте.
В отливной сосуд наливают воду до уровня боковой трубки. После этого в сосуд погружают плавающее тело (рис. 140), предварительно взвесив его в воздухе. Опустившись в воду, тело вытесняет объем воды, равный объему погруженной в нее части тела. Взвесив эту воду, находят, что ее вес (архимедова сила) равен силе тяжести, действующей на плавающее тело, или весу этого тела в воздухе.
Проделав такие же опыты с любыми другими телами, плавающи
ми в
разных жидкостях воде, спирте, растворе соли, можно убедиться, что если тело
плавает в жиДкости, то вес вытесненной им лсиДкости равен весу этого тела в
возДухе.
Легко доказать, что если плотность сплошного тверДого тела
больше плотности жиДкости, то тело в такой жиДкости тонет. 'Тело с меньшей
плотностью всплывает в этой жиДкости. Кусок железа, например, тонет в воде, но
всплывает в ртути. Тело же, плотность которого равна плотности жидкости, оста 
ется
в равновесии внутри жидкости.
Плавает на поверхности воды и лед, так как его плотность меньше плотности воды.
Чем меньше плотность тела по сравнению с плотностью жидкости,
тем меньшая часть тела погружена в жидкость (рис, 141)
Парафин
Пробка
Рис
140 Рис
Глаад IIL Давлонио твердых тел, жидхослей и газов
При равных плотностях тела и жИДКОСТИ тело плавает внутри жидкости на любой глубине.
Две несмешивающиеся жидкости, например вода и керосин, рас
полагаются
в сосуде в соответствии со своими плотностями: в ниж-
ней части сосуда — более плотная вода р -
1000 , сверху — более МЗ кг легкий керосин р 800
Средняя плотность живых организмов, населя{ощих водную среду,
мало отличается от плотности воды, поэтому их вес почти полностью
уравновешивается архимедовой силой. Благодаря этому водные животные не
нуждаются в столь прочных и массивных скелетах, как наземные. По этой же
причине эластичны стволы водных 
растений,
Плавательный пузырь рыбы легко меняет свой объем. Когда рыба
с помощью мышц опускается на большую глубину и давление воды на нее
увеличивается, пузырь сжимается, объем тела рыбы уменьшается и она не
выталкивается вверх, а плавает в глубине. При 
подъеме плавательный
пузырь и объем всего тела рыбы увеличивает
ся и она плавает уже
на меньшей глубине. Таким образом рыба может в определенных пределах
регулировать глубину своего погружения. Киты регулируют глубину своего
погружения за счет уменьшения и увеличения объема легких.
Вопросы
При каком условии тело, находящееся в
жидКОСТИ, тонет? плавает? всплывает? 2. Как показать на опыте, что вес
жидкости, вытесненной плаВЕПОЩИМ телом, равен весу тела в воздухе? З. Чему
равна выталкивающая 
сила, которая действует на тело, плавающее на поверхности жидкости? 4. Как
зависит глубина погружения в жидкость плавающего тела от его плотности? 5.
Почему водные животные не нуждаются в прочных скелетах?
6. Какую роль играет плавательный пузырь у рыб? 7. Как регулируют глубину погружения киты?
Упражнение 25
1. На весах уравновесили отливной сосуд с водой (рис. 142, а). В воду опустили деревянный брусок. Равновесие весов сначала нарушилось (рис- 142, б). Но когда вся вода, вытесненная плавающим
Глава III. .№впенле твердых тел, мид•ссеи и тазов
бруском, вытекла из сосуда, равновесие весов восстановилось (рис. 142, е). Объясните это явление.
2. 
На рисунке
143 изображено одно и то же тело, плавающее в двух разных жидкостях. Плотность
какой жидкости больше? Почему? Что можно сказать о силе тяжести, действующей на
тело, и архимедовой силе в том и другом случае?
Рис. 142 Рис. 143
З. Яйцо (или картофелина) тонет в пресйой воде, но плавает в соленой. Объясните почему. Пронаблюдайте это сами на опыте,
4. Изобразите графически силы, действующие на тело, плавающее на воде; всплывающее на поверхность воды, тонущее в воде.
5. Пользуясь таблицами плотности 2—4, определите, тела из каких металлов будут плавать в ртути, а какие — тонуть.
Французский ученый Декарт (1596-—1650) для
демонстрации 
некоторых гидростатических явлений
придумал прибор,
Высокий стеклянный сосуд (банку) наполняли водой, оставляя
сверху сосуда небольшой объем воздуха. В этот сосуд опускали небольшую полу
стеклянную фигурку. Фигурку заполняли частично водой и частично воздухом так,
чтобы она только немного выходила из воды. Сверху стеклянный сосуд ПЛОТНО
закрывали куском тонкой кожи. Нажимая на кожу, можно было заставить фигурку
плавать в воде и на воде, а также тонуть.
Изготовьте такой прибор и проделайте с
опыты.
Фигурку замените небольшим Рев. поплавком, а сосуд закройте резиновой пленкой
(рис 144, а, На рисунке 144, б изображен другой вариант этого прибора)
Объясните действие прибора. Продемонстрируйте на этом прибое ре законы плавания тел.
S 51 . Плавание судов
суда, плавающие по рекам, озерам, морям и океанам, построены
из разных материалов с различной плотностью. Корпус судов обычно 
делают из
стальных листов. Все внутренние крепления, придающие 
судам прочность, также
изготовляют из металлов. Для постройки судов используют различные материалы,
имеющие по сравнению с водой как 66.льшую, так и меньшую плотность.
Благодаря чему же суда держатся на воде, принимают на борт и перевозят большие грузы?
Опыт с плавающим телом (S 50) показал, что тело вытесняет
своей подводной частью столько воды, что вес этой воды равен весу тела 
ввоздухе.
Это справедливо и для любого судна.
Вес воды, вытесняемой подводной частью судна, равен весу судна с грузом в воздухе или силе тяжести, действующей на судно с грузом.
Глубину, на которую судно погружается в воду, называют
осадкой. Наибольшая допускаемая осадка отмечена на корпусе судна красной
линией, называемой ватерлинией (от голланд. ватер 
вода).
Вес ВОДы, вытесняемой суДном при погружении до ватерЛИНИИ, равный силе тяжести, Действующей на суДно с грузом, называется воДоизмещением суДна.
Сейчас для перевозки нефти строят суда водоизмещением 5 ООО ООО кН (5 • 106 кН) и больше, т е имеющие вместе с грузом массу 500 ООО т (5 • 10 5 т) и более.
Если из водоизмещения вычесть вес самого судна, то получим грузоподъемность этого судна. Грузоподъемность показывает вес груза, перевозимого судном.
Судостроение существовало еще в Древнем
Египте, Финикии, 
Древнем Китае
В России судостроение зародилось на рубеже XVII—--XV111 вв.
Сооружались главным образом военные корабли, но именно в России были созданы
первый ледокол, суда с двигателем внутреннего сгора
ния, атомный ледокол
«Арктика» .
Вопросы
1 . На чем основано плавание судов? 2. Что называют осадкой судна?
з. Что такое ватерлиния о 4. Что называют водоизмещением судна?
Упражнение 26
1. Как изменится осадка корабля при переходе из реки в море? ответ объясните.
2. Сила тяжести, • действующая на судно, 100 ООО кН. КакоЙ объем воды вытесняет это судно?
з.Плот, плывущий по реке, имеет площадь 8 м2 . После того как на него поместили груз, его осадка увеличилась на 20 см. Каков вес помещенного на плот груза?
1. На рисунке 145 изображены два прибора, плавающие в воде, называемые ареометрами.
Пояснение. Эти приборы используются для измерения плотности жидкости. Первый ареометр, изображенный на рисунке 145, а, предназначен для жидкостей, имеющих плотность меньшую, чем вода.
Деления на нем нанесены сверху вниз. Второй 1000 (рис.
145, б) для жидкостей с плотностью большей, чем вода. Деления на нем нанесены
снизу вверх. Цифрой 1000 обозначена плотность воды:
кг р = 1000
м
а) Объясните действие таких приборов.
б) Используя пробирку или деревянную па-
лочку и кусочки свинца, изготовьте ареометры для жидкостей, имеющих плотности 66льплую и
меньшую, чем вода.
Рис.. 345 
2. Налейте в стакан воды, введите в
воду конец пипетки и выпускайте из нее понемногу воздух, Затем наберите в
пипетку немного жидкого масла и пускаите его под водой по капле. Что вы
наблюдаете? Сделайте вывод.
S 52. Воздухоплавание
С давних времен люди мечтали о возможности летать над облаками, плавать в
воздушном океане, как они плавали по морю. Для воздухо
авания вначале использовали воздушные
шары (рис. 146), которые раньше наполняли нагретым воздухом, сейчас -—
водородом или гелием.
Для того чтобы шар поднялся в воздух, необходимо, чтобы архимедова сила (выталкивающая) FA, действующая на шар, была больше силы тяжести тяне т. е. > к тяж-
По мере поднятия шара вверх архимедова сила, действующая на него, уменьшается (FA gpV), так как плотность верхних слоев атмосферы меньше, чем у поверхности Земли. Чтобы подняться выше, с шара сбрасывают специально взятый для этой цели груз (балласт) и этим облегчают шар. В конце концов шар достигает своей предельной высоты подъема. Для спуска шара из его оболочки при помощи специального клапана выпускают часть газа.
В горизонтальном направлении воздушный шар перемещается
только под действием ветра, поэтому он называется аэростатом (от греч. аэр
.-„--. воздух, стато — стоящий). Для исследования верхних 
слоев
атмосферы, стратосферы еще не так давно применялись огромные воздушные шары —
стратостаты.
До того как научились строить большие самолеты для перевозки по воздуху
пассажиров и грузов, применяли управляемые аэростаты 
Дирижабли. Они имеют
удлиненную форму, под корпусом подвешивается гондола для пассажиров и гондола с
двигателем, который приводит в движение пропеллер.
Воздушный шар не только сам поднимается вверх, но может поднять и некоторый груз: кабину, людей, приборы. Поэтому, для того чтобы узнать, какой груз может поднять воздушный шар, необходимо определить его поДъемнџю силу. Рис, 146
Пусть, например, в воздух запущен шар объемом наполненныи гелием. Масса гелия, запол-
кг з
няюгцая оболочку шара, будет равна: т г prV
0,1890 —3 • 40 м
м
7,2 кг, а его вес равен: Р г щпг', Р г 9,8
— • 7,2 кг 71 Н. Вытал-
кг кивающая же, сила (архимедова),
действующая на этот шар в возду-
хе, равна весу воздуха объемом 40 з Т.
е. РА овоздру; ТА
н кг
= — • — •40 520 Н.
кг мз
Значит, этот шар может поднять груз весом 520 Н — 71 Н 
449
Н. Это и есть его подъемная сила.
Шар такого же объема, но наполненный водородом, может поднять груз весом
479 Н. Значит, подъемная сила его больше, чем ша
ра, наполненного гелием. Но все же
чаще используют гелий, так как он не горит и поэтому безопаснее. Водород же
горючий газ.
Гораздо проще осуществить подъем и спуск шара, наполненного горячим воздухом. Для этого под отверстием, находящимся в нижней части •ймара, располагают горелку. При помощи газовои горелки можно регулировать температ ру воздуха, а значит, его плотность и выталкивающую сил . Чтобы шар поднялся выше, ДОСТ&ТОЧНО сильнее нагреть воздух в нем, увеличив пламя горелки. При уменьшении пламени горелки температура воздуха в шаре уменьшается и шар опускается вниз.
Можно подобрать такую температуру шара, при которой вес шара и кабины будет равен выталкивающей силе. Тогда •шар повиснет в воздухе и с него будет легко проводить наблюдения.
Глава 111. Длнление твердых тел. жидкостей и газов
По мере развития науки происходилии существенные
изменения в воздухоплавательной технике. Появилась возможность для созда
ния
новых оболочек для аэростатов, которые стали прочными, морозоустойчивыми и легкими.
Достижения в области радиотехники, электроники, автоматики позволили создать беспилотные аэростаты. Эти аэростаты используются для изучения воздушных течений, для географических и медико-биологических исследований в нижних слоях атмосферы.
Вопросы
Почему воздушные шары наполняют
водородом или гелием? 2. Как рассчитать подъемную силу шара, наполненного
гелием? З. Почему уменьшается выталкивающая сипа, действующая на шар, по мере
его подъема? 4. Как регулируют высоту подъема воздушного шара, наполненного
горячим воздухом?
Упражнение 27
1. На весах
уравновешена бутылка, внутри которой находится 
сжатый воздух. Через
пробку бутылки пропущена стеклянная трубка с краном, к наружному концу которой
привязана оболочка резинового шара (рис. 147, а). Если часть воздуха из бутылки
перейдет в оболочку и раздует ее (рис. 147, б), то равновесие весов нарушится.
Объясните наблюдаемое явление.
Рис 147 рис. 149
2. На весах уравновешен легкий стеклянный шар. Если поместить весы под колокол воздушного насоса и откачать воздух, то равновесие весов нарушится (рис. 148). Почему?
РАБОТА И МОЩНОСТЬ.
ЭНЕРГИя
В обыденной жизни словом «работа» мы называем всякий полезный труд рабочего, инженера, ученого, учащегося.
Понятие работы в физике несколько иное. Это определенная
физическая величина, а значит, ее можно измерить. В физике изуча
ют прежде
всего механическую работу.
Рассмотрим примеры механической работы.
Поезд движется под действием силы тяги электровоза, при
этом совершается механическая работа. При выстреле из ружья сила давления
пороховых газов совершает работу — перемещает пулю вдоль ствола, скорость пули
при этом увеличивается.
Из этих примеров видно, что механическая работа совершается, когда тело движется под действием силы.
Механическая работа совершается и в том случае, когда сила, действуя на тело (например, сила трения), уменьшает скорость его движения. Желая передвинуть шкаф, мы с силой на него надавливаем, но если он при этом в движение не приходит, то механической работы мы не совершаем,
Можно представить себе случай, когда тело движется без участия сил (по инерции), в этом случае механическая работа также не совершается.
Итак, механическая работа совершается, только когда на тело действует сила и оно движется.
Нетрудно понять, что чем 66.льшая сила действует ца тело и чем длиннее путь, который проходит тело под действием этой силы, тем ббльшая совершается работа.
5 Физика
Учебник д,Пй 7 к,пхса
Глада ГУ. Работа мошность„ Энергия
Механическая работа прямо пропорциональна приложенной силе и прямо пропорциональна пройденному пути.
Поэтому условились измерять механическую работу произведением силы на путь, пройденный по направлению этой силы:
работа = сила х путь, или
где А — работа, F — сила и s — пройденный путь.
За еДиницу работы принимают работу, совершаемую силой в 1 Н, на пути, равном 1 м.
Единица работы — Джоуль (Дж) названа в честь английского ученого Джоуля. Таким образом,
Используются также и КИЛОДЖОУЛИ, (кДж).
1 кдж 1000 Дж;
1 дж - 0,001 кдж. формулаА = Fs применима в том случае, когда сила постоянна и совпадает с направлением движения тела,
Если направление силы совпадает с направлением движения тела, то данная сила совершает положительную работу.
Если же движение тела происходит в направлении, противоположном направлению приложенной силы, например, силы трения скольжения, то данная сила совершает отрицательную работу. А = -FTPS.
Если направление силы, дей ствунэщей на тело, перпендикулярно направлению движения, то эта сила работы не совершает, работа равна нулю:
В дальнейшем, говоря о механической работе, мы будем кратко называть ее одним словом — работа.
Пример. Вычислите работу, совершаемую при подъеме гранитной плиты объемом 0,5 м з на высоту 20 м. Плотность гранита
кг
2500 
м
Глава ГУ. Раоотп мОи НАОСГЬ„ Энергмп
Запишем условие задачи и решим ее.
|
дано:
кг р = 2500 20 м |
|
9 |
Решение:
— сила, которую нужно
приложить, чтобы равномерно поднимать плиту вверх. Эта сила по модулю равна
силе тяжести тяне действующей на плиту, т. е. F = Етяж. А силу тяжести можно
определить по массе плиты: Щя ж — gm. Массу плиты вычислим, зная ее объем и плотность
гранита: т pV; s П, т. е. путь равен высоте подъема.
кг
Итак, т - 2500 — ' 0,5 м з 1250 кг.
н
1250 кг- 12 250 н.
кг
А = 12 250 Н • 20 м = 245 000 дж 245 кДж.
Ответ: А = 245 кДж.
Вопросы 
1. Какие два условия необходимы для совершения механической работы? 2. От каких двух величин зависит совершенная работа? З. Что принимают за единицу работы? 4. Дайте определение единицы работы 1 Дж. Какие еще единицы работы вы знаете?
1. В каких из нижеперечисленных случаев совершается механическая работа: мальчик влезает на дерево; девочка играет на пианино; вода давит на стенку сосуда; вода падает с плотины?
2. По гладкому горизонтальному льду катится стальной шарик. Допустим, что сопротивление движению шарика (трение о лед, сопротивление воздуха) отсутствует. Совершается ли при этом работа?
З. При помощи подъемного крана подняли груз массой 2500 кг на высоту 12 м. Какая работа при этом совершается?
4. Какая работа совершается при подъеме гидравлического молота массой 20 т на высоту 120 см?
5•
1. Вычислите механическую работу, которую вы совершаете, равномерно поднимаясь с первого на второй этаж здания школы. Все необходимые данные получите сами, результат запишите в тетрадь.
2. Рассчитайте, какую механическую работу вы совершаете, равномерно проходя 1 км пути по горизонтальной дороге, Результаты запищите в тетрадь.
Указание. Человек, равномерно идя по ровному горизонтальному пути, совершает примерно 0,05 той работы, которая требовалась бы для поднятия этого человека на высоту, равную длине пути.
На совершение одной и той же работы различным двигателям требуется разное время. Например, подъемный кран на стройке за несколько минут поднимает на верхний этаж здания сотни кирпичей. Если бы эти кирпичи перетаскивал рабочий, то ему для этого потребовалось бы несколько часов. Другой пример. Гектар земли лошадь может вспахать за 10—12 ч, трактор же с многолемешным плугом эту работу выполнит за 40—50 мин.
Ясно, что подъемный кран ту же работу совершает быстрее, чем 
рабочий,
а трактор — быстрее, чем лошадь. Быстроту выполнения работы характеризуют
особой величиной, называемой мощностью.
Мощность равна отношению работы ко времени, за которое она была совершена.
Чтобы вычислить мощность, наДо работу разделить на время, в течение которого совершена эта работа.
мощность 
время 
и
где — мощность, А — работа, t —- время выполнения работы.
Мощность величина постоянная, когда за
каждую секунду со
вертается одинаковая работа, в других
случаях отношение определяет среднюю мощность:
За еДиницу мощности принимают такую мощность, при которой в 1 с совершается работа в 1 Дж.
Эту единицу называют ваттом (Вт) в честь английского ученого Уатта.
Итак,
1 ватт — 1 джоуль , или 1 Вт = 1 дж
1 секунда с
Ватт (джоуль в секунду)
В технике широко используют более крупные единицы мощности
киловатт (кВт), мегаватт (МВт).
1 мвт 1 000 000 вт 1 вт 0,000001 мвт
1
квт 1000 вт 1 вт 0,001 квт
1 мвт 0,001 вт 1 вт 1000 мвт
Пример. Найти мощность потока воды, протекающей через плотину, если высота падения воды 25 м, а расход ее — 120 мз в минуту.
Запишем условие задачи и решим ее.
|
Дано: h= 25 м v— 120 мз кг р = 1000 — м
9,8 ц кг |
|
|
Решение:
Масса падающей воды: т = pV,
т = 1000 • 120 120 000 кг (12 • 104 кг).
МЗ
Сила тяжести, действующая на воду:
F gm,
9,8 120 000 кг- 1 200 000 н (12 •
10 5 н).
кг
Работа, совершаемая потоком в минуту:
А = 1 200 000 Н. 25 м = ЗО 000 000 дж (3 • 10 7 Дж).
Мощность потока: лт = — ,
зо 000 000 дж 500
000 вт = 0,5 мвт.
60 с
Ответ: N = 0,5 МВт.
53 Физи«я- Учебних для 7 (ЛДССЗ
глава Ш. Работа и мошнОСТЬ. Энеогия
Что показывает мощность? 2. Как
вычислить мощность, зная работу и время? З. Как называется единица мощности Э
4. Какие единицы мощности используют в технике? 5. Как, зная мощность и
время работы, рассчитать работу?
Упражнение 29
1. С плотины высотой 22 м за 10 мин падает 500 т воды. Какая мощность развивается при этом?
2. Какова мощность человека при ходьбе, если за 2 ч он делает 10 ООО шагов и за каждый шаг совершает 40 Дж работы?
З. Какую работу совершает двигатель мощностью 100 кВт за 20 мин?
4. Транспортер за 1 ч поднимает 30 м з песка на высоту 6 м. Вычислите необходимую для этой работы мощность двигателя. Плот-
кг ность песка 1500
5. Выразите в киловаттах и мегаваттах мощность: 2500 Вт; 100 вт.
Выразите в ваттах мощность: 5 кВт; 2,3 кВт; 0,3 кВт; 0,05
МВт; 0,001 МВт. 
б. Штангист поднял штангу массой 125 кг на высоту 70 см за 0,3 с. Какую среднюю мощность развил спортсмен при этом?
Задание 181. Вычислите мощность, которую вы развиваете, равномерно поднимаясь медленно и быстро с первого на второй или третий этаж школы. Все необходимые данные получите сами.
2. Установите по паспорту мощность электродвигателей пылесоса, мясорубки, кофемолки.
3. Установите, на какую мощность рассчитаны двигатели автомобилей, которые вы знаете.
5.3•
Глава пт. Работа и мошность. Энергия
С незапамятных времен человек использует для совершения механической работы различные приспособления.
Каждому известно, что тяжелый предмет (камень, шкаф, станок), который невозможно передвинуть непосредственно, сдвигают с места при помощи достаточно длинной палки — рычага (рис. 149, 150).
Рис. 149 Рис. 150
С помощью рычагов три тысячи лет назад при строительстве пирамид в Древнем Египте передвигали и поднимали на большую высоту тяжелые каменные плиты (рис. 151).
Рис. i5l
Глава Ш. Работа А мОЩнОСтЬ. Знеотв•
Во многих случаях, вместо того чтобы поднимать тяжелый
груз на некоторую высоту, его вкатывают или втаскивают на ту же высоту по
наклонной плоскости (рис. 1.52) или поднимают с помощью блоков (рис. 153).
Приспособления, служащие для преобразования силы, называют механизмами.
|
|
Рис. 152 |
наклонная плоскость и
ее разновидности — клин, винт. В большинстве случаев простые механизмы
применяют для того, чтобы получить выигрыш в силе, т. е. увеличить силу,
действующую на тело, в несколько раз.
Простые механизмы имеются и в бытовых, и во всех сложных заводских и фабричных машинах, которые режут, скручиВтоТ и штампуют большие ЛИСТЫ стали или вытягивают тончайшие нити, из которых делают ткани, Эти же механизмы можно обнаружить и в современных сложных автоматах, печатных и счетных машинах.
1 . Что называют простыми механизмами? 2. Для какой цели
применяют простые меха
низмы? Какой простой механизм применяли в Египте при строительстве
пирамид? Рис. 153
Рассмотрим самый простой и распространенный механизм 
рычаг.
На рисунках 149 и 150 показано, как рабочий для поднятия груза использует в качестве рычага лом. В первом случае рабочий с силой F нажимает на конец лома В, во втором приподнимает конец В.
Рабочему нужно преодолеть вес груза Р — силу, направленную вертикально вниз. Он поворачивает для этого лом вокруг оси, проходящей через единственную непоДвижнџю точку лома точку его опоры О. Сила 17 , с которой рабочий действует на рычат, меньше силы Р, таким образом, рабочий получает выигрыш в силе. Припомощи рычага можно поднять такой тяжелый груз, который без рычага поднять нельзя.
На рисунке 154 изображен рычаг, ось вращения которого О (точка опоры) расположена между точками приложения сил А и В. На рисунке 155 показана схема этого рычага. Обе силы F1 и F2, действующие на рычаг, направлены в одну сторону.
Кратчайшее расстояние между точкой опоры и прямой, вдоль которой действует на рычаг сила, называется плечом силы.
Чтобы найти плечо силы, надо из точки опоры опустать перпенДикуляр на ЛИНИЮ Действия силы.
Длина этого перпендикуляра и будет плечом данной силы. На рисунке 155 показано, что ОА — плечо силы F1; ОВ — плечо силы E2. Силы, действующие на рычаг, могут повернуть его вокруг оси в двух направлениях: по ходу или против хода часовой стрелки. Так, сила
|
|
|
|
Рис. 155
Глава щ, Pi00t' И моЩнОСТь Эне:тив
F1 (см. рис. 154) вращает рычаг по ходу
часовой стрелки, а сила F2 
вращает его ПРОТИВ хода часовой стрелки.
Условие, при котором рычаг находится в равновесии под деиствием приложенных к нему сил, можно установить на опыте. При этом надо помнить, что результат действия силы зависит не только от ее числового значения (модуля), но и от того, в какой точке она приложена к телу и как направлена.
К рычагу (см. рис. 154) по обе стороны от точки опоры подвешивают различные грузы так, чтобы рычаг каждый раз оставался в равновесии. Действующие на рычаг силы равны весам этих грузов. Для каждого случая измеряют модули сил и их плечи. Из опыта, изображенного на рисунке 154, видно, что сила 2 Н уравновешивает силу 4 Н. При этом, как видно из рисунка, плечо меньшей силы в 2 раза больше плеча большей силы.
На основании таких опытов было установлено условие (правило) равновесия рычага.
Рычаг находится в равновесии тогда, когда силы, действующие на него, обратно пропорциональны плечам этих сил.
Это правило можно записать в виде формулы:
где F1 и F2 — силы, действующие на рычаг, l1 и l2 — плечи этих сил (см. рис. 155).
Правило равновесия рычага было установлено Архимедом около 287—212 гг. до н, э.
Из этого правила следует, что меньшей силой можно
уравновеситн•при помощи рычага ббльшую силу. Пусть одно плечо рычага в 2 раза
больше другого (см. рис. 154). Тогда, прикладывая в 
точке А силу,
например, в 400 Н, мс»КНО в точке В уравновесить рычаг силой, равной 800 Н.
Чтобы поднять еще более тяжелый груз, нужно увеличить длину плеча рычага, на
которое действует рабочий.
Пример. С ПОМОЩЬю рычага рабочий поднимает плиту массой 240 кг (см. рис. 149). Какую силу прикладывает он к большему плечу рычага, равному 2,4 м, если меньшее плечо равно 0,6 м?
Запишем условие задачи и решим ее.
|
Дано: т — 240 кг н 9,8 — кг [2 |
|
|
|
|
|
2400 н. |
|
Тогда F1 |
0,6 м 2400 н • 600 н.
|
|
Решение:
По правилу равновесия
рычага 
откуда F1 — 
, где F2 Р— вес плиты.
Вес плиты Р = gm,
н
2,4 м Ответ.• 
600 Н.
в нашем примере рабочий преодолевает силу 2400 Н, прикладывая
к рычагу силу 600 Н. Он получает выигрыш в силе в 4 раза. Но при этом плечо, на
которое действует рабочий, в 4 раза длиннее того, на которое действует вес
плиты (l1 : [2 2,4 м •
Применяя правило рычага, можно меньшей силой уравновесить ббльшую силу. При этом плечо меньшей силы должно быть длиннее плеча большей силы.
1. Что представляет собой рычаг? 2. Что называют плечом силы? З. Как найти плечо силы? 4. Какое действие оказывают на рычаг силы?
5. В чем состоит правило равновесия рычага? 6. Кто установил правило равновесия рычаге
вам уже известно правило равновесия рычага:
Пользуясь свойством пропорции (произведение ее крайних чле-
нов равно произведению средних членов), запишем его в таком вид
F1l1 = F2l2.
В левой части равенства стоит произведение силы F1 на ее плечо [1, а в правой — произведение силы F2 на ее плечо [2.
Произведение модуля силы, вращающей тело, на ее плечо навывается моментом силы; он обозначается буквой М. Следовательно,
Рычаг находится в равновесии под деиствием двух сил, если момент силы, вращающей его по часовои стрелке, авен моменту силы, вращающей его против часовой стрелки.
Это правило, называемое пратплом моментов, можно записать
в 
виде
формулы:
мт = ль.
Действительно, в рассмотренном нами опыте (S 56) действующие на рычаг силы были равны 2 11 л Н, их плечи соответственно со. ставляли 4 и 2 деления рычага, т. е. моменты этих сил одинаковы при равно есии рычага.
Момент силы, как и всякая физическая величина, может быть 
измерена.
За ,еДиницу «момента силы принимается момент 
силы 1 Н, плечо
которой равно 1 м.
Эта единица называется ньютон„метр (Н • м).
Момент силы характеризует действие силы и доказывает, что оно
зависит одновременно и от модуля силы, и от ее плеча. Действительно, мы уже
знаем, например, что действие силы на дверь зависит и от модуля силы, и от
того, где приложена сила. Дверь тем легче повер
нуть, чем дальше от
оси вращения приложена действующая на нее сила. Гайку легче отвернуть длинным
гаечным ключом, чем корот
кита. Ведро тем легче поднять из колодца,
чем длиннее ручка вброта, 
ит. д.
1 . Что называется моментом силы? Как выражается момент силы через модуль силы и ее плечо? 2. В чем состоит правило моментов? З. Что принимают за единицу момента силы? Как называется эта единица?
Глава Ш. Работо •я мощность. Энеогир•
Правило рычага (или правило моментов) лежит в основе действия различного рода инструментов и устройств, применяемых в технике и быту там, где требуется выигрыш в силе или в пути.
Выигрыш в силе мы имеем при работе с ножницами. нож
НИЦЬ[
это рычаг (рис. 156), ось вращения которого проходит через винт, соединяющий
обе половины ножниц. Действующей силой F1 является мускульная сила руки
человека, сж им ающего ножницы. Противодействующей силой 172 сила сопротивления
того материала, который режут ножницами. В зависимости от назначения ножниц их
устройство бывает различным. Конторские ножницы, предназначенные Рис. 156 для
резки б и, имеют длинные лезвия и чти такой же длины ручки- Для резки бумаги не
требуется бОЛЬШОЙ силы, а длинным лезвием удобнее резать по прямой линии.
Ножницы для резки листового Рис, 157 металла (рис. 157) имеют ручки гораздо
длиннее лезвий, так как сила сопротивления металла велика и для ее
уравновешивания плечо действулощей силы приходится значительно увеличивать. Еще
больше разрис, 158 ница между длиной ручек и расстоянием режущей части от оси
вращения в кусачках (рис. 158), предназначенных для перекусывания проволоки.
Рычаги различного вида имеются у многих машин. Ручка швейной машины, педали или ручной тормоз велосипеда, педали автомобиля и трактора, клавиши пианино — все это примеры рычагов, используемых в данных машинах и инструментах.
Примеры применения рычагов это рукоятки тисков и верстаков, рычаг сверлильного станка и т. д.
На принципе рычага основано действие и рычажных весов (рис. 159). Учебные весы, изображенные на рисунке 48 (с. 42), дейстВуют как равноплечий рычаг. В Десятичных весах (рис, 159, г) плечо, к которому подвешена чашка с гирями, в 10 раз длиннее плеча, несущего груз. Это значительно упрощает взвешивание больших грузов. Взвешивая груз на десятичных весах, следует умножить массу гирь на 10.
а)
Рис. 159
Устройство весов для взвешивания грузовых вагонов автомобилей также основано на правиле рычага.
Рычаги встречаются также в разных частях тела животных и че
ловека.
Это, например, конечности, челюсти. Много рычагов можно указать в теле насе
:омых, птиц, в строении растений.
1. Пользуясь рисунком 156, объясните действие ножниц как рычага.
2. Объясните, почему ножницы для резки листового металла и кусачки (см. рис. 157 и 158) дают выигрыш в силе. З. Приведите примеры применения рычагов в быту, в технике.
Упражнение 30
1. Укажите точку опоры и плечи рычагов, изображенных на рисунке 160.
 |
а) б)
в) г) д)
Рис 160
З. Пользуясь рисунком 161, объясните, почему при гребле мы
получаем проигрыш в силе и для чего это нужно.
4. На рисунке 162 изсБражен разрез предохранительного клапана. Рассчитайте, какой груз надо повесить на рычаг, чтобы пар через клапан не выходил. Давление в котле в 12 раз больше нор- Рис, 161 мального атмосферного давле-
ния. Площадь клапана S = З см 2, вес клапана и вес рычага не
учитываты Плечи сил измерьте по рисунку. Куда нужно переместить груз, ес
ли давление пара в котле увеличится?
уменьшится? Ответ обоснуйте.
Рис 162 Рис- 163
5. На рисунке 163 изображен подъемный кран. Рассчитайте, какой груз можно поднимать при помощи этого крана, если масса противовеса 1000 кг. Сделайте расчет, пользуясь равенством моментов сил.
Блок представляет собой колесо с желобом, укрепленное в обойме. По желобу блока пропускают веревку, трос или цепь.
Неподвижным блоком называют такой блок, ось которого закреплена и при подъеме грузов не поднимается и не опускается (рис. 164).
IV. мощность. Энергия
Рис,
Неподвижный блок можно рассматривать к равноплечий рычаг, у которого плечи сил равны радиусу колеса (рис, 165): ОА ОВ = r, Такой блок не дает выигрыша в силе (F1 F2), но позволяет менять направление действия силы.
Подвижный блок — это блок, ось которого поднимается и опус
кается
вместе с грузом (рис. 166). На рисунке 167 показан соответствующиЙ ему рычаг: О
— точка опоры рычага, ОА— плечо силы Р и ОВ плечо силы Е. Так как плечо ОВ в 2
раза больше плеча 04, то сила в 2 раза меньше силы Р:
Таким образом, подвижный блок дает выигрыш
в силе в Раза.
о 
Рис рус. Т 67
Это можно доказать и пользуясь
понятием момента силы. При равновесии блока моменты сил F и Р равны друг другу.
Но плечо силы равно диаметру блока ОВ, плечо силы Р — его радиусу ОА. При
равенстве моментов силы имеютнеравные плечи. Значит, меньше та сила, плечо
которой больше. Поскольку плечо силы в 2 раза больше плеча силы Р, то сама сила
в 2 раза меньше силы Р.
Обычно на практике применяют комбинацию неподвижного блока с подвижным (рис. 168). Неподвижный блок применяется только для уд“тва. Он не дает выигрьшја в силе, но изменяет направление действия силы, например позволяет поднимать груз, стоя на земле. Рис 168
Вопросы1 . Какой блок называют неподвижным, а какой подвижным? 2. Для какой цели применяют неподвижный блок? З. Какой выигрыш в силе дает подвижный блок? 4. Можно ли рассматривать неподвижный и подвижный блоки как рычаги? Начертите схемы таких рычагов. 5. Назовите примеры применения блока.
S 60. Равенство работ при использовании простых механизмов.
«Золотое
правило» механики
Рассмот нные нами простые механизмы
применяют при совершении работы в тех случаях, когда надо действием одной силы
уравновесить другую силу.
Естественно, возникает вопрос: давая выигрыш в силе или в пути, не дают ли простые механизмы выигрыша и в работе? Ответ на поставленный вопрос можно получить из опыта.
Уравновесив на рычаге две какие-нибудь
разные по модулю силы F1 и F2 (рис. 169), Рис.
IV, мощносгь. Энергмя
ПРИВОДЯТ рычаг в движение. При этом оказывается, что за одно и то же время точка приложения меньшей силы F2 проходит больший путь $2, а точка приложения большей силы Р1 — меньший путь Sl, Измерив эти пути и модули сил, находят, что пути, пройден ные точ К0МИ приложения сил на рычаге, обратно пропорциональны силам:
Таким образом, действуя на длинное плечо рыч га, мы выигрываем в силе, но при этом во столько же раз проигрываем в пути.
Произведение сиЛы на путь s есть работа. Наши опыты показывануг, что работы, совершаемые силами, приложенными к рычагу, равны друг другу:
FIS1 F2S2, т. е. Ат = 442.
Итак, при использовании рычага выигрыша в работе не получают.
Пользуясь рычагом, мы можем выиграть или в силе, или в
расстоянии. Если мы силу приложим к длинному плечу, то выиграем в силе, но во
столько же раз проиграем в расстоянии. Действуя же си
лой на короткое плечо
рычага, мы выиграем в расстоянии, но во столько же раз проиграем в силе.
Существует легенда, что Архимед, восхищенный открытием правила рычага,
воскликнул: «Дайте мне точку опоры, и я подниму Землю!»
Конечно, Архимед не мог бы справиться с такой задачей, если бы даже ему и дали точку опоры (которая должна была бы находиться вне Земли) и рычаг нужной длины.
Для подъема Земли всего на Т см длинное плечо рычага должно было бы описать дугу огромной длины. Для перемещения длинного
конца рычага по этому пути, например со скоростью 1 , потребовас лись бы миллионы лет.
Не Дает выигрыша в работе и неподвижный
блок, в чем легко убедиться на опыте (см. рис. 165). Пути, проходимые точками 
приложения
сил и F2, одинаковы, одинаковы и силы, а значит, одинаковы и работы.
Можно измерить и сравнить между собой работы, совершаемые с 
помощью
подвижного блока. Чтобы при помощи подвижного блока
Глава пр. РаЬптл и мощность Энергия
поднять груз на
высоту Ь, необходимо конец веревки, к которому прикреплен динамометр, как
показывает опыт (рис. 170), переместить на высоту 2h.
Таким образом, получая выигрыш в силе в 2 раза, проигрывают в 2 раза в пути, следовательно, и пОДвижныЙ блок не Дает выигрыша в работе.
Многовековая практика показала, что ни один из механизмов не Дает выигрыша
в работе. Применяют же различные механизмы для того, чтобы в зависимости от
условий 
боты выиграть в силе или в пути.
Уже древним ученым было известно правило, применимое ко всем механизмам: во сколько раз выигрываем В СИ.ље, ВО столько раз проигрываем в расстояНИИ. Это правило назвали «золотым правалом» механики.
Какое соотношение существует между
силами, деиствующими на рычаг, и плечами этих сил (см. рис. 154)? 2. Какое соотношение
существует между путями, пройденными точками приложения рис 
сил на рычаге, и этими силами? З. В
чем проигрывают, пользуясь рычагом, дающим ВЫИГРЫШ в силе? 4. Во сколько раз
проигрывают в пути, используя для поднятия грузов подВИЖныЙ блок? 5. В чем
состоит «золотое правило» механики?
Упражнение З 1
1. С помощью подвижного блока груз подняли на высоту 1,5 м. На какую длину при этом был вытянут свободный конец веревки?
2. Рабочий с помощью подвижного блока поднял груз на высоту 7 м, прилагая к свободному концу веревки силу 160 Н. Какую работу он совершил? (Вес блока и силу трения не учитывать.) З. Как применить блок для выигрыша в расстоянии?
дл МОтНОСТь Энегиме;
4. Как можно соединить друг с другом неподвижные и подвижные блоки, чтобы получить выигрыш в силе в 4 раза? в 6 раз?
5. Решите задачу 2, учитывая вес блока, равный 20 Н.
Докажите, что закон равенства работ («Хоуое правило» механики) применим к гидравлической машине. Трение медсду поршнями и стенками сосудов не учитывайте.
Указание. Используйте для доказательства рисунок 132. Когда малый поршень под действием силы F1 опускается вниз на расстояние hl, он вытесняет некоторый объем жидкости. На столько же увеличивается объем жидкости под большим поршнем, который при этом поднимается на высоту h2.
Рассматривая устройство и действие рычага, мы не учитывали трение, а также вес рычага. В этих идеальных условиях работа, совершенная приложенной силой (эту работу мы будем называть полной), равна полезной работе по подъему грузов или преодолению какого-либо сопротивления.
На практике совершенная с помощью механизма полная работа всегда несколько больше полезной работы.
Часть работы совершается против силы трения в механизме и ло перемещению его отдельных частей. Так, применяя подвижный блок, приходится дополнительно совершать работу по подъему самого блока, веревки и по преодолению силы трения в оси блока.
Какой бы механизм мы ни взяли, полезная работа, совершенная с его помощью, всегда составляет лишь часть полной работы. Следовательно, обозначив полезную работу буквой Ап, а полную (затраченную) — буквой Аз, можно записать:
Ап < Аз,
ИЛИ
1.
Отношение полезной работы к полной работе называется коэффициентом полезного действия механизма.
Сокращенно коэффициент полезного действия обозначается кпд.
кпд
КПД обычно выражают в процентах и обозначают греческой буквой тт (читается «эта»):
— • 100 0/0.
Пример. На коротком плече рычага подвешен груз массой 100 кг. Для его подъема к длинному плечу приложили силу 250 Н. Груз подняли на высоту h1 0,08 м, при этом точка приложения движущей силы опустилась на высоту h2 = 0,4 м. Найти КПД рычага.
Запишем условие задачи и решим ее.
Решение:
• 100 0 0.
Полная (затраченная) работа А = Fh2. Полезная работа Ап = Ph1.
Р gm. н Р = 
кг- 1000 Н.
кг 
Ап = 1000 Н • 0,08 м = 80 Дж. Аз 250 Н • м- 100 Дж.
80 дж 
100 дж
Ответ: 80 0/0 .
Но «золотое правило» механики выполняется и в этом случае. Часть полезно боты 20 0/0 ее — расходуется на преодоление трения в оси рычага и противления воздуха, а также на движение самого рычага.
КПД любого механизма всегда меньше 100 0/0 Конструируя механизмы, стремятся увеличить их КПД. Для этого уменьшают трение в осях механизмов и их вес.
1 . Какую работу называют полезной, какую — полной? 2. Почему при применении механизмов для подъема грузов и преодоления других сопротивлений полезная работа не равна полной? З. Что такое коэффициент полезного деиствия механизма? 4. Может ли КПД быть больше единицы? Ответ обоснуйте, 5. Как можно увеличить КПД(7
тобы на заводах и фабриках могли работать
станки и машины, 
их приводят в движение электродвигатели,
которые расходуют при этом электрическую энергию
Автомобили и самолеты, тепловозы и теплоходы работают, расходуя энергию
сгорающего топлива, гидротурбины — энергию па 
дающей с высоты воды. Да и сами мы,
чтобы жить и работать, возобновляем запас своей энергии при помощи пищи.
Слово «энергия» употребляется нередко и в быту. Так, например
людей,
которые могут быстро выполнять большую работу, называют энергичными,
обладающими большой энергией. Что же такое энер
гия? Чтобы ответить на
этот вопрос, рассмотрим примеры
Сжатая пружина (рис. 171), распрямляясь, может совершить
работу, например поднять на высоту груз (рис. 172) или заставить двигаться
тележку.
171 Рис
172
Глава IV. Рљоота и мощность, Энергия
Рис, 173
Поднятый над землей неподвижный груз не совершает работы, но если этот груз упадет, то он совершит работу (например, может забить в землю сваю).
Способностью совершить работу обладает и всякое движущееся тело. Так, скатившийся с наклонной плоскости стальной шарик А (рис. 173), ударившись о деревянный брусок В, передвигает его на некоторое расстояние. При этом совершается работа.
Если тело или несколько взаимодействующих между собой тел (система тел) могут совершить работу, то говорят, что они обладают энергией.
Энергия физическая величина, показывающая, какую работу может совершить тело (или несколько тел). Энергию выражают в СИ в тех же единицах, что и работу, т. е. в Джоулях.
Чем 
работу может
совершить тело, тем большей энергией оно облаДает.
При совершении работы энергия тел изменяется. Совершенная работа равна изменению энергии.
Вопросы1 . На каких примерах можно показать, что работа и энергия физические величины, связанные друг с другом? 2. В каком случае можно сказать, что тело обладает энергией? З. Назовите единицы, в которых ВЫРаукают работу и энергию.
Потенциальной (от лат. потенциа — возможность) энергией пазывается энергия, которая определяется взаимным положением взаимодействулощих тел или частей одного и того же тела.
Потенциальной энергией, например, обладает тело, поднятое относительно поверхности Земли, потому что энергия тела зависит от взаимного положения его и Земли и их взаимного притяжения. Если считать потенциальную энергию тела, лежащего на Земле, равной нулю, то потенциальная энергия тела, поднятого на некоторую высоту, определится работой, которую совершит сила тяжести при падении тела на Землю. Обозначим потенциальную энергию тела Ел. Поскольку Еп = А, а работа, как мы знаем, равна произведению силы на путь, то
где F — сила тяжести.
Значит, в этом•случае и потенциальная энергия Еп равна:
Еп = Fh, или Еп = gmh,
где g -е— ускорение свободного падения, т — масса тела, — высота, на которую поднято тело.
Огромной потенциальной энергией обладает вода в реках, удерживаемая плотинами. Падая вниз, вода совершает работу, приводя в движение мощные турбины электростанций.
Потенциальную энергию молота копра
(рис. 174) используют в строительстве для совершения работы по забиванию свай.
Открывая дверь с пружиной, совершают работу по растяжению (или сжатию) пружины. За счет приобретенной энергии пружина, сокращаясь (или распрямляясь), совершает работу, закрывая дверь.
Энергию сжатых и закрученных пружин используют, например, в ручных часах, разнообразных заводных игрушках и пр.
Потенциальной энергией обдаДает всякое упругое Деформированное тело. Потенциальную энергию сжатого газа используют в работе тепловых двигателей, в отбойных молотках, которые широко применяют в горной промышленности, при строительстве дорог, выемке твердого грунта и т. д.
Энергия, которой обладает тело вследствие своего движения, называется кинетической (от греч. кинема — движение) энергией.
Кинетическая энергия тела обозначается буквой
Ек
Движущаяся вода, приводя во вращение турбины гидроэлектростанций, расходует свою кинетическую энергию и совершает работу. Кинетической энергией обладает и движущийся воздух — ветер.
От чего зависит кинетическая энергия? Обратимся к опыту (см. рис. 173). Если скатывать шарик А с разных высот, то можно заметить, что чем с большей высоты скатывается шарик, тем больше его скорость и тем дальше он передвигает брусок, т. е. совершает бблъшую работу. Значит, кинетическая энергия тела зависит от его скорости.
За счет скорости большой кинетической энергией обладает
летящая пуля.
Кинетическая энергия тела зависит и от его массы. Еще раз обратимся к опыту (см. рис. 173), но будем скатывать с наклонной плоскости другой шарик — большей массы. Брусок В передвинется дальше, т. е- будет совершена ббльшая работа. Значит, и кинетическая энергия второго шарика больше, чем первого.
Чем больше масса тела и скорость, с которой оно движется, тем больше его кинетическая энергия.
Для того чтобы определить кинетическую энергию тела, применяют формулу:
2
2 
где т — масса тела, — скорость движения тела.
Кинетическую энергию тел используют в технике. Удерживаемая
плотиной вода обладает, как было уже сказано, большой потенциальной энергией.
При падении с плотины вода движется и имеет 
такую. же большую
кинетическую энергию. Она приводит в движение турбину, соединенную с
генератором электрического тока. За счет кинетической энергии воды
вырабатывается электрическая 
энергия.
Энергия движущейся воды имеет большое значение в народном хозяйстве. Эту энергию используют с помощью мощных гидроэлектростанций.
Энергия падающей воды является экологически чистым источником энергии в отличие от энергии топлива.
Все тела в природе относительно условного нулевого значения обладают либо потенциальной, либо кинетической энергией, а иногда той и другой вместе. Например, летящий самолет обладает относительно Земли и кинетической и потенциальной энергией.
Мы ознакомились с двумя видами механической энергии, Иные виды энергии (электрическая, внутренняя и др.) будут рассмотрены в других разделах курса физики.
1 . Какую энергию называют потенциальной? 2. Приведите примеры тел, обладающих потенциальной энергией. З, Как показать, что деформированная пружина обладает потенциальной энергией? 4. Какую энергию называют кинетической? От каких величин она зависит? 5. В каком случае кинетическую энергию тела считают равной нулю? 6, Назовите случаи, когда тела обладают кинетической энергией. 7. Где используют кинетическую энергию текущей воды?
Упражнение 32
1. Какой потенциальной энергией
относительно Земли обладает 
тело массой 100 кг на высоте 10 м?
2. В
каких местах реки — у истоков или в устье — каждый куби
ческий метр воды
обладает большей потенциальной энергией? Ответ 
обоснуйте.
З. В какой реке — горной или равнинной — каждый кубическии 
метр
текущей воды обладает большей кинетической энергией? Почему?
4. Определите, какой кинетической энергией будет обладать пуля, вылетевшая из ружья. Скорость ее при вылете из ружья равна
600 , а масса — 7,5 г.
с
В природе, технике и быту можно часто наблюдать превращение одного вида механической энергии в другой: потенциальной в кинетическую и кинетической в потенциальную. Например, при падении
Глава дг. Работа и
мощность ЭНЕРГИЯ
воды с плотины ее
потенциальная энергия превращается в кинетическую. В качающемся маятнике
периодически эти виды энергии переходят друг в друга.
Явление превращения одного вида механической энергии в друго е
оиень удобно наолюдать на приборе, изображенном на рисунке 175.
Накручивая на ось нить, поднимают диск прибора. Диск, поднятый вверх, обладает
некоторой потенциальной энергией. Если его отпустить, то он, вращаясь, начнет
падать. По мере падения потенциальная энергия диска уменьшается, но вместе с
тем возрастает его кинетическая энергия. конце падения диск обладает таким
запасом кинетической энергии, что может опять подняться почти до прежней
высоты. (Часть энергии расходуется на работу против силы трения, поэтому диск
не достигает первоначальной высоты.) Поднявшись Рис, 175 вверх, диск снова
падает, а затем снова поднимается. В этом опыте при движении диска вниз его 
потенциальная
энергия превращается в кинетическую, а при движении вверх кинетическая энергия
превращается в потенциальную.
Превращение энергии из одного вида в другой происходит
также при ударе двух каких-нибудь упругих тел, например резинового мяча о пол
или стального шарика о стальную плиту.
Если поднять над стальной плитой стальной шарик (рис. 176) и затем выпустить его из рук, то он будет падать. По мере падения шарика его потенциальная энергия убывает, а кинетическая растет, так как увеличивается скорость движения шарика. При ударе шарика о плиту произойдет сжатие как шарика, так и плиты, Кинетическая энергия, которой шарик обладал, превратится в потенциальную энергию сжатой плиты и сжатого шарика. Затем благодаря действию упругих сил плита и шарик примут почти первоначальную форму. Шарик отскочит от плиты, а их потенци-
альная энергия вновь превратится в кинетическую энергию шарика: шарик отскочит вверх со скоростью, почти равной скорости, которой обладал в момент удара о плиту. При подъеме вверх скорость шарика, а следовательно, и его кинетическая энергия уменьшаются, потенциальная энергия растет. Отскочив от плиты, шарик поднимается почти до той же высоты, с которой начал падать. В верхней точке подъема вся кинетическая энергия шарика вновь превратится в потенциальную.
Явления природы обычно сопровождаются превращением одного вида энергии в другой.
Энергия может и передаваться от одного тела к другому. Так,
например, при стрельбе из лука потенциальная энергия натянутой те
тивы
переходит в кинетическую энергию летящей стрелы.
Вопросы1 . Как на опыте можно показать превращение одного вида механичесой энергии в другой? 2. Какие превращения энергии происходят при падении воды с плотины? З. Какие превращения энергии происходят при ударе стального шарика о стальную плиту?
Упражнение 33
1. Укажите превращение одного вида энергии в другой в следующих случаях: а) при падении воды водопада; б) при бросании мяча вертикально вверх; в) при закручивании пружины наручных часов; г) на примере дверной пружины.
2. Массы падающих тел одинаковы. Одинаковы
ли значения потенциальной энергии тел на одной и той же высоте и одинаковы ли
значения кинетической энергии на этой высоте?
З. Приведите примеры тел, обладающих одновременно
кинетической и потенциальной энергией. 
ЛАБОРАТОРНЫЕ РАБОТЫ
Определение цены деления измерительного прибора
Цель работы определить цену деления измерительного ци
линдра
(мензурки), научиться пользоваться им и определять с его помощью объем
жидкости.
Приборы и материалы: измерительный цилиндр (мензурка), стакан с водой, небольшая колба и другие сосуды.
Указания к работе
1. Рассмотрите измерительный цилиндр, обратите внимание на его деления. Ответьте на следующие вопросы:
1) Какой объем жидкости вмещает измерительный цилиндр, ес
ли
жидкость налита:
а) до верхнего штриха; б) до первого снизу штриха, обозначенного цифрой, отличной от нуля?
2) Какой объем жидкости помещается: а)
между 2-м и 3-м штрихами, обозначенными цифрами; б) между соседними (самыми
близкими) Жлтрихами мензурки?
2. Как называется последняя вычисленная вами величина? Как определяют цену деления шкалы измерительного прибора?
Запомните: прежде чем проводить измерения физической величины с помощью измерительного прибора, определите цену деления его шкалы.
З. Рассмотрите рисунок 7 учебника и определите цену деления изображенной на нем мензурки.
Лаборатоџ•.ьјо рлЬоте•
4. Налейте в измерительный цилиндр воды,
50
определите и запишите, чему равен объем налитой воды.
40
П р и м е ч а н и е. Обратите внимание на правильное положение глаза при отсчете объема жидкости. Вода у стенок сосуда немного приподнимается, в средней же части сосуда поверхность жидкости почти плоская. Глаз следует направить на деление, совпадающее с плоской частью поверхности (рис. 177).
5. Налейте полный стакан воды, потом осторожно перелейте воду в измерительный 177 цилиндр. Определите и запишите с учетом погрешности, чему равен объем налитой воды. Вместимость стакана будет такой же.
6. Таким же образом определите вместимость колбы, аптечных склянок и других сосудов, которые находятся на вашем столе.
7. Результаты измерений запишите в таблицу 6.
Таблица 6
|
№ опыта |
Название сосуда |
Объем жидкости |
з |
Вместимость сосуда Vc, смз |
|
1 2 з |
Стакан Колба Пузырек |
|
|
|
Измерение размеров малых тел
Цель работы научиться выполнять измерения способом рядов.
Приборы и материалы: линейка, дробь (или горох), иголка.
Указания к работе
1. Положите вплотную к линейке несколько (20—25 штук) дробинок (или горошин) в ряд. Измерьте длину ряда и вычислите диаметр одной дробинки.
Рис. 178 таблицу 7.
 |
|
S опыта |
Число частиц в ряду |
Длина ряда мм |
Размер одной частищы мм |
|
|
1(горох) 2(пшено) |
|
|
|
|
|
З (молекула) |
|
|
на фотографии |
истинный размер |
|
|
|
|||
Измерение массы тела на рычажных весах
Цель работы — научиться пользоваться рычажными весами и с их помощью определять массу тел.
Приборы и материалы: весы е разновесами, несколько небольших тел разной массы.
€ 
7 уп.ае.са
Указания к
1. Придерживаясь правил взвешивания, измерьте массу нескольких твердых тел с точностью до 0,1 г.
2. Результаты измерений запишите в таблицу 8.
Таблица 8
|
№ опыта |
Масса тела |
г |
|
1 2 |
|
|
Правила взвешивания
1.
 |
6олее легкую чашку
нужно положить полоски бумаги, картона и т. п.
2. Взвешиваемое тело кладут на левую чашку весов, а гири — на правую.
З. Во избежание порчи весов взвешиваемое тело и гири нужно 
опускать
на чашки осторожно, не роняя их даже с небольшой высоты.
4. Нельзя взвешивать тела более тяжелые, чем указанная на весах предельная нагрузка,
5.
На чашки весов нельзя класть мокрые, грязные, горячие тела, 
насыпать
без использования подкладки порошки, наливать жидкости.
6. Мелкие гирл нужно брать только пинцетом (рис. 179), положив взвешиваемое тело на левую чашку, на правую кладут
гирю, имеющую массу,
немного 66.льтую, чем масса взвешиваемого тела (подбирают на глаз с последующей
проверкой). При несоблюдении этого правила нередко случается, что мелких гирь
не хватает приходится взвеши-
Рис.
379 ванне начинать сначала.
Лабораторные
работы
Если гиря перетянет чашку, то ее ставят обратно в футляр, если же не перетянет — оставляют на чашке. Затем то же проделывают со следующей гирей меньшей массы и т. д., пока не будет достигнуто равновесие.
Уравновесив тело, подсчитывают общую массу гирь, лежащих на
чашке весов. Затем переносят гири с чашки весов в футляр.
Проверяют, все ли гири положены в футляр, находится ли каждая из них на предназначенном для нее месте.
Измерение объема тела
Цель работы — научиться определять объем тела с помощью измерительного цилиндра.
Приборы и материалы: измерительный цилиндр (мензурка), те
ла
неправильной формы небольшого объема (гайки, фарфоровые ролики, кусочки металла
и др.), нитки,
Указания к работе
1. Определите цену деления мензурки.
2. Налейте в мензурку столько воды, чтобы тело можно было полностью погрузить в воду, и измерьте ее объем.
З. Опустите тело, объем которого надо
измерить, в воду, удерживая его за нитку (рис. 180), и снова измерьте объем
жидкости.
4.
Проделайте опыты, описанные в пунктах 2 и З, с некоторыми 
другими
у
вас телами. 
5. Результаты измерений запишите в таблицу 9.
Таблица 9
|
№ опыта |
Название тела |
Началытыи объем жидкости В мензурке у1, см |
Объем жидкости и тела V2, см |
Объем тела
|
|
|
|
|
|
|
Лабораторные
Дополнительное задание
Если тело неправильной формы не входит в мензурку, то его
объем можно определить с помощью отливного сосуда (рис. 181). Перед измерением
сосуд наполняют водой до отверстия отливной труб
кие При погружении в
него тела часть воды, равная объему тела, выливается. Измерив мензуркой ее
объем, определяют объем погруженного в жидкость тела.
Рис.
180 Рис.
Определение плотности твердого тела
Цель работы --— научиться определять плотность твердого тела с помощью весов и измерительного цилиндра.
Приборы и материалы: весы с разновесами, измерительный цилиндр (мензурка), твердое тело, плотность которого надо определить, нитка (рис. 182).
Лабораторные работн
Рис, 182
Указания к работе
1. Повторите по учебнику S 21 «Плотность вещества».
2. Измерьте массу тела на весах (см. лабораторную работу № З).
З. Измерьте объем тела с помощью мензурки (см. лабораторную работу № 4).
4. Рассчитайте по формуле р --- плотность данного тела.
5. Результаты измерений и вычислений занесите в таблицу 10.
Таблица 10
|
Надым И е вещества |
Масса тела |
Объем тела V. смз |
Плотность вещества. р |
|
|
см |
кг |
|||
|
|
|
|
|
|
Градуирование пружины и измерение сил динамометром
Цель работы — научиться градуировать пружину, получать шкалу с любой
(заданной) ценой деления и с ее помощью измерять силы.
Приборы и материалы: динамометр, шкала которого закрыта бумагой, набор грузов массой по 102 г, штатив с муфтой, лапкой и кольцом.
Физика дпа
Указания к
1. Прочитайте в учебнике S 28 «Динамометр» .
2.
Укрепите динамометр с закрытой шкалой вертикально в лапке
штатива. Отметьте горизонтальной чертой начальное по 
ложение указателя
динамометра, это будет нулевая отметка шкалы.
З. Подвесьте к крючку динамометра груз, масса которого 102 г. На этот груз действует сила тяжести, равная 1 Н. -С такой же силой груз растягивает пружину динамометра. Эта сила уравновешивается силои упругости, возникающей в пружине при ее растяжении (деформации).
Новое положение указателя динамометра также отметьте гори 
зонтальной
чертой на бумаге.
П р и м е ч а н и е. Грузы массой 102 
можно
получить, прибавив 2 г (колечко из проволоки) к имеющимся грузам массой 
100
г.
4. Затем подвешивайте к динамометру второй, третий, четвертый грузы той же массы (102 г), каждый раз отмечая черточками на бумаге положение указателя (рис. 183).
5.
Снимите динамометр со штатива и против горизонтальных черточек,
начиная с верхней, проставьте числа
4... Выше числа О напишите: «ньютон» ,
6.
Измерьте расстояния между соседними черточками. Одинаковы ли они?
По
чему
(см. S 27)? На основании сделанного вывода. скажите, с какой силой растянут
пружину грузы массой 51 г; 153 г.
7. Не подвешивая к динамометру грузы,
получите шкалу с ценой деления 0,1 Н.
8.
Измерьте проградуированным динамометром вес какого-нибудь
тела, например кольца от штатива, лапки штати
ва, груза.
9.
Нарисуйте проградуированный ди-
Рис 
намометр.
Определение выталкивающей силы, действующей на погруженное в жидкость тело
Цель работы обнаружить на опыте выталкивающее действие жидкости на погруженное в нее тело и определить выталкивающую силу,
Приборы и материалы: динамометр, штатив с муфтой и лапкой, два тела разного объема, стаканы с водой и насыщенным раствором соли в воде.
Указания к работе
1. Повторите по учебнику S 49 «Архимедова сила» .
2. Укрепите динамометр на штативе и подвесьте к нему на нити тело. Отметьте и запишите в таблице показание динамометра. Это будет вес тела в воздухе.
З. Подставьте стакан с водой и опускайте муфту с лапкой и динамометром, пока все тело не окажется под водой. Отметьте и запишите в таблицу показание динамометра. Это будет вес тела в воде,
4. По полученным данным вычислите выталкивающую силу, действующую на тело.
5. Вместо чистой воды возьмите насыщенный раствор соли и снова определите выталкивающую силу, действующую на то же тело.
6. Подвесьте к динамометру тело другого объема и определите указанным способом (см. пункты 2 и З) выталкивающую силу, действующую на него в воде.
7. Результаты запишите в таблицу 11.
Таблица 11
|
Жидкость |
Вес тела в воздухе Р, Н |
Вес тела в жидкости Р1, Н |
Выталкивающая сила Е, Н
|
|||
|
|
Р |
|
|
|
17v 2 |
|
|
Вода Насыщенный раствор соли в воде |
|
|
|
|
|
|
На основе выполненных опытов сделайте выводы.
От каких величин зависит значение выталкивающей силы?
Выяснение условий плавания тела в жидкости
Цель работы — на опыте выяснить условия, при которых тело плавает и при которых тонет.
Приборы и материалы: весы с разновесами, измерительный цилиндр (мензурка), пробирка-цодлавок с пробкой, проволочный крючок, сухой песок, фильтровальная бумага или сухая трянка.
Указания к работе
1. Повторите по учебнику S 50 «Плавание тел» .
2. Насыпьте в пробирку столько песка, чтобы она, закрытая пробкой, плавала в мензурке с водой в вертикальном положении и часть ее находилась над поверхностью воды,
З. Определите выталкивающую силу, действующую на пробирку. Она равна весу воды, вытесненной пробиркой. Для нахождения этого веса определите сначала объем вытесненной воды. Для этого отметьте уровни воды в мензурке до и после погружения пробирки в воду, Зная объем вытесненной воды и плотность, вычислите ее вес.
4.
 |
Выньте пробирку из воды, протрите ее фильтровальной бумагой или
тряпкой. пределите на весах массу пробирки с точностью до 1 г и рассчитайте
силу тяжести, действующую на нее, она равна весу пробирки с леском в воздухе.
5. Насыпьте в пробирку еще немного песка. Вновь определите выталкивающую силу и силу тяжести. Проделайте это несколько раз, пока пробирка, закрытая пробкой, не утонет.
6. Результаты измерений и вычислений занесите в таблицу 12. Отметьте, когда пробирка плавает и когда тонет или ЕСД,ЛЬЈВает.
Таблица 12
|
№ опыта |
Выталкивающая сила, действујощая на пробирку, Н, 17 gp,ev |
Вес пробирки с песком Р, Н, Р А'тгт |
Поведение пробирки в воде (плавает пробирка или тонет) |
|
1 2 з |
|
|
|
7. Сделайте вывод об условии плавания тела
в жидкости.
Выяснение условия равновесия рычага
Цель работы проверить на опыте, при каком соотношении сил и их плеч рычаг находится в равновесии. Проверить на опыте правило моментов.
Приборы и материалы: рычаг на штативе, набор грузов, измерительная линейка, динамометр (рис, 184).
Указания к работе
1. Повторите по учебнику S 56 «Рычаг. Равновесие сил на рычаге» .
2. Уравновесьте
рычаг, вращая гайки на его концах так, чтобы 
он расположился
горизонтально.
З. Подвесьте два груза на левой части рычага на расстоянии, 
равном
примерно 12 см от оси вращения. Опытны»,« путем устано
вите, на каком
расстоянии вправо от оси вращения надо подвесить:
 |
новесие.
4. Считая, что каждый груз весит 1 Н, запишите данные и измеренные величины в таблицу 13.
Таблица 13
|
М опыта |
Сила на левой Части рычага, Н
|
Плечо см |
Сила на правой части рычага, Н |
Плечо см |
Отношение сил и плеч |
|
|
|
|
|||||
|
1 2 з |
|
|
|
|
|
|
5. Вычислите отношение сил и отношение плеч для каждого из опытов и полученные результаты запищите в последний столбик таблицы,
6. Проверьте, подтверждают ли результаты опытов условие равновесия рычага под действием приложенных к нему сил и правило моментов сил (5 57).
Лабораторные рд0оты
Дополнительное задание
Подвесьте три груза справа от оси вращения рычага на расстояНИИ 5 см.
С помощью динамометра определите, какую силу нужно приложить
на расстоянии 15 см от оси вращения правее грузов, чтобы 
удерживать рычаг в
равновесии (см. рис, 184).
рис. 184
Как направлены в этом случае силы,
действующие на рычаг? Запишите длину плеч этих сил. Вычислите отношение сил и
плеч 
для этого случая и сделайте
соответствующий вывод.
Определение КПД при подъеме тела по наклонной плоскости
Цель работы — убедиться на опыте в том, что полезная работа, выполненная с помощью простого механизма (наклонной плоскости), меньше полной.
Приборы и материалы: доска, динамометр, измерительная лента или ЛИНеИКа, брусок, штатив с муфтой и лапкой (рис. 185).
Указания к работе
1. Повторите по учебнику S 61 «Коэффициент полезного деЙствия механизма» .
Рис. 185
2. Определите с помощью динамометра вес бруска.
З. Закрепите доску в лапке штатива
внаклонном положении.
4. Положите брусок на доску, прикрепив к нему динамометр.
5.
Перемещайте брусок
с постоянной скоростью вверх по наклон 
ной доске.
6. Измерьте с помощью линейки путь s, который проделал брусок, и высоту наклонной плоскостиЬ.
7. Измерьте силу тяги Е.
8.
Вычислите полезную работу по формуле Ап
затраченкую — по
формуле Аз Fs.
! . Определите КПД аклонной плоскости:
А 
п ,
100 0 0
Аз
10. Результаты измерений и вычислений
занесите в таблицу 14,
Таблица 14
|
|
|
Ап, ДЖ |
|
F,'FI |
Аз, Дж |
• лоси, |
|
|
|
|
|
|
|
|
Дополнительное задание
1. Используя «золотое правило» механики, рассчитайте, какой выигрьпл в силе дает наклонная плоскость, если не учитывать трение.
2. Измените высоту наклонной плоскости и
для нее определите полезную, полную работу и КПД
МАТЕРИАЛ ДЛЯ ЧТЕНИЯ
К числу основных опытных доказательств того, что молекулы движутся, относится явление, которое первым наблюдал в 1827 г. английский ботаник Броун, рассматривая в микроскоп споры растений, находящиеся в жидкости.
Подобный опыт можно проделать, пользуясь краской или тушью,
предварительно растертой до таких мельчайших крупинок, которые видны лишь в
микроскоп. Размешав краску в воде, рассматри
вают полученную смесь
в микроскоп.
Можно увидеть, что крупинки краски непрерывно движутся. Самые мелкие из них беспорядочно перемещаются с одного места в другое, более крупные лишь беспорядочно колеблются. Такое перемещение спор растений в жидкости и наблюдал Броун. Поэтому движение очень мелких твердых частиц, находящихся в жидкости, и называют броуновским Движением.
Наблюдения показывают, что броуновское движение никогда не 
прекращается,
В капле воды (если не давать ей высохнуть) движение крупинок можно наблюдать в
течение многих дней, месяцев, лет. Оно не прекращается ни летом, ни зимой, ни
днем, ни ночью. В кусках кварца, пролежавших в земле тысячи лет, попадаются
иногда капельки воды, замурованные в нем. В этих капельках тоже наблюдали
броуновское движение плавающих в воде частиц.
Причина броуновского движения заключается в непрерывном,
никогда не прекращающемся движении молекул той жидкости, в которой находятся
крупинки твердого тела. Конечно, эти крупинки во много раз крупнее самих
молекул, и когда мы видим под микроскопом движение крупинок, то не следует
думать, что мы видим движение самих молекул. Молекулы нельзя видеть в обычный
микроскоп, 
но об их существовании и движении мы можем
судить по тем уда-
Р.ам, которые они производят, толкая
крупинки краски и заставляя 
их двигаться.
Можно привести такое сравнение. Группа людей играет на воде в
огромный
мяч. Они толкают мяч, и от толчков мяч движется то в од
ном, то в д рутом
направлении. Если наблюдать эту игру издали, то людей не видно, а беспорядочное
движение мяча происходит как будто без причины.
Так же мы не видим молекул, но понимаем, что от их толчков непрерывно и беспорядочно двигаются крупинки краски.
Открытие броуновского движения имело большое значение для изучения строения вещества. Оно показало, что тела Действительно состоят из отДельных частиц — молекул и что молекџлы нахоДятся в непрерывном беспоряДоњном Движении.
Мы живем в век начала освоения космоса, в век полетов космических кораблей вокруг Земли, на Луну и на другие планеты Солнечной системы. Нам часто приходится слышать и читать о том, что летчики-космонавты и все предметы на космическом корабле во время его свободного полета находятся в особом состоянии, называемом состоянием невесомости. Что же это за состояние и можно ли его наблюдать на Земле?
Невесомость -— сложное физическое явление. Однако некоторые представления о состоянии невесомости можно получить и в начале изучения физики.
4апомним, что иод весом тела мы понимаем
силу, с которой тело 
вследствие притяжения к Земле давит.на
подставку или растягивает 
подвес.
Представим себе такой случай: опора или подвес вместе с телом свободно падают. Ведь опора и подвес тоже телб, и на них также действует сила тяжести. Каков в этом случае будет вес тела, т. е. с какой силой тело будет действовать на опору или подвес?
Обратимся к опыту. Для опыта берут небольшое тело и подвешивают его к пружине (рис. 186, а), другой конец которой прикреплен к неподвижной опоре. Под действием силы тяжести тело начинает двигаться вниз, поэтому пружина растягивается до тех пор, пока возникшая в ней сила упругости не уравновесит силу тяжести. Затем пережигают нить, удерживающую пружину с телом, пружина вместе с телом падает. Наблюдая за пружиной, замечают, что растяжение ее исчезло
Материал для
(рис. 186, б). И пока пружина с телом
паДает, она остается нерастянутой. 
Следовательно, падающее тело не
Действует на паДающую вместе с телом пружину, В этом случае вес тела равен
нулю, но сила тяжести не равна нулю, она по-прежнему действует на тело и
заставлает его падать. Точно так же если тело и поДставка, на которой оно лежит,
ОџДут свободно паДать, то такое тело перестанет давить на подставку.
Следовательно, в этом случае вес тела буДепт равен нулю.
Подобные явления наблюдаются и на спутнике, обращающемся
вокруг Земли. 
Сам спутник и все находящиеся в нем тела,
включая космонавта, обращаясь во-
|
а) |
|
О) |
круг
Земли, как бы непрерывно свободно падают на Землю, Вследствие этого все на- |
|
|
Рис, 186 |
|
ходящиеся в спутнике тела не давят на |
подставки, а
подвешенные к пружине не растягивают ее. Про такие 
ела говорят, что они
находятся в состоянии невесомости.
Не закрепленные в корабле-спутнике тела свободно парят.
Жид,кость, налитая в сосуд, не давит на дно и стенки сосуда, поэтому она не
вытекает через отверстие в сосуде. Маятники часов покоятся в лю
бом положении,
в котором их поставили. Космонавту, чтобы удержать руку или ногу в вытянутом
положении, не требуется никакого усилия. У него исчезает представление о том,
где верх и где низ. Если сообщить какому-нибудь телу скорость относительно
кабины спутника, то оно будет двигаться прямолинейно и равномерно, пока не
столкнется с другими телами.
Вокруг Солнца движутся 9 больших планет (рис. 1,87). Все они 
удерживаются
около Солнца силами тяготения. Эти силы очень ве
лики. Например, между
Солнцем и Землей действует сила тяготения, равная примерно ЗО 000 000 000 000
000 000 000 Н З , 10 22 Н, или З • 10 19 кН. Большое
числовое значение этой силы объясняется тем, что массы Солнца и Земли очень
велики.
Среди больших планет Солнечной системы наименьшую массу имеет Меркурий — его масса почти в 19 раз меньше массы Земли.
п 
Рис. 187 Рис.
Масса самой большой планеты Солнечной системы
— Юпитера 
в 318 раз больше массы Земли. Вокруг
многих планет движутся их спутники, которые также удерживаются вблизи планет
силами тяготения. Спутник нашей Земли Луна самое близкое к нам небес
ное
тело. Расстояние между Луной и Землей равно в среднем 380 ООО км, Масса Луны в
81 раз меньше массы Земли,
Чем меньше масса планеты, тем с меньшей силой она притягивает к себе тела. Сила тяжести на поверхности Луны в б раз меньше силы тяжести, действующеи на поверхности Земли. Например, автомобиль, масса которого 600 кг, на Луне весил бы не 6000 н, как на Земле, а 1000 Н (рис, 188). Чтобы покинуть Луну, тела должны иметь ско-
км рость не 11 ,
как на Земле, а 2,если бы человек высадил-
с ся на Юпитер, масса которого во много раз больше массы Земли, то там онвесил. бы почти в З раза больше, чем на Земле.
Кроме 9 больших планет с их спутниками, вокруг Солнца
движется группа очень маленьких планет, которые называют астероиДами. Даже
самая большая из этих планет Ц е р е р а — по радиусу почти в 20 раз, а по
массе в 7500 раз меньше Земли. Сила тяжести на этих планетах так мала, что
человек, оттолкнувшись 
от поверхности такой планеты, мог бы
улететь с нее.
Вот как описывает К. Э. Циолковский в одном из рассказов условия пребывания человека на астероиде Веста, который имеет массу в 60 ООО раз меньшую массы Земли: «На Земле я могу свободно нести еще одного человека такого же веса, как я. На Весте с такою же легкостью могу нести в 30 раз больше, т. е. 60 человек. На Земле я могу подпрыгнуть на 50 см. На Весте такое же усилие дает прыжок на
Матероов див
зо м. это высота десятиэтажного дома или огромнейшей сосны. Там легко перепрыгивать через рвы и ямы шириной в порядочную реку, Можно перепрыгивать через 15-метровые деревья и дом. И это без разбега .
Свойством жидкости передавать во все стороны производимое
на нее давление объясняется явление, известное в физике под названи
ем
«гидростатический парадокс. (этим еловом называют неожиданное явление, не
соответствующее обычным представлениям). Рас
смотрим его.
На рисунке 189 изображены три сосуда различной формы, но с одинаковой площадью дна и одинаковой высотой столба жидкости в них. Масса жидкости в этих сосудах различна, но давление на дно во всех трех сосудах одинаково, его можно рассчитать по формуле: р gph.
А так как площадь дна у всех сосудов одинакова, то и сила, с
ко
торой
жидкость давит на дно этих сосудов, одна и та же. Она равна весу вертикального
столба АВГ)С' жидкости: Р gphS, здесь S площадь дна.
Эгот вывод легко проверить на опыте с прибором, изображенным на рисунке
190. Дном трех сосудов (1, 2, З, рис. 190) служит резино
вая пленка, укрепленная в стойке
прибора. Сосуды поочередно ввинчивают в стойку прибора и наливают в них воду,
дно при этом прогиба-
[ еџвдјљ
, и его движение передается стрелке. ОПыТ
показывает, что при оди ковых высотах столбов воДы е сосџДах стрелка от
клоняептсз на одно и то же шисло Делении ШКоЛЫ. А это означает, что сила, с
которой лсиДкость Давит на дно сосуда, не зависит от формы сосџДа, она равна
весу вертикального столба, основанием которого является дно сосуДа, а высотой —
высота столба лсцДкости,
Это утверждение, хотя оно нами обосновано и подтверждено опы
том,
все же кажется неправдоподобным парадоксальным. Однако ничего парадоксального в
нем нет, его можно объяснить законом Паскаля.
Рис- 190 Рис. 191
Рассмотрим «рисунок 191- На площадку МАГ дна
сосуда действует сила, равная весу столба жидкости KMNL, которая производит
давлежне pgh. По закону Паскаля такое давление передается и на площадкиАМ и NB.
Тогда сила, действующая на все дно АВ, будет равна весу вертикального столба
жидкости ABDC. Эта сила больше веса 
жидкост•й в сосуде З (см. рис. 190),
меньше веса жидкости в сосуде 2 и равна весу жидкости в сосуде 1.
Представьте себе, что суженную часть сосуда (см. рис. 191) мы
сделаем еще тоньше и длиннее. Тогда совсем небольшим количест
вом воды мы
сможем создать большое давление на дно. Таким опы
том поразил своих
современников в 1648 г. Паскаль. В прочную, наполненную водой н закрытую со
всех сторон бочку он вставил узкую
трубку (рис. 192) и, поднявшись на
балкон второго этажа дома, вылил в эту трубку кружку воды. Давление на стенки
бочки так возросло, что планки (клепки) бочки разошлись и вода из бочки стала
выливаться.
Глубина океанов достигает нескольких километров. Поэтому на дне океана огромное давление, Так, например, на глубине 10 км (а есть и ббльшие глубины) давление составляет около 100 000 000 Па (100 000 кПа).
Несмотря на это, вследствие малой сжимаемости воды, плотность ее на дне океанов лишь немного больше, чем вблизи поверх-
НОСТИ.
Как показывают специальные исследоГ{1НИЯ, и на таких
больших океанских глубинах живут рыбы и некоторые другие живые существа.
Организм этих рыб приспособлен к существованию в условиях большого давления. Их
тела способны выдержать давление в миллионы паскалеи. Понятно, что такое же
давление существует и внутри самих рыб.
Человек при специальной тренировке может без особых предохранительных средств погружаться на глубины до 80 м, давление воды на таких глубинах около 800 кПа. На ббльших глубинах, если не принять специальных мер защиты, грудная клетка человека может не выдержать давления воды.
При очистке дна рек, ремонте подводных частей кораблей, плотин, при подъеме затонувших судов людям приходится работать под водой на разной глубине. Дл: этого при- Рис. 302 меняют специальные воЭолазные костюмы
(рис. 193),
Водолазный костюм изготовляют из прорезиненной ткани и надевают его поверх
теплой одежды. На верхнюю часть костюма навинчивают металлический шлем с
окошками из толстого стекла, Ботинки водолаза имеют свинцовые подошвы, а на его
грудь и спину надевают свинцовые грузы, иначе водолаз в своем костюме не
погрузится в воду, В шлем по шлангу непрерывно подают воздух для дыхания.
Однако шланг стесняет движения водолаза под водой и уменьшает расстояние, на
которое он может удаляться от места погружения. На глубину до 90 м водолазы
могут опускаться под воду, беря с собой запас сжатого воздуха, накачанного в
прочные стальные баллоны. Такое снаряжение называют аквалангом (см. рис. 193),
Аквалангом пользуются и спортсмены-пловцы.
Для исследования моря на больших глубинах используют батисферы и батискафы (см. рис, 193), Батисферу опускают в море на стальном тросе со специального корабля. Батискаф не связан тросом с кораблем, он имеет собственный двигатель и может передвигаться на большой глубине в любом направлении.
Свойство газов передавать давление используют в технике при устройстве различных пневматичесћ>их машин (от лат. пневматикос воздушный; это машины, работающие посред-
Рис. 193 ством сжатого воздуха) и инструментов.
Сжатый воздух, например, применяют в работе заклепочных и отбойных молотков.
На рисунке 194 (слева) показана схема устройства отбойного молотка. Сжатый воздух подают по шлангу 1. Особое устройство 2, называемое золотником, направляет его поочередно то в верхнюю, то в нижнюю часть цилиндра. Поэтому воздух давит на поршень З то
Рис, 194 Рис. 195
с одной, то с другой стороны, что вызывает быстрое возвратно-поступательное движение поршня и пики молота 4. Последняя наносит быстро следующие друг за другом удары, внедряется в грунт или в уголь и откалывает его куски.
Существуют пескоструйные аппаратьь, которые дают сильнуто
струю воздуха, смешанного с песком. Их используют для очистки стен. Нередко
можно видеть работу специальных аппаратов, при
меняемых для окраски
стен, где краску распыляет сжатый воздух.
Сжатым воздухом Откр»ываот двери вагонов поездов метро и троллейбусов.
 |
При открывании стоп-крана сжатый воздух выпускается из
магистральной трубы, вследствие чего давление в правой части тормозного
цилиндра уменьшается. Сжатый же воздух, находящийся в девой части тормозного
цилиндра и в резервуаре, выйти не может, этому мешает клапан 2. Под действием
сжатого воздуха поршень тор
мозного цилиндра перемещается вправо,
прижимая тормозную колодку к ободу колеса, отчего и происходит торможение.
При наполнении магистральной трубы сжатым воздухом тормозные
КОЛОДУ<И отжимаются пружинами от колес
Изучение атмосферного давления имеет большую поучительнуто историю. Как и многие другие научные открытия, оно тесно связано с практическими потребностями людей.
Устройство насоса было известно еще в глубокой древности.
ОднаКО и древнегреческий ученый Аристотель, н его последователи объясняли
движение воды за поршнем в трубе насоса тем, что «при
рода боится пустоты».
Истинная же причина этого явления —-- давление атмосферы им была неизвестна.
В конце первой половины XVII в. во Флоренции — богатом торговом городе Италии строили так называемые всасывающие насосы. Он состоит из вертикально расположенной трубы, внутри которой имеется поршень. При подъеме поршня вверх за ним поднимается вода (см. рис. 116). При помощи этих насосов хотели поднимать воду на большую высоту, но насосы «отказывались» это делать.
 |
насосы не могут
поднять воду выше, чем на 18 итальянских локтей (— 10 м). Но разрешить вопрос
до конца он не успел. После смерти Галилея эти научные исследования продолжил
его ученик — Торричеллн. Торричелли занялся и изучением явления поднятия воды
за поршнем в трубе насоса, Для опыта он предложил использовать длинную
стеклянную трубку, а вместо воды взять ртуть. Впервые такой опыт (S 42) был
проделан его учеником Вивиани в 1643 г.
Раздумывая над этим опытом, Торричелли пришел к заключению, что ИстИнноЙ причиной поднятия в трубке ртути является давление воздуха, а не боязнь пустоты» Это давление производит воздух своим весом. (А что воздух имеет вес — было доказано Галилеем.)
Об опытах Торричелли узнал французский ученый Паскаль, Он
повторил опыт Торричелли с ртутью и водой. Однако Паскаль считал, что•для
окончательного доказательства факта существования ат
мосферного давления
необходимо проделать опыт Торричелли один раз у подножия какой-нибудь горы, а
другой раз на вершине ее и измерить в обоих случаях высоту ртутного столба в
трубке. Если бы на вершине горы столб ртути оказался ниже, чем у подножия ее,
то отсюда следовало бы заключить, что ртуть в трубке действительно
поддерживается атмосферным давлением.
«Легко понять, говорил Паскаль, — что у подножия горы воздух оказывает большее давление, чем на вершине ее, меж тем как
Рис. Рис. 197
нет никаких оснований предполагать, чтобы природа испытывала ббльшую
боязнь пустоты внизу, чем вверху»
Такой опыт был проведен, он показал, что давление воздуха на вершине той
горы, где проводились опыты, было почти на 100 мм РТ. ст. 
меньше, чем у подножия горы. Но
Паскаль этим опытом не ограничился. Чтобы еще раз доказать, что ртутный столб в
опыте Торричелли удерживается атмосферным давлением, Паскаль поставил другой
опыт, который он образно назвал доказательством пустоты в пустоте.
 |
женного на рисунке
196, где А —- прочный полый стеклянный сосуд, в который пропущены и впаяны две
трубки: одна — от барометра Б, другая (трубка с открытыми концами) от барометра
В.
Прибор устанавливают на тарелку воздушного насоса. В начале
опыта давление в сосуде А равно атмосферному, оно измеряется раз
ностью высот
h столбов ртути в барометре Б. В барометре же В ртуть стоит на одном уровне.
Затем из сосуда А воздух выкачивается насосом. По мере удаления воздуха уровень
ртути в левом колене баро
метра Б понижается, а в левом колене
барометра В повышается. Когда воздух будет полностью удален из сосуда А,
уровень ртути в узкой трубке барометра Б упадет и сравняется с уровнем ртути в
его широком колене. В узкой же трубке барометра В ртуть под действием
атмосферного давления поднимается на высоту h (рис. 197). Этим опытом Паскаль
еще раз доказал существование атмосферного давления.
Опыты Паскаля окончательно опровергли теорию Аристотеля о «60язни пустоты» и подтвердили существование атмосферного давления.
Существует легенда о том, как Архимед пришел к открытию, что выталкивающая сила равна весу жидкости в объеме тела.
Царь Гиерон (250 лет до н. э.) поручил ему проверить
честность мастера, изготовившего золотую корону. Хотя корона весила столько,
сколько было отпущено на нее золота, царь заподозрил, что она 
изготовлена
из сплава золота с другими, более дешевыми металлами. Архимеду было поручено
узнать, не ломая короны, есть ли в ней примесь.
Достоверно неизвестно, каким методом пользовался Архимед, но можно предположить следующее. Сначала он нашел, что кусок чистого золота в 19,3 раза тяжелее такого же объема воды. Иначе говоря, плотность золота в 19,3 раза больше плотности воды.
Архимеду надо было найти плотность вещества короны, Если эта плотность оказалась бы больше плотности воды не в 19,3 раза, а в меньшее число раз, значит, корона была изготовлена не из чистого золота.
Взвесить корону было легко, но как найти ее объем, ведь
корона была очень сложной формы. Много дней мучила Архимеда эта задача. И вот
однажды, находясь в бане, он погрузился в наполненную водой ванну, и его
внезапно осенила мысль, давшая.решение задачи. Ликующий и возбужденный своим
открытием, Архимед восклик
нут. «Эврика! Эврика!» , что значит:
«Нашел! Нашел!»
Архимед взвесил корону сначала в воздухе, затем в воде. По разнице в весе он рассчитал выталкивающую силу, равную весу воды в объеме короны. Определив затем объем короны, он смог вычислить ее плотность, а зная плотность, ответить на вопрос царя: нет ли примесей дешевых металлов в золотой короне? Плотность вещества короны оказалась меньше плотности чистого золота. Тем самым мастер был изобличен_ђ обмане, а наука обогатилась замечательный открытием.
Задача о золотой короне побудила Архимеда заняться вопросом о плавании тел. В результате появилось замечательное сочинение «О плавающих телах», которое дошло до нас. В этом сочинении Архимедом сформулировано:
Тела, которые тяжелее жиДњости, буДучи опущены в нее, погружаются все глубже, пока не Достигают. дна, и, пребывая в жиДкости, теряют в своем весе столько, СКОЛЬКО весит жиДкость, взятая в оббеме тел.
Материал пля чтения
S 9. Энергия движущейся воды и ветра, Гидравлические и ветряные двигатели
Всякое тело, поднятое над Землей, обладает потенциальной
энергией. Это в равной степени относится и к воде. Например, вода объ
емом
1 мз на высоте 50 м обладает потенциальной энергией:
Е 
9,8 Ц •
1000 • 1м з • 50 м = 500 ООО Дж 500 кДж. м
При падении воды с этой высоты совершится работа А— 500 кДж.
Но в природе сравнительно редко встречаются большие водопады. Чаще всего русла рек имеют небольшой уклон. В этих случаях для создания давления (напора), необходимого для работы гидравлических двигателей, приходится поднимать уровень воды в реке искусственно, при помощи плотин. За счет энергии поднятой воды гидравлические двигатели могут совершать механическую работу.
Один из простейших и древнейших двигателей водяное колесо. Наиболее совершенные гидравлические двигатели воДяные турбины. В таких турбинах вода отдает энергию колесу, приводя в движение лопасти турбины. Рабочее колесо турбины соединено с валом электрического генератора, дающего электрический ток.
Ветряные Двигатели используют энергию Движущегося возДуха —- ветра. Энергию ветра иногда называют энергией «голубого угля».
Ветер представляет собой источник
дешевой энергии, но этот источник энергии обладает большим непостоянством, — в
этом его неудобство.
Ветряные двигатели известны с древнейших времен. Современный довольно мощный ветряной двигатель изображен на рисунке 198. Двиэкущиеся массы воздуха оказывают давление на наклонные плоскости крыльев ветряных двигателей и приводят их в движение. Вращательное движение крыльев при помощи системы передач передается механизмам, выполняющим какую-либо работу.
Экономически целесообразно использовать 
ветродвигательные
установки там, где ветры дуют часто и сильно. Например, в Поволжье, Казахстане,
на Алтае. Удобно их использовать и в отдаленных районах, куда не поступает
энергия
чтения
от электростанций, куда трудно подвозить топливо, например в дальних или высокогорных экспедициях. Они, как и гидравлические двигатели, имеют преимущества перед двигателями, в которых источником энергии служит топливо или радиоактивное вещество.
Во-первых, водяные и воздушные двигатели, после того как они построены, уже не требуют затрат на топливо. Энергия, используемая в них, — энергия текущей воды и ветра поставляется самой природой, возобновляется.
Во-вторых, работа этих двигателей не сопровождается
выделением вредных отходов: газов, образующихся при сгорании топлива или 
радиоактивных
отходов, т. водяных и ветряных двигателях используются экологически чистые
источники энергии. В некоторых местах применяют еще один вид экологически
чистых двигателей, использующих энергию приливов и отливов воды в морях и
океанах, причиной которых является сила всемирного тяготения.
5 10. Центр тяжести тела
При создании машин, механизмов и различных конструкций важно
знать, при каких условиях они будут устойчивыми, т. е, находиться в равновесии.
Каким же образом можно добиться равновесия тела? Возьмем линейку и, обвязав ее
петлей, подвесим на нити. Затем, перемещая петлю по линеике, можно найти положение,
в котором линейка удет находиться в равновесии. В этом случае говорят, что
линейка подвешена в центре тяжести. Центр тяжести имеется 
каждого
тела. Что же такое центр тяжести? Гааделим мысленно тело на несколько частей.
На каждую часть будет действовать сила тяжести, которая всегда направлена
вертикально вниз (рис. 199).
Точку приложения равнодействурщей сил тяжести, действующих на отдельные части тела, называют центром тяжести тела (см. рис. 199).
Матщлекв• доп чтонив
0) в)
Рис, 200
Как же найти центр тяжести в различных твердых телах?
Проделаем следующий опыт. Возьмем фигуру неправильной формы из картона (рис.
200, а) и подвесим ее на гвоздь вместе с, отвесом. На фигуру действуют две
силы: сила тяжести и сила упругости. Поскольку картон находится в покое, то эти
две силы озаимно уравновешиваются, т. е. они равны по величине и направлены в
разные стороны, Это значит, что точки приложения сил лежат на одной
вертикальнои прямой, отмеченной отвесом,
Проведем на фигуре вертикальную линию по отвесу. Затем
подвесим ее в другой точке и снова проведем по отвесу вертикальную лиНИк) (рис.
200, б). Сколько бы ни проводили таким способом ЛИНИЙ, 
все они пересекутся в
однои точке, которая и будет центром тяжести тела С (рис. 200, в). Проверить
это можно, если на острие карандаша поместить фигуру в наиденном центре
тяэкести. Она окажется в равновесии (рис. 200, г).
Во время опыта мы несколько раз меняли положение картонной фигуры, но центр тяжести ее оставался в одной и той же точке.
Рис, 201 Рис. 202
При любом положении тела центр тяжести его нахоДится в одной и той же точке.
Например, центр тяжести шара лежит в его геометрическом центре, у цилиндра он находится на середине линии, соединяющей центры его оснований, у параллелепипеда — в точке пресечения диагоналей (рис. 201). Иногда центр тяжести может находиться и вне тела. Например, у кольца он лежит на пересечении диаметров Фис. 202).
Положение центра тяжести может изменяться только при изменении относительного расположения частей тела.
11. Условия
равновесия тел
Раздел механики, изучающий условия равновесия тел, называется статикой.
Рассмотрим различные случаи равновесия тел, имеющих одну точку опоры.
Повесим на гвоздь линеику так, чтобы она заняла положение равновесия (рис. 203, а). Если линейку отклонить в сторону, то под действием силы тяжести она возвратится в прежнее положение,
Равновесие, при котором выведенное из положения равновесия тело вновь к нему возвращается, называют устойчивым.
При устойчивом равновесии центр тяжести тела расположен ниже оси вращения и нахоДится на вертикальной прямой, прохоДящей через эту ось.
Теперь расположим линейку таким образом, чтобы центр тяжести находился на одной вертикальной линии с точкой опоры, но выше нее (рис. 203, б). Если линейку вывести из положения равновесия, то
Рисе. 203
Материал для чтения
она больше в начальное положение не вернется, так как сила тяжести, действующая на линейку, препятствует этому.
Равновесие, при котором выведенное из равновесия тело не возвращается в начальное положение, называют неустойчивым.
При неустойчивом равновесии центр тяжести тела расположен выше осц вращения и нахоДится на вертикальной прямой, прохоДящей через эту ось.
Подвесим линейку на гвоздь так, чтобы центр тяжести линейки и точка опоры совпадали (рис. 203, в), Линейка от толнков будет менять свое положение, но равновесия не потеряет.
Равновесие называют безразличным, если при отклонении или перемещении тела оно остается в равновесии.
При безразличном равновесии ось вращения тела проходит через его центр тяжести, при атом центр тяжести тела остается на одном и том же уровне при любых положениях тела.
Шарик, находящийся в устойчивом равновесии, показан на рисунке 204, а, в неустойчивом — на рисунке 204, б и в безразличном — на рисунке 204, в.
Вид равновесия можно установить по изменению положения Центра
тяжести тела, когда его выводят из состояния равновесия. Если центр тяжести при
этом поднимается, равновесие устойчивое, если центр тяжести при этом
опускается, равновесие тела неустойчивое, 
если центр тя•жести в
любом положении тела остается на одном уров-
не, то равновесие тела безразличное.
В устойчивом
равновесии находится любое тело, висящее на нити: лампа, люстра, грузик отвеса
и т. д.
а)В безразличном
равновесии находятся колеса автомобиля, велосипеда и другие вращающиеся части
машин, у которых ось вращения проходит через их центр тяжести.
Цирковые артисты, например, при ходьбе по канату сохраняют равновесие, изменяя положение своего центра тяжести.
Теперь рассмотрим
условия равновесия тел, имеющих площадь опоры. Большинство предметов,
окружающих нас. опирается на некоторую площадь. Например, дома, аврис „ 204
томобили, сталки и т. д.
Материал для чтения
бу в)
Рис, 205
Возьмем призму на шарнирах (рис. 205, а). К центру тяжести призмы прикрепим отвес. Будем постепенно менять форму призмы.
Равновесие призмы остается устойчивым, пока линия отвеса про
ходит
через площадь опоры (рис. 205, б). Как только линия отвеса оказывается на
границе площади опоры, равновесие становится неустойчивым (рис. 205, 6). При
незначительном отклонении вправо призма опрокидывается.
Об устойчивости положения тела можно также судить по величи
не
угла поворота, необходимого для приведения тела в неустойчивое равновесие .
Чтобы тело заняло положение неустойчивого равновесия, его
надо повернуть вокруг оси, проходящей через линию опоры. Чем боль
ше угол (х,
на который нужно для этого повернуть тело (рис. 206), тем устойчивеё
первоначальное положение тела.
Величина угла поворота, а следовательно, и устойчивость тела
зависят от размеров площади, на которую оно опирается, и от поло
жения его
центра тяжести.
б)
Рис. 206
От ы к упражнениям
Упр. 4. З. 657 
.
5. 4 м 
Упр. 5. 2. 16,2 км.
Упр. 
м . З. = кг.
4.
о 12 120 кг . 5. 1,6
см см
Упр. 8. 1. 0,4 кг; 0,5 кг; 6,8 кг. 2. 120 см з . З. 4 кг, 4. - 53.
Упр. 9. 1. 34 н; 4 н; 15 кн; - 0,6 н.
2. 500 н; з н. з. 71 кг, 5. 50 н; 50 н. 
Упр. 11. 1. 900 н. 2. 10 н. з. 700 н.
Упр. 12. 2. 47 кпа; = в З раза. З. 6000 кпа (6 103 кпа). 4. 1500 Па; в 10 раз меньше.
Упр. 14. З. Изменилось. Одинаково.
Упр. 15. 1. 6 кпа; 4,8 кпа; 82 кпа. 2. 112 000 кпа. З. 50 см 2 .
Упр. 19. 1. 10,3 м. 2. 28,4 кн.
Упр. 20. г) 1000 ГПа, 750 мм РТ. ст.
Упр. 21. 2 - 460 м. З. 1013 гПа. 4. 162 кн.
Упр. 22. 1. 10,3 м, 2. = 13 м; 76 см.
Упр. 23. 1. 120 т. 2. В 90 раз, в 100 раз.
Упр. 24. з. 0,98 н; 0,784 н. 4. 45 кн; 25,5 кн.
Упр. 26, 1. Уменьшится. 2. 10 000 М З . з. 16 кн.
Упр. 28. з. зоо кдж. 4, 240 кд
Упр. 29. 1. 180 квт. 2. = 55 вт. з. 120 000 кдж. 4. 750 вт.
6. 2,9 квт.
Упр. 30. 5. 416 кг
Упр. 31. 1. З м. 2. 2240 Дж. 5. 2380 Дж. Упр. 32. 1. 10 кдж, 4. 1350 Дж.
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ
S 1. Что изучает физика
Некоторые физические термины
З. Наблюдения и опыты
S 4. Физкгческие величины, Измерение физических величин
S 5. Точность и погрешность измерений . S 6. Физика и техника .
лава
ПЕРВОНАЧАЛЬНЫЕ СВЕДЕНИЯ О СТРОЕНИИ ВЕЩЕСТВА
S 7. Строение вещества 
16
S 8. Молекулы
18
S 9. Диффузия
в газах, жидкостях и твердых телах20 S 10. Взаимное притяжение и отталкивание
молекул
. 23
S 11. Агрегатные состояния вещества. 26
S 12. Различие в молекулярном
строении твердых тел, жидкостей и газов . . . 28
Глава П
ВЗАИМОДЕЙСТВИЕ ТЕЛ
S 13. Механическое движениезо
S 14. Равномерное и неравномерное движение. . 32
S 15. Скорость. Единицы скорости
S 16. Расчет пути и времени движения. 
38
S 17. Инерция 
. 40
S 18. Взаимодействие тел. . 42 S 19.
Масса тела. Единицы массы. . .44 S 20. Измерение массы тела на весах 
. 46
S 21. Плотность вещества . .
48
S 22. Расчет массы и объема тела по его плотности .52
S 23. Сила . . 54
S 24 .
57
S 25. . 59
S 26, Вес тела . 61
S . 62 S 28.Динамометр . 65 S 29, Сложение двух сил, направленных по одной прямой.
РаАћодействующая сил .
68
S 30. Сила трения70
S 31. Трение покоя73
S 32. Трение в природе и технике . 74
Глава III
ДАВЛЕНИЕ ТВЕРДЫХ ТЕЛ, ЖИДКОСТЕЙ И ГАЗОВ
S 33.
Давление. Единицы давления 
, 77 S 34. Способы уменьшения и
увеличения давления . 
. 80 S 35. Давление газа
82
S 36. Передача давления жидкостями и газами. Закон Паскаля ,
85
S 37. Давление в жидкости и газе
88
S 38. Расчет давления жидкости на дно и стенки сосуда
90
S 39. Сообщающиеся сосуды
93
S 40. Вес воздуха. Атмосферное давление. . . . . .
97 S 41. Почему существует воздушная
оболочка Земли
99
S 42. Измерение атмосферного давления. Опыт Торричелли . . 101
S 43. Барометр-анероид 105
. 106
S 45. Манометры , . . 108
S 46. Поршневой жидкостный насос . по
S 47. Гидравлический пресс . 111
S . 114
S 49. Архимедова сила . 117 S 50. Плавание тел 120
S 51. Плавание судов. . . 124
S 52. Воздухоплавание . 126
Глава
РАБОТА И МОЩНОСТЬ. ЭНЕРГИЯ
S 53. Механическая работа. Единицы работы
129 S 54. Мощность. Единицы мощности 132
S 55. Простые механизмы . 136
S 56. Рычаг. Равновесие сил на рычаге 137
S 57, Момент силы. 140
S 68. Рычаги в технике, быту и природе . . . , 142 S 59. Применение закона равновесия рычага к блоку 145 S 60. Равенство работ при использовании простых механизмов.
«Золотое правило» механики.
147
S 61. Коэффициент полезного действия механизма
150
S 62. Энергия
152
S 63. Потенциальная и кинетическая энергия
153
S 64. Превращение одного вида механической энергии в другой .
, 
156
Лабораторные работы . . ,
. 
. 159
Материал для чтения 172
S 1. Броуновское движение 172 S 2. Невесомость . . . . . . . . . . . 1 73
S З. Сила тяжести на других планетах . 174 S 4. Гидростатический парадокс. Опыт Паскаля . 176
S 5, Давление на дне морей и океанов. Исследование морских глубин . 178
S 6. Пневматические машины и инструменты . 179
S 7. История открытия атмосферного давления . . 181
S 8, Легенда об Архимеде . . 183
|
|
|
ΌΡΟΦα
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
кг
сины в и 
з
930 г
щаться вверх и вниз.
К простым механизмам относятся: ры• чаг
и его разновидности — блок, ворот;
