удк 373.167.1:512 ББК 22.141я721

Александрова Л. А.

А46 Алгебра. 8 класс. Контрольные работы для учащихся общеобразовательных учреждений / Л. А. Александрова ; под ред. А. Г. Мордковича. 2-е изд., стер. — М. : Мнемозина, 2009.

ISBN 9786-346-01304-4

Пособие включает примерное тематическое планирование курса алгебры в 8-м классе и контрольные работы в четырех вариантах по всем темам курса. удк 373.167.1:512

ББК 22.141я721

Учебное издание

Александрова Лидия Александровна

АЛГЕБРА

8 класс

КОНТРОЛЬНЫЕ РАБОТЫ для учащихся общеобразовательных учреждений

Генеральный директор издательства М. И. Безвиконная

Главный редактор К. И. Куровский. Редактор С. В. Бахтина

Оформление и художественное редактирование: Т. С. Богданова

Технический редактор Г. З. Кузнецова. Корректор Л. В. Яковлева

Компьютерная верстка: А. А. Горкин

Санитарно-эпидемиологическое заключение

 77.99.60.953.Д.003577.04.09 от 06.04.2009.

Подписано в печать 18.06.09. Формат 60х90 ¹/16. Бумага офсетная. Гарнитура «Школьная». Печать офсетная. Усл. печ. л. 2,5. Тираж ЗО 000 экз. Заказ № 317.

Издательство «Мнемозина». 105043, Москва, ул. 6-я Парковая, 29 б. тел.: 8 (499) 367 5418, 367 5627, 367 6781; факс: 8(499) 165 9218.

                            E-mail: ioc@mnemozina.ru         www.mnemozina.ru

Магазин «Мнемозина»

(розничная и мелкооптовая продажа книг, «КНИГА — ПОЧТОЙ»). 105043, Москва, ул. 6-я Парковая, 29 б.

Тел./факс: 8 (495) 783 8284; тел.: 8 (495) 783 8285.

E-mail: magazin@mnemozina.ru

Торговый дом «Мнемозина» (оптовая продажа книг).

Тел. [факс: 8 (495) 665 6031 (многоканальный). E-mail: td@mnemozina.ru

Отпечатано в ООО «Финтрекс».

115477, Москва, ул. Кантемировская, 60.

 «Мнемозина», 2007

О «Мнемозина», 2009

О Оформление. «Мнемозина», 2009

ISBN 9786-346-01304-4                                             Все права защищены

ПРЕДИСЛОВИЕ

Предлагаемый сборник контрольных работ предназначен для тех учителей математики, которые используют в своей преподавательской деятельности УМК, созданный авторским коллективом под руководством А. Г. Мордковича. Обращаем внимание учителя на то, что сборник ориентирован на переработанные издания учебника и задачника, опубликованные издательством «Мнемозина» в 2007 году.

Сборник включает 9 контрольных работ. Каждая из них представлена в четырех вариантах, причем в ряде случаев третий и четвертый варианты чуть сложнее, чем первый и второй (это облегчит учителю дифференцированный подход к учащимся). Последняя работа является итоговой, рассчитанной на 2 урока. Она охватывает содержание всего годичного курса алгебры и проводится при наличии соответствующих возможностей в период завершающего повторения.

Все контрольные работы имеют единую структуру. Каждый вариант состоит из трех частей. Первая часть (до первой черты) включает материал, соответствующий базовому уровню математической подготовки учащихся. Выполнение этой части контрольной работы гарантирует школьнику получение удовлетворительной оценки. Вторая часть (от первой до второй черты) содержит задания, несколько более сложные с технической точки зрения. Третья часть (после второй черты) включает задания, которые в определенном смысле можно охарактеризовать как творческие. Чтобы получить хорошую оценку, учащийся должен выполнить кроме базовой части вторую или третью часть работы. Чтобы получить отличную оценку, ученику необходимо выполнить все три части работы.

Советуем не снижать итоговую оценку за контрольную работу при наличии одной ошибки или погрешности, допущенной учащимся в базовой части работы.

В конце пособия приведено примерное тематическое планирование из расчета З часа в неделю.

з

.N2 1

1

1. При каких значениях переменной алгебраическая дробь

 не имеет смысла?

5- 3х

2. Найдите значение выражения 25 — при х = —1,5.

З. Выполните действия:

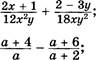
а)в) 2а(а — 1) 2а(а + 1) '

6)г) 2х—4 — х² — 2х'

4.   Прогулочный теплоход по течению реки проплывает 12 км за такое же время, что и 10 км против течения. Найдите скорость течения реки, если собственная скорость теплохода 22 км/ч.

5.   Докажите, что при всех допустимых значениях перемен-

                                                          10           1           1

ной значение выражения 25 — U 5 + Н — 5 _           положительно.

4

.М 1

2

1.  При каких значениях переменной алгебраическая дробь  не имеет смысла?

                                                                                    4 — 7х2        6х2

2.  Найдите значение выражения 2—х           2—х

з при х = —

З. Выполните действия:

              а) 18а2Ь         24ab² '                ) 4у(у - 3)        4у(у + 3)'

б)

4.  Туристы проплыли на лодке по озеру 18 км за такое же время, что и 15 км против течения реки, впадающей в озеро. Найдите скорость движения лодки по озеру, если скорость течения реки 2 км/ч.

5.  Докажите, что при всех допустимых значениях переменной значение выражения + 2 а4 _ 4 _ 2 отрицательно.

5

1

                         а + 4 80²                                             3х2у-з 2     (3x)3z-2

5⁴ • 0,2-2

      2. Вычислите:              

1252

З. Решите уравнение х + 81х-1 = 18.

5. Из пункта М в пункт N, находящийся на расстоянии 4,5 км от пункта М, вышел пешеход. Через 45 мин вслед за ним выехал велосипедист, скорость которого в З раза больше скорости пешехода. Найдите скорость пешехода, если в пункт л^т он прибыл одновременно с велосипедистом.

Ль

2

 Т² — 64 (2С)³ • а^б 5m 15 т ²

2 ⁵ • 0,5-6

2. Вычислите:

163

З. Решите уравнение 64х + х-1 = -16.

5. Из города А в город В, находящийся на расстоянии 200 км от города А, выехал автобус. Через 1 ч 20 мин вслед за ним выехал автомобиль, скорость которого в 1,5 раза больше скорости автобуса. Найдите скорость автобуса, если в город В он прибыл одновременно с автомобилем.

9

Х

8

т² — 10mn + 25n² . т — 5n.

12т3п2

85 • 0,2-15

2. Вычислите:

1014

З. Решите уравнение 25х — х

5. Лодка по течению реки проходит 12 км на 30 мин быстрее, чем такое же расстояние против течения реки. Найдите собственную скорость лодки, если скорость течения реки 2 км/ч.

4

2512 . 0,5-24

2. Вычислите:

1025

З. Решите уравнение х — 100х-1 = О

5. Расстояние между пристанями 40 км. Теплоход проплывает от одной пристани до другой и возвращается обратно за З ч 40 мин. Найдите скорость течения реки, если собственная скорость теплохода 22 км/ч.

1

1. Вычислите:

2. Постройте график функции у = а. Найдите:

а) наименьшее и наибольшее значения этой функции на отрезке [4; 71;

б) координаты точки пересечения графика этой функции с прямой х — 2у = О. а-зса

З. Сократите дробь

4.  Сравните значения выражений А и В, если

А = 0,12² + 0,05² , В =

5.  Докажите равенство        = 71 - 1265.

6 + 35

2 Вычислите:

   а) 0,40 • 66 +666;       б) 6i.

2. Постройте график функции у =            Найдите:

а) наименьшее и наибольшее значения этой функции на отрезке [5; 91;

б) координаты точки пересечения графика этой функции с прямой х + Зу = О.

З. Сократите дробь

4. Сравните значения выражений А и В, если

    А =                  В = 0,17² - 0,08² .

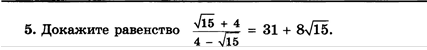
.М

З

1.  Вычислите:

2.  Постройте график функции у = а. Найдите:

а) наименьшее и наибольшее значения этой функции на отрезке [2; 41;

б) координаты точки пересечения графика этой функции с прямой х — Зу + 2 = О.

З. Сократите дробь

4—2

4. Сравните значения выражений А и В, если

в = 0,2² - 0,12² .

5 + 2 6

Л)

4

Вычислите:

а) 0,16 . б          б)

2. Постройте график функции у =            Найдите:

а) наименьшее и наибольшее значения этой функции на отрезке [1; 6);

б) координаты точки пересечения графика этой функции с прямой х + 4у + З = О. ь -20+1

З. Сократите дробь

4. Сравните значения выражений А и В, если

А = 0,24² + 0,1² , В =

3 - 2 2

.N2

1

0,5х² . С помощью ка найдите:

а) значение функции, если аргумент равен —2; З; 4;

б) значения аргумента, при которых значение функции равно 2;

в) значения аргумента, при которых у < 2;

г) наименьшее и наибольшее значения функции на отрезке [—1; 2].

2. Решите графически уравнение

х

З. Известно, что график функции у = — проходит через точх ку 4). Найдите значение коэффициента К. Принадлежит ли графику этой функции точка В(2ј5; —20)?

4. Даны функции у = f(x) и у = (х), где f(x) = х² , а g(x) = 3х² . При каких значениях аргумента выполняется равенство f(2x + 3) = + 2)?

N2

2

5

график функции у — С помощью

найдите:

а) значение функции, если аргумент равен —10; —2; 5;

б) значения аргумента, при которых значение функции равно —5;

в) значения аргумента, при которых у > 1;

г) наименьшее и наибольшее значения функции на отрезке [—5; —1].

2. Решите графически уравнение —0,5х² = х — 4.

З. Известно, что график функции у = — проходит через точ-

х ку С(8; —3). Найдите значение коэффициента Ь. Принадлежит ли графику этой функции точка            446)?

4. Даны функции у = f(x) и у = g(x), где f(x) = 4х² , а g(x) = х² . При каких значениях аргумента выполняется равенство

З

—2х² . С помощью ка найдите:

а) значение функции, если аргумент равен —1; 1,5; 2;

б) значения аргумента, при которых значение функции равно —8;

в) значения аргумента, при которых у < —2;

г) наименьшее и наибольшее значения функции на отрезке [—2; 1].

2. Решите графически уравнение     = —1х1.

х

З. Известно, что график функции у = bx² проходит через точку В(2; 12). Найдите значение коэффициента К. Принадлежит ли графику этой функции точка  24)?

4.  Даны функции у = f(x) и у = (х), где f(x)

При каких значениях аргумента выполняется равенство

5.  Решите уравнение 9х² - 24х + 16 = 5.

контрольнАЯ

Вариант 4

6

график функции у —— • С помощью

найдите:

а) значение функции, если аргумент равен —1; 1,5; 6;

б) значения аргумента, при которых значение функции равно 2;

в) значения аргумента, при которых у < 2;

г) наименьшее и наибольшее значения функции на отрезке [1; З].

2. Решите графически уравнение 0,5х² = 1х

З. Известно, что график функции у = Кх² проходит через точку ЦЗ; —36). Найдте значение коэффициента К. Принадлежит ли графику этой функции точка  48)?

4.  Даны функции у = f(x) и у = (х), где f(x)

При каких значениях аргумента выполняется равенство 4х² - 4) - + 2) = -1?

5.  Решите уравнение 16х² + 24х + 9 = 5.

.N2 б

1

2

                                                          —           Укажите область

определения функции.

2. Постройте график функции у = х² — 2х — З. С помощью графика найдите:

а) промежутки возрастания и убывания функции;

б) наименьшее значение функции;

в) при каких значениях х у < О.

З. Решите графически уравнение —х² 2х + 8 = О.

4.   Решите графически систему уравнений y = lx - 3l.

5.   Найдите значение параметра р и напишите уравнение оси симметрии параболы, заданной формулой у = .r² + рх — 24, если известно, что точка с координатами (4; О) принадлежит этой параболе.

Л)

2

= — 2. Укажите множество значений функции.

2. Постройте график функции у = —х² + 2х + З. С помощью графика найдите:

а) промежутки возрастания и убывания функции;

б) наибольшее значение функции;

в) при каких значениях х у < О.

З. Решите графически уравнение х² — 2х — 8 = О.

4. Решите графически систему уравнений у = lxl + 4,

-5

5. Найдите значение параметра р и напишите уравнение оси симметрии параболы, заданной формулой у = х² + рх + 35, если известно, что точка с координатами (5; О) принадлежит этой параболе.

Ль

З

з

= х + 1. Укажите множе-

ство значений функции.

2. Постройте график функции у = —2х² — 4х + 6. С помощью графика найдите:

а) промежутки возрастания и убывания функции;

б) наибольшее значение функции;

в) при каких значениях х у > О.

З. Решите графически уравнение х² + 3х — 4 = О.

4.   Решите графически систему уравнений у = ј-г;-ј + 1,

5.   Найдите значение параметра р, если известно, что прямая х = —1 является осью симметрии параболы у = рх² — ф + 12)х — 15.

.М

4

1.  Постройте график функции у = —463. Укажите область определения функции.

2.  Постройте график функции у = 0,5х² — х — 1,5. С помощью графика найдите:

а) промежутки возрастания и убывания функции;

б) наименьшее значение функции;

в) при каких значениях х у > О.

З. Решите графически уравнение —х² + 3х + 4 = О.

4.   Решите графически систему уравнений

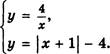
5.   Наидите значение параметра р, если известно, что прямая х = З является осью симметрии параболы у = 2рх² - Ф- 11)х + 17.

Г•Г2

1

число корней

в) х⁴ — 10х² + 9 = О.

З. Одна сторона прямоугольника на 9 см больше другой. Найдите стороны прямоугольника, если его площадь равна 112 см ² .

25 — х² — 5+ х х— 5

5. При каких значениях параметра р уравнение 4х² + рх + 9 = О имеет один корень?

и

«М

2 число корней

в) - 13х² + 36 = о.

З. Один катет прямоугольного треугольника на 5 см меньше другого. Найдите длину каждого катета, если площадь этого треугольника равна 42 см ² .

5. При каких значениях параметра р уравнение х² — рх + р = О имеет один корень?

25

                      контрольнм             .м

Вариант З число корней

     б) 0,5х² — х — 8 = О. уравнение:

             а) + 7х - 60 = О;           б) —х² — 3х — ⁵ 4 = О;

в) (х^а - 22)² - 2(х² - 22) - З = О.

З. Одна сторона прямоугольника на 14 см меньше другой. Найдите стороны прямоугольника, если его диагональ равна 26 см.

5. При каких значениях параметра р уравћение (р + 2)х² + (р + + 2 = О имеет один корень?

26

                            КОНТРОЛЬНАЯ                 .М

Вариант 4 число корней

            4х — 5х — 9 = О;         6) -16х² + 24х - 9 = о.

уравнение:

         а) х² + 19х + 48 = О;        6) -8х² + 16х + 10 = о;

в) (3х² - - 4(3х² - 4) - 5 = о.

З. Гипотенуза прямоугольного треугольника равна 17 см, а разность длин катетов равна 7 см. Найдите длину каждого катета данного треугольника.

5. ПЬи каких значениях параметра р уравнение ф — 1)х² + ф — 1)х — 1 = О имеет один корень?

27.

.М

1 уравнение:

               х      10х + 22 = О;         б) х² — 110х + 216 = о.

 + 9х + 14

2. Сократите дробь * - 49 З. Упростите выражение

10- зх • х- 4 - в- х- 12 - х + 3

4.  Из пункта А в пункт В, находящийся на расстоянии 240 км от пункта А, одновременно выехали два автомобиля: «ГАЗ-53» и «Газель». Скорость автомобиля «Газель» на 20 км/ч больше скорости автомобиля «ГАЗ-53», поэтому «Газель» прибыла в пункт В на 1 ч раньше. Найдите скорость каждого автомобиля.

5.  Разность корней квадратного уравнения х2 равна 4. Найдите корни уравнения и значение q.

28

контролыия

Вариант 2

уравнение:

              х      6х + 4 = О;          б) х² + 106х + 693 = О.

* - 64

     2. Сократите дробь х.2 _     + 24 •

З. Упростите выражение з         6х        1 . 8х- 13 х + 4 * + х —12 х — 3

4.  Автомобиль проехал 60 км по автостраде и 32 км по шоссе, затратив на весь путь 1 ч. Найдите скорость автомобиля на каждом участке пути, если по автостраде он двигался на 20 км/ч быстрее, чем по шоссе.

5.  Отношение корней квадратного уравнения х² + 2х + q = О равно 6. Найдите корни уравнения и значение q.

29

З

уравнение:

               7х     6х + 1 = О;         6) 3х² - 124х - 84 = о.

.r² + — 21

2. Сократите дробь 2х2 + 11х — 21'

З. Упростите выражение х

4.  Туристы, осматривая достопримечательности края, проплыли сначала 24 км по течению реки„ затем 10 км по озеру. Возвращаясь домой тем эк. маршрутом, они затратили на путь против течения рени столько же времени, сколько на путь по течению реки и по озеру. Найдите скорость движения лодки по течению реки, если скорость течения равна З км/ч.

5.  При каком отрицательном значении параметра р один из корней квадратного уравнения х² + рх + 36 = О на 4 меньше другого?

50

4

уравнение:

         3х — 4х — 1 = О;        б) 5х² —

3х² - 25х - 18

2. СОКРаТИТе дробь

З. Упростите выражение

            х² —                            х                               8

178х + 105 = о.

х + 3 х — 4 * — 3х— 4 х + 1

4. В озеро впадают 2 притока, скорость течения в каждом из которых З км/ч. База А расположена на первом притоке в 30 км от озера, база В — на втором притоке в 48 км от озера. Расстояние по озеру от одного притока до другого 27 км. Бригада рыбнадзора на моторной лодке плывет от базы А к базе В (по первому притоку, по озеру и по второму притоку), при этом время движения от базы А до устья второго притока равно времени движения лодки по второму притоку. С какой скоростью движется моторная лодка по второму притоку?

б. При каком положительном значении параметра р один из корней квадратного уравнения х ^а — рх + 48 = О в 8 раза больше другого?

31

8

1

З. Найдите область определения выражения 2 — 5х.

4— 2х

4.  Докажите, что функция у =  5 убывает.

5.  При каких значениях параметра р уравнение х² + 2рх — 7р = О не имеет корней?

Вариант З

1.  Решите неравенство:

            а) 3(4х - 1) > -5(5 + 2х);           6) х + 35 - 6х² < о.

2.  Решите уравнение:

З. Найдите область определения выражения (х² + 6х)-1

6

4.  Докажите, что функция у =  + 4 возрастает при х > О.

5.  При каких значениях параметра р уравнение х ² — 2ф — 1)х + 4р² = О имеет не более одного корня?

32

8

2

неравенство:

            а) 9х - 11 > 5(2х - 3);         

2. Решите уравнение:

1

З. Найдите область определения выражения

2

5. При каких значениях параметра р уравнение рх² — 2рх + 9 = О имеет два корня?

Вариант 4

З. Найдите область определения выражения 4х — х² .

4

4.   Докажите, что функция у =  убывает при х > 2.

5.   При каких значениях параметра р уравнение х² - 2ф +     + 16 = о имеет хотя бы один корень?

38

итоговМ КОНТРОЛЬНАЯ РАБОТА

Вариант 1

график функции у = х² 2х. Найдите:

а) наименьшее и наибольшее значения функции на отрезке [О; 31;

б) промежутки возрастания и убывания функции;

в) решения неравенства х^а — 2х < О.

2. Решите уравнение 10х² — х — 60 = О.

З. При каких значениях переменной квадрат двучлена бр + 1 больше произведения выражений 9р — 1 и 4р + 5? Укажите наибольшее целое число, удовлетворяющее этому условию.

4. На предприятии по изготовлению вычислительной техники должны были в определенный срок собрать 180 компьютеров. Собирая в день на З компьютера больше, чем было запланировано, специалисты выполнили задание на З дня раньше срока. Сколько компьютеров в день собирали специалисты?

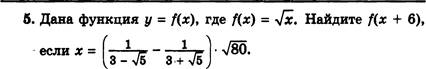
2 у 4х — х^а . Найдите:

а) наименьшее и наибольшее значения функции на отрезке [О; З);

б) промежутки возрастания и убывания функции;

в) решения неравенства 4х² — х^а < О.

2. Решите уравнение 14х² + 25х — 84 = О.

З. При каких значениях переменной разность квадратов выражений 4q и 8 меньше произведения выражений 8q + 7 и и — 9? Укажите наибольшее целое число, удовлетворяющее этому условию.

4.  Завод получил заказ на изготовление в определенный срок ЗОО новых электронных игр. Изготавливая в день на 10 игр больше запланированного, завод выполнил заказ на 1 день раньше срока. Сколько электронных игр в день изготавливал завод?

5.  Дана функция у = f(x), где f(x) = а. Найдите f(x — 5), если х =

З у —х2 + 6х — 8. Найдите:

а) наименьшее и наибольшее значения функции на отрезке [2; 5];

б) промежутки возрастания и убывания функции;

в) решения неравенства —х² + 6х — 8 > О.

2. Решите уравнение 15х² — 16х — 15 = О.

З. При каких значениях переменнбй разность квадратов выражений 5t и 6 не меньше квадрата разности выражений 5t и 4? Укажите наименьшее целое число, удовлетворяющее этому условию.

4. На переезде у семафора автомобиль был задержан на 6 мин. Чтобы прибыть в пункт назначения вовремя, он увеличил скорость на 10 км/ч. Найдите скорость автомобиля после переезда, если расстояние между переездом и пунктом назначения равно 42 км.

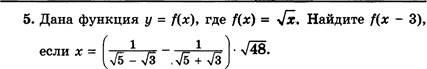
36

4

у х² — 6х + 5. Найдите:

а) наименьшее и наибольшее значения функции на отрезке [1; 41;

б) промежутки возрастания и убывания функции;

в) решения неравенства х^а — 6х + 5 > О.

2. Решите уравнение 35х² + 24х — 35 = О.

З. При каких значениях переменной квадрат суммы выражений 7у и З не больше суммы квадратов выражений 7у и 9? Укажите наибольшее целое число, удовлетворяющее этому условию.

4.   Автобус был задержан с выездом на 9 мин. Чтобы прибыть в пункт назначения вовремя, водитель увеличил намеченную скорость на 10 км/ч. Найдите скорость автобуса, если расстояние, которое он проехал, равно 30 км.

5.   Дана функция у = f(x), где f(x) = G. Найдите f(x + 1),

если х

37

ПРИМЕРНОЕ ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ

З ч в неделю, всего 102 ч в год

                                                                                                    Итого:             18

Г л а в а З. Квадратичная функция, функция у = — х

38

Окончание табл.

                                                                                                     Итого:             17

Г л а в а 4. Квадратные уравнения

                                                                                                    Итого:             21

Г л а в а 5. Неравенства

S 31.Свойства числовых неравенств                                                           з

S 32.Исследование функций на монотонность з S 33.Решение линейных неравенств 2 S 34.Решение квадратных неравенств з

        Контрольная работа ЛФ 8                                              1

S 35.Приближенные значения действительных чисел, погрешность приближения, приближение

СОДЕРЖАНИЕ

Предисловие

Контрольная работа № 1 Контрольная работа № 2