Учебное пособие «Информатика и ИКТ» предназначено для изучения информатики и информационно-компьютерных технологий в учреждениях начального и среднего профессионального образования, реализующих образовательную программу среднего (полного) общего образования, при подготовке квалифицированных рабочих и специалистов среднего звена. Настоящее учебное пособие представляет собой краткое изложение основных положений учебной дисциплины «Информатика и ИКТ». Темы пособия содержат изложение основных вопросов дисциплины, и примеры решения задач , что делает его пригодным и для самообразования. Предназначено для студентов 1 курса, изучающих дисциплину «Информатику и ИКТ».

Коми Республикаса йöзöс велöдан министерство

«Сыктывкарса сервис да связь колледж»

уджсикасö велöдан канму учреждение Министерство образования Республики Коми

государственное профессиональное образовательное учреждение

«Сыктывкарский колледж сервиса и связи»

(ГПОУ «СКСиС»)

Информатика и ИКТ

Учебное пособие

Часть 2

В помощь студентам изучающим Информатику и ИКТ

Подготовила:

преподаватель Информатики и ИКТ

Белева Л.Ф.

Сыктывкар-2015 г.

Содержание

Введение 2

Измерение информации

1.1. Подходы к измерению информации 3

1.2. Содержательный (вероятностный) подход к определению количества 3

1.3. Единицы измерения информации 4

1.4. Вычисление количества информации для событий с различными вероятностями 7

1.5. Алфавитный подход к измерению информации 10

Системы счисления

2.1. Системы счисления 13 2.2. Развернутая форма числа 13

2.3. Системы счисления, используемые в компьютерах 14

2.4. Перевод целых чисел из десятичной системы счисления в другую 14 2.5. Перевод числа из двоичной системы счисления в десятичную 15

2.6. Перевод правильных дробей из десятичной системы счисления в с основанием 18 S систему счисления с основанием S

2.7. Перевод неправильных дробей из десятичной системы счисления в с 19 основанием S

2.8. Перевод чисел из системы счисления с основанием 2 в систему счисления с 19 основанием 2ⁿ и обратно (Перевод дробных чисел) 2.9. Перевод чисел из системы счисления с основанием 2 в систему счисления с 20 основанием 2ⁿ и обратно (Перевод дробных чисел)

2.10 Перевод чисел из систем счисления с основанием q=2ⁿ в двоичную систему 21

Двоичная арифметика

3.1. Двоичная арифметика 22

3.2. Основы машинной арифметики с двоичными числами 25

3.3. Коды чисел 25

3.4. Особенности сложения чисел в обратном и дополнительном кодах 26 Арифметические действия над числами в различных системах счисления

4.1. Сложение и вычитание в 8-ой с/с 28

4.2. Сложение и вычитание в 16-ой с/с 28

4.3. Умножение 29

4.4. Деление 29

Дискретное (цифровое) представление информации

5.1. Дискретное представление информации 31

5.2. Аналоговый и дискретный способ кодирования 31

5.3. Кодирование изображений 32 5.4. Графические форматы файлов 34

5.5. Информационный объем растрового графического изображения 35

5.6. Кодирование звуковой информации 39

5.7. Характеристики оцифрованного звука 40 Основы логики и логические основы компьютера

6.1. Основы логики 42

6.2. Алгебра высказываний 43

6.3. Логические выражения и таблицы истинности 48

6.4. Законы алгебры логики 51

Задачи 57

Литература 70

Пояснительная записка

Учебное пособие «Информатика и ИКТ» предназначено для изучения информатики и информационно-компьютерных технологий в учреждениях начального и среднего профессионального образования, реализующих образовательную программу среднего (полного) общего образования, при подготовке квалифицированных рабочих и специалистов среднего звена.

Настоящее учебное пособие представляет собой краткое изложение основных положений учебной дисциплины «Информатика и ИКТ».

Темы пособия содержат изложение основных вопросов дисциплины, и примеры решения задач , что делает его пригодным и для самообразования.

Предназначено для студентов 1 курса, изучающих дисциплину «Информатику и ИКТ».



Измерение информации

1.1. Подходы к измерению информации

Как измерить информацию? Часто мы говорим, что, прочитав статью в журнале или просмотрев новости, не получили никакой информации, или наоборот, краткое сообщение может оказаться для нас информативным. В то же время для другого человека та же самая статья может оказаться чрезвычайно информативной, а сообщение — нет. Информативными сообщения являются тогда, когда они новы, понятны, своевременны, полезны. Но то, что для одного понятно, для другого — нет. То, что для одного полезно, ново, для другого — нет. В этом проблема определения и измерения информации.

При всем многообразии подходов к определению понятия информации, с позиции измерения информации нас будут интересовать два из них: определение К. Шеннона, применяемое в математической теории информации (содержательный подход), и определение А. Н. Колмогорова, применяемое в отраслях информатики, связанных с использованием компьютеров (алфавитный подход).

1.2. Содержательный (вероятностный) подход к определению количества

информации

Согласно Шеннону, информативность сообщения характеризуется содержащейся в нем полезной информацией — той частью сообщения, которая снимает полностью или уменьшает неопределенность какой-либо ситуации.

По Шеннону, информация — уменьшение неопределенности наших знаний.

Неопределенность некоторого события — это количество возможных исходов данного события. Так, например, если из колоды карт наугад выбирают карту, то неопределенность равна количеству карт в колоде. При бросании монеты неопределенность равна 2.

Содержательный подход часто называют субъективным, так как разные люди (субъекты) информацию об одном и том же предмете оценивают по-разному.

Но если число исходов не зависит от суждений людей (случай бросания кубика или монеты), то информация о наступлении одного из возможных исходов является объективной.

Если сообщение уменьшило неопределенность знаний ровно в два раза, то говорят, что сообщение несет 1 бит информации.

1 бит — объем информации такого сообщения, которое уменьшает неопределенность знания в два раза.

Рассмотрим, как можно подсчитать количество информации в сообщении, используя содержательный подход.

Пусть в некотором сообщении содержатся сведения о том, что произошло одно из N равновероятных (равновозможных) событий. Тогда количество информации i, заключенное в этом сообщении, и число событий N связаны формулой: 2ⁱ = N. Эта формула носит название формулы Хартли. Получена она в 1928 г. американским инженером Р. Хартли.

Если N равно целой степени двойки (2, 4, 8, 16 и т.д.), то вычисления легко произвести "в уме". В противном случае количество информации становится нецелой величиной, и для решения задачи придется воспользоваться таблицей логарифмов либо определять значение логарифма приблизительно (ближайшее целое число, большее).

Количество информации в сообщении об одном из N равновероятных событий: i = log ₂N.

	N	i	N	i	N	i	N	i
	1	0,0000	17	4,0874	33	5,0443	49	5,6147
	2	1,0000	18	4,1699	34	5,0874	50	5,6438
	3	1,5849	19	4,2479	35	5,1292	51	5,6724
	4	2,0000	20	4,3219	36	5,1699	52	5,7004
	5	2,3219	21	4,3923	37	5,2094	53	5,7279
	6	2,5849	22	4,4594	38	5,2479	54	5,7548
	7	2,8073	23	4,5235	39	5,2854	55	5,7813
	8	3,0000	24	4,5849	40	5,3219	56	5,8073
	9	3,1699	25	4,6438	41	5,3575	57	5,8328
	10	3,3219	26	4,7004	42	5,3923	58	5,8579
	11	3,4594	27	4,7548	43	5,4262	59	5,8826
	12	3,5849	28	4,8073	44	5,4594	60	5,9068
	13	3,7004	29	4,8579	45	5,4918	61	5,9307
	14	3,8073	30	4,9068	46	5,5235	62	5,9542
	15	3,9068	31	4,9542	47	5,5545	63	5,9772
	16	4,0000 0	32	5,0000 0	48	5,5849 6	64	6,0000 0
Таблица 2.

Пример 1. Какое количество информации можно получить при угадывании числа из интервала от 1 до 11? В этом примере N=11. Чтобы найти i (количество информации),

необходимо воспользоваться таблицей. По таблице i = 3,45943 бит.

1.3. Единицы измерения информации

Как уже было сказано, основная единица измерения информации — бит.

8 бит составляют 1 байт.

Наряду с байтами для измерения количества информации используются более крупные единицы:

1 Кбайт (один килобайт) = 2¹⁰ байт = 1024 байта;

1 Мбайт (один мегабайт) = 2²⁰ байт = 1024 Кбайта; 1 Гбайт (один гигабайт) = 2³⁰байт = 1024 Мбайта.

В последнее время в связи с увеличением объѐмов обрабатываемой информации входят в употребление такие производные единицы, как:

1 Терабайт (Тб) =2⁴⁰ = 1024 Гбайта;

1 Петабайт (Пб) = 2⁵⁰= 1024 Тбайта.

Пример 1. При бросании монеты возможны 2 события (случая) – монета упадѐт орлом или решкой, причѐм оба события равновероятны (при большом количестве бросаний количество случаев падения монеты орлом и решкой одинаковы). После получения сообщения о результате падения монеты неопределѐнность знаний уменьшилась в 2 раза, и, поэтому, количество информации, полученное при, этом равно 1 бит.

Задача 1.

В коробке 32 карандаша, все карандаши разного цвета. Наугад вытащили красный. Какое количество информации при этом было получено?

Дано: Решение.

N = 32 Так как вытаскивание карандаша любого цвета из Найти: имеющихся в коробке 32 карандашей является i -? равновероятным, то число возможных событий равно 32.

N = 2ⁱ; 32 = 2⁵; i = 5 бит.

Ответ: 5 бит. Задача 2.

При угадывании целого числа в некотором диапазоне было получено 8 бит информации.

Сколько чисел содержит этот диапазон?

Дано: Решение. i =8 2ⁱ = N;

Найти: 2⁸=256

N - ? Ответ:256 чисел.

Вопросы:

1. Какие подходы к измерению информации вам известны?

2. Какова основная единица измерения информации?

3. Приведите формулу подсчета количества информации при уменьшении неопределенности знания.

4. Что такое бит, байт, килобайт, мегабайт, гигабайт?

5. Как определить количество информации при равновероятных событиях?

Задания для самостоятельного выполнения: Задача 3.

Сообщение о том, что ваш друг живет на 10 этаже, несет 4 бита информации. Сколько этажей в доме?

Задача 4.

В коробке лежат 8 разноцветных карандашей.

Какое количество информации содержит сообщение, что достали красный карандаш?

Задача 5.

В корзине 16 шаров. Все шары разного цвета. Сколько информации несет сообщение о том, что из корзины достали красный шар?

Задача 6.

Группа школьников пришла в бассейн, в котором 4 дорожки для плавания. Тренер сообщил, что группа будет плавать на дорожке номер 3. Сколько информации получили школьники из этого сообщения?

Задача 7.

При угадывании целого числа в некотором диапазоне было получено 5 бит информации.

Сколько чисел содержит этот диапазон?

Задача 8.

В книге 512 страниц. Сколько информации несет сообщение о том, что закладка лежит на какой-либо странице?

Задача 9.

При угадывании целого числа в некотором диапазоне было получено 6 бит информации.

Сколько чисел содержит этот диапазон?

Задача 10.

Выразить:

a) 3 Кб в байтах и битах; 81920 бит в байтах и Кб;

b) 3072 Мб в Гб и Кб; 12288 бит в Кб и байтах;

c) 5 Кб в байтах и битах; 4096 Мб в Кб и Гб.

d) 2 Гб в байтах и битах; 4096 Гб в Кб и Мб.

Домашнее задание:

Задача 11.

Сообщение о том, что Даша живет во 2 подъезде, несет 3 бита информации. Сколько подъездов в доме?

Задача 12.

В барабане для розыгрыша лотереи находятся 64 шара. Сколько информации содержит сообщение о первом выпавшем номере?

Задача 13.

В библиотеке имеется 16 стеллажей. Каждый из которых содержит 8 полок. Сколько информации содержит сообщение, что книга находится на верхней полке первого стеллажа?

Задание 14.

Переведи в байты. Переведи в килобайты.

a) 15 Кб, 256 Кб, 2500 Кб. a) 7168 байт, 7680 байт, 2 Мб, 5 Гб.

b) 72 Кб, 340 Мб, 7340032 Кб. b) 2560 байт, 257 Мб.

1.4*. Вычисление количества информации для событий с различными вероятностями

Возвращаясь к рассмотренным выше формулам, можно сказать, что формула является частным случаем, так как применяется только к равновероятным событиям. В жизни же мы сталкиваемся не только с равновероятными событиями, но и событиями, которые имеют разную вероятность реализации.

1. В коробке 20 карандашей, из них 15 красных и 5 чѐрных. Вероятность вытащить наугад красный карандаш больше, чем чѐрный.

2. В пруду живут 8000 карасей, 2000 щук и 40000 пескарей. Самая большая вероятность для рыбака – поймать в этом пруду пескаря, на втором месте – карася, на третьем – щуку.

Как вычислить количество информации в сообщении о таком событии?

Для этого необходимо использовать следующую формулу.

i= log₂(l/p), где i — это количество информации, р — вероятность события. Вероятность события выражается в долях единицы и вычисляется по формуле:

р = К / N, где К — величина, показывающая, сколько раз произошло интересующее нас событие, N — общее число возможных исходов какого-то процесса.

Что такое логарифм?

Логарифмом числа а по основанию b называется показатель степени, в которую надо возвести число a, чтобы получить число b.

Количество информации в случае различных вероятностей событий определяется по

формуле: Формула Шеннона:

(американский учѐный, 1948 г.) I ^pi^log₂^pi где Pi – вероятность i-го события, N - i1

количество возможных событий

Вопросы:

1. Приведите примеры событий с одинаковой вероятностью, с разной вероятностью.

2. Как определить количество информации для событий с различными вероятностями?

3. Что такое логарифм?

Задания для самостоятельного выполнения:

Задача 1.

В мешке находятся 20 шаров. Из них 15 белых и 5 красных. Какое количество информации несет сообщение о том, что достали: а) белый шар; б) красный шар.

Дано: К_б=15; К_к=5;

Найти: i_б-?; i_к-?

Решение:

1. p=K/N

2. Найдем вероятность того, что достали белый шар: р_б = 15 / 20 = 0,75.

3. Найдем вероятность того, что достали красный

шар: р_к= 5 / 20 = 0,25.

4. Найдем количество информации в сообщении о вытаскивании белого шара: i_б = log₂ (1/ р_б) = log₂(l/0,75) = log₂ 1,3 =1,15470 бит.

5. Найдем количество информации в сообщении о вытаскивании красного шара: i_К = log₂ (1/ р_к) = log₂(1/0,25) = log₂4 = 2 бит.

Ответ: количество информации в сообщении о том, что достали белый шар, равно 1,1547 бит. Количество информации в сообщении о том, что достали красный шар, равно 2 бит.

Задача 2.

В коробке лежат кубики: 10 красных, 8 зеленых, 5 желтых, 12 синих. Вычислите вероятность доставания кубика каждого цвета и количество информации, которое при этом будет получено.

Дано:

К_к=10; К_з=8; К_ж=5; К_с=12; Найти:

р_к-?; р_з-?; р_ж-?:р_с-? i_к-?;i_з-?; i_ж-?;i_с-?

Решение:

1. Всего кубиков в коробке N = 10 + 8 + 5 + 12 = 35.

2. Найдем вероятности:

р_к = 10 / 35 ≈ 0,29, р_з = 8/ 35 ≈ 0,22, р_с= 12/35 ≈ 0,34,

р_ж = 5/35 ≈ 0,14.

3. Найдем количество информации:

i_c = log₂ ( 1/0,34) = log₂2,9 = 1,5360529 бит,

i_к = log₂ ( 1/0,29) = log₂3,4 = 1,7655347 бит, i_з= log₂ (1/0,22) = log₂4,5 = 2,169925 бит, i_ж=log₂ (l/0,14) = log₂7,l = 2,827819 бит.

Ответ: наибольшее количество информации мы получим при доставании желтого кубика по причине качественной связи между вероятностью и количеством информации.

Задача 3.

В ящике лежат перчатки (белые и черные). Среди них - 2 пары черных. Сообщение о том, что из ящика достали пару черных перчаток, несет 4 бита информации. Сколько пар белых перчаток было в ящике?

Дано: Решение:

Кч=2;

i_ч = 4 бита;

Найти:

К_б - ?

1. i_ч, = log₂ (l/p_ч), 4 = log₂ (l/p_ч), 1/р_ч = 16.

2. р_ч = 1/16 - вероятность доставания черных перчаток.

3. р_ч = K_ч/N, К_ч/р_ч, N = 216 = 32- всего перчаток.

4. К_б= N- К_ч =32- 2 = 30 пар белых.

Ответ: 30 пар белых перчаток.

Задания для самостоятельного выполнения:

Задача 4.

В коробке находятся кубики трех цветов: красного, желтого и зеленого. Причем желтых в два раза больше красных, а зеленых на 6 больше чем желтых. Сообщение о том, что из коробки случайно вытащили желтый кубик, содержало 2 бита информации. Сколько было зеленых кубиков?

Задача 5.

Студенты группы изучают один из трех языков: английский, немецкий или французский.

Причем 12 студентов не учат английский. Сообщение, что случайно выбранный студент Петров изучает английский, несет log₂3 бит информации, а что Иванов изучает французский – 1 бит. Сколько студентов изучают немецкий язык?

Задача 6.

В колоде содержится 32 карты. Из колоды случайным образом вытянули туза, потом его положили обратно и перетасовали колоду. После этого из колоды опять вытянули этого же туза. Какое количество бит информации в сумме содержат эти два сообщения?

Задача 7.

В составе 16 вагонов, среди которых К – купейные, П – плацкартные и СВ – спальные. Сообщение о том, что ваш друг приезжает в СВ несет 3 бита информации. Определите, сколько в поезде вагонов СВ.

Домашнее задание:

Задача 8.

В корзине лежат 8 черных шаров и 24 белых. Сколько информации несет сообщение о том, что достали черный шар?

Задача 9.

В коробке лежат 64 цветных карандаша. Сообщение о том, что достали белый карандаш, несет 4 бита информации. Сколько белых карандашей ныло в корзине?

Задача 10.

В классе 30 человек. За контрольную работу по математике получено 15 пятерок, 6 четверок, 8 троек и 1 двойка. Какое количество информации в сообщении о том, что Андреев получил пятерку?

1.5. Алфавитный подход к измерению информации

При алфавитном подходе к определению количества информации отвлекаются от содержания информации и рассматривают информационное сообщение как последовательность знаков определенной знаковой системы.

С позиций computer science носителями информации являются любые последовательности символов, которые хранятся, передаются и обрабатываются с помощью компьютера. Согласно Колмогорову, информативность последовательности символов не зависит от содержания сообщения, алфавитный подход является объективным, т.е. он не зависит от субъекта, воспринимающего сообщение.

Алфавит - все множество используемых в языке символов. Обычно под алфавитом понимают только буквы, но поскольку в тексте могут встречаться знаки препинания, цифры, скобки, то мы их тоже включим в алфавит. В алфавит также следует включить и пробел, т.е. пропуск между словами.

Мощность алфавита - полное количество символов алфавита.

Сообщения, записанные с помощью символов ASCII, используют алфавит из 256 символов. Сообщения, записанные по системе UNICODE, используют алфавит из 65 536 символов.

Мощность русского алфавита - 33 знака, английского - 28, двоичного кода - 2 , компьютерного текста - 256.

Будем использовать следующие обозначения: N — мощность алфавита, К — количество символов в тексте, i — количество информации, которое несет каждый символ алфавита, It — объем информации, содержащейся в тексте.

Алфавитный подход к измерению количества информации.

Алфавитный подход позволяет определить количество информации, заключенной в тексте.

Если допустить, что все символы алфавита встречаются в тексте с одинаковой частотой (равновероятно), то количество информации, которое несет каждый символ, вычисляется по формуле: i =Log₂ N, или 2ⁱ= N.

Чтобы определить объем информации в сообщении при алфавитном подходе, нужно последовательно решить задачи:

1. Определить количество информации (i) которое несет каждый символ алфавита по формуле 2ⁱ = N, где N — мощность алфавита

2. Определить количество символов в сообщении (K) 3. Вычислить объем информации по формуле: It = i * K.

Задача 1.

Найти объем сообщения, содержащего 200 знаков 16-символьного алфавита.

Дано:

N = 16;

K = 200;

Найти:

It - ?

Решение.

1. N = 2ⁱ, 16=2ⁱ.

2. i = 4бита.

3. It = K · i, It=200 · 4=800 бит = 100 байт.

Ответ: 100 байт Задача 2.

Сообщение занимает 3 страницы по 25 строк. В каждой строке записано по 60 символов. Сколько символов в использованном алфавите, если все сообщение содержит 2250 байтов?

Дано: s=3; x=25; y=60; It = 2250 байта;

Найти:

N -?

Решение.

1. К = 3·25·60 = 4500 символов в тексте.

2. It = K · i, i = It / K.

3. i = 2250 · 8 / 4500 = 4 бита.

4. N = 2ⁱ; N = 2⁴; N = 16 символов.

Ответ: 16 символов Вопросы:

1. Какие существуют два подхода к измерению информации?

2. Что такое алфавит, мощность алфавита?

3. Что такое информационный вес символа в алфавите?

4. Каким образом можно подсчитать количество информации в сообщении?

Задания для самостоятельного выполнения:

Задача 3.

Можно ли уместить на одну дискету книгу, имеющую 432 страницы, причем на каждой странице этой книги 46 строк, а в каждой строке 62 символа?

Примечание: на дискету помещается 1,44 Мб.

Задача 4.

Книга, набранная с помощью компьютера, содержит 150 страниц, на каждой странице — 40 строк, в каждой строке — 60 символов. Каков объем информации в книге?

Задача 5.

Сообщение, записанное буквами из 32-х символьного алфавита, содержит 30 символов.

Какой объем информации оно несѐт?

Задача 6.

Сообщение, записанное буквами из 128-символьного алфавита, содержит 100 символов.

Какой объем информации оно несет?

Задача 7.

Информационный объем текста, подготовленного с помощью компьютера, равен 3.5 Кбайт. Сколько символов содержит этот текст?

Задача 8.

Информационное сообщение объемом 2 Кб содержит 8192 символа. Сколько символов содержит алфавит, при помощи которого было записано это сообщение?

Задача 9.

Информационное сообщение объемом 1,5 Кб содержит 3072 символа. Сколько символов содержит алфавит, при помощи которого было записано это сообщение?

Домашнее задание:

Задача 10.

Сколько килобайт составляет сообщение, содержащее ,12288 бит?

Задача 11.

Объем сообщения, содержащего 2048 символов, составил 1/512 часть Мбайта. Каков размер алфавита, с помощью которого записано сообщение?

Задача 12.

Для записи сообщения использовался 64-х символьный алфавит. Каждая страница содержит 30 строк. Все сообщение содержит 8775 байтов информации и занимает 6 страниц. Сколько символов в строке?

Задача 13.

Пользователь компьютера, хорошо владеющий навыками ввода информации с клавиатуры, может вводить в минуту 100 знаков. Мощность алфавита, используемого в компьютере, равна 256. Какое количество информации в байтах может ввести пользователь в компьютер за 1 минуту?

Системы счисления 2.1. Системы счисления

Система счисления – это система записи чисел с помощью определенного набора цифр.

Системы счисления делятся на следующие виды:

1. непозиционные (кодовые) системы; 2. позиционные системы.

Непозиционной называется такая система счисления, в которой количественный эквивалент каждой цифры не зависит от ее положения (места, позиции) в записи числа.

Примером непозиционной системы, которая сохранилась до наших дней, может служить Римская система счисления.

В системе значение цифры не зависит от ее положения в числе. Например, в числе ХХХ цифра Х встречается трижды, а в каждом случае обозначает одну и туже величину 10, а в сумме ХХХ это 30.

Система счисления называется позиционной, если значение цифры зависит от ее места

(позиции) в записи числа.

К позиционным системам счисления относятся двоичная, десятичная, восьмеричная, шестнадцатеричная.

Десятичная система счисления пришла в Европу из Индии, где она появилась не позднее VI века н.э.

Например, в записи 555, сделанной в десятичной системе счисления, использована одна цифра 5, но в зависимости от занимаемого ею места она имеет разное количественное значение – 5 единиц, 5 десятков или 5 сотен. Позиция цифры в числе называется разрядом. Основанием системы счисления называется количество знаков или символов, используемых для изображения числа в данной системе счисления.

2.2. Развернутая форма числа

Из курса математики вам известно, что цифры десятичной записи числа – это просто коэффициенты его представления в виде суммы степеней числа – основания системы счисления:

25076 = 2·10000 + 5·1000 + 0·100 + 7·10 + 6·1 = 2·10⁴ +5·10³ + 0·10² +7·10¹ +6·10⁰

При записи чисел значение каждой цифры зависит от ее положения. Место для цифры в числе называется разрядом, а количество цифр в числе разрядностью. На самом деле числа можно записывать как сумму степеней не только числа 10, но и любого другого натурального числа, большего 1.

Развернутой формой записи числа называется такая запись:

а₄а₃а₂а₁а₀ = а₄*q⁴ + a₃*q³ + a₂*q² + a₁*q¹ + a₀*q⁰ , где а4,а3,а2,а1,а0 –цифры числа, q –основание степени.

Пример 1. Получить развернутую форму числа 75124.

Решение: 75 124₁₀ = 7·10⁴ + 5·10³ + 1·10² + 2·10¹ + 4·10⁰.

2.3. Системы счисления, используемые в компьютерах

Двоичная система счисления. Для записи чисел используются только две цифры – 0 и 1. Выбор двоичной системы объясняется тем, что электронные элементы, из которых строятся ЭВМ, могут находиться только в двух хорошо различимых состояниях. По существу эти элементы представляют собой выключатели. Как известно выключатель либо включен, либо выключен. Благодаря таким особенностям двоичная система стала стандартом при построении ЭВМ.

Восьмеричная система счисления. Для записи чисел используется восемь чисел

0,1,2,3,4,5,6,7.

Шестнадцатеричная система счисления. Для записи чисел в шестнадцатеричной системе необходимо располагать уже шестнадцатью символами, используемыми как цифры. В качестве первых десяти используются те же, что и в десятичной системе. Для обозначения остальных шести цифр (в десятичной они соответствуют числам 10,11,12,13,14,15) используются буквы латинского алфавита – A,B,C,D,E,F.

Таблица соответствия систем счисления.

Десятичная	Двоичная	Восьмеричная	Шестнадцатеричная
0	0	0	0
1	1	1	1
2	10	2	2
3	11	3	3
4	100	4	4
5	101	5	5
6	110	6	6
7	111	7	7
8	1000	10	8
9	1001	11	9
10	1010	12	А
11	1011	13	В
12	1100	14	С
13	1101	15	D
14	1110	16	Е
15	1111	17	F

2.4. Перевод целых чисел из десятичной системы счисления в другую

Правило перевода целых чисел из десятичной системы счисления в систему с основанием q:

1. Последовательно выполнять деление исходного числа и получаемых частных на q до тех пор, пока не получим частное, меньшее делителя.

2. Полученные при таком делении остатки – цифры числа в системе счисления q – записать в обратном порядке (снизу вверх).

Пример 1. Перевести 2610 в двоичную систему счисления. А10→А2

Решение:

26:2=13 0

13:2=6 1

6:2=3 0

3:2=1 1

1:2=0 1 Ответ: 26₁₀=11010₂

2.5. Перевод числа из двоичной системы счисления в десятичную.

Это перевод – как бы обратный к изложенному выше. Его наиболее просто осуществить, основываясь на позиционности двоичной системы счисления. Уже отмечалась правомерность записи двоичного числа в виде суммы степеней основания системы счисления, то есть степеней двойки. Сделав такую запись, надо подсчитать десятичное значение полученной суммы:

Пример 2. Перевести число 110102 в десятичную систему счисления. А2 →А10

Решение:

24 23 22 21 20

1 1 0 1 0₂

11010₂⁼0·2⁰ +1· 2¹ + 0· 2²+1· 2³ +1· 2⁴ =0+2+0+8+16=26₁₀

Ответ: 11010₂=26₁₀

Пример 3. Перевести 1910 в троичную систему счисления. А10→А3

Решение:

19:3=6 1

6:3=2 0

2:3=0 2

Ответ: 19₁₀=201₃

Пример 4. Перевести число 2013 в десятичную систему счисления. А3→ А10

Решение:

32 31 30

2 0 1₂

201₂⁼1·3⁰ +0· 3¹ + 2· 3²=1+0=2*9=19₁₀ Ответ: 201₃=19₁₀

Пример 5. Перевести 24110 в восьмеричную систему счисления. А10→А8

Решение:

241:8=30 1

30:8=3 6

3:8=0 3

Ответ: 241₁₀=361₈

Пример 6. Перевести число 3618 в десятичную систему счисления. А8→ А10

Решение:

82 81 80

3 6 1₂

361₂⁼1·8⁰ +6· 8¹ + 3· 8²=1+0=1+48+192₁₀ Ответ: 361₈=241₁₀

Пример 7. Перевести 362710 в шестнадцатеричную систему счисления. А10→А16

Решение:

3627:16=226 11

226:16=14 2

14:16=0 14

Т.к. в шестнадцатеричной системе счисления 14 – Е, а 11 – В, то получаем ответ Е2В16. Ответ: 3627₁₀=E2B₁₆

Пример 8. Перевести E2B₁₆ в десятичную систему счисления. А₁₆→ А₁₀

Решение:

162 161 160

E 2 B

E 2 B₁₆= B·16⁰+2·16¹ +E·16²₌ B·1+2·16+E·16·16 =11·1+2·16 +14·16·16=3627₁₀

Ответ: E2B₁₆=3627₁₀

Пример 9. Перевести 1 0 1 1 , 0 1 1₂ в десятичную систему счисления. А₂→ А₁₀

Решение:

1 0 1 1 , 0 1 1₂= 1·2³+0·2²+1·2¹+1·2⁰+0·2^-1+1·2^-2+1·2^-3=8+2+1+1/4+1/8=11,375₁₀

Вопросы:

1. Что такое системы счисления?

2. Что называется основанием системы счисления?

3. Какие виды систем счисления вы знаете?

4. Приведите пример непозиционной системы счисления.

5. А почему она считается непозиционной системой счисления?

6. Какая система называется позиционной?

7. Что называется развернутой записью числа?

Задания для самостоятельного выполнения:

Задание 1.

Перевести десятичное число 247 в двоичную, восьмеричную и шестнадцатеричную системы.

Для проверки:247₁₀=11110111₂=367₈=F7₁₆

Задание 2.

Переведите двоичную дробь в десятичную: a) 11,001; b) 110,11; c) 100,011.

Задание 3.

Раскодируйте координаты и постройте фигуру.

1. (10; 1111)

2. (1000; 10000)

3. (1011; 10110)

4. (1110; 10000)

5. (10100; 1111)

7. (10010; 100)

8. (1011; 111)

9. (100; 100)

10. (110; 1010)

11. (10; 1111)

6. (10000; 1010)

Задание 4.

Дано: а = 21₁₀, b = 23₈.

Какое из чисел с, записанных в двоичной системе, отвечает условию b < с < а?

a) 10000; b) 10001; c) 11000; d) 10100.

Домашнее задание:

Задание 5.

Перевести числа в двоичную, восьмеричную и шестнадцатеричную сиcтемы:71₁₀, 240₁₀,

125₁₀.

Задание 6.

Отметить и последовательно соединить на координатной плоскости точки, координаты которых записаны в двоичной системе счисления

1. (1, 11)

2. (101, 11)

3. (101, 1001)

4. (1000, 110)

5. (101, 11)

6. (1010, 110)

7. (1001, 1)

8. (11, 1)

9. (1, 11)

10. (101, 1001)

11. (101, 1010)

12. (1000, 1010)

13. (1000, 1001)

14. (101, 1001)

Задание 7.

Чему равно число х в десятичной системе счисления, если х = 10₅ + 10₂  10₃Задание 8.

Дано: a  A5₁₆, b247₈.

Какое из чисел c , записанных в двоичной системе, отвечает условию a ?

a) 10100101; b) 10100110; c) 10101000; d) 10100111.

Задание 9.

В таблице приведена часть кодовой таблицы AСSII:

Символ	1	3	А	Y	Z	а	b
Десятичный	49	51	65	89	90	97	98
Восьмеричный	61	63	101	131	132	141	142

Каков восьмеричный код символа «z»?

a) 122; b) 172; c) 121; d) 173.

Задание 10.

Автоматическое устройство осуществило перекодировку двух информационных сообщений равной длины из 16-битной кодировки Unicode в 8-битную кодировку в дно новое сообщение, которое при этом увеличилось на 240 байт.

Какова длина каждого из исходных сообщений в символах.

Задание 11.

Записать числа в порядке убывания: 15₁₀, 10111010₂, 217₈, 1F₁₆.

2.6. Перевод правильных дробей из десятичной системы счисления в систему счисления с основанием S

1. Последовательно умножить данное число и получаемые дробные части произведения на основание новой системы счисления (S) до тех пор, пока дробная часть произведения не станет равна нулю или не будет достигнута требуемая точность представления числа.

2. Полученные целые части произведений, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления.

3. Составить дробную часть числа в новой системе счисления, начиная с целой части первого произведения.

Примеры:

a. В двоичную: b. В восьмеричную: c. В шестнадцатеричную:

Ответ: 0,15₁₀= 0,00100₂=0,11463₈=0,26666₁₆

2.7. Перевод неправильных дробей из десятичной системы счисления в систему

счисления с основанием S

Перевод неправильных дробей из десятичной системы счисления в систему счисления с основанием S выполняется отдельно для целой и дробной частей по вышеизложенным правилам с последующим соединением этих частей в одну запись – неправильную дробь, представленную уже в новой системе счисления.

Задания для самостоятельного выполнения:

Задание 1.

Переведите десятичную дробь в дробь системы счисления (двоичную, восьмеричную, шестнадцатеричную) с точность до указанного количества знаков после запятой:

a) 0,75; два знака

b) 0,2; три знака

c) 0,9; четыре знака

d) 0,45; три знака

Задание 2.

Переведите данное число в десятичной системе счисления в двоичную, восьмеричную, а затем в шестнадцатеричную систему счисления:

a) 153,25₁₀ c) 98,45₁₀

b) 3,5₁₀ d) 712,5₁₀

Домашнее задание:

Задание 3.

a) 0,85; два знака

b) 0,23; три знака Задание 4.

c) 0,322; четыре знака

d) 0,251; три знака

a) 670,25₁₀ c) 8,25₁₀

b) 162,5₁₀ d) 72,52₁₀

2.8. Перевод чисел из системы счисления с основанием 2 в систему счисления с

n и обратно (Перевод целых чисел) основанием 2

Для того чтобы целое двоичное число записать в системе счисления с основанием q=2ⁿ, нужно:

1. Двоичное число разбить справа налево на группы по n цифр в каждой.

2. Если в последней левой группе окажется меньше n разрядов, то ее надо дополнить слева нулями до нужного числа разрядов.

3. Рассмотреть каждую группу как n-разрядное двоичное число и записать ее соответствующей цифрой в системе счисления с основанием q=2ⁿ.

Пример 1. Число 1011000010001100102 переведем в восьмеричную систему счисления. Разбиваем число справа налево на триады и под каждой из них записываем соответствующую восьмеричную цифру:

101 100 001 000 110 010

5 4 1 0 6 2

Получаем восьмеричное представление исходного числа: 5410628.

Пример 2. Число10000000000111110000111₂ переведем в шестнадцатеричную систему счисления.

Разбиваем число справа налево на тетрады и под каждой из них записываем соответствующую шестнадцатеричную цифру:

0100 0000 0000 1111 1000 0111 4 0 0 F 8 7

Получаем шестнадцатеричное представление исходного числа: 400F8716.

2.9. Перевод чисел из системы счисления с основанием 2 в систему счисления с

n и обратно (Перевод дробных чисел) основанием 2

Для того, чтобы дробное двоичное число записать в системе счисления с основанием q=2ⁿ, нужно:

1. Двоичное число разбить слева направо на группы по n цифр в каждой.

2. Если в последней правой группе окажется меньше n разрядов, то ее надо дополнить справа нулями до нужного числа разрядов.

Рассмотреть каждую группу как n-разрядное двоичное число и записать ее соответствующей цифрой в системе счисления с основанием q=2n.

Пример 3. Число 0,101100012 переведем в восьмеричную систему счисления.

Разбиваем число слева направо на триады и под каждой из них записываем соответствующую восьмеричную цифру:

0, 101 100 010

0, 5 4 2

Получаем восьмеричное представление исходного числа: 0,5428.

Пример 4. Число 0,1000000000112 переведем в шестнадцатеричную систему счисления. Разбиваем число слева направо на тетрады и под каждой из них записываем соответствующую шестнадцатеричную цифру:

0, 1000 0000 0011

0, 8 0 3

Получаем шестнадцатеричное представление исходного числа: 0,80316

2.10. Перевод чисел из систем счисления с основанием q=2ⁿ в двоичную систему

Для того, чтобы произвольное число, записанное в системе счисления с основанием q=2ⁿ, перевести в двоичную систему счисления, нужно каждую цифру этого числа заменить ее n-значным эквивалентом в двоичной системе счисления.

Пример 5. Переведем шестнадцатеричное число 4АС3516 в двоичную систему счисления.

В соответствии с алгоритмом:

4 А С 3 5 0100 1010 1100 0011 0101

Получаем: 1001010110000110101 ₂.

Задания для самостоятельного выполнения:

Задание 1.

Переведите двоичные числа в восьмеричную систему счисления:

a) 1010001001011; c) 1010,00100101; e) 1110,01010001;

b) 1011001101111; d) 110001000100; f) 1000,1111001.

Задание 2.

Переведите двоичные числа в шестнадцатеричную систему счисления:

a) 1010001001011; c) 110001000100; e) 1110,01010001;

b) 1011001101111; d) 1010,00100101; f) 100,1111001.

Задание 3.

Переведите восьмеричные и шестнадцатеричные числа в двоичную систему счисления:

a) 266₈;

b) 266₁₆;

Домашнее задание:

Задание 4.

1270₈;

10,23₈;

2A1916 10,23₁₆.

Перевести числа в восьмеричную и шестнадцатеричную системы счисления:

a) 0,10110000111₂

b) 111100001,0111₂

Задание 5.

c) 11101001000,11010010₂

d) 11101101,11011₂

Перевести числа в шестнадцатеричную систему счисления.

a) 1101000101011₂b) 100000011,000101110₂

Задание 6.

Переведите восьмеричные и шестнадцатеричные числа в двоичную систему счисления:

а) 213₈; b) 13,51₈; c) 11,22₁₆;

Задание 7.

Чему равна сумма чисел 718 и 5416?

a) 215₈; b) 105₈;

Задание 8.

Чему равна сумма чисел 448.и 5916?

a) 103₁₀; b) 1011₂;

c) 1000101₂; d) 145₈.

c) А1₁₆; d) 175₈.

Двоичная арифметика

3.1. Двоичная арифметика

Правила выполнения арифметических действий над двоичными числами задаются таблицами двоичных сложения, вычитания и умножения.

Правила двоичного сложения

Правила двоичного вычитания

Правила двоичного умножения

0 + 0 = 0

0 + 1 = 1

1 + 0 = 1

1 + 1= 10

0 – 0 = 0

1 – 0 = 1

1 – 1 = 0

10 – 1 = 1

0  0 = 0

0 1 = 0

1  0 = 0

1  1 = 1

При сложении двоичных чисел в каждом разряде производится сложение цифр слагаемых и переноса из соседнего младшего разряда, если он имеется. При этом необходимо учитывать, что 1+1 дают нуль в данном разряде и единицу переноса в следующий.

Пример 1. Выполнить сложение двоичных чисел:

1 a. b. 1 1 1 c.

1010 1101,01 1 1 1 1 1 1

110111

+ 11 + 111,10 + 1011101

1101 10100,11

10010100

При вычитании двоичных чисел в данном разряде при необходимости занимается 1 из старшего разряда. Эта занимаемая 1 равна двум 1 данного разряда.

Пример 2. Выполнить вычитание двоичных чисел:

Умножение двоичных чисел производится по тем же правилам, что и для десятичных с помощью таблиц двоичного умножения и сложения.

Пример 3. Выполнить умножение двоичных чисел:

a . 101

*11

+ 101

101

1111

b .

1010

*101

1010

⁺ 0

1010

110010

c .

1110

*110

0000

+ 1110

1110

1010100

Деление двоичных чисел производится по тем же правилам, что и для десятичных. При этом используются таблицы двоичного умножения и вычитания.

Пример 4. Выполнить деление двоичных чисел:

10 10

l l

1001,10

-100,01

101,01

_l10 _l1 10

1011001

-100111

110010

l 10 _l 10

100110

- 10001

10101

a. b. c.

11000 110

110

100

000

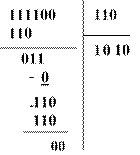Задания для самостоятельного выполнения:

Задание 1.

Сложить два числа в двоичной системе счисления. Результат проверить при помощи десятичной системы счисления.

a) 110110+ 1011010 c) 10011,01+ 1001,101

b) 1011101+ 1000100

d) 1010101+ 1010000

Задание 2.

Выполнить вычитание двух чисел в двоичной системе счисления. Результат проверить при помощи десятичной системы счисления.

a) 101010,10111- 100100,01 c) 1110011 – 101100

b) 1011001- 100011 d) 1001011- 101000

Задание 3.

Выполнить умножение двух чисел в двоичной системе счисления. Результат проверить при помощи десятичной системы счисления.

a) 101·101 c) 1011·1001

b) 1110·1010 d) 1100·1011

Задание 4.

Выполнить деление в двоичной системе счисления.

a) 100111000: 11000 = 1101 b) 111111000: 101010 = 1100

Домашнее задание:

Задание 5.

Выполните сложение и проверьте ответы:

a) 101011 + 1011 = 110110 d)

b) 101 + 11 = 1000 e)

c) 10110 +101 = 101001010 f)

Задание 6.

Выполните вычитание и проверьте ответы:

1110011 – 101100=1000111

1001011- 101000=100011

10101 + 10011 = 101000

a) 100 – 1 = 11 d)

b) 10101 – 110 = 1111 e)

c) 10000 – 101 = 1011 f)

10101 – 1010 = 1011

10111 – 1011 = 1100

10101– 101=10000

Задание 7.

Выполните умножение и проверьте ответы:

a) 101 · 11 = 1111

b) 1001 · 11 = 11011

c) 10101 · 1011 = 11100111

d) 1101 · 101 = 1000001

e) 1101 · 1001 = 1110101

f) 101 ^. 110 = 1001110

Задание 8.

a) 1111 : 101 = 11

b) 1111 : 11 = 101

c) 11100111 : 1011 = 10101

d) 111111 : 111 = 1001

Выполните деление и проверьте ответы:

3.2. Основы машинной арифметики с двоичными числами

Любая информация (числа, команды, записи и т. п.) представляется в ЭВМ в виде двоичных кодов фиксированной или переменной длины. Отдельные элементы двоичного кода, имеющие значение 0 или 1, называют разрядами или битами. Двоичный код состоящий из 8 разрядов носит название байта. Для записи чисел также используют 32разрядный формат (машинное слово), 16-разрядный формат (полуслово) и 64-разрядный формат (двойное слово).

3.3. Коды чисел

В ЭВМ в целях упрощения выполнения арифметических операций применяют специальные коды для представления чисел. Использование кодов позволяет свести операцию вычитания чисел к арифметическому сложению кодов этих чисел. Применяются прямой, обратный и дополнительный коды чисел. Прямой код используется для представления отрицательных чисел в запоминающем устройстве ЭВМ, а также при умножении и делении. Обратный и дополнительный коды используются для замены операции вычитания операцией сложения, что упрощает устройство арифметического блока ЭВМ. К кодам выдвигаются следующие требования:

1) Разряды числа в коде жестко связаны с определенной разрядной сеткой.

2) Для записи кода знака в разрядной сетке отводится фиксированный, строго определенный разряд. Например, если за основу представления кода взят один байт, то для представления числа будет отведено 7 разрядов, а для записи кода знака один разряд. Прямой код. Прямой код двоичного числа совпадает по изображению с записью самого числа. Значение знакового разряда для положительных чисел равно 0, а для отрицательных чисел 1.

Пример 1. В случае, когда для записи кода выделен один байт, для числа +1101 прямой код 0,0001101, для числа –1101 прямой код 1,0001101.

Обратный код

Обратный код для положительного числа совпадает с прямым кодом. Для отрицательного числа все цифры числа заменяются на противоположные (1 на 0, 0 на 1), а в знаковый разряд заносится единица.

Пример 2.

Для числа +1101 прямой код 0 , 0001101; обратный код 0,0001101.

Для числа –1101 прямой код 1 , 0001101; обратный код 1,1110010.

Дополнительный код

Дополнительный код положительного числа совпадает с прямым кодом.

Для отрицательного числа дополнительный код образуется путем получения обратного кода и добавлением к младшему разряду единицы.

Пример 3. Для числа +1101:

прямой код обратный код дополнительный код

0,0001101 0,0001101 0,0001101

Для числа –1101: прямой код обратный код дополнительный код

1,0001101 1,1110010 1,1110011

3.4. Особенности сложения чисел в обратном и дополнительном кодах

При сложении чисел в дополнительном коде возникающая единица переноса в знаковом разряде отбрасывается.

При сложении чисел в обратном коде возникающая единица переноса в знаковом разряде прибавляется к младшему разряду суммы кодов.

Если результат арифметических действий является кодом отрицательного числа, необходимо преобразовать его в прямой код. При этом обратный код преобразуется в прямой заменой цифр во всех разрядах кроме знакового на противоположные. Дополнительный код преобразуется в прямой также, как и обратный, с последующим прибавлением единицы к младшему разряду.

Пример 1. Сложить X и Y в обратном и дополнительном кодах.

1) Сложим числа пользуясь правилами двоичной арифметики: X= 1010, Y= -11;

1010

- 11

111

2) Сложим числа используя коды:

Прямой код

Сложение в обратном коде

Сложение в дополнительном коде

X _{п р}=0,0001010

Y _{п р}=1,0000011

X _обр= 0,0001010

Y _обр= 1,1111100

10,0000110

(X+Y) _обр=0,0000 111

X _доп= 0,0001010

Y _доп= 1,1111101

10,0000111

отбрасывается

(X+Y) _доп=0,0000111

Так как результат сложения является кодом положительного числа (знак 0), то (X+Y)_обр=(X+Y)_доп=(X+Y)_пр.

Вопросы:

1. Дать определение дополнительного, обратного и прямого кода для положительного и отрицательного числа.

2. Сформулировать алгоритмы сложения в обратном и дополнительном коде.

Задания для самостоятельного выполнения:

Задание 1.

Записать число в прямом, обратном и дополнительном кодах:

a) 11010; b) –11101; c) –101001; d) –1001110.

Задание 2.

Вычислить:

a) X= 11010;

Y= –10011;

d) X= 1011001;

Y= –111011;

Задание 3.

Вычислить:

b) X= 1110100;

Y= –100110;

e) X= 11110101;

Y= –1001010;

Домашнее задание:

c) X= 1110100;

Y= –101101;

f) X= 11011010;

Y= –101010.

a) X= 10010;

Y= –1001;

b) X= 101010;

Y= –10110;

X= 1000100;

Y= –111101;

d) X= 10110;

Y= –1101;

e) X= 110110;

Y= –11110;

f) X= 1110100;

Y= –110011;

Арифметические действия над числами в различных системах счисления

4.1. Сложение и вычитание в 8-ой с/с

При выполнении этих действий в 8-ой с/с необходимо соблюдать следующие правила:

1. в записи результатов сложения и вычитания могут быть использованы только цифры восьмеричного алфавита;

2. десяток восьмеричной системы счисления равен 8, т.е. переполнение разряда наступает, когда результат сложения больше или равен 8.

3. В этом случае для записи результата надо вычесть 8, записать остаток, а к старшему разряду прибавить единицу переполнения;

4. если при вычитании приходится занимать единицу в старшем разряде, эта единица переносится в младший разряд в виде восьми единиц.

4.2. Сложение и вычитание в 16-ой с/с

При выполнении этих действий в 16-ой с/с необходимо соблюдать следующие правила:

1. при записи результатов сложения и вычитания надо использовать цифры шестнадцатеричного алфавита: цифры, обозначающие числа от 10 до 15 записываются латинскими буквами, поэтому, если результат является числом из этого промежутка, его надо записывать соответствующей латинской буквой;

2. десяток шестнадцатеричной системы счисления равен 16, т.е. переполнение разряда поступает, если результат сложения больше или равен 16, и в этом случае для записи результата надо вычесть 16, записать остаток, а к старшему разряду прибавить единицу переполнения;

3. если приходится занимать единицу в старшем разряде, эта единица переносится в младший в виде шестнадцати единиц.

Примеры:

6 ( 8 ) + 7 ( 8 ) 25 ( 8 )

7+6=13=8+5

1+1=2

311,2 _{( 8 )}

^- 73,6 _{( 8 )}

215,4 _{( 8 )}

b. c.

07 ( 8 ) 0F ( 1 6 ) + 01 ( 8 ) + 06 ( 1 6 )

10 ( 8 ) 15 ( 1 6 )

7+1=8+0 15+6=21=16+5

0+1=^{^[1]}

С9,4 ( 1 6 )

2+8-6=4 3В,С ( 1 6 )

1-1+8-3=5

1-1+8 -7=1 8D,8 _{( 1
6 )}

4.3. Умножение

4-С+16=4-12+16=8

9-1-В+16=9-1-11+16=13

С-3-1=12-3-1=8

Выполняя умножение многозначных чисел в различных позиционных системах счисления, можно использовать обычный алгоритм перемножения чисел в столбик.

4.4. Деление

Деление в любой позиционной системе счисления производится по тем же правилам, как и деление, углом в десятичной системе.

Примеры:

16 _{( 8 )} *

17 ( 8 )

142 +

322 ( 8 )

6 · 7 = 4 2= 8 · 5 +2

5 +7 =1 2= 8+ 4

4 +6 =1 0= 8+ 2

5·7=35₁₀=4∙8+3=35₈

17 _{( 1 6 )} *

16 ( 1 6 )

8 A

4 2= 16 · 2 + 1 0= A

6 +2 =8

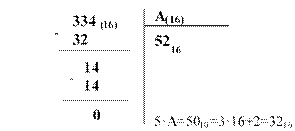2·A=20·10=1·16+4=14₁₆

Задания для самостоятельного выполнения:

Задание 1. Выпишите целые числа, принадлежащие следующим числовым промежуткам:

a) [14₈; 20₈] в восьмеричной системе;

b) [28₁₆; 30₁₆] в шестнадцатеричной системе.

Задание 2.

Выполнить арифметические операции в 8-й и16-й СС:

a) 67₈ + 23₈ = 112₈ e) AF₁₆ + 97₁₆ = 146₁₆

b) 67₈ – 23₈ = 44₈ f) AF₁₆ – 97₁₆ = 18₁₆

c) 67₈ · 23₈ = 2025₈ g) AF₁₆ · 97₁₆ = 6739₁₆

d) 74₈ : 24₈ = 3₈h) 5A₁₆ : 1E₁₆ = 3₁₆

Задание 3.

Выполнить арифметические операции в 8-й и16-й СС:

a) 45₈+ 36₈ = 103₈n) 6EF5₁₆ : 5F₁₆ = 12B₁₆

b) 274₈ + 76₈ = 372₈o) 24₈ · 16₈ = 430₈

c) 521₈ + 377₈ = 1120₈p) 24E₁₆ · 12₁₆ = 297C

d) 38₁₆ + 25₁₆ = 5D₁₆q) 623₈ · 41₈ = 31763₈

e) 78C₁₆ + 9B₁₆ = 827₁₆r) A,5₁₆ · 2,B₁₆ = 1B,B7₁₆

f) B8C4₁₆ + F9D₁₆ = C861₁₆s) 52₈ : 3₈ = 16₈

g) B8C4₁₆ + F9D₁₆ = C861₁₆t) 313₈ : 7₈ = 35₈

h) F47₁₆ + D98₁₆ = 1CDF₁₆u) 250₈ : 16₈ = 14₈

i) F47₁₆ + D98₁₆ = 1CDF₁₆v) 1552₈ : 23₈ = 56₈

j) 1435₈ – 746₈ = 467₈w) 5E8₁₆ : 12₁₆ = 54₁₆

k) 235₈ – 71₈ = 144₈x) 63C₁₆ : 39₁₆ = 1C₁₆

l) A5₁₆ – 19₁₆ = 8C₁₆ y) 6EF5₁₆ : 5F₁₆ = 12B₁₆

m) 9A23₁₆ – ABC₁₆ = 8F67₁₆ z) 53₈ · 4₈ = 254₈

Домашнее задание:

Задание 4.

Выполните действия:

a) 4 312₈ + 2 727₈; b) 314₅ + 232₅; c) 3 79В₁₆ + 2 DЕ5₁₆;

d) 6 714₈ – 3 505₈; e) А 256₁₆ – 9Е8₁₆; f) 2 431₅ – 1 302₅;

g) 7 0А9₁₆· 138₁₆;	h) 665₇ · 43₇;	i) 42₆ · 31₆;
j) 5 250₈ : 76₈;	k) А 178₁₆ : 102₁₆;	l) 404 401₅ : 113₅;

m) 1 011 101 001,101₂ + 10 111 011,011₍₂₎ + 1 110 100,111₍₂₎,

Задание 5.

Решите уравнение:

a) 120х : 200 = 1022 в троичной системе счисления;

b) (b + 311) – 55 = 253 в шестеричной системе счисления;

c) (3 666 + k) × 148 = 1 534 874 в девятеричной системе счисления.

Задание 6.

Выполните действия:

a) ABC,F₁₆+123,4₁₆= e) 745,1₈+123,7₈=

b) 563,7₁₆+ED,4₁₆= f) 563,7₈+10,4₈=

c) 111,9₁₆+FF,1₁₆= g) 125,6₈+37,3₈=

d) AC7,3₁₆-4B8,4₁₆=h) 234,5₈*21₈=

Дискретное (цифровое) представление информации

5.1. Дискретное представление информации

Вся информация, которую обрабатывает компьютер должна быть представлена двоичным кодом с помощью двух цифр 0 и 1. Эти два символа принято называть двоичными цифрами или битами. С помощью двух цифр 0 и 1 можно закодировать любое сообщение. Это явилось причиной того, что в компьютере обязательно должно быть организованно два важных процесса: кодирование и декодирование.

Кодирование – преобразование входной информации в форму, воспринимаемую компьютером, т.е. двоичный код.

Декодирование – преобразование данных из двоичного кода в форму, понятную человеку. С точки зрения технической реализации использование двоичной системы счисления для кодирования информации оказалось намного более простым, чем применение других способов. Действительно, удобно кодировать информацию в виде последовательности нулей и единиц, если представить эти значения как два возможных устойчивых состояния электронного элемента:

0 – отсутствие электрического сигнала; 1 – наличие электрического сигнала. Эти состояния легко различать. Недостаток двоичного кодирования – длинные коды. Но в технике легче иметь дело с большим количеством простых элементов, чем с небольшим числом сложных.

Вам приходится постоянно сталкиваться с устройством, которое может находится только в двух устойчивых состояниях: включено/выключено. Конечно же, это хорошо знакомый всем выключатель. И в основу представления чисел в компьютере была положена именно двоичная система счисления.

Способы кодирования и декодирования информации в компьютере, в первую очередь, зависит от вида информации, а именно, что должно кодироваться: числа, текст, графические изображения или звук.

5.2. Аналоговый и дискретный способ кодирования

Человек способен воспринимать и хранить информацию в форме образов (зрительных, звуковых, осязательных, вкусовых и обонятельных). Зрительные образы могут быть

сохранены в виде изображений (рисунков, фотографий и так далее), а звуковые — зафиксированы на пластинках, магнитных лентах, лазерных дисках и так далее.

Информация, в том числе графическая и звуковая, может быть

представлена в аналоговой или дискретной форме. При аналоговом

Рис.21 представлении физическая величина принимает бесконечное множество значений, причем ее значения изменяются непрерывно. При дискретном представлении физическая величина принимает конечное множество значений, причем ее величина изменяется скачкообразно.

Приведем пример аналогового и дискретного представления информации. Положение тела на наклонной плоскости и на лестнице задается значениями координат X и У. При движении тела по наклонной плоскости его координаты могут принимать бесконечное множество непрерывно изменяющихся значений из определенного диапазона, а при движении по лестнице — только определенный набор значений, причем меняющихся скачкообразно.

Примером аналогового представления графической информации может служить, например, живописное полотно, цвет которого изменяется непрерывно, а дискретного — изображение, напечатанное с помощью струйного принтера и состоящее из отдельных точек разного цвета. Примером аналогового хранения звуковой информации является виниловая пластинка (звуковая дорожка изменяет свою форму непрерывно), а дискретного — аудиокомпакт-диск (звуковая дорожка которого содержит участки с различной отражающей способностью).

Преобразование графической и звуковой информации из аналоговой формы в дискретную производится путем дискретизации, то есть разбиения непрерывного графического изображения и непрерывного (аналогового) звукового сигнала на отдельные элементы. В процессе дискретизации производится кодирование, то есть присвоение каждому элементу конкретного значения в форме кода.

Дискретизация – это преобразование непрерывных изображений и звука в набор дискретных значений в форме кодов.

5.3. Кодирование изображений

Создавать и хранить графические объекты в компьютере можно двумя способами – как растровое или как векторное изображение. Для каждого типа изображений используется свой способ кодирования.

Растровое изображение представляет собой совокупность точек (пикселей) разных цветов. Пиксель - минимальный участок изображения, цвет которого можно задать независимым образом.

В процессе кодирования изображения производится его пространственная дискретизация. Пространственную дискретизацию изображения можно сравнить с построением изображения из мозаики (большого количества маленьких разноцветных стекол). Изображение разбивается на отдельные маленькие фрагменты (точки), причем каждому фрагменту присваивается значение его цвета, то есть код цвета (красный, зеленый, синий и так далее).

Для черно-белого изображения информационный объем одной точки равен одному биту (либо черная, либо белая – либо 1, либо 0).

Для четырех цветного – 2 бита. Для 16 цветов – 4 бита.

Для 8 цветов необходимо – 3 бита. Для 256 цветов – 8 бит (1 байт).

Качество изображения зависит от количества точек (чем меньше размер точки и, соответственно, больше их количество, тем лучше качество) и количества используемых цветов (чем больше цветов, тем качественнее кодируется изображение).

Для представления цвета в виде числового кода используются две обратных друг другу цветовые модели: RGB или CMYK. Модель RGB используется в телевизорах, мониторах, проекторах, сканерах, цифровых фотоаппаратах… Основные цвета в этой модели: красный (Red), зеленый (Green), синий (Blue). Цветовая модель CMYK используется в полиграфии при формировании изображений, предназначенных для печати на бумаге.

Цветные изображения могут иметь различную глубину цвета, которая задается количеством битов, используемых для кодирования цвета точки.

Если кодировать цвет одной точки изображения тремя битами (по одному биту на каждый цвет RGB), то мы получим все восемь различных цветов.

R		G		B		Цвет
	1		1		1	белый
	1		1		0	желтый
	1		0		1	пурпурный
	1		0		0	красный
	0		1		1	голубой
	0		1		0	зеленый
	0		0		1	синий
	0		0		0	черный

На практике же, для сохранения информации о цвете каждой точки цветного изображения в модели RGB обычно отводится 3 байта (т.е. 24 бита) - по 1 байту (т.е. по 8 бит) под значение цвета каждой составляющей. Таким образом, каждая RGB-составляющая может принимать значение в диапазоне от 0 до 255 (всего 2⁸=256 значений), а каждая точка изображения, при такой системе кодирования может быть окрашена в один из 16 777 216 цветов.

Такой набор цветов принято называть True Color (правдивые цвета), потому что человеческий глаз все равно не в состоянии различить большего разнообразия.

Векторное изображение представляет собой совокупность графических примитивов (точка, отрезок, эллипс…). Каждый примитив описывается математическими формулами.

Кодирование зависит от прикладной среды.

Достоинством векторной графики является то, что файлы, хранящие векторные графические изображения, имеют сравнительно небольшой объем.

Важно также, что векторные графические изображения могут быть увеличены или уменьшены без потери качества.

5.4. Графические форматы файлов

Форматы графических файлов определяют способ хранения информации в файле (растровый или векторный), а также форму хранения информации (используемый алгоритм сжатия).

Наиболее популярные растровые форматы:

BMP; GIF; JPEG; TIFF; PNG

Bit MaP image (BMP) — универсальный формат растровых графических файлов, используется в операционной системе Windows. Этот формат поддерживается многими графическими редакторами, в том числе редактором Paint.

Tagged Image File Format (TIFF) — формат растровых графических файлов, поддерживается всеми основными графическими редакторами и компьютерными платформами. Включает в себя алгоритм сжатия без потерь информации. Используется для обмена документами между различными программами. Рекомендуется для использования при работе с издательскими системами.

Graphics Interchange Format (GIF) — формат растровых графических файлов, поддерживается приложениями для различных операционных систем. Включает алгоритм сжатия без потерь информации, позволяющий уменьшить объем файла в несколько раз. Рекомендуется для хранения изображений, создаваемых программным путем (диаграмм, графиков и так далее) и рисунков (типа аппликации) с ограниченным количеством цветов (до 256). Используется для размещения графических изображений на Web-страницах в Интернете.

Portable Network Graphic (PNG) — формат растровых графических файлов, аналогичный формату GIF. Рекомендуется для размещения графических изображений на Web-страницах в Интернете.

Joint Photographic Expert Group (JPEG) — формат растровых графических файлов, который реализует эффективный алгоритм сжатия (метод JPEG) для отсканированных фотографий и иллюстраций. Алгоритм сжатия позволяет уменьшить объем файла в десятки раз, однако приводит к необратимой потере части информации. Поддерживается приложениями для различных операционных систем. Используется для размещения графических изображений на Web-страницах в Интернете.

5.5. Информационный объѐм растрового графического изображения Расчѐт информационного объѐма растрового графического изображения (количества информации, содержащейся в графическом изображении) основан на подсчѐте количества пикселей в этом изображении и на определении глубины цвета (информационного веса одного пикселя).

Итак, для расчѐта информационного объѐма растрового графического изображения используется формула V=iXY, где V – это информационный объѐм растрового графического изображения, измеряющийся в байтах, килобайтах, мегабайтах;

XY – количество пикселей (точек) в изображении, определяющееся разрешающей способностью носителя информации (экрана монитора, сканера, принтера); i – глубина цвета, которая измеряется в битах на один пиксель.

Глубина цвета задаѐтся количеством битов, используемым для кодирования цвета точки.

Глубина цвета связана с количеством отображаемых цветов формулой

N=2ⁱ, где N – это количество цветов в палитре, i – глубина цвета в битах на один пиксель.

Задание 1.

Определить требуемый объем видеопамяти для различных графических режимов экрана монитора, если известна глубина цвета на одну точку.

Режим экрана		Глуб	ина цвета (бит на точку)
Режим экрана	4	8	16	24	32
640 на 480
800 на 600
1024 на 768
1280 на 1024

Решение:

1. Всего точек на экране (разрешающая способность): 640 · 480 = 307200

2. Необходимый объем видеопамяти V= 4 бит · 307200 = 1228800 бит = 153600 байт = 150 Кбайт.

Аналогично рассчитывается необходимый объем видеопамяти для других графических режимов.

Ответ:

Режим экрана		Глубина цвета (бит на точку)
Режим экрана	4	8	16	24	32
640 на 480	150 Кб	300 Кб	600 Кб	900 Кб	1,2 Мб
800 на 600	234 Кб	469 Кб	938 Кб	1,4 Мб	1,8 Мб
1024 на 768	384 Кб	768 Кб	1,5 Мб	2,25 Мб	3 Мб
1280 на 1024	640 Кб	1,25 Мб	2,5 Мб	3,75 Мб	5 Мб

Задание 2.

Черно-белое (без градаций серого) растровое графическое изображение имеет размер 10

10 точек. Какой объем памяти займет это изображение?

Дано:

XY=10 ·10:

N=2;

Найти:

V - ?

Задание 3.

Решение:

1. Количество точек X·Y =100.

2. Так как всего 2 цвета черный и белый, то глубина цвета равна 1 ( 2¹=2).

3. Объем видеопамяти равен 100·1=100 бит

Ответ:100 бит.

Для хранения растрового изображения размером 128 x 128 пикселей отвели 4 КБ памяти.

Каково максимально возможное число цветов в палитре изображения?

Дано:

XY=128128;

V=4 Кбайт;

Найти:

N - ?

Решение:

1. Количество точек XY=128·128=16384 точек или пикселей.

2. Объем памяти на изображение 4 Кб выразим в битах, так как V=I·X·Y вычисляется в битах:

4 Кб=4·1024=4 096 байт = 4096·8 бит =32768 бит

3. Найдем глубину цвета i=V/(X·Y) =

32768:16384=2.

4. N=2ⁱ, где N – число цветов в палитре. N=4

Ответ:4 цвета.

Задание 4.

Какой объем видеопамяти необходим для хранения четырех страниц изображения, если битовая глубина равна 24, а разрешающая способность дисплея- 800  600 пикселей.

Дано:

XY=800  600; i=24; s=4;

Найти:

V-?

Решение:

1. Найдем объем видеопамяти для одной страницы: 800·600·24=11520000 бит =1440000 байт =1406,25 Кб ≈1, 37 Мб

2. 1,37·4 =5,48 Мб ≈5.5 Мб

Ответ: 5.5 Мб

Задание 5.

Определить объем видеопамяти компьютера, который необходим для реализации графического режима монитора High Color с разрешающей способностью 1024  768 точек и палитрой цветов из 65536 цветов.

Дано: Решение:

XY=1024  768; 1. По формуле K=2ⁱ, где K – количество цветов, i –

N=65536; глубина цвета определим глубину цвета.

Найти: 2ⁱ=65536.

V-?

2. Глубина цвета составляет: i = log₂65536 =16 бит

Количество точек изображения равно: 1024·768 = 786 432 .

3. Требуемый объем видеопамяти равен: 16 бит · 786 432 = 12 582 912 бит = 1572864 байт = 1536 Кб =1,5 Мб.

Ответ: 1,5 Мб Вопросы:

1. Что такое пиксель?

2. Чем отличаются растровые и векторные изображения?

3. Перечислите характеристики растрового изображения.

4. Как связаны между собой палитра и глубина цвета?

5. Что такое графический режим экрана монитора?

6. Что такое палитра цветов в системе цветопередачи RGB?

7. Назовите форматы растровых графических файлов?

8. В чѐм заключается растровое кодирование?

9. Как кодируется черно-белое изображение?

10. Из каких основных цветов складываются оттенки?

11. Сколько бит отводится на каждый из основных цветов?

12. Сколько различных оттенков основного цвета при этом можно закодировать?

13. Сколько цветов включает в себя цветовая палитра современных компьютеров?

Задания для самостоятельного выполнения:

6. Достаточно ли видеопамяти объемом 256 Кбайт для работы монитора в режиме 640

 480 и палитрой из 16 цветов?

7. Укажите минимальный объем памяти (в килобайтах), достаточный для хранения любого растрового изображения размером 256  256 пикселей, если известно, что

в изображении используется палитра из 2¹⁶цветов. Саму палитру хранить не нужно.

8. Используются графические режимы с глубинами цвета 8, 16. 24, 32 бита. Вычислить объем видеопамяти, необходимые для реализации данных глубин цвета при различных разрешающих способностях экрана.

9. Сколько секунд потребуется модему, передающему сообщения со скоростью 28800 бит/с, чтобы передать цветное растровое изображение размером 640 480 пикселей, при условии, что цвет каждого пикселя кодируется тремя байтами?

10. Сколько секунд потребуется модему, передающему сообщения со скоростью 14400 бит/сек, чтобы передать цветное растровое изображение размером 800600 пикселей, при условии, что в палитре 16 миллионов цветов?

11. Современный монитор позволяет получать на экране 16777216 различных цветов.

Сколько бит памяти занимает 1 пиксель?

Домашнее задание:

12. Каков минимальный объем памяти (в байтах), достаточный для хранения чернобелого растрового изображения размером 3232 пикселя, если известно, что в изображении используется не более 16 градаций серого цвета.

13. Монитор работает с 16 цветной палитрой в режиме 640400 пикселей. Для кодирования изображения требуется 1250 Кбайт. Сколько страниц видеопамяти оно занимает?

14. Страница видеопамяти составляет 16000 байтов. Дисплей работает в режиме

320400 пикселей. Сколько цветов в палитре?

15. Сканируется цветное изображение размером 1010 см. Разрешающая способность сканера 600 dpi и глубина цвета 32 бита. Какой информационный объем будет иметь полученный графический файл.

16. Объем видеопамяти равен 256 Кб. Количество используемых цветов -16. Вычислите варианты разрешающей способности дисплея.

17. Часть страниц многотомной энциклопедии является цветными изображениями в шестнадцати цветовой палитре и в формате 320 640 точек. Страницы, содержащие текст, имеют формат — 32 строки по 64 символа в строке. Сколько страниц книги можно сохранить на жестком магнитном диске объемом 20 Мб, если каждая девятая страница энциклопедии — цветное изображение?

18. Определить максимально возможную разрешающую способность экрана для монитора с диагональю 15" и размером точки экрана 0,28 мм.

5.6. Кодирование звуковой информации

Звук представляет собой звуковую волну с непрерывно меняющейся амплитудой и

частотой. Звуковые колебания можно представить в виде графика, горизонтальная ось которого – время, а вертикальная ось – амплитуда.

Для человека звук тем громче, чем больше амплитуда сигнала, и чем выше тон, чем больше частота сигнала.

Частота – физическая величина, показывающая, сколько

колебаний произошло за 1 секунду. Измеряется в герцах.

Считается, что диапазон частот, которые слышит человек, составляет от 20 Гц до 20 кГц.

Непрерывный сигнал не несет в себе информации, поэтому он должен быть превращен в последовательность двоичных нулей и единиц - двоичный (цифровой) код. Оцифровку звука выполняет специальное устройство на звуковой плате. Называется оно аналого-цифровой преобразователь (АЦП). Обратный процесс — воспроизведение закодированного звука производится с помощью цифроаналогового преобразователя (ЦАП).

Подробнее рассмотрим эти процессы. В процессе кодирования непрерывного звукового сигнала производится дискретизация по времени, или, как говорят, «временная дискретизация».

Временная дискретизация – процесс, при котором, во время кодирования непрерывного звукового сигнала, звуковая волна разбивается на отдельные маленькие временные участки, причем для каждого такого участка устанавливается определенная величина амплитуды. Чем больше амплитуда сигнала, тем громче звук. Данный метод называется импульсноамплитудной модуляцией РСМ (Pulse Code Modulation).

Таким образом, гладкая кривая заменяется на последовательность «ступенек». Каждой «ступеньке» присваивается значение громкости звука (1, 2, 3…). Чем больше «ступенек», тем большее количество уровней громкости выделено в процессе кодирования, и тем большее количество информации будет нести значение каждого уровня и более качественным будет звучание.

5.7. Характеристики оцифрованного звука

Качество звука зависит от двух характеристик — глубины кодирования и частоты дискретизации. Рассмотрим эти характеристики.

Глубина кодирования звука (I) — это количество бит, используемое для кодирования различных уровней сигнала или состояний. Тогда общее количество таких состояний или уровней( N) можно вычислить по формуле: N = 2ⁿ .Современные звуковые карты обеспечивают 16-битную глубину кодирования звука, и тогда общее количество различных уровней будет: N =2^I= 65536.

Частота дискретизации (М) — это количество измерений уровня звукового сигнала в единицу времени. Эта характеристика показывает качество звучания и точность процедуры двоичного кодирования. Измеряется в герцах (Гц). Одно измерение за одну секунду соответствует частоте 1 Гц, 1000 измерений за одну секунду — 1 килогерц

(кГц). Частота дискретизации звукового сигнала может принимать значения от 8 до 48 кГц. Для кодировки выбирают одну из трех частот: 44,1 КГц, 22,05 КГц, 11,025 КГц. При частоте 8 кГц качество дискретизированного звукового сигнала соответствует качеству радиотрансляции, а при частоте 48 кГц — качеству: звучания аудио-CD.

Высокое качество звучания достигается при частоте дискретизации 44,1 кГц и глубины кодирования звука, равной 16 бит. Для мрачного, приглушенного звука характерны следующие параметры: частота дискретизации 11-кГц, глубина кодирования — 8 бит.

Размер цифрового моноаудиофайла (V) измеряется по формуле:

V =D*T*I, где D –частота дискретизации (Гц), T – время звучания или записи звука, I разрядность регистра (разрешение).

Размер цифрового стереоаудиофайла (V) измеряется по формуле:

V =2*D*T*I, сигнал записан для двух колонок, так как раздельно кодируются левый и правый каналы звучания. Задание 1.

Звук воспроизводится в течение 10 секунд при частоте дискретизации 22,05 кГц и глубине звука 8 бит. Определить его размер (в байтах).

Дано:

T=10 сек;

D=22,05 кГц;

I=8 bit;

Найти V-?

Решение:

D= 22,05·1000 = 220500 Гц.

I = 8/8=1 байт.

Т = 10 секунд.

V = 220500·10·I = 220500 байт.

Ответ: 220500 байт.

Задание 2.

Определить объем памяти для хранения цифрового аудиофайла, время звучания которого составляет две минуты при частоте дискретизации 44.1 кГц и расширении 16 бит.

Дано: Решение:

T=2 мин; 1. D =44,1· 1000=44100 Гц.

D=44,1 кГц ; 2. Т=2 мин=2·60=120 с.

I=16 bit; 3. V=D·Т·I=44100·120·16=84672000бит=

Найти V-? =10584000байт=10335,9375Кб=10,094Мб.

Ответ: 220500 байт.

Вопросы:

1. Что такое звук в природе?

2. Что такое частота звука?

3. Какой спектр частот мы можем слышать?

4. Какие параметры определяют качество звука?

5. Что такое временная дискретизация?

6. Что такое глубина кодирования?

Задания для самостоятельного выполнения:

3. Определить объем памяти для хранения моноаудифайла, время звучания которого составляет пять минут при частоте дискретизации 44 кГц и глубине кодирования 16 бит.

4. Какой должна быть частота дискретизации и глубина кодирования для записи звуковой информации длительностью 2 минуты, если в распоряжении пользователя имеется память объемом 5б1 МБайта.

5. Объем свободной памяти на диске -5,25 Мбайта, глубина кодирования -8. Звуковая информация записана с частотой дискретизации 44,1 КГц. Какова длительность звучания такой записи.

5. Одна минута записи звуковой информации занимает на диске 1,3 Мбайта, глубина кодирования равна 16. С какой частотой дискретизации записан звук.

6. Объем свободной памяти на диске — 0,01 Гб, разрядность звуковой платы — 16. Какова длительность звучания цифрового аудиофайла, записанного с частотой дискретизации 44100 Гц?

7. Какой объем памяти требуется для хранения цифрового аудиофайла с записью звука высокого качества при условии, что время звучания составляет 3 минуты.

Домашнее задание:

8. Рассчитайте время звучания моноаудиофайла, если при 16-битном кодировании и частоте дискретизации 32 кГц его объем равен:

a) 700 Кбайт; b) 6300 Кбайт

9. Вычислить, сколько байт информации занимает на компакт-диске одна секунда стереозаписи (частота 44032 Гц, 16 бит на значение). Сколько занимает одна минута? Какова максимальная емкость диска (считая максимальную длительность равной 80 минутам)?

10. Определите качество звука (качество радиотрансляции, среднее качество, качество аудио-CD) если известно, что объем моноаудиофайла длительностью звучания в 10 сек. равен:

a) 940 Кбайт; b) 157 Кбайт.

11. Определите длительность звукового файла, который уместится на гибкой дискете 3,5”. Учтите, что для хранения данных на такой дискете выделяется 2847 секторов объемом 512 байт.

a) при низком качестве звука: моно, 8 бит, 8 кГц;

b) при высоком качестве звука: стерео, 16 бит, 48 кГц.

Основы логики и логические основы компьютера

6.1. Основы логики

Первые учения о формах и способах рассуждений возникли в странах Древнего Востока (Китай, Индия), но в основе современной логики лежат учения, созданные в 4 веке до нашей эры древнегреческими мыслителями. Основы формальной логики заложил Аристотель, который впервые отделил логические формы речи от ее содержания. Он исследовал терминологию логики, подробно разобрал теорию умозаключений и доказательств, описал ряд логических операций, сформулировал основные законы мышления. Логика изучает внутреннюю структуру процесса мышления, который реализуется в таких естественно сложившихся формах как понятие, суждение, умозаключение и доказательство.

Понятие. Понятие — это форма мышления, отражающая наиболее существенные свойства предмета, отличающие его от других предметов. В структуре каждого понятия нужно различать две стороны: содержание и объем. Содержание понятия составляет совокупность существенных признаков предмета. Чтобы раскрыть содержание понятия, следует выделить признаки, необходимые и достаточные для выделения данного предмета по отношению к другим предметам.

Объем понятия определяется совокупностью предметов, на которую оно распространяется, и может быть представлено в форме множества объектов, состоящего из элементов множества.

Высказывание. Высказывание (суждение) — это форма мышления, выраженная с помощью понятий, посредством которой что-либо утверждают или отрицают о предметах, их свойствах и отношениях между ними.

О предметах можно судить верно или неверно, то есть высказывание может быть истинным или ложным. Истинным будет суждение, в котором связь понятий правильно отражает свойства и отношения реальных вещей.

Обоснование истинности или ложности простых высказываний решается вне алгебры логики. Например, истинность или ложность высказывания: «Сумма углов треугольника равна 180 градусов» устанавливается геометрией, причем — в геометрии Евклида это высказывание является истинным, а в геометрии Лобачевского — ложным.

В естественном языке высказывания выражаются повествовательными предложениями. Высказывание не может быть выражено повелительным или вопросительным предложением, оценка истинности или ложности которых невозможна. Высказывания могут выражаться с помощью математических, физических, химических и прочих знаков. Из двух числовых выражений можно составить высказывания, соединив их знаками равенства или неравенства.

Умозаключение. Умозаключение — это форма мышления, посредством которой из одного или нескольких суждений, называемых посылками, по определенным правилам логического вывода получается новое знание о предметах реального мира (вывод).

Доказательство. Доказательство есть мыслительный процесс, направленный на подтверждение или опровержение какого-либо положения посредством других несомненных, ранее обоснованных доводов. Доказательство по своей логической форме не отличается от умозаключения. Однако, если в умозаключении заранее исходят из истинности посылок и следят только за правильностью логического вывода, в доказательстве подвергается логической проверке истинность самих посылок.

6.2. Алгебра высказываний

Алгебра в широком смысле этого слова — наука об общих операциях, аналогичных сложению и умножению, которые могут выполняться над различными математическими объектами (алгебра переменных и функций, алгебра векторов, алгебра множеств и так далее). Объектами алгебры логики являются высказывания.

Виды высказываний (суждений):

= общее – начинается со слов: все, всякий, каждый, ни один;

= частное – начинается со слов: некоторые, большинство и т. п.; = единичное - во всех других случаях.

Алгебра логики отвлекается от смысловой содержательности высказываний. Ее интересует только один факт — истинно или ложно данное высказывание, что дает возможность определять истинность или ложность составных высказываний алгебраическими методами.

Простые высказывания в алгебре логики обозначаются заглавными латинскими буквами:

А = {Аристотель — основоположник логики}; В = {На яблонях растут бананы}.

Истинному высказыванию ставится в соответствие 1, ложному — 0. Таким образом,

А = 1, В = 0.

Составные высказывания на естественном языке образуются с помощью союзов, которые в алгебре высказываний заменяются на логические операции. Логические операции задаются таблицами истинности и могут быть графически проиллюстрированы с помощью диаграмм Эйлера-Венна.

Логическая операция КОНЪЮНКЦИЯ (логическое умножение):

= в естественном языке соответствует союзу и;

= в алгебре высказываний обозначение &;

= в языках программирования обозначение And.

A	B	A&B
0	0	0
0	1	0
1	0	0
1	1	1

Конъюнкция — это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания истинны.

В алгебре множеств конъюнкции соответствует операция пересечения множеств, то есть множеству, получившемуся в результате умножения множестве и В, соответствует множество, состоящее из элементов, принадлежащих одновременно двум множествам.

Логическая операция ДИЗЪЮНКЦИЯ (логическое сложение):

= в естественном языке соответствует союзу или;

= обозначение  ;

= в языках программирования обозначение Or.

A	B	A B
0	0	0
0	1	1
1	0	1
1	1	1

Дизъюнкция — это логическая операция, которая каждым двум простым высказываниям ставит в соответствие составное высказывание, являющееся ложным тогда и только тогда, когда оба исходных высказывания ложны и истинным, когда хотя бы одно из двух образующих его высказываний истинно.

В алгебре множеств дизъюнкции соответствует операция объединения множеств, то есть множеству, получившемуся в результате сложения множеств А и В, соответствует множество, состоящее из элементов, принадлежащих либо множеству А, либо множеству В.

Логическая операция ИНВЕРСИЯ (отрицание):

= в естественном языке соответствует словам неверно, что... и частице не;

= обозначение A ,¬A;

= в языках программирования обозначение Not.

A	A
0	1
1	0

Отрицание — это логическая операция, которая каждому простому высказыванию ставит в соответствие составное высказывание, заключающееся в том, что исходное высказывание отрицается.

В алгебре множеств логическому отрицанию соответствует операция дополнения до универсального множества, то есть множеству, получившемуся в результате отрицания

множества А, соответствует множество A , дополняющее его до универсального множества.

Логическая операция ИМПЛИКАЦИЯ (логическое следование): = в естественном языке соответствует обороту если ..., то ...; = обозначение ,→.

A	B	AB
0	0	1
0	1	0
1	0	1
1	1	1

Импликация — это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся ложным тогда и только тогда, когда условие (первое высказывание) истинно, а следствие (второе высказывание) ложно.

Логическая операция ЭКВИВАЛЕНЦИЯ (равнозначность):

= в естественном языке соответствует оборотам речи тогда и только тогда; в том и только в том случае;

= обозначения , ,~.

A	B	A B
0	0	0
0	1	0
1	0	0
1	1	1

Эквиваленция — это логическая операция, ставящая в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны.

A	B	A B
0	0	0
0	1	1
1	0	1

Логическая операция Исключающее ИЛИ (строгая дизъюнкция): = в естественном языке соответствует оборотам речи либо… либо случае;

= обозначение _.

Исключающее ИЛИ – это логическая операция, значение которой истинно тогда, когда истинно либо одно из простых высказываний, либо другое, но не оба сразу.

Логические операции имеют следующий приоритет: действия в скобках, инверсия, &,  , ,.

Пример 1. Определите истинность составного высказывания:

( A & B )&(C D), состоящего из простых высказываний:

А = {Принтер — устройство вывода информации}, В = {Процессор — устройство хранения информации},

С = {Монитор — устройство вывода информации},

D = {Клавиатура — устройство обработки информации}.

Сначала на основании знания устройства компьютера устанавливаем истинность простых высказываний: А = 1, В = 0, С= 1, В = 0.

Определим теперь истинность составного высказывания, используя таблицы истинности

логических операций: (1&0 )&(1 0) = (0&l)&(l 0) = 0. Составное высказывание ложно.

Вопросы:

1. Что такое логика?

2. Кто является основоположником логики, как науки?

3. В чем состоит отличие формальной логики от математической логики?

4. Что такое суждение?

5. Приведите пример истинного суждения.

6. Приведите пример ложного суждения.

7. Приведите пример высказывания, не являющегося суждением.

8. На какие типы можно разделить высказывания?

9. Что такое логические константы?

10. Что такое логические выражения?

Задания для самостоятельного выполнения:

Задание 1.

Найдите значения логических выражений:

a) (1 1) (l 0); b) (0&1)&1; c) 1&(1 1)&1;

d) ((l 0) l) 1; e) ((l l) 0)&(0 0); f) ((l 0)&(0 l);

g) ((l&l) 0)&(0 l); h) ((0 0) 0)&(0&l); i) (1&0)  1;

j) ((l&0) 1)&(1 l); k) ((0&l)&0) (0 0); l) ((0&0)  0)&(l l).

Задание 2.

Даны два простых высказывания: А = {2∙ 2 = 4}, В = {2 ∙ 2 = 5}.

Какие из составных высказываний истинны:

a) A ;

Задание 3.

B ;

c) А&В;

d) A B;

e) А→В

f) А B?

Даны высказывания: А={3∙3=9}, В={3∙3=10}. Определите истинность высказываний:

a) А; b) B ;

Задание 4.

Даны высказывания: высказываний:

a) А; b) B ;

Задание 5.

c) А&В;

А={5+7=13},

c) А&В;

d) A B;

В={5+7=12}.

d) A B;

e) A

Определите

e) A

f) B?

истинность

f) B?

Для какого имени истинно высказывание:

¬ (Первая буква имени гласная → Четвертая буква имени согласная)?

a) ЕЛЕНА b) ВАДИМ c) АНТОН d) ФЕДОР

Задание 6.

Для какого символьного выражения неверно высказывание:

Первая буква гласная → ¬ (Третья буква согласная)?

a) abedc b) becde c) babas d) abcab

Домашнее задание:

Задание 5.

Даны простые высказывания: А = {5>3}, В = {2=3} и С = {4<2}.

Определите истинность составных высказываний:

c) (A B)&C→ (A&C) (B&C); d) (A&B) C (A C)&(A&B)).

Задание 6.

Даны простые высказывания:

А = {Принтер — устройство ввода информации},

В = {Процессор — устройство обработки информации},

С = {Монитор — устройство хранения информации}, D = {Клавиатура — устройство ввода информации}.

Определите истинность составных высказываний:

a) (A&B)&(C D); c) (А&В) → (В&С);

b) (A B)  (C&D); d) А В.

Задание 7.

Дано составное высказывание не (не А и В), где А и В — простые высказывания.

В каком случае данное высказывание будет ложным?

Задание 8.

Выполните поразрядное логическое сложение двоичных чисел:

a) 100 и 110; b) 1010 и 1000; c) 101010 и 111111.

Задание 9.

Для какого числа X истинно высказывание (X > 2)(X > 5)→(X < 3)

a) 5 b) 2 c) 3 d) 4

Задание 10.

Для какого из значений числа Z высказывание ((Z > 2)(Z > 4)) →(Z > 3) будет ложным?

a) 1 b) 2 c) 3 d) 4

Задание 11.

Для какого имени истинно высказывание:

¬ (Первая буква имени согласная → Третья буква имени гласная)?

a) ЮЛИЯ b) ПЕТР c) АЛЕКСЕЙ d) КСЕНИЯ

6.3. Логические выражения и таблицы истинности

Таблицу, показывающую, какие значения принимает составное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний, называют таблицей истинности составного высказывания.

Составные высказывания в алгебре логики записываются с помощью логических выражений. Для любого логического выражения достаточно просто построить таблицу истинности.

Алгоритм построения таблицы истинности:

1. подсчитать количество переменных п в логическом выражении;

2. определить число строк в таблице, которое равно т = 2ⁿ;

3. подсчитать количество логических операций в логическом выражении и определить количество столбцов в таблице, которое равно количеству переменных плюс количество операций;

4. ввести названия столбцов таблицы в соответствии с последовательностью выполнения логических операций с учетом скобок и приоритетов;

5. заполнить столбцы входных переменных наборами значений;

6. провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной в п.4 последовательностью.

Задание 1.

Для формулы A&(BB &C ) построить таблицу истинности алгебраически и с использованием электронных таблиц.

1) Количество логических переменных 3, следовательно, количество строк в таблице истинности должно быть 2³ = 8.

2) Количество логических операций в формуле 5, следовательно количество столбцов в таблице истинности должно быть 3 + 5 = 8.

A	B	C	B	C	B &C	B ( B &C )	A&( BB &C )
0	0	0	1	1	1	1	0
0	0	1	1	0	0	0	0
0	1	0	0	1	0	1	0
0	1	1	0	0	0	1	0
1	0	0	1	1	1	1	1
1	0	1	1	0	0	0	0
1	1	0	0	1	0	1	1
1	1	1	0	0	0	1	1

Задание 2.

Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z.

Дан фрагмент таблицы истинности выражения F:Какое выражение соответствует F?

1) ¬X  ¬Y  ¬Z 2) X  Y  Z 3) X  Y  Z 4) ¬X  ¬Y  ¬Z

Решение:

1) нужно для каждой строчки подставить заданные значения X, Y и Z во все функции, заданные в ответах, и сравнить результаты с соответствующими значениями F для этих данных

2) если для какой-нибудь комбинации X, Y и Z результат не совпадает с соответствующим значением F, оставшиеся строчки можно не рассматривать, поскольку для правильного ответа все три результата должны совпасть со значениями функции F

3) перепишем ответы в других обозначениях:

1) X Y Z 2) X YZ 3) X Y Z 4) X Y Z

4) первое выражение, X Y Z , равно 1 только при X Y  Z  0

5) второе выражение, X YZ , равно 1 только при X Y  Z 1

6) третье выражение, X Y Z , равно нулю только при X Y  Z  0

7) наконец, четвертое выражение, X Y Z равно нулю только тогда, когда X Y  Z 1, а в остальных случаях равно 1, что совпадает с приведенной частью таблицы истинности

X	Y	Z	F	X Y Z	X YZ	X Y Z	X Y Z
1	0	0	1	0 ×	0 ×	1	1
0	0	0	1	–	–	0 ×	1
1	1	1	0	–	–	–	0

Задания для самостоятельного выполнения:

Задание 1.

Составьте таблицы истинности для следующих логических выражений:

a) F=(X&Y)  Z.

b) F=X&Y Z.

c) F= X v Y& ¬ Z

c) F= ¬ (X Y) & (Y X).

d) F= ¬ ((X Y) & (Z X)) & (Z Y).

e) F= A&B&C&D.

f) F= (A B) & (B A B).

g) F= A  B &D.

Задание

X	Y	Z	F
0	1	0	0
1	1	0	1
1	0	1	0

Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F?

a) X  ¬Y  Z b) X  Y  Z c) X  Y  ¬Z d) ¬X  Y  ¬Z

Задание 3.

X	Y	Z	F
0	1	0	0
1	1	0	1
1	0	1	0

a) ¬X  Y  ¬Z b) X  Y  ¬Z c) ¬X  ¬Y  Z d) X  ¬Y  Z

Домашнее задание:

Задание 4.

Построить таблицы истинности для следующих формул:

a) A (BB →C ); c) (A B)&( A B )

b) А&(В&B →C ); d) A (BB )&A (B→С)

Задание 5.

X	Y	Z	F
0	0	0	1
0	0	1	0
0	1	0	0

Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F

(см. таблицу справа). Какое выражение соответствует F?

a) X  Y  Z b) ¬X  ¬Y  Z c) X  Y  ¬Z d) ¬X  ¬Y  ¬Z

Задание 6.

X	Y	Z	F
0	0	0	1
0	0	1	0
0	1	0	1

a) ¬X  ¬Y  Z b) ¬X  ¬Y  Z c) X  Y  ¬Z d) X  Y  Z

6.4. Законы алгебры логики

Логические законы и правила преобразования логических выражений.

Законы логики отражают наиболее важные закономерности логического мышления. В алгебре высказываний законы логики записываются в виде формул, которые позволяют проводить эквивалентные преобразования логических выражений в соответствии с законами логики.

Закон тождества. Всякое высказывание тождественно самому себе: А=А

Закон непротиворечия. Высказывание не может быть одновременно истинным и ложным. Если высказывание А- истинно, то его отрицание не А должно быть ложным. Следовательно, логическое произведение высказывания и его отрицания должно быть

ложно: A&A  0 ( A A  0 ₎

Закон исключенного третьего. Высказывание может быть либо истинным, либо ложным, третьего не дано. Это означает, что результат логического сложения

высказывания и его отрицания всегда принимает значение истина: A A 1 ( A A 1)

Закон двойного отрицания. Если дважды отрицать некоторое высказывание, то в

результате мы получим исходное высказывание:AA

Кроме логических законов, важное значение для выполнения преобразований логических выражений имеют правила алгебраических преобразований. Многие из них имеют аналоги в обычной алгебре.

Законы Моргана

Логическое умножение Логическое сложение

A&B  A BA B  A&B

A B  A BA B  A B

Правило коммутативности. В обычной алгебре слагаемые и множители можно менять местами. В алгебре высказываний можно менять местами логические переменные при операциях логического умножения и логического сложения:

Логическое умножение Логическое сложение

A&B  B&AAB  B A

AB  B A AB  B A

Правило ассоциативности. Если в логическом выражении используются только операция логического умножения или только логического сложения, то можно пренебрегать скобками или произвольно их расставлять:

Логическое умножение Логическое сложение

(A&B)&C  A&(B&C) (A B) C  A(B C)

(A B)C  A(BC)(A B) C  A(B C)

Правило дистрибутивности. В отличии от обычной алгебры, где за скобки можно выносить только общие множители, в алгебре высказываний можно выносить за скобки как общие множители, так и общие слагаемые:

Дистрибутивность умножения Дистрибутивность сложения относительно сложения относительно умножения

(A&B) (A&C)  A&(B C)(A B)&(AC)  A(B&C)

(A B)  (AC)  A(B C) (A B)(AC)  A (BC)

Операция с константами

A0  A _,A11A&0  0 _,A&1 A

A0  A_,A11A0  0 _,A1 A

A A A

A A A

A&A A

A A A

Идемпотенция Поглощение

A (A&B)  AA&(A B)  A

A (A B)  AA(A B)  A

Склеивание

(A& B)  (A& B)  B(A B)&(A B)  B

(A B)  (A B)  B(A B)(A B)  B

Правила Блейка-Порецкого

A (A&B)  A B A&(A B)  A&B

A (A B)  A BA(A B)  AB

Упрощение логических выражений:

Можно заменить операции  ,  , _ на их выражения через И, ИЛИ и НЕ:

А В  АВ  АВ ; А В  А В = AB

А  В ( А В)(B  A) = ( A B)( A B) = = АВ АВ = AB  AB

Пример 1.

Рассмотрим в качестве примера применения законов логики и правил алгебры логики преобразование логического выражения.

_{Пусть нам необходимо
упростить логическое выражение:}(A&B)  (A&B)

Решение:

Воспользуемся правилом дистрибутивности и вынесем за скобки А:

(A&B) (A&B)  A&(B  B) ( (AB)  (AB)  A(B  B))

По закону исключенного третьего : B  B 1 ( B  B 1),

следовательно: A&(B  B)  A&1 A .

Законы и правила преобразования логических выражений позволяют упростить сложное выражение и, не применяя таблиц истинности, найти ответ при решении задач.

Задание 1.

Укажите, какое логическое выражение равносильно выражению A  ¬(¬B  C). 1) ¬A  ¬B  ¬C 2) A  ¬B  ¬C 3) A  B  ¬C 4) A  ¬B  C

Решение:

1) перепишем заданное выражение и ответы в других обозначениях: A(B C)

ответы: 1) A  B C 2) A B C 3) ABC 4) AB C

2) посмотрев на заданное выражение, видим инверсию (операцию «НЕ») для сложного выражения в скобках, которую раскрываем по формуле де Моргана,

A(B C)  AB C

а затем используем закон двойного отрицания по которому B  B : A B C  A BC 3) таким образом, правильный ответ – 3 .

Задание 2.

Укажите, какое логическое выражение равносильно выражению ¬(A  ¬B) ¬(A  B) A  B 1) ¬B  A 2) A  B  ¬B 3) A  B  ¬A 4) ¬A

Решение:

1) перепишем заданное выражение в других обозначениях:(AB)(AB) AB

ответы: 1) B  A 2) AB B 3) AB A 4) A

2) проще всего упростить заданное выражение; сначала раскрываем инверсию сложных выражений, используя законы де Моргана:

(A B)(A B) AB  AB AB  AB

3) выносим за скобки A в первых двух слагаемых и используем закон исключения

третьего B B 1: AB  AB  AB  A(B  B) AB  A  AB

4) наконец, применяем распределительный закон для операции «И» и еще раз закон

исключения третьего A  A 1: A  A B  (A  A)(A  B)  A  B

5) дальше не упрощается

6) теперь замечаем, что такого ответа нет среди предложенных вариантов!

7) это означает, что ответы тоже можно упростить; упрощаем ответы 2 и 3, применяя распределительный закон и закон исключения третьего

ответы: 2) AB  B  (A B)(B  B)  A B

3) AB  A  (A A)(B  A)  B  A  A  B видим, что упрощенное выражение для ответа 3 совпало с упрощенным исходным выражением таким образом, правильный ответ – 3.

Задание 3.

Упростите логические выражения.

a) A (A& B) ; b) A&(A B) ; c) (A B)&(B  A)&(C  B)

Решение:

a) A (A& B) =(A A) &(A B) 1&(A B)  A B ;

b) A&(A B)  (A& A)  (A& B)  0  (A& B)  A& B ;

Задания для самостоятельного выполнения:

1) Укажите, какое логическое выражение равносильно выражению ¬(A  ¬B  C) ?

a) ¬A  B  ¬C b) A  ¬B  C c) ¬A  ¬B  ¬C d) ¬A  B  ¬C

2) Какое логическое выражение равносильно выражению ¬ (A  B)  ¬C ?

a) ¬A  B  ¬C b) (¬A  ¬B)  ¬C c) (¬A  ¬B)  C d) ¬A  ¬B  ¬C

3) Укажите, какое логическое выражение равносильно выражению ¬ (¬А  B)?

a) A  ¬B b) ¬A  B c) B  ¬A d) A  ¬B

4) Какое логическое выражение равносильно выражению ¬(А  ¬B) ?

a) A  B b) A  B c) ¬A  ¬B d) ¬A  B

5) Какое логическое выражение эквивалентно выражению ¬(¬A  ¬B)  C ?

a) (A  ¬B)  C b) A  B  C c) (A → ¬B) C d) ¬(A  ¬B) C

6) Какое логическое выражение эквивалентно выражению A  ¬(¬B  ¬C)?

a) A  B  C b) A  B  ¬C c) A  (B  C) d) (A  ¬B)  ¬C

7) Какое логическое выражение эквивалентно выражению ¬(A  B)  ¬C?

a) (A  B)  ¬C b) (A  B)  C c) (¬A  ¬B)  ¬C d) (A  B)  C

8) Какое логическое выражение эквивалентно выражению ¬(A  ¬B)  ¬C?

a) A  B  C b) ¬(A  B)  C c) ¬(A  C)  B d) ¬(A  C)  B

9) Какое логическое выражение эквивалентно выражению ¬(¬A  B)  ¬C?

a) (A  B)  ¬C b) (A  B)  C c) (A  ¬B)  ¬C d) (A  ¬B)  ¬C 10) Какое логическое выражение эквивалентно выражению ¬(A  B) → C?

a) ¬A  B  C b) A  B  C

11) Упростите логические выражения:

c) ¬(A  B)  C d) ¬A  ¬B  ¬C

g) (X &Y Y &Z  Z & X

h) A&B  (B&C)

A&B  D  A BX Y  X &Y

f) (X  Z)&(X  Z)&(Y  Z) l) (A B) (B  A)

12) Какая из формул является тождественно истинной, а какая тождественно ложной?

a) А(АВ)(АВ) b) X(XY)

13) Какие два из четырѐх высказываний эквивалентны?

a)A B  C; b)(A B)  C; c)(AB)C; d)ABC;

Домашнее задание:

14) Какое логическое выражение эквивалентно выражению ¬(¬ A  ¬ B) C?

a) ¬ A  B  ¬ C; b) (¬ A  ¬ B) ¬C; c) (A  B) C d) A  B  C

15) Какое логическое выражение эквивалентно выражению A  ¬(B  ¬ C)?

a) A  ¬B  C; b) A  ¬B  ¬C; c) A  ¬B  ¬C d) A  ¬B  C

16) Какое логическое выражение эквивалентно выражению ¬(A  ¬B  ¬C)?

a) ¬A  B  C ; b) ¬A  B  ¬C ; c) ¬A  B  C d) A  B  ¬C

17) Какое логическое выражение эквивалентно выражению ¬(¬A  (¬B  C))?

a) ¬A  ¬B  C; b) A  ¬B  ¬C; c) A  B  ¬C d) A  ¬B  C

18) Упростите логические выражения:

a) A&Y  X &Y

b) (X  Z)&(X  Z)&Y

d) (X &(YY)& X)

e) A B & B  Cl) XXYY & X &Y

f) AAm) (A  A)  A

Задачи:

1. Как представлено число 83₁₀ в двоичной системе счисления?

a) 1001011₂ b) 1100101₂ c) 1010011₂ d) 101001₂

2. Сколько единиц в двоичной записи числа 195?

a) 5 b) 2 c) 3 d) 4

3. Сколько единиц в двоичной записи числа 173?

a) 7 b) 5 c) 6 d) 4

4. Как представлено число 25 в двоичной системе счисления?

a) 1001₂ b) 11001₂ c) 10011₂ d) 11010₂

5. Как представлено число 82 в двоичной системе счисления?

a) 1010010₂ b) 1010011₂ c) 100101₂ d) 1000100₂

6. Как записывается число A87₁₆ в восьмеричной системе счисления?

a) 435₈ b) 1577₈ c) 5207₈ d) 6400₈

7. Как записывается число 754₈ в шестнадцатеричной системе счисления?

a) 738₁₆ b) 1A4₁₆ c) 1EC₁₆ d) A56₁₆

8. Для хранения целого числа со знаком используется один байт.

Сколько единиц содержит внутреннее представление числа (-128)?

a) 1 b) 2 c) 3 d) 4

9. Дано: a  9D₁₆, b  237₈. Какое из чисел С, записанных в двоичной системе счисления, удовлетворяет неравенству a  C  b?

a) 10011010 b) 10011110 c) 10011111 d) 11011110

10. Объем сообщения – 7,5 Кбайт. Известно, что данное сообщение содержит 7680 символов. Какова мощность алфавита?

a) 77 b) 256 c) 156 d) 512

11. Дан текст из 600 символов. Известно, что символы берутся из таблицы размером 16 на 32. Определите информационный объем текста в битах.

a) 1000 b) 2400 c) 3600 d) 5400

12. Мощность алфавита равна 256. Сколько Кбайт памяти потребуется для сохранения

160 страниц текста, содержащего в среднем 192 символа на каждой странице?

a) 10 b) 20 c) 30 d) 40

13. Объем сообщения равен 11 Кбайт. Сообщение содержит 11264 символа. Какова мощность алфавита?

a) 64 b) 128 c) 256 d) 512

14. Для кодирования секретного сообщения используются 12 специальных значковсимволов. При этом символы кодируются одним и тем же минимально возможным количеством бит. Чему равен информационный объем сообщения длиной в 256 символов?

a) 256 бит b) 400 бит c) 56 байт d) 128 байт

15. Мощность алфавита равна 64. Сколько Кбайт памяти потребуется, чтобы сохранить

128 страниц текста, содержащего в среднем 256 символов на каждой странице?

a) 8 b) 12 c) 24 d) 36

16. Для кодирования нотной записи используется 7 значков-нот. Каждая нота кодируется одним и тем же минимально возможным количеством бит. Чему равен информационный объем сообщения, состоящего из 180 нот?

a) 180 бит b) 540 бит c) 100 байт d) 1 Кбайт

17. В корзине лежат 8 черных шаров и 24 белых. Сколько бит информации несет сообщение о том, что достали черный шар?

a) 2 бита b) 4 бита c) 8 бит d) 24 бита

18. В коробке лежат 64 цветных карандаша. Сообщение о том, что достали белый карандаш, несет 4 бита информации. Сколько белых карандашей было в коробке?

a) 4 b) 8 c) 16 d) 32

19. За четверть Василий Пупкин получил 20 оценок. Сообщение о том, что он вчера получил четверку, несет 2 бита информации. Сколько четверок получил Василий за четверть?

a) 2 b) 4 c) 5 d) 10

20. В некоторой стране автомобильный номер длиной 6 символов составляется из заглавных букв (всего используется 12 букв) и десятичных цифр в любом порядке. Каждый символ кодируется одинаковым и минимально возможным количеством

бит, а каждый номер – одинаковым и минимально возможным количеством байт.

Определите объем памяти, необходимый для хранения 32 автомобильных номеров.

a) 192 байта b) 120 байт c) 32 байта d) 128 байт

21. В некоторой стране автомобильный номер длиной 5 символов составляется из заглавных букв (всего используется 30 букв) и десятичных цифр в любом порядке. Каждый символ кодируется одинаковым и минимально возможным количеством бит, а каждый номер – одинаковым и минимально возможным количеством байт.

Определите объем памяти, необходимый для хранения 50 автомобильных номеров.

a) 100 байт b) 150 байт c) 200 байт d) 250 байт

22. Световое табло состоит из светящихся элементов, каждый из которых может гореть одним из трех различных цветов. Сколько различных сигналов можно передать с помощью табло, состоящего из четырех таких элементов (при условии, что все элементы должны гореть)?

a) 4 b) 16 c) 64 d) 81

23. Автоматическое устройство осуществило перекодировку информационного сообщения на русском языке, первоначально записанного в 8-битном коде, в 16битную кодировку Unicode. При этом информационное сообщение увеличилось на 2048 байт. Каков был информационный объем сообщения до перекодировки?

a) 1024 байт b) 2048 бит c) 2 Кбайта d) 2 Мбайта

24. Считая, что каждый символ кодируется 16-ю битами, оцените информационный объем следующей фразы в кодировке Unicode: В шести литрах 6000 миллилитров.

a) 1024 байта b) 1024 бита c) 512 байт d) 512 бит

25. Автоматическое устройство осуществило перекодировку информационного сообщения на русском языке, первоначально записанного в 16-битном коде Unicode,

в 8-битную кодировку

КОИ-8. При этом информационное сообщение уменьшилось на 800 бит. Какова длина сообщения в символах?

a) 50 b) 100 c) 200 d) 800

26. В таблице ниже представлена часть кодовой таблицы ASCII:

Символ	1	5	J	K	P	j	k
Десятичный код	49	53	74	75	80	106	107
Шестнадцатеричный код	31	35	4A	4B	50	6A	6B

Каков шестнадцатеричный код символа «p» ?

a) 70₁₆ b) 85₁₆ c) 6F₁₆ d) СЕ₁₆

27. В таблице ниже представлена часть кодовой таблицы:

Символ	С	Т	У	Я	с	т	у
Десятичный код	145	146	147	159	225	226	227
Шестнадцатеричный код	91	92	93	9А	E1	E2	E3

Каков шестнадцатеричный код символа «я» ?

a) 2A1₁₆ b) DF₁₆ c) EF₁₆ d) 180₁₆

28. Вычислите сумму чисел x и y, при x = 56₈, y = 1101001₂. Результат представьте в двоичной системе счисления.

a) 11110111₂ b) 1000111₂ c) 11001100₂ d) 10010111₂

29. Вычислите сумму чисел x и y, при x = 5A₁₆, y = 1010111₂. Результат представьте в восьмеричной системе счисления.

a) 151₈ b) 261₈ c) 433₈ d) 702₈

30. Вычислите сумму чисел x и y, при x = 127₈, y = 10010111₂. Результат представьте в десятичной системе счисления.

a) 214 b) 238 c) 183 d) 313

31. Вычислите A81₁₆ + 377₁₆. Результат представьте в той же системе счисления.

a) 21B₁₆ b) DF8₁₆ c) C92₁₆ d) F46₁₆

32. Чему равна разность чисел 101₁₆ и 110111₂?

a) 312₈ b) 12₈ c) 32₁₆ d) 64₁₆

33. Какое логическое выражение эквивалентно выражению ¬(A  ¬B  C)?

a) ¬A  B  ¬C; b) ¬A  B  ¬C; c) ¬A  (B  C) d) ¬A  B  ¬A  ¬C

34. Какое логическое выражение эквивалентно выражению ¬(A  ¬B) ¬C  D?

a) A  ¬B  C  ¬D; b) A  ¬B  C  D; c) ¬A  B  ¬C  D d) ¬A  B  ¬C  D

X	Y	Z	F
1	1	1	1
1	1	0	1
1	0	1	1

35. Дан фрагмент таблицы истинности выражения F

(см. таблицу справа). Какое выражение соответствует F?

a) X  Y  Z b) ¬X  ¬Y  Z c) X  Y  Z d) X  Y  ¬Z

X	Y	Z	F
0	0	0	0
0	1	1	1
1	0	0	1

36. Дан фрагмент таблицы истинности выражения F (см. таблицу справа). Какое выражение соответствует F?

a) (X  ¬Y)→ Z b) (X  Y)→ ¬Z c) X  (¬Y → Z) d) X  Y  ¬Z

37. В таблице приведена стоимость перевозки пассажиров между соседними населенными пунктами. Укажите схему, соответствующую.

	A	B	C	D	E
A		1	4		1
B	1		2
C	4	2		3
D			3
E	1

D B A C B

2 1 1 A

^A¹^СD 1 B 2 С A 5 D 3 B D

38. Между четырьмя местными аэропортами: ОКТЯБРЬ, БЕРЕГ, КРАСНЫЙ и СОСНОВО, ежедневно выполняются авиарейсы. Приведѐн фрагмент расписания перелѐтов между ними:

Аэропорт вылета Аэропорт прилета Время вылета Время прилета

СОСНОВО	КРАСНЫЙ	06:20	08:35
КРАСНЫЙ	ОКТЯБРЬ	10:25	12:35
ОКТЯБРЬ	КРАСНЫЙ	11:45	13:30
БЕРЕГ	СОСНОВО	12:15	14:25
СОСНОВО	ОКТЯБРЬ	12:45	16:35
КРАСНЫЙ	СОСНОВО	13:15	15:40
ОКТЯБРЬ	СОСНОВО	13:40	17:25
ОКТЯБРЬ	БЕРЕГ	15:30	17:15
СОСНОВО	БЕРЕГ	17:35	19:30
БЕРЕГ	ОКТЯБРЬ	19:40	21:55

Путешественник оказался в аэропорту ОКТЯБРЬ в полночь (0:00). Определите самое раннее время, когда он может попасть в аэропорт СОСНОВО.

a) 15:40 b) 16:35 c) 17:15 d) 17:25

39. Для кодирования букв А, Б, В, Г решили использовать двухразрядные последовательные двоичные числа (от 00 до 11 соответственно). Если таким способом закодировать последовательность символов ГБАВ и записать результат в шестнадцатеричной системе счисления, то получится:

a) 132₁₆ b) D2₁₆ c) 3102₁₆ d) 2D₁₆

40. Для кодирования букв А, Б, В, Г решили использовать двухразрядные последовательные двоичные числа (от 00 до 11 соответственно). Если таким способом закодировать последовательность символов ГБВА и записать результат шестнадцатеричным кодом, то получится:

a) 138₁₆ b) DBCA₁₆ c) D8₁₆ d) 3120₁₆

41. Для 5 букв латинского алфавита заданы их двоичные коды (для некоторых букв - из двух бит, для некоторых - из трех). Эти коды представлены в таблице:

a b c d e

000 110 01 001 10

Определите, какой набор букв закодирован двоичной строкой 1100000100110

a) baade b) badde c) bacde d) bacdb

42. Цепочка из трех бусин формируется по следующему правилу: На первом месте в цепочке стоит одна из бусин А, Б, В. На втором – одна из бусин Б, В, Г. На третьем месте – одна из бусин А, В, Г, не стоящая в цепочке на первом или втором месте.

Какая из следующих цепочек создана по этому правилу:

a) АГБ b) ВАГ c) БГГ d) ББГ

43. Для составления 4-значных чисел используются цифры 1, 2, 3, 4, 5, при этом соблюдаются следующие правила:

i. На первом месте стоит одна из цифр 1, 2 или 3.

ii. После каждой четной цифры идет нечетная, а после каждой нечетной - четная

iii. Третьей цифрой не может быть цифра 5.

Какое из перечисленных чисел получено по этим правилам?

a) 4325 b) 1432 c) 1241 d) 3452

Какая из перечисленных цепочек создана по этим правилам?

44. Сколько существует четырехзначных чисел, в которых есть ровно две восьмерки, не стоящие рядом?

a) 216 b) 234 c) 224 d) 243

45. Сколько существует четырехзначных чисел, составленных из разных четных цифр?

a) 96 b) 120 c) 500 d) 625

46. Сколько существует четырехзначных чисел, которые делятся на 5?

a) 900 b) 1000 c) 1800 d) 2000

47. Сколько существует четырехзначных чисел, не превышающих 3000, в которых ровно две цифры «3»?

a) 36 b) 54 c) 81 d) 162

48. В чемпионате по шахматам участвовало 40 спортсменов. Каждый с каждым сыграл по одной партии. Сколько всего партий было сыграно?

a) 780 b) 800 c) 1560 d) 1600

49. В вазе лежат яблоко, груша, персик и абрикос. Кате разрешили выбрать два каких-то фрукта. Сколько у Кати вариантов выбора?

a) 6 b) 12 c) 16 d) 24

50. У Паши есть 6 воздушных шариков разного цвета. Три из них он хочет подарить

Маше. Сколькими способами он может это сделать?

a) 6 b) 12 c) 20 d) 60

51. Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 26, запись которых в троичной системе счисления оканчивается на

22?

52. Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 30, запись которых в четверичной системе счисления оканчивается на 31?

53. Укажите через запятую в порядке возрастания все десятичные натуральные числа, не превосходящие 17, запись которых в троичной системе счисления оканчивается на две одинаковые цифры?

54. Укажите, сколько всего раз встречается цифра 3 в записи чисел 19, 20, 21, …, 33 в системе счисления с основанием 6.

55. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 31 оканчивается на 4.

56. В системе счисления с некоторым основанием десятичное число 83 записывается в виде 123. Укажите это основание. В системе счисления с некоторым основанием десятичное число 144 записывается в виде 264. Укажите это основание.

57. Каково наибольшее целое положительное число X, при котором истинно высказывание: ((X - 1) < X) → (40 > X·X)

58. Укажите значения переменных K, L, M, N, при которых логическое выражение (¬(M  L)  K) → ((¬K  ¬M)  N) ложно. Ответ запишите в виде строки из четырех символов: значений переменных K, L, M и N (в указанном порядке). Так, например, строка 1101 соответствует тому, что K=1, L=1, M=0, N=1.

59. Каково наименьшее натуральное число X, при котором высказывание ¬(X·X < 9) → (X >(X + 2)) будет ложным?

60. Исполнитель КАЛЬКУЛЯТОР имеет только две команды, которым присвоены номера:

1. умножь на 3

2. вычти 2

Выполняя команду номер 1, КАЛЬКУЛЯТОР умножает число на экране на 3, а выполняя

команду номер 2, вычитает из числа на экране 2. Напишите программу, содержащую не более 5 команд, которая из числа 1 получает число 23. Укажите лишь номера команд. Например, программа 11221 – это программа:

i. умножь на 3 ii. умножь на 3

iii. вычти 2 iv. вычти 2

v. умножь на 3,

которая преобразует число 1 в число 15.

61. Три ученика из разных школ на вопрос, в какой школе учатся, ответили:

Артем: я учусь в школе №534, а Кирилл – в школе №76. Кирилл: я учусь в школе №534, а Артем – в школе №105.

Максим: я учусь в школе №534, а Артем – в школе №76.

Каждый из них один раз сказал правду и один раз солгал. В каких школах учатся Артем, Кирилл и Максим? В ответе перечислите подряд без пробелов числа, соответствующие номерам школ в указанном порядке имен, например 53410576.

62. На перекрестке произошло дорожно-транспортное происшествие, в котором участвовали автобус (А), грузовик (Г), легковой автомобиль (Л) и маршрутное такси (М). Свидетели происшествия дали показания инспектору ГИБДД. Первый свидетель считал, что первым на перекресток выехал автобус, а маршрутное такси было вторым. Другой свидетель полагал, что последним на перекресток выехал легковой автомобиль, а вторым был грузовик. Третий свидетель уверял, что автобус выехал на перекресток вторым, а следом за ним – легковой автомобиль. В результате оказалось, что каждый из свидетелей был прав только в одном из своих утверждений. В каком порядке выехали машины на перекресток? В ответе перечислите подряд без пробелов первые буквы названий транспортных средств в порядке их выезда на перекресток, например АМЛГ.

63. Три друга Олег, Борис и Арсений, закончив институт, разъехались по разным городам. И вот спустя несколько лет, они, встретившись на вечере встречи выпускников, решили разыграть своего товарища. На его вопрос, где они теперь живут, друзья ответили:

Олег: я живу в Екатеринбурге, а Борис - в Мурманске.

Борис: я живу в Волгограде, а Олег - в Мурманске.

Арсений: я живу в Мурманске, а Олег - в Волгограде.

Каждый из них один раз сказал правду и один раз солгал. Где живут Арсений, Борис и Олег? В ответе перечислите подряд без пробелов первые буквы названий городов, соответствующие именам друзей в указанном порядке, например ВМЕ.

64. Скорость передачи данных через ADSL-соединение равна 128000 бит/с. Передача текстового файла через это соединение заняла 1 минуту. Определите, сколько символов содержал переданный текст, если известно, что он был представлен в 16битной кодировке Unicode.

65. Информационное сообщение объемом 2.5 Кбайт передается со скоростью 2560 бит/мин. За сколько минут будет передано данное сообщение?

66. Модем передает данные со скоростью 7680 бит/с. Передача текстового файла заняла 1,5 мин.

67. Определите, сколько страниц содержал переданный текст, если известно, что он был представлен в 16-битной кодировке Unicode, а на одной странице – 400 символов.

68. Средняя скорость передачи данных с помощью модема равна 36 864 бит/с. Сколько секунд понадобится модему, чтобы передать 4 страницы текста в 8-битной кодировке КОИ8, если считать, что на каждой странице в среднем 2 304 символа?

69. Скорость передачи данных через модемное соединение равна 4096 бит/с. Передача текстового файла через это соединение заняла 10 с. Определите, сколько символов содержал переданный текст, если известно, что он был представлен в 16-битной кодировке Unicode.

70. Передачи данных через ADSL-соединение заняла 2 минуты. За это время был передан файл, размер которого 3 750 Кбайт. Определите минимальную скорость (бит/c), при которой такая передача возможна.

71. Записано 7 строк, каждая имеет свой номер – от «0»- до «6»-й. В начальный момент в строке записана цифра 0 (ноль). На каждом из последующих 6 шагов выполняется следующая операция: в очередную строку записывается удвоенная предыдущая строка, а в конец строки приписывается очередная цифра (на i-м шаге приписывается цифра i). Для удобства в скобках пишется номер строки (начиная с

0). Ниже показаны первые строки, сформированные по описанному правилу:

(0) 0

(1) 001

(2) 0010012

(3) 001001200100123

Какая цифра стоит в последней строке на 123-м месте (считая слева направо)?

72. Цепочки символов (строки) создаются по следующему правилу: первая строка состоит из одного символа, это цифра 1. Каждая из следующих цепочек создается так: сначала записывается порядковый номер данной строки, далее дважды записывается вся цепочка цифр из предыдущей строки. Первые 4 строки, созданные по этому правилу, выглядят следующим образом:

211

3211211

432112113211211

Сколько раз в общей сложности встречаются в 10-й строке нечетные цифры (1,3, 5, 7,9)?

73. На сервере news.edu находится файл list.txt, доступ к которому осуществляется по протоколу ftp. Фрагменты адреса данного файла закодированы буквами А, В, С ... G

(см. таблицу). Запишите последовательность этих букв, которая кодирует адрес указанного файла в Интернете.

74. Петя записал IP-адрес школьного сервера на листке бумаги и положил его в карман куртки. Петина мама случайно постирала куртку вместе с запиской. После стирки Петя обнаружил в кармане четыре обрывка с фрагментами IP-адреса. Эти фрагменты обозначены буквами А, Б, В и Г. Восстановите IP-адрес. В ответе укажите последовательность букв, обозначающих фрагменты, в порядке, соответствующем IP-адресу.

75. В таблице приведены запросы к поисковому серверу. Расположите обозначения запросов в порядке убывания количества страниц, которые найдет поисковый сервер по каждому запросу. Ответ запишите в виде последовательности соответствующих букв.

d) Информатика | Excel

76. В таблице приведены запросы к поисковому серверу, условно обозначенные буквами от А до Г. Расположите запросы в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу. Ответ запишите в виде последовательности соответствующих букв.

а ) Гренландия & Климат & Флора & Фауна b ) Гренландия & Флора

с) (Гренландия & Флора) | Фауна

d) Гренландия & Флора & Фауна

77. Производится одноканальная (моно) звукозапись с частотой дискретизации 16 кГц и 32-битным разрешением. Запись длится 8 минут, ее результаты записываются в файл, сжатие данных не производится. Какое из приведенных ниже чисел наиболее близко к размеру полученного файла, выраженному в Мбайтах?

1) 30 2) 45 3) 75 4) 85

78. Производится двухканальная (стерео) звукозапись с частотой дискретизации 16 кГц и глубиной кодирования 32 бит. Запись длится 12 минут, ее результаты записываются в файл, сжатие данных не производится. Какое из приведенных ниже чисел наиболее близко к размеру полученного файла, выраженному в мегабайтах?

1) 30 2) 45 3) 75 4) 90

Список использованной литературы:

1. Практикум по информатике и информационным технологиям. Учебное пособие для общеобразовательных учреждений/Н.Д. Угринович, Л.Л. Босова, Н.И. Михайлова. – 3-е изд. – М. БИНОМ. Лаборатория знаний, 2010. – 394 с.

2. Информатика: Учебник для среднего профессионального образования. Изд. 2-е, испр./ Михеева Е.В., Титова О.И., - ИЦ «Академия», 2008.

3. Е. А. Колмыкова, И. А. Кумскова. Информатика: учебное пособие для студентов средних профессиональных учебных заведений. – ИЦ «Академия», 2010.

4. Информатика 10-11 класс. Базовый курс. Теория / Под ред. Н.В.Макаровой. – СПб.:

Питер, 2010. – 675 с.: ил.

5. Информатика и информационные технологии. Учебник для 10-11 классов/Н.Д.

Угринович. – М. БИНОМ. Лаборатория знаний, 2010. – 511 с.: ил.

6. Семакин Е.Г. Информатика и ИКТ. Базовый уровень: учебник для 10-11 классов. М.

:БИНОМ. Лаборатория знаний, 2008. — 246 с.: ил.

7. http://school497.ru/download/u/01/urok4/les4.html

8. http://kpolyakov.narod.ru/index.htm

9. http://ivan101.narod.ru/gos/pril/18etapy-postr-modeley.htm

10. http://umk-model.narod.ru/p6.html

[1] FA _{( 1 6 )}

Коми Республикаса йöзöс велöдан министерство «Сыктывкарса сервис да связь колледж» уджсикасö велöдан канму учреждение

Введение 2

Пояснительная записка Учебное пособие «Информатика и

Измерение информации 1.1. Подходы к измерению информации

Рассмотрим, как можно подсчитать количество информации в сообщении, используя содержательный подход

Единицы измерения информации

Найти: 2 8 =256

Задача 10. Выразить: a) 3

Для этого необходимо использовать следующую формулу

Найдем количество информации в сообщении о вытаскивании красного шара: i

Кч=2; i ч = 4 бита;

В коробке лежат 64 цветных карандаша

Чтобы определить объем информации в сообщении при алфавитном подходе, нужно последовательно решить задачи: 1

Задания для самостоятельного выполнения:

Для записи сообщения использовался 64-х символьный алфавит

Основанием системы счисления называется количество знаков или символов, используемых для изображения числа в данной системе счисления

А 11 1011 13

Решение : 2 4 2 3 2 2 2 1 2 0 1 1 0 1 0 2 11010 2 = 0·2 0 +1· 2…

Т.к. в шестнадцатеричной системе счисления 14 –

Задание 4. Дано: а = 21 10 , b = 23 8

Задание 9.

Ответ: 0,15 10 = 0,00100 2 =0,11463 8 =0,26666 16 2

Переведите данное число в десятичной системе счисления в двоичную, восьмеричную, а затем в шестнадцатеричную систему счисления: a) 670,25 10 c) 8,25 10 b) 162,5 10…

Если в последней правой группе окажется меньше n разрядов, то ее надо дополнить справа нулями до нужного числа разрядов

Пример 5. Переведем шестнадцатеричное число 4АС35 16 в двоичную систему счисления

Задание 7. 23 Чему равна сумма чисел 71 8 и 54 16 ? a) 215 8 ; b) 105 8 ;

Пример 2. Выполнить вычитание двоичных чисел:

Сложить два числа в двоичной системе счисления

Задание 2. Выполнить вычитание двух чисел в двоичной системе счисления

Задание 8. a) 1111 : 101 = 11 b) 1111 : 11 = 101 c) 11100111 : 1011 = 10101 d) 111111 : 111 =…

Пример 1. В случае, когда для записи кода выделен один байт, для числа +1101 прямой код 0,0001101, для числа – 1101 прямой код 1,0001101

Пример 1. Сложить X и Y в обратном и дополнительном кодах

Задание 2. Вычислить: a)

Примеры: a. 6 ( 8 ) + 7 ( 8 ) 25 ( 8 ) 7+6=13=8+5 1+1=2 d

Деление в любой позиционной системе счисления производится по тем же правилам, как и деление, углом в десятичной системе

AF 16 – 97 16 = 18 16 b) 67 8 · 23 8 = 2025 8 g)

Задание 6. Выполните действия: a)

И в основу представления чисел в компьютере была положена именно двоичная система счисления

Дискретизация – это преобразование непрерывных изображений и звука в набор дискретных значений в форме кодов

R ed), зеленый ( G reen), синий (

Форматы графических файлов определяют способ хранения информации в файле (растровый или векторный), а также форму хранения информации (используемый алгоритм сжатия)

Итак, для расчѐта информационного объѐма растрового графического изображения используется формула

Задание 2. Черно-белое (без градаций серого) растровое графическое изображение имеет размер 10  10 точек

Дано: X  Y=800  600; i =24; s=4;

Из каких основных цветов складываются оттенки? 2

Сканируется цветное изображение размером 10  10 см

Подробнее рассмотрим эти процессы

Высокое качество звучания достигается при частоте дискретизации 44,1 кГц и глубины кодирования звука, равной 16 бит

Дано:

Рассчитайте время звучания моноаудиофайла, если при 16-битном кодировании и частоте дискретизации 32 кГц его объем равен: a) 700

Материалы на данной страницы взяты из открытых истончиков либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

23.04.2017

Учебное пособие. Информатика и ИКТ.

1.1. Подходы к измерению информации

1.2. Содержательный (вероятностный) подход к определению количества

1.3. Единицы измерения информации

1.4*. Вычисление количества информации для событий с различными вероятностями

1.5. Алфавитный подход к измерению информации

Системы счисления 2.1. Системы счисления

2.2. Развернутая форма числа

2.3. Системы счисления, используемые в компьютерах

2.4. Перевод целых чисел из десятичной системы счисления в другую

2.5. Перевод числа из двоичной системы счисления в десятичную.

2.7. Перевод неправильных дробей из десятичной системы счисления в систему

2.8. Перевод чисел из системы счисления с основанием 2 в систему счисления с

2.9. Перевод чисел из системы счисления с основанием 2 в систему счисления с

2.10. Перевод чисел из систем счисления с основанием q=2n в двоичную систему

3.2. Основы машинной арифметики с двоичными числами

3.3. Коды чисел

6 ( 8 ) + 7 ( 8 ) 25 ( 8 )

07 ( 8 ) 0F ( 1 6 ) + 01 ( 8 ) + 06 ( 1 6 )

17 ( 8 )

322 ( 8 )

16 ( 1 6 )

Коми Республикаса йöзöс велöдан министерство «Сыктывкарса сервис да связь колледж» уджсикасö велöдан канму учреждение

Введение 2

Пояснительная записка Учебное пособие «Информатика и

Измерение информации 1.1. Подходы к измерению информации

Рассмотрим, как можно подсчитать количество информации в сообщении, используя содержательный подход

Единицы измерения информации

Найти: 2 8 =256

Задача 10. Выразить: a) 3

Для этого необходимо использовать следующую формулу

Найдем количество информации в сообщении о вытаскивании красного шара: i

Кч=2; i ч = 4 бита;

В коробке лежат 64 цветных карандаша

Чтобы определить объем информации в сообщении при алфавитном подходе, нужно последовательно решить задачи: 1

Задания для самостоятельного выполнения:

Для записи сообщения использовался 64-х символьный алфавит

Основанием системы счисления называется количество знаков или символов, используемых для изображения числа в данной системе счисления

А 11 1011 13

Решение : 2 4 2 3 2 2 2 1 2 0 1 1 0 1 0 2 11010 2 = 0·2 0 +1· 2…

Т.к. в шестнадцатеричной системе счисления 14 –

Задание 4. Дано: а = 21 10 , b = 23 8

Задание 9.

Ответ: 0,15 10 = 0,00100 2 =0,11463 8 =0,26666 16 2

Переведите данное число в десятичной системе счисления в двоичную, восьмеричную, а затем в шестнадцатеричную систему счисления: a) 670,25 10 c) 8,25 10 b) 162,5 10…

Если в последней правой группе окажется меньше n разрядов, то ее надо дополнить справа нулями до нужного числа разрядов

Пример 5. Переведем шестнадцатеричное число 4АС35 16 в двоичную систему счисления

Задание 7. 23 Чему равна сумма чисел 71 8 и 54 16 ? a) 215 8 ; b) 105 8 ;

Пример 2. Выполнить вычитание двоичных чисел:

Сложить два числа в двоичной системе счисления

Задание 2. Выполнить вычитание двух чисел в двоичной системе счисления

Задание 8. a) 1111 : 101 = 11 b) 1111 : 11 = 101 c) 11100111 : 1011 = 10101 d) 111111 : 111 =…

Пример 1. В случае, когда для записи кода выделен один байт, для числа +1101 прямой код 0,0001101, для числа – 1101 прямой код 1,0001101

Пример 1. Сложить X и Y в обратном и дополнительном кодах

Задание 2. Вычислить: a)

Примеры: a. 6 ( 8 ) + 7 ( 8 ) 25 ( 8 ) 7+6=13=8+5 1+1=2 d

Деление в любой позиционной системе счисления производится по тем же правилам, как и деление, углом в десятичной системе

AF 16 – 97 16 = 18 16 b) 67 8 · 23 8 = 2025 8 g)

Задание 6. Выполните действия: a)

И в основу представления чисел в компьютере была положена именно двоичная система счисления

Дискретизация – это преобразование непрерывных изображений и звука в набор дискретных значений в форме кодов

R ed), зеленый ( G reen), синий (

Итак, для расчѐта информационного объѐма растрового графического изображения используется формула

Задание 2. Черно-белое (без градаций серого) растровое графическое изображение имеет размер 10  10 точек

Дано: X  Y=800  600; i =24; s=4;

Из каких основных цветов складываются оттенки? 2

Сканируется цветное изображение размером 10  10 см

Подробнее рассмотрим эти процессы

Высокое качество звучания достигается при частоте дискретизации 44,1 кГц и глубины кодирования звука, равной 16 бит

Дано:

Рассчитайте время звучания моноаудиофайла, если при 16-битном кодировании и частоте дискретизации 32 кГц его объем равен: a) 700

2.10. Перевод чисел из систем счисления с основанием q=2ⁿ в двоичную систему