умножение без таблицы умножения проект 9 класс

Оглавление

Введение…………………………………………………………………..2
1. Русско-крестьянский способ умножения…………………………….3
2. Умножение с помощью прямых………………………………………4   
2.1. Умножение двухзначного числа на двухзначное………………….4            
2.2. Умножение трехзначного числа на двухзначное…………….…....4
3. Умножение при помощи кругов…………..4                                                      
3.1. Умножение двухзначного числа на двухзначное……….........…..5-6            
3.2. Умножение трехзначного числа на двузначное.............................7-8            
3.3. Умножение трехзначного числа с нулем на двузначное….……9-11
3.4. Умножение трехзначного числа на трехзначное.............................11     
Заключение                                                                                  
Литература.

Введение

Вы не сможете выполнить умножения многозначных чисел - хотя бы даже двузначных - если не помните наизусть всех результатов умножения однозначных чисел, т. е. того, что называется таблицей умножения.

В школе изучают таблицу умножения, а затем учат детей умножать числа в столбик. Разумеется, это не единственный способ умножения. На самом деле, существует несколько десятков способов умножения многозначных чисел.

Но проблема в том, что не все современные ученики  хорошо знают таблицу умножения?  Потому возник вопрос: «Не существуют ли способов перемножать числа и без знания таблицы умножения?».

Таким образом, я выдвинул гипотезу: нельзя ли выполнить умножение больших чисел без знания таблицы умножения.

Объектом моего исследования являются математическое действие умножения; предметом исследования - различные способы умножения.

Цель проекта: ознакомление с различными способами умножения натуральных чисел, не используемых на уроках, для вычисления которых достаточно устного счета или применения карандаша, ручки и бумаги.

Задачи: Найти и разобрать различные способы умножения.

Рассмотреть методы умножения, при которых не нужно знать таблицу умножения. Расширить круг примеров, решенных указанным способом.

Развить навыки самостоятельной работы: поиск информации, отбор и оформление найденного материала.

Актуальность темы проекта. Для современного ученика умножать числа — это не проблема, так как он знает таблицу умножения и с помощью действия умножения легко справится с заданием. Но не все дети знают таблицу умножения, и не все выполняют его с интересом. А научиться умножать это жизненная необходимость. Поэтому научить детей умножать можно и другими интересными способами.

Методы: поисковый метод с использованием научной и учебной литературы, интернета;

исследовательский метод при определении способов умножения;

практический метод при решении примеров.

Способы умножения

Мало кто подозревает, что нынешние способы выполнения арифметических действий тоже не всегда были так просты и удобны, так прямо и быстро приводили к результату.

Не всем умножение дается легко и просто. А уж тем более умножать большие числа.

За тысячелетия развития математики было придумано много способов умножения.  Кроме таблицы умножения, все они громоздкие, сложные и трудно запоминаются.  Считалось, что для овладения искусством быстрого умножения нужно особое природное дарование. Простым людям, не обладающим особым математическим даром, это искусство недоступно.

Предки наши пользовались гораздо более громоздкими и медленными приемами. Но возможно, среди них есть более интересные и увлекательные способы умножения.  Посмотрим некоторые из них.

«Русский крестьянский способ»

В России среди крестьян был распространен способ, который не требовал знания всей таблицы умножения. Здесь необходимо лишь умение умножать и делить числа на 2.

Напишем одно число слева, а другое справа на одной строке (рис. 3).  Левое число будем делить на 2, а правое – умножать на 2 и результаты записывать в столбик.

Если при делении возник остаток, то его отбрасывают. Умножение и деление на 2 продолжают до тех пор, пока слева не останется 1.

Затем вычеркиваем  те строчки из столбика, в которых слева стоят четные числа. Теперь сложим оставшиеся числа в правом столбце.

Рис. 2 «Русский крестьянским способом»

Ответ – 1972026.

Этот способ интересен, но как мы видим его можно применить, только если знаешь деление на 2.

Умножение с помощью прямых (китайский)

Давайте посмотрим  еще более интересные способы умножения. В этих случаях нам таблица умножения не нужна.

Умножение двухзначного числа на двухзначное

При умножении чисел считаются точки пересечения прямых, которые соответствуют  количеству цифр каждого разряда обоих множителей.

Пример: умножим 31 на 12. В первом множителе 3 десятка и 1единица, значит строим 3 параллельные прямые и чуть дальше 1 прямую.

Во втором множителе 1 десяток и 2 единицы. Строим параллельно 1 и поодаль 3 прямые, пересекающие прямые первого множителя.

Прямые пересеклись в точках, количество которых и есть ответ, то есть   31 х 112 = 372

Умножение трехзначного числа на двухзначное

Пример: умножим 213 на 13.

В первом множителе 2 сотки,1 десяток и 3 единицы, значит строим сначала 2 параллельные прямые, чуть дальше 1 прямую и чуть дальше 3 параллельные прямые.

Во втором множителе 1 десяток и 3 единицы. Так же параллельно строим прямые, но в другом направлении.

Далее разделяем их дугой как показано ниже и читаем точки пересечения.

Прямые пересеклись в точках, количество которых и есть ответ, то есть 213 х 13 = 2769.

Забавно и интересно, придется точки пересечения считать.  В общем, без таблицы умножения можно обойтись!

Умножение при помощи кругов (японский)

Этот способ умножения –с использованием кругов и линий. Не менее забавный и интересный чем предыдущий.  Даже чем-то на него похож.

В Интернете был указан только один пример умножения двузначного числа на двузначное, но я его исследовал и применил к многозначным числам. Давайте разберем подробнее.

Умножение двузначных чисел

13 х 24 = 312

Последовательность работы.

1) Чертим круги, так как второй множитель двузначное число, то и два столбца. В первом ряду по одному кругу, во втором ряду по три круга.

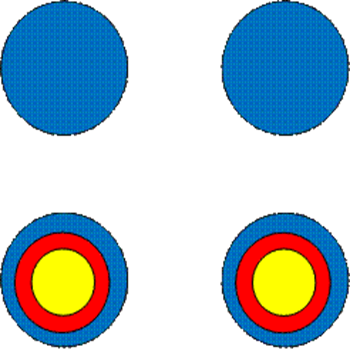
2) Второй множитель число 24, то круги, которые в первом столбце делим на две части, а круги, которые во втором столбце делим на четыре части.

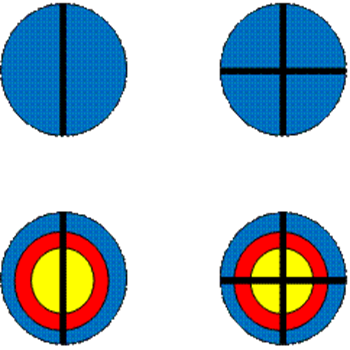
3) Проводим прямые и считаем точки.

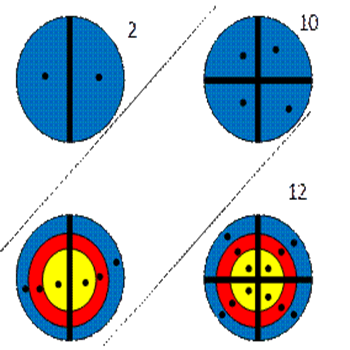
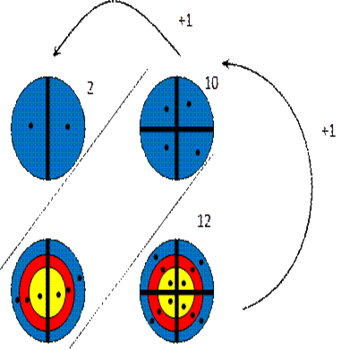
Ответ записывается следующим образом, смотрим снизу-вверх количество точек 12, 2 – последняя цифра результата, один в уме, количество точек во второй области 10 и +1, того 11, 1 пишем и один в уме, количество точек в третьей области 2 и +1, того 3. Ответ – 312.

Я провел самостоятельное исследование и определил способ решения еще трех примеров:

Умножение трехзначного числа на двузначное.

Умножение трехзначного числа с нулем на двузначное.

Умножение трехзначного числа на трехзначное.

Все примеры, приведенные для показа данного метода придуманы и решены самостоятельно.

Умножение трехзначного числа на двузначное

132 · 21 = 2772

Решения примера данного типа не было, я дорабатывал его самостоятельно.

Алгоритм.

1) Чертим круги, так как второй множитель двузначное число, то и два столбца. В первом ряду по одному кругу, во втором ряду по три круга, в третьем ряду по два круга.

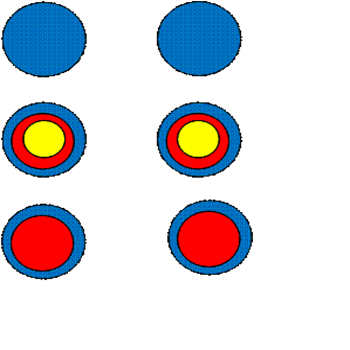
2) Второй множитель число 21, то круги, которые в первом столбце делим на две части, а круги, которые во втором столбце так и остаются.

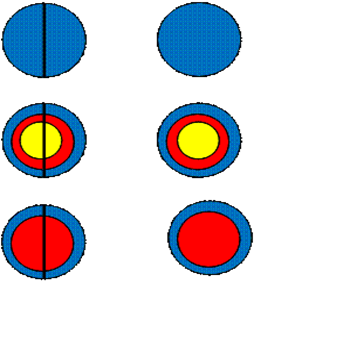
3) Проводим прямые и считаем точки.

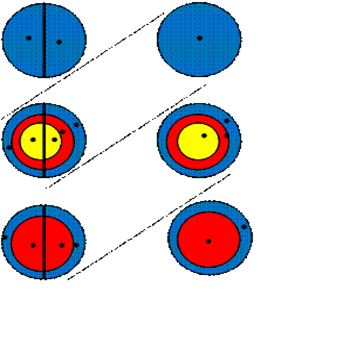
Ответ записывается следующим образом, смотрим сверху вниз, по часовой стрелке, количество точек в первой области 2, количество точек во второй области 7, в третьей области 7, в четвертой области 2.

Ответ – 2772.

Умножение трехзначного числа с нулем на двузначное

203 х 21= 4263

Последовательность работы.

Алгоритм такой же, как при умножении трехзначного числа на двузначное, но круг, обозначающий ноль, чертим пунктирной линией -  это воображаемая линия, точек на ней не существует.

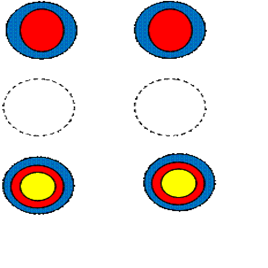
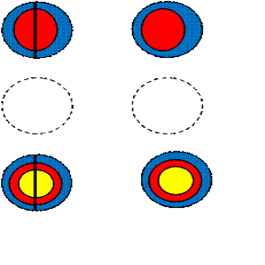
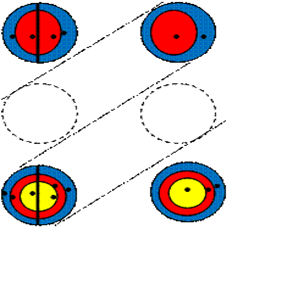
Ответ: 4263

Умножение трехзначного числа на трехзначное

123х 121= 14883

Решения примера данного типа тоже не было

Алгоритм.

4) Чертим круги, так как второй множитель трехзначное число, то и три столбца. В первом ряду по одному кругу, во втором ряду по два круга, в третьем ряду по три круга (рис. 17)

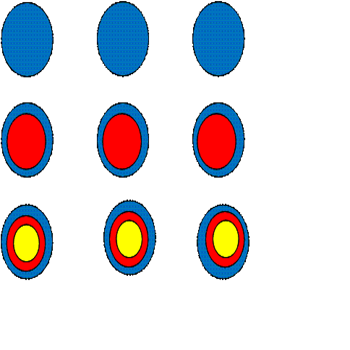
5) Второй множитель число 121, то круги, которые в первом и третьем столбце так и остаются, а круги, которые во втором столбце делим на две части (рис. 18).

6)

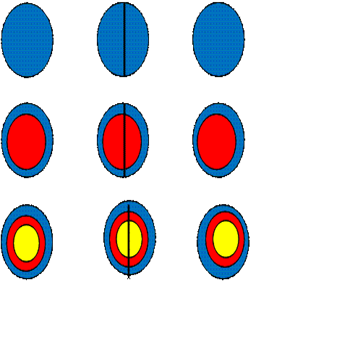
7) Проводим прямые и считаем точки (рис. 19).

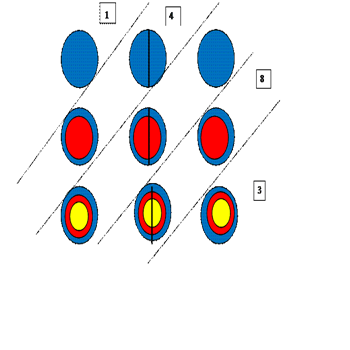
Ответ записывается следующим образом, смотрим снизу-вверх количество точек 3-последняя цифра результата, количество точек во второй области 8, в третьей области 5, в четвертой области 2. Ответ – 14883.

Заключение

При выполнении данной работы над проектом по математике на тему "Умножение без таблицы умножения" мне понадобились не только те знания, которые были у меня, но и работа с дополнительной литературой и с интернет ресурсами.

В процессе выполненной исследовательской работы по математике на тему "Умножение без таблицы умножения" получены следующие выводы и результаты.

1. В ходе работы над исследовательским проектом "Умножение без таблицы умножения" я нашел и освоил различные способы умножения многозначных чисел и могу констатировать следующее:

большинство способов умножения многозначных чисел основаны на знании таблицы умножения;

способ «решетчатое умножение» ничуть не хуже, чем общепринятый. Он даже проще, поскольку в клетки таблицы заносятся числа прямо из таблицы умножения без одновременного сложения, присутствующего в стандартном методе;

многие приемы умножения, которые мы встретили в разных источниках, опираются на знание таблицы умножения. «Русский крестьянский способ умножения» не требовал знаний таблицы. Достаточно только уметь умножать и делить на два.

2. Исследовав методы умножения, которые можно назвать методами умножения с помощью кругов и прямых, я доказал, что существуют способы умножения чисел, для которых достаточно наличие карандаша и бумаги и знаний таблицы умножения не требуется.

Работая над этой темой "Умножение без таблицы умножения", я узнал, что существует много различных, забавных способов умножения.

Своей работой над проектом я доказал, что моя гипотеза верна, не нужно обладать сверхъестественными способностями, чтобы умножать числа. Есть очень интересные и увлекательные способы умножения.

Но все-таки наш способ умножения самый простой и быстрый и в общем, таблицу умножения все-таки знать нужно!

Литература

1. Кордемский Б. А., Ахадов А. А. Удивительный мир чисел: Книга учащихся,- М. Просвещение, 1986.

2. Минских Е. М. «От игры к знаниям», М., «Просвещение» 1982г.

3. Свечников А. А. Числа, фигуры, задачи М., Просвещение, 1977г.

4. Депман И. «Рассказы о математике».  – Ленинград.: Просвещение, 1954. – 140 с.

5. Корнеев А.А.  Феномен русского умножения. История. http://numbernautics.ru/

6. Олехник  С. Н., Нестеренко Ю. В., Потапов М. К.  «Старинные занимательные задачи». –  М.: Наука. Главная редакция физико-математической литературы, 1985. – 160 с.

7. Перельман Я.И. Быстрый счет. Тридцать простых приемов устного счета. Л., 1941 — 12 с.

8. Перельман Я.И.  Занимательная арифметика. М.Русанова,1994--205с.

9. Энциклопедия «Я познаю мир. Математика». – М.: Астрель Ермак, 2004.

10.Энциклопедия для детей. «Математика». – М.: Аванта +, 2003. – 688 с. 

11. Депман И. Я., Виленкин Н. Я. За страницами учебника математики: Пособие для учащихся 5-6 кл. сред.шк.-М.: Просвещение, 1989.

12. Занимательная арифметика. Перельман Я. И.Издание:8Год изд.:1954

13. Энциклопедия для детей. Т.11 Математика. М: Аванта+ 2003г.

14. Как постепенно дошли люди до настоящей арифметики с таблицей. Общедоступные очерки для любителей арифметики. Составитель: В. Билюстин. М:1939г. .

15. Интернет ресурсы

Скачано с www.znanio.ru