Управление запасами

Задача скачана с сайта www.MatBuro.ru

Еще примеры: https://www.matburo.ru/ex_emm.php?p1=emmuz

©МатБюро - Решение задач по математике, экономике, статистике

Управление запасами

Пример решения задачи

Фирме по строительству судов требуется 20000 заклепок в год, расходуемых с постоянной интенсивностью. Организационные издержки составляют 0,5 тыс. р. за партию, цена одной заклепки — 10 р. Издержки на хранение одной заклепки оценены в 12,5% ее стоимости.

Найти         оптимальный      размер       партии        поставки,   оптимальную продолжительность цикла и оптимальное число поставок за год.

Решение:

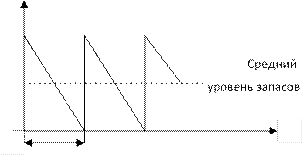Обозначим:

g – годовой спрос; g = 20000 b – организационные издержки; b = 0,5 тыс.р.

s – цена товара; s = 0,01 тыс. р.

        Продолжитель                                                                          h – издержки содержания запасов; h

ность цикла

= 0,01*0,125=0,00125 тыс. р.

q – размер партии поставки

Общие издержки в течение года:

С = С₁ + С₂ + С₃, 

где С₁ – общие организационные издержки; С₂ – стоимость товаров; С₃ – общие издержки содержания запасов.

             g                 g                                                      20000           10000

С₁ =  ⋅b , где        - количество партий; С₁ =     ⋅0,5 =  ; q   q          q          q

C₂ = s⋅ g; C₂ = 0,01⋅20000= 200;

1

Задача скачана с сайта www.MatBuro.ru

Еще примеры: https://www.matburo.ru/ex_emm.php?p1=emmuz

©МатБюро - Решение задач по математике, экономике, статистике

                  q            q                                                                                                           q

C₃ = h⋅ , где  - среднее количество запасов на складе; C₃ = 0,00125⋅

                  2            2                                                                                                           2

                             10000                           q

Имеем ^С =   + 200+ 0,00125       . q     2

Найдём q_опт , чтобы издержки С были минимальными.

С_q′ = −¹⁰⁰⁰⁰₂   + 0,000625 = 0 ⇒ ¹⁰⁰⁰⁰₂            = 0,000625⇒q² =16000000 ⇒q_опт =   16000000 = 4000 q          q

 ед.

s   20000  365 п – число поставок; n_опт =   =            =5; t =            =73 дня.

                                                                     qопт             4000                 nопт

Ответ: Оптимальный размер партии составляет 4000заклепок; число поставок – 5; продолжительность цикла – 73 дня.

2