Уравнения смешанного типа: логарифмические, показательные и тригонометрические. (Профильный уровень).

Уравнения из материалов ЕГЭ профильного уровня смешанного тип

         Логарифмические и тригонометрические уравнения.

 1. а)  Решите уравнение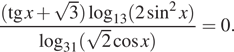

б)  Найдите все корни этого уравнения, принадлежащие отрезку

Решение. 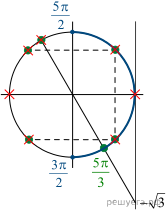а)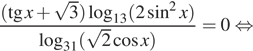  

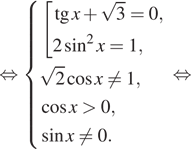
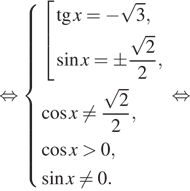
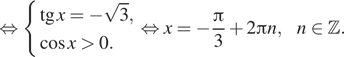
б)  С помощью числовой окружности отберём корни, принадлежащие отрезку Получим число

Ответ: а)    б)

2. а)  Решите уравнение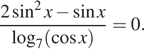

б)  Найдите все корни этого уравнения, принадлежащие отрезку

Решение. а)  Перейдём к системе: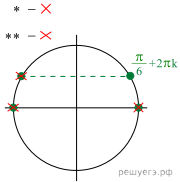

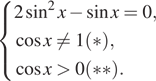
Решаем уравнение системы

Получаем:

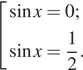
С учётом всех ограничений

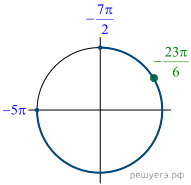
б)  С помощью числовой окружности отберём корни, принадлежащие отрезку Получим число

Примечание. Отбор корней может быть обоснован и любым другим способом: с помощью графика, решения двойных неравенств и т. п.

Ответ: а) б)

3. а)  Решите уравнение

б)  Найдите все корни этого уравнения, принадлежащие отрезку

Решение. 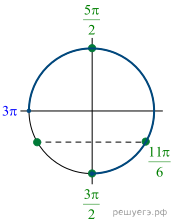а)  Из данного уравнения получаем:

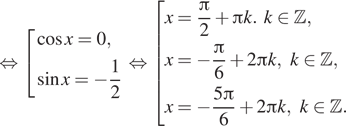
б)  С помощью числовой окружности отберём корни, принадлежащие отрезку Получим числа:

Ответ: а) б)

4. а)  Решите уравнение

б)  Найдите все корни этого уравнения, принадлежащие отрезку

Решение. а)  Пусть тогда откуда или

Далее имеем:

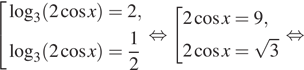
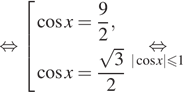
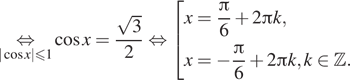
б)  Найдём на числовой оси корни, лежащие на отрезке

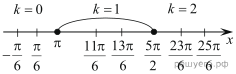
Из рисунка видно, что заданному отрезку принадлежат корни и

Ответ: а) ; б) ;

5. а)  Решите уравнение:

б)  Укажите корни этого уравнения, принадлежащие отрезку

Решение. 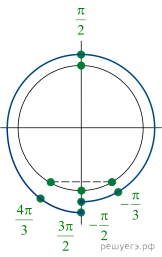а)  Запишем исходное уравнение в виде: Заметим, что выражение, стоящее под знаком логарифма, приравнено к положительному числу, поэтому исследовать ОДЗ не требуется.

Для решения полученного тригонометрического уравнения используем формулу синуса двойного угла откуда получаем откуда или

Из уравнения находим: или

Из уравнения находим:

б)  С помощью числовой окружности отберём корни, принадлежащие отрезку Получим числа:

Ответ: а) б)

6. а)  Решите уравнение

б)  Найдите все корни этого уравнения, принадлежащие отрезку

Решение. a)  Пусть тогда имеем:

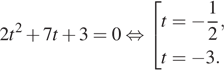
Вернёмся к исходной переменной:

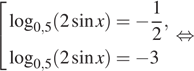
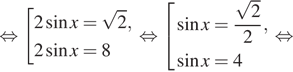
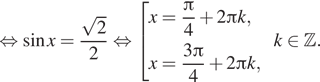
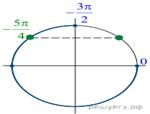
б)  С помощью числовой окружности отберём корни уравнения, принадлежащие заданному отрезку (см. рис.), получим число

Ответ: а) б)

7. а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

Решение. a)  Пусть тогда имеем:

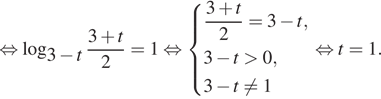
Вернёмся к исходной переменной:

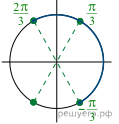
б)  При помощи единичной окружности отберём корни, лежащие на отрезке Получаем числа

Ответ: а) б)

8. а)  Решите уравнение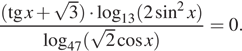

б)  Укажите корни этого уравнения, принадлежащие интервалу

Решение. а)  Заметим, что выражения под логарифмами должны быть положительны, а знаменатель не равен нулю, то есть корни уравнения должны удовлетворять следующим условиям:

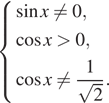
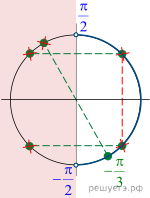
При выполнении этих условий уравнение равносильно совокупности

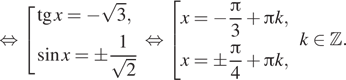
Условиям удовлетворяет только

б)  Имеем:

Единственным решением полученного двойного неравенства является которому соответствует корень

Ответ: а) б)

9. а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

Решение. а)  Заметим, что должны быть выполнены следующие условия: то есть При этих условиях применим к правой части формулу и получим равносильное уравнение

При тех же условиях имеем:

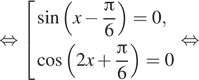
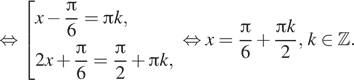
Из найденной серии ограничениям удовлетворяет только корень

б)  Очевидно, что единственный корень п. а) не лежит в указанном промежутке, то есть удовлетворяющих условию корней нет.

Ответ: а) б) корней нет.

10. а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

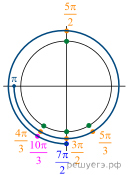Решение. а)  Решим уравнение:

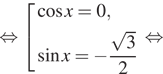
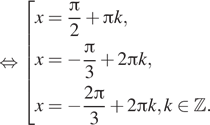
б)  Отберем корни при помощи тригонометрической окружности (см. рис.). На заданном промежутке лежат корни:

11. а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

Решение. а)  Сделаем замену получим:

Таким образом,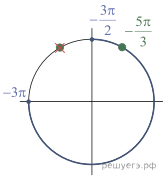

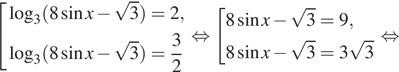
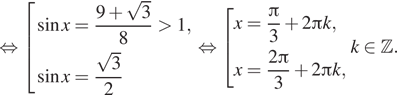
б)  Корни, лежащие на отрезке найдем при помощи тригонометрической окружности. Получим

Ответ: а) б)

12. а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

Решение. а)  Преобразуем уравнение при условиях (⁎). Имеем:

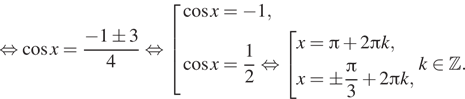
Условиям (⁎) удовлетворяет только серия

б)  Длина отрезка равна π, поэтому из найденной серии решений в отрезок может попасть не более одного корня. Следовательно, число соответствующее   — единственное решение, лежащее в этом отрезке.

Ответ: а) б)

13. а)  Решите уравнение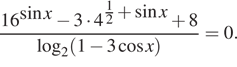

б)  Укажите корни этого уравнения, принадлежащие отрезку

Решение. 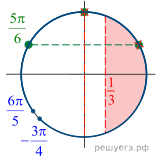а)  При условии и исходное уравнение сводится к квадратному относительно показательной функции:

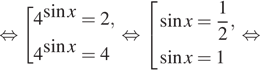
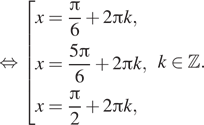
Условию равносильности удовлетворяет только серия

б)  Отберём корни при помощи единичной окружности (см. рис.). Подходит только

Ответ: а) б)

14. а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

Решение. а)  Первый множитель обращается в нуль, если то есть при откуда или При аргумент логарифма отрицателен, при   — положителен. Число −4  — посторонний корень.

Второй множитель обращается в нуль, если то есть если откуда или При подкоренное выражение отрицательно, при   — положительно. Число −2  — посторонний корень.

Тем самым корнями уравнения являются числа 2 и 4.

б)  Расставим корни и концы отрезка в порядке возрастания:

Значит, подходит только 2.

Ответ: а) б) 2.

15. а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

Решение. 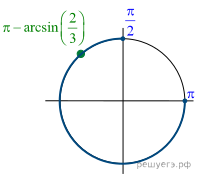а)  Заметим, что при условии исходное уравнение равносильно следующим::

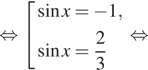
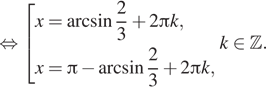
б)  Отберём корни при помощи единичной окружности. Подходит

Ответ: а) б)

16. а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

Решение. а)  Заметим, что уравнение имеет смысл только при и Преобразуем его при этом условии:

б)  Отберём корни при помощи единичной окружности. Подходит

Ответ: а) б)

17. а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

Решение. а)  Выражение положительно и отлично от единицы при условиях При этих условиях уравнение эквивалентно следующим:

При и получим , что не удовлетворяет условию. При получим , что также не удовлетворяет условию. Следовательно, условию эквивалентности удовлетворяет только

б)  Отберем корни при помощи двойного неравенства:

При найденном значении k находим:

Ответ: а) б)

18. а)  Решите уравнение

б)  Найдите все корни этого уравнения, принадлежащие отрезку

Решение. а)  Перейдем к одному основанию, получим

откуда пологая получаем:

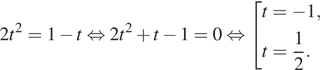
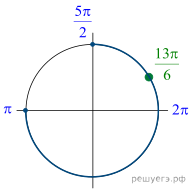
Вернемся к исходной переменной; получим:

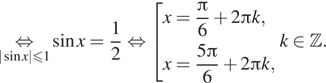
б)  На отрезке лежит корень

Ответ: а) б)

19. а)  Решите уравнение

б)  Найдите все корни уравнения, принадлежащие промежутку

Решение. а)  Область определения уравнения задается системой соотношений: Последнее условие означает, что оно выполнено при всех значениях переменной. Условие эквивалентно условию что верно, если одновременно и

При указанных условиях и поэтому при переходе к основаниям и не произойдет потери решений. Получаем

откуда следует, что

Сделаем замену тогда а значит, левая часть уравнения записывается в виде

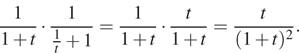
Решим уравнение:

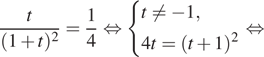
Таким образом,

Условию на синус и косинус удовлетворяет только

б)  Отберем корни при помощи двойного неравенства:

Найденному значению k соответствует корень

Ответ: а) б)

20. а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

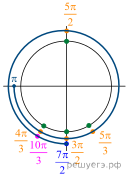Решение. а)  Решим уравнение:

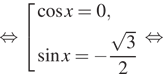
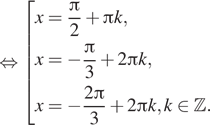
б)  Отберем корни при помощи тригонометрической окружности (см. рис.). На заданном промежутке лежат корни:

                     Решить самостоятельно.

1. а)  Решите уравнение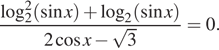

б)  Найдите все корни этого уравнения, принадлежащие отрезку

2. а)  Решите уравнение

б)  Найдите все корни этого уравнения, принадлежащие отрезку

3. а)  Решите уравнение

б)  Найдите решения уравнения из отрезка

4. а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

5. а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

6. а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

7. а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

8. а)  Решите уравнение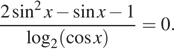

б)  Укажите корни этого уравнения, принадлежащие отрезку

9. а)  Решите уравнение

б)   Найдите все корни уравнения, принадлежащие отрезку

10. а)  Решите уравнение

б)  Найдите все корни уравнения, принадлежащие отрезку

                                         Ответы.

1. а) б)   (№14)

2. а) б)      (№20)

3. а) б)          (№33)

4. : а) б)     (№43)

5. а) б)      (№49)

6. : а) б)   (№56)

7. : а) б)    (№69)

8. : а) б)      (№79)

9. : а) б)     (№84)

10. : а) б)        (№88)