Урок 17. РЕШЕНИЕ ЗАДАЧ ПО ТЕМЕ «РАВНОБЕДРЕННЫЙ ТРЕУГОЛЬНИК»

Урок 17
РЕШЕНИЕ ЗАДАЧ ПО ТЕМЕ  «РАВНОБЕДРЕННЫЙ ТРЕУГОЛЬНИК»

Цели: изучить свойство биссектрисы (медианы, высоты) равнобедренного  треугольника,  проведенной  к  основанию;  изучить  признак равнобедренного треугольника и закрепить знание свойств равнобедренного треугольника  при  решении  задач;  развивать логическое мышление учащихся.

Ход урока

I. Проверка домашнего задания учащихся.

1. Один учащийся на доске готовит доказательство теоремы о свойстве углов при основании равнобедренного треугольника.

2. Второй  учащийся  решает  на  доске домашнюю задачу № 117 (по рис. 67).

3. Устно по готовым чертежам на доске (см. рис. 1–3) решаем задачи, предварительно повторив материал в ходе ответов учащихся на контрольные вопросы 10–12 на с. 50.

Найдите DВА.

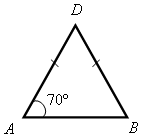
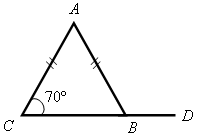
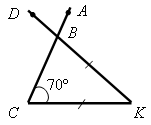
Рис. 1                                      Рис. 2                                         Рис. 3

II. Изучение нового материала.

1. Сформулировать и записать признак  равнобедренного  треугольника  (обратная  теорема  свойства  углов  равнобедренного  треугольника):

Если в треугольнике два угла равны, то он равнобедренный.

2. Решить задачу № 111 (по рис. 65) устно по заранее заготовленному чертежу на доске.

3. Изучить теорему о биссектрисе равнобедренного треугольника, проведенной к основанию (рис. 64):

1) перед изучением теоремы повторить первый признак равенства треугольников; повторить определение биссектрисы, медианы и высоты треугольника; определение и свойство смежных углов треугольника;

2) учить учащихся при формулировке теоремы выделять, что дано, что надо доказать; учить краткой записи доказательства теоремы.

4. Объяснение учителя. Мы установили, что биссектриса, медиана и высота равнобедренного треугольника, проведенные к основанию, совпадают. Поэтому справедливы также утверждения:

1) Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.

2) Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой.

5. Устно решить задачу № 110.

III. Решение задач на закрепление изученного материала.

1. Решение задач (устно) по готовым чертежам (заранее изготовить плакаты с рисунками, см. рис. 1–5).

Найдите DВА  (учить  учащихся  читать  чертеж  по  обозначениям на нем).

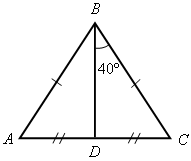
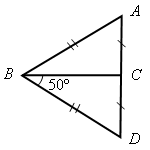
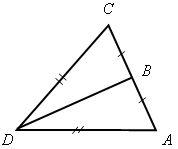
      Рис. 1                                         Рис. 2                                      Рис. 3

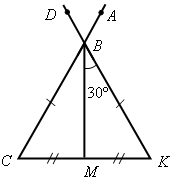
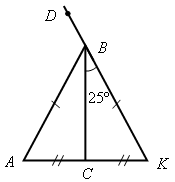
Рис. 4                                                           Рис. 5

2. Решить задачу № 119 с записью решения на доске и в тетрадях.

Решение

1) По условию ЕF – биссектриса DDЕK и DЕF = 43°, тогда

DЕK = 2 · DЕF = 43° · 2 = 86°.

2) EF – медиана равнобедренного DЕK (по свойству биссектрисы, проведенной к основанию), тогда KF = DK; KF = 16 : 2 = 8 (см).

3) ЕF – высота равнобедренного DЕK (свойство биссектрисы, проведенной к основанию равнобедренного треугольника).

Значит, ЕFD = ЕFK = 90°.

Ответ: KF = 8 см; DЕK = 86°; ЕFD = 90°.

3. Решить задачу  № 120 (а)  с  записью  решения  на  доске  и  в  тетрадях.

IV. Итоги урока.

Домашнее задание: повторить п. 15; изучить пункты 16–18, ответить на вопросы 4–13 на с. 50; решить задачи №№ 114, 118 и 120 (б).