Урок 28. КОНТРОЛЬНАЯ РАБОТА № 2 «ТРЕУГОЛЬНИКИ»

Урок 28

КОНТРОЛЬНАЯ РАБОТА № 2 «ТРЕУГОЛЬНИКИ»

Цель: проверить знания, умения и навыки учащихся по усвоению и применению изученного материала.

Ход урока

I. Организация учащихся на выполнение работы.

II. Выполнение работы по вариантам.

Вариант I

1. На рисунке 1 отрезки АВ и СD имеют общую середину О. Докажите, что DАО = СВО.

2. Луч АD – биссектриса угла А. На сторонах угла А отмечены точки В и С так, что АDВ = АDС. Докажите, что АВ = АС.

3. Начертите равнобедренный треугольник АВС с основанием ВС. С помощью циркуля и линейки проведите медиану ВВ₁ к боковой стороне АС.

Вариант II

1. На рисунке 2 отрезки МЕ и РK точкой D делятся пополам. Докажите, что KМD = РЕD.

2. На сторонах угла Д отмечены точки М и K так, что DМ = DK. Точка Р лежит внутри угла D и РK = РМ. Докажите, что луч DР – биссектриса угла МDK.

3. Начертите равнобедренный треугольник АВС с основанием АС и острым углом В. С помощью циркуля и линейки проведите высоту из вершины угла А.

Вариант III
(для более подготовленных учащихся)

1. На  рисунке  3  прямые  АВ и СD  пересекаются в точке Е, СЕ = ВЕ, С = В; АА₁ и DD₁ – биссектрисы треугольников АСЕ и DВЕ. Докажите, что АА₁ = DD₁.

2. На  сторонах  угла  А  отмечены  точки  В  и  С  так,  что  АВ = АС. Точка М лежит внутри угла А и МВ = МС. На прямой АМ отмечена точка D так, что точка М лежит между точками А и D. Докажите, что ВМD =
= СМD.

3. Начертите равнобедренный тупоугольный треугольник АВС с основанием ВС и с тупым углом А. С помощью циркуля и линейки проведите:

а) высоту треугольника АВС из вершины угла В;

б) медиану треугольника АВС к стороне АВ;

в) биссектрису треугольника АВС угла А.

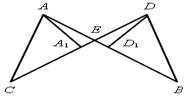
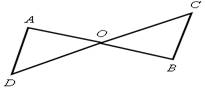
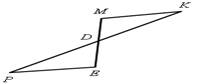
     Рис. 1                                              Рис. 2                                    Рис.3

III. Итоги урока.

Домашнее задание:  повторить материал пунктов 2–21.