Урок 51. НЕКОТОРЫЕ СВОЙСТВА ПРЯМОУГОЛЬНЫХ ТРЕУГОЛЬНИКОВ

Урок 51
НЕКОТОРЫЕ СВОЙСТВА ПРЯМОУГОЛЬНЫХ
ТРЕУГОЛЬНИКОВ

Цели: рассмотреть некоторые свойства прямоугольных треугольников и показать, как они применяются при решении задач.

Ход урока

I. Анализ результатов контрольной работы.

II. Изучение нового материала.

1. Устно решить задачу № 254 (использовать демонстрационный равнобедренный прямоугольный треугольник).

2. Решить задачу № 255 на доске и в тетрадях.

Так как СF DЕ по условию, то треугольник СFЕ – прямоугольный, в нем CFЕ = 90°, Е = 63°; тогда ЕСF = 180° – (90° + 63°) = 27°.

Ответ: 27°.

3. Рассмотреть свойство 1° и посоветовать учащимся запомнить его, поскольку оно часто используется при решении задач.

4. Доказательство свойств 2° и 3° следует провести учителю самому с записью условия и заключения прямого и обратного утверждений на доске в виде таблицы. Эту таблицу учащиеся должны воспроизвести в своих тетрадях.

III. Закрепление изученного материала.

1. Устно решить задачи по готовым чертежам на доске:

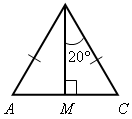
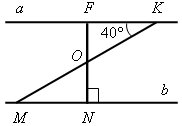
Рис. 1                                                                  Рис. 2   

1) Дано: АВС (рис. 1).

    Найти: углы АВС.

2) Дано: а || b (рис. 2).

    Найти: углы треугольника MON.

2. Решить задачу № 257 на доске и в тетрадях.

Решение

CАВ = 180° – 120° = 60° (смежные  углы),  тогда В = 90° – 60° =
= 30° (по свойству 1°); АС = АВ (свойство 2°; катет, лежащий против угла в 30°).

По  условию  АС + АВ  =  18 см;  АВ + АВ = 18 см;  1АВ  =  18 см, АВ = 12 см; значит, АС = 18 – 12 = 6 (см).

Ответ: АВ = 12 см; АС = 6 см.

3. Решить задачу № 260.

Ответ: D = С = 30°; М = 120°.

IV. Итоги урока.

Домашнее задание: изучить п. 34; повторить пункты 15–33; ответить на вопросы 10 и 11 на с. 90; решить №№ 256, 259.

Скачано с www.znanio.ru