Урок алгебры в 9 классе "Решение уравнений с одной переменной"

Тема урока « Обобщение по теме « Решение уравнений с одной переменной».
Цель урока: Обобщить знания учащихся о целых и дробных рациональных уравнениях.

Образовательные задачи: систематизировать знания и умения учащихся по применению методов решения целых и дробных рациональных уравнений, готовить учащихся к ГИА.

Развивающие: развивать умения наблюдать, сравнивать, обобщать, анализировать математические ситуации.
Воспитательные: воспитывать такие качества личности, как познавательная активность, самостоятельность, упорство в достижении цели.
Тип урока: обобщающий

Ход урока

Эпиграф к уроку «Весь смысл жизни заключается в бесконечном завоевании неизвестного, в вечном усилии познать большее»

1. Организационный момент. Мотивация. Сообщение темы и цели урока.

Сегодня у нас обобщающий урок по теме  «Уравнения с одной переменной»
Н.Е.Жуковский сказал: “В математике есть своя красота, как в живописи и поэзии”. Сегодня на уроке мы ещё раз увидим всю красоту такой математической структуры как уравнения. Ведь уравнения - одна из сквозных тем всего курса математики, проходящая красной линией с 1 по 11 класс. И нет в математике ничего изящнее, чем красиво решённое уравнение. В этом году вам предстоит сдавать экзамены, и математика обязательный предмет. Поэтому одной из задач нашего урока является подготовка  к экзамену. Девиз   урока   «Математика   учит   преодолевать   трудности   и   исправлять   собственные   ошибки» 

2.   Актуализация знаний учащихся по теме.

     Повторение теории по решению уравнений

• Что называется уравнением?

Ответ: Уравнение – это равенство, содержащее переменную, значение которой надо найти.

• Дайте определение корня уравнения

                       Ответ: Корень уравнения – это значение переменной, обращающее уравнение в   верное числовое равенство.

• Что значит решить уравнение?

Ответ: Решить уравнение – это значит найти все его корни или доказать что их нет.

• Какие уравнения называются равносильными?

          Ответ: Уравнения, имеющие одни и те же корни, называются равносильными.

• Сформулируйте свойства уравнений.

    Ответ:

ü  Если в уравнении перенести слагаемое из одной части в другую, изменив   его знак, то получится уравнение, равносильное данному;

ü  Если обе части уравнения умножить или разделить на одно и то же число, отличное от нуля, то получится уравнение, равносильное данному.

• Перечислите общие методы решения уравнений с одним неизвестным.

     Ответ: Разложение на множители, замена переменной, графический.

• Какие уравнения называются целыми, а какие дробными?

           Ответ:  

ü  Рациональные уравнения, в которых левая и правая части являются целыми выражениями, называются целыми.

ü  Рациональные уравнения, в которых левая или правая части являются дробными выражениями, называются дробными рациональными уравнениями.

• Назовите виды целых уравнений, их стандартный вид.    

Ответ:

а) Линейное;

б) квадратное;

в) уравнение высших порядков (биквадратным, возвратное, симметрическое);

г) уравнения содержащие модуль;

д) уравнения с параметром.

• Дайте алгоритм решения дробных рациональных уравнений.

Ответ:                         

1. Найти общий знаменатель дробей, входящих в уравнение;
2. Умножить обе части уравнения на общий знаменатель;
3. Решить полученное целое уравнение;
4. Исключить из его корней те, которые обращают в нуль общий знаменатель.

Мы знаем, что правильно выбранный метод часто

позволяет существенно упростить решение, поэтому все изученные нами методы

всегда нужно держать в зоне своего внимания, чтобы решать конкретные

уравнения наиболее подходящим методом.

·         Определить способ решения уравнения

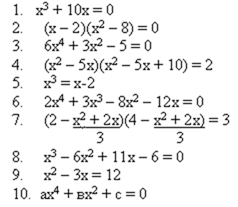
II. Основная часть

Но знания теории теряет свою силу, если они не находят своего применения на практике. Первая индивидуальная работа на сегодня – это тестовая работа на знание теории 

Тест

1. Определи степень уравнения  x(x²-4)=0:

a. Уравнение первой степени

b. Уравнение второй степени

c. Уравнение третьей степени

d. Степень равна нулю

2. Определи вид уравнения         :

a. Квадратное

b. Дробное рациональное

c. Целое

3.Корнями какого уравнения являются числа -2; 0; 2:

a.  х³ – 4х = 0

b.  х (х² – 4х + 4) = 0

c.  х³ – 2х = 0

d. х³ – 4х + 4 = 0

4.Выберите уравнение из списка, которое не имеет корней:

a. (x+1)²=0

b. x²+1=0

       c. x²+x=0

d. x²- x=0

5.Найди корни уравнения: х (х – 2) (х + 3) (5 – х) = 0

a.       0; -3; 2; 5

2. 0; 2; 3; 5
3. -2;-5; 3
4. 0;2; 3; -5

6.Найди корни уравнения: 3x²+x=0

a.       0; 

2. 0; -
3. Корней нет

Сколько корней имеет уравнение 5х²+75=0 ?

           а) один корень

б) два корня

в) не имеет корней

с) имеет бесконечное множество корней

  7. Распределите уравнения на две группы:  Целые уравнения  и дробные рациональные уравнения

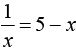
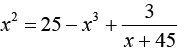
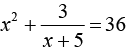
8. Какую замену можно сделать, чтобы решить уравнение

9. Какие из данных уравнений являются биквадратными?

10. При каких значениях переменной дробь 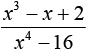 не имеет смысла?

2; -2; 16; 0

11. Найдите корень уравнения .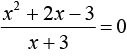

12. Чему равна сумма корней уравнения 

0; 4;-3; 3.

IV. Закрепление умений и навыков решать целые уравнения, используя при этом различные приемы и методы.

Самостоятельная работа «Уравнения с одной переменной»

V.Домашнее задание:

№358 (в,ж),364

VI.Итог урока. Рефлексия.

Итак, сегодня на уроке мы обобщили такую важную тему, как решение уравнений. Конечно, школьная линия уравнений на этом не заканчивается, но полученные на этом уроке знания найдут своё применение   сдаче экзамена   в 9 классе и в 11классе  , и в дальнейшем при изучении математики.

А закончить урок мне хочется афоризмом Ж.Даламбера:

«Алгебра щедра. Зачастую она даёт человеку больше, чем он у неё спрашивает».

Уравнение - это золотой ключ, открывающий все математические сезамы».                                    

Станислав Коваль

Всего хорошего! Урок закончен.

Мне приходиться делить своё время между политикой и уравнениями. Однако уравнение, по-моему, гораздо важнее, потому что политика существует только для данного момента, а уравнение будет существовать вечно.

                                                                                                   Эйнштейн А