
Александрова Светлана Федоровна,
Учитель математики
МБОУ г. Иркутска СОШ №1
Урок математики
с использованием технологии развития критического мышления
7 класс
Тема урока: «Умножение многочлена на многочлен».
Тип урока: урок открытия нового знания.
Цель урока: создать условия для усвоения и осмысления алгоритма умножения многочлена на многочлен.
Деятельностная цель: формирование способности обучающихся к новому способу действия – умножению многочлена на многочлен.
Образовательная цель: совершенствование умений складывать, вычитать многочлены, умножать одночлены на многочлен, расширение способов преобразований выражений при изучении темы «Многочлены» за счет включения в нее алгоритма умножения многочлена на многочлен.
Познавательная задача: организовать деятельность учащихся по совершенствованию умений преобразовывать многочлены, формированию умения умножать многочлен на многочлен.
Развивающая задача: продолжить формирование умений и навыков работы с научным текстом, умения анализировать информацию, способность ее оценивать, использовать; развитие логического мышления, сознательного восприятия учебного материала.
Воспитательная задача: повышение интереса к процессу обучения и активного восприятия учебного материала, развитие коммуникативных навыков работы в парах, группах.
Практическая задача: формирование навыков критического мышления как творческого, аналитического, последовательного и структурированного мышления, формирование навыков самообразования.
Планируемые образовательные результаты:
Предметные: расширение понятийной базы по теме «Многочлены» за счет включения в неё новых элементов: умножение многочлена на многочлен; отработка правила умножения многочлена на многочлен.
Метапредметные: представлять конкретное содержание и сообщать его в устной и письменной форме; вступать в диалог, а также участвовать в коллективном обсуждении проблем; умение аргументировать свою точку зрения, спорить и отстаивать свою позицию; поиск и выделение необходимой информации; умение структурировать знания; выдвижение гипотез и их обоснование; умение наблюдать; умение обобщать полученные данные.
Личностные: проявлять дисциплинированность, трудолюбие и упорство в достижении поставленных целей; умение бескорыстно оказывать помощь своим сверстникам, находить с ними общий язык; формирование активности; развитие коммуникативных способностей обучающихся; формирование у обучающихся познавательного интереса к предмету.
Форма урока: проблемный урок с использованием технологии развития критического мышления (ТРКМ).
Используемые технологии: технология развития критического мышления.
Используемые приемы: мозговой штурм, «верные, неверные утверждения», ИНСЕРТ.
Оборудование: презентация PowerPoint, раздаточный материал.
Ход урока:
1. Мотивирование к учебной деятельности (3мин.).
Добрый день! Приятно видеть всех вас в классе, и я очень надеюсь, что сегодня у нас состоится полезный, продуктивный урок. Сегодня вы будете работать в парах, в группах, индивидуально. Каждый из вас будет осуществлять самооценку своей деятельности на уроке, используя листы самооценки и критерии оценивания. (Приложение №1)
Теоретическая разминка (мозговой штурм)
Учащийся отвечает на 5 вопросов, которые задают одноклассники.
На данном этапе предпочтительна фронтальная форма деятельности. Все дети втягиваются в процесс обучения, приобретают умения совершенствовать уже имеющиеся знания, а значит, осознают познавательную задачу.
Примерные вопросы:
1. Какое выражение называют одночленом?
2. Какой одночлен называют одночленом стандартного вида?
3. Какой многочлен называют многочленом стандартного вида?
4. Что называют коэффициентом одночлена?
5. Что такое многочлен?
6. Что является членами многочлена?
7. Какие одночлены называются подобными членами?
8. Как определить степень многочлена?
9. Сформулируйте правило умножения одночленов.
10. Сформулируйте правило умножения одночлена на многочлен.
2. Актуализация и фиксирование индивидуального затруднения в пробном учебном действии (3 мин.).
- Над освоением какой темы мы с вами работаем? («Многочлены»)
- Что вы уже знаете? (понятия многочлена, одночлена, многочлена стандартного вида, подобных членов многочлена, степени многочлена...)
- Что умеете? (приводить одночлены и многочлены к стандартному виду, определять степень многочлена, складывать, вычитать многочлены, умножать одночлен на многочлен...).
- Конечно, это лишь начало, вам предстоит еще многому научиться. Но чтобы двигаться дальше посмотрим, что вы действительно знаете и умеете.
Устная работа (задания на карточках).
1. Упростите: -7х2+7х2+х2 ; 13 - 5а - а; 3х+5+8х
2. Выполните умножение: 3ху · 5х2у; -2х2у3· 4ху5; - 0,8х2у3 · (-10х3у).
3. Раскройте скобки: 7(х – у); 3х (х2+ 4у3); 5х2 (2х – 3х2)
- Какие действия выполняли в заданиях 1, 2 и 3? (1 – приведение подобных, 2 - умножение одночлена на одночлен, 3 - умножение одночлена на многочлен).
- Где практически мы применяем эти правила? (упрощение выражений, решение уравнений, приведение многочленов к стандартному виду)
3. Выявление места и причины затруднения (4 мин.).
Самостоятельная работа.
Ученикам предлагается упростить выражения.
Упростите выражения:
|
I вариант |
II вариант |
|
1) 2 a2 (a-2b) |
1) 5х(2х2+1) |
|
2) 8x-6y+7x-y |
2) 5b - 2c - 6c - 3b |
|
3) 5x ∙ 3x3 |
3) 5 x3 ∙ 7x6 |
|
4) -6ax3 ∙ 9x2 |
4) -2a2b ∙ 4a3 |
|
5) (6x2y2-3y2-7x2) ∙5x2y2 |
5) -4ху2(2х3-5у2+3ху) |
|
6) (2а+3) ∙ (3а - 2) |
6) (4х+7) ∙ (2х-3) |
По окончании работы ученики проверяют правильность решения заданий, проводят самооценку (за каждый правильный ответ – 1 балл). (Приложение №2)
|
Верные ответы |
|
|
I вариант |
II вариант |
|
1) 2a3 -4a2b |
1) 10х3 +5х |
|
2) 15x-7y |
2) 2b - 8c |
|
3) 15x4 |
3) 35 x9 |
|
4) -54ax5 |
4) -8a5b |
|
5) 30x4y4-15x2y4-35x4y2 |
5) -8х4у2 +20ху4- 12х2у3 |
|
6) 6а2+5а - 6 |
6) 8х2+2х - 21 |
- С какими трудностями вы встретились при выполнении заданий?
- Какое задание вы не смогли выполнить? (6 задание)
- Что в нем необходимо было выполнить? (умножить многочлен на многочлен)
4. Формулировка темы урока, цели и задач (3 мин.).
- Как вы думаете, чем мы будем заниматься на уроке?
- Можете ли вы сформулировать тему урока? («Умножение многочлена на многочлен»).
- Можете ли вы сейчас это сделать верно?
- Что для этого нам необходимо знать и уметь? (знать алгоритм умножения многочлена на многочлен и научиться его применять)
- Какие цели перед собой вы можете поставить? (ученики формулируют цели урока: научиться умножать многочлен на многочлен, преобразовывать выражения, применяя правило умножения многочлена на многочлен)
Сегодня на уроке вы сформулируете алгоритм умножения многочлена на многочлен и научитесь его применять.
Предлагаю спланировать учебную работу следующим образом:
- Изучить текст §11 п.29 стр.136 в рабочих листах с извлечением материала параграфа (в них можно свободно делать рукописные пометки), используя прием ИНСЕРТ - прием смысловой маркировки текста.
V - уже знал (а)
+ - новое
– - думал (а) иначе
? - не понял (а)
- Заполнить таблицу «Верите ли вы, что…»
- Сформулировать алгоритм умножения многочлена на многочлен.
- Поработать с обучающей карточкой.
- Выполнить предложенное задание и объяснить его выполнение одноклассникам.
- Закрепить полученный алгоритм при выполнении преобразований многочленов.
5. Изучение нового материала (9 мин.).
На столах у вас лежат карточки с вопросами. Все они начинаются со слов «Верите ли вы, что…». Ответ на вопрос может быть только «да» или «нет». Если «да», то справа от вопроса в первом столбце поставьте знак «+», если «нет», то знак «-». Если сомневаетесь, поставьте знак «?». Работая над текстом §11 п.29, заполните столбец А таблицы. Работайте в парах. (Приложение №3)
|
№ п/п |
Вопросы: |
А |
Б |
|
Верите ли вы, что… |
|||
|
1. |
Умножая многочлен на многочлен, применяем правило умножения одночлена на многочлен |
|
+ |
|
2. |
Умножив многочлен на многочлен, мы получили одночлен |
|
- |
|
3. |
Умножив двучлен на двучлен, получим многочлен из 4 одночленов |
|
+ |
|
4. |
Умножив двучлен на трехчлен, получим многочлен из 5 одночленов |
|
- |
|
5. |
Чтобы умножить многочлен на многочлен, надо каждый член одного многочлена сложить с каждым членом другого многочлена |
|
- |
|
6. |
Ещё учёные Древней Греции, используя правила вычисления площадей, получали многочлены |
|
+ |
|
7. |
Алгебра, оперировавшая не числами, а отрезками, площадями, объёмами, названа геометрической алгеброй |
|
+ |
|
8. |
Многочлены играют важную роль в алгебраической геометрии, применяются для кодирования информации |
|
+ |
Работа над текстом §11 п.29 стр.136, текстом в рабочих листах. (Приложение №4)
Рабочий лист.
Умножение многочлена на многочлен
Рассмотрим, как можно умножить многочлен на многочлен на примере произведения
(а + b)(с + d).
Обозначим двучлен а + b какой-либо одной буквой, например буквой х, и раскроем скобки в произведении х(с + d) по правилу умножения одночлена на многочлен. Затем букву х заменим двучленом а + b и опять раскроем скобки. Получим
(а + b)(с + d) = х(с + d) = хс + х d = (а + b)с + (а + b) d = ас + bс + аd + bd.
Таким образом,
![]()
(а + b)(с + d) = ас + bс + аd + bd.
Каждый член второго многочлена умножили на каждый член первого многочлена
![]() А можно так:
А можно так:

![]()
![]() (а + b)(с + d) = ас + аd + bс + bd
(а + b)(с + d) = ас + аd + bс + bd
Каждый член первого многочлена умножили на каждый член второго многочлена
Умножив многочлен на многочлен, мы получили многочлен.
Произведение двух многочленов всегда можно представить в виде многочлена.
Чтобы умножить многочлен на многочлен, надо каждый член одного многочлена умножить на каждый член другого и полученные произведения сложить.
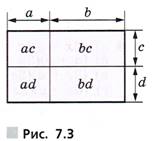
С помощью рисунка 7.3 полученное равенство для положительных а, b, с и d можно показать геометрически: площадь прямоугольника со сторонами а + b и с + d равна сумме площадей четырёх прямоугольников, стороны которых равны а и с, b и с, а и d, b и d.
Интересно, что именно так, используя правила вычисления площадей, получали подобные равенства учёные Древней Греции. Величины они изображали отрезками, произведение аb называли прямоугольником, выражение а2 — квадратом. Такая алгебра, оперировавшая не числами, а отрезками, площадями, объёмами, т.е. выраженная геометрическим языком, много веков спустя была названа геометрической алгеброй.
Одну из главных ролей многочлены играют в алгебраической геометрии, изучающей множества, определенные как решения систем многочленов, т.к. они обладают свойствами, необходимыми при преобразовании коэффициентов умножения многочленов.
Многочлены содержат в себе символьные исчисления, которые с 20 века стали использовать как способ передачи данных. Была предложена идея кодирования сообщения, которую успешно используют и в настоящее время.
Обсуждение текста параграфа §11 п.29 учебника.
- Что вы уже знали, что для вас – новое, а что вы не поняли?
- Как умножить многочлен на многочлен?
- Как вы думаете, разные результаты получатся, если один ученик каждый член второго многочлена умножил на каждый член первого многочлена, а второй ученик каждый член первого многочлена умножил на каждый член второго многочлена?
- Что делать, если при умножении получатся подобные одночлены?
- Давайте попробуем сформулировать алгоритм умножения многочлен на многочлен
Алгоритм умножения многочлена на многочлен.
1. Каждый член первого многочлена умножаем на каждый член второго многочлена
2. Полученные произведения складываем
3. Приводим подобные слагаемые
6. Первичное закрепление с проговариванием во внешней речи (6 мин.).
Обучающиеся приступают к умножению многочленов в группах с проговариванием алгоритма решения вслух, а затем один ученик из группы показывает решение у доски по алгоритму. (Приложение №5)
Обучающая карточка №1
Тема: «Умножение многочлена на многочлен»
Алгоритм действий:
1. Каждый член первого многочлена умножаем на каждый член второго многочлена
2. Полученные произведения складываем
3. Приводим подобные слагаемые
![]() Пример. Умножьте многочлены:
Пример. Умножьте многочлены:
![]()
![]() (х + 3)(х
+ 2) = х2 + 2х + 3х + 6= х2 + 5х + 6
(х + 3)(х
+ 2) = х2 + 2х + 3х + 6= х2 + 5х + 6
Задание. Умножьте многочлены: (х + 3)(х + 1)
Обучающая карточка №2
Тема: «Умножение многочлена на многочлен»
Алгоритм действий:
1. Каждый член первого многочлена умножаем на каждый член второго многочлена
2. Полученные произведения складываем
3. Приводим подобные слагаемые
![]() Пример. Умножьте многочлены:
Пример. Умножьте многочлены:
![]()
![]() (b + 3)( b - 2) = b 2 - 2 b + 3 b - 6= b 2 + b - 6
(b + 3)( b - 2) = b 2 - 2 b + 3 b - 6= b 2 + b - 6
Задание. Умножьте многочлены: (b + 5)( b - 2)
Обучающая карточка №3
Тема: «Умножение многочлена на многочлен»
Алгоритм действий:
1. Каждый член первого многочлена умножаем на каждый член второго многочлена
2. Полученные произведения складываем
3. Приводим подобные слагаемые
![]() Пример. Умножьте многочлены:
Пример. Умножьте многочлены:
![]() (2х + 1)(2х
+ 5) = 4х2 + 10х + 2х + 5= 4х2 + 12х + 5
(2х + 1)(2х
+ 5) = 4х2 + 10х + 2х + 5= 4х2 + 12х + 5
Задание. Умножьте многочлены: (3х + 2)(х + 3)
Обучающая карточка №4
Тема: «Умножение многочлена на многочлен»
Алгоритм действий:
1. Каждый член первого многочлена умножаем на каждый член второго многочлена
2. Полученные произведения складываем
3. Приводим подобные слагаемые
![]() Пример. Умножьте многочлены:
Пример. Умножьте многочлены:
![]()
![]() (5у - 1)(у - 3)
= 5у2 –15у – у + 3= 5у2 –16у + 3
(5у - 1)(у - 3)
= 5у2 –15у – у + 3= 5у2 –16у + 3
Задание. Умножьте многочлены: (y - 4)(3у -4)
Ответы: 1) х2 + 4х + 3 2) b 2 + 3b – 10 3) 3х2 + 11х + 6 4) 3у2 –16у + 16
Обсуждение решений.
- Какие затруднения при умножении многочленов испытали?
- На каких этапах выполнения заданий можно допустить ошибки?
7. Закрепление (6 мин.).
Самостоятельная работа.
Решение №677 (а, б, в), №678 (а, б, в)
Ответы:
|
№677 (а, б,в) |
№678 (а, б,в) |
|
(2m+1)(2m+5) = 4m2+12m+5 |
(2x-y)(x+y) = 2x2 + xy – y2 |
|
(3x+2)(x+3) = 3x2+11x+6 |
(a+b)(2a+3b) = 2a2+5ab+3b2 |
|
(5m-1)(m+1) = 5m2 + 4m - 1 |
(3c+a)(2c-a) = 6c2 - ac - a2 |
- Какие затруднения при умножении многочленов испытали?
- На каких этапах выполнения заданий можно допустить ошибки?
- Что нужно сделать, чтобы уверенно выполнять умножение многочленов?
Возвратимся к заданию 6 в самостоятельной работе, которую мы выполняли в начале урока и попробуем решить задания.
(2а+3) ∙ (3а - 2) = 6а2 – 4а +9а – 6 = 6а2+5а - 6
(4х+7) ∙ (2х-3) = 8х2 – 12х+ 14х – 21 = 8х2+2х – 21
8. Домашнее задание (2 мин.):
§ 11 п.29, №677 (г, д, е), №678 (г, д, е), №679(а, б, в)
В дополнительной литературе или с помощью Интернет ресурсов постарайтесь найти области применения многочленов.
9. Рефлексия (2 мин.). Подведем итоги.
- Какую задачу пришлось решать сегодня на уроке?
- Как умножить многочлен на многочлен?
- Какие правила, способы действий нужно знать, чтобы правильно выполнять умножение многочлена на многочлен?
Нам предстоит еще на двух уроках совершенствовать умения умножать многочлены, и вы, ребята, разовьете свои умения преобразовывать многочлены.
Эмоциональная рефлексия.
Перед вами лежат ключи определенного цвета. Поднимите ключ:
- зеленый, если вам все понятно по теме урока, вы были успешны;
- желтый, если у вас возникли трудности, но вы их преодолевали;
- красный, если вы многое не поняли и у вас остались вопросы.
Самооценка (2мин.).
Лист самооценки _________________________
Фамилия, имя
|
№ п/п |
Вид работы |
Количество баллов |
Критерии самооценки
«3» - 11- 16 баллов «4» - 17-21 балла «5» - 22 и более баллов |
|
|
1. |
Теоретическая разминка (за каждый верный ответ по 1 б.) |
|
||
|
2. |
Самостоятельная работа «Упростите выражения» (до 5 б.) |
|
||
|
3. |
Заполнение таблицы «Верите ли вы, что…» (до 8 б.) |
|
||
|
Итого баллов: |
||||
|
4. |
Работа с обучающей карточкой (2 б.), на месте – 1б. за каждый пример |
|
||
|
5. |
Самостоятельная работа. Решение упражнений №677 (а, б, в), №678 (а, б, в) + задание 6 (за каждое верно выполненное задание – 2б) |
|
||
|
Отметка: |
Литература.
1. Алгебра 7 класс : учеб. для общеобразоват. учреждений Ю.Н. Макарычев, Н.Г. Миндюк,
С. Б.Суворова под редакцией С.А. Теляковского; М.: Просвещение, 2018г.
Интернет ресурсы.
1. http://www.13min.ru/video-uroki/video-uroki-matematika-mnogochleny/
2. http://www.ipo.spb.ru/iumk2/MATH_XXI-10/Modules/M_1.2/M_1.2.html
Директор школы Багмат Л.Н.
Приложение №1
Лист самооценки _________________________
Фамилия, имя
|
№ п/п |
Вид работы |
Количество баллов |
Критерии самооценки
«3» - 11- 16 баллов «4» - 17-21 балла «5» - 22 и более баллов |
|
|
1. |
Теоретическая разминка (за каждый верный ответ по 1 б.) |
|
||
|
2. |
Самостоятельная работа «Упростите выражения» (до 5 б.) |
|
||
|
3. |
Заполнение таблицы «Верите ли вы, что…» (до 8 б.) |
|
||
|
Итого баллов: |
||||
|
4. |
Работа с обучающей карточкой (2 б.), на месте – 1б. за каждый пример |
|
||
|
5. |
Решение упражнений №677 (а, б, в), №678 (а, б, в) + задание 6 (за каждое верно выполненное задание – 2б)
|
|
||
|
Отметка: |
Приложение №2
Упростите выражения:
|
I вариант |
II вариант |
|
1) 2 a2 (a-2b) |
1) 5х(2х2+1) |
|
2) 8x-6y+7x-y |
2) 5b - 2c - 6c - 3b |
|
3) 5x ∙ 3x3 |
3) 5 x3 ∙ 7x6 |
|
4) -6ax3 ∙ 9x2 |
4) -2a2b ∙ 4a3 |
|
5) (6x2y2-3y2-7x2) ∙5x2y2 |
5) -4ху2(2х3-5у2+3ху) |
|
6) (2а+3) ∙ (3а - 2) |
6) (4х+7) ∙ (2х-3) |
|
Верные ответы |
|
|
I вариант |
II вариант |
|
1) 2a3 -4a2b |
1) 10х3 +5х |
|
2) 15x-7y |
2) 2b - 8c |
|
3) 15x4 |
3) 35 x9 |
|
4) -54ax5 |
4) -8a5b |
|
5) 30x4y4-15x2y4-35x4y2 |
5) -8х4у2 +20ху4- 12х2у3 |
|
6) 6а2+5а - 6 |
6) 8х2+2х - 21 |
Приложение №3
|
№ п/п |
Вопросы: |
А |
Б |
|
Верите ли вы, что… |
|||
|
1. |
Умножая многочлен на многочлен, применяем правило умножения одночлена на многочлен |
|
|
|
2. |
Умножив многочлен на многочлен, мы получили одночлен |
|
|
|
3. |
Умножив двучлен на двучлен, получим многочлен из 4 одночленов |
|
|
|
4. |
Умножив двучлен на трехчлен, получим многочлен из 5 одночленов |
|
|
|
5. |
Чтобы умножить многочлен на многочлен, надо каждый член одного многочлена сложить с каждым членом другого многочлена |
|
|
|
6. |
Ещё учёные Древней Греции, используя правила вычисления площадей получали многочлены |
|
|
|
7. |
Алгебра, оперировавшая не числами, а отрезками, площадями, объёмами названа геометрической алгеброй |
|
|
|
8. |
Многочлены играют важную роль в алгебраической геометрии, применяются для кодирования информации |
|
|
Приложение №4
Рабочий лист.
Умножение многочлена на многочлен
Рассмотрим, как можно умножить многочлен на многочлен на примере произведения
(а + b)(с + d).
Обозначим двучлен а + b какой-либо одной буквой, например буквой х, и раскроем скобки в произведении х(с + d) по правилу умножения одночлена на многочлен. Затем букву х заменим двучленом а + b и опять раскроем скобки. Получим
(а + b)(с + d) = х(с + d) = хс + х d = (а + b)с + (а + b) d = ас + bс + аd + bd.
Таким образом,
![]()
(а + b)(с + d) = ас + bс + аd + bd.
Каждый член второго многочлена умножили на каждый член первого многочлена
![]() А можно так:
А можно так:
 |
![]()
![]() (а + b)(с + d) = ас + аd + bс + bd.
(а + b)(с + d) = ас + аd + bс + bd.
Каждый член первого многочлена умножили на каждый член второго многочлена
Умножив многочлен на многочлен, мы получили многочлен.
Произведение двух многочленов всегда можно представить в виде многочлена.
Чтобы умножить многочлен на многочлен, надо каждый член одного многочлена умножить на каждый член другого и полученные произведения сложить.
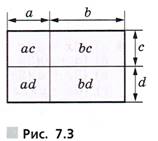
С помощью рисунка 7.3 полученное равенство для положительных а, b, с и d можно показать геометрически: площадь прямоугольника со сторонами а + b и с + d равна сумме площадей четырёх прямоугольников, стороны которых равны а и с, b и с, а и d, b и d.
Интересно, что именно так, используя правила вычисления площадей, получали подобные равенства учёные Древней Греции. Величины они изображали отрезками, произведение аb называли прямоугольником, выражение а2 — квадратом. Такая алгебра, оперировавшая не числами, а отрезками, площадями, объёмами, т.е. выраженная геометрическим языком, много веков спустя была названа геометрической алгеброй.
Одну из главных ролей многочлены играют в алгебраической геометрии, изучающей множества, определенные как решения систем многочленов, т.к. они обладают свойствами, необходимыми при преобразовании коэффициентов умножения многочленов.
Многочлены содержат в себе символьные исчисления, которые с 20 века стали использовать как способ передачи данных. Была предложена идея кодирования сообщения, которую успешно используют и в настоящее время.
Приложение №5
Обучающая карточка №1
Тема: «Умножение многочлена на многочлен»
Алгоритм действий:
1. Каждый член первого многочлена умножаем на каждый член второго многочлена
2. Полученные произведения складываем
3. Приводим подобные слагаемые
![]() Пример. Умножьте многочлены:
Пример. Умножьте многочлены:
![]()
![]() (х + 3)(х
+ 2) = х2 + 2х + 3х + 6= х2 + 5х + 6
(х + 3)(х
+ 2) = х2 + 2х + 3х + 6= х2 + 5х + 6
Задание. Умножьте многочлены: (х + 3)(х + 1)
Обучающая карточка №2
Тема: «Умножение многочлена на многочлен»
Алгоритм действий:
1. Каждый член первого многочлена умножаем на каждый член второго многочлена
2. Полученные произведения складываем
3. Приводим подобные слагаемые
![]() Пример. Умножьте многочлены:
Пример. Умножьте многочлены:
![]()
![]() (b + 3)( b - 2) = b 2 - 2 b + 3 b - 6= b 2 + b - 6
(b + 3)( b - 2) = b 2 - 2 b + 3 b - 6= b 2 + b - 6
Задание. Умножьте многочлены: (b + 5)( b - 2)
Обучающая карточка №3
Тема: «Умножение многочлена на многочлен»
Алгоритм действий:
1. Каждый член первого многочлена умножаем на каждый член второго многочлена
2. Полученные произведения складываем
3. Приводим подобные слагаемые
![]() Пример. Умножьте многочлены:
Пример. Умножьте многочлены:
![]() (2х + 1)(2х
+ 5) = 4х2 + 10х + 2х + 5= 4х2 + 12х + 5
(2х + 1)(2х
+ 5) = 4х2 + 10х + 2х + 5= 4х2 + 12х + 5
Задание. Умножьте многочлены: (3х + 2)(х + 3)
Обучающая карточка №4
Тема: «Умножение многочлена на многочлен»
Алгоритм действий:
1. Каждый член первого многочлена умножаем на каждый член второго многочлена
2. Полученные произведения складываем
3. Приводим подобные слагаемые
![]() Пример. Умножьте многочлены:
Пример. Умножьте многочлены:
![]()
![]() (5у - 1)(у - 3)
= 5у2 –15у – у + 3= 5у2 –16у + 3
(5у - 1)(у - 3)
= 5у2 –15у – у + 3= 5у2 –16у + 3
Задание. Умножьте многочлены: (y - 4)(3у -4)
Ответы: 1) х2 + 4х + 3 2) b 2 + 3b – 10 3) 3х2 + 11х + 6 4) 3у2 –16у + 16
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.