Урок по решению исследовательской задачи в компьютерной программе «Живая геометрия» по теме: «Сечение многогранников»
Урок по решению исследовательской задачи в компьютерной программе «Живая геометрия» по теме: «Сечение многогранников»
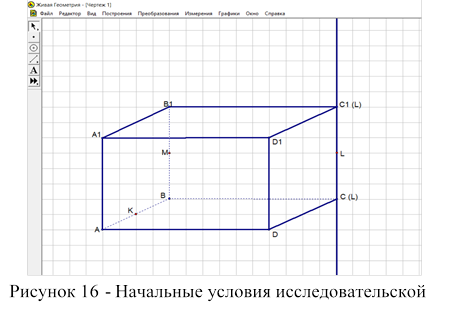
Ученикам 10-го класса предлагается задача: определить вид сечения параллелепипеда, в котором 2 точки М и К середины граней ВВ1 и АВ соответственно, а точка L движется по прямой содержащей ребро СС1. [17]
И исследуйте при каком расположении точки L сечение МКL будет иметь вид: а) трапеция; в) параллелограмм; г) треугольник.
Учитель подсказывает что необходимо построить хотя бы 3 сечения, так чтобы точка L:
1) Совпадала с точкой С1
2) Лежала между точками С1 и С (частный случай середина СС1)
3) Совпадала с точкой С
 |
Предполагается индивидуальная форма работы над задачей. В компьютерной программе «Живая математика» учащиеся строят произвольный параллелепипед ABCDA1B1C1D1, на ВВ1 и АВ отмечают середины граней М и К соответственно и точку L, которая движется по прямой содержащей ребро СС1 (рис 16).
Изменяя положение точки L (по подсказкам учителя) и достраивая каждый раз сечение параллелепипеда, учащиеся высказывают гипотезы о виде сечения параллелепипеда:
1)
 |
Если точка L совпадает с точкой С1, то сечение – трапеция (рис. 17).
2)
 |
Если точка L лежит между точками С1 и С (частный случай середина СС1), то сечение – параллелограмм. (рис. 18)
3)
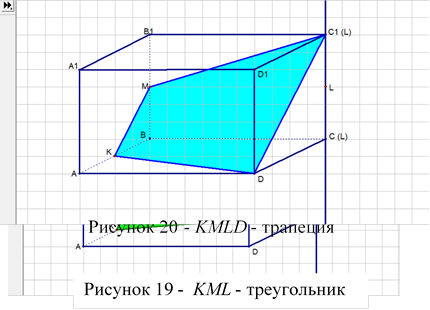
Если
точка L совпадает
с точкой С, то сечение – треугольник (рис. 19).
 |
Первая гипотеза: “KMLD – трапеция” доказывается на уроке методом эвристической беседы (рис. 20).
Учитель: Давайте посмотрим, как мы строили данную фигуру. Почему мы соединили точки К и М ; М и С1(L)?
Ученики: Так как обе пары точек находятся в одной плоскости.
Учитель: Как мы построили прямую LD?
Ученики: Секущая плоскость пересекает параллельные грани по параллельным отрезкам, поэтому KM ççLD
Учитель: Почему мы соединили точки D и K?
Ученики: Так как они находятся в одной плоскости
Учитель: Какую фигуру мы в итоге получили и почему?
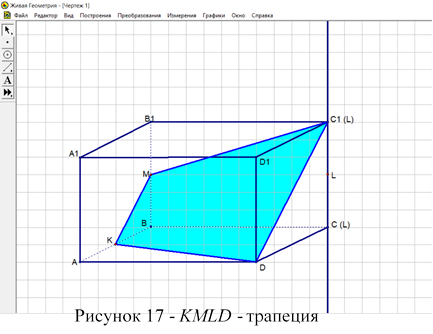
Ученики: Сечением является трапеция. Трапеция – четырехугольник, у которого две стороны параллельны, а две другие не параллельны, что мы и можем увидеть исходя из построения.
Ученики оформляют описание построения в тетрадях:
1. Соединим КМ – т.к. в одной плоскости
2. Соединим ML – т.к. в одной плоскости
3. Проведем через точку L прямую параллельную МК (по правилу построения параллельных отрезков в параллельных плоскостях)
LD ççKM
4. Соединим DK – т.к. в одной плоскости
KMLD – искомое сечение – трапеция (LD ççKM).
Далее класс делится на две группы. Каждая группа получает задание доказать одну из гипотез:
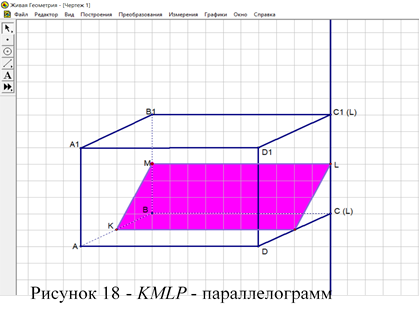
· Если точка L лежит между точками С1 и С (частный случай середина СС1), то сечение – параллелограмм.
· Если точка L совпадает с точкой С, то сечение – треугольник.
Затем представитель каждой группы выходит к доске и показывает свой чертеж и построение.
Для более сильного класса можно предложить: определить вид сечения параллелепипеда, в котором 2 точки М и К середины граней ВВ1 и АВ соответственно, а точка L движется по прямой содержащей ребро СС1. Причем точка LÎCC1 и может находиться на ребре, а может выходить за пределы ребра СС1.
В итоге одно построение так же рассматривается сообща, а в последствии можно разделить класс так же на 2 группы, но теперь у каждой группы будет уже 2 задания разного уровня сложности.
Домашнее задание: составить две задачи на построение сечений многогранников с использованием полученных знаний.
Подведение итогов урока, выставление оценок.
Урок по решению исследовательской задачи в компьютерной программе «Живая геометрия» по теме: «Сечение многогранников»
Изменяя положение точки L (по подсказкам учителя) и достраивая каждый раз сечение параллелепипеда, учащиеся высказывают гипотезы о виде сечения параллелепипеда: 1)
Первая гипотеза: “ K MLD – трапеция” доказывается на уроке методом эвристической беседы (рис
Ученики: Сечением является трапеция
© ООО «Знанио»
С вами с 2009 года.
