Урок по теме Решение задач разными способами 5 класс

Тема урока: решение задачи несколькими способами

Тип урока: обобщение полученных знаний

Метод обучения: исследовательский

Планируемые результаты:

Личностные: оценивать процесс и результат своей работы, а также оценивать работу своих одноклассников

.Метапредметные: будут учиться искать и выделять необходимую информацию, анализировать, сравнивать, классифицировать объекты по выделенным признакам, учиться ставить учебную задачу; планировать свою деятельность, сотрудничать с учителем и одноклассниками, оценивать действия партнёров по работе

.Предметные: учащиеся научатся применять правила о порядке выполнения действий.

Проблема:  Сколькими способами можно решить одну и ту же задачу? А зачем мне нужно знать разные способы решения?

Ход урока

Предполагаемые ответы учащихся:

·         для того чтобы найти наиболее рациональное решение;

·         поиск рационального (краткого, «красивого») решения – это увлекательное занятие и неплохая «зарядка для ума».

 

Задача: В трех ящиках 127 кг яблок. Когда из первого ящика взяли 21 кг, из второго – 9 кг, а из третьего – 7 кг, во всех ящиках яблок стало поровну. Сколько килограммов яблок было в первом ящике первоначально?

 

                          Решение:

1 случай: 

    Составим краткую запись задачи.

             Было                  взяли            осталось

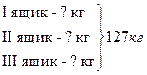
                поровну

  

2 случай: схематический чертеж задачи.

 

 1 способ

1) 21 + 9 = 30 (кг) – взяли яблок  из I и II ящиков

2) 30 + 7 = 37 (кг) – взяли яблок из трех ящиков

3) 127 – 37 = 90 (кг) – осталось яблок в трех ящиках

4) 90 : 3 = 30 (кг) – осталось яблок в каждом ящике

5) 30 + 21 = 51 (кг) – было яблок в первом ящике первоначально

 

 

    2 способ

1) 21 +7 = 28 (кг) – взяли яблок из I и III ящиков

2) 28 + 9 – 37 (кг) – взяли яблок из трех ящиков

3) 127 – 37 = 90 (кг) – осталось яблок в трех ящиках

4) 90 : 3 = 30 (кг) – осталось яблок в каждом ящике

5) 30 + 21 = 51 (кг) – было яблок в первом ящике первоначально

 

 

 

  3 способ

1) 9 + 7 = 16 (кг) – взяли яблок из II и III ящиков

2) 16 + 21 = 37 (кг) – взяли яблок из трех ящиков

3) 127 – 37 = 90 (кг) – осталось яблок в трех ящиках

4) 90 : 3 = 30 (кг) – осталось яблок в каждом ящике

5) 30 + 21 = 51 (кг) – было яблок в первом ящике первоначально

 

 

 

 Что же служит теоретической основой разных способов решения этой задачи?

Чтобы узнать, сколько килограммов яблок осталось во всех трех ящиках, нужно от числа, выражающего исходное количество яблок, отнять число, выражающее количество яблок, которое взяли из трех ящиков. Чтобы узнать, сколько всего яблок взяли, надо сложить три числа, т.е. найти сумму 21+ 9 + 7. А это можно сделать по-разному, преобразовывая данное выражение в тождественно равное на основе арифметических действий:

 (21 + 9) +7 = (21 + 7) + 9 = (7 + 9) + 21.

 Эти преобразования и определили три способа решения задачи, которые легко найти, используя для нахождения остатка яблок в трех ящиках буквы. Обозначим буквой  m – количество яблок во всех трех корзинах, буквами a, b, c – количество яблок, взятого из первого, второго и третьего ящиков соответственно, а буквой p – остаток яблок в трех ящиках, тогда получим: 

                      p  =  m – (a+  b + c).

 Найти значение последнего выражения можно шестнадцатью способами, используя свойства сложения и вычитания.

1. m – ((a+  b) + c)

2. m – (a+ ( b + c))

3. m – (b + (a + c))

4. m – (a+  b + c)

5. m – a –  b – c

6. m – a –  c – b

7. m – b – a– c

8. m – b – c – a

9. m – c – a – b

10. m – c – b –  a 

11.  m –a –  (b + c)

12.  m – b –  (a + c)

13.  m – c –  (a + b)

14. m – ( a + b) –  c

15 m – (a + c) –  b

16. m – (b + c) –  a

 

 А это означает, что задача имеет 16 способов решения. Во всех случаях сначала мы определяем, сколько всего яблок осталось после того, когда из каждого ящика взяли определенное число килограммов.

 

   4 способ

1) 21 + 9 + 7 = 37 (кг) – взяли яблок из трех ящиков

2) 127 – 37 = 90 (кг) – осталось яблок в трех ящиках

3) 90 : 3 = 30 (кг) – осталось яблок в каждом ящике

4) 30 + 21 = 51 (кг) – было яблок в первом ящике первоначально

 

 

   5 способ

1) 127 – 21 = 106 (кг) – осталось яблок в трех ящиках после взятия из первого ящика

2) 106 – 9 = 97 (кг) – осталось яблок в трех ящиках после взятия из первого и второго ящиков

3) 97 – 7 = 90 (кг) –  осталось яблок в трех ящиках

4) 90 : 3 = 30 (кг) – осталось яблок в каждом ящике

5) 30 + 21 = 51 (кг) – было яблок в первом ящике первоначально

 

6 способ

1) 127 – 21 = 106 (кг) –

2) 106 – 7 = 99 (кг) –

3) 99 – 9 = 90 (кг) – осталось яблок в трех ящиках

4) 90 : 3 = 30 (кг) – осталось яблок в каждом ящике

5) 30 + 21 = 51 (кг) – было яблок в первом ящике первоначально

 

7 способ

1) 127 – 9 = 118 (кг) – осталось яблок в трех ящиках после взятия из второго ящика

2) 118 – 21 = 97 (кг) – осталось яблок в трех ящиках после взятия из второго и первого ящиков

3) 97 – 7 = 90 (кг) – осталось яблок в трех ящиках

4) 90 : 3 = 30 (кг) – осталось яблок в каждом ящике

5) 30 + 21 = 51 (кг) – было яблок в первом ящике первоначально

 

8 способ

1) 127 – 9 = 118 (кг) – осталось яблок в трех ящиках после взятия из второго ящика

2) 118 – 7 = 111 (кг) – осталось яблок в трех ящиках после взятия из второго и третьего ящиков

3) 111 – 21 = 90 (кг) –  осталось яблок в трех ящиках

4) 90 : 3 = 30 (кг) – осталось яблок в каждом ящике

5) 30 + 21 = 51 (кг) – было яблок в первом ящике первоначально

 

9 способ

1) 127 – 7 = 120 (кг) – осталось яблок в трех ящиках после взятия из третьего ящика

2) 120 – 21 = 99 (кг) – осталось яблок в трех ящиках после взятия из третьего и первого ящиков

3) 99 – 9 = 90 (кг) –  осталось яблок в трех ящиках

4) 90 : 3 = 30 (кг) – осталось яблок в каждом ящике

5) 30 + 21 = 51 (кг) – было яблок в первом ящике первоначально

 

 

10 способ

1) 127 – 7 = 120 (кг) – осталось яблок в трех ящиках после взятия из третьего ящика

2) 120 – 9 = 111 (кг) – осталось яблок в трех ящиках после взятия из третьего и второго ящика

3) 111 – 21 = 90 (кг) –  осталось яблок в трех ящиках

4) 90 : 3 = 30 (кг) – осталось яблок в каждом ящике

5) 30 + 21 = 51 (кг) – было яблок в первом ящике первоначально

 

11 способ

1) 9 + 7 = 16 (кг) – взяли яблок из второго и третьего ящиков

2) 127 – 21 = 106 (кг) – осталось яблок в трех ящиках после взятия из первого ящика

3) 106 – 16 = 90 (кг) –  осталось яблок в трех ящиках

4) 90 : 3 = 30 (кг) – осталось яблок в трех ящике   

5) 30 + 21 = 51 (кг) – было яблок в первом ящике первоначально

 

12 способ

1) 21 + 7 = 28 (кг) – взяли яблок из первого и третьего ящиков

2) 127 – 9 = 118 (кг) – осталось яблок в трех ящиках после взятия из второго ящика

3) 118 – 28 = 90 (кг) –  осталось яблок в трех ящиках

4) 90 : 3 = 30 (кг) – осталось яблок в каждом ящике

5) 30 + 21 = 51 (кг) – было яблок в первом ящике первоначально

 

13 способ

1) 21 + 9 = 30 (кг) – взяли яблок из первого и второго ящиков

2) 127 –  7 = 120 (кг) – осталось яблок в трех ящиках после взятия из третьего ящика

3) 120 – 30 = 90 (кг) –  осталось яблок в трех ящике

4) 90 : 3 = 30 (кг) – осталось яблок в каждом ящике

5) 30 + 21 = 51 (кг) – было яблок в первом ящике первоначально

 

14 способ

1) 21 + 9 = 30 (кг) – взяли яблок из первого и второго ящиков

2) 127 –  30 = 97 (кг) – осталось яблок в трех ящиках после взятия из первого и второго ящиков 3) 97 – 7 = 90 (кг) – осталось яблок в трех ящике   

4) 90 : 3 = 30 (кг) – осталось яблок в каждом ящике

5) 30 + 21 = 51 (кг) – было яблок в первом ящике первоначально

 

15 способ

1) 21 + 7 = 28 (кг) – взяли яблок из первого и третьего ящиков

2) 127 – 28 = 99 (кг) – осталось яблок в трех ящиках после взятия из первого и третьего ящиков

3) 99 – 9 = 90 (кг) –  осталось яблок в трех ящике

4) 90 : 3 = 30 (кг) – осталось яблок в каждом ящике

5) 30 + 21 = 51 (кг) – было яблок в первом ящике первоначально

 

16 способ

1) 9 + 7 = 16 (кг) – взяли яблок из второго и третьего ящиков

2) 127 – 16 = 111 (кг) –  осталось яблок в трех ящиках после взятия из второго и третьего ящиков                                            

3) 111 – 21 = 90 (кг) – осталось яблок в трех ящиках

4) 90 : 3 = 30 (кг) – осталось яблок в каждом ящике

5) 30 + 21 = 51 (кг) – было яблок в первом ящике первоначально

 

 Существуют и другие способы решения данной задачи.

 

 

 

 

 

 

3 случай: графическую модель задачи.

 

 

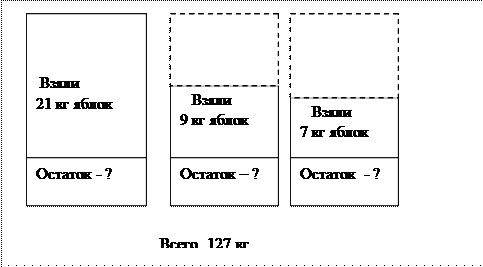
 В этих вариантах решения сначала надо определить, сколько яблок было бы во всех трех ящиках первоначально, если бы в каждом из них яблок было столько, сколько в первом ящике.

 

17 способ

1) 21 – 9 = 12 (кг ) – добавить во второй ящик, чтобы было яблок одинаково, как в первом ящике

2) 21 – 7 = 14 (кг) – добавить в третий ящик, чтобы было яблок одинаково, как в первом ящике

3) 12 + 14 = 26 (кг) – добавили в два последние ящики

4) 127 + 26 = 153 (кг) – стало в трех ящиках

5) 153 : 3 = 51 (кг) – было яблок в первом ящике первоначально

 

18 способ

1) 21 – 9 = 12 (кг ) – добавить во второй ящик, чтобы было яблок одинаково, как в первом ящике

2) 21 – 7 = 14 (кг) – добавить в третий ящик, чтобы было яблок одинаково, как в первом ящике

3) 127 + 12= 139 (кг) – стало в трех ящиках после добавления во второй ящик

4) 139 + 14 = 153 (кг) – стало в трех ящиках после добавления во третий ящик

5) 153 : 3 = 51 (кг) – было яблок в первом ящике первоначально

 

19 способ

1) 21 – 7 = 14 (кг ) – добавить в третий ящик, чтобы было яблок одинаково, как в первом ящике

2) 21 – 9 = 12 (кг) – добавить во второй ящик, чтобы было яблок одинаково, как в первом ящике

3) 12 + 14 = 26 (кг) – добавили в два последние ящики

4) 127 + 26 = 153 (кг) – стало в трех ящиках

5) 153 : 3 = 51 (кг) – было яблок в первом ящике первоначально

 

20  способ

1) 21 – 7 = 14 (кг ) – добавить в третий ящик, чтобы было яблок одинаково, как в первом ящике

2) 21 – 9 = 12 (кг) – добавить во второй ящик, чтобы было яблок одинаково, как в первом ящике

3) 127 + 12= 139 (кг) – стало в трех ящиках после добавления во второй ящик

4) 139 + 14 = 153 (кг) – стало в трех ящиках

5) 153 : 3 = 51 (кг) – было яблок в первом ящике первоначально

 

21 способ

1) 21 – 7 = 14 (кг ) – добавить в третий ящик, чтобы было яблок одинаково, как в первом ящике

2) 21 – 9 = 12 (кг) – добавить во второй ящик, чтобы было яблок одинаково, как в первом ящике

3) 127 + 14= 141 (кг) – стало в трех ящиках после добавления в третий ящик

4) 141 + 12 = 153 (кг) – стало в трех ящиках

5) 153 : 3 = 51 (кг) – было яблок в первом ящике первоначально

Рефлексия: сколько способов получилось? Какой способ самый рациональный?