«Арифметическая и геометрическая прогрессии»

МОУ СОШ №9

Тиридатова Е.Н.

 

«Прогрессио – движение вперёд»

 

«Прогрессио – движение вперёд» - урок комбинированных задач по теме «Арифметическая и геометрическая прогрессии»

 Цели урока: - повторение и обобщение изученного  материала  путём решения комбинированных задач;  развитие познавательного интереса к математике.

Задачи:

Образовательные:

- совершенствовать навыки решения разнообразных задач по использованию формул  арифметической и геометрической прогрессий;

- применять свои знания в практических ситуациях;

-расширять знания учащихся путём решения нестандартных задач;

Развивающие:

- развивать математический кругозор, мышление, математическую речь;

Воспитательные:

-воспитывать стремление к непрерывному совершенствованию;  воспитывать чувство прекрасного;

-формировать отношения взаимной ответственности при совместной работе;

Тип урока: отработка умений и навыков, применение знаний при решении комбинированных задач.

Форма проведения: личное соревнование с использованием презентации.          

Длительность : 2 учебных часа.

К уроку прилагается презентация Приложение1.ppt

Эпиграф урока.

Закончился 20-ый век.

Куда стремится человек?

Изучены космос и море,

Строенье звёзд и вся Земля.

Но математиков зовёт

Известный лозунг:

«Прогрессио – движение вперёд».

 

ХОД УРОКА.    

Ι. Организационный момент.                                            

II. Сценка «Мужик и купец».

(Стол. На столе – самовар; у окна сидит купчиха. Входит купец )

 Купец: Послушай, жена! На базаре я встретил глупого мужика и заключил с ним выгодную сделку.

Жена: Какую?

Купец: Он каждый день будет приносить мне по 100 000 рублей, а я ему в первый день отдам копейку. Ты слышишь, копейку за 100 000 рублей. Во второй день за 100 000- две копейки, в третий- 4 копейки и так целый месяц. А он мне целый месяц будет носить каждый день по 100 000 рублей!

Жена: Откуда у этого глупца столько денег?

Купец: Это не наше дело. Об одном жалею, что заключил договор только на 1 месяц. Боюсь, что этот чудак поймёт, что его обманывают, и не принесёт свои деньги.

(Раздаётся стук.  Жена выглядывает в окно.)

Жена: Там кто-то пришел!

Купец: Это он.  (Входит мужик)

Мужик: Получай, купец, свои деньги и отдай мою копейку. (Взяв копейку, уходит)

Купец: Как я боялся, что он не придёт! А вдруг завтра он не придёт? Или придёт и заберёт свои деньги?

Жена: Успокойся! Если он сегодня не понял, что его обманывают, не думаю, что он поймёт это завтра. Говорят же: «Если дурак, то надолго».

Купец: Так-то оно так, да всё равно боязно. 

Ведущий: Каждый день мужик приносил по 100 000 рублей и забирал свои копейки. Вначале купец радовался и не задумывался над тем, сколько он отдаёт мужику. На 24 день он отдал уже более 83000 рублей.

Купец: О горе мне, горе! Мужик оказался не так глуп! Какой я глупец! Разве можно заключать сделки на базаре!

Ведущий: Видите, ребята, сколь неожиданными бывают результаты, когда не знаешь математику. Вероятно, купец не оказался бы в безвыходном положении, знай он хоть чуть-чуть математику.

 

«Так о чём же, ребята, пойдёт сегодня речь?»

III . Сообщение темы и целей урока.

Конечно о прогрессиях.  Но встретим мы её в комбинированных нестандартных задачах. Сегодня мы должны обобщить и систематизировать знания и умения, приобретённые при изучении  прогрессий, а также вспомнить, насколько математика может быть занимательной. Нам предстоит поработать и с формулами, вспомнить, как решаются уравнения и строятся графики, посадить «волшебное дерево» и услышать исторические факты, решить задачу и написать тест. 

А вот почему же в конце месяца купец посчитал себя глупцом?

Сколько пришлось заплатить каждому?

I V. Устная работа

1.Считают «мужик» и «купец» 

 «Мужик» заплатил :  S₃₀ = 100 000∙ 30 = 3 000 000рублей.

 «Купец» заплатил : 1; 2; 4;…       q=2/1=2.

S₃₀ =1∙ (2³⁰  - 1):(2-1)= 2 ³⁰ -1=1 073 741 824 -1 =1 073 741 823 коп.=

= 10 738 418 руб.23коп

2.Найди ошибку.(Текст решения на слайде)

В то время пока двое подсчитывают суммы, следующий ученик комментирует решение и находит ошибку в решенном неравенстве:

х²+ х(-1-1/2-1/4-…) – 8 < 0,

Имеем в скобках сумму бесконечно убывающей геометрической прогрессии, которая равна  S=1/(1-1/2)=2, и  тогда неравенство приобретает вид   

 х² -2x -8 <0.

Рассмотрим функцию у = х² -2х -8. График парабола, «ветви» вверх, т.к. а=1, 1>0.

Нули функции: 4; -2.

Построим параболу схематично:

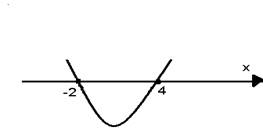Ответ: (-2;4).

V. Работа с формулами.

Герберт Спенсер, английский философ, когда-то сказал: «Дороги не те знания, которые откладываются в мозгу, как жир, дороги те, которые превращаются в умственные мышцы».

Проверим, кто из вас порадовал бы Герберта Спенсера.

восприятие речи на слух. Проговариваю название формулы один раз, а учащиеся пишут номер формулы (двое у доски, остальные под копирку на листочках, повернувшись так, чтобы работать спиной к доске).

Вопросы к формулам

1.Сумма бесконечно убывающей геометрической прогрессии.                                                    

 2.Формула n-го члена арифметической прогрессии.

 3.Сумма n-первых членов арифметической прогрессии.

 4.Сумма n-первых членов геометрической прогрессии.

 5.Формула n-го члена геометрической прогрессии.

 6.Свойство членов арифметической прогрессии.

 7.Свойство членов геометрической прогрессии.

 8.Знаменатель геометрической прогрессии.

 9.Разность арифметической прогрессии.

 

Формулы.

1. a_n = a₁ + ( n-1)d

2. b_n = b₁∙ q^n-1                                                                                           

3. S_n.

4. S_n =

5. S =.

6. a_n = .

7. b_n=

8. d = a_{n + 1} – a_n.

9. q =                                               

Листочки с каждого ряда собирает дежурный помощник. Выполняем проверку по коду.

Получили 9-значное число  513 426 798.

Это КОД  ОТВЕТА.

 

VI.  Практическая часть урока.

«Умение решать задачи – практическое искусство, подобное плаванию или катанию на лыжах, или игре на фортепиано; научиться этому можно лишь, подражая избранным образцам и постоянно тренируясь»,- говорил Д.Пойа.

 

1.Задача. Три числа составляют арифметическую прогрессию. Найдите эти числа, если их сумма равна 27, а при уменьшении первого числа на  1, уменьшении  второго на 3 и при увеличении третьего на 3, получили геометрическую прогрессию.

 

Дано: а₁+а₂ +а₃=27 –сумма трёх членов арифметической прогрессии; а₁-1; а₂ -3; а₃+3- геометрическая прогрессия

Найти: а₁; а_2;  а_3.

 

 

 

Решение.  ,       ,       

                      q  =                  

 

   =9 – d,               

             (8 - d)(d + 12)=36.

 

d² +4d-60=0,

d₁=6,   d₂=-10.

Если  d₁=6, то ; .

Если  d₂=-10, то ; .

Ответ:  если арифметическая прогрессия 3; 9; 15, то геометрическая прогрессия 2; 6; 18.

Если арифметическая прогрессия 19; 9; -1, то геометрическая прогрессия 18; 6; 2.

 

Нестандартные  комбинированные задачи по теме «Прогрессии» мы можем встретить и при решении уравнений, неравенств, при построении графиков функций.

 

2. Решите неравенство:

 (3х+)() > 0.

          6-слагаемых            6-слагаемых

Двое учащихся упрощают скобки в данном неравенстве. Сумма 6-ти слагаемых арифметической прогрессии равна (-18) . Сумма 6-ти слагаемых геометрической  прогрессии равна 126.

Неравенство перепишется в виде : (3х-18)(х+126)>0.

Третий ученик решает его методом интервалов.

 

Ответ: (-  ∞; -126) U  (6; +  ∞).

VII . Проверка  домашнего задания.

Мы знаем легенду об изобретателе шахмат, которая гласит, что изобретатель шахмат Сета попросил у индусского царя Шерам за своё изобретение столько пшеничных зёрен, сколько их получится, если на первую клетку шахматной доски положить одно зерно, на вторую – в два раза  больше, т. е. 2 зерна, на третью – ещё в два раза больше, т.е. 4 зерна, и т.д. до 64-й клетки. Одно из домашних заданий заключалось в том, чтобы посчитать современными способами и записать, сколько зёрен должен был получить изобретатель шахмат?

S₆₄ = 2⁶⁴ – 1 = 18 446 744 073 709 551 615.

18 квинтильонов  446 квадрильонов  744 триллиона 73 миллиарда (биллиона) 709миллионов  551 тысяча 615.

Современники сказали бы так:

 S₆₄ = 1, 84∙ 10 ¹⁹ – стандартный вид данного числа.

Если бы индусскому царю Шерам удалось засеять пшеницей площадь всей поверхности Земли, считая и моря, и океаны, и горы, и пустыни, и Арктику с Антарктикой, и получить удовлетворительный результат, то, пожалуй, лет за 5 он смог бы рассчитаться.

 

Мы ещё посмотрели сценку о мужике и купце. А когда же стали встречаться первые упоминания о прогрессиях?

VIII. Сообщаются краткие исторические сведения, приготовленные учащимися.

В клинописных табличках вавилонян, как и в египетских папирусах, относящихся ко 2 тысячелетию до нашей эры, встречаются примеры арифметических и геометрических прогрессий. Первые теоретические сведения, связанные с прогрессиями, дошли до нас в документах Древней Греции. Некоторые формулы, относящиеся к прогрессиям, были известны и индийским учёным.

Правило для нахождения суммы членов произвольной арифметической прогрессии даётся в «Книге  абака» (1202г.) Леонардо Фибоначчи. А общее правило для суммирования любой конечной геометрической прогрессии встречается в книге Н. Шюке «Наука о числах», увидевшей свет  в 1484 году.

 

IX. Практическая часть. (продолжение)

Великому Эйнштейну приходилось делить время между политикой и уравнениями. Он говорил: «Однако уравнения, по-моему, гораздо важнее. Политика существует только для данного момента, а уравнения будут существовать вечно».

3. Итак, уравнение, содержащее прогрессию.

х²  -3 |х | = 2+1+1/2+…

Решение: S= 2/(1-1/2)=4.

Уравнение приобретает вид  х²  -3 |х | -4=0.

1) Если х ≥  0, то х²  -3х  - 4 =0. Его корни 4 и -1;

              х= -1 не удовлетворяет условию х ≥   0.

2) Если х < 0, то х²  +3х  - 4=0. Его корни -4 и 1;

              х=1 не удовлетворяет условию х <    0.

Ответ: 4; - 4.

                                                     

4. Построить график функции:

                                                                                 

    у = .                                                 Решение.  1+sin30+sin² 30+sin³ 30+...=1+1/2+1/4+1/8+...- сумма бесконечно убывающей геометрической прогрессии, т.к. q=1/2.

S= 1/(1-1/2)=2.

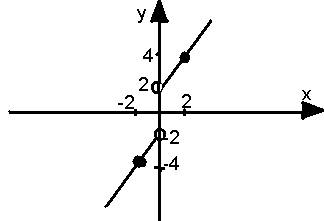
Функция приобретает вид:  1) у = х +2, если х > 0

2) у = х - 2, если х < 0.

Область определения х ≠0. У доски работают 2 ученика, каждый строит свою часть графика.

 

В нашей школе стало  традицией: выпускники школы, заложив однажды «аллею выпускников»,  продолжают эту традицию каждую новую весну.

Но пока ещё зима, самое время посадить «волшебное дерево».

5. Логическая задача.

Волшебное дерево, первоначальная высота которого 1 м, каждый день увеличивает свою высоту в 2 раза. При этом через 36 дней оно  «достанет» до Луны. Через сколько дней оно достало бы до Луны, если бы его высота в начальный момент времени была 8м?

Решение: через 33 дня. Один день-2м. Два дня-4м. Три дня-8м.    36-3=33 дня.

X. Индивидуальная работа .

В этом году вы принимаете эстафетную палочку от 11 классов и тоже сдаёте свой экзамен по алгебре в форме тестов ЕГЭ. Следующий тест позволит проверить вашу готовность к нему по теме  « Прогрессии». (Текст теста по вариантам ).

Решается тест в тетради, записывается в тетради номер ответа, тесты сдаются и выполняется проверка по коду. Привожу пример теста.

     Вариант 1.

1.  (а_n )-арифметическая прогрессия, а₁ =10; d = - 0,1. Найди а₄  .

1)      9,7     2) 97        3) -97         4) 10,3       5) – 10,3

2. В геометрической прогрессии b₁  ; b₂    ; 4; 8;…. Найди b₁  .

1)- 4     2) 1        3) 1/4        4) 1/8       5) – 1

3. (b_n  ) – геометрическая прогрессия. Найди b₆  , если  b₁  = 4; q = 1/2

1)      - 1/8    2) 1,25        3) 1/8        4)12,5       5) – 1,25

4. Найди сумму бесконечной геометрической прогрессии 12;6;…

     1) 6     2) - 12        3) -24        4) 24       5)  12

5.   Представь    в виде  обыкновенной    дроби    число   0, (1).

1) 9     2) 11/9        3) -1/9        4) - 9       5) 1/9

6. Найди сумму 100 – первых членов последовательности (x _n ), если         x _n  =2n +1.

     1)10200     2) 20400        3)1200        4) 102       5) 1020

7. Найди  S₄  ,  (b_n  ) – геометрическая прогрессия и  b₁  = = 1, q = 3.

     1) 81     2) 40        3) 80        4) -80       5) – 40

Код  ответов 1234542

 

XΙ . Подведение итогов.

Итак, сегодня мы в нестандартных  комбинированных заданиях   обобщили и систематизировали знания и умения, приобретённые при изучении  прогрессий, , поработали с формулами, вспомнили, как решаются уравнения и строятся графики, встретились с занимательной математикой и посадили «волшебное дерево» при решении занимательной логической задачи, услышали исторические факты, решили задачу и написали тест. (Итоги подводят ученики)

Урок сегодня завершён,

Но каждый должен знать:

Познание, упорство, труд

К прогрессу в жизни приведут.

 

XΙΙ. Выставление оценок.

За работу с формулами и тестом каждый учащийся получает оценки в журнал. Дополнительные оценки получают те, кто был активен на уроке.  

XΙΙΙ. Домашнее задание - творческое: составить 3 комбинированных задачи по теме «Прогрессии»   и их решения оформить на  альбомном листе.