Вычисления и преобразования тригонометрических выражений в задачах ЕГЭ

Методическое пособие для подготовки учеников к ЕГЭ

Тема: Вычисление и преобразование тригонометрических выражений.

Шарапова  Д.А.

 

Содержание

 

1.      Модуль 1. Теоретическая часть по теме «Тригонометрические выражения»

2.      Модуль 2. Ключевые задачи. Примеры решения задач.

3.      Модуль 3. Задачи для отработки практических навыков.

4.      Модуль 4. Задачи для зачета по данной теме.

5.      Модуль 5. Домашнее задание.

6.      Модуль 6. Варианты ЕГЭ по теме «Вычисление и преобразование тригонометрических выражений»

7.      Модуль 7. Ответы .

8.      Литература

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Модуль 1. Теоретическая часть по теме «Тригонометрические выражения»

 

1.      Понятие синуса, косинуса, тангенса и котангенса числового аргумента

 

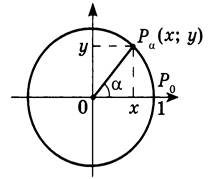Рассмотрим единичную окружность, т.е. окружность с центром в начале координат и радиусом 1.

Def:Синусом числа α называется ордината точки  , образованной поворотом точки  вокруг начала координат на угол α радиан.

 Обозначается : , т.е.  – ордината точки .

 

Def:Косинусом числа α называется абсцисса точки , полученной поворотом точки   вокруг начала координат на угол α  радиан.

Обозначается: , т.е.  – абсцисса точки .

 

Синус и косинус определены для любого числа  .

 

, 

 

Def:Тангенсом числа  называется отношение  синуса числа  к его косинусу:

Тангенс определен для всех , кроме тех значений, при которых , т.е.

 

 

Def:Котангенсом числа  называется отношение косинуса числа  к его синусу:

Котангенс определен для все , кроме тех значений, при которых , т.е

 

Для окружности произвольного радиуса R определение тригонометрических функций выглядит следующим образом:

 

;   ;   ;  

 

Если , то справедливы равенства:

 

 

Пример 1. Найдите значение выражения:

a)    

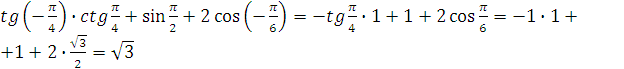
b)   

 

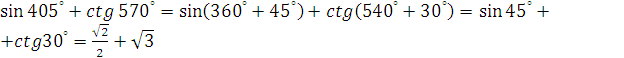
Пример 2. Определите знак выражения:

 

a)      т.к.  - угол II четверти, то - угол III четверти, то .

b)       т.к.  - угол II четверти, то- угол III четверти, то .

 

 

2.      Соотношение между тригонометрическими функциями одного аргумента.

 

Основное тригонометрическое тождество:

 

 

Следствия:

 

Пример 1. Могут ли одновременно быть справедливы равенства:

a)       и  

Решение:

Так как рассматриваются функции синус и косинус одного и того же аргумента, то должно выполняться основное тригонометрическое тождество:

, но .

Поэтому равенства  и  одновременно справедливы, быть не могут (т.к. не выполняется основное тригонометрическое тождество).

 

b)       и

       Решение:

Так как рассматриваются функции синус и косинус одного и того же аргумента, то должно выполняться основное тригонометрическое тождество:

, но .

Основное тригонометрическое тождество выполняется. Значит, равенства, данные в условии, одновременно справедливы.

 

Пример 2. Найдите значения тригонометрических функций числа , зная, что  и .

    Решение:

Так как по условию , то - принадлежит II четверти. Поэтому

;

 

 

 

3.      Произведение тангенса и котангенса одно и того же аргумента.

 

 

Пример 1. Могут ли быть справедливы равенства:

a)    

b)   

Решение:

 Поскольку , то :

a)       , равенства справедливы, т.к. выполняется тождество.

b)     , равенства не справедливы, т.к. не выполняется тождество.

 

Пример 2. Упростите:

Решение:

Так как , то

 

 

 

 

 

 

 

 

 

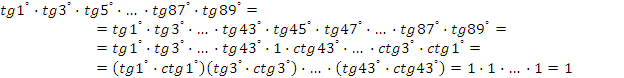
4.      Зависимость между тангенсом и косинусом одного аргумента.

 

 

 

Пример. Упростите:

   Решение:

 

 

 

 

5.      Зависимость между котангенсом и синусом одного аргумента.

 

 

 

Пример. Вычислите значения тригонометрических функций, если , - угол IV четверти.

   Решение:

Так как - угол IV четверти, то , , .

Известно, что  . Отсюда

   

Но  поэтому

 

 

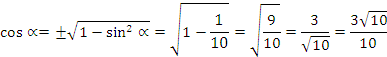
6.      Формулы сложения

 

A.    Синус суммы и разности

 

Def:Синус суммы двух аргументов равен сумме произведений синуса первого аргумента на косинус второго и косинус первого аргумента на синус второго:

 

 

Def:Синус разности двух аргументов равен разности произведений синуса первого аргумента на косинус второго и косинус первого аргумента на синус второго:

 

 

 

Пример1. Вычислите:

a)    

b)    

  Решение:

a)   

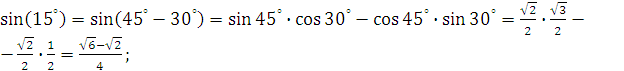
b)   

 

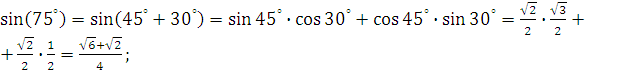
Пример 2. Найдите значение выражений:

a)    

b)    

Решение:

a)    

b)    

 

 

B.    Косинус суммы и разности

 

Def:Косинус суммы двух аргументов равен разности произведений косинуса первого аргумента на косинус второго и синуса первого аргумента на синус второго:

 

 

Def:Косинус разности двух аргументов равен сумме произведений косинуса первого аргумента на косинус второго и косинус первого аргумента на синус второго:

 

 

Пример . Вычислите:

a)    

b)    

Решение:

a)    

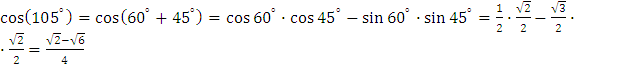
b)    

 

 

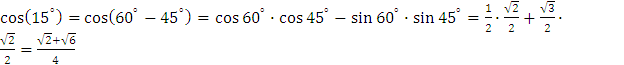
C.    Тангенс и котангенс  суммы и  разности.

 

 

 

Пример 1. Вычислите:

a)        

b)       

 Решение:

a)      

b)     

 

 Пример 2. Докажите тождество:

 

Доказательство:

Тогда из данного равенства имеем:

 

 

 

 

 

 

7.      Следствия из формул сложения

 

                                                                                                                                         I.           Синус двойного аргумента

 

Def: Синус двойного аргумента равен удвоенному произведению синуса и косинуса данного аргумента:

 

 

Пример 1. Вычислите:

Решение:

. Найдем .

Так как , то - угол III четверти, т.е. .

 

Итак,

 

Пример 2. Вычислите:

Решение:

 

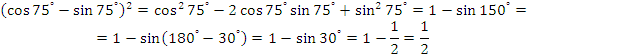
                                                                                                                                 II.           Косинус двойного аргумента.

 

Def: Косинус двойного аргумента равен разности квадратов косинуса и синуса данного аргумента.

 

 

 

Пример . Вычислите:

a)     

b)    

Решение:

a)     

b)    

 

 

 

 

 

 

 

                                                                                                                              III.           Тангенс двойного аргумента.

 

 

Пример. Вычислите:

a)    

b)   

Решение:

a)    

b)    

 

 

8.      Формулы приведения

 

 Def: Тригонометрические функции аргументов  могут быть выражены через функции аргумента  с помощью формул, которые называются формулами приведения.

Def:  Два угла называются дополнительными, если из сумма равна , для них справедливы равенства:

 

 

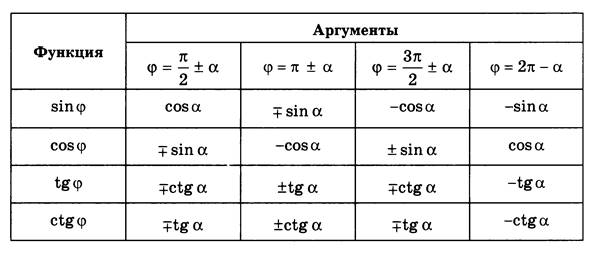
Чтобы облегчить запоминание формул приведения для преобразования выражений вида:

 

 

удобно пользоваться такими правилами:

a)    перед приведенной функций ставится тот знак, который имеет исходная функция, если

b)    функция меняется на «кофункцию».

Примеры к этому правилу приведены в таблице.

 

Пример. Найдите значение:

a)    

b)   

Решение:

a)    

b)   

 

 

9.      Тождественные преобразования тригонометрических выражений

 

 

 

 

 

 

 

 

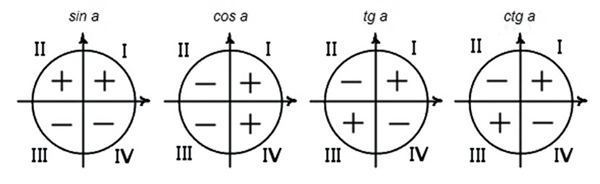
10.  Знаки тригонометрических функций по координатным четвертям.

11.   

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Модуль 2. Ключевые задачи. Примеры решения задач.

 

Разделим задачи на блоки:

1.     Нахождение значения выражения.

2.     Нахождение тригонометрических функций, если значение одной известно.

3.     Применение формул приведения и основных тригонометрических преобразований.

4.     Разные задачи.

 

 

1.      Нахождение значения выражения.

Пример 1.                            

Решение:

Данные значения углов табличные, подставляем и вычисляем:

Пример 2.

Решение:

Косинус угла    - это табличное значение. С косинусом угла   поступим следующим образом – выделим период, применим формулу приведения, и далее вычислим:

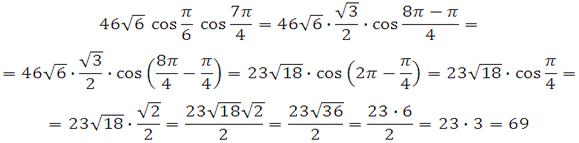
Пример 3.

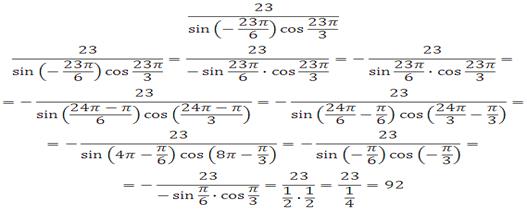
Пример 4.

Решение:

Применяем свойство чётности косинуса и нечётности синуса, далее вычисляем:

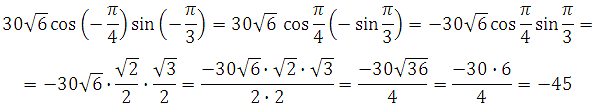
Пример 5.

Решение:

Используем формулу синуса двойного аргумента. Затем выделим период и применим свойство периодичности:

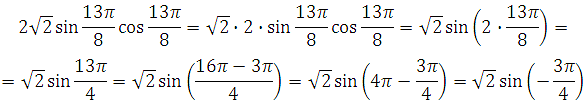
Далее применим свойство нечётности синуса и формулу приведения:

Пример 6.

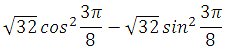
Решение:

Вынесем за скобку общий множитель и применим формулу косинуса двойного аргумента:

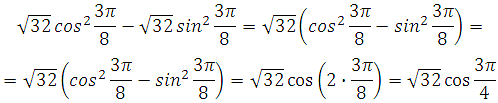
Далее используем формулу приведения и вычислим:

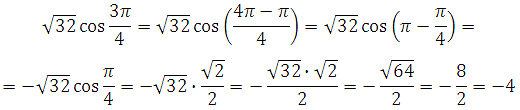
Пример 7.

Решение:

Выделим общий множитель и вынесем его за скобку, затем применим формулу косинуса двойного аргумента:

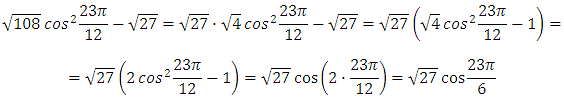
Далее выделим период, используем свойство периодичности и свойство чётности косинуса, вычисляем:

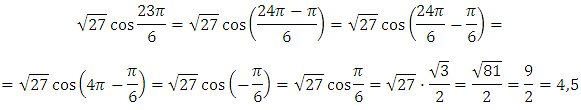
Пример 8.

Решение:

Выделим общий множитель и вынесем его за скобку, затем применим формулу косинуса двойного аргумента:

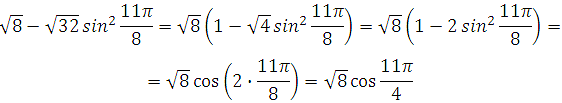
Далее выделим период и применим формулу приведения:

 

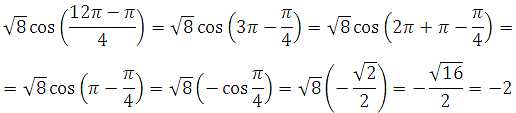
Пример 9.

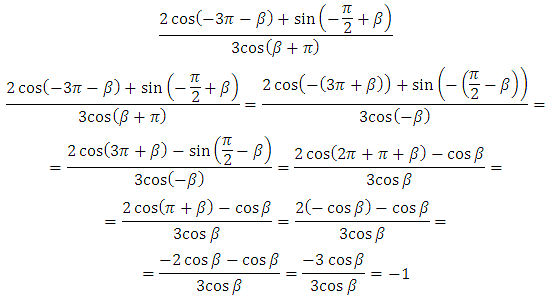
Пример 10.

 

 

 

 

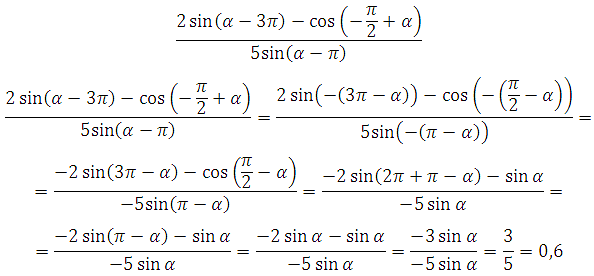
2.      Нахождение тригонометрических функций, если значение одной известно.

Пример 1.Найдите tg α, если

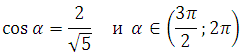
Решение:

В этом и подобных примерах необходимо знать основное тригонометрическое тождество (его вообще нужно помнить всегда), а также формулу тангенса:

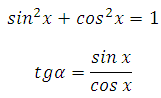
Косинус угла нам известен. Из формулы основного тригонометрического тождества  мы можем найти значение синуса. Затем подставить их в формулу тангенса.

Теперь важный момент: необходимо определить знак синуса для заданного интервала. Это интервал от 270 до 360 градусов (четвёртая четверть).  Значение синуса в этой четверти отрицательное, поэтому:

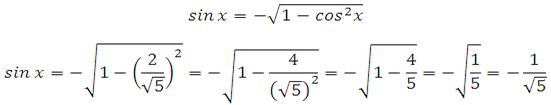
Таким образом:

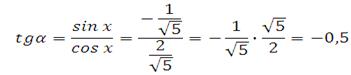
Пример 2.   Найдите tg α, если

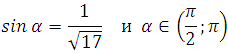
Решение:

В этом и подобных примерах необходимо знать основное тригонометрическое тождество (его вообще нужно помнить всегда), а также формулу тангенса:

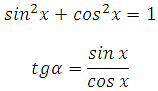
Cинус угла нам известен. Из формулы основного тригонометрического тождества  мы можем найти значение синуса. Затем подставить их в формулу тангенса.

Определяем знак косинуса для заданного интервала. Это интервал  от 90 до 180 градусов (вторая четверть). Значение косинуса в этой четверти отрицательное. Поэтому

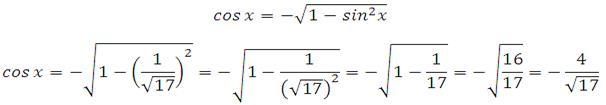
Таким образом:

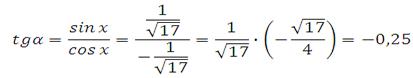
Пример 3.   Найдите 5cos α, если

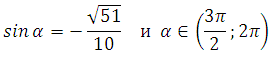
Решение:

Необходимо найти косинус угла. Из формулы основного тригонометрического тождества следует, что cos²x = 1– sin²x и

Определим знак косинуса. Угол принадлежит интервалу от 270 до 360 градусов  (четвёртая четверть).  Значение косинуса в этой четверти  положительное, поэтому:

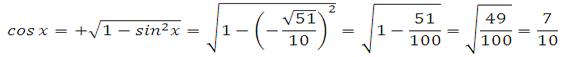
Таким образом, 5cos α = 5∙0,7 = 3,5

 

Пример 4   Найдите 0,1sin α, если

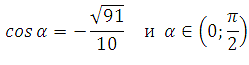
Необходимо найти синус угла. Из формулы основного тригонометрического тождества следует, что sin²x = 1– cos²x  и

Определим знак синуса. Угол принадлежит интервалу от 0 до 90 градусов  (первая четверть).  Значение синуса в этой четверти  положительное, поэтому:

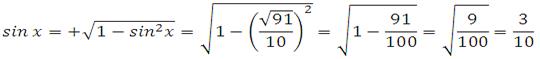
Таким образом 0,1sin α = 0,1∙0,3 = 0,03

 

Пример 5.   Вычислить , если .

Решение:

Так как . Воспользовавшись формулой  , получаем 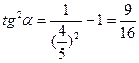. При   будет  Поэтому .

Пример 6. Известно, что

Найдите , ,  
Решение:  Поскольку из условия задачи следует неравенство 
то, учитывая знак синуса, находим, что точка P_a принадлежит 4-й четверти. Поэтому 

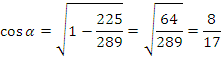
Пример 7. Известно, что . Найдите

Решение:

Учитывая знак тангенса и условие задачи 

 находим, что точка P_a принадлежит 4-й четверти. Поэтому 

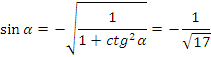
Пример 8. Известно, что . Найдите

Решение:

Из условия -3p < a < -2p и неравенства sinacosa > 0 следует, что  точка P_a принадлежит 3-й четверти. Следовательно, sina+cosa < 0.

Кроме того, 

Поэтому

 

Пример 9. Известно, что . Найдите

Решение: Возведем обе части данного равенства в квадрат: 

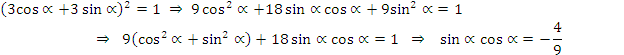
Пример 10.

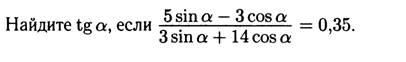
Решение:

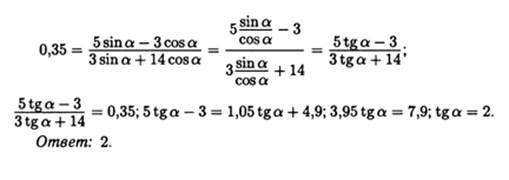
3.      Применение формул приведения и основных тригонометрических преобразований.

Пример 1.  Найдите значение выражения

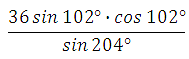
Решение:

Используем формулу синуса двойного аргумента:

Выражение в числителе «сворачиваем»:

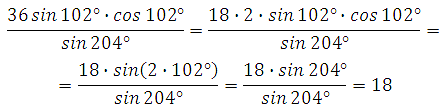
Второй путь: можно было использовать эту же формулу преобразовав знаменатель.

Пример 2.  Найдите значение выражения

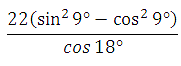
Для решения этого примера достаточно знать формулу косинуса двойного аргумента:

Преобразуем знаменатель:

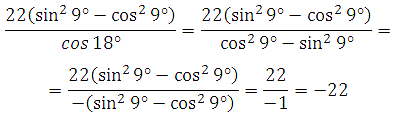
Пример 3. Найдите значение выражения

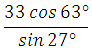
В данном случае 63 градуса представляем как разность 90⁰ – 27⁰

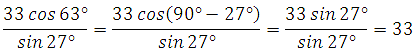
Пример 4. Найдите значение выражения

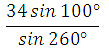
Представим 100⁰ как разность 360⁰ – 260⁰,  применим свойство периодичности нечётности синуса:

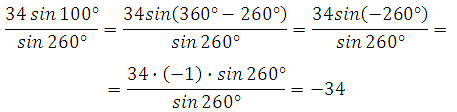
Пример 5. Найдите значение выражения

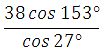
Используем формулу приведения косинуса. Представим 153⁰ как разность 180⁰– 27⁰:

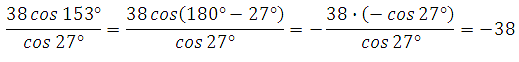
Пример 6.  Найдите значение выражения

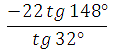
Используем формулу приведения для тангенса. Представим 148⁰ как разность 180⁰ – 32⁰:

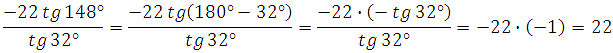
Пример 7. Найдите значение выражения

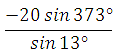
Представим 373⁰ как сумму 360⁰ + 13⁰,  используем свойство периодичности:

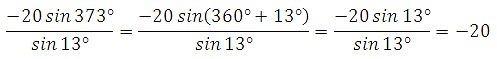
Пример 8. Найдите значение выражения

Используем формулы приведения:

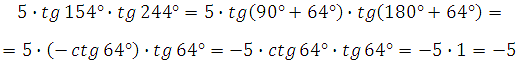
Применили формулу тригонометрии:

 

Пример 9.  Найдите значение выражения

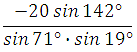
Применяем формулу синуса двойного аргумента в числителе, и формулу приведения в знаменателе:

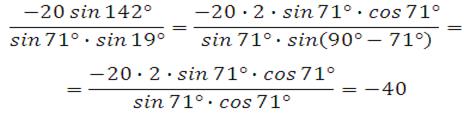
Пример 10. Найдите значение выражения

Применяем формулу синуса двойного аргумента:

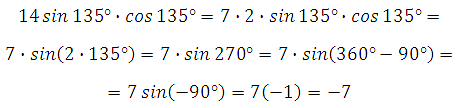
Пример 11.  Най­ди­те зна­че­ние вы­ра­же­ния

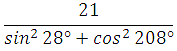
Используем формулу приведения и основное тригонометрическое тождество:

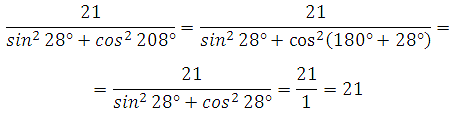
Пример 12. Най­ди­те зна­че­ние вы­ра­же­ния

Косинус функция чётная, то есть

Её период равен 2Пn, то есть

Значит

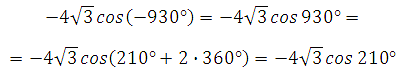
Используем формулу приведения для косинуса:

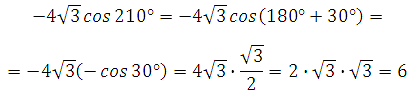
4.      Различные задачи.

1)     Задача. («Ломоносов»,2007 )  Вычислите: , если 

Решение:

Обозначим искомую величину за x. Раскрывая скобки, получим:

Слагаемые сгруппированы так , чтобы получились формулы.

2)     Задача. (МГУ, ф-т почвоведения, 2008) Вычислите , если

 .

Решение:

Поскольку  положителен и , угол - угол II четверти: . Значит, его косинус отрицателен:

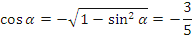
Отсюда

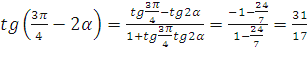
3)     Задача. (МГУ, ф-т почвоведения, 2000)  Найдите

a)     

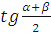
b)     , если известно, что

Решение:

Имеем:   

Разделив последние два равенства, друг на друга получим:

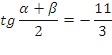
Теперь возведем последние два равенства в квадрат и сложим:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

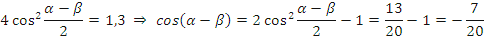
Модуль 3. Задачи для отработки практических навыков.

 

1.      Нахождение значения выражения.

1.      Вычислите

2.      Вычислите

3.      Най­ди­те зна­че­ние вы­ра­же­ния .

4.      Най­ди­те зна­че­ние вы­ра­же­ния .

5.      Най­ди­те зна­че­ние вы­ра­же­ния .

6.      Най­ди­те зна­че­ние вы­ра­же­ния .

7.      Най­ди­те зна­че­ние вы­ра­же­ния .

8.      Най­ди­те зна­че­ние вы­ра­же­ния .

9.      Най­ди­те зна­че­ние вы­ра­же­ния .

10.  Най­ди­те зна­че­ние вы­ра­же­ния .

11.  Най­ди­те зна­че­ние вы­ра­же­ния .

12.  Най­ди­те зна­че­ние вы­ра­же­ния .

13.  Най­ди­те зна­че­ние вы­ра­же­ния .

14.  Най­ди­те зна­че­ние вы­ра­же­ния .

15.  Най­ди­те зна­че­ние вы­ра­же­ния .

16.  Най­ди­те зна­че­ние вы­ра­же­ния .

17.  Най­ди­те зна­че­ние вы­ра­же­ния: .

18.  Най­ди­те зна­че­ние вы­ра­же­ния .

19.  Най­ди­те зна­че­ние вы­ра­же­ния .

20.  Най­ди­те зна­че­ние вы­ра­же­ния .

21.  Най­ди­те , если .

22. 

23. 

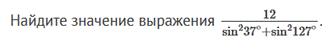
24. 

25. 

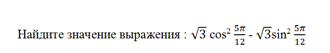
26. 

2.      Нахождение тригонометрических функций, если значение одной известно.

1)     Найдите , если 

2)     («Ломоносов», 2007) Вычислите: , если

a.     

3)     (МГУ, ф-т гос.управления,2010) Найдите  и , если известно, что а

4)     Най­ди­те , если и .

5)     Най­ди­те , если и

6)     Най­ди­те , если и .

7)     Най­ди­те , если и .

8)     Най­ди­те , если .

9)     Най­ди­те , если

10) Най­ди­те , если .

11) Най­ди­те , если .

12) Най­ди­те , если .

13) Най­ди­те если и

14) Най­ди­те если и

15)

16)

17)

18)

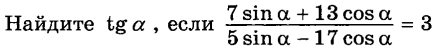
19)

20)

21)

22)

 

 

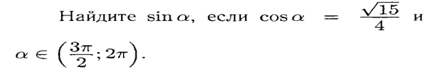
3.      Применение формул приведения и основных тригонометрических преобразований.

1)     Най­ди­те , если .

2)     Най­ди­те зна­че­ние вы­ра­же­ния , если .

3)     Най­ди­те , если и .

4)     Най­ди­те , если и .

5)     Най­ди­те , если

6)  Най­ди­те , если .

7)     Най­ди­те , если .

8)     Най­ди­те зна­че­ние вы­ра­же­ния , если .

9)     Най­ди­те зна­че­ние вы­ра­же­ния , если .

10) Най­ди­те зна­че­ние вы­ра­же­ния .

11) Най­ди­те зна­че­ние вы­ра­же­ния .

12) Най­ди­те зна­че­ние вы­ра­же­ния .

13) Най­ди­те зна­че­ние вы­ра­же­ния .

14) Най­ди­те зна­че­ние вы­ра­же­ния .

15) Най­ди­те зна­че­ние вы­ра­же­ния .

16) Най­ди­те зна­че­ние вы­ра­же­ния .

17) Най­ди­те зна­че­ние вы­ра­же­ния .

18)

19)

20)

21)

22)  

 

 

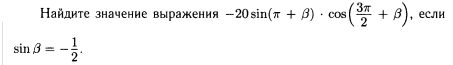
4.      Разные задачи.

1)      Докажите тождество:

2)      Покажите, что:  

3)      Докажите:

4)      Най­ди­те зна­че­ние вы­ра­же­ния .

5)      Най­ди­те зна­че­ние вы­ра­же­ния .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Модуль 4. Задачи для зачет по данной теме.

 

Зачет № 1.  Нахождение значения выражения.

Найдите значения выражений:

1)    

2)    

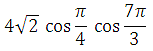
3)    

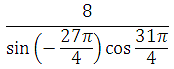
4)    

5)    

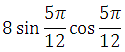
6)    

7)    

8)    

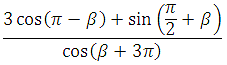
9)    

 

 

 

 

 

 

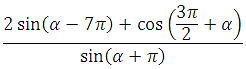
Зачет №2 Нахождение тригонометрических функций, если значение одной известно.

 

Найдите значение если известно:

1)      Найдите  tg² α, если 

 

2)   Найдите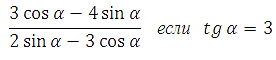

 

 

3)      Найдите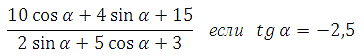

 

4)      Найдите tg α, если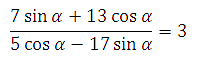

 

 

5)      Найдите tg α, если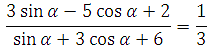

 

6)     Найдите 24cos2α, если sinα = – 0,2. 

7)      Найдите 9cos2α, если cosα = 1/3

 

8)      Найдите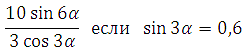 

 

9)      Найдите значение выражения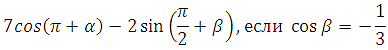

 

 

10)   Найдите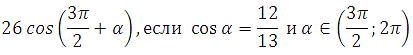

 

 

 

 

Зачет №3   Применение формул приведения и основных тригонометрических преобразований.

1)    Найдите значение выражения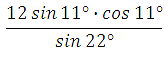

 

2)   Найдите значение выражения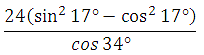

 

Найдите значение выражения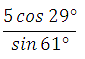

3)    

4)   Найдите значение выражения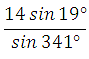

 

5)   Найдите значение выражения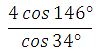

 

 

6)   Найдите значение выражения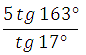

 

7)   Найдите значение выражения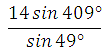

 

 

8)   Найдите значение выражения

 

9)   Найдите значение выражения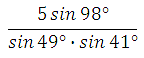

 

 

10) Найдите значение выражения

11) Найдите значение выражения

12) Найдите значение выражения

13) Найдите значение выражения

 

 

Модуль 5. Домашнее задание.

 

1.Упростите выражения:

 

a)   

b)   

c)   

d)   

e)   

f)     .

2. Вычислите:

a)   

b)    ;

c)    ;

d)    ;

e)   

3. Известно, что sin α – cos α = 0,3. Найти:

a)    sin²α;

b)    sin⁴α + cos⁴α;

c)      sin⁶α + cos⁶α.

 

4.Найти tg α, если 

5. Вычислить cos α, если cos2α = 3/4 и 

6. Найти значение выражения: 

7. Вычислить sin10º sin30º sin50º sin70º .

8. Упростить выражение: .

9. Доказать тождество при 

10. Найти значение следующих тригонометрических выражений: sin 2α, cos 2α, tg 2α, если 

11.* Вычислить значение выражения:

Модуль 6. Варианты ЕГЭ по теме «Вычисление и преобразование тригонометрических выражений»

 

 

Вариант 1

Вопрос 1. Найдите значение выражения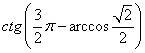 

Вопрос 2. Найдите значение выражения 

Вопрос 3. Найдите значение выражения 

Вопрос 4. Найдите значение выражения 

Вопрос 5. Найдите значение выражения 

Вопрос 6. Найдите значение выражения 

 

Вариант 2

1)     Най­ди­те зна­че­ние вы­ра­же­ния , если .

2)     Най­ди­те  если  и 

3)     Най­ди­те , если .

4)     Най­ди­те зна­че­ние вы­ра­же­ния .

5)     Най­ди­те , если .

6)     Най­ди­те , если .

7)     Най­ди­те зна­че­ние вы­ра­же­ния 

8)     Най­ди­те , если .

9)     Най­ди­те зна­че­ние вы­ра­же­ния .

10) Най­ди­те , если .

Вариант 3

1)       Най­ди­те , если  и .

2)      Най­ди­те , если  и .

3)       Най­ди­те , если .

4)      Най­ди­те , если  и 

5)      Най­ди­те зна­че­ние вы­ра­же­ния .

6)      Най­ди­те зна­че­ние вы­ра­же­ния .

7)      Най­ди­те  если  и 

8)      Най­ди­те зна­че­ние вы­ра­же­ния 

9)      Най­ди­те , если .

10)  Най­ди­те зна­че­ние вы­ра­же­ния: .

Вариант 4.                                                                           

 

А1. Упростите выражение:      7cos²– 5 + 7sin²

                             1) 1 + cos²;              2)  2;               3)       –12 ;             4) 12.

 

А2. Найдите значение выражения   

                                   1) 0;                     2) 2 ;                     3) –1 ;                  4) –2.

 

А3. Найдите значение выражения 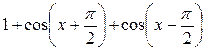  при

                                       1) 1 ;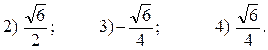          

 

А4. Упростите выражение: sincos  +  sincos  – cos 

 

     

 

А5. Упростите выражение:      

 

                                            ;              

 

А6. Найдите ,если ,  

                                                                           

 

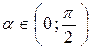
А7. Найдите значение выражения 

                             1)  1;         2)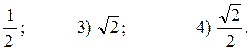

А8. Упростите выражение: 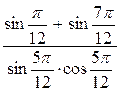       1) 0;     2) –1;      3) ;     4) -2

 

 

Вариант 5. 

                                                                         

А1. Упростите выражение:  cosx  +  tgx sinx 

                                     1) 1;    2)   2cosx;       3) cosx + sinx;         4)  

 

А2. Найдите значение выражения    

                              1) 0,5 ;          2) –4 ;           3) 4;                4) –4.

 

А3. Найдите значение выражения 

                                

 

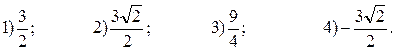
А4. Упростите выражение: 

 

       

 

А5. Упростите выражение: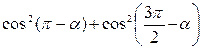     

                                                   

 

А6.  Найдите ,если ,  

                          

 

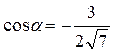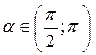
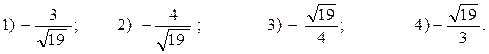
А7. Найдите значение выражения 

                  

 

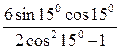
А8.  Упростите выражение: 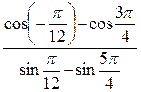    1) 1;     2) 0,5 ;      3) –4 ;     4) .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Модуль 7. Ответы .

1.      Модуль 3.

№ темы	1	2	3	4	5	6	7	8	9	10	11	12	13	14
1	0,5	-0,5	6	-24	36	2	-16	-6	6	18	-12	-5	7	12
2	0,69	-0,5		-3	5	1	-1	22,08	7	8	2,25	-7	-0,2	-0,75
3	4,2	-28	0,6	-10	-2,5	-9	5	3	4	5	-14	-4	-5	14
4				2	1

 

№ темы	15	16	17	18	19	20	21	22	23	24	25	26
1	6	12	-3	-1,5	-1,5	-1,5	31,96	2	12	36	-1,5	-13
2	-0,4	2,25	-9	8	2	-0.68	1,75	-0,25
3	10	10	2	4	3	-24	-104	5
4

 

2.      Модуль 4. Задачи для зачета по данной теме.

1)     Зачет №1: 1) 36, 2) 2, 3) -16, 4) -12, 5) 2, 6) -1,5, 7) -1,5, 8) 2, 9) 1

2)     Зачет №2: 1) 7, 2)-9, 3) 5, 4)8, 5)2, 6) 22,08, 7)-7, 8)4, 9)3  10)10

3)     Зачет №3: 1)6, 2)-24, 3)5, 4)-14, 5)-4, 6)-5, 7)14, 8)-5, 9)10, 10) -3, 11)-6, 12)6, 13)18

 

 

 

3.      Модуль 5. Домашнее задание.

№ задания	ответ	№ задания	ответ
1	а) , b), c), d)0, e)1, f)	7	,
2	a)0, b)1 , с), d), e)	8
3	a)0,91 b)0,545 c)0,3175	9	---
4	7	10
5		11	0
6	1

 

 

 

 

4. Модуль 6. Варианты ЕГЭ по теме «Вычисление и преобразование  тригонометрических выражений»

 

№ варианта	1	2	3	4	5	6	7	8	9	10
1	1	0,5	-17	22	6	4
2	12,8	-0,8	0,25	36	8	2	-1	5	22	-5
3	-1	0,7	11,08	-0,5	-34	44	-1/5	-30	-7	-7
4	2	4	1	2	1	2	2	4
5	4	1	2	4	1	4	4	4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Литература.

1)     http://alexlarin.net

2)     http://reshuege.ru

3)     http://fipi.ru

4)     http://www.matematikvn.ru/ege-oge/ege-avtorskie-materialy.php

5)     http://xn----etbbfc5ae1a3k.xn--p1ai/?level=trigonometricheskie-vyrazheniya

6)     http://matematikalegko.ru/vichislnie-viragenii/trigonometricheskie-vyrazheniya-chast-6.html

7)      ЕГЭ 3000 задач с ответами по математике. Все задания группы В/ А.Л.Семенов, И.В. Ященко, И.Р. Высоцкий, Д.Д. Гущин, М.А. Посицельская, С.Е. Посицельский, С.А.Шестаков, Д.Е.Шноль, П.И. Захаров, А.В. Семенов, В.А. Смирнов; под редакцией А.Л Семенова, И.В. Ященко – 3 изд. перераб. и доп. – М. Издательство «Экзамен», 2012.-543,(1) с.

8)     Математика. Подготовка к ЕГЭ- 2014 учебно- методическое пособие/ Под редакцией Ф.Ф. Лысенко, С.Ю. Кулабухова. – Ростов – на- Дону: Легион-М, 2013-416с. – («Готовимся к ЕГЭ»)

9)     ЕГЭ 2008. Математика. Учебно-тренировочные материалы для подготовки учащихся/ Под редакцией Семенов П.В., Краснянская К. А. и др. ФИПИ-М.:Интелект-Центр, 2007.-240с.

10) ЕГЭ-2008:математика:реальные задании/ авт.-сост. В.В.Кочагин, Е.М. Бойченко, Ю.А.Глазков и др. – М.: АСТ: Астрель, 2008. – 125,[3] с. – (ФИПИ)