Урок "Применение производной к исследованию функции"

Дисциплина: Математика

Преподаватель: Фомченко Ольга Леонидовна

Дата проведения: 27.04.2022 г.

Группа: 1-14

Тема урока:  Применение производной к исследованию функции.

Тип урока: практическая работа

Вид урока: комбинированный

Цели урока:

I. Обучающие:

- усвоение студентами основных понятий изученных ранее тем;

- применение правила нахождения производных при исследовании функций;

- осуществление студентами самостоятельного применения знаний.

II. Развивающие:

         - развитие познавательного интереса к дисциплине;

         - развитие внимания, логического мышления.

III. Воспитывающая:

        - формирование навыков по применению знаний, полученных на уроке в  

           жизни;

       - воспитание положительного отношения к знаниям.

Задачи урока:

-      обеспечить в ходе урока усвоение (повторение, закрепление) следующих основных понятий, законов и теорий, научных фактов (преподаватель вписывает их возможные наименования);

-      сформировать (продолжить формирование, закрепить) следующие специальные умения по данному предмету (преподаватель приводит их возможный перечень);

-      сформировать (продолжить формирование, закрепить) следующие общеучебные навыки и умения (например, навыки планирования ответа, навыки самоконтроля и др.);

-      формировать у учащихся умение выделять главное, существенное в изучаемом материале, сравнивать, обобщать изучаемые факты, логически излагать свои мысли (например, предусмотреть с этой целью в ходе занятия дополнительные контрольные вопросы, сравнение понятий, оглавление текста и пр.);

-      восполнить следующие типичные пробелы в знаниях, общеучебных и специальных навыках и умениях учащихся данного класса;

-      обеспечить контроль знаний и умений по тем;

-      подвести учащихся к пониманию сущности изучаемого материала.

-       

Межпредметные  связи: физика, механика, химия (изучение скорости  изменения  процессов) и т.д.

Методы обучения: продуктивные (эвристическая беседа), объяснительно – иллюстративный, логический (анализ, абстрагирование).

Формы организации познавательной деятельности на уроке: фронтальная, групповая, индивидуально – обособленная.

Приёмы повышения внимания и интереса студентов к изучаемой теме:

® наводящие вопросы, помогающие выбору правильных путей решения задачи, одновременно указывающие на различные подходы к ней;

® задания на индивидуальное речевое проговаривание правил, определений;

® предъявление студентам переформулированных вопросов, заданий, облегчающих понимание их смысла;

® намёк – подсказка, содержащий готовую информацию;

® задания на определение степени достоверности;

® мультимедийное сопровождение.

Самостоятельная работа студентов на уроке: запись основных понятий; ответы на поставленные вопросы; выполнение практической работы.

Оснащение урока: учебники Колмогорова А.Н. "Алгебра и начала анализа", 10-11 класс, раздаточный материал, мультимедийное сопровождение.

 

Макроструктура урока:

1. Организационный момент (2 мин)

2. Мотивация (2 мин)

3. Актуализация опорных знаний и умений (10 мин)

4. Изучение нового материала (54 мин)

5. Восприятие и осмысление нового материала (8 мин)

 6. Первичное закрепление, самостоятельная работа (10 мин)

 7. Домашнее задание (2 мин)

8. Рефлексия (2 мин)

Ход урока:

1. Организационный момент

-      приветствие;

-      проверка отсутствующих.

2. Мотивация

-       сообщение цели и темы урока;

-       представление плана урока.

3. Актуализация опорных знаний и умений

Проводится математический диктант на знание определения производной функции в точке, геометрического и физического смысла производной, правил вычисления производных (после выполнения математического диктанта, студенты тут же проверяют правильность ответов и оценивают себя):

1.  Дать определение производной функции в точке (Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю).
2. В чем состоит геометрический смысл производной (Геометрический смысл производной: производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке).

3. Раскрыть физический смысл производной (Физический смысл производной: производная пути по времени равна скорости прямолинейного движения).

4. Решить два примера, нахождение производной:

·        3х² – 5х – 6; ответ 6х – 5

·        х ⁵ + 3х³ – 4х; ответ 5х⁴ + 9х² – 4

5 правильных ответов – «5»,

4 правильных ответа – «4»

3 правильных ответа – «3»

2 правильных ответа – «2»

4.  Изучение нового материала

Понятие производной – одно из важнейших в математике. С помощью производной учитывая её механический смысл и геометрический смысл, можно решать самые разнообразные задачи, относящиеся к любой области человеческой деятельности. В частности, с помощью производных стало возможным подробное исследование функций, что позволило очень точно строить их графики, находить их наибольшие и наименьшие значения и т. д.

Одной из основных задач, возникающих при исследовании функции, является нахождение промежутков возрастания и убывания. Такой анализ легко сделать с помощью производной.

Но прежде чем приступить к исследованию функций вспомним, какие функции называются возрастающими (убывающими).

Функция f(x)  называется возрастающей на некотором интервале, если в точках этого интервала большему значению аргумента соответствует большее значение функции, и убывающей, если большему значению аргумента соответствует меньшее значение функции.

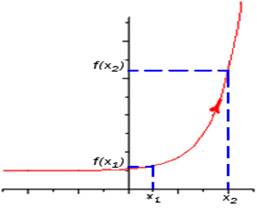
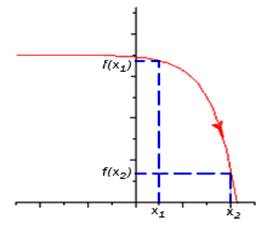
И так, давайте сейчас сформулируем следующие утверждения:

Достаточный признак возрастания функции: Если f '(х) > 0 в каждой точке интервала I, то функция f возрастает на I.

Достаточный признак убывания функции: Если f '(х) < 0 в каждой точке интервала I, то функция f убывает на I.

Сформулируем теперь правило нахождения интервалов возрастания и убывания функции f(x).

1.     Находим область определения функции f(x).

2.     Вычисляем производную f’(x) данной функции.

3.     Находим точки, в которых f’(x)=0 или не существует. Эти точки называются критическими для функции f(x).

4.     Делим область определения функции этими точками на интервалы. Они являются интервалами возрастания и убывания функции.

5.     Исследуем знак f’(x) на каждом интервале. Если f’(x)›0, то на этом интервале f(x)  возрастает; если f’(x)‹0, то на таком интервале функция f(x)  убывает.

Рассмотрим теперь нахождение промежутков возрастания/убывания на конкретном примере функции.

 

 

 

Пример №1. Найти промежутки возрастания/убывания функции

y=2x³-3x²-36x+5.

1.     Область определения: R. Функция непрерывна.

2.     Вычисляем производную : y’=6x²-6x-36.

3.     Находим критические точки: y’=0.

x²-x-6=0

Д=1-4*(-6)*1=1+24=25

x₁=-2, x₂=3

4.     Делим область определения на интервалы:

5.     Функция возрастает при xϵ(-∞;-2]υ[3;+∞),  функция убывает при xϵ[-2;3].

Пример №2. Найти промежутки возрастания/убывания функции y=x³-3x².

1.     Область определения: R. Функция непрерывна.

2.     Вычисляем производную : y’=3x²-6x.

3.     Находим критические точки: y’=0.

x²-2x=0

x(x-2)=0

x₁=0 и x₂=2

4.     Делим область определения на интервалы:

5.     Функция возрастает при xϵ(-∞;0]υ[2;+∞),  функция убывает при xϵ[0;2].

Но помимо нахождения промежутков возрастания и убывания функции с помощью производной можно ещё определить точки экстремума (точки максимума/минимума).

Сначала вспомним необходимые определения и понятия.

Опр. 1. Точку x₀ называют точкой минимума функции f(x), если у этой точки существует окрестность, для всех точек которой выполняется неравенство f(x) ≥ f(x₀).

Опр. 2. Точку x₀ называют точкой максимума функции f(x), если у этой точки существует окрестность, для всех точек которой выполняется неравенство f(x) ≤ f(x₀).

Сформулируем соответствующее утверждение, его называют теоремой Ферма:

 Необходимое условие экстремума. Если точка х₀ является точкой экстремума функции f и в этой точке существует производная f ', то она равна нулю: f '( х₀ ) = 0.

Из теоремы Ферма следует, что при нахождении точек экстремумов функции требуется в первую очередь найти ее критические точки. При этом часто помогают такие достаточные условия существования экстремума в точке.

Признак максимума функции. Если функция f непрерывна в точке х₀, а

f '(х) > 0 на интервале (а;х₀) и f '(х) < 0 на интервале (х_0; b), то точка х₀ является точкой максимума функции f.

Признак минимума функции. Если функция f непрерывна в точке х₀, а

f '(х) < 0 на интервале (а;х₀) и f '(х) > 0  на интервале (х_0; b), то точка х₀ является точкой минимума функции f.

 

 

Удобно пользоваться упрощенной формулировкой:

Если производная меняет знак с «+» на «-», то точка будет являться точкой максимума, если с «-» на «+», то точка будет точкой минимума.

Рассмотрим теперь на примерах исследование функции на возрастание/убывание и экстремумы.

Пример №3. Найти экстремумы функции y=-2x³-3x²+12x-4.

1.     Область определения: R. Функция непрерывна.

2.     Вычисляем производную : y’=-6x²-6x+12.

3.     Находим критические точки: y’=0.

x²+x-2=0

D=1-4*1*(-2)=1+8=9

x₁=-2 и x₂=1

4.     Делим область определения на интервалы:

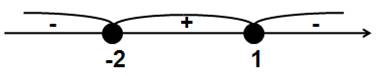
5.     Функция возрастает при xϵ(-∞;0]υ[2;+∞),  функция убывает при xϵ[0;2].

6.     Видно, что в точке x=-2 знак производной меняется с минуса на плюс. Поэтому критическая точка x= -2 – точка минимума. Найдём минимум функции y_min= -24. В точке x=1 знак меняется с плюса на минус. Поэтому критическая точка x= 1 – точка максимума. Найдём максимум функции: y_max= 3.

 

 

 

 

 

5. Восприятие и осмысление нового материала

1.                 Определение возрастающей (убывающей) функции (достаточный признак).

2.                 Критические точки функции (необходимое условие экстремума: теорема Ферма).

3.                 Условия существования экстремума в точке (признак максимума и минимума функции).

4.                 Алгоритмы исследования функции на возрастание/убывание и экстремумы.

6.     Первичное закрепление.

-       Решение студентами следующих примеров:

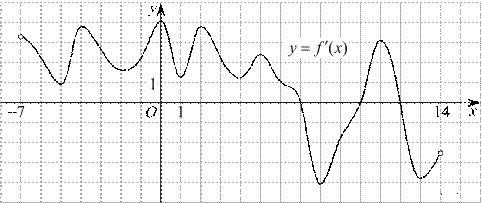            Рис.1  

1. На рисунке 1 изображен график производной функции f(x), определенной на интервале (−7; 14). Найдите количество точек максимума функции f(x) на отрезке [−6; 9].

 

 

2. Найти промежутки возрастания и убывания и точки экстремума функции

 y = - 3

 

ответы:

 1) 1

 2) возрастает на  ( U, убывает на

- 1 – точка максимума, 1 – точка минимума.

-        взаимопроверка студентами работ с предоставлением правильных ответов;

7.     Задание на дом: № 281, 290 (в, г), Колмогоров А.Н. «Алгебра и начала анализа», 10-11 класс, глава II, §6, п. 22, п. 23.

 

 

8.     Рефлексия:

- насколько баллов из  пяти оцениваешь свою работу сегодня?

- что оказалось наиболее трудным для понимания?

- какие моменты необходимо усилить, доработать в дальнейшем?