ГОУ ЛНР «Станично-Луганская средняя школа пгт Петровка»

 

 

 

 

 

         Урок закрепления знаний по алгебре в 10-м классе по теме «Математическое кафе "Иррациональные уравнения"».

 

 

 

 

 

 

 

 

 

Подготовила учитель математики и информатики

Мошонская Евгения Александровна

 

 

 

Урок закрепления знаний по алгебре в 10-м классе по теме «Математическое кафе "Иррациональные уравнения"».

Цели:

Обучающие.

1.     Обобщить и закрепить методы решения иррациональных уравнений.

2.     Создать условия контроля (самоконтроля и взаимоконтроля).

Развивающие.

1.     Развитие операций мышления (обобщение, анализ, выделение существенного). Развитие внимания.

2.     Развития навыков сотрудничества.

3.     Развитие  речевой культуры,  математического кругозора.

Воспитательные.

1.     Воспитание сознательного отношения к изучению алгебры.

2.     Воспитание  уверенности в своих знаниях;

3.      Воспитание умения слушать других;

4.     Содействовать воспитанию интереса к математике;

5.     Воспитание  объективности и честности при контроле знаний;

6.     Воспитание культуры поведения.

 

Тип урока: урок закрепления и систематизации знаний.

 

Оборудование:  мультимедийный проектор,  презентация,  раздаточный материал,  ноутбуки.

План урока (меню кафе)

 

№	Этапы урока
1	Планерка (орг. момент)
2	Вчерашнее меню (дом. зад.)
3	Салат «Математический винегрет» (актуализация опорных знаний)
4	Первое блюдо (самостоятельная работа)
5	Гимнастика для глаз
6	Напитки «Красочный коктейль» (научный эксперимент)
7	Математические орешки (тест)
8	Второе блюдо (мозговая атака)
9	Десерт (дом. зад., итог)
10	Книга отзывов и предложений (рефлексия)

        Перед началом урока класс разбивается на подгруппы. Парты расставлены так, чтобы имитировать расположение столиков в кафе.

Ход урока

I.                  Организационный момент (планерка):

        Учитель: Здравствуйте, ребята. Добрый день, уважаемые гости, приглашаю Вас в математическое кафе “Иррациональные уравнения”. ( На экране  «Меню кафе», на столах у каждой группы тоже есть меню). Предлагаю посмотреть сегодняшнее меню.

Эйнштейн говорил так: “Мне приходится делить время между политикой и уравнениями. Однако, уравнения, по-моему, гораздо важнее. Политика существует для данного момента, а уравнения будут существовать вечно”.

Как Вы знаете, прославился он именно уравнением, названным “уравнение Эйнштейна”. Вот и мы займемся уравнениями: закрепим знания по теме “Иррациональные уравнения”, повторим методы решения уравнений, покажем использование информационных технологий на разных этапах урока.

    Давайте задумаемся и ответим, для чего нам нужно уметь решать иррациональные уравнения?

          На протяжении всего урока вы будете работать с  «Картой успеха».  (Учитель знакомит учащихся с «Картой успеха».)  На каждом этапе урока вы будете выставлять в карту успеха баллы за каждое задание выполненное правильно. Итак, начинаем наш урок.

      Улыбнитесь! Удачи всем!

      Чтобы не было проблем!

Запишите в тетради число, тему урока.

 

II.                Проверка домашнего задания (вчерашнее меню).

      Учитель: Проверить домашнее задание помогут нам наши консультанты. Они остановятся на алгоритме решения. (На экране высвечивается решение уравнений, двое учащихся поясняют последовательность шагов.)  Если ваше решение совпадает с представленным на доске, поставьте в карте успеха 2 балла.

 

III.           Актуализация опорных знаний (салат «Математический винегрет»).

Учитель:  Обобщим теоретические знания по пройденной теме и параллельно пройдемся по основным вопросам теории открытия иррациональности.  Как сказал Лобачевский: «Чем больше я знаю, тем больше умею».

     Иррациональное в переводе с греческого “уму непостижимое, неизмеримое, немыслимое”. Открытие иррациональности опровергало теорию Пифагора, что “всё есть число”. Предание говорит, что ученик Пифагора, выдавший смертным эту тайну погиб во время кораблекрушения, ниспосланного богами. Пифагорейцы, изгнавшие его из общины, еще при жизни соорудили ему могилу, как бы умершему.

  Учитель: История развития теории иррациональности знает много ученых – исследователей. Назовем некоторых из них, отвечая на вопросы теории, которая является фундаментом, для решения иррациональных уравнений.

 

Работа в группах. (Каждая группа получает кроссворд, разгадав его правильно, учащиеся получают имя ученого)

 

Вопросы для первого кроссворда.

1.     Что требуется для полученных значений переменной при решении иррациональных уравнений? (проверка)

2.     Способ, которым проводится проверка решений иррациональных уравнений. (подстановка)

3.     Как называется знак корня?( радикал)

4.     Сколько решений имеет уравнение х² = а, если а < 0? (ноль)

5.     Как называются уравнения, в которых под знаком корня содержится переменная? (иррациональное)

6.     Как называется корень второй степени? (квадратный)

 Учащийся 1 группы.   Получилось слово Евклид. Евклид – это великий ученый, он жил в 3 веке до нашей эры в Древней Греции. Известно, что он был приглашен в Александрию царем Птолемеем I Сотером для организации математической школы. Книга 10 главного труда Евклида – «Начала», посвящена  теории иррациональности.

Учитель: Понятие иррациональности ассоциируется с изображением корня. Греческие математики вместо слов “извлечь корень” говорили “найти сторону квадрата по его заданной величине (площади)”. Знак корня впервые появился в 1525 году. За это время его изображение менялось. Кто ввел это изображение, нам скажут учащиеся 2 группы.

 

 Вопросы для второго кроссворда.

1.     Сколько решений имеет уравнение х²=0. (одно)

2.     Корень какой степени существует из любого числа? (нечетной )

3.     Как называется корень третей степени? (кубический)

4.     Сколько решений имеет уравнение х²=а, если а >0 ? (два)

5.     Как называется корень уравнения, который получается в результате неравносильных преобразований? ( постороннний)

6.     Корень какой степени существует только из неотрицательного числа? (четной)

Учащийся 2  группы.   И так впервые изображение корня ввёл Декарт, французский ученый. Им положено начало исследования важных свойств алгебраических уравнений.

Учитель: Кто же ввел современное изображение корня?

Вопросы для третьего кроссворда.

1.   Как называется равенство двух алгебраических выражений? (уравнение)

2.   Как называют значение переменной, при котором уравнение обращается в верное числовое равенство (корень)

3.   Какая черта личности поможет при решении иррациональных уравнений? (трудолюбие)

4.   Какой должен быть взгляд на уравнения, что бы не вычисляя сказать ответ? (пристальный)

5.   Как называют уравнения, если они имеют одни и те же корни или не имеют корней вообще? (равносильные)

6.   Как называется иррациональное выражение, содержащее противоположное арифметическое действие? (сопряженное)

Учащийся 3  группы.   Это Ньютон – английский физик, открывший основные законы природы, законы Ньютона. Он ввёл современное изображение корня.

Учитель: Мы повторили теорию решения иррациональных уравнений, которая является фундаментом для познания мира.

(Если каждая группа справилась с заданием правильно, то каждый ученик выставляет себе в «Карте успеха» 1 балл)

IV.            Самостоятельная работа (первое блюдо)

      Учитель:  Как сказал Суворов «Непреодолимого ничего нет». Откройте текстовый документ «Самостоятельная работа». Решите задания и в течение 5 минут напечатайте ответ. По истечении времени проверти правильные ответы. Заполните карту успеха. (Каждый правильный ответ оценивается 1баллом)

V.                Минутка релаксации

 

VI.            Научный  эксперимент  (напитки «Красочный коктейль»).

 Учитель:  Ректор института землеустройства при анализе ошибок абитуриентов сказал, что большинство ошибок связано с формальным и поверхностным оформлением решения иррациональных уравнений.  Поэтому вам необходимо решить уравнение   
   различными способами. Затем мы проанализируем оформление решения одного и того же уравнения, насколько удачны они в логическом, языковом и коммуникативном аспектах.

Решение 1. Возведем обе части уравнения в квадрат и преобразуем полученное уравнение:

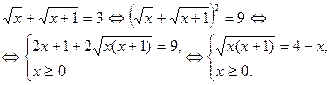
Вновь возведем обе части уравнения в квадрат:

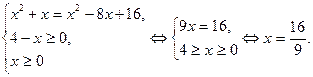
Ответ: .

Решение 2. Пусть , .

                    a+b=3

    Это уравнение отражает связь между новыми переменными, существующую в силу исходного уравнения. Для того чтобы решить задачу, попытаемся найти еще какое-либо соотношение, связывающее введенными переменными. Поскольку  и выражаются через , выразим их друг через друга уже в силу самой произведенной замене. Нетрудно заметить, что

a²  -  b²= x – x – 1 = - 1

Получим систему:

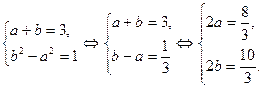
Следовательно, , откуда  и .

Проверка показывает, что - корень исходного уравнения.

Решение 3. Область определения уравнения

        
                               

 

Отделим один квадратный корень: 

Возведем обе части уравнения в квадрат:

 

 

                                                       

 

                                                       

 

 

Решить уравнение :    =33 (дополнительно)

 

VII .  Тестирование (математические орешки).

 Учитель: Следующий этап урока я бы назвала опорой на ранее изученное. Откройте документ «Тестирование». Решите задания в течение нескольких минут. Занесите набранное количество баллов в «Карту успеха».

 

VIII. Мозговая атака (второе блюдо).

Учитель: Ребята, я вам предлагаю проверить, правильно ли решены уравнения?

  =

      x – 2 = 2x – 1

      - 2x + x= 2 – 1

       x = -1

Ответ: -1.

 верное решение

 =

x – 2 = 2x – 1       x = -1

  x – 2 ≥ 0             x ≥ 2

 

Ответ: решений нет.

Проверка:  х=7 не удовлетворяет

Ответ: х=0

 

 

IX. Подведение итогов.  Домашнее задание (десерт)

       Учитель: У каждого из вас заполнена карта успеха, где в течение урока вы выставляли себе баллы, набранные на каждом  этапе урока. Подведем итог и выставим себе оценку.

Итак, у нас есть лидер, это ……, приглашаю для награждения. Посвящается в великие магистры и награждается символом мудрости – совой.

Домашнее задание индивидуальное.

 

X. Рефлексия (книга отзывов и предложений)

Притча: Шёл мудрец, а навстречу ему три человека, которые везли под горячим солнцем тележки с камнями для строительства. Мудрец остановился и задал каждому по вопросу. У первого спросил: «Что ты делал целый день?» И тот с ухмылкой ответил, что целый день возил проклятые камни. У второго спросил мудрец: «А что ты делал целый день?», и тот ответил: «А я добросовестно выполнял свою работу». А третий улыбнулся, его лицо засветилось радостью и удовольствием: «А я принимал участие в строительстве храма!»

 — Ребята! Давайте мы попробуем с вами оценить каждый свою работу за урок.

 — Кто работал так, как первый человек?

(Заливают смайлик зеленым цветом).

 — Кто работал добросовестно?

(Заливают смайлик синим цветом).

 — Кто принимал участие в строительстве храма науки?

(Заливают смайлик красным цветом).

“Да, мир познания не гладок.
И знаем мы со школьных лет
Загадок больше, чем разгадок
И поискам предела нет!”