Урок в 5 классе "Прямоугольный параллелепипед. Куб."

Тема: Прямоугольный параллелепипед. Куб

Тип урока: урок изучение нового материала. 

Цели урока:

 1)Получить представление о прямоугольном параллелепипеде (кубе), через предметы из окружающего мира, имеющих форму прямоугольного параллелепипеда (куба);

рассмотреть из каких элементов состоят эти геометрические  фигуры;

познакомиться с измерениями прямоугольного параллелепипеда;

научиться находить общую длину ребер и площадь поверхности параллелепипеда.

2) Развивать логическое мышление, внимательность, пространственное мышления, умения применять полученные знания на практике.

3) Воспитывать аккуратность, уважение друг к другу.

Оборудование: Компьютер, модели прямоугольного параллелепипеда и куба.

Весь иллюстративный материал демонстрируется на мониторе компьютера в виде презентации к данному уроку.

Ход урока.

1.     Организационный момент.

2.     Изучение нового материала.

Окружающий нас мир состоит из огромного количества разных по форме, цвету и размеру предметов. Многие предметы окружающего нас мира имеют одинаковую форму.

Сегодня мы рассмотрим с вами прямоугольный параллелепипед и куб. С предметами, которые имеют форму прямоугольного параллелепипеда и куба, вы сталкиваетесь практически каждый день.  Форму прямоугольного параллелепипеда имеют: кирпич, обувная коробка, и др.

Ребята, приведите еще примеры предметов из вашей жизни, которые имеют форму прямоугольного параллелепипеда.

(Примерные ответы детей: спичечный коробок, аквариум, класс, в котором мы находимся и т. д.)

На рисунке 1 изображены примеры предметов, имеющие форму параллелепипеда.

                                         Рис.1

 Поверхность прямоугольного параллелепипеда состоит из 6 прямоугольников, которые называются гранями прямоугольного параллелепипеда. Противоположные грани прямоугольного параллелепипеда равны. Грань, на которую поставлен параллелепипед, и ей противоположную называют нижним и верхним основаниями. Остальные четыре грани называют боковыми гранями.

Стороны граней параллелепипеда называют рёбрами, их - двенадцать.

Вершины граней называются вершинами параллелепипеда, их в параллелепипеде восемь. Все перечисленные элементы прямоугольного параллелепипеда вы можете увидеть на рисунке 2.

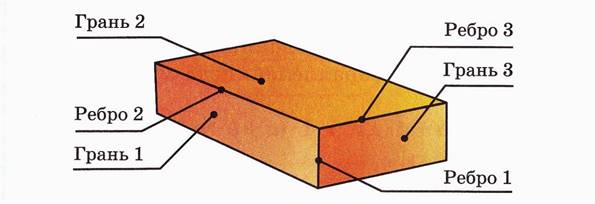
                                                   Рис. 2

Назовите на рисунке 3: а) грани параллелепипеда;

                                         б) равные грани параллелепипеда;

                                         в) ребра параллелепипеда;

                                         г) равные ребра параллелепипеда;

                                         д) вершины параллелепипеда;

                                         е) основания параллелепипеда;

                                         ж) боковые грани параллелепипеда.                                        

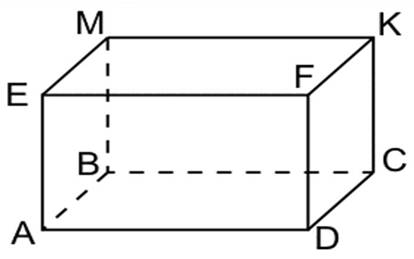
                                     Рис. 3

Каждая вершина является общим концом трёх рёбер. Длины этих ребер называют измерениями параллелепипеда: длиной, шириной и высотой.

Причем, длину обозначают – а, ширину – b, высоту – с.

Смотрим рисунок 4.

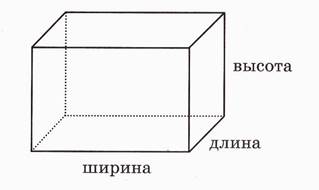
                                           Рис. 4                              

Прямоугольный параллелепипед, у которого все измерения равны, называется кубом.

Что вы можете сказать о размерах граней и ребер куба?

3. Физкультминутка.

4. Практическая часть урока.

а) Сколько проволоки понадобиться на изготовление каркаса куба с ребром 10 см?

б) Найдите площадь поверхности куба с длиной ребра 5 см?

в) Найдите длину ребер и площадь поверхности параллелепипеда, изображенного на рисунке 5.

                                                    А                            В

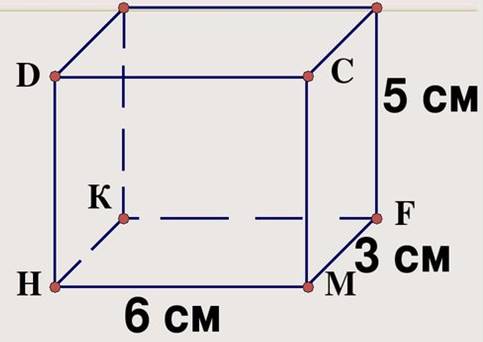
                                                        Рис. 5

       г) Дан куб с диной ребра а см. Найдите длину всех ребер и площадь поверхности куба.

           (Напомнить учащимся, что мы получили формулы для нахождения общей длины ребер и площади поверхности куба)

   д) Дан прямоугольный параллелепипед с длиной – а см, шириной – b см и высотой – с см. Найдите длину всех ребер параллелепипеда и его площадь поверхности.

            (Напомнить учащимся, что мы также получили формулы для нахождения общей длины ребер и площади поверхности параллелепипеда)

е) Решите самостоятельно. Найдите длину ребер и площади поверхности прямоугольного параллелепипеда, изображенного на рисунке 6. (Можете использовать формулы, полученные в предыдущем задании)

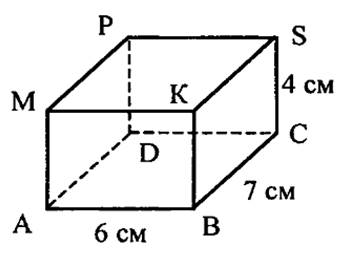
                                      Рис. 6             

е) Задания из учебника: № 371 (б), 374.

5. Подведение итогов урока

·        С каким геометрическим  фигурами мы познакомились сегодня на уроке?

·        Сколько граней у параллелепипеда?

·         Сколько ребер у параллелепипеда?

·         Сколько вершин у параллелепипеда?

6. Комментирование и выставление отметок

 7. Домашнее задание.  Глава 3, § 17, № 371 (а), 373. (Герасимов В.Д. и другие)