
Публикация является частью публикации:
Урок
53
Умножение на 5. Решение задач
Цели урока: совершенствовать навыки решения задач действиями умножение и деление; закреплять знание табличных случаев умножения и деления на 2, 3, 4; продолжить формирование умений вычислять периметр многоугольника; развивать глазомер и внимание.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Вставьте пропущенные числа и продолжите ряды.
|
а) |
82 |
|
|
|
58 |
52 |
46 |
|
|
|
22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) |
|
|
24 |
35 |
46 |
|
|
|
90 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
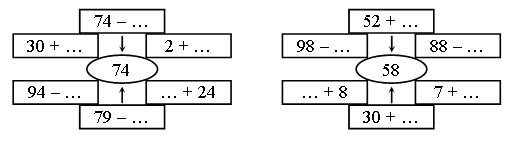
|
|
|
|
в) |
96 |
|
|
60 |
50 |
41 |
33 |
|
|
|
|
|
|
|
|
2. Задача.
Длина тела енота 69 см, а длина его хвоста на 45 см меньше. Придумайте и напишите такой вопрос, чтобы задача решалась в два действия. Решите задачу.

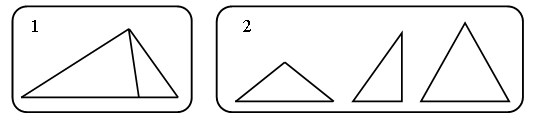
3. В каждой рамке обведите треугольник с большим, чем у других, периметром. Если нужно, выполните измерения и вычисления.
III. Сообщение темы урока.
– Рассмотрите рисунок на доске:
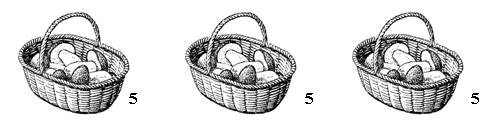
– Составьте по нему задачу. (Миша, Маша и Катя собирали грибы. Каждый собрал по 5 грибов. Сколько всего грибов собрали дети?)
– Как быстро решить эту задачу? (Умножением.)
– Сегодня будем решать задачи на умножение.
IV. Работа по теме урока.
Задание № 8 (с. 6).
– Прочитайте задачу.
– Что известно? Что требуется узнать?
Рассмотрев рисунок, учащиеся увидят, что в лагере 5 палаток. Так как по условию задачи в каждой палатке поселилось 3 человека, то задача решается так:

Решение: 3 · 5 = 15 (чел.).
Ответ: 15 человек.
– Какими данными нужно дополнить текст задачи, чтобы ее можно было решить без рисунка?
З а д а ч а. В лагере 5 палаток. Туристы поселились по 3 человека в палатке. Сколько всего человек живет в лагере?
Задание № 9 (с. 6).
– Прочитайте задачу и выполните рисунок к ее условию.
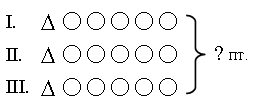
Решение: 1) 1 · 3 = 3 (пт.) – было уток.
2) 5 · 3 = 15 (пт.) – было утят.
3) 15 + 3 = 18 (пт.) – всего.
Ответ: 18 птиц.
Задание № 10 (с. 6).
– Рассмотрите чертеж.
– Как называется данная фигура?
– Как называется этот многоугольник? (Пятиугольник.)
– Что такое периметр многоугольника?
– Выполните необходимые измерения и вычислите периметр пятиугольника разными способами.
Запись: а = 1 см.
Р = 1 + 1 + 1 + 1 + 1 = 5 (см).
Р = 1 · 5 = 5 (см).
Ответ: 5 см.

V. Повторение пройденного материала.
1. Работа в печатной тетради № 2.
Задание № 4.
Запись:
Задание № 6.
Можно предложить карточки-помощницы:
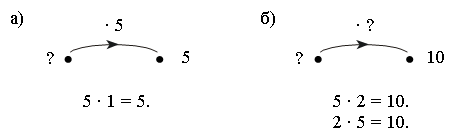
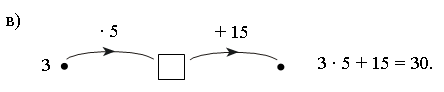
2. Работа по учебнику.
Задание № 28, 29 (с. 10).
Учащиеся работают самостоятельно. Работы сдают на проверку учителю.
Задание № 39 (с. 12).
– Какое время показывают каждые часы? (7 часов и 12 часов.)
– Какое время они будут показывать через час? (7 + 1 = 8 (ч); 12 + 1 = 13 (ч).)
Далее учитель может рассказать учащимся об истории создания календаря.
Справочный материал для учителя
Из истории календаря
– Вы уже знаете, что календарь появился много тысяч лет назад. Но каким он был? Похожим на современный или другим?
Сначала люди вообще не записывали чисел, а завязывали узелки на веревочках, представляя, что каждый узелок – это один день, или делали зарубки на деревянных брусках. Год в календарях древних начинался не зимой, как у нас, а летом. Отсчет вели от самого продолжительного дня в году, по нашему календарю это 21 июня. Календари были солнечные и лунные в зависимости от того, за каким небесным телом велось наблюдение. Год по солнечным и лунным календарям начинался в разное время. Представляете, как было неудобно людям ориентироваться во временах года!
Но вот четыре тысячи лет назад в Англии создали первый письменный календарь. Он был высечен из камня. Само слово календарь произошло от латинского калере, обозначавшее выкликать, выкрикивать. Специальные служащие криками объявляли появление серпа луны в начале месяца. В то время у людей было множество приспособлений, которые мы можем назвать календарем. И все же наиболее удачным оказался египетский календарь, составленный по солнечному году. Египтяне установили, что в году 12 месяцев по 30 дней в каждом и еще 5 добавочных дней. Все трудности при создании календаря возникали по причине того, что ни месяц, ни год нельзя было разделить на целое число суток. И эти «лишние» доли, накапливаясь за годы, образовывали новые сутки. Чтобы решить эту проблему, император Юлий Цезарь приказал прибавлять эти новые сутки к каждому четвертому году, который называли високосным, т. е. 365 дней + 1 день. Но и эта мера оказалась недостаточной. Тогда римский папа Григорий III приказал с 4 октября сразу перейти к 15 октября, нагнав таким образом упущенные 10 суток. С этого момента начался новый стиль счисления времени, при котором високосными нельзя было считать года 1700, 1800, 1900, 2100, 2200, 2300 и т. д. Этот стиль назвали григорианским в честь его учредителя Григория III и распространили во многих государствах, в том числе и у нас. Летосчисление договорились вести условно от Рождества Христова, а новый год начинать с 1 января.
VI. Итог урока.
– Что нового узнали на уроке?
– Как вычислить периметр многоугольника?
Домашнее задание: № 11 (учебник); № 1, 16 (рабочая тетрадь).
Урок
54
Умножение и деление на 5. Решение задач
Цели урока: составить таблицу деления на 5; рассмотреть особые случаи деления на единицу и деления нуля; совершенствовать навыки решения составных задач разными способами; продолжить формирование умений решать задачи геометрического содержания; развивать логическое мышление и умение рассуждать.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Вставьте числа и знаки действий, чтобы получились верные равенства.
|
53 – 3 … = 41 |
45 … – 8 = 32 |
|
72 – 2 … = 64 |
64 … + 9 = 59 |
|
83 – 3 … = 73 |
88 … – 9 = 71 |
|
65 – 5 … = 72 |
57 … + 3 = 63 |
|
66 – 6 … = 69 |
33 … – 6 = 24 |
2. Задача.
Вера и Коля набрали по 60 ягод земляники. Коля отдал Вере 12 ягод. Сколько ягод стало у Веры и сколько у Коли?
3. Чем похожи многоугольники? В чем их отличие?
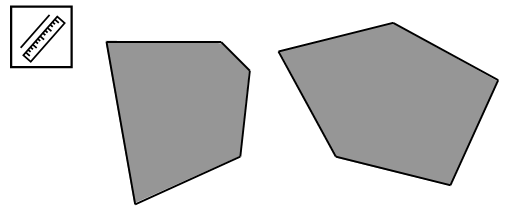
– Какому многоугольнику соответствует каждое выражение и что оно обозначает?

III. Сообщение темы урока.
– Используя рисунок, составьте верные равенства:
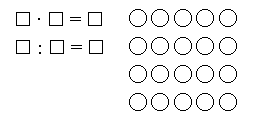
– Сегодня на уроке мы составим таблицу деления на 5.
IV. Изучение нового материала.
Учитель проводит фронтальную работу по составлению таблицы деления на 5.
– Вставьте пропущенные числа в «окошки», чтобы равенства были верными.
|
5 · 1 = |
5 · 2 = |
5 · 3 = |
5 · 4 = |
|
: 5 = |
: 5 = |
: 5 = |
: 5 = и т. д. |
Далее учащиеся сравнивают свою таблицу с таблицей деления на 5 (учебник, с. 7).
Задание № 12 (с. 7).
Используя таблицу умножения и деления на 5, учащиеся выполняют деление.
Задание № 14 (с. 7).
Запись: 0 · 5 = 0
0 : 5 = 0
– Объясните, какое число получилось. Почему?
Задание № 16 (с. 7).
– Прочитайте задачу.
– Что известно? Что требуется узнать?
– Запишите условие задачи в таблице.
|
Количество |
Количество |
Всего |
|
? х. одинаковое ? х. |
5 кл. |
20 х. |
|
3 кл. |
? х. |
Решение: 1) 20 : 5 = 4 (х.) – в 1 клетке.
2) 4 · 3 = 12 (х.) – в 3 клетках.
Ответ: 4 хомячка, 12 хомячков.
Задание № 17 (с. 7).
– Прочитайте текст. Является ли он задачей? Почему?
– Что известно? Что требуется узнать?
– Заполните таблицу:
|
Количество |
Количество |
Всего |
|
5 ф. |
? с. |
30 ф. |
|
одинаковое |
? с. |
15 ф. |
Решение: 1) 30 : 5 = 6 (с.) – заняли 30 фото.
2) 15 : 5 = 3 (с.) – заняли 15 фото.
Ответ: 6 страниц, 3 страницы.

V. Повторение пройденного материала.
1. Работа в печатной тетради № 2.
Задание № 5.
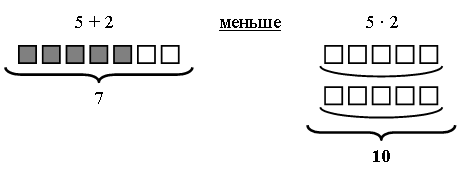
Все вычисления учащиеся выполняют устно, но так как они еще незнакомы со знаками «>» и «<», то решение оформляется так:
5 · 3 меньше 3 · 6
7 · 5 больше 7 · 4
8 · 5 равно 5 · 8
Сильные учащиеся выполняют сравнение, не производя вычисления.
Задание № 7.
– Прочитайте задачу.
– Что известно? Что требуется узнать?
– Решите задачу разными способами.
Решение:
I способ:
1) 1 · 5 = 5 (р.).
2) 5 + 5 = 10 (р.) или 5 · 2 = 10 (р.).
– Монетой какого достоинства можно заменить все Катины монеты по 1 рублю? (Одной монетой достоинством 5 рублей.)
– Сколько действий теперь надо выполнить, чтобы ответить на вопрос задачи? (Одно действие.)
II способ:
1) 5 · 2 = 10 (р.).
– Какой способ решения вам понравился больше?
2. Работа по учебнику.
Задание № 35 (с. 12).
– Какие фрукты лежат на тарелке?
– Обозначим название этих фруктов первой буквой. (Я – яблоко, Г – груша, А – апельсин.)
– Сколькими способами можно выбрать один плод? (Тремя способами.)
– Как изменится решение, если на тарелке лежат яблоко и апельсин?
– Как изменится решение, если на тарелке лежат яблоко, апельсин, груша и банан?
Задание № 36 (с. 12).
После чтения задания учитель проводит беседу.
– Чему равна сумма двух чисел? (32.)
– Что вам известно про одно слагаемое?
При затруднении в решении учитель использует карточку-помощницу.
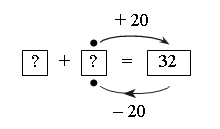
Решение: 32 – 20 = 12.
Значит, сложим числа 20 + 12 и получим 32.
Задание № 37 (с. 12).
Все фигуры, изображенные на чертеже, – многоугольники. Данное задание можно использовать для тренировки учащихся в выполнении логической операции классификации. Попросите детей разбить фигуры на группы так, чтобы в каждой были многоугольники с равным числом сторон (а значит, и углов, и вершин). Получатся 2 группы:
I группа – фигуры 3, 4 и 1 – четырехугольники.
II группа – фигура 2 – пятиугольник.
Задание № 38 (с. 12).
Каждое число в нижней клетке является результатом умножения числа в верхней клетке на такое же число, поэтому в пустую клетку надо поставить число 25 : 5 · 5 = 25.
VI. Итог урока.
– Что нового узнали на уроке?
– Назовите признаки четырехугольника.
– Назовите признаки пятиугольника.
Домашнее задание: № 13, 15 (учебник); № 2, 3 (рабочая тетрадь).
Урок
55
Умножение и деление на 5. Пятая часть
числа
Цели урока: ввести понятие «пятая часть числа»; учить находить пятую часть числа действием деление; совершенствовать навыки построения геометрических фигур; развивать умение анализировать и сравнивать.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Разгадайте закономерность и продолжите ряды чисел:
а) 99, 78, 57, … , … , … ;
б) 15, 30, 45, … , … , … ;
в) 1, 11, 23, 37, … , … , … ;
г) 12, 24, 36, … , … , … ;
д) 87, 76, 65, … , … , … .
2. Задача.
Подумайте, что нужно изменить в текстах задач, чтобы выражение 9 – 6 было решением каждой?
1) На двух скамейках сидели 6 девочек. На одной из них 9 девочек. Сколько девочек сидело на второй скамейке?
2) В саду 9 кустов красной смородины, а кустов черной смородины на 6 больше. Сколько кустов черной смородины в саду?
3) В гараже 9 легковых машин и 6 грузовых. Сколько всего машин в гараже?
3. Назовите пары отрезков, у которых одинаковая длина. Проверьте себя!
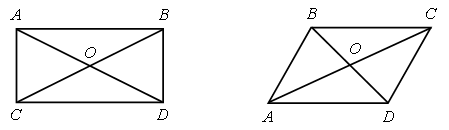
III. Сообщение темы урока.
– Рассмотрите иллюстрации на доске:
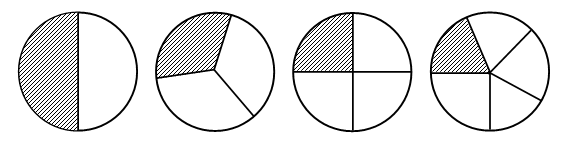
– Какая часть круга закрашена на каждом рисунке?
– Сегодня на уроке мы научимся находить пятую часть числа.
IV. Изучение нового материала.
– Используя фишки, выполните действие: 20 : 5.
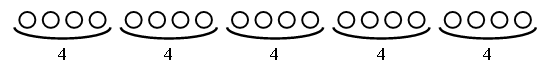
20 : 5 = 4.
– Покажите пятую часть числа 20.
– Чему она равна?
– Как найти пятую часть какого-нибудь числа? (Надо это число разделить на 5.)
Далее учащиеся читают правило на с. 8 учебника.
Задание № 21 (с. 8).
– Что значит найти пятую часть числа?
Решение:
|
10 : 5 = 2 |
35 : 5 = 7 |
|
40 : 5 = 8 |
20 : 5 = 4 и т. д. |
Задание № 22 (с. 8).
– Можно ли сразу узнать длину пятой части отрезка 3 дм 5 см? (Нет, так как надо длину данного отрезка выразить в сантиметрах.)
Решение: 1) 3 дм 5 см = 35 см;
2) 35 : 5 = 7 (см) – пятая часть отрезка.
Ответ: 7 см.
Задание № 23 (с. 9).
– Прочитайте текст. Является ли он задачей?
– Что вам известно? Что требуется узнать?
– Запишите кратко условие задачи.
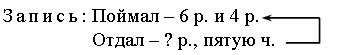
Решение: 1) 6 + 4 = 10 (р.) – поймал.
2) 10 : 5 = 2 (р.) – отдал.
Ответ: 2 р.
Задание № 24 (с. 9).
– Что известно в задании?
– Составьте схему к условию задания.
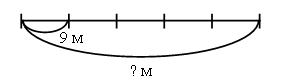
Решение: 9 · 5 = 45 (м).

V. Повторение пройденного материала.
1. Работа по учебнику.
Задание № 40 (с. 13).
Первая часть задания продолжает линию логических задач на перебор возможных вариантов решения.
Возможные варианты оплаты покупки:
1. За ластик: монетами 1 р. и 2 р. – 1 вариант.
2. За карандаш: монетами 1 р., 2 р. и 2 р. или монетой 5 р. – 2 варианта.
3. За блокнот: монетами 1 р., 2 р., 2 р. и 5 р. или монетами 5 р. и 5 р. – 2 варианта.
Для того чтобы ответить на вопросы второй части задания, необходимо предварительно выполнить ряд вычислений:
1. 1 + 2 + 2 + 5 + 5 = 15; 15 р. – всего денег было у Юли.
2. 1) 5 + 10 = 15; 15 р. – стоимость карандаша и блокнота.
2) 15 р. = 15 р. – значит, Юле хватит денег на покупку карандаша и блокнота.
3. 1) 5 · 2 = 10; 10 р. – стоят два карандаша.
2) 10 + 3 = 13; 13 р. – стоят два карандаша и ластик.
3) 13 р. меньше 15 р. – значит, Юле хватит денег на покупку двух карандашей и ластика.
4. 1) 3 · 3 = 9; 9 р. стоят три ластика.
2) 9 р. меньше 15 р. – значит, Юле хватит денег на покупку ластиков.
5. 1) 3 + 5 + 10 = 18; 18 р. – стоимость всех трех предметов.
2) 18 р. больше 15 р., значит, Юле не хватит денег на покупку всех трех предметов.
Разобрать задание вместе с классом можно во время устной фронтальной работы.
Задание № 41 (с. 13).
– Какие фигуры необходимо построить?
– Как они расположены?
Чертеж:
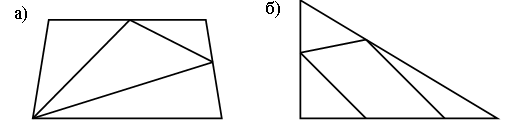
Задание № 42 (с. 13).
Разобрать и решить задачу можно устно, фронтально. Для того чтобы ответить на поставленный вопрос, надо сначала выяснить, сколько всего примеров записано на карточке. Сделать это можно по-разному: просто последовательно пересчитать примеры или найти их число вычислением. (Способ 1: на карточке 2 столбика по 6 примеров. Всего: 2 · 6 = 12 примеров. Способ 2: на карточке 6 строк по 2 примера. Всего: 6 · 2 = 12 примеров.)
Теперь можно ответить на вопрос задачи. 12 примеров записали по 4 в столбик, значит, в каждом столбике будет 3 примера (12 : 4 = 3).
В качестве дополнительного задания можно предложить устно выполнить все вычисления на карточке.
2. Работа в печатной тетради № 1.
Задание № 176.
Запись: Решение: 2 · 3 = 6 (д.) – всего.
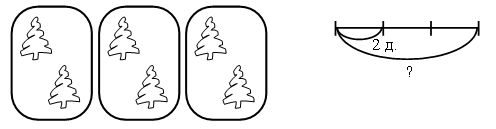
Ответ: 6 деревьев.
VI. Итог урока.
– Что нового узнали на уроке?
– Как найти пятую часть числа?
Домашнее задание: № 18, 19 (учебник); № 8, 14 (рабочая тетрадь).
Урок
56
Умножение и деление на 5. Пятая часть
числа.
Самостоятельная работа
Цели урока: закреплять знание табличных случаев умножения и деления на 2, 3, 4, 5; совершенствовать умение находить доли числа действием деление; познакомить учащихся с историей русских мер массы; развивать внимание и логическое мышление.
Ход урока
I. Организационный момент.
II. Устный счет.
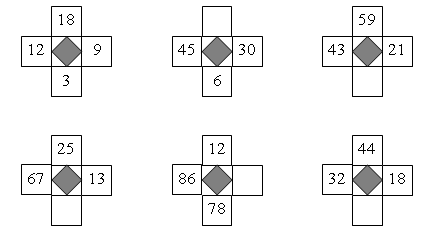
1. Догадайтесь, какие числа нужно вставить в «окошки».
2. Сравните тексты задач. Чем они похожи? Чем отличаются?
|
На верхней полке 10 книг. На нижней – столько же. Сколько книг на нижней полке? |
|
|
|
На верхней полке 10 книг. На нижней – столько же. Сколько книг на двух полках? |
3. Догадайтесь, какому из прямоугольников соответствует каждое выражение и что оно обозначает:
|
(3 · 2) + (8 · 2) |
3 · 4 |
(4 · 2) + (3 · 2) |

III. Сообщение темы урока.
– Сегодня мы будем совершенствовать умение находить пятую часть числа действием деление.
IV. Работа по теме урока.
1. Работа по учебнику.
Статья «Путешествие в прошлое» (с. 10).
Из истории мер массы.
Система мер у русского народа
– Сегодня мы узнаем, как люди научились определять массу различных предметов. Определите, что весит больше: карандаш или тетрадь? Теперь возьмите 8 карандашей в одну руку и тетрадь в другую. Что получилось? Значит, 1 тетрадь весит 8 карандашей. Вот мы и придумали новую единицу массы – «1 карандаш». Теперь в «карандашах» можно измерять все что угодно. Так поступали древние торговцы, используя различные подручные средства. Например, на Руси древнейшей мерой массы была гривна (или фунт) – кусок металла, масса которого по нынешним меркам равна примерно 410 граммам. Фунт делится на 96 золотников. Почему именно на 96, ведь гораздо проще было бы использовать круглое число? Оказывается, древние гири весили 1, 2, 3, 6, 12, 24, 48 золотников. Если все гири сложить вместе, то получится 1 + 2 + 3 + 6 + 12 + 24 + 48 = 96 золотников. Так, 1 золотник весил примерно 4 грамма. Помните пословицу: «Мал золотник, да дорог»? Действительно, золотник весил очень мало.
В аптекарском деле применялась унция, которая равна примерно 30 граммам. Чтобы измерить более тяжелые предметы, использовался пуд, который равнялся 40 фунтам, или 16 кг, тонна (столько весила бочка с жидкостью), берковец (корзина, заполненная доверху).
Далее учитель предлагает решить старинные задачи (с. 10 учебника).
Решение первой старинной задачи следующее: 5 · 2 = 10, то есть 10 пудов. С ней могут справиться даже самые слабоуспевающие ученики. Сильным же детям в качестве дополнительной работы можно предложить такое задание: «Сколько примерно килограммов зерна получил крестьянин с каждой копны ржи? Решите задачу с помощью микрокалькулятора». Для того чтобы ответить на вопрос, ученики должны воспользоваться материалом рубрики «Путешествие в прошлое», в котором говорится, что 1 пуд – это примерно 16 кг. Так как с каждой копны получили по 5 пудов, то это примерно 16 · 5 = 80, то есть 80 кг зерна.
Перед решением второй старинной задачи надо обратить внимание детей на то, что пятак – это медная монета достоинством 5 копеек.
Решение: 5 · 4 = 20.
Ответ: мальчик получил одну серебряную монету достоинством 20 копеек.
2. Работа в печатной тетради № 2.
Задание № 10.
Учитель может предложить карточки-помощницы.
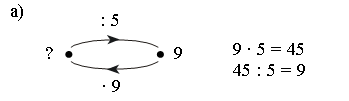
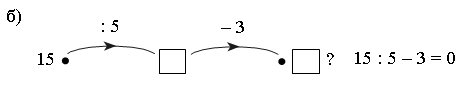
– Решите данные примеры.
– Подчеркните только те примеры, ответы которых делятся на 5.
– Сравните числа, которые делятся на 5. Какой вывод вы можете сделать?
Признак делимости чисел на 5.
Если число оканчивается на 0 или 5, то оно делится на 5.
– Назовите несколько своих чисел, которые можно разделить на 5.
V. Итог урока.
Урок
57
Умножение на 6
Цели урока: составить таблицу умножения шести и умножения на 6; совершенствовать навыки составления и преобразования задач; закреплять табличные случаи умножения и деления на 2, 3, 4, 5; развивать умение рассуждать и доказывать.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Поставьте «+» или «– » так, чтобы равенства были верными.
|
64 … 3 … 30 = 91 |
79 … 6 … 60 = 13 |
|
72 … 7 … 50 = 29 |
87 … 2 … 20 = 69 |
|
8 … 2 … 53 = 63 |
61 … 9 … 20 = 50 |
|
94 … 50 … 5 = 49 |
42 … 8 … 40 = 10 |
2. Сколько на чертеже:
кругов ;
квадратов ;
треугольников ?
Обведите кривые линии.
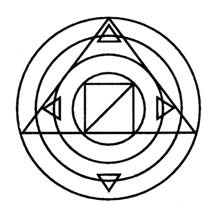
3. Щенок тяжелее котенка. С помощью стрелочки ↑ исправьте ошибки художника.
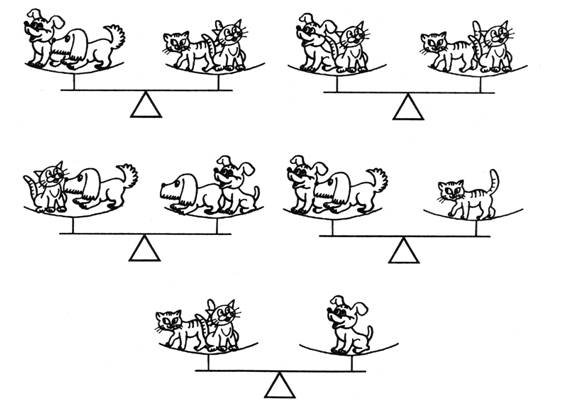
III. Сообщение темы урока.
– Прочитайте примеры, записанные на доске.
|
2 · 7 |
4 · 7 |
6 · 7 |
5 · 7 |
– Значения каких примеров вы сможете назвать?
– Какой пример будет «лишним»? Почему?
– Сегодня на уроке мы составим таблицу умножения на 6.
IV. Изучение нового материала.
Задание № 1 (с. 14).
– Рассмотрите иллюстрацию в учебнике.
– Сколько коробок лежит на столе? (7.)
– Сколько карандашей в каждой коробке? (6.)
– Сколько всего карандашей в 7 коробках?
– Как решил задачу Волк? (Он использовал сложение.)
– Как решил Заяц? (Он использовал умножение.)
– Кто из них быстрее справился с заданием? Почему?
Далее учащиеся, используя фишки, составляют таблицу умножения числа 6 и записывают ее в тетрадь.
Задание № 2 (с. 15).
Используя фишки, учащиеся находят результаты умножения чисел.
Задание № 4 (с. 15).
Учащиеся сравнивают результаты умножения.
Запись:
6 · 3 равно 3 · 6, так как 6 · 3 = 18 и 3 · 6 = 18;
6 · 7 равно 7 · 6, так как 6 · 7 = 42 и 7 · 6 = 42;
6 · 9 равно 9 · 6, так как 6 · 9 = 54 и 9 · 6 = 54.
Вывод: при перестановке множителей результат умножения не изменяется.
Задание № 5 (с. 15).
Запись: 6 · 0 = 0.
0 · 6 = 0.
Вывод:
· При умножении какого-нибудь числа на нуль получится нуль.
· При умножении нуля на какое-нибудь число получится нуль.
Задание № 6 (с. 15).
Используя таблицу умножения числа 6, учащиеся составляют и записывают таблицу умножения на 6.

V. Повторение пройденного материала.
1. Работа по учебнику.
Задание № 28 (с. 20).
При решении данной задачи целесообразно использовать «машины» в качестве моделей, описывающих содержание задачи и помогающих найти способ ее решения:
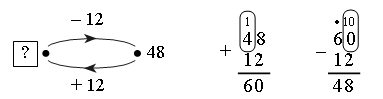
Ответ: 60.
2. Работа в печатной тетради № 1.
Задание № 180.
– Рассмотрите рисунок.
– Сколько ячеек в подставке для яиц?
6 · 5 = 30 (ячеек).
– Сколько яиц на подставке?
|
I способ: |
II способ: |
|
4 · 2 + 3 · 4 = 20 (яиц). |
6 · 3 + 2 = 20 (яиц). |
Ответ: 30 ячеек; 20 яиц.
Задание № 181.
– Рассмотрите иллюстрацию и составьте по ней задачу.
Задача. В каждой коробке 6 карандашей. Сколько карандашей в 4 таких коробках?
Решение:
|
I способ: |
II способ: |
|
6 + 6 + 6 + 6 = 24 (к.). |
6 · 4 = 24 (к.). |
Ответ: 24 карандаша.
Справочный материал для учителя
Умножение на пальцах
– Пальцевой счет был необходим в торговых местах, где сталкивались представители разных народов, не имевших общего языка. Знаки, изображаемые на пальцах, были понятны всем без слов. Этот прием умножения используется для чисел, которые больше 5, но меньше 10:
|
6 · 9 |
6 · 8 |
6 · 7 |
6 · 6 |
|
7 · 9 |
7 · 8 |
7 · 7 |
7 · 6 |
|
8 · 9 |
8 · 8 |
8 · 7 |
8 · 6 |
|
9 · 9 |
9 · 8 |
9 · 7 |
9 · 6 |
Чтобы выполнить умножение на пальцах, нужно вытянуть на одной и другой руках столько пальцев, на сколько единиц каждый множитель превышает число 5. Сумма чисел вытянутых пальцев дает десятки произведения. Произведение чисел, соответствующее оставшимся незагнутым пальцам, дает единицы ответа. Полученные десятки и единицы нужно сложить. Это будет искомым произведением. Например, нужно было умножить 7 на 8. На одной руке показывали 3 пальца (8 > 5 на 3), на другой 2 (7 > 5 на 2). 3 + 2 = 5 – это десятки произведения чисел 7 · 8. На одной руке остались незагнутыми 2 пальца, на другой – 3. 2 · 3 = 6 – это единицы произведения: 7 и 8. Итак, 7 · 8 =50 + 6 = 56.
VI. Итог урока.
– Что нового узнали на уроке?
– Как найти долю от числа?
– Что означает запись: «3 · 6»?
Домашнее задание: № 27 (учебник); № 19, 20 (рабочая тетрадь).
Урок
58
Умножение на 6. Решение задач
Цели урока: совершенствовать навыки решения составных задач, задач на нахождение периметра; закреплять табличные случаи умножения и деления на 2, 3, 4, 5, 6; продолжить формирование вычислительных навыков; развивать глазомер и внимание.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Соедините выражения с одинаковыми значениями.
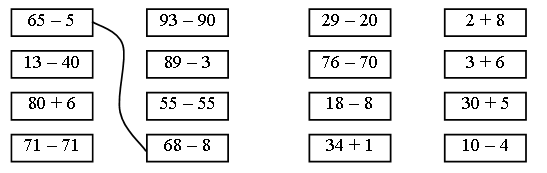
2. Задача.
На елке висело несколько игрушек. Когда на нее повесили еще 8, то на елке стало 15 игрушек. Сколько игрушек было на елке? Выберите схему, которая подходит к данной задаче:
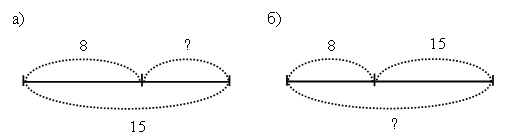
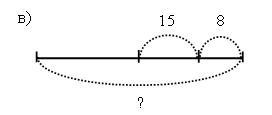
– Выберите выражение, которое является решением задачи:
![]()
3. Найдите закономерность и сделайте чертежи.
III. Сообщение темы урока.
– Рассмотрите иллюстрацию на доске и составьте по ней задачу.
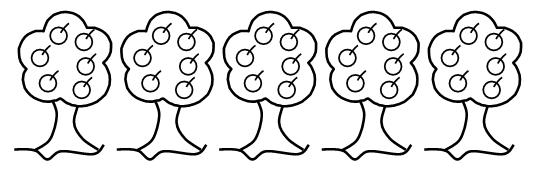
З а д а ч а. В саду росло 5 яблонь. С каждого дерева сорвали по 6 яблок. Сколько сорвали плодов?
– Сегодня на уроке мы будем решать задачи, используя таблицу умножения на 6.
IV. Изучение нового материала.
Задание № 7 (с. 15).
– Прочитайте задачу.
– Что известно? Что требуется узнать?
– Выполните рисунок к данной задаче и решите ее.
|
Запись: |
∆∆∆∆ |
4 + 4 + 4 + 4 + 4 + 4 = 24 (д.). |
|
|
∆∆∆∆ |
4 · 6 = 24 (д.) – построили. |
|
|
∆∆∆∆ |
Ответ: 24 дома. |
|
|
∆∆∆∆ |
|
|
|
∆∆∆∆ |
|
|
|
∆∆∆∆ |
|
Задание № 8 (с. 15).
– Прочитайте текст. Является ли он задачей? Почему?
– Что известно? Что требуется узнать?
– Запишите условие задачи в таблицу.
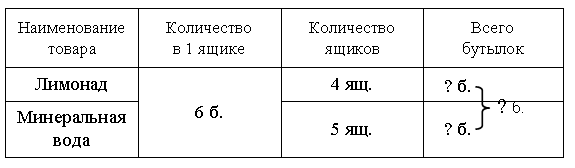
Решение:
I способ:
1) 6 · 4 = 24 (б.) – в 4 ящиках.
2) 6 · 5 = 30 (б.) – в 5 ящиках.
3) 24 + 30 = 54 (б.) – всего.
II способ:
1) 4 + 5 = 9 (ящ.) – всего.
2) 6 · 9 = 54 (б.) – всего.
Ответ: 54 бутылки.
Задание № 9 (с. 16).
– Рассмотрите чертежи.
– Как называются эти фигуры? (Многоугольники.)
– Назовите признаки многоугольников.
– Как называется первый многоугольник? (Восьмиугольник.)
– Как называется второй многоугольник? (Двадцатиугольник.)
– Чем схожи эти многоугольники? (Они невыпуклые.)
– Назовите признаки выпуклых и невыпуклых многоугольников.
– На сколько квадратов разделена каждая фигура? Подсчитайте их количество разными способами.
Решение:
|
|
I способ |
|
1-я фигура: |
6 + 6 + 2 + 2 + 6 + 6 = 28 (кв.). |
|
|
II способ |
|
|
6 · 4 + 2 · 2 = 28 (кв.). |
|
|
I способ |
|
2-я фигура: |
6 + 6 + 4 + 4 + 4 + 4 + 2 + 2 = 32 (кв.) |
|
|
или |
|
|
6 + 6 + 6 + 6 + 2 + 2 + 2 + 2 = 32 (кв.). |
|
|
II способ |
|
|
6 · 2 + 4 · 4 + 2 · 2 = 32 (кв.) |
|
|
или |
|
|
6 · 4 + 2 · 4 = 32 (кв.). |
– Какой способ оказался лучше?
Задание № 11 (с. 16).
– Рассмотрите фигуры. Как они называются?
– Чем они похожи? (Количеством углов, вершин, сторон.)
– Чем они отличаются? (Стороны имеют разную длину.)
– Чему равны стороны первого шестиугольника? (2 см.)
– Чему равны стороны второго шестиугольника? (1 см.)
– Периметр какого шестиугольника больше? Почему?
– Вычислите периметр этих шестиугольников.
Решение: 1) 2 + 2 + 2 + 2 + 2 + 2 = 12 (см).
2 · 6 = 12 (см).
2) 1 + 1 + 1 + 1 + 1 + 1 = 6 (см).
1 · 6 = 6 (см).

V. Повторение пройденного материала.
1. Работа по учебнику.
Задание № 30 (с. 20).
Учащиеся читают названия единиц величин.
– Выберите из них единицы длины. (Аршин, метр, дециметр.)
– Какие единицы массы? (Пуд, килограмм.)
– Какие единицы остались? (Единицы времени – неделя, час.)
Справочный материал для учителя
Как люди научились измерять время
– Считать предметы мы умеем с первого класса. Это очень просто – один, два, три... Измерить расстояние тоже несложно. А как и чем измерять время? Самыми древними «часами», которые никогда не останавливались и не ломались, оказалось солнце. Утро, вечер, день – не очень-то точные мерки, но поначалу первобытному человеку этого было достаточно. Потом люди стали больше наблюдать за небом и обнаружили, что через определенное время на небосклоне появляется яркая звезда. Эти наблюдения сделали египтяне, и они же назвали эту звезду Сириус. Когда появлялся Сириус, в Египте отмечали наступление Нового года. Так возникла хорошо известная сейчас мера времени – год. Оказалось, что промежуток между появлениями Сириуса состоит из 365 дней. Как видите, подсчеты древних египтян были достаточно точными. Ведь и наш год состоит из 365 дней. Но год слишком уж долгая мера времени. А для того чтобы вести хозяйство: посев, сбор, подготовку урожая, – нужны были более мелкие единицы времени, и люди вновь обратились к небу и звездам. На этот раз на помощь пришла луна, или, по-другому, – месяц. Все вы наблюдали за луной и знаете, что через определенное время она меняет свою форму: от тоненького серпа до яркого круглого диска (полнолуния). Промежуток между двумя полнолуниями и назвали месяцем. Оказалось, что месяц состоит примерно из 29 дней. Вот как точно в Древнем мире умели определять время.
А семидневная неделя возникла в Вавилоне благодаря тем планетам, которые появлялись на небосклоне и были известны вавилонянам:
суббота – день Сатурна;
воскресенье – день Солнца;
понедельник – день Луны;
вторник – день Марса;
среда – день Меркурия;
четверг – день Юпитера;
пятница – день Венеры.
Если бы в Вавилоне были известны и другие планеты нашей Солнечной системы, возможно, наша неделя состояла бы не из 7, а из 9, 10 или 8 дней. Смена этих светил в течение месяца происходила примерно 4 раза. Вот и оказалось, что в месяце 4 недели. Итак, самое сложное – найти мерки времени – было сделано уже в Древнем мире. Этими мерами пользуются по сей день. Только вот называют их по-разному. На Руси название дней недели произошли от порядкового номера дня в неделе:
понедельник – по неделе; начинающий неделю;
вторник – второй день;
среда – середина недели;
четверг – четвертый день;
пятница – пятый день;
суббота, воскресенье – эти названия пришли из церковного словаря.
Выходит, что все главные меры времени (год, месяц, неделя) люди позаимствовали у природы еще много лет назад. Хотя этими мерками нельзя было измерить точное время, но главный шаг все-таки был сделан.
2. Работа в печатной тетради № 2.
Задание № 24.
Решение задачи представлено в непривычной для учащихся форме – в виде схемы. Разбор задачи можно организовать так. Предложите детям внимательно рассмотреть схему решения задачи.
– Во сколько действий решается задача? (В 2 действия.)
– Что предлагается найти в первом действии? (Сколько рам изготавливает один столяр за 2 дня.)
– Чему равен результат? (6 рам.)
– Впишите полученный результат в нужное «окошко».
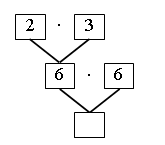
– Что предлагается найти во втором действии? (Сколько рам изготовят за 2 дня 6 столяров.)
– Выполните вычисления. (6 · 6 = 36.)
– Закончите оформление решения задачи.
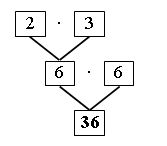
Ответ: 36 рам.
В качестве дополнительного задания можно предложить учащимся придумать другой способ решения этой задачи, а затем устно разобрать его.
1) 3 · 6 = 18 – столько рам изготовляют 6 столяров за 1 день;
2) 18 · 2 = 36 – столько рам изготовят 6 столяров за 2 дня.
VI. Итог урока.
– Что нового узнали на уроке?
– Как люди научились измерять время?
Домашнее задание: № 12 (учебник); № 21, 22 (рабочая тетрадь).
Урок
59
Умножение на 6. Деление на 6
Цели урока: составить таблицу деления на 6; совершенствовать навыки решения задач разными способами; закреплять ранее изученные табличные случаи умножения и деления; развивать логическое мышление.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Поставьте «+» или «–» так, чтобы равенства были верными.
|
79 … 50 … 6 = 23 |
18 … 60 … 40 = 38 |
|
45 … 5 … 30 = 10 |
51 … 40 … 30 = 61 |
|
10 … 6 … 80 = 84 |
89 … 6 … 2 = 81 |
|
7 … 3 … 57 = 67 |
8 … 2 … 7 = 17 |
2. Задача.
В ящике 12 баклажанов, а в корзине 10. Все баклажаны из корзины переложили в ящик. Сколько баклажанов стало в ящике?
3. Дети рисовали многоугольники и превращали их в портреты.
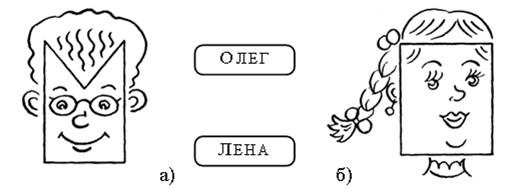
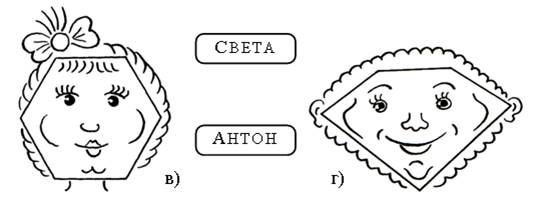
Число сторон в многоугольниках Олега и Светы одинаковое. Периметры многоугольников Светы и Антона равны между собой.
III. Сообщение темы урока.
– Рассмотрите рисунок на доске.

– Какие примеры можно составить к данной иллюстрации?
+ + + + =
· =
: =
– Вставьте числа в «окошки», используя этот рисунок.
– Какие трудности у вас возникли?
– Сегодня на уроке мы составим таблицу деления на 6.
IV. Изучение нового материала.
Учащиеся, используя фишки и опорные примеры на умножение, составляют таблицу деления на 6.
|
1 · 6 = |
2 · 6 = |
3 · 6 = |
4 · 6 = |
|
: 6 = |
: 6 = |
: 6 = |
: 6 = и т. д. |
Далее учащиеся сравнивают свою таблицу деления на 6 с таблицей, данной в учебнике (с. 17).
Задание № 13 (с. 17).
Используя таблицу умножения на 6, учащиеся выполняют деление.
36 : 6 = 6, так как 6 · 6 = 36.
18 : 6 = 3, так как 6 · 3 = 18 и т. д.
Задание № 15 (с. 17).
– Прочитайте задачи.
– Решите каждую задачу.
|
Решение: 18 : 6 = 3 (п.) – получилось. Ответ: 3 пучка. |
Решение: 18 : 3 = 6 (р.) – в 1 кучке. Ответ: 6 редисок. |
– Сравните решения этих задач. Чем они похожи?
– Как называются эти задачи? (Это обратные задачи.)
– Составьте и запишите еще одну обратную задачу.
З а д а ч а. Все редиски связали в 3 пучка по 6 редисок в каждом. Сколько всего редисок связали?
Решение:
6 · 3 = 18 (п.) – всего.
Ответ: 18 пучков.
Задание № 16 (с. 18).
Запись: 6, 12, 18, 24, 30, 36, 42, 48.

V. Повторение пройденного материала.
1. Работа по учебнику.
Задание № 17 (с. 18).
– Прочитайте текст. Является ли он задачей? Почему?
– Что известно в задаче?
– Что надо узнать?
– Запишите условие задачи в таблице.
|
Книг в 1 подарке |
Количество |
Всего |
|
4 кн. 2 кн. |
? п. |
54 кн. |
Решение: 1) 4 + 2 = 6 (кн.) – в 1 подарке.
2) 54 : 6 = 9 (п.) – получилось.
Ответ: 9 подарков.
Задание № 18 (с. 18).
– Прочитайте задачу.
– Что известно? Что требуется узнать?
– Запишите условие этой задачи в таблицу.

Решение:
I способ: 1) 18 : 6 = 3 (к.) – из I рулона.
2) 12 : 6 = 2 (к.) – из II рулона.
3) 3 + 2 = 5 (к.) – всего.
II способ: 1) 18 + 12 = 30 (м) – всего.
2) 30 : 6 = 5 (к.) – всего.
Ответ: 5 комплектов.
Задание № 29 (с. 21).
При решении данной задачи целесообразно использовать «машины» в качестве моделей, описывающих содержание задачи и помогающих найти способ ее решения.
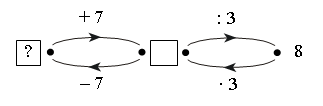
Решение:
1) 8 · 3 = 24.
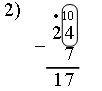
Ответ: 17.
2. Работа в печатной тетради № 2.
Задание № 30.
Вывод: у Маши 4 шарика, а у Кати – 3 шарика, так как по условию у Маши шариков не меньше, чем у Кати.
VI. Итог урока.
– Что нового узнали на уроке?
– Как связано деление с умножением?
Домашнее задание: № 19 (учебник); № 23, 25 (рабочая тетрадь).
Урок
60
Умножение и деление на 6.
Шестая часть числа
Цели урока: ввести понятие «шестая часть числа»; учить находить шестую часть числа; продолжить работу по составлению и чтению математических графов; совершенствовать вычислительные навыки; развивать умение анализировать и рассуждать.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Догадайтесь, как связаны числа с рисунками, и заполните пустые «окошки».
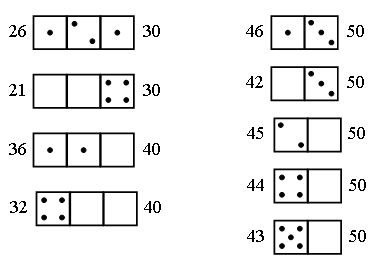
2. Задачи.
Сравните тексты задач. Чем они похожи, чем отличаются? Решите каждую задачу.
|
Из зала сначала вынесли 24 стула, потом еще 10. На сколько стульев в зале стало меньше? Сколько стульев осталось в зале? |
|
Из зала сначала вынесли 24 стула, потом еще 10. На сколько стульев в зале стало меньше? Сколько стульев осталось, если в зале было 84 стула? |
3. Карлсон отрезал пятую часть полотенца Фрекен Бок. Обведите отрезанный кусок полотенца.
III. Сообщение темы урока.
– Рассмотрите рисунки.

– Чем они похожи?
– Какая часть четырехугольника закрашена на каждом рисунке?
– Какие трудности у вас возникли?
– Сегодня на уроке мы узнаем, как вычислить шестую часть числа.
IV. Изучение нового материала.
– Используя фишки, выполните деление: 18 : 6.
![]()
– Покажите одну шестую часть числа 18. Чему равна шестая часть числа 18? (3.)
– Как же найти шестую часть числа? (Надо разделить число на 6.)
– Прочитайте правило в учебнике на с. 18.
Задание № 20 (с. 18).
– Что значит «найти шестую часть числа»?
|
Запись: |
12 : 6 = 2 |
48 : 6 = 8 |
|
|
24 : 6 = 4 |
36 : 6 = 6 и т. д. |
Задание № 21 (с. 19).
– Прочитайте задачу.
– Что известно? Что требуется узнать?
Для того чтобы ответить на первый вопрос задачи, надо найти шестую часть числа 36, то есть 36 разделить на 6 (36 : 6 = 6). Значит, в день рабочие собирали по 6 машин. При ответе на второй вопрос задачи, скорее всего, дети будут рассуждать так: «Так как рабочие каждый день собирали 6 машин, а всего было собрано 36 машин, то, чтобы выяснить, сколько дней длилась работа, надо 36 разделить на 6 (36 : 6 = 6). Значит, работа длилась 6 дней».
– Можно ли ответить на второй вопрос задачи, не выполняя вычисления? (Действительно, в выполнении вычислений нет необходимости. Из условия задачи следует, что вся работа была разделена на 6 равных частей. На выполнение одной части требуется один день, значит, на выполнение всей работы потребуется 6 дней.)
Задание № 23 (с. 19).
– Прочитайте задачу.
– Что известно? Что требуется узнать?
– Нарисуйте схему к данной задаче.
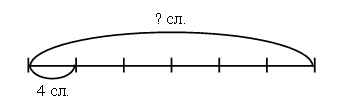
Решение: 4 · 6 = 24 (сл.) – всего.
Ответ: 24 сл.

V. Повторение пройденного материала.
1. Работа по учебнику.
Задание № 30 (с. 21).
– Прочитайте задачу.
– Что известно в задаче? Что требуется узнать?
– Все ли данные потребуются для решения этой задачи?
– Объясните, почему мы не учитываем при решении задачи тот факт, что в журналы выставлялись оценки в течение 5 дней.
Запись: Всего – 40 оц.
«Пятерок» – 10 оц.
«Четверок» – 15 оц.
«Троек» – ? оц.
Решение:
40 – 10 – 15 = 15 (оц.) – «троек».
Ответ: 15 оценок.
2. Работа в печатной тетради № 2.
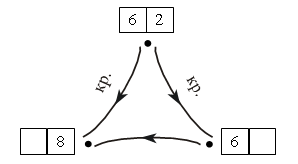
Задание № 31.
– Что изображено в тетради? (Граф.)
– Какое отношение изображено на этом графе? (Отношение «больше».)
Желательно устно перебрать с учащимися все возможные варианты чисел, которые могут стоять в «окошках».
|
Для числа |
|
8 |
– это числа 1, 2, 3, 4, и 5. |
|
Для числа |
6 |
|
– это числа 0 и 1. |
VI. Итог урока.
– Что нового узнали на уроке?
– Как найти шестую часть числа?
– Решите кроссворд.
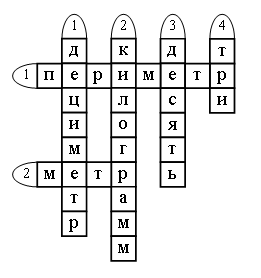
По горизонтали:
1. Сумма длин сторон многоугольника. 2. Мера длины.
По вертикали:
1. Мера длины. 2. Мера массы. 3. Неизвестное число (5 + 5 = ). 4. Наименьшее число вершин многоугольника.
Домашнее задание: № 22 (учебник); № 27 (рабочая тетрадь).
Урок
61
Умножение и деление на 6. Шестая часть
числа
Цели урока: учить находить шестую часть числа; совершенствовать вычислительные навыки; продолжить формирование умений решать геометрические задачи, выполнять чертежи; развивать внимание и логическое мышление.
Ход урока
I. Организационный момент.
II. Устный счет.
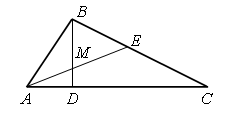
1. Сколько отрезков на чертеже?
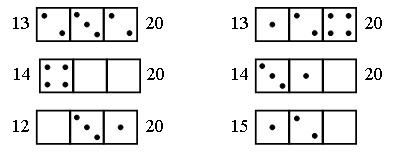
2. Догадайтесь, как связаны числа с рисунками, и заполните пустые «окошки».
3. Задача.
При озеленении проспекта планировалось высадить 100 деревьев. По одной стороне проспекта посадили 40, а по другой – 60 деревьев. Был ли выполнен план посадки деревьев?
4. Знайка сделал чертеж:
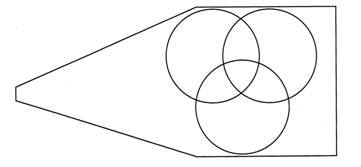
Он написал на нем все натуральные числа от 2 до 18. Из них в левый круг попали числа, которые делятся на 2, в правый – на 3, в нижний – на 4. Запишите эти же числа так, как это сделал Знайка.
III. Сообщение темы урока.
– Рассмотрите рисунки на доске.

– Чем они похожи?
– Чем отличаются?
– Сегодня мы продолжим учиться находить шестую часть числа и число по его шестой части.
IV. Работа по теме урока.
– На каком из чертежей закрашена шестая часть фигуры?
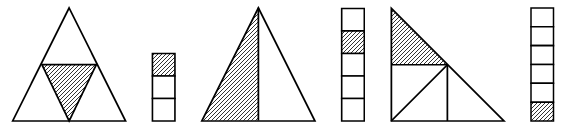
– Как найти шестую часть числа?
Задание № 23 (с. 19).
Учитель предлагает учащимся карточку-помощницу.
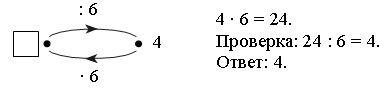
Задание № 25 (с. 19).
– Как найти число, если известна его шестая часть? (Надо значение шестой части умножить на 6.)
Запись:
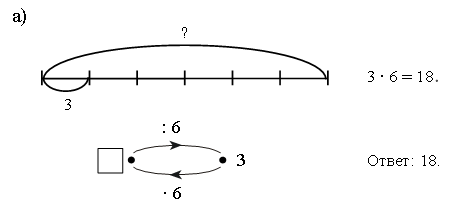
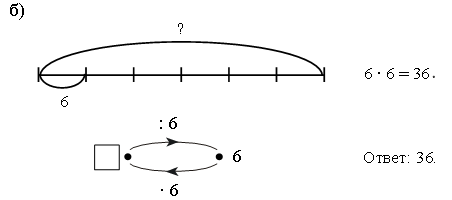
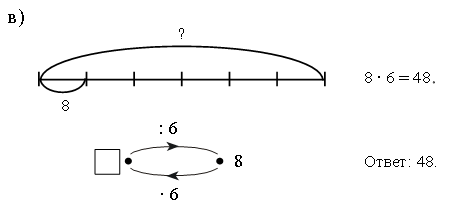
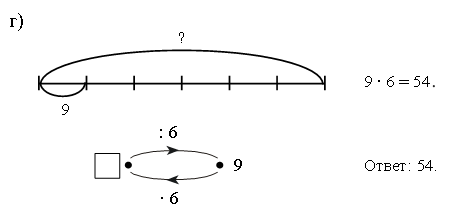
Задание № 24 (с. 19).
Правы оба мальчика, так как половина квадрата равна трем шестых части квадрата.
ФИЗКУЛЬТМИНУТКА
V. Повторение пройденного материала.
1. Работа по учебнику.
Задание № 31 (с. 21).
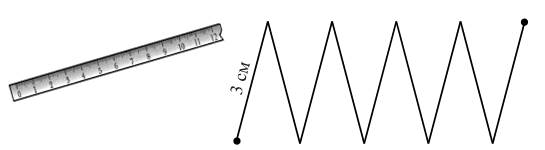
– Рассмотрите рисунок. Как измеряли длину цепочки мальчики?
– Каким инструментом пользовались ребята?
– Кто правильно проводил измерения? (Вова.)
– Какие ошибки допустил Миша? (Надо измерять от нуля линейки.)
– Какие ошибки допустил Сева? (Сева не выровнял цепочку по линейке.)
Справочный материал для учителя
История линейки
– Знаете ли вы, что в 1989 году у линейки был юбилей? Ей исполнилось 200 лет. Однако линейкой пользовались и в более ранние времена. В Средневековье, например, немецкие монахи для разметки линий на листках пергамента (так называлась бумага) пользовались тонкими свинцовыми пластинками. А в ряде стран Европы, в том числе и в Древней Руси, для этих целей применялись железные прутья. Их называли шильцами. В разных странах люди измеряли одно и то же расстояние по-разному. Это было очень неудобно. Наконец, во Франции в 1789 году решено было ввести единую систему мер. В Париже изготовили платиновые линейки с делениями, которые стали образцами мерок для всего мира. По их образцу изготовили деревянные линейки. В Россию линейка попала после войны 1812 года в качестве военного трофея.
2. Работа по карточкам.
Задание 1.
Какая часть фигуры закрашена?
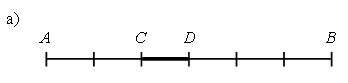
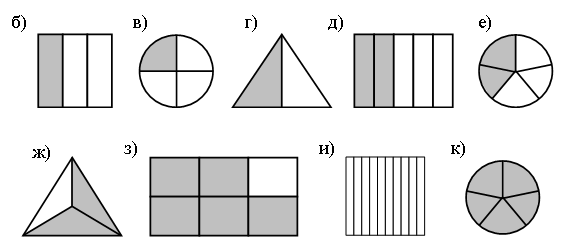
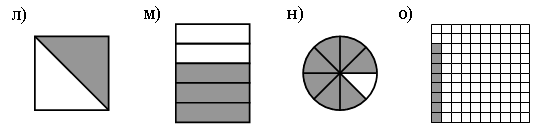
Задание 2.
Какую часть на рисунке составляет:
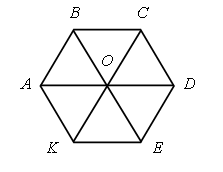
а) треугольник АВО от четырехугольника АВСО;
б) треугольник АВО от четырехугольника ABCD;
в) четырехугольник АВСО от четырехугольника ABCD;
г) четырехугольник АВСО от шестиугольника ABCDEK?
Задание 3.
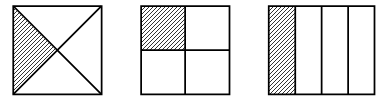
Начертите квадрат со стороной 4 см.
Разделите тремя способами этот квадрат на четыре равные части.
Решение:
3. Работа в печатной тетради № 2.
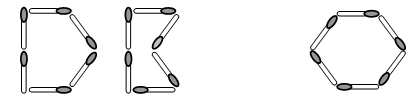
Задание № 26.
– Как можно назвать многоугольники, если на один многоугольник требуется 6 палочек?
а) треугольник; б) четырехугольник;

в) пятиугольник; г) шестиугольник.
Задание № 186.
|
Число |
6 |
12 |
18 |
|
Половина числа |
3 |
6 |
9 |
|
Треть числа |
2 |
4 |
6 |
|
Шестая часть числа |
1 |
2 |
3 |
Вывод: половина числа больше третьей части этого же числа, а треть числа всегда больше шестой части этого числа.
VI. Итог урока.
– Что нового узнали на уроке?
– Можно ли сравнивать доли числа?
Домашнее задание: № 28, 29 (рабочая тетрадь).
Урок
62
Контрольная работа по теме
«Табличное умножение и деление»
Цели урока: проверить усвоение знаний таблицы умножения и деления на 2, 3, 4, 5, 6; сформированность навыков решения задач.
I вариант
1. Используя числа 6, 3, 24, 18, 4, запишите восемь верных равенств.
2. Масса одной тыквы 5 кг. Чему равна масса четырех таких тыкв?
3. Чем похожи выражения в каждом столбике:
|
(40 – 35) · 6 |
(3 + 5) · 4 |
|
(50 – 41) · 3 |
(8 + 1) · 5 |
|
(60 – 52) · 4 |
(2 + 4) · 6 |
|
(70 – 63) · 5 |
(3 + 6) · 3 |
|
(80 – 73) · 2 |
(2 + 6) · 5 |
|
(90 – 84) · 8 |
|
Запишите каждое выражение в виде произведения двух чисел.
Вычислите значения этих произведений.
4. Что обозначают данные выражения и как они связаны с рисунком:
|
3 · 2 |
3 · 4 |
3 · 6 |
3 · 8 |
|
3 · 3 |
3 · 5 |
3 · 7 |
3 · 9 |
Найдите значение каждого произведения.
5.* В одной корзине помещается 6 кг грибов. Используя данное условие, составьте две задачи, решение которых можно записывать так:
![]()
II вариант
1. Используя числа 5, 8, 30, 6, 40, запишите восемь верных равенств.
2. Масса ящика с яблоками равна 6 кг. Чему равна масса пяти таких ящиков с яблоками?
3. Чем похожи выражения в каждом столбике:
|
(50 – 46) · 5 |
(5 + 3) · 5 |
|
(60 – 53) · 4 |
(4 + 2) · 4 |
|
(70 – 61) · 3 |
(3 + 3) · 6 |
|
(80 – 77) · 2 |
(8 + 1) · 3 |
|
(90 – 88) · 6 |
(4 + 3) · 3 |
|
(100 – 95) · 5 |
(6 + 2) · 2 |
Запишите каждое выражение в виде произведения двух чисел.
Вычислите значения этих произведений.
4. Что обозначают данные выражения и как они связаны с рисунком:
|
4 · 2 |
4 · 6 |
|
4 · 3 |
4 · 7 |
|
4 · 4 |
4 · 8 |
|
4 · 5 |
4 · 9 |
Найдите значение каждого выражения.
5.* На одной машине можно перевезти 5 коробок с игрушками. Используя данное условие, составьте две задачи, решение которых можно записать так:
![]()
Урок
63
Работа над ошибками. Решение задач
Цели урока: провести анализ выполненной контрольной работы; совершенствовать умение решать задачи; развивать умения анализировать и рассуждать.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Задача.
В корзине было 16 яблок, а в пакете – 8.
Взяли 7 яблок. Сколько всего яблок осталось в корзине и в пакете вместе?
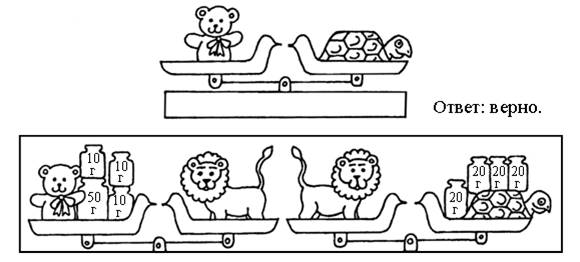
2. Рассмотрите рисунок.
Весы в рамке нарисованы верно. Верно ли нарисованы весы вне рамки? Если неверно, исправьте ошибку художника с помощью стрелочек ↓↑.
3. Вставьте числа и запишите верные равенства:
|
57 + 20 + = 82 |
61 – 20 – = 38 |
|
57 + 20 + = 85 |
61 – 20 – = 37 |
|
57 + 20 + = 81 |
61 – 20 – = 39 |
|
57 + 20 + = 84 |
61 – 20 – = 36 |
4. Задача на смекалку.
От домика Лисы к домику Волка ведут три дороги, а от домика Волка к берлоге Медведя – две дороги.
Сколькими способами Лиса может прийти в гости к Медведю?
Рисунок на доске:
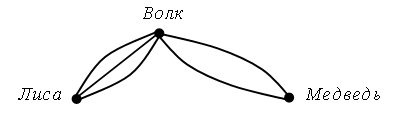
Ответ: шестью способами.
III. Сообщение результатов выполнения контрольной работы.
IV. Работа над ошибками.

V. Самостоятельная работа по карточкам.
Карточка А
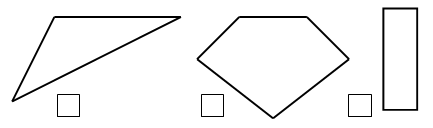
Под каждым многоугольником запишите номер отрезка, длина которого равна периметру этого многоугольника.

Карточка В
Соедините линией кружок с номером задачи и карточку со схематическим чертежом к ней. Закрасьте одним цветом кружок с номером задачи и рамку с ее решением.


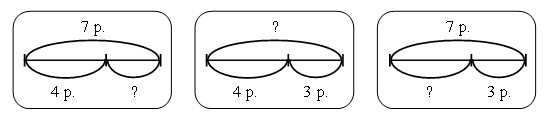
Карточка С
1) От ленты длиной 10 м сначала отрезали 2 м, а затем еще 5 м. Сколько метров ленты осталось?
Решите задачу двумя способами.
1-й способ 2-й способ
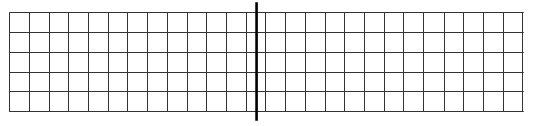
2) На сколько больше страниц прочитала Оля вечером, чем утром, если утром она прочитала 9 страниц, а вечером – 12 страниц?
VI. Итог урока.
Урок
64
Площадь фигуры. Единицы площади
Цели урока: ввести термин «площадь фигуры»; познакомить учащихся с единицами площади (квадратным метром, квадратным дециметром, квадратным сантиметром) и их обозначениями; закреплять табличные случаи умножения и деления на 2, 3, 4, 5, 6; совершенствовать навыки вычисления доли числа; развивать умения анализировать и обобщать.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Сколько треугольников вы видите на чертеже?
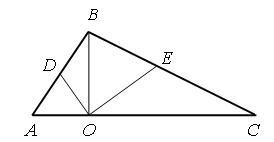
2. Вставьте пропущенные числа.
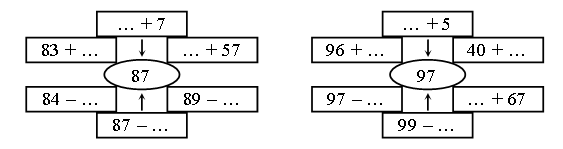
3. Задачи.
а) В столовом сервизе 12 глубоких и столько же мелких тарелок. Сколько тарелок в этом сервизе?
б) Уже прошло 30 минут урока. Через 5 минут прозвенит звонок. Сколько минут продолжается урок в нашей школе?
4. Заштрихуйте передние грани кубов, изображенных верно.
III. Сообщение темы урока.
– Как называются данные на доске фигуры?
– Что их объединяет? (Это многоугольники, стороны которых равны 2 см.)
– Как найти периметр каждого многоугольника?
![]() =
2 · 3 = 6 (см) или 2 + 2 + 2 = 6 (см).
=
2 · 3 = 6 (см) или 2 + 2 + 2 = 6 (см).
![]() =
2 · 4 = 8 (см) или 2 + 2 +2 + 2 = 8 (см).
=
2 · 4 = 8 (см) или 2 + 2 +2 + 2 = 8 (см).
![]() = 2 · 5 = 10 (см) или 2 + 2 + 2 + 2 + 2 = 10 (см).
= 2 · 5 = 10 (см) или 2 + 2 + 2 + 2 + 2 = 10 (см).
– Как найти площадь этих фигур?
– Какие трудности у вас возникли?
– Сегодня на уроке мы узнаем, что называют площадью фигуры.
IV. Изучение нового материала.
Задание № 1 (с. 22).
– Мастер облицовывает плитками в ванной комнате две стены. Каждая плитка квадратной формы с длиной стороны 1 дм. Ее площадь считают равной одному квадратному дециметру. Записывают так: 1 дм2.
– Рассмотрите таблицу в учебнике.
– Сколько плиток пошло на облицовку одной стены? (12.)
– Другой стены? (15.)
– На какую стену мастер израсходовал больше плиток?
– Назовите площадь каждой стены в квадратных дециметрах. (12 дм2 и 15 дм2.)
– Площадь какой стены больше и почему?
– Прочитайте определение квадратного дециметра на с. 22 учебника.
– Сформулируйте определение квадратного сантиметра. (Квадратным сантиметром называют площадь квадрата с длиной стороны 1 см.)
– Сформулируйте определение квадратного метра.
– Квадратный сантиметр, квадратный дециметр, квадратный метр – это единицы площади.
Их обозначают так: см2, дм2, м2.
– Покажите вырезанные из бумаги квадраты площадью 1 дм2, 1 см2 и 1 м2.
– Сравните попарно площади этих квадратов, накладывая меньший квадрат на больший.
– В квадрате площадью 1 дм2 может уместиться ровно 100 квадратов площадью 1 см2, а в квадрате площадью 1 м2 – ровно 100 квадратов площадью 1 дм2.
Справочный материал для учителя
Фигура на рисунке 1 состоит из 8 квадратов со стороной 1 см каждый. Площадь одного такого квадрата называют квадратным сантиметром. Пишут: 1 см2. Значит, площадь всей фигуры равна 8 см2.
Если какую-нибудь фигуру можно разбить на р квадратов со стороной 1 см, то ее площадь равна р см2.
Прямоугольник на рисунке 2 состоит из 3 полос, каждая из которых разбита на 5 квадратов со стороной 1 см. Весь прямоугольник состоит из 5 · 3 = 15 таких квадратов, и его площадь равна 15 см2.
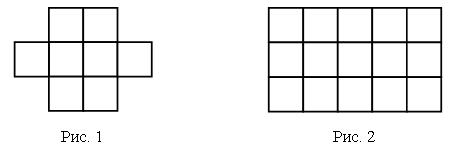
Чтобы найти площадь прямоугольника, надо умножить его длину на ширину.
Запишем это правило в виде формулы. Площадь прямоугольника обозначим буквой S, его длину – буквой а, а ширину – буквой b.
Получаем формулу площади прямоугольника:
![]()
Две фигуры называют равными, если одну из них можно так наложить на вторую, что эти фигуры совпадут.
Площади равных фигур равны. Их периметры тоже равны.
Линия KLMN на рисунке 3 разбивает прямоугольник ABCD на две части. Одна из частей имеет площадь 12 см2, а другая – 9 см2. Площадь всего прямоугольника равна 3 · 7, то есть 21 см2. При этом 21 = 12 + 9.
Площадь всей фигуры равна сумме площадей ее частей.
Отрезок АС разбивает прямоугольник на два равных треугольника: ABC и ADC (рис. 4).
Площадь каждого треугольника равна половине площади всего прямоугольника.
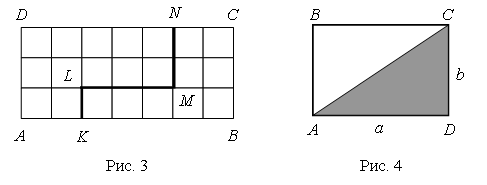
· Квадратной единицей называют не квадрат, а его площадь.
· Квадратным сантиметром называют площадь квадрата с длиной стороны 1 см.
· Квадратным дециметром называют площадь квадрата с длиной стороны 1 дм.
· Квадратным метром называют площадь квадрата с длиной стороны 1 м.
! Следите за правильным применением учащимися терминологии. В быту дети довольно часто слышат, как взрослые говорят о том, что площадь такой-то комнаты или квартиры равна 15 м, 60 м и т. д. Разъясните, что в этих случаях речь идет о площадях 15 м2, 60 м2, а не о длинах.
– Рассмотрите рисунок на с. 23 учебника и объясните, как найти площадь фигуры. (Надо разделить фигуры на квадраты с длиной стороны 1 см и пересчитать, сколько получилось квадратов.)
Задание № 2 (с. 23).
Учащиеся читают величины, записанные единицами площади.
Задание № 3 (с. 23).
Выполняя задание, учащиеся устанавливают взаимосвязь между двумя изученными единицами площади: 1 дм2 = 100 см2.
Не следует требовать от учащихся знания наизусть этой зависимости.
Задание № 4 (с. 23).
Для выполнения задания учащиеся используют палетку. Цель задания – научить детей измерять площадь фигур с помощью палетки. Сначала объясните ученикам, как надо накладывать палетку на фигуру, чтобы было удобно выполнять измерения, и только потом переходите к практической работе. Рассуждать дети должны примерно так: «В голубой фигуре ровно 13 квадратов. Площадь каждого квадрата – 1 см2, значит, площадь фигуры – 13 см2.
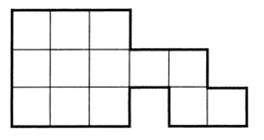
В желтой фигуре ровно 12 квадратов (их площадь – 12 см2), 6 половинок квадратов (их площадь – 3 см2) и 4 четвертинки квадрата (их площадь – 1 см2). Следовательно, площадь желтой фигуры:
12 + 3 + 1 = 16, то есть 16 см2».

V. Повторение пройденного материала.
1. Работа по учебнику.
Задание № 11 (с. 25).
|
12 : 2 = 6 |
6 : 2 = 3 |
40 : 4 = 10 |
15 : 3 = 5 |
8 : 2 = 4 |
|
12 : 3 = 4 |
6 : 3 = 2 |
40 : 5 = 8 |
15 : 5 = 3 |
8 : 4 = 2 |
|
12 : 4 = 3 |
6 : 6 = 1 |
|
|
|
|
12 : 6 = 2 |
|
|
|
|
Вывод: чтобы найти неизвестный делитель, надо делимое разделить на значение частного.
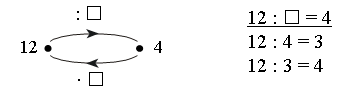
Задание № 13 (с. 25).
Ответ: пятая часть, четвертая часть и две шестых части.
2. Работа в печатной тетради № 2.
Задание № 35.
Чертеж:

Ответ: 10 см2.
Задание № 192.
Ответ: 7 см2 и 8 см2.
VI. Итог урока.
– Что нового узнали на уроке?
– Назовите единицы измерения площади фигуры.
Домашнее задание: № 10, 12 (учебник); № 32, 191 (рабочая тетрадь).
Урок
65
Площадь фигуры. Единицы площади
Цели урока: продолжить формирование умений определять площадь фигуры приемом пересчитывания квадратов, на которые разделена фигура; совершенствовать навыки работы с математическими графами; развивать логическое мышление и умение рассуждать.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Вставьте пропущенные числа.
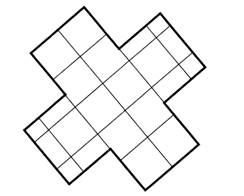
2. Задача.
Почтальон принес в наш дом 2 десятка газет и 8 журналов – в каждую квартиру что-нибудь одно. Сколько квартир получили газету или журнал?
3. Рассмотрите чертеж:
а) Какая фигура «лишняя»?
б) У какой фигуры 6 вершин, 5 граней, 9 ребер?
в) У какой фигуры только одна вершина?
г) В чем сходство и различие фигур 4 и 5?
д) Названия каких из этих фигур ты знаешь?
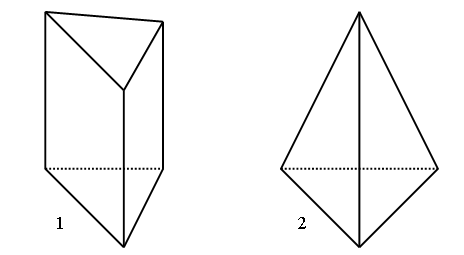
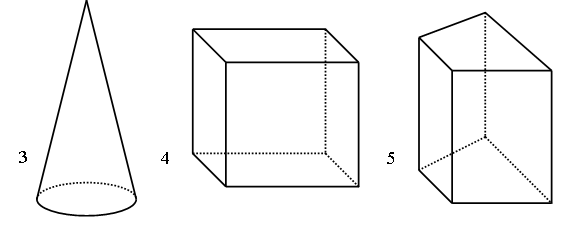
III. Сообщение темы урока.
– Сегодня на уроке будем определять площадь различных геометрических фигур.
IV. Изучение нового материала.
Задание № 5 (с. 24).
Предложите учащимся выполнить чертеж клумб не в тетради, а на отдельном листе бумаги. Это позволит легко организовать самостоятельную проверку. Для этого дети вырезают ножницами изображения клумб и накладывают их друг на друга. Если четырехугольная «клумба» полностью уместится на треугольной, то задание выполнено верно.
Задание № 6 (с. 24).
Чертежи:
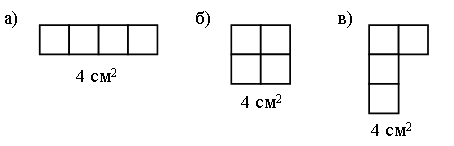
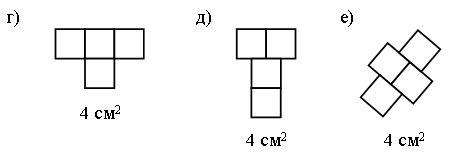
Задание № 7 (с. 24).
– Прочитайте текст. Является ли он задачей? Почему?
– Что известно? Что надо узнать?
– Запишите кратко условие задачи и решите ее.

Решение:
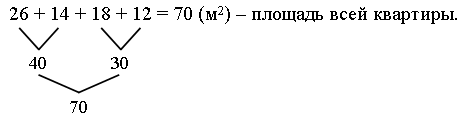
Ответ: 70 м2.

V. Повторение пройденного материала.
1. Работа в печатной тетради № 2.
Задание № 34.
Площадь фигуры № 1 – 6 см2.
Площадь фигуры № 2 – 8 см2.
Площадь фигуры № 3 – 7 см2.
Сложнее всего найти площадь фигуры № 4. Учащиеся должны рассуждать примерно так: «В синей фигуре 10 квадратов (их площадь – 10 см2) и 4 половинки (их площадь – 2 см2). Следовательно, площадь красной фигуры:
10 + 2 = 12, то есть 12 см2».
Площадь фигуры № 5 – 20 см2.
Площадь фигуры № 6 – 32 см2.
2. Работа по учебнику.
Задание № 16 (с. 26).
· Пять больше трех.
· Двадцать шесть больше трех.
· Двадцать шесть больше пяти.
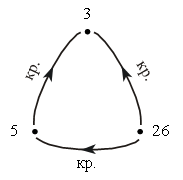
– Какое отношение задает первый граф? (Отношение «больше».)
– Какое отношение задает второй граф? (Отношение «меньше».)
· 20 меньше 70.
· 15 меньше 70.
· 15 меньше 20.
· 15 меньше 81.
· 20 меньше 81.
· 70 меньше 81.
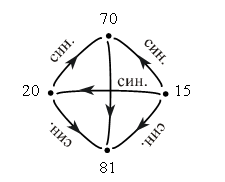
Задание № 17 (с. 26).
– Прочитайте текст. Является ли он задачей? Почему?
– Что известно? Что требуется узнать?
– Запишите кратко условие задачи и решите ее.
Запись:
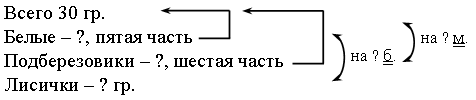
Решение:
1. Сколько белых грибов принес Миша?
30 : 5 = 6 (гр.)
2. Сколько подберезовиков принес?
30 : 6 = 5 (гр.)
3. Сколько принес лисичек?
20 – 5 – 6 = 9 (гр.)
4. На сколько больше нашел лисичек, чем белых грибов?
9 – 6 = 3 (гр.)
5. На сколько меньше нашел подберезовиков, чем белых грибов?
6 – 5 = 1 (гр.)
VI. Итог урока.
– Что нового узнали на уроке?
– Какие правила математических граф вам известны?
Домашнее задание: № 14, 15 (учебник); № 195 (рабочая тетрадь).
Урок
66
Площадь фигуры. Единицы площади
Цели урока: совершенствовать навыки определения площади фигуры; закреплять умение решать задачи с величинами «цена», «количество», «стоимость»; развивать внимание и логическое мышление.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Разгадайте правило, по которому записан каждый ряд чисел и продолжите его.
19, 17, 15, …
71, 73, 75, …
44, 46, 45, 47, 46, …
23, 26, 24, 27, …
91, 95, 92, 96, 93, …
2. Задача.
Аудиокассета рассчитана на 60 минут записи. На этой кассете у меня уже записана музыка, звучащая 56 минут. Уместится ли на кассете еще одна песня, запись которой занимает 4 минуты?
3. Рассмотрите чертеж.
Выберите фигуру, которую нужно нарисовать.
III. Сообщение темы урока.
– Прочитайте величины, записанные на доске.
– Зачеркните «лишнюю» величину в каждой строке:
а) 91 см, 10 дм, 100 м, 29 см2, 41 дм;
б) 45 кг, 24 дм2, 83 см2, 15 дм2, 43 м2;
в) 25 м2, 68 м2, 38 см2, 74 м2, 91 см2.
– Сегодня на уроке будем определять площадь различных многоугольников.
IV. Изучение нового материала.
Задание № 8 (с. 24).
– Прочитайте задание.
– Какую форму должен иметь кусок ткани? (Форму квадрата.)
– Какой длины должны быть стороны квадрата? (По 6 см.)
– Какой вывод вы можете сделать? (Для заплатки потребуется кусок ткани квадратной формы со сторонами по 6 см.)
– Изобразите такую заплатку в тетради.

– Найдите площадь заплатки.
Решение: 6 + 6 + 6 + 6 + 6 + 6 = 36 (см2).
Задание № 9 (с. 24).
– Чему равна площадь квадратной обертки? (25 см2.)
– Что вы можете сказать о квадрате? (У квадрата все стороны равны.)
– Чему равна длина сторон этой обертки? (5 см2.)
– Сделайте проверку. Постройте в тетради квадрат с длинами сторон по 5 см и убедитесь, что его площадь равна 25 см2.
Работа по карточкам.
Закрасьте: 20 см2 – синим цветом;
5 см2 – красным цветом;
30 см2 – зеленым цветом.
– Какая площадь 1 дм2 осталась
незакрашенной? ![]()
Учащиеся работают самостоятельно.
Работы сдаются учителю на проверку.

V. Повторение пройденного материала.
1. Работа по учебнику.
Задание № 18 (с. 26).
– Прочитайте текст. Является ли он задачей? Почему?
– Что известно? Что требуется узнать?
– Запишите кратко условие задачи и решите ее.
Разложили – в 6 с. по ? к.
Решение: 1) 10 – 2 = 8 (к.) – со II грядки.
2) 10 + 8 = 18 (к.) – всего.
3) 18 : 6 = 3 (к.) – в каждой сетке.
Ответ: 3 к.
Задание № 20 (с. 26).
– Прочитайте задачу.
– Что известно? Что требуется узнать?
– Запишите условие задачи в таблицу.

Решение: 1) 3 · 4 = 12 (р.) – стоимость сырков.
2) 12 + 28 = 40 (р.) – стоимость всей покупки.
Ответ: 40 рублей.
Задание № 22 (с. 27).
– Рассмотрите рисунок и составьте по нему задачу.
Задача. В мотке было 30 м. Отрезали 12 м 50 см. Какой длины канат остался в мотке?
– Можно ли сразу ответить на вопрос задачи?
– Запишите кратко условие задачи.
Запись: Было – 30 м.
Отрезали – 12 м 50 см.
Осталось – ?
Решение:
30 м – 12 м 50 см = 17 м 50 см
Ответ: 17 м 50 см.
2. Работа в печатной тетради № 2.
Задания № 36, 37, 38.
Эти задания являются подготовительными для введения отношений «больше в...» и «меньше в...».
VI. Итог урока.
– Что нового узнали на уроке?
– Что называют площадью фигуры?
– Назовите единицы площади.
Домашнее задание: № 19 (учебник); № 39, 40 (рабочая тетрадь).
Урок
67
Практическая работа по теме
«Площадь фигуры. Единицы площади»
Цели урока: проверить умения и навыки вычисления площади фигуры; развивать практические навыки, внимание и умение анализировать.
Ход урока
I. Организационный момент.
II. Практическая работа.
Задание № 1.
Дорисуйте фигуру так, чтобы получился прямоугольник, площадь которого равна:
а) 9 см2, б) 21 см2,
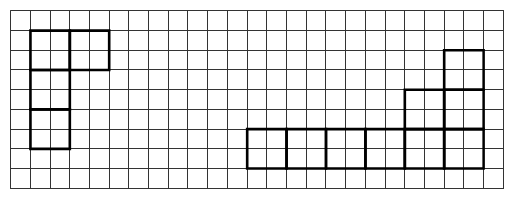
в) 15 см2, г) 18 см2,
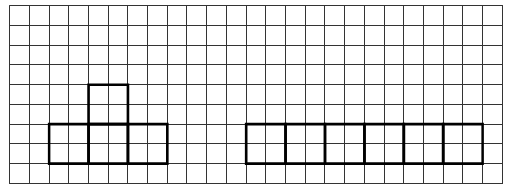
д) 27 см2.
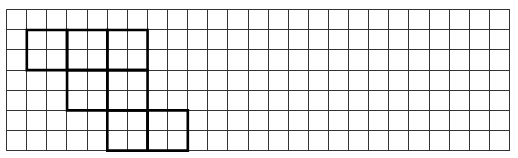
Задание № 2.
Вычислите периметр и площадь фигуры удобным способом.

Задание № 3.
Разделите фигуру на многоугольники площадью 4 см2. Если сможете, найдите несколько решений.
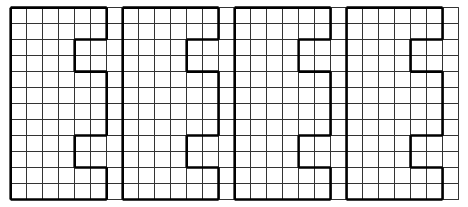
|
Чему равны у этой фигуры площадь |
|
|
|
|
|
|
|
|
|
и периметр |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
? |
Выберите любое из ваших решений и составьте из полученных четырех многоугольников другую фигуру, не выходящую за границу прямоугольника:

|
Чему равны у этой фигуры площадь |
|
|
|
|
|
|
|
|
|
и периметр |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
? |
III. Итог урока.
Тематическое планирование
|
Номер |
Тема урока |
Кол-во часов |
|
1 |
2 |
3 |
|
Тема
2: Таблица умножения однозначных чисел |
||
|
68 |
Умножение семи и на 7 |
1 |
|
69 |
Умножение на 7. Решение задач |
1 |
|
70 |
Умножение и деление на 7 |
1 |
|
71 |
Умножение и деление на 7. Седьмая часть числа |
1 |
|
72 |
Умножение восьми и на 8 |
1 |
|
73 |
Умножение на 8. Решение задач |
1 |
|
74 |
Умножение и деление на 8 |
1 |
|
75–76 |
Умножение и деление на 8. Восьмая часть числа |
2 |
|
77 |
Умножение девяти и на 9 |
1 |
|
78 |
Умножение на 9. Решение задач |
1 |
|
79 |
Умножение и деление на 9 |
1 |
|
80–81 |
Умножение и деление на 9. Девятая часть числа |
2 |
|
82 |
Контрольная работа по теме «Умножение и деление на 7, 8, 9» |
1 |
|
83 |
Работа над ошибками. Решение задач |
1 |
|
84–88 |
Во сколько раз больше или меньше? |
5 |
|
89–90 |
Решение задач на увеличение и уменьшение в несколько раз |
2 |
|
91–96 |
Нахождение нескольких долей числа |
6 |
|
97 |
Контрольная работа по теме «Решение арифметических задач» |
1 |
|
98 |
Работа над ошибками. Решение задач |
1 |
|
Тема 3: Выражения |
||
|
99–101 |
Названия чисел в записях действий |
3 |
|
102– |
Числовые выражения |
3 |
|
105– |
Составление числовых выражений |
3 |
|
108– |
Угол. Прямой угол |
3 |
Окончание табл.
|
1 |
2 |
3 |
|
111– |
Прямоугольник. Квадрат |
3 |
|
114– |
Свойства прямоугольника |
2 |
|
116– |
Площадь прямоугольника |
3 |
|
119 |
Контрольная работа по теме «Выражения» |
1 |
|
120 |
Работа над ошибками |
1 |
|
121 |
Повторение по теме «Сложение, вычитание, умножение и деление чисел в пределах 100» |
1 |
|
122– |
Повторение по теме «Арифметические задачи» |
2 |
|
124 |
Повторение по теме «Фигуры и величины» |
1 |
|
125– |
Резервные |
12 |
Урок 68
Умножение семи и на 7
Цели: составить таблицу умножения семи и умножения на семь; совершенствовать вычислительные навыки; развивать внимание и умение рассуждать.
Ход урока
I. Организационный момент.
I. Устный счет.
1. Сколько отрезков на чертеже?
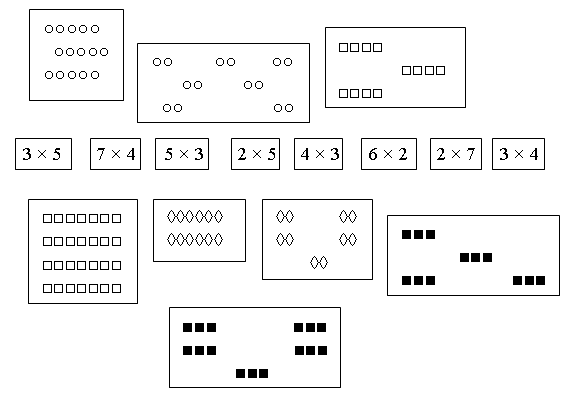
2. Соедините выражения с рисунками:
3. Задача.
Сколько костюмов можно составить, имея 4 блузки и 6 юбок, если каждая блузка подходит к каждой юбке по размеру и расцветке?
4. Выберите фигуру, которую нужно нарисовать.
III. Сообщение темы урока.
Учитель. Рассмотрите рисунок на доске.
– Как быстро можно вычислить массу яблок в трех ящиках?
– Сегодня мы составим таблицу умножения на 7.
IV. Изучение нового материала.
Задание № 1 (с. 28).
– Прочитайте задачу.
– Что известно? Сколько дней в одной неделе?
– Что требуется узнать?
– Сравните решения Волка и Зайца (на с. 28 учебника).
– Кто из них быстрее справился с заданием? (Волк прибавлял число 7 четыре раза, а Заяц, используя таблицу умножения числа 7, сразу назвал ответ: 7 · 4 = 28.)
Далее учащиеся самостоятельно составляют таблицу умножения числа 7.
– Используя таблицу умножения числа 7, составьте и запишите таблицу умножения на число 7.
Учащиеся выполняют задание № 4 (с. 29).
Задание № 2 (с. 28).
– Используя калькулятор (или цветные фишки), сравните результаты умножения.
7 × 3 равно 3 × 7 6 × 7 равно 7 × 6
Вывод: от перестановки множителей значение произведения не изменяется.
Задание № 3 (с. 29).
Запись:
7 × 0 = 0; 0 × 7 = 0.
Вывод: при умножении любого числа на нуль получим нуль. При умножении нуля на любое число получим нуль.
Задание № 6 (с. 29).
– Прочитайте текст. Является ли он задачей? Почему?
– Что известно?
– Что требуется узнать?
– Выполните рисунок и решите задачу.

V. Повторение пройденного материала.
1. Работа по учебнику.
Задание № 28 (с. 32).
Важно, чтобы при работе над этим заданием учащиеся не пошли по пути выполнения вычислений, а опирались на взаимосвязь действий умножения и деления.
Учитель может предложить карточки-помощницы:
– Рассмотрите данную схему.
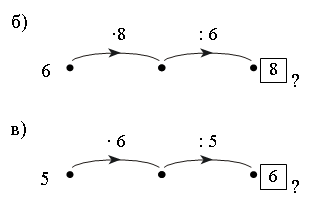
– Надо ли выполнять вычисления? (Надо 12 разделить на 3, а затем результат умножить на 3. Так как умножение на 3 обратно делению на 3, то, последовательно выполняя эти действия, мы получим первоначальное число 12.)
Запись:
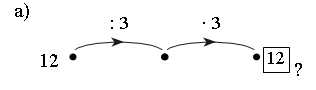
Задание № 30 (с. 33).
– Рассмотрите рисунок.
– Что вам известно? (Известна цена карандаша и цена тетради.)
– Составьте задачу, решением которой будет схема + . (Сколько стоит вся покупка?)
– Составьте задачу, решением которой будет схема – . (На сколько дороже тетрадь, чем карандаш?)
2. Работа в печатной тетради № 2.
Задание № 41.
Результаты умножения в третьем и четвертом столбиках учащиеся находят, используя переместительное свойство умножения.
Задание № 43.
Учащиеся работают самостоятельно, осуществляя взаимопроверку в парах.
Задание № 42.
– Как найти следующие несколько чисел, которые тоже делятся на 7?
– Используя схему, заполните «окошки».
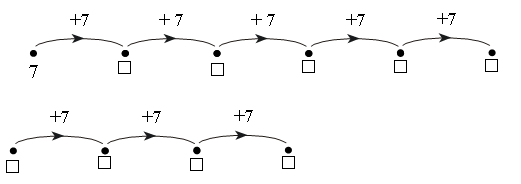
– Проверьте свои действия с помощью калькулятора.
VI. Итог урока.
– Что нового узнали на уроке?
– Что обозначает запись: 7 · 2?
Домашнее задание: № 5, 29 (учебник); № 44 (рабочая тетрадь).
Урок 69
Умножение на 7. РЕШЕНИЕ ЗАДАЧ
Цели: закреплять табличные случаи умножения на 2, 3, 4, 5, 6, 7; совершенствовать вычислительные навыки решения составных задач; продолжить формирование умений составлять и читать математические графы; развивать умение анализировать и сравнивать.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Заполните таблицу:
|
Первое слагаемое |
38 |
|
5 |
60 |
16 |
4 |
|
69 |
|
Второе слагаемое |
8 |
40 |
|
|
80 |
|
3 |
|
|
Значение суммы |
|
74 |
87 |
93 |
|
34 |
89 |
70 |
2. Задача.
Когда тетя Ася встала на весы, они показали 78 кг. А она мечтает иметь массу, равную хотя бы 70 кг. На сколько килограммов тетя Ася хочет похудеть?
3. Узнайте по рисунку, чей путь короче.
III. Сообщение темы урока.
Учитель. Рассмотрите схемы на доске.
□ + □ + □ + □ + □ + □
□ ∙ □
– Могут ли данные схемы быть решениями задач?
Сегодня на уроке мы будем решать задачи и закреплять знание таблицы умножения на 7.
IV. Изучение нового материала.
Задание № 7 (с. 29).
– Прочитайте текст.
– Является ли он задачей? Почему?
– Что известно в задаче?
– Что требуется узнать?
– Выполните схему к данной задаче и решите ее.
Запись:
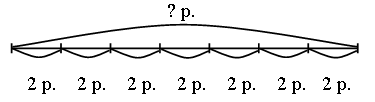
Решение:
2 · 7 = 14 (р.).
Ответ: 14 р.
Задание № 8 (с. 29).
– Прочитайте задачу. Кого называют туристами?
– Что известно в задаче?
– Что требуется узнать?
– Как быстро решить эту задачу?
Решение:
4 · 7 = 28 (чел.).
Ответ: 28 человек.
Задание № 10 (с. 29).
– Прочитайте задачу.
– Что известно в задаче?
– Что требуется узнать?
– Запишите условия задачи в таблицу.

Решение:
1) 7 ∙ 4 = 28 (шт.) – в 4 гроздьях.
2) 28 + 12 = 40 (шт.) – всего.
Ответ: 40 штук.

V. Повторение пройденного материала.
1. Работа в печатной тетради № 2.
Задание № 45.
– Прочитайте задачу.
– Что известно в задаче? Что требуется узнать?
– Сколько дней брали по 7 литров воды? (9 дней.)
– Сколько литров воды взяли из бочки? (7 ∙ 9 = 63 (л).)
– Сколько литров воды было в бочке? (63 + 37 = 100 (л).)
Задание № 46.
Это задание учащиеся выполняют методом подбора, вспоминая соответствующие табличные случаи умножения.
Задание № 47.
Запись: б) ○○○○○○○
а) ○○○○○○○●●● ○○○○○○○
7 + 3 = 10. ○○○○○○○
7 ∙ 3 = 21.
2. Работа по учебнику.
Задание № 31 (с. 33).
– Прочитайте текст.
– Является ли он задачей? Почему?
– Что известно? Что требуется узнать?
– Рассмотрите чертеж. Какие данные содержит рисунок?
– Можно ли эту задачу решить без рисунка?
– Сформулируйте условие задачи так, чтобы все данные содержались в тексте и не было необходимости использовать иллюстрацию.
– Запишите кратко условие этой задачи.
Запись условия задачи:
Было – 16 см.
1-й жук – 4 см.
2-й жук – 3 см.
Осталось – ? (см).
– Решите задачу разными способами.
1-й способ.
1) 3 + 4 = 7 (см) – проползли оба жука.
2) 16 – 7 = 9 (см) – осталось.
2-й способ.
1) 16 – 3 = 13 (см).
2) 13 – 4 = 9 (см).
Задание № 32 (с. 34).
– Рассмотрите чертеж. Какие фигуры здесь изображены?
– Что такое площадь?
– Чему равна площадь каждой фигуры?
Запись:
7 см², 14 см², 28 см², 11 см², 14 см².
– Площади каких фигур равны?
Задание № 34 (с. 34).
– Что такое «граф»?
– Как показать на графе отношение «меньше»?
– Прочитайте высказывание о каждой паре чисел.
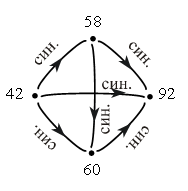
Ответ: 42 меньше 58;
42 меньше 60;
42 меньше 90;
58 меньше 60;
58 меньше 90;
60 меньше 90.
VI. Итог урока.
– Что нового узнали на уроке?
– Назовите единицы площади.
– Какие правила математических граф вам известны?
Домашнее задание: № 33, 13 (учебник); № 56 (рабочая тетрадь).
Урок 70
Умножение и ДЕЛЕНИЕ на 7
Цели: составить таблицу деления на 7; рассмотреть связь действия умножения с действием деления; совершенствовать вычислительные навыки; повторить порядок выполнения действий в выражениях со скобками; развивать умение анализировать и делать выводы.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Сколько отрезков на чертеже?
2. Вставьте цифры в «окошки», чтобы получились верные равенства:
7 – 4 = 70 8 – 40 = 38 2 + 20 = 62
6 – 5 = 64 3 + 20 = 83 5 + 20 = 74
5 + 3 = 58 7 – 50 = 47 7 + 20 = 93
4 + 6 = 48 2 + 70 = 92 9 – 60 = 19
3. Задача.
а) В упаковке 2 десятка таблеток. Сегодня я уже принял 3 таблетки. Сколько таблеток осталось в упаковке?
б) Пачка вафель стоит 8 р. Нужно купить 5 таких пачек. Сколько это будет стоить?
4. Игра «Стрелок».
– Составьте выражения по схеме: + = 100.

III. Сообщение темы урока.
– Какое действие является обратным умножению? (Деление.)
– Какое действие обратно действию умножения на 7?
– Сегодня на уроке мы составим таблицу деления на 7.
IV. Изучение нового материала.
Используя фишки, учащиеся самостоятельно составляют таблицу деления на 7.
7 · 1 = 7 · 2 = 7 · 3 = И т. д.
׃ 7 = ׃ 7 = ׃ 7 = И т. д.
Далее учащиеся сравнивают свою таблицу деления на 7 с таблицей, данной в учебнике (на с. 29).
Задание № 11 (с. 30).
– Какие фигуры изображены на рисунке?
– На сколько квадратов разделен каждый четырехугольник?
Запись:
5 · 7 = 35 (кв.);
7 · 7 = 49 (кв.).
Задание № 12 (с. 30).
Вероятно, при решении этой задачи учащиеся будут рассуждать так: «Сначала нужно узнать, сколько яблок получили все дети (6 · 7 = 42), затем – сколько всего персиков получили дети (6 · 8 = 48). Теперь можно ответить на вопрос задачи («Сколько всего фруктов получили ребята?»): 42 + 48 = 90».
Дополнительно можно попросить учащихся решить задачу другим способом. Сначала узнаем, сколько фруктов получил каждый ребенок. Для этого надо сложить 7 и 8. А затем нужно узнать, сколько всего фруктов получили ребята. Для этого результат предыдущего действия умножим на 6.
Вычисления учащиеся могут выполнять с помощью микрокалькулятора. Потом сравнивают ответы, полученные при решении задачи обоими способами.
Задание № 15 (с. 30).
Используя схемы, учащиеся составляют равенства.
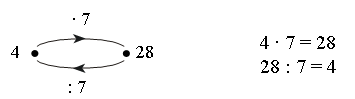
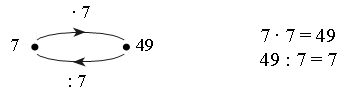
Задание № 16 (с. 30).
Ответы:
а) умножению на 7 обратным действием является деление на 7;
б) делению на 7 обратным действием является умножение на 7;
в) умножению на 6 обратным действием является деление на 6;
г) делению на 5 обратным действием является умножение на 5.
– Поясните каждый ответ примерами.
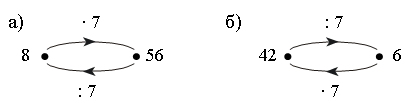
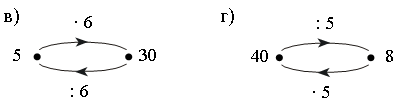

V. Повторение пройденного материала.
1. Работа в печатной тетради № 2.
Задание № 55.
Работу над заданием можно построить следующим образом.
Учитель задает вопросы:
– Сколько пчелок на рисунке? (2.)
– По сколько ромашек мы обведем каждой линией? (Тоже по 2.)
– Проведите линии. Сколько раз мы обвели по 2 ромашки? (7 раз.)
Учитель предлагает классу сделать вывод.
Вывод: мы получили ромашек 7 раз по столько, сколько пчелок.
Задание № 57.
Учащиеся самостоятельно выполняют умножение, осуществляя взаимопроверку в парах.
2. Работа по карточкам.
– Найдите значения выражений.
I вариант
14 – (11 – 3) (3 · 7) ׃ 1
12 – (5 + 7) (20 ׃ 4) · 7
8 + (16 – 6) (8 · 6) ׃ 8
9 + (14 – 10) (25 ׃ 5) · 6
(16 – 6) + 3 (56 ׃ 8) + 3
(7 – 0) + 7 15 – (20 ׃ 4)
(15 + 1) – 8 8 + (49 ׃ 7)
(20 – 1) – 9
II вариант
(5 + 5) + 7 9 · (40 ׃ 5)
(6 + 6) – 10 6 · (12 ׃ 4)
(3 + 9) – 2 56 ׃ (14 ׃ 2)
(7 + 7) – 8 28 ׃ (24 ׃ 6)
12 – (5 + 7) 0 ׃ (5 + 9)
6 + (2 + 8) (3 · 6) ׃ 9
(18 – 10) + 4 (42 ׃ 6) + 10
18 – (11 – 2)
III вариант
(15 – 6) + 9 42 ׃ (7 ׃ 1)
(18 – 9) + 10 24 ׃ (54 ׃ 9)
(13 – 8) – 4 (3 · 2) · 8
(10 + 7) – 8 (4 · 9) ׃ 6
(8 + 8) – 8 (25 ׃ 5) – 5
(7 + 7) – 10 40 – (5 · 8)
19 – (18 – 8) (7 · 8) – 6
(9 + 9) – 1
VI. Итог урока.
– Что нового узнали на уроке?
– Как связано деление с умножением?
Домашнее задание: задание № 14 (учебник); № 53, 54 (рабочая тетрадь).
Урок 71
Умножение
и ДЕЛЕНИЕ на 7.
СЕДЬМАЯ ЧАСТЬ ЧИСЛА
Цели: ввести понятие «седьмая часть числа»; учить вычислять седьмую часть числа; продолжить формирование умений решать составные задачи; развивать логическое мышление.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Суммы трех чисел, написанных вдоль сторон треугольника, имеют одинаковые значения.
Найдите эти значения и недостающие слагаемые.
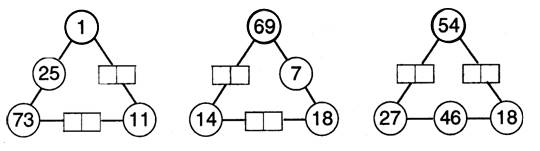
2. Задача.
Ленту разрезали на 6 одинаковых по длине кусков по 3 метра. Какой длины была лента?
3. Выберите фигуру, которую нужно нарисовать.
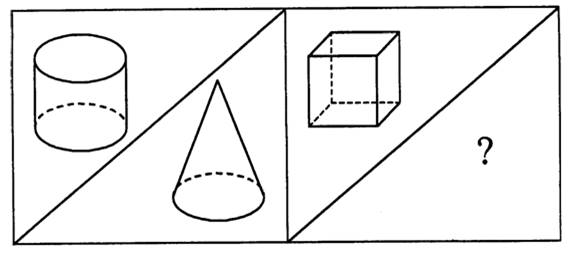
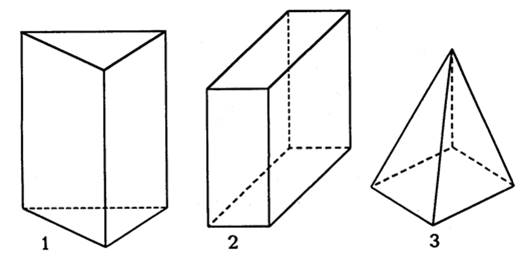
III. Сообщение темы урока.
– Рассмотрите фигуры на доске.
– Что их объединяет? (Это четырехугольники, которые разделили на равные части.)
– Какая часть четырехугольника закреплена на каждом рисунке?
– Сегодня на уроке мы узнаем, как найти седьмую часть числа.
IV. Изучение нового материала.
Используя цветные фишки, учащиеся выполняют задание учителя.
– Выполните действие: 14 ׃ 7.
14 ׃ 7 = 2.
– Покажите седьмую часть числа 14.
– Как найти седьмую часть числа? (Надо разделить данное число на 7.)
Задание № 23 (с. 31).
Запись:
7 ׃ 7 = 1 42 ׃ 7 = 6
21 ׃ 7 = 3 56 ׃ 7 = 8 и т. д.
Задание № 24 (с. 32).
– Прочитайте задачу.
– Какую часть февраля составляет одна неделя февраля? (Четвертую часть, так как в феврале 4 недели.)
– Какую часть недели составляет один день? (Седьмую часть, так как в неделе семь дней.)
Задание № 25 (с. 32).
Используя карточку-помощницу, учащиеся находят неизвестное число.
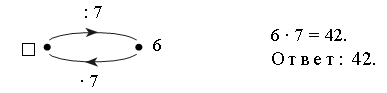
Задание № 26 (с. 32).
– Прочитайте задачу.
– Что известно? Что требуется узнать?
– Выполните схему к этой задаче.
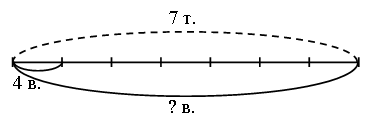
Решение: 4 · 7 = 28 (в.) – сварила мама.
Ответ: 28 в.
Задание № 27 (с. 32).
– Какая часть круга вырезана на первом рисунке? (Четвертая часть.)
– Какая часть круга вырезана на втором рисунке? (Седьмая часть.)
– Начертите четырехугольник и разделите его на семь равных частей.
– Синим цветом закрасьте седьмую часть фигуры.
– Красным цветом закрасьте две седьмых части четырехугольника.
– Какая часть фигуры закрашена? (Три седьмых.)
– Какая часть фигуры осталась незакрашенной? (Четыре седьмых.)

V. Повторение пройденного материала.
1. Работа в печатной тетради № 2.
Задание № 50.
– Прочитайте задачу.
– Что известно?
– Что требуется узнать?
– Запишите кратко условие задачи.
Запись условия:

Осталось – ? (м).
Решение:
1) Сколько метров прошел Федя?
63 ׃ 7 = 9 (м).
2) Сколько метров осталось пройти?
63 – 9 = 54 (м).
Ответ: 54 м.
Задание № 52.
«Изюминка» упражнения в том, что по условию требуется закрасить седьмую часть круга, а на чертеже изображена окружность, разбитая на семь равных частей. Поэтому, чтобы выполнить задание, учащиеся должны сделать некоторые дополнительные построения.
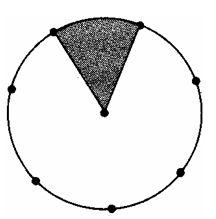
2. Работа по учебнику.
Задание № 17 (с. 31).
Учащиеся самостоятельно выполняют деление и осуществляют взаимопроверку в парах.
VI. Итог урока.
– Что нового узнали на уроке?
– Как вычислить седьмую часть числа?
– Назовите признаки окружности.
Домашнее задание: задание № 22 (учебник); № 48, 49, 51 (рабочая тетрадь).
Урок 72
УМНОЖЕНИЕ ВОСЬМИ И НА 8
Цели: составить таблицу умножения восьми и умножения на восемь; закреплять ранее изученные табличные случаи умножения и деления; совершенствовать вычислительные навыки; развивать внимание и память.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Вставьте числа в «окошки»:
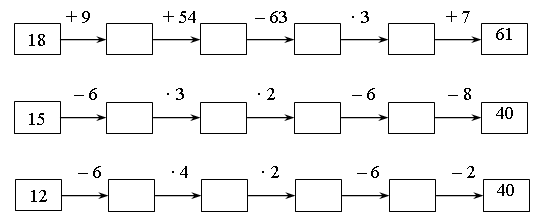
2. Задача.
Бак автомобиля «Волга» вмещает 55 л бензина, а автомобиля «Москвич» – 35 л. На сколько литров меньше вмещает бак автомобиля «Москвич»?
3. Математический диктант.
– Сложите двузначное число с однозначным и запишите только ответы.
28 + 4 64 + 5 30 + 7 35 + 6
32 + 6 18 + 3 49 + 8 56 + 7
48 + 3 25 + 7 18 + 4 64 + 3
72 + 8 12 + 8 21 + 9 81 + 4
56 + 4 72 + 7 27 + 8 47 + 3
42 + 9 14 + 8 24 + 2 88 + 2
36 + 7 35 + 1 16 + 7 55 + 5
68 + 5 21 + 5 15 + 9 33 + 7
III. Сообщение темы урока.
– Рассмотрите рисунок.
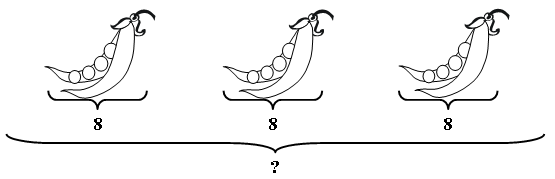
– Как быстро узнать, сколько всего горошин?
– Сегодня на уроке мы составим таблицу умножения.
IV. Изучение нового материала.
Задание № 1 (с. 35).
– Рассмотрите рисунок.
– Сколько подарков в каждом ряду?
– Сколько рядов?
– Как узнать, сколько приготовили новогодних подарков?
– Как решил задачу Волк?
– Как решил задачу Заяц?
– Кто из них быстрее справился с заданием?
Далее учащиеся составляют и записывают в тетрадь таблицу умножения числа 8.
– Сравните свою таблицу с таблицей в учебнике.
Задание № 2 (с. 35).
Используя калькулятор, учащиеся сравнивают значения произведений.
9 · 8 равно 8 · 9
9 · 8 = 72 8 · 9 = 72
Вывод: умножать числа можно в любом порядке.
Задание № 3 (с. 36).
Учащиеся выполняют записи:
0 · 8 = 0
8 · 0 = 0
Задание № 4 (с. 36).
Учащиеся составляют таблицу умножения на число 8.
Задание № 5 (с. 36).
– Прочитайте текст.
– Является ли он задачей? Почему?
– Что известно в задаче?
– Что требуется узнать?
– Выполните рисунок и решите задачу.
Решение:
9 · 8 = 72 (ст.) – всего.

Ответ: 72 ст.

V. Повторение пройденного материала.
1. Работа в печатной тетради № 2.
Задание № 59.
Учитель может предложить карточку-помощницу.
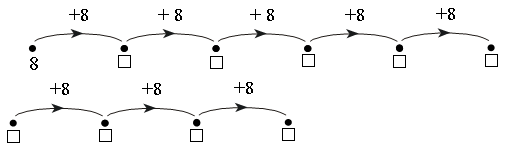
Задание № 61.
Перед непосредственным выполнением задания внимательно рассмотрите с учащимися иллюстрацию.
Выясните, что доска для игры в шахматы разбита на 8 рядов квадратов по 8 в каждом. Причем в ряду по 4 белые и черные клетки.
В шахматы играют 2 человека: один – белыми фигурами, а другой – черными.
В начале игры фигуры устанавливаются по краям доски в 2 ряда. В одном ряду – только пешки, а в другом – разные фигуры (можно их назвать и показать: король, ферзь, два слона, два коня и две ладьи).
Далее можно переходить к письменной части задания.
2. Работа по учебнику.
Задание № 26 (с. 39).
Учащиеся составляют карточки-помощницы.
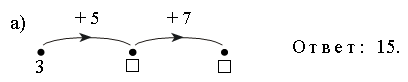
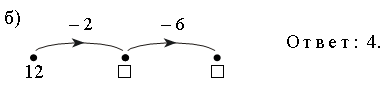
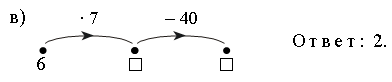
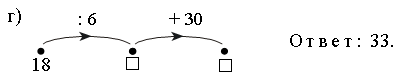
Задание № 27 (с. 39).
Важно, чтобы при ответе на данный вопрос учащиеся дали исчерпывающие ответы, то есть указали все возможные пары чисел, удовлетворяющие условию. Только в том случае задание считается выполненным. При этом удобно последовательно перебирать по порядку все числа, начиная с 0, и находить каждому из них (если возможно) пару. Тем самым исключается возможность пропуска какой-нибудь пары.
Запись:
1 · 12 = 12
2 · 6 = 12
3 · 4 = 12
Задание № 28 (с. 39).
Запись:
0 + 12 = 12 4 + 8 = 12
1 + 11 = 12 5 + 7 = 12
2 + 10 = 12 6 + 6 = 12
3 + 9 = 12
Задание № 29 (с. 39).
Запись:
7 : 1 = 7 21 : 3 = 7
14 : 2 = 7 28 : 4 = 7
VI. Итог урока.
– Что нового узнали на уроке?
– Что означают записи: «4 · 8» и «8 · 5»?
Домашнее задание: № 11, 30 (учебник); № 63 (рабочая тетрадь).
Урок 73
Умножение на 8. Решение задач
Цели: совершенствовать навыки решения составных задач разными способами; продолжить формирование умений строить и читать математические графы; закреплять табличные случаи умножения и деления; развивать умение анализировать и рассуждать.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Сравните числа в первом и во втором столбиках. Найдите сумму чисел первого столбика.
Догадайтесь, как можно быстро вычислить сумму чисел второго столбика.
6 16
7 17
8 18
9 19
2. Какой знак действия нужно поставить, чтобы получились верные равенства?
87 … 49 = 38 50 … 8 = 42
78 … 19 = 59 90 … 4 = 86
3. Составьте задачу по таблице.
|
Цена |
Количество |
Стоимость |
|
5 р. |
3 конверта |
? р. |
4. Отметьте, на каких чертежах правильно изображен цилиндр.
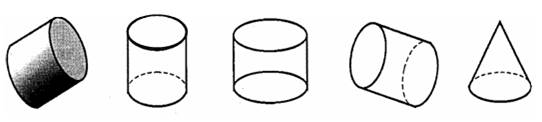
III. Сообщение темы урока.
– Сегодня на уроке мы будем решать задачи и повторять таблицу умножения на 8.
IV. Изучение нового материала.
Задание № 7 (с. 36).
– Прочитайте текст. Является ли он задачей? Почему?
– Что известно в задаче?
– Что требуется узнать?
– Запишите условие задачи в таблицу.
|
Кол-во в 1 пучке |
Кол-во пучков |
Всего редиски |
|
8 шт. |
9 п. |
? шт. |
Решение:
8 · 9 = 72 (шт.) – всего.
Ответ: 72 штуки.
Задание № 8 (с. 36).
– Прочитайте задачу.
– Что известно?
– Что надо узнать?
– Запишите условие задачи в таблицу.
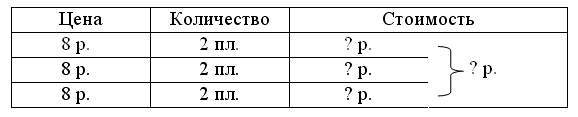
Решение:
1-й способ.
1) Сколько стоят 2 плитки шоколада?
8 · 2 = 16 (р.).
2) Сколько стоит вся покупка?
16 + 16 + 16 = 48 (р.).
2-й способ.
1) Сколько плиток шоколада купили?
2 · 3 = 6 (пл.).
2) Сколько стоит вся покупка?
8 · 6 = 48 (р.).
Ответ: 48 рублей.
Задание № 9 (с. 36).
– Прочитайте задачу.
– Что известно? Что требуется узнать в задаче?
– Заполните таблицу.

Решение:
1) 8 · 3 = 24 (р.) – стоимость моркови.
2) 25 – 24 = 1 (р.) – дороже капуста, чем морковь.
3) 25 + 24 = 49 (р.) – стоимость всей покупки.
Ответ: на 1 р. дороже; 49 р.
Задание № 10 (с. 36).
– Прочитайте задачу.
– Что известно? Что требуется узнать в задаче?
– Запишите кратко условие задачи.
Запись условия задачи:
Было – 6 рядов по 8 ст.
Вынесли – ? ст.
Осталось – 46 ст.
Решение:
1) 8 · 6 = 48 (ст.) = было.
2) 48 – 46 = 2 (ст.) – вынесли.
Ответ: 2 стула.

V. Повторение пройденного материала.
1. Работа по учебнику.
Задание № 32 (с. 40).
Это задание является подготовительным для введения правила нахождения площади прямоугольника.
– Рассмотрите данные фигуры. Как они называются?
– Что такое площадь? Как узнать площадь каждого многоугольника?
– Стороны многоугольников разбиты точками на отрезки. Измерьте длину этих отрезков. (Учащиеся проводят измерение линейкой прямо на чертеже в учебнике. Отрезки равны 1 см.)
– Разбейте каждый многоугольник на квадраты, мысленно проводя горизонтальные и вертикальные отрезки через отмеченные на сторонах точки, и подсчитайте число получившихся квадратов.
Решение: в зеленом многоугольнике будет 2 ряда квадратов по 4 в каждом, следовательно, его площадь: 8 смІ (4 · 2 = 8). А в розовом многоугольнике будет 3 ряда квадратов по 8 в каждом, значит, его площадь: 24 смІ (8 · 3 = 24).
– Выполните проверку, используя палетку.
Задание № 33 (с. 40).
– Рассмотрите графы. Какое отношение задано на первом графе? (Отношение «больше».)
– Прочитайте каждое высказывание на первом графе.
· 56 больше 30.
· 56 больше 28.
· 30 больше 28.
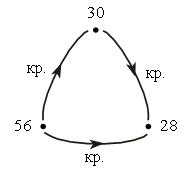
– На сколько 56 больше каждого из остальных чисел?
Запись:
56 – 30 = 26.
56 – 28 = 28.
– Какое отношение задано на втором графе? (Отношение «меньше».)
– Прочитайте каждое высказывание на втором графе.
· 36 меньше 62.
· 36 меньше 47.
· 36 меньше 100.
· 47 меньше 62.
· 47 меньше 100.
· 62 меньше 100.
– На сколько 36 меньше каждого из остальных чисел?
Запись:
100 – 36 = 64.
47 – 36 = 11.
62 – 36 = 26.
2. Работа в печатной тетради № 2.
Задание № 62.
На первый вопрос задачи учащиеся без труда смогут ответить самостоятельно. А перед выполнением второй части задания стоит провести небольшую подготовительную работу. Спросите у детей: «Сколько же таблеток купила мама?» (24.)
– Что известно о ежедневном приеме таблеток? (Принимают по одной таблетке 4 раза в день.)
– Сколько же нужно таблеток на один день? (1 · 4 = 4.)
Теперь, когда выяснено, сколько всего куплено таблеток и сколько таблеток расходуется каждый день, дети могут самостоятельно завершить решение.
Решение:
1) 8 · 3 = 24 (т.) всего.
2) 24 : 4 = 6 (дн.) – хватит.
Задание № 23.
– Прочитайте задачу.
– Что известно? Что потребуется узнать?
Учитель может предложить записать условие задачи в таблицу.

Решение:
1-й способ.
1) 2 · 8 = 16 (п.) – больших.
2) 6 · 8 = 48 (п.) – маленьких.
3) 16 + 48 = 64 (п.) – всего.
2-й способ.
1) 2 + 6 = 8 (п.) – на 1 пиджак.
2) 8 · 8 = 64 (п.) – всего.
Ответ: 64 п.
VI. Итог урока.
– Что нового узнали на уроке?
– Назовите правила чтения математических графов.
Домашнее задание: № 6, 31 (учебник); № 64 (рабочая тетрадь).
Урок 74
Умножение и ДЕЛЕНИЕ на 8
Цели: составить таблицу деления на 8; учить использовать знание таблицы умножения для решения задач; совершенствовать вычислительные навыки; продолжить формирование умений строить и читать математические графы; развивать внимание и умение анализировать.
Ход урока
I. Организационный момент.
II. Устный счет.
1. По какому правилу подобраны выражения в каждой паре? Догадайтесь, в каких парах значения выражений будут одинаковыми.
43 + 8 72 + 5 54 + 7 68 + 5
48 + 3 75 + 2 57 + 4 65 + 8
63 – 4 85 – 6 42 – 8 76 – 7
64 – 3 86 – 5 48 – 2 77 – 6
– Проверьте себя, вычислив значения всех выражений.
2. Ответьте на вопросы:
а) Назовите самое большое из данных чисел, которое делится на 3: 1, 2, 3, 4, 5, 6, 7.
б) Назовите самое большое число до 5 (до 10, до 14), которое делится на 3.
в) Какое самое большое число до 22 делится на 4? на 5? на 6? на 7?
3. Задача.
В саду посадили 14 кустов крыжовника, по 7 кустов в каждом ряду. Сколько было рядов?
III. Сообщение темы урока.
– Рассмотрите рисунок на доске.
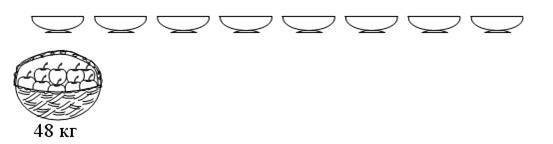
– Составьте задачу по этому рисунку.
– Какое действие надо выполнить для решения этой задачи?
– Сегодня на уроке мы составим таблицу деления на 8.
IV. Изучение нового материала.
Используя цветные фишки, учащиеся составляют на доске таблицу деления на 8.
Запись на доске:
8 · 1 = 8 · 2 = 8 · 3 = 8 · 4 =
׃ 8 = ׃ 8 = ׃ 8 = ׃ 8 = 4
Далее учащиеся сравнивают составленную таблицу деления и таблицу, данную в учебнике (на с. 37).
Задание № 12 (с. 37).
Используя данные схемы, учащиеся составляют равенства.
Запись:
5 · 8 = 40 8 · 8 = 64 9 · 8 = 72
40 ׃ 8 = 5 64 ׃ 8 = 8 72 ׃ 8 = 9
Задание № 14 (с. 37).
– Прочитайте текст. Является ли он задачей? Почему?
– Что известно в задаче? Что требуется узнать?
– Выполните схему к данной задаче.
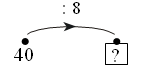
Решение:
40 ׃ 8 = 5 (к.) – было у Маши.
Ответ: 5 кур.
Задание № 15 (с. 38).
– Прочитайте задачу.
– Что известно? Что требуется узнать?
– Заполните таблицу и решите задачу.
|
Цена |
Количество |
Стоимость |
|
8 р. |
? (человек) |
72 р. |
Решение:
72 ׃ 8 = 9 (чел.).
Ответ: 9 человек.

V. Повторение пройденного материала.
1. Работа по учебнику.
Задание № 34 (с. 41).
– Прочитайте текст. Является ли он задачей?
– Что известно в задаче?
– Что требуется узнать?
– В какой форме написано требование?
– Решите задачу и начертите оба отрезка.
– Имеет ли это задание одно решение? (Два решения, так как не сказано «больше» или «меньше» красный отрезок, чем зеленый.)
Решение:
1) 5 + 2 = 7 (см).
2) 5 – 2 = 3 (см).
2. Работа в печатной тетради № 2.
Задание № 65.
Учащиеся самостоятельно анализируют схемы и заполняют «окошки».
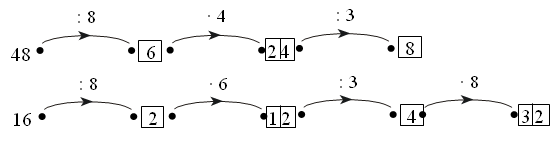
Задание № 66.
Учащиеся должны записать следующие примеры:
6 · 8 = 48 7 · 8 = 56
8 · 6 = 48 8 · 7 = 56
48 ׃ 6 = 8 56 ׃ 7 = 8
48 ׃ 8 = 6 56 ׃ 8 = 7
Задание № 67.
– Прочитайте задачу.
– Что известно в задаче?
– Что требуется узнать?
– Запишите кратко условие задачи.
Было – 60 п.
Красили – ? (дн.), по 8 п.
Осталось – 12 п.
Решение:
1) Сколько парт покрасили?
60 – 12 = 48 (п.).
2) Сколько дней красили?
48 ׃ 8 = 6 (дн.).
Ответ: 6 дней.
VI. Итог урока.
– Что нового узнали на уроке?
– Как связано деление с умножением?
– Назовите правила чтения математических граф.
Домашнее задание: № 13 (учебник); № 72 (рабочая тетрадь).
Урок 75
Умножение
и ДЕЛЕНИЕ на 8.
ВОСЬМАЯ ЧАСТЬ ЧИСЛА
Цели урока: ввести понятие «восьмая часть числа»; учить находить восьмую часть числа; совершенствовать практические навыки в построении чертежей; продолжить формирование умений решать составные задачи разными способами; развивать логическое мышление.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Как получили следующее число цепочки из предыдущего?
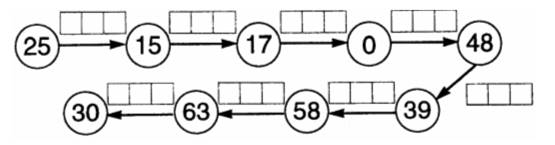
2. Задача.
Дети посадили 16 дубков в 2 одинаковых ряда. Сколько дубков было в каждом ряду?
3. Выберите фигуру, которую нужно нарисовать.
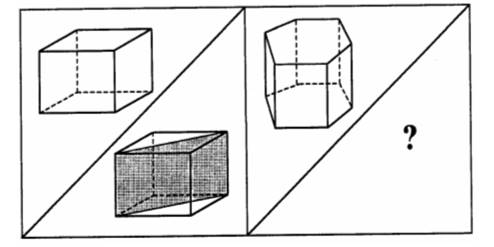
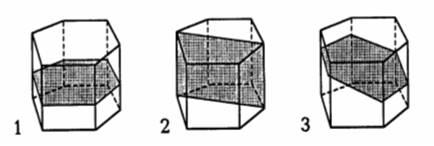
III. Сообщение темы урока.
– Рассмотрите рисунки на доске.
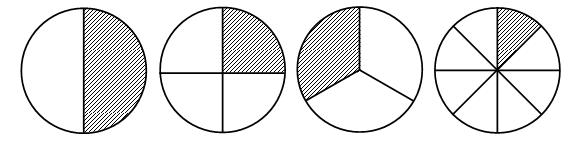
– Как называются эти фигуры?
– Какая часть закрашена на каждом круге?
– Сегодня на уроке будем определять восьмую часть числа.
IV. Изучение нового материала.
Учащиеся выполняют действия с цветными фишками.
– Разложите 16 фишек по 8 в каждом ряду.

– Покажите восьмую часть фишек.
– Как найти восьмую часть числа?
Запись на доске:
16 ׃ 8 = 2.
Задание № 21 (с. 39).
Запись:
24 ׃ 8 = 3 (см).
56 ׃ 8 = 7 (см).
16 ׃ 8 = 2 (см).
Учитель должен обратить внимание учащихся на то, что восьмая часть величины – это тоже величина, а не число. 3 см – это восьмая часть 24 см.
Задание № 22 (с. 39).
– Прочитайте задачу.
– Что известно в задаче? Что требуется узнать?
– Запишите кратко условие задачи.
Запись:
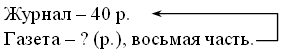
Решение: 40 ׃ 8 = 5 (р.).
Ответ: 5 р.
Задание № 24 (с. 39).
– Прочитайте текст. Является ли он задачей?
– Что известно? Что требуется узнать?
– Запишите кратко условие задачи.
Запись:
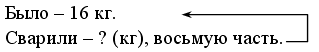
Осталось – ? (кг).
Решение:
1) 16 ׃ 8 = 2 (кг) – сварили.
2) 16 – 2 = 14 (кг) – осталось.
Ответ: 14 кг.

V. Повторение пройденного материала.
1. Работа по учебнику.
Задание № 35 (с. 41).
– Прочитайте задачу.
– Что известно в задаче?
– Что требуется узнать?
– Запишите кратко условие задачи.
Запись:
Было – ? чел.
В театр – 5 (чел.), это шестая часть.
В цирк – ? (чел.).
Решение:
1) Сколько человек было в классе?
5 · 6 = 30 (чел.).
2) Сколько человек поехало в цирк?
30 – 5 = 25 (чел.).
Ответ: 25 человек.
2. Работа в печатной тетради № 2.
Задание № 68.
Запись в таблице:
|
Число |
8 |
16 |
|
Половина числа |
4 |
8 |
|
Четверть числа |
2 |
4 |
|
Восьмая часть числа |
1 |
2 |
– Сравните половину и четверть числа.
– Сравните четверть и восьмую часть каждого числа.
– Какой вывод можно сделать?
Задание № 69.
Учащиеся выполняют чертежи:
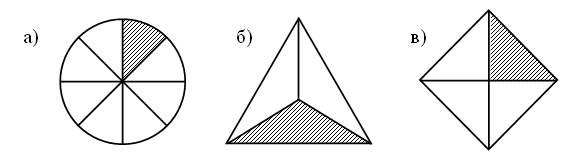
3. Фронтальная работа по таблице.
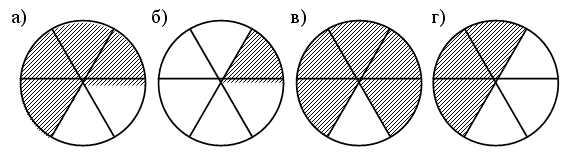
– На сколько равных частей разделен каждый круг?
– Сколько частей каждого круга заштриховано?
– Какая это часть круга?
– Можно ли утверждать, что у первого круга закрашены две третьих части?
– Можно ли утверждать, что у последнего круга закрашена половина?
VI. Итог урока.
– Что нового узнали на уроке?
– Как вычислить восьмую часть числа?
– Можно ли сравнивать доли числа?
Домашнее задание: № 31 (учебник); № 71 (рабочая тетрадь).
Урок 76
Умножение
и ДЕЛЕНИЕ на 8.
ВОСЬМАЯ ЧАСТЬ ЧИСЛА
Цели: совершенствовать навыки решения задач на нахождение доли от числа и решения составных задач разными способами; закреплять табличные случаи умножения и деления на 8; развивать внимание и умение анализировать.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Какие цифры нужно вставить в «окошки», чтобы получились верные равенства?
8 – 3 = 7 9 – 4 = 6
5 – 6 = 4 7 – 8 = 2
4 – 7 = 3 6 – 2 = 8
– Чем похожи все равенства?
2. Задача.
В спортивном кружке занимались 10 девочек, а мальчиков – на 2 меньше, чем девочек. Сколько всего детей занималось в спортивном кружке?
3. Математический диктант.
– Вычтите однозначное число из двузначного и запишите только ответы.
50 – 5 43 – 3 28 – 6 36 – 2
40 – 8 58 – 8 54 – 3 99 – 6
30 – 9 44 – 4 48 – 7 24 – 1
20 – 4 89 – 9 79 – 4 76 – 3
41 – 2 37 – 8 42 – 4 44 – 6
96 – 7 52 – 3 53 – 6 51 – 4
64 – 5 15 – 6 61 – 5 26 – 9
83 – 4 98 – 9 95 – 9 17 – 6
III. Сообщение темы урока.
– Сегодня на уроке мы будем вычислять доли от числа и закреплять знание таблицы умножения и деления на 8.
IV. Работа по теме урока.
1. Работа по учебнику.
Задание № 18 (с. 38).
– Рассмотрите данные на рисунке фигуры.
– Чем они похожи?
– Чему равна площадь каждой фигуры? (Зеленая фигура – 17 смІ, красная – 10 смІ.)
Задание № 19 (с. 38).
Это одна из задач, подготавливающих введение отношений «больше в...», «меньше в...». При обсуждении ее решения удобно в качестве модели использовать фишки.
– Выложите в ряд столько желтых фишек, сколько открыток у Пети, а ниже выложите красные фишки так, чтобы их было 3 раза по столько, сколько желтых фишек (то есть столько, сколько открыток у Лены).
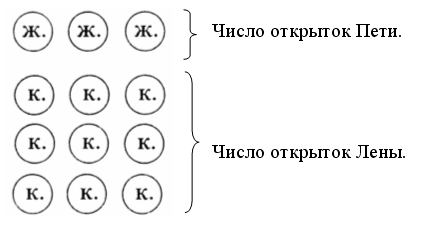
– Какое арифметическое действие нужно выполнить, чтобы выяснить, сколько открыток у Лены? (Надо 4 умножить на 3.)
– Запишите условие задачи.
Решение:
4 · 3 = 12 (откр.).
Ответ: 12 открыток.
Задание № 25 (с. 39).
– Прочитайте задачу.
– Что известно? Что требуется узнать?
– Запишите кратко условие задачи.
Запись условия:
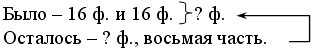
Решение:
1-й способ.
1) 16 + 16 = 32 (ф.) – всего.
2) 32 ׃ 8 = 4 (ф.) – осталось.
Ответ: 4 фартука.
2-й способ.
1) 16 : 8 = 2 (ф.) – осталось белых.
2) 16 : 8 = 2 (ф.) – осталось черных.
3) 2 + 2 = 4 (ф.) – осталось всего.
Ответ: 4 фартука.
– Какой способ более удобный?
Задание № 38 (с. 41).
– Какую фигуру называют треугольником?
– Какую фигуру называют окружностью?
– Начертите треугольник и окружность так, чтобы у этих фигур были три общие точки.
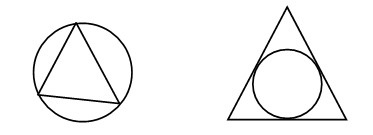
2. Работа в печатной тетради № 2.
Задание № 70.
Выполнение задания рекомендуется дополнить следующей устной фронтальной работой.
– Сколько всего детей изображено на рисунке? (Четверо.)
– По сколько яблок мы обведем каждой линией? (Обведем тоже по 4.)
– Проведите линии. Сколько раз мы обвели по 4 яблока? (4 раза.)
– Сделайте вывод. (У нас получилось яблок 4 раза по столько, сколько детей.)
Задание № 31.
Задание лучше выполнять, используя не линейку, а циркуль, последовательно откладывая на числовом луче отрезки нужной длины.

Начиная с этого задания, учащиеся будут постепенно привыкать для изображения отрезков использовать не только линейку, но и циркуль.

V. Самостоятельная работа.
1. Вставь числа в «окошки», чтобы получились верные равенства:
8 · 6 = 8 + 8 + 8 + + 8 · 8 = 8 · – 8
8 · 7 = 8 · 6 + 8 · 3 = 8 + 8 +
8 · 9 = 9 · 9 – 8 · 5 = 8 · + 8
5 · 8 = · 5 8 · 5 = 8 · – 8
2. Запиши выражения в виде произведения двух чисел и найди их значения:
(75 – 67) · 4 (62 – 53) · 8
(81 – 72) · 3 (55 – 47) · 7
(44 – 36) · 5 (37 – 28) · 6
3. Какому рисунку соответствует каждое выражение и что оно обозначает?
![]()

– Проверь себя, пользуясь линейкой и вычислениями.
–
Начерти ломаную линию, которой соответствует выражение: ![]()
VI. Итог урока.
– Что нового узнали на уроке?
– Как вычислить восьмую часть числа?
Урок 77
Умножение ДЕВЯТИ И на 9
Цели: составить таблицу умножения девяти и на девять; совершенствовать навыки решения задач умножением и делением; развивать внимание и умение анализировать.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Вставьте знаки действий, чтобы получились верные равенства:
7 … 5 … 9 … 15 = 18 8 … 7 … 6 = 9
30 … 20 … 9 … 1 = 18 4 … 8 … 3 = 9
14 … 7 … 8 … 3 = 18 12 … 5 … 2 = 9
2. Задача.
На первой стройке работало всего 20 подъемных кранов, затем на вторую стройку перевели 4 больших и 6 малых кранов. Сколько кранов осталось на первой стройке?
3. Выберите фигуры, которые нужно нарисовать.
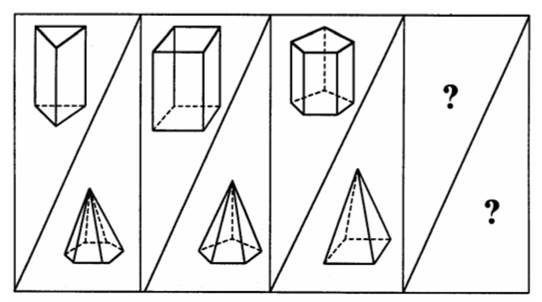
III. Сообщение темы урока.
– Рассмотрите рисунки на доске.
– На сколько всего частей разделен каждый круг?
– Сколько всего частей получилось? (9 + 9 + 9 + 9 = 36.)
– Сегодня на уроке мы узнаем, как быстро ответить на этот вопрос, составим таблицу умножения на 9.
IV. Изучение нового материала.
Задание № 1 (с. 42).
– Рассмотрите рисунок в учебнике.
– Сколько растет елочек в каждом ряду? (9.)
– Сколько всего рядов елочек? (3.)
– Как узнать, сколько елочек в трех рядах?
– Как решил задачу Волк? (Сложил: 9 + 9 + 9 = 27.)
– Как решил задачу Заяц? (Умножил: 9 · 3 = 27.)
– Кто из них быстрее справился с заданием? Почему?
– Рассмотрите таблицу умножения числа 9.
– Какие примеры из нее вам уже знакомы?
– О каком примере вы только что узнали? (9 · 9 = 81.)
Задание № 2 (с. 42).
Используя таблицу умножения числа 9, учащиеся составляют и записывают таблицу умножения на число 9.
Далее учащиеся выполняют вычисления предложенных примеров.
Задание № 3 (с. 43).
– Прочитайте текст. Является ли он задачей? Почему?
– Что известно в задаче? Что требуется узнать?
– При необходимости можете выполнить рисунок.
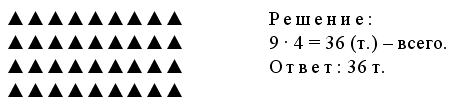
Задание № 4 (с. 43).
– Какие фигуры изображены на рисунке? (Многоугольники.)
– Как называются данные многоугольники? (Четырехугольники.)
– На сколько квадратов разделен зеленый четырехугольник?
Запись: 9 + 9 + 9 = 27 (кв.).
9 · 3 = 27 (кв.).
– Какой способ вам понравился больше? Почему?
– На сколько квадратов разделен желтый четырехугольник?
Запись: 9 + 9 + 9 + 9 + 9 + 9 + 9 + 9 + 9 = 81 (кв.).
9 · 9 = 81 (кв.).
– Какой способ более удобный?
Задание № 5 (с. 43).
– Сколько кирпичей в каждом ряду? (9 кирпичей.)
– Сколько рядов в этой кладке? (5 рядов.)
– Из скольких кирпичей состоит кладка?
Запись: 9 · 5 = 45 (к.).

V. Повторение пройденного материала.
1. Работа по учебнику.
Задание № 26 (с. 46).
Учитель должен обратить внимание учащихся на то, что сравнение в каждом случае можно проводить и без выполнения вычислений.
Запись: 7 · 8 больше 5 · 8; 6 · 0 меньше 6 · 1;
12 ׃ 3 больше 12 ׃ 4; 2 + 2 равно 2 · 2. И т. д.
2. Работа в печатной тетради № 2.
Задание № 81.
Это задание предваряет введение правила нахождения площади прямоугольника.
Задание состоит из двух частей:
а) разбить четырехугольник на квадраты с длиной стороны 1 см;
б) найти площадь четырехугольника.
Учитель обращает внимание учащихся на то, что в первой части задания для откладывания на сторонах четырехугольника отрезков длиной 1 см удобнее использовать циркуль.
Затем учащиеся по линейке проводят отрезки:

В итоге четырехугольник получился разбитым на квадраты площадью 1 смІ. Теперь переходим к выполнению второй части задания. При этом дети могут рассуждать двумя способами.
1-й способ.
В четырехугольнике 2 ряда квадратов по 8 в каждом. Следовательно, его площадь: 8 · 2 = 16 (смІ).
2-й способ.
В четырехугольнике 8 столбцов квадратов по 2 в каждом. Значит, его площадь: 2 · 8 = 16 (смІ).
VI. Итог урока.
– Что нового узнали на уроке?
– Что такое площадь?
– Какую фигуру называют четырехугольником?
Домашнее задание: № 27, 28 (учебник); задание № 73 (рабочая тетрадь).
Урок 78
Умножение на 9. РЕШЕНИЕ ЗАДАЧ
Цели: совершенствовать навыки решения составных задач; закреплять табличные случаи умножения и деления на 2, 3, 4, 5, 6, 7, 8; развивать логическое мышление.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Впишите недостающие цифры:
58 5 6 93 7
+ 1 – 23 + 27 – 8 – 0
0 5 5 7 7
2. Задача.
В кассе кинотеатра было 98 билетов. Продали 60 взрослых и 8 детских.
Сколько билетов осталось в кассе?
3. Математический диктант.
– Выполните сложение двузначных чисел и запишите только ответы:
40 + 20 36 + 20 60 + 30 36 + 10
10 + 50 48 + 40 20 + 41 60 + 32
80 + 20 74 + 10 30 + 70 53 + 40
20 + 29 30 + 40 16 + 80 13 + 80
14 + 25 12 + 27 23 + 14 63 + 15
36 + 12 11 + 11 50 + 49 17 + 12
56 + 23 48 + 21 36 + 22 28 + 31
64 + 11 74 + 15 44 + 44 42 + 57
4. Выберите картинку.

III. Сообщение темы урока.
– Сегодня на уроке будем учиться решать задачи и выполнять умножение на 9.
IV. Изучение нового материала.
Задание № 7 (с. 43).
– Прочитайте текст. Является ли он задачей? Почему?
– Что известно в задаче? Что требуется узнать?
– Запишите условие задачи в виде схемы и решите ее.
Запись:
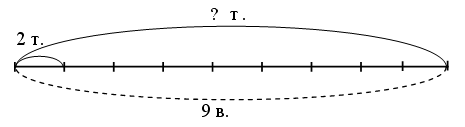
Решение:
2 · 9 = 18 (т.).
Ответ: 9 т.
Задание № 8 (с. 43).
– Прочитайте условие задачи.
– Что известно? Что требуется узнать?
– Заполните таблицу по данному условию:

Решение:
1) 6 · 9 = 54 (пуг.) – пришили к 9 пиджакам.
2) 54 + 8 = 62 (пуг.) – пришили всего.
Ответ: 62 пуговицы.
Задание № 9 (с. 44).
– Прочитайте условие задачи.
– Что известно? Что требуется узнать?
– Заполните таблицу по данному условию:

Учащиеся должны понимать, что на первый вопрос («В каком из населенных пунктов домов больше?») можно ответить, не выполняя вычислений.
Действительно, чтобы найти, сколько домов в деревне, надо 9 умножить на 3. А чтобы найти, сколько домов в поселке, надо 8 умножить на 9. И без вычислений видно, что 8 · 9 (или, что то же самое, 9 · 8) больше 9 · 3, поэтому в поселке домов больше, чем в деревне.
А вот для того чтобы ответить на второй вопрос («На сколько домов в поселке больше, чем в деревне?»), уже необходимо выполнить вычисления.
Решение:
1) Сколько домов в первой деревне?
9 · 3 = 27 (д.).
2) Сколько домов во второй деревне?
8 · 9 = 72 (д.).
3) На сколько домов больше во второй деревне?
72 – 27 = 45 (д.).
Ответ: на 45 домов больше.
Задание № 10 (с. 44).
Это одна из задач, предваряющих введение отношений «больше в...», «меньше в...». Решение лучше начать с моделирования ситуации, описанной в задаче, с помощью фишек. Попросите учащихся выложить в ряд столько желтых фишек, сколько попугайчиков в маленькой клетке, а ниже выложить красные фишки так, чтобы их было в 2 раза по столько, сколько желтых фишек (то есть столько, сколько было канареек).
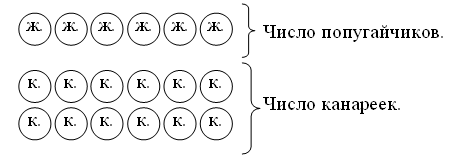
– Какое арифметическое действие нужно выполнить, чтобы найти число канареек в большой клетке? (Надо 6 умножить на 2.)
– Запишите решение этой задачи.
Решение:
6 · 2 = 12 (к.).
Ответ: 12 канареек.

V. Повторение пройденного материала.
1. Работа по учебнику.
Задание № 29 (с. 46).
– Прочитайте задачу.
– Что известно? Что требуется узнать?
– Запишите кратко условие задачи.
Запись:
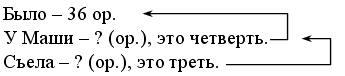
Осталось – ? (ор.).
Решение:
1) Сколько орехов у Маши?
36 ׃ 4 = 9 (ор.).
2) Сколько орехов съела Маша?
9 ׃ 3 = 3 (ор.).
3) Сколько орехов осталось у Маши?
9 – 3 = 6 (ор.).
Ответ: 6 орехов.
2. Работа в печатной тетради № 2.
Задание № 83.
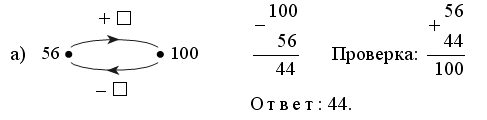
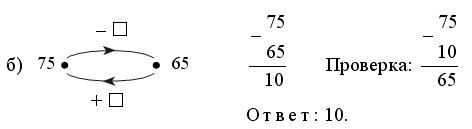
VI. Итог урока.
– Что нового узнали на уроке?
Домашнее задание: № 6 (учебник); задания № 82, 84 (рабочая тетрадь).
Урок 79
Умножение и деление на 9
Цели: составить таблицу деления на 9; совершенствовать навыки решения и составления обратных задач; закреплять навыки вычисления периметра многоугольников; развивать умение рассуждать и обобщать.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Догадайтесь, по какому правилу составлены схемы, вставьте числа в «окошки».
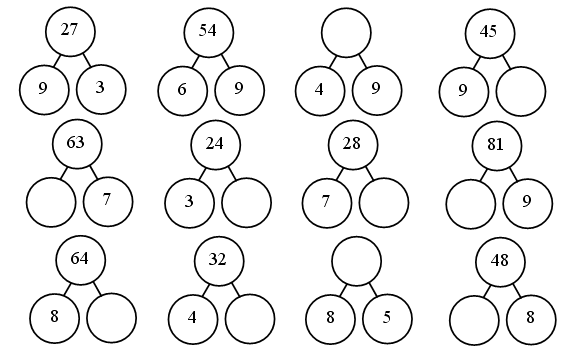
2. Поставьте знаки «+» или «–».
69 … 40 … 8 = 21 17 … 70 … 2 = 89
75 … 5 … 30 + 40 31 … 60 … 7 = 98
20 … 6 … 2 = 24 61 … 8 … 9 = 60
8 … 2 … 47 = 57 34 … 4 … 6 = 36
3. Задача.
За три дня рабочие отремонтировали 24 троллейбуса: в первый день 8 троллейбусов, во второй – 10. Сколько троллейбусов они отремонтировали в третий день?
4. Выберите фигуру, которую нужно нарисовать.
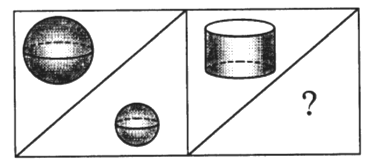
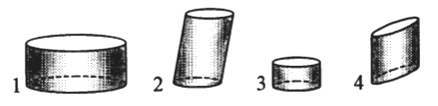
III. Сообщение темы урока.
– Рассмотрите, как составлены столбики примеров на доске.
18 ׃ 2 =
18 ׃ 3 =
18 ׃ 6 =
18 ׃ = 2
– Чем они похожи?
– Чем отличаются?
– Вставьте числа в «окошки».
– Какие трудности у вас возникли?
– Сегодня на уроке мы составим таблицу деления на 9.
IV. Изучение нового материала.
Учащиеся, используя цветные фишки и записи на доске, составляют таблицу деления на 9.
9 · 1 = 9 · 2 = 9 · 3 = 9 · 4 =
׃ 9 = ׃ 9 = ׃ 9 = ׃ 9 = 4 и т. д.
Далее учащиеся сравнивают свою таблицу деления с таблицей в учебнике на с. 44.
Задание № 12 (с. 44).
По каждой схеме надо составить равенства.
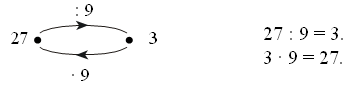
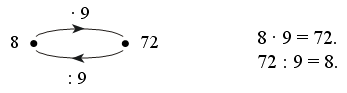
Задание 14, с. 45.
– Прочитайте текст. Является ли он задачей? Почему?
– Что известно? Что требуется узнать?
– Каким действием узнать длину стороны девятиугольника? (Делением.)
– На сколько надо разделить периметр? Почему? (Надо 36 разделить на 9, так как у девятиугольника девять сторон.)
Решение:
36 : 9 = 4 (см).
Ответ: 4 см.
Задание № 15 (с. 45).
– Прочитайте условие задачи.
– Что известно? Что требуется узнать?
– Заполните условие задачи в таблицу:
|
В 1 стакане |
Количество стаканов |
Всего кусочков |
|
? кус. |
9 ст. |
18 кус. |
Решение:
1) 18 : 9 = 2 (кус.).
Ответ: 2 кусочка.

V. Повторение пройденного материала.
1. Работа по учебнику.
Задание № 30 (с. 47).
Запись условия обеих задач:
Было – 100 кг. Было – ? кг.
Продали – ? (кг). Продали – 80 кг.
Осталось – 20 кг. Осталось – 20 кг.
Решение: Решение:
100 – 20 = 80 (кг) – продали. 80 + 20 = 100 (кг) – было.
Ответ: 80 кг. Ответ: 100 кг.
– Сравните обе задачи. Чем они похожи?
– Чем различаются?
– Можно ли составить еще одну похожую задачу?
– Запишите кратко условие третьей задачи и решите ее.
Запись условия третьей задачи:
Было – 100 кг.
Продали – 80 кг.
Осталось – ? кг.
Решение:
100 – 80 = 20 (кг) – осталось.
Ответ: 20 кг.
Задание № 31 (с. 47).
– Какая фигура изображена? (Многоугольник.)
– Какую фигуру называют многоугольником?
– Как называется этот многоугольник? (Четырехугольник.)
– Что надо знать, чтобы вычислить периметр четырехугольника?
– Измерьте в сантиметрах длины сторон этого четырехугольника и вычислите его периметр.
Запись:
5 + 5 + 2 + 4 = 16 (см).
2. Работа в печатной тетради № 2.
Задание № 79.
– Прочитайте условие задачи.
– Что вам известно?
– Что требуется узнать?
«Изюминка» этой задачи в том, что за стол сели не только 8 Таниных подруг, но и она сама.
Решение:
1) Сколько девочек будет за столом?
8 + 1 = 9 (чел.).
2) Сколько пирожных досталось каждой девочке?
18 : 9 = 2 (п.).
Ответ: 2 п.
Задание № 85.
Учащиеся работают самостоятельно, после чего учитель проводит фронтальную проверку по вопросам:
– Сколько ежей на рисунке? (Четверо.)
– По сколько грибов вы обвели каждой линией? (По 4.)
– Сколько раз вы обвели линией по 4 гриба? (5 раз.)
– Какой вывод можно сделать? (У нас получилось грибов 5 раз по столько, сколько опят.)
VII. Итог урока.
– Что нового узнали на уроке?
– Назовите признаки многоугольников.
Домашнее задание: № 13, 16 (учебник); № 74–76 (рабочая тетрадь).
Урок 80
Умножение
и деление на 9.
ДЕВЯТАя ЧАСТЬ ЧИСЛА
Цели: ввести понятие «девятая часть числа»; учить находить девятую часть числа с помощью деления; совершенствовать практические умения по построению геометрических фигур; закреплять знание табличных случаев умножения и деления; развивать внимание и умение анализировать.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Разгадайте правило, по которому составлены схемы, вставьте числа в «окошки».
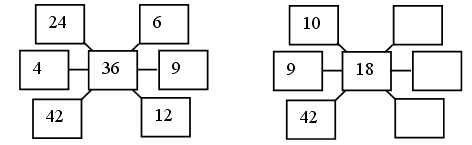
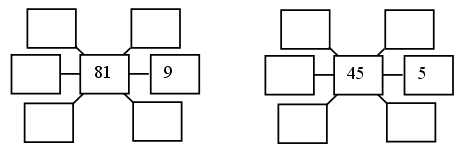
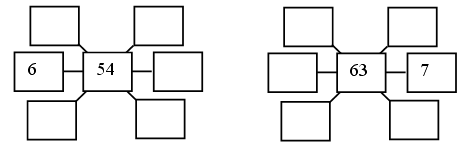
2. Задача.
Ваня собрал летом коллекцию красивых камней. В двух коробках у него было по 6 камней в каждой и в одной коробке 4 камня. Сколько всего камней у Вани?
3. Математический диктант.
Выполните вычитания и запишите только ответы.
60 – 10 30 – 20 96 – 30 99 – 90
50 – 30 60 – 40 61 – 50 80 – 8
90 – 50 70 – 40 76 – 70 36 – 20
80 – 70 80 – 50 54 – 10 47 – 30
54 – 21 57 – 17 55 – 22 63 – 32
38 – 16 68 – 18 77 – 44 58 – 58
63 – 41 42 – 12 66 – 55 47 – 46
79 – 28 71 – 11 99 – 77 98 – 97
III. Сообщение темы урока.
– Рассмотрите рисунки на доске.
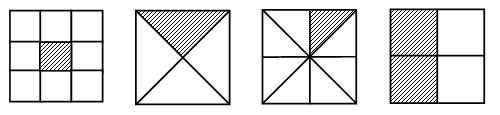
– Какие фигуры здесь изображены?
– Чем они похожи?
– У какой фигуры закрашена девятая часть числа?
– Как найти девятую числа?
– Сегодня на уроке мы будем решать задачи и вычислять девятую часть числа.
IV. Изучение нового материала.
Задание № 19 (с. 45).
– Рассмотрите данные в учебнике фигуры.
– Как они называются? (Это многоугольники.)
– Какую фигуру называют многоугольником? Назовите признаки многоугольника.
– Как называется первый многоугольник? (Восьмиугольник.)
– Какая часть восьмиугольника закрашена? (Восьмая часть.)
– Как найти восьмую часть числа? (Число разделить на восемь.)
– Как называется второй многоугольник? (Четырехугольник.)
– Назовите признаки четырехугольника.
– Какая часть четырехугольника закрашена? (Девятая часть.)
– Как найти девятую часть числа? (Число разделить на девять.)
Задание № 21 (с. 45).
Подготовительная работа к выполнению этого упражнения была проведена ранее в рабочих тетрадях № 1, 2 (учащиеся уже проводили наблюдения и делали выводы, но для конкретных чисел).
В этом задании второклассники подходят к более высокому уровню обобщения: чем большую часть любого числа мы находим, тем меньшее число получаем.
Значит, восьмая часть числа больше, чем девятая часть этого же числа.
Задание № 22 (с. 46).
чертеж:

– Чему равна девятая часть отрезка АВ?
9 : 9 = 1 (см).
Задание № 23 (с. 46).
– Как найти девятую часть любого числа?
Запись:
72 : 9 = 8 54 : 9 = 6
63 : 9 = 7 18 : 9 = 2
Задание № 24 (с. 46).
– Прочитайте текст. Является ли он задачей? Почему?
– Что известно в задаче?
– Что требуется узнать?
– Заполните условие задачи в таблицу:
|
В 1 день |
Количество дней |
Всего страниц |
|
6 с. |
? дн. |
54 с. |
|
9 с. |
? дн. |
54 с. |
Решение:
1) 54 : 6 = 9 (дн.) – если читает по 6 страниц.
2) 54 : 9 = 6 (дн.) – если читает по 9 страниц.
Ответ: 9 дней; 6 дней.
Задание № 25 (с. 46).
Учитель может предложить карточки-помощницы для выполнения этого задания.
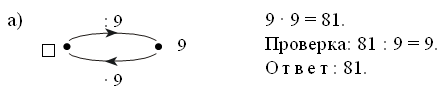
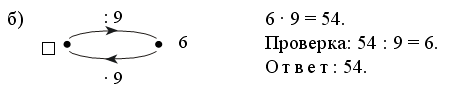
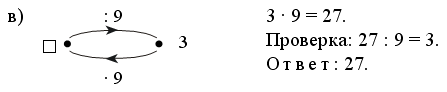

V. Повторение пройденного материала.
1. Работа в печатной тетради № 2.
Задание № 86.
– Сколько куриц на рисунке? (Три.)
– Сколько яиц снесла каждая курица? (Пять.)
– По сколько яиц мы нарисуем под каждой курицей? (По пять.)
– Сколько раз по 5 яиц получилось? (3 раза.)
– Как выяснить, сколько яиц мы нарисовали? (5 умножить на 3.)
– Сколько же яиц получилось? (15.)
Задание № 87.
– Что изображено на чертеже? (Окружность.)
– Назовите признаки окружности.
– Что называют радиусом окружности?
– Измерьте длину радиуса данной окружности. (Радиус равен 4 см.)
– Чему будет равен радиус, который составляет половину радиуса данной окружности? (4 : 2 = 2 (см).)
– Начертите окружность, радиус которой равен 2 см.
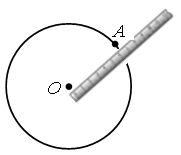
Примечание. Учитель должен обратить внимание учащихся на то, что измерить длину радиуса данной окружности можно без построения самого радиуса. Для этого на окружности выбирается и отмечается произвольная точка и с помощью линейки измеряется расстояние между центром окружности и выбранной точкой. Это расстояние и является длиной радиуса окружности.
2. Работа по учебнику.
Задание № 32 (с. 47).
– Какую фигуру называют треугольником?
– Какую фигуру называют кругом?
– Изобразите данные фигуры так, чтобы их пересечением был круг.
Чертеж:
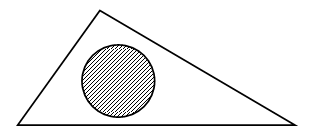
– Изобразите данные фигуры так, чтобы их пересечением был треугольник.
Чертеж:
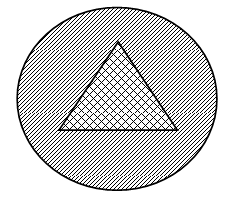
Задание № 33 (с. 47).
– Рассмотрите рисунок (а).
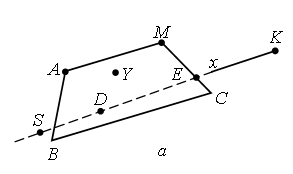
– Какие фигуры здесь изображены? (Многоугольник, луч, точки.)
– Назовите признаки многоугольника.
– Как называется данный многоугольник? (Четырехугольник.)
– Назовите признаки луча.
– Назовите точки, которые лежат на данном четырехугольнике. (А, В, С, М, Е.)
– Назовите точки, которые не лежат на данном четырехугольнике. (S, Y, D, K.)
– Какие из отмеченных точек лежат на луче КХ? (Учащиеся, используя линейку, продолжают луч КХ и отмечают точки Е, D, S, которые лежат на луче КХ.)
– Рассмотрите рисунок (б). Какие фигуры здесь изображены? (Треугольник АС D, луч КХ и точки Е и М.)
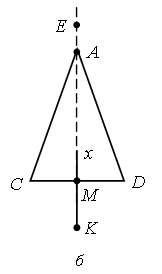
– Какие из отмеченных точек многоугольника лежат на луче КХ? (Точки М, А. Е лежат на луче КХ.)
VI. Итог урока.
– Что нового узнали на уроке?
– Как найти девятую часть числа?
– Назовите признаки окружности.
Домашнее задание: № 20, 16 (учебник); задание № 78 (рабочая тетрадь).
Урок 81
Умножение
и деление на 9.
ДЕВЯТАя ЧАСТЬ ЧИСЛА
Цели: совершенствовать вычислительные навыки; закреплять знание табличных случаев умножения и деления; развивать внимание и умение рассуждать, анализировать и обобщать.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Догадайтесь, какие числа нужно вставить в «окошки».
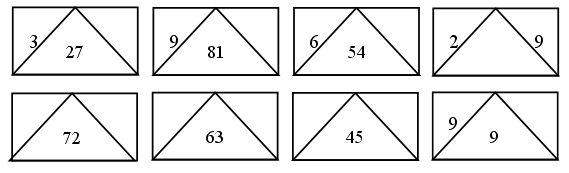
2. Разгадайте правила и продолжите ряды чисел:
а) 13, 15, 19, 25, 33, … , … , … ;
б) 81, 84, 80, 83, 79, … , … , … ;
в) 9, 12, 16, 21, 27, 34, … , … , … .
3. Задача.
Вася нарисовал трехэтажный дом. На первом этаже он нарисовал двери и 6 окон, а на двух верхних этажах по 8 окон. Сколько окон в этом доме нарисовал Вася?
4. Выберите фигуру, которую нужно нарисовать.
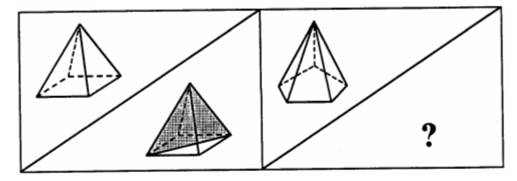
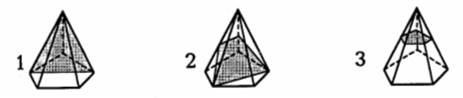
III. Сообщение темы урока.
– Сегодня на уроке продолжим работу с таблицей умножения и деления на 9.
IV. Работа по теме урока.
Задание № 17 (с. 45).
– Прочитайте текст. Является ли он задачей? Почему?
– Что известно в задаче? Что требуется узнать?
– Запишите условие задачи в таблицу:
|
В 1 букете |
Количество букетов |
Всего цветов |
|
? гв. (одинаков.) |
9 б. |
5 гв. |
|
8 б. |
? гв. |
Решение:
1) Сколько гвоздик в одном букете?
45 : 9 = 5 (гв.).
2) Сколько гвоздик в 8 таких букетах?
5 · 8 = 40 (гв.).
Ответ: 40 гвоздик.
Задание № 18 (с. 45).
– Прочитайте задачу.
– Что известно? Что требуется узнать?
– Запишите условие задачи в таблицу:
|
В 1 день |
Количество дней |
Всего консервов |
|
? б. (одинаков.) |
9 дн. |
36 б. |
|
7 дн. |
? б. |
Решение:
1) Сколько банок консервов израсходовали в 1-й день?
36 : 9 = 4 (б.).
2) Сколько банок израсходовали за неделю?
4 : 7 = 28 (б.).
Ответ: 28 банок.

V. Самостоятельная работа.
Задание № 1.
– Не выполняя вычислений, найди в каждом столбике «лишнее» выражение:
9 · 5 8 · 4 7 · 4
9 · 6 – 6 8 · 5 – 4 7 · 3 + 3
9 · 4 + 9 8 · 3 + 8 7 · 3 + 7
9 · 6 – 9 8 · 5 – 8 7 · 5 – 7
Задание № 2.
– Какому рисунку соответствует каждое выражение?
9 · 3 9 · 4 9 · 2 3 · 9 4 · 9 2 · 9
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Задание № 3.
– Пользуясь числовым лучом, найди значения выражений:
8 · 4 8 · 5 + 8 8 · 8 – 8 8 · 4 + 8 8 · 2
Задание № 4.
– Разгадай правила, по которым записаны ряды чисел, и продолжи каждый ряд. Чем похожи и чем отличаются эти числовые ряды?
16, 24, 32, …
8 · 2, 8 · 3, 8 · 4, …
2 · 8, 3 · 8, 4 · 8, …
VI. Итог урока.
– Как вычислить девятую часть числа?
– Как деление связано с умножением?
Домашнее задание: рабочая тетрадь, задание № 80.
Урок 82
КОНТРОЛЬНАЯ
РАБОТА ПО ТЕМЕ
«УМНОЖЕНИЕ И ДЕЛЕНИЕ НА 7, 8, 9»
Цели: проверить усвоение табличных случаев умножения и деления на 7, 8, 9; проверить умение решать задачи, навык нахождения доли от числа.
Ход урока
I. Организационный момент.
II. Контрольная работа.
I вариант
1. Вставь пропущенный множитель.
9 ∙ □ + 8 = 53 9 ∙ □ + 38 = 92
9 ∙ □ + 30 = 75 9 ∙ □ – 19 = 35
9 ∙ □ – 8 = 37 9 ∙ □ + 7 = 61
9 ∙ □ + 18 = 63 9 ∙ □ – 5 = 49
9 ∙ □ – 27 = 18 9 ∙ □ + 6 = 60
2. Вставь в «окошки» знаки действий, чтобы получились верные равенства.
9 ∙ 2 = 9 □ 9 9 ∙ 5 = 9 □ 4 □ 9
9 ∙ 2 = 27 □ 9 9 ∙ 5 = 9 □ 18 □ 18
9 ∙ 3 = 9 □ 9 □ 9 9 ∙ 6 = 50 □ 4
9 ∙ 3 = 20 □ 7 9 ∙ 6 = 9 □ 5 □ 9
9 ∙ 4 = 9 □ 3 □ 9 9 ∙ 7 = 9 □ 9 □ 9 □ 9
9 ∙ 4 = 9 □ 5 □ 9 9 ∙ 7 = 70 □ 7
3. Задача.
На каждое платье расходуется 3 метра ткани. Сколько метров ткани потребуется на 9 таких платьев?
4. Дорисуй каждую картинку так, чтобы число кругов на ней было равно значению произведения.
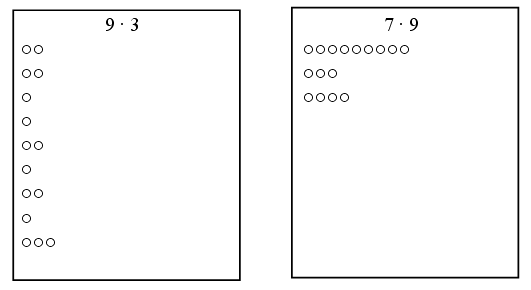
5. Вычисли пятую часть чисел: 40, 25, 50.
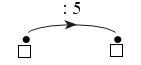
II вариант
1. Вставь пропущенный множитель.
9 ∙ □ + 6 = 51 9 ∙ □ + 7 = 61
9 ∙ □ + 9 = 54 9 ∙ □ – 5 = 49
9 ∙ □ + 19 = 64 9 ∙ □ + 8 = 62
9 ∙ □ + 29 = 74 9 ∙ □ – 6 = 48
2. Вставь в «окошки» знаки действий, чтобы получились верные равенства.
9 ∙ 2 = 48 □ 30 9 ∙ 5 = 81 □ 47 □ 11
9 ∙ 2 = 9 □ 3 □ 9 9 ∙ 5 = 9 □ 7 □ 18
9 ∙ 3 = 9 □ 2 □ 9 9 ∙ 6 = 9 □ 7 □ 9
9 ∙ 3 = 50 □ 23 9 ∙ 6 = 63 □ 9
9 ∙ 4 = 9 □ 5 □ 9 9 ∙ 7 = 9 □ 8 □ 9
9 ∙ 4 = 20 □ 16 9 ∙ 7 = 9 □ 6 □ 9
3. Задача.
В каждый пакет помещается 9 яблок. Сколько поместится яблок в 4 такие пакета?
4. Дорисуй каждую картинку так, чтобы число кругов на ней было равно значению произведения.
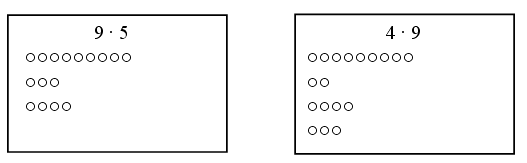
5. Вычисли шестую часть чисел: 42, 36, 60.
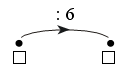
Урок 83
РАБОТА
НАД ОШИБКАМИ.
РЕШЕНИЕ ЗАДАЧ
Цели: провести анализ выполненной контрольной работы; совершенствовать умения решать составные задачи; развивать умение анализировать и рассуждать.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Расшифруйте слово.
|
26 + 73 |
Е |
20 – 5 |
М |
|
40 – 36 |
Л |
8 + 8 |
К |
|
100 – 94 |
А |
22 – 4 |
С |
|
38 – 22 |
К |
46 – 40 |
А |
Ключ:
|
18 |
15 |
99 |
16 |
6 |
4 |
16 |
6 |
|
|
|
|
|
|
|
|
|
Ответ: смекалка.
2. Геометрическое задание.
– Какие фигуры изображены на чертеже?
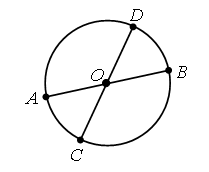
– Назовите признаки окружности.
– Назовите все изображенные на рисунке отрезки.
– Какие из отрезков являются радиусами?
– Что можете сказать об их длине?
– Какие отрезки являются диаметрами?
– Какая у них длина?
3. Игра «В стручки».
Во времена царя Гороха
Под смех и шутки скомороха
Царь, нацепив свои очки,
Играл с царицею в стручки.
Ты знаешь, как они играли?
Я сообщаю все детали!

– Перед вами такое число. Вы его узнали? (Число XIV.)
– Переложите только один стручок, превратите в число 5.
Решение:
Х – V = V.
10 – 5 = 5.
III. Сообщение о результатах выполнения контрольной работы.
IV. Работа над ошибками.

V. Самостоятельная работа по карточкам.
Карточка А
– Устно реши задачи. Соедини линией кружок с номером задачи и карточку, на которой записано выражение для ее решения.
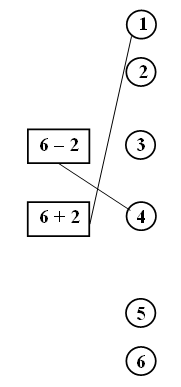
• Юре 6 лет, а его сестра на 2 года старше. Сколько лет сестре?
• Таня отрезала от ленты сначала 6 дм, а затем 2 дм. Сколько всего дециметров Таня отрезала от ленты?
• На парте было 6 тетрадей. Юля положила 2 тетради в портфель. Сколько тетрадей осталось на парте?
• На первой клумбе расцвело 6 тюльпанов, а на второй – на 2 тюльпана меньше. Сколько тюльпанов расцвело на второй клумбе?
• В городе 6 театров и 2 музея. На сколько больше в городе театров, чем музеев?
• Во дворе 6 девочек. Из них 2 девочки играют в куклы, а остальные прыгают через веревочку. Сколько девочек прыгают через веревочку?
Карточка В
Из пакета взяли 7 яблок и 5 груш. Узнай по этому условию:
1) На сколько больше яблок, чем груш, взяли из пакета?
2) Сколько всего яблок и груш взяли из пакета?
Если задача решается сложением, номер вопроса обведи 0, если вычитанием – .
Карточка С
1) Вставь в кружок около каждой задачи знак действия, с помощью которого она решается.
![]() В
кроссворде 15 слов. Катя уже отгадала 8 слов. Сколько слов ей осталось
отгадать?
В
кроссворде 15 слов. Катя уже отгадала 8 слов. Сколько слов ей осталось
отгадать?
![]() С
одной яблони дети сорвали 10 яблок, а с другой – 8. Сколько всего яблок дети
сорвали с двух яблонь?
С
одной яблони дети сорвали 10 яблок, а с другой – 8. Сколько всего яблок дети
сорвали с двух яблонь?
![]() На
диске записано 15 песен, а на кассете – на 8 песен меньше. Сколько песен
записано на кассете?
На
диске записано 15 песен, а на кассете – на 8 песен меньше. Сколько песен
записано на кассете?
![]() Жене
11 лет, а Саше 8. На сколько лет Женя старше Саши?
Жене
11 лет, а Саше 8. На сколько лет Женя старше Саши?
2) Запиши решение той задачи, для которой дан схематический чертеж. Поставь на нем около чисел наименования.
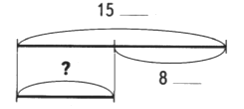
VI. Игра «Капитаны» на знание табличных случаев умножения.
Рифы отделяют корабль от островов, на одном из которых пираты зарыли клад. Безопасный путь к этому месту лежит через проходы в рифах, на которых произведения имеют значения, данные в записке.
![]()

– Восстанови стертые цифры и нарисуй путь к месту, где зарыт клад.
VII. Итог урока.
Урок 84
ВО СКОЛЬКО РАЗ БОЛЬШЕ ИЛИ МЕНЬШЕ?
Цели: рассмотреть краткое сравнение чисел; ввести отношение «во сколько раз больше или меньше»; совершенствовать навыки нахождения доли от числа; продолжить работу по формированию вычислительных навыков; развивать внимание, логическое мышление и умение обобщать.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Вставьте числа в «окошки».
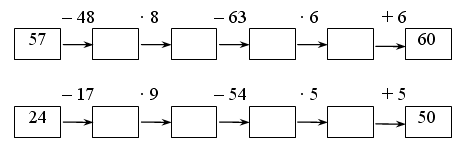
2. Задачи.
1) Приготовили 9 оправ для очков. Сколько потребуется стекол, чтобы изготовить очки?
2) Если разложить пирожные в коробки по 6 штук, потребуется 8 коробок. Сколько всего пирожных?
3. Геометрия на спичках.
1) Уберите 2 палочки так, чтобы квадратов не осталось.
|
|
|
|
2) Уберите 2 палочки так, чтобы осталось 2 квадрата.
3) Уберите одну палочку так, чтобы среди оставшихся фигур был только один квадрат. Какие еще остались многоугольники? Сколько их?
4) Уберите одну палочку так, чтобы осталось 2 квадрата.
5) Уберите три палочки так, чтобы осталось 2 квадрата. Какой еще остался многоугольник?
4. Что изменилось?
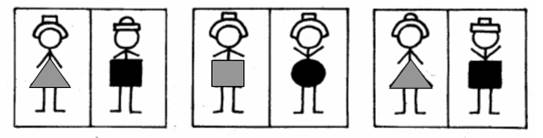
III. Сообщение темы урока.
– Рассмотрите рисунок на доске.
![]()
– Каких фигур больше? (Кругов.)
– На сколько кругов больше, чем треугольников? (6 – 3 = 3.)
– Каких фигур меньше?
– На сколько треугольников меньше, чем кругов?
– Сегодня на уроке мы познакомимся с новым отношением «во сколько раз больше или меньше».
IV. Изучение нового материала.
Справочный материал для учителя
Каждому учителю начальных классов хорошо известно, как трудно дается детям усвоение понятий, связанных с отношениями «больше в...» и «меньше в...». Дело, однако, не столько в том, что эти отношения являются более сложными и труднодоступными, чем отношения «больше на...» и «меньше на...», а в том, что учащиеся очень часто смешивают понятия «больше в...» и «больше на...», «меньше в...» и «меньше на...».
Возникает много и других трудностей. Так, сами понятия «больше в...» и «меньше в...» усваиваются по-разному: легче понимается отношение «больше в...» и намного труднее – «меньше в...». Говорят, что одних предметов в 4 раза больше, чем других, а, записывая решение, число умножают на 4.
Нельзя не учитывать и то обстоятельство, что с данными понятиями дети редко встречались в своей практике; сами фразы типа «число 6 в 5 раз меньше числа 30» по структуре трудны, и необходимо приложить немало усилий, чтобы научить каждого ученика правильно произносить эти фразы и понимать их смысл.
В целях предупреждения смешивания отношений следует как можно чаще сопоставлять отношения «больше в...» и «больше на...», «меньше в...» и «меньше на...». Большое значение имеет подготовительная работа, которую целесообразно проводить задолго до изучения данной темы.
Необходимо провести подготовительные упражнения:
1. У Миши 3 ореха (выкладываем фишки), у Пети – 2 раза по столько орехов (выкладываем орехи Пети фишками другого цвета).
2. Предлагается рисунок, на котором изображены, например, 3 зеленых и 12 красных яблок, и задаются вопросы: «Сколько зеленых яблок? Сколько раз по столько нарисовано красных яблок?» Ответ на второй вопрос находится практическим путем: каждые 3 красных яблока обводятся замкнутой линией («кладем» по 3 яблока на блюдца). Получается, что красных яблок 4 раза по столько, сколько зеленых. Иллюстрировать задачи можно на доске в классе, используя картинки с изображениями животных, растений, игрушек, плодов и др.
* * *
работа по учебнику (с. 48).
– Рассмотрите рисунок в учебнике.
– Сколько синих воздушных шариков нарисовал художник? (2.)
– А сколько раз по 2 он нарисовал красных шариков? (3 раза по 2.)
– Красных шариков больше, чем синих. Их в 3 раза больше, чем синих, потому что их 3 раза по столько, сколько синих. О синих шариках можно сказать, что их в 3 раза меньше, чем красных.
Задание № 1 (с. 48–49).
Это задание лучше выполнять устно, фронтально. В каждом случае надо, прежде всего, рассмотреть иллюстрацию.
Работу можно организовать по следующим вопросам.
Рисунок 1.
– Посмотрите на рисунок. Какие предметы изображены на рисунке? (Мячи и кубики.)
– Сколько всего мячей? (Три.)
– Обратите внимание, кубики сложены в башенки. Сколько кубиков в каждой башенке? (Тоже три.)
– Сколько всего башенок по 3 кубика? (Четыре.)
– Значит, кубиков 4 раза по столько, сколько мячиков. Делаем вывод: кубиков в 4 раза больше, чем мячиков, а мячиков – в 4 раза меньше, чем кубиков.
Если у учащихся будут возникать затруднения, можно использовать модели (фишки).
Рисунок 2.
– Что изображено на втором рисунке? (Ёжики и грибки.)
– Сколько всего ёжиков? (Два.)
– Сколько всего грибков? (Четыре.)
– Мысленно разбейте грибки на группы, по 2 грибка в каждой, то есть в каждой группе должно быть по столько грибков, сколько всего ёжиков. Сколько групп получилось? (Две.)
– Значит, у нас грибков 2 раза по столько, сколько ёжиков. Делаем вывод: грибков в 2 раза больше, чем ёжиков, а ёжиков в 2 раза меньше, чем грибков.
Рисунок 3.
– Рассмотрите рисунок (на с. 49). На нем изображены тарелки с фруктами. Какие фрукты разложены по тарелкам? (Сливы и груши.)
– По сколько фруктов на каждой тарелке? (По 4 сливы или груши.)
– Значит, фруктов на каждой тарелке поровну: по 4 штуки.
– Сколько тарелок со сливами? (5 тарелок.)
– Сколько тарелок с грушами? (1 тарелка.)
– Значит, слив у нас 5 раз по столько, сколько груш. Делаем вывод: слив в 5 раз больше, чем груш; а груш в 5 раз меньше, чем слив.
Задание № 2 (с. 49).
Учащиеся устно вставляют пропущенные слова в предложения: «больше» или «меньше».
Задание № 3 (с. 49) (фронтально).
Задание № 4 (с. 49).
Учащиеся читают новые предложения:
• Воробьев в 3 раза больше, чем ворон.
• Юбок в 4 раза больше, чем блузок.
• Стаканов в 8 раз меньше, чем чашек.
• Гвоздик в 6 раз меньше, чем роз.

V. Повторение пройденного материала.
1. Работа в печатной тетради № 2.
Задание № 88.
чертеж:
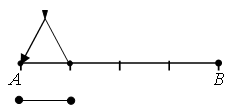
– Во сколько раз длина красного отрезка больше длины зеленого? (В 4 раза больше.)
– Во сколько раз длина зеленого отрезка меньше длины красного? (В 4 раза меньше.)
Задание № 89.
чертеж:
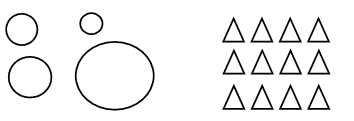
– Сколько кругов изображено на рисунке? (4.)
– Изобразите 3 раза по столько треугольников, сколько кругов.
– Сколько получилось треугольников? (4 · 3 = 12.)
– Во сколько раз их больше, чем кругов? (В 3 раза больше.)
2. Работа по учебнику.
Задание № 18 (с. 53).
– Как найти третью часть числа? Пятую часть числа? Шестую часть числа?
Запись:
30 : 3 = 10 30 : 5 = 6 30 : 6 = 5
Задание № 19 (с. 53).
Учитель может предложить карточки-помощницы.
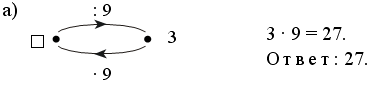
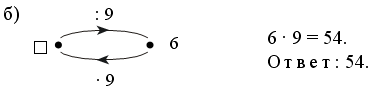
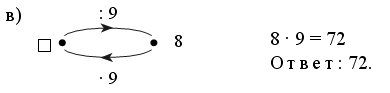
Задание № 20 (с. 53).
Учащиеся работают самостоятельно в парах.
VI. Итог урока.
– Что нового узнали на уроке?
– Какое действие необходимо выполнить, чтобы узнать, во сколько раз больше (меньше)?
– Как найти долю от числа?
Домашнее задание: № 21 (учебник); задания № 97, 98, 99 (рабочая тетрадь).
Урок 85
ВО СКОЛЬКО РАЗ БОЛЬШЕ ИЛИ МЕНЬШЕ?
Цели: продолжить формирование умений выполнять кратное сравнение чисел; совершенствовать вычислительные навыки; закреплять умения решать составные задачи; развивать умение анализировать и сравнивать.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Вставьте пропущенные знаки действий, чтобы получились верные равенства:
9 … 9 … 72 = 9 3 … 9 … 9 = 36
(16 … 7) … 8 = 72 4 … 9 … 18 = 18
6 … (11 … 2) = 54 (16 … 7) … 3 = 27
2. Задачи.
1) Луковицы тюльпанов высадили в 4 ряда по 8 штук. Сколько луковиц высадили?
2) Булочка стоит 4 рубля. Сколько булочек можно купить на 12 рублей?
3. Магические рамки.
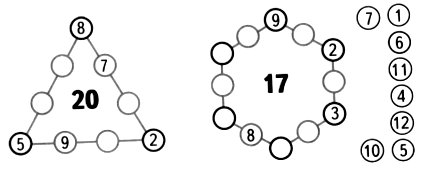
4. Определи длину лент.
Красная лента длиннее синей, но короче желтой. Покажите, какая лента красная.

III. Сообщение темы урока.
– Прочитайте ряд чисел, записанных на доске:
2, 5, 10, 7, 1, 4, 50, 9.
– На какие две группы можно разделить эти числа? (Однозначные и двузначные.)
– Используя цветные фишки, ответьте на вопрос: во сколько раз 5 меньше, чем 10?

Ответ: в 2 раза меньше.
– Во сколько раз 10 меньше, чем 50?
– Можно ли ответить на этот вопрос, используя фишки?
– Сегодня на уроке мы узнаем, каким арифметическим действием можно ответить на этот вопрос.
IV. Изучение нового материала.
Используя цветные фишки, учащиеся отвечают на вопрос учителя.
– Сколько раз по два содержится в числе 6? (Три раза.)
![]()
– Какое действие вы выполнили? (6 : 2 = 3 (раза).)
– Произносят так: 6 больше, чем 2, в 3 раза, и 2 меньше, чем 6, в 3 раза.
Далее учащиеся читают правило в учебнике (на с. 50).
Задание № 5 (с. 50).
Запись:
15 : 5 = 3 (раза) – 15 больше, чем 5.
15 – 5 = 10 (ед.) – 15 больше, чем 5.
15 – 5 = 10 (ед.) – 5 меньше, чем 15.
15 : 5 = 3 (раза) – 5 меньше, чем 15.
Задание № 6 (с. 50).
Справочный материал для учителя
Решая такие задачи, как, например, «узнать, во сколько раз 3 меньше 18», некоторые дети выполняют неверную запись: 3 : 18 = 6, хотя правильно формулируют правило сравнения чисел. Нужно заранее предупреждать подобные ошибки, предлагая учащимся до выполнения записи назвать большее число, меньшее число, выяснить, какое число на какое надо делить, и только после этого разрешать им делать запись.
Запись:
49 : 7 = 7 42 : 6 = 7
35 : 5 = 7 63 : 7 = 9
64 : 8 = 8 72 : 9 = 8
20 : 4 = 5 40 : 5 = 8
Задание № 7 (с. 50).
– Прочитайте текст. Является ли он задачей? Почему?
– Что известно в задаче? Что требуется узнать?
– Запишите кратко условие задачи.
Запись:
У Пети – 3 откр. во ? (раз) б.
У Тани – 9 откр. на ? м.
Решение:
1) Во сколько раз у Тани открыток больше, чем у Пети?
9 : 3 = 3 (раза).
2) На сколько открыток у Пети меньше, чем у Тани?
9 – 3 = 6 (откр.).
Ответ: в 3 раза больше; на 6 открыток меньше.

V. Повторение пройденного материала.
1. Работа по учебнику.
Задание № 22 (с. 53).
Учащиеся рассуждают следующим образом:
100 : 2 = 50.
(100 – это 10 десятков, поэтому 100 : 2 = 10 д. : 2 = 5 д. = 50.)
40 · 2 = 80.
(40 – это 4 десятка, поэтому 40 · 2 = 4 д. · 2 = 8 д. = 80.)
10 · 5 = 50.
(10 – это 1 десяток, поэтому 10 · 5 = 1 д. · 5 = 5 д. = 50.)
60 : 6 = 10
(60 – это 6 десятков, поэтому 60 : 6 = 6 д. : 6 = 1 д. = 10.)
Задание № 24 (с. 53).
– Прочитайте условие задачи.
– Что известно?
– Что требуется узнать?
– Запишите кратко условие задачи и решите ее.
Запись:
Было – 90 смІ.
Отрезали – 18 смІ.
Осталось – ? смІ.
Решение:
90 – 18 = 72 (смІ).
Ответ: 72 смІ.
2. Работа в печатной тетради № 2.
Задание № 90.
Запись:

Задание № 92.
Учащиеся заполняют таблицу.
|
10 |
20 |
40 |
72 |
21 |
36 |
|
5 |
4 |
5 |
9 |
3 |
6 |
|
2 |
5 |
8 |
8 |
7 |
6 |
VI. Итог урока.
– Что нового узнали на уроке?
– Как узнать, во сколько раз одно число больше (меньше), чем другое?
– Назовите единицы измерения площади фигуры.
Домашнее задание: № 23 (учебник); задания № 91 (рабочая тетрадь).
Урок 86
ВО СКОЛЬКО РАЗ БОЛЬШЕ ИЛИ МЕНЬШЕ?
Цели: совершенствовать навыки решения задач на кратное сравнение; закреплять умения решать задачи с величинами «цена», «количество», «стоимость»; продолжить формирование вычислительных навыков; развивать внимание и мышление.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Вставь в «окошки» знаки действий, чтобы получились верные равенства.
9 · 8 = 9 7 9 9 · 9 = 9 7 18
9 · 8 = 9 9 9 9 36 9 · 9 = 9 6 27
9 · 8 = 9 5 27 9 · 9 = 9 5 36
9 · 8 = 90 9 9 9 · 9 = 63 9 9
2. Задачи.
а) Длина бассейна – 8 м. Петя проплыл туда и обратно 4 раза. Сколько метров проплыл Петя?
б) Сколько шнурков нужно для 8 пар ботинок?
3. Геометрия на спичках.
а) Сколько всего на чертеже квадратов? Сколько на нем всего многоугольников?

б) Уберите одну палочку так, чтобы осталось 3 квадрата. Найдите несколько решений.
в) Уберите одну палочку так, чтобы осталось 2 квадрата. Найдите несколько решений.
г) Уберите две палочки так, чтобы осталось 3 квадрата. Найдите два решения и сравните их.
д) Уберите две палочки так, чтобы остался 1 квадрат. Какие еще остались многоугольники?
4. Выберите нужную картинку и вставьте в пустой квадрат.

III. Сообщение темы урока.
– Сегодня на уроке будем решать задачи с отношениями «на несколько больше (меньше)» и «в несколько раз больше (меньше)».
IV. Работа по теме урока.
Задание № 8 (с. 50).
– Рассмотрите рисунок. Какие фигуры здесь изображены? (На нем изображены синий и красный отрезки.)
– На сколько частей точками разбит синий отрезок? (На 5 частей.)
– Выполните измерения и выясните, чему равна длина каждой такой части. (2 см.)
– Значит, синий отрезок разбит на 5 равных отрезков длиной 2 см. Измерьте длину красного отрезка. (Тоже 2 см.)
– Сколько раз красный отрезок будет «укладываться» в синем? (5 раз.)
– Делаем вывод: синий отрезок в 5 раз длиннее красного, а красный отрезок в 5 раз короче синего.
Задание № 9 (с. 50).
Это задание лучше выполнить фронтально.
· Если 28 больше 4 в 7 раз, то 4 меньше 28 в 7 раз.
· Если 56 больше 7 в 8 раз, то 7 меньше 56 в 8 раз и т. д.
Задание № 10 (с. 51).
– Прочитайте текст. Является ли он задачей? Почему?
– Что известно в задаче? Что требуется узнать?
– Запишите кратко условие задачи.
Запись:
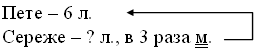
– Что значит «Петя в 3 раза старше Сережи»?
– Продолжите предложение: «Сережа в … , чем Петя».
Решение:
6 : 3 = 2 (г.) – Сереже.
Ответ: 2 года.
Задание № 11 (с. 51).
– Рассмотрите рисунок в учебнике.
– Назовите самое высокое дерево. (Ель.)
– Во сколько раз ель выше рябины? (В 3 раза.)
– Во сколько раз рябина ниже ели? (В 3 раза.)
– Во сколько раз береза выше рябины? (В 2 раза.)
– Во сколько раз рябина ниже березы? (В 2 раза.)
Задание № 12 (с. 51).
– Прочитайте задачу.
– Что известно в задаче? Что требуется узнать?
– Запишите кратко условие задачи.
Запись:
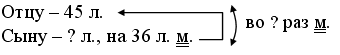
Решение:
1) Сколько лет сыну?
45 – 36 = 9 (л.).
2) Во сколько раз сын моложе отца?
45 : 9 = 5 (раз).
Ответ: в 5 раз моложе.

V. Повторение пройденного материала.
1. Работа по учебнику.
Задание № 25 (с. 54).
– Прочитайте задачу.
– Что известно? Что требуется узнать?
– Запишите кратко условие задачи и решите ее с помощью выражения.
Запись:
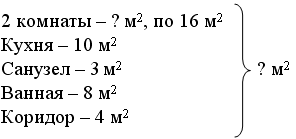
Решение:
16 + 16 + 10 + 3 + 8 + 4 = 57 (м2).
Ответ: 57 м2.
Задание № 26 (с. 54).
– Прочитайте задачу.
– Что известно? Что требуется узнать?
– Заполните таблицу по условию этой задачи.
|
Цена |
Количество |
Стоимость |
|
9 р. |
? к. |
45 р. |
|
? к. |
36 р. |
Решение:
1) 45 : 9 = 5 (к.) – стоят 45 р.
2) 36 : 9 = 4 (к.) – стоят 36 р.
Ответ: 5 к., 4 к.
2. Работа в печатной тетради № 2.
Задание № 94.
– Прочитайте задачу.
– Что известно в задаче? Что требуется узнать?
При затруднении учащиеся могут оформить краткую запись условия этой задачи.
Запись:
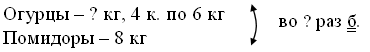
Далее учащиеся решают задачу по схеме:
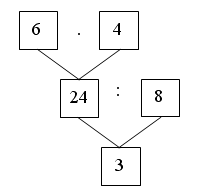
Ответ: в 3 раза больше огурцов, чем помидоров.
VI. Итог урока.
– Что нового узнали на уроке?
– Назовите единицы измерения площади.
– Что означает выражение «во сколько раз больше (меньше)»?
Домашнее задание: № 27 (учебник); № 93 (рабочая тетрадь).
Урок 87
ВО СКОЛЬКО РАЗ БОЛЬШЕ ИЛИ МЕНЬШЕ?
Цели: совершенствовать навыки решения составных задач на кратное сравнение; закреплять знания геометрических фигур, умения читать чертеж; продолжить подготовительную работу по ознакомлению с уравнениями; развивать умение рассуждать.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Выполните действия и вставьте числа в «окошки».
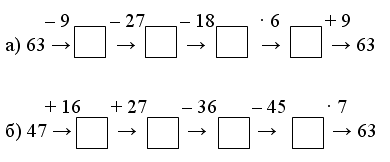
2. Задачи.
а) Маша пригласила на свой день рождения подруг. Для гостей она приготовила 18 предметов – ложки, вилки и ножи. Сколько гостей ожидает Маша?
б) На каждую куртку пришили 5 пуговиц. Сколько всего курток, если использовали 40 пуговиц?
3. Рассмотрите рисунок.
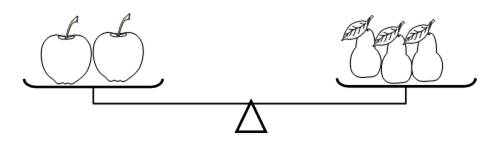
– Какой фрукт тяжелее: яблоко или груша?
4. Что изменилось? Что не изменилось?

III. Сообщение темы урока.
– Сегодня на уроке продолжим выполнение заданий с отношениями «во сколько раз больше (меньше)» и «на сколько больше (меньше)».
IV. Работа по теме урока.
1. Работа по учебнику.
Задание № 13 (с. 51).
– Рассмотрите схему. На какое число умножает «машина»?
Это задание является подготовительным к решению уравнений вида: 4 · х = 8.
– Из «машины» вышло число большее, чем 4, в несколько раз. На сколько умножает «машина»? (На столько, во сколько раз 8 больше, чем 4.)
– Как узнать, во сколько раз 8 больше, чем 4? (8 : 4 = 2.)
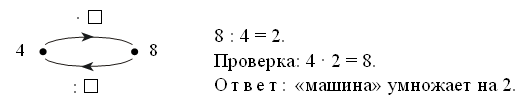
Задание № 14 (с. 52).
Данное задание является подготовительным к решению уравнений вида: 12 : у = 2.
– Рассмотрите схему. На какое число делит «машина»?
– Из «машины» вышло число, меньшее 12 в несколько раз. На сколько же «машина» делит? (На столько, во сколько раз 12 больше 2.)
– Как узнать, во сколько раз 12 больше, чем 2? (Надо большее число (12) разделить на меньшее (2).)
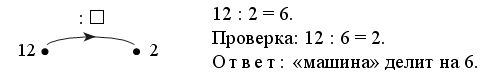
2. Работа в печатной тетради № 2.
Далее учащиеся самостоятельно выполняют задание № 96 в рабочей тетради № 2.
Запись:

12 : 4 = 3. 24 : 3 = 8. 18 : 2 = 9.
Ответ: а) 3; б) 8; в) 9.

V. Повторение пройденного материала.
1. Работа по учебнику.
Задание № 28 (с. 54).
– Рассмотрите рисунки в учебнике.
– Сколько квадратов на первом рисунке? (Четыре.)
– Назовите их. (АХOY, АМКВ, APSN, AEДС.)
– Сколько квадратов на втором рисунке? (Шесть.)
– Назовите их. (АЕСР, ДМКВ, АМОД, МОКЕ, КОВС, ВОДР.)
2. Самостоятельная работа по карточкам (5–7 мин).
Задание № 1.
Дорисуй круги так, чтобы число кругов справа было больше, чем число кругов слева:
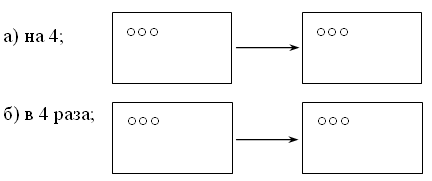
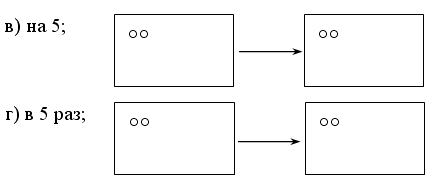
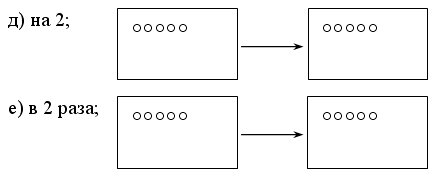
Задание № 2.
Вставь пропущенные слова и числа так, чтобы высказывания соответствовали рисунку:
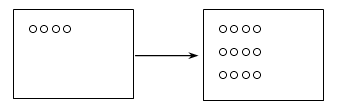
а) Справа … 8 кругов … , чем слева.
б) Справа кругов … 3 … , чем слева.
в) Слева … 8 кругов … , чем справа.
3. Работа в печатной тетради № 2.
Задание № 95.
В помощь слабоуспевающим учащимся можно предложить следующую карточку-помощницу:
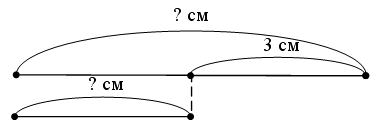
Длины отрезков: 3 см и 6 см.
VI. Итог урока.
– Что нового узнали на уроке?
– Назовите признаки квадратов.
Домашнее задание: учебник, № 17, 29.
Урок 88
ВО СКОЛЬКО РАЗ БОЛЬШЕ ИЛИ МЕНЬШЕ?
Цели: совершенствовать умения решать составные задачи на кратное и разностное сравнение; закреплять умения вычислять периметр и площадь прямоугольника; развивать внимание и логическое мышление.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Вставьте в «окошки» знаки действий, чтобы получились верные равенства.
9 ∙ 8 = 80 □ 8 9 ∙ 9 = 90 □ 9
9 ∙ 8 = 9 □ 9 □ 9 9 ∙ 9 = 9 □ 8 □ 9
9 ∙ 8 = 90 □ 18 9 ∙ 9 = 9 □ 9 □ 9 □ 9 + 45
2. Задачи.
а) Цена килограмма яблок – 6 р. Какое наибольшее количество яблок можно купить, имея 50 р.?
б) С огорода принесли 24 помидора. Четвертую часть их израсходовали для приготовления салата. Сколько помидоров пошло на салат?
3. Геометрия на спичках.
а) Сложите такую фигуру. Сколько в ней квадратов? Какие еще есть многоугольники? Сколько их?

б) Уберите две палочки так, чтобы не осталось ни одного квадрата.
в) Уберите одну палочку так, чтобы остался 1 квадрат. Какие еще остались многоугольники? Сколько их? Найдите два решения.
г) Уберите две палочки так, чтобы осталось 2 квадрата.
д) Уберите три палочки так, чтобы осталось 2 квадрата. Найдите два решения.
е) Переложите две палочки так, чтобы стало 2 квадрата.
4. Как связаны числа с рисунками?

III. Сообщение темы урока.
– Сегодня на уроке будем решать задачи и повторим отношения «больше (меньше) в несколько раз», «во сколько раз больше (меньше)».
IV. Работа по теме урока.
1. Работа по учебнику.
Учащиеся читают текст в учебнике (с. 52).
– Выполните рисунок к данному тексту.
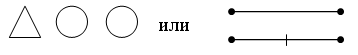
– Почему детей оказалось в 2 раза больше, чем взрослых?
Задание № 15 (с. 52).
– Прочитайте текст. Является ли он задачей?
– Что известно? Что требуется узнать?
– Выполните рисунок к данному условию.
– Надо ли выполнять действие, чтобы ответить на вопрос задачи?
– Во сколько раз детей больше, чем взрослых? (так как на каждого взрослого приходится 7 детей, то детей в 7 раз больше, чем взрослых; взрослых в 7 раз меньше, чем детей.)
Задание № 16 (с. 52).
– Прочитайте задачу.
– Что известно? Что надо узнать?
– Запишите кратко условие этой задачи.
Запись:
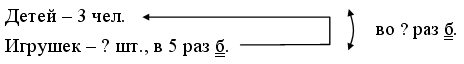
– Можно ли ответить на этот вопрос, не зная, что детей трое? (Нельзя, так как мы не знаем, сколько было игрушек.)
Скорее всего, учащиеся предложат решить задачу так.
Решение:
1) Сколько всего игрушек у детей?
5 · 3 = 15 (шт.).
2) Во сколько раз игрушек больше, чем детей?
15 : 3 = 5 (раз).
Ответ: в 5 раз больше.
Для того чтобы наметить другой путь решения, надо ситуацию, представленную в задаче, смоделировать на фишках. Сначала выложим в ряд столько желтых фишек, сколько всего играло детей:

Под каждой желтой фишкой выложим в столбик столько красных фишек, сколько игрушек было у каждого ребенка:
Игрушек 5 раз по столько, сколько детей. Значит, игрушек в 5 раз больше, чем детей.
Дополнительно спросите у учащихся: «Изменится ли ответ, если играть будут 6 детей, но игрушек у каждого опять будет по 5?» (Нет. Игрушек снова будет в 5 раз больше, чем детей.) «А изменится ли ответ, если играть будут трое детей, но игрушек у каждого будет 7?» (Да. Игрушек будет в 7 раз больше, чем детей.)
Делаем вывод: ответ на вопрос задачи не зависит от числа играющих детей. Важно только, сколько игрушек у каждого ребенка.
Задание № 17 (с. 52).
– Прочитайте задачу.
– Что известно? Что требуется узнать?
– Надо выполнять действия, чтобы узнать, «во сколько раз книг больше, чем полок». (Не надо, так как ясно, что книг в 20 раз больше, чем полок.)
– Можно ли узнать, на сколько число полок меньше числа книг? (Нельзя, так как в задаче неизвестно, сколько было книг.)
– Ответьте на этот вопрос задачи, если полок было 5.
Запись:
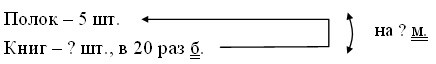
Решение:
1) 20 · 5 = 100 (шт.) – книг.
2) 100 – 5 = 95 (шт.) – меньше полок, чем книг.
Ответ: на 95 шт. меньше.
2. Работа в печатной тетради № 2.
Задание № 100.
Учащиеся вполне могут самостоятельно справиться с заданием, но предварительно обсудите с ними план выполнения работы:
1. Разбить фигуру на квадраты площадью 1 см2. Для этого каждую сторону четырехугольника разделить точками на последовательные отрезки длиной 1 см и через отмеченные точки провести горизонтальные и вертикальные отрезки.
2. Подсчитать площадь фигуры в квадратных сантиметрах.
3. Определить длину каждой стороны четырехугольника в сантиметрах.
4. Вычислить периметр фигуры.
Задание № 98.
Разбейте это задание на варианты. Для того чтобы учащимся было легче справиться с работой, подскажите им, что раскрашивание удобно начинать с того ряда, в котором уже есть цветной шар.
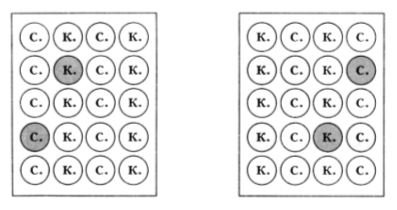

V. Самостоятельная работа по теме урока.
Задание № 1.
– Рассмотрите рисунки в учебнике.
– Измерьте длину каждого отрезка.

– Объясните, что обозначают выражения:
12 : 6 6 : 2 12 : 2
Задание № 2.
– Рассмотрите рисунок.
– Какие арифметические действия нужно выполнить, чтобы ответить на вопросы?
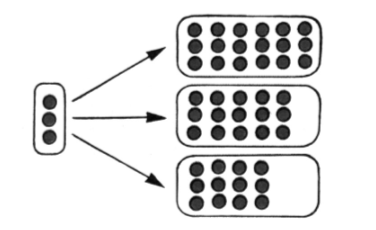
а) Во сколько раз слева кругов меньше, чем справа?
б) На сколько слева кругов меньше, чем справа?
в) На сколько справа кругов больше, чем слева?
г) Во сколько раз справа кругов больше, чем слева?
VI. Итог урока.
– Что нового узнали на уроке?
– Как вычислить площадь фигуры?
– Как найти периметр четырехугольника?
Домашнее задание: № 96 (рабочая тетрадь).
Урок 89
РЕШЕНИЕ
ЗАДАЧ НА УВЕЛИЧЕНИЕ
И УМЕНЬШЕНИЕ В НЕСКОЛЬКО РАЗ
Цели: учить решать задачи на увеличение и уменьшение числа в несколько раз; продолжить формирование умений находить симметричные фигуры, строить оси симметрии; совершенствовать вычислительные навыки; развивать умение анализировать и сравнивать.
Ход урока
I. Организационный момент.
II. Устный счет.
1. По какому признаку можно разбить ряды чисел на две группы?
8, 16, 24, 32, 40, 48, …
7, 14, 21, 28, 35, 42, …
4, 12, 20, 28, 36, 44, …
2, 10, 18, 26, 34, 42, …
4, 11, 18, 25, 32, 39, …
5, 13, 21, 29, 37, 45, …
2. Задача.
В спортивный лагерь приехали школьники, тренеры и воспитатели, всего 96 человек. Тренеров было 4 человека, воспитателей столько же. Сколько было школьников?
3. Геометрия на спичках.

а) Уберите две палочки так, чтобы квадратов не осталось. Какие остались многоугольники? Сколько их?
б) Уберите три палочки так, чтобы осталось 3 квадрата. Какие еще остались многоугольники? Сколько их?
в) Переложите три палочки так, чтобы в получившейся фигуре оказался 1 квадрат. Найдите разные решения. Какие еще получились многоугольники?
г) Переложите три палочки так, чтобы получилась другая фигура из четырех квадратов.
III. Сообщение темы урока.
Задача.
Тетрадь в 6 раз дешевле книги, а ручка в 3 раза дороже тетради.
Выберите схему, которая соответствует данному условию, и ответьте на следующие вопросы.
Во сколько раз:
а) тетрадь дешевле ручки?
б) ручка дешевле книги?
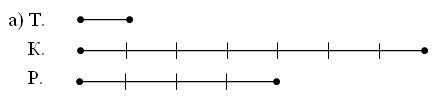
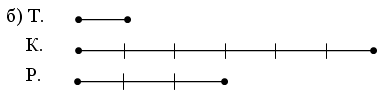
– Сегодня на уроке будем решать задачи с соотношениями «в несколько раз больше», «в несколько раз меньше».
IV. Изучение нового материала.
Учитель предлагает детям прочитать и решить задачи, данные в учебнике (с. 55).
– Прочитайте самостоятельно первую задачу.
– Что известно? Что надо узнать?
– Рассмотрите рисунок к этой задаче. Объясните ее решение.
– Прочитайте вторую задачу.
– Объясните решение этой задачи, данное в учебнике.
(10 : 5 = 2).
Далее учитель предлагает учащимся другой способ решения задачи, основанный на использовании «машины»; может быть, для некоторых слабоуспевающих детей он окажется более понятным.
Итак, по условию яблок в 5 раз меньше, чем слив. Это значит, что слив в 5 раз больше, чем яблок. Нужно найти число яблок. Слив – 10. Число 10 в 5 раз больше неизвестного числа яблок. Поэтому если неизвестное число яблок умножить на 5, то получится 10:
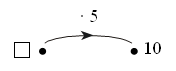
Дальнейшее решение ясно.
Задание № 1 (с. 56).
– Прочитайте задачу.
– Сколько помидоров лежит на столе? (Четыре.)
– Выложите перед собой в ряд столько желтых фишек, сколько помидоров лежит на столе.

– Что нам известно об огурцах? (Их в 2 раза больше, чем помидоров.)
– Что это значит? (Огурцов 2 раза по столько, сколько помидоров.)
– Выложим столько красных фишек, сколько огурцов на столе. Как это сделать? (Надо выложить 2 раза по столько красных фишек, сколько желтых фишек на столе.)
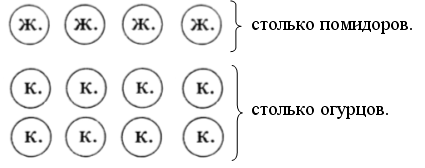
– Какое действие надо выполнить, чтобы найти число огурцов на столе? (Надо 4 умножить на 2.)
– Запишем решение задачи в тетрадь.
Решение:
4 · 2 = 8 (ог.).
Ответ: 8 огурцов.
Задание № 2 (с. 56).
– Прочитайте задачу и рассмотрите рисунок.
– Сколько стаканов смородины набрал брат? (Двенадцать.) Выложим перед собой в ряд столько желтых фишек, сколько стаканов набрал брат.
![]()
– Что нам известно о том, сколько стаканов ягод набрала сестра? (Она набрала в 3 раза меньше стаканов, чем брат.)
– Что это значит? (На каждые три стакана брата приходится один стакан сестры.)
– Разложенные желтые фишки разбейте на кучки по 3 штуки в каждой.
![]()
– Сколько получилось кучек? (Четыре.)
– Чтобы получить этот результат, какое арифметическое действие надо выполнить? (12 разделить на 3.)
– Значит, сколько стаканов смородины набрала сестра? (Четыре.)
– Выложите красных фишек столько, сколько стаканов смородины набрала сестра.

– Запишите решение задачи в тетрадь.
Решение:
12 : 3 = 4 (ст.).
Ответ: 4 стакана.

V. Повторение пройденного материала.
1. Работа по учебнику.
Задание № 9 (с. 57).
– Рассмотрите примеры. Чем они похожи? (Одинаковые числа и арифметические действия.)
– Чем отличаются? (По-разному стоят скобки, поэтому разный порядок действий.)
– Выполните действия:
(3 · 2) · 4 = 24 (32 : 8) : 2 = 2
3 · (2 · 4) = 24 32 : (8 : 2) = 8
Задание № 10 (с. 57).
– Какие фигуры изображены? (Круг, многоугольники.)
– Назовите признаки круга.
– Как называются данные многоугольники? (Четырехугольники.)
– Назовите признаки четырехугольника.
– Какой четырехугольник «лишний»? (Желтый, так как это невыпуклый многоугольник.)
– Что называют осью симметрии?
– Правильно ли проведены оси симметрии фигуры?
– Выполните проверку с помощью зеркала.
– Сколько осей симметрии имеет круг?
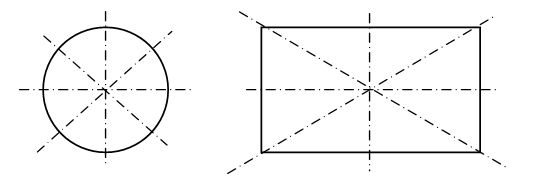
– Сколько осей симметрии имеет второй четырехугольник?
2. Работа с вырезанными фигурами.
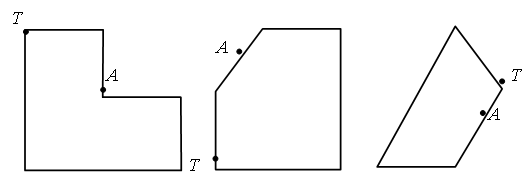
– Проведите ось симметрии в каждой фигуре, если она проходит через точку А.
– Обозначьте буквой Е точку, симметричную Т относительно этой оси.
3. Работа в печатной тетради № 2.
Задание № 103.
– Рассмотрите иллюстрацию. Что вам известно? Составьте задачу по данной иллюстрации.
Задача. В кувшине 3 л молока. В ведре на 5 л молока больше, чем в кувшине. А во фляге в 4 раза больше молока, чем в кувшине. Сколько литров молока во фляге? сколько литров молока в ведре?
– Запишите решение задачи по действиям.
Решение:
1) Сколько литров молока в ведре?
3 + 5 = 8 (л).
2) Сколько литров молока во фляге?
3 · 4 = 12 (л).
Ответ: 12 л, 8 л.
Далее учитель задает дополнительно вопросы:
– Изменится ли решение задачи, если кувшин, флягу и ведро наполнили не молоком, а водой?
– Изменится ли решение задачи, если ее формулировка будет звучать так: в кувшине 3 л молока, это на 5 л меньше, чем в ведре, и в 4 раза меньше, чем во фляге. Сколько литров молока в ведре? Сколько литров молока во фляге? (Решение задачи не изменится.)
4. Работа по карточкам.
Используя данные условия и вопросы, составьте задачи. Соедините линией карточки с условием и вопросом. Устно решите полученные задачи. В каждый кружок запишите знак действия, с помощью которого решается задача.


VI. Итог урока.
– Что нового узнали на уроке?
– Какие фигуры называют симметричными?
Домашнее задание: № 101, 102 (рабочая тетрадь).
Урок 90
РЕШЕНИЕ
ЗАДАЧ НА УВЕЛИЧЕНИЕ
И УМЕНЬШЕНИЕ В НЕСКОЛЬКО РАЗ
Цели: совершенствовать умения решать задачи на увеличение и уменьшение числа в несколько раз; продолжить формирование навыков строить и читать математические графы; закреплять умения решать задачи с величинами «цена», «количество», «стоимость», развивать внимание и логическое мышление.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Выполните действия и вставьте числа в «окошки».
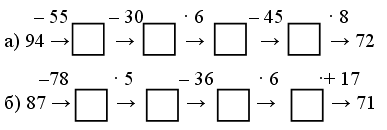
2. Задача.
Дети поехали на экскурсию в трех автобусах. В одном было 20 детей, в другом – на 5 больше, а в третьем – столько же, сколько в первом. Сколько детей поехало на экскурсию?
– Какая схема соответствует условию данной задачи?
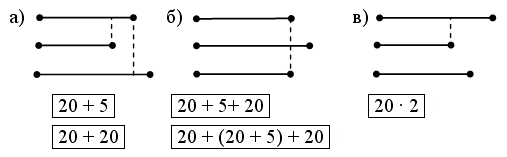
– Что обозначают выражения, записанные по условию этой задачи?
3. Геометрия на спичках.
а) Уберите две палочки так, чтобы не осталось квадратов. Какие остались многоугольники? Сколько их?
б) Уберите три палочки так, чтобы не осталось квадратов. Какой остался многоугольник?
в) Уберите три палочки так, чтобы осталось 3 квадрата. Найдите два решения.
III. Сообщение темы урока.
– Рассмотрите рисунки на доске.
Объясните, что обозначают выражения, записанные под каждой картинкой, и по-разному прочитайте их:
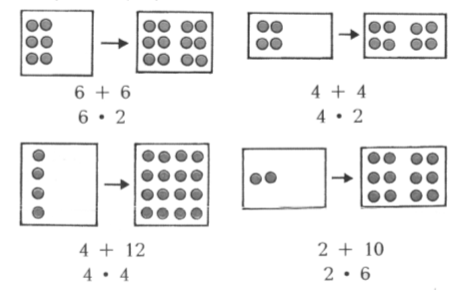
– Сегодня на уроке продолжим знакомство с задачами на увеличение и уменьшение в несколько раз.
IV. Работа по теме урока.
Задание № 3 (с. 56).
– Прочитайте задачу.
– Что известно? Что требуется узнать?
– Что называют «ценой»?
– Используя цветные фишки, покажите решение этой задачи.
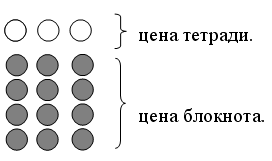
Решение:
3 · 4 = 12 (р.) – цена блокнота.
Ответ: 12 рублей.
– Что можно сказать о цене блокнота, если тетрадь дешевле, чем блокнот? (Блокнот дороже, чем тетрадь.)
Задание № 4 (с. 56).
– Прочитайте текст. Является ли он задачей?
– Что известно в задаче?
– Так как ручка в 3 раза дороже карандаша, то сколько карандашей можно купить вместо одной ручки? (Три.)
– А как узнать, сколько денег будут стоить эти карандаши? (2 рубля умножить на 3.)
– Сколько это рублей? (6 рублей.)
Далее учитель предлагает учащимся рассмотреть решение этой задачи на доске, которое записано заранее. (Пояснения к каждому действию появляются по ходу обсуждения способа решения.)
Запись на доске:
1) 2 · 3 = 6 (р.) – столько рублей будет стоить одна ручка или карандаши, которые можно купить вместо одной ручки.
2) 6 : 2 = 3 (шт.) – столько карандашей можно купить вместо одной ручки.
Ответ: 3 карандаша.
– Сравните оба способа решения данной задачи (полученного в ходе устной работы и записанного на доске).
Задание № 5 (с. 56).
– Прочитайте задачу.
– Что известно? Что требуется узнать?
– Заполните таблицу и решите эту задачу.

Решение:
1) 3 · 2 = 6 (р.) – цена ручки.
2) 6 · 4 = 24 (р.) – стоят 4 ручки.
Ответ: 24 рубля.

V. Повторение пройденного материала.
1. Работа по учебнику.
Задание № 12 (с. 58).
– Что изображено в учебнике? (Графы.)
– Какое отношение задано на первом графе? (Отношение «меньше».)
– Какое отношение задано на втором графе? (Отношение «больше».)
– Прочитайте все высказывания о числах 5, 16 и 18.
Высказывания:
• 5 меньше 16; • 18 больше 5;
• 5 меньше 18; • 18 больше 16;
• 16 меньше 18; • 16 больше 5;
• 5 равно 5; • 5 равно 5;
• 16 равно 16; • 16 равно 16;
• 18 равно 18; • 18 равно 18.
2. Работа в печатной тетради № 2.
Задание № 106.
– Прочитайте задачу.
– Что известно? Что требуется узнать?
– Найдите в задаче лишнее данное и подчеркните его.
– Подумайте и запишите такой вопрос, чтобы при решении задачи нужно было использовать все данные.
Варианты вопросов:
• Сколько лет живет ласточка?
• На сколько лет меньше живет ласточка, чем ворона?
• На сколько лет больше живет сорока, чем ласточка?
Далее устно разбирается план решения всех составленных задач. Одна задача оформляется в тетради.
– Запишите на доске кратко условие задачи.
Запись:
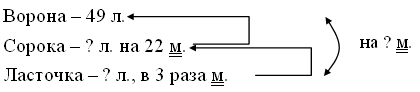
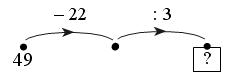
Решение:
1) Сколько лет живет сорока?
49 – 22 = 27 (л.).
2) Сколько лет живет ласточка?
27 : 3 = 9 (л.).
3) На сколько лет меньше живет ласточка, чем ворона?
49 – 9 = 40 (л.).
Ответ: на 40 лет меньше.
Задание № 109.
На левом чертеже изображен граф отношения «больше», а на первом – граф отношения «меньше». После проведения недостающих стрелок схемы будут выглядеть так:
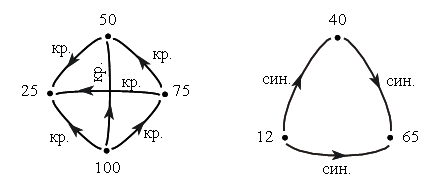
– Прочитайте все высказывания о числах, изображенные с помощью графов.
Высказывания:
• 50 больше 25; • 12 меньше 40;
• 75 больше 25; • 12 меньше 65;
• 75 больше 50; • 40 меньше 65.
• 100 больше 25;
• 100 больше 50;
• 100 больше 75;
VI. Итог урока.
– Что нового узнали на уроке?
– Назовите правила чтения математических граф.
Домашнее задание: № 11 (I столбик, учебник); № 105, 107 (рабочая тетрадь).
Урок 91
нахождение нескольких долей числа
Цели: учить решать задачи на нахождение нескольких долей числа; совершенствовать навыки построения и чтения математических граф; закреплять навыки построения числового луча и умения находить координаты заданных точек; развивать умение рассуждать и анализировать.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Выполните действия и вставьте числа в «окошки».
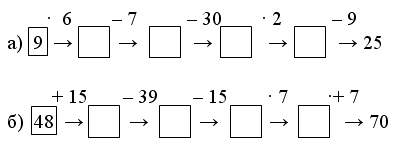
2. Задачи.
а) Купили десяток яиц. Из 5 яиц приготовили омлет и 2 яйца сварили вкрутую. Сколько яиц осталось?
б) У Ани 18 кубиков. Сколько кубиков не хватит, чтобы расставить все имеющиеся кубики на пяти полках по 4 штуки?
3. Закройте «лишнюю» картинку.

4. Геометрия на спичках.
а) Сложите два квадрата из восьми палочек.
б) Уберите одну палочку и сложите такие же два квадрата из оставшихся семи.
в) Проверьте: у вас получилось такое решение?

г) подумайте: почему удалось сложить два квадрата из семи палочек?
д) Сложите два треугольника из шести палочек.
е) Уберите одну палочку и сложите такие же два треугольника из оставшихся пяти.
ж) Подумайте, почему удалось сложить два треугольника из пяти палочек.
III. Сообщение темы урока.
– Рассмотрите иллюстрации на доске.
– Какими числовыми выражениями можно записать изменения слева направо? А справа налево?

– Сегодня будем решать задачи на увеличение и уменьшение в несколько раз.
IV. Работа по теме урока.
Задание № 6 (с. 57).
– Рассмотрите иллюстрацию в учебнике. Прочитайте текст. Является ли он задачей? Почему?
– Что известно в задаче? Что требуется узнать?
– Заполните таблицу и решите задачу.
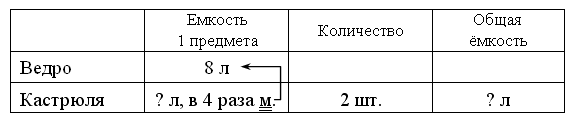
Решение:
1) 8 : 4 = 2 (л) – в одной кастрюле.
2) 2 · 2 = 4 (л) – в двух кастрюлях.
Ответ: 4 литра.
Задание № 7 (с. 57).
– Прочитайте задачу.
– Что известно? Что требуется узнать?
Если у учащихся возникнут затруднения при ответе на первый вопрос задачи, посоветуйте им построить граф отношения больше.
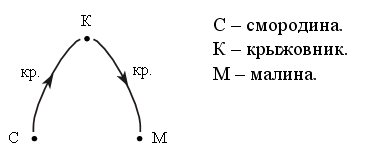
Разбирая граф, дети увидят, что больше всего было саженцев смородины, а меньше всего – малины. Затем попросите учеников высказать предположение о том, во сколько раз смородины было больше, чем малины. Вероятнее всего, будут два мнения: одни скажут, что в 2 раза, а другие – что в 4 раза.
Предложите детям проверить эти предположения на конкретных примерах.
Пример 1. Пусть смородины было 16 кустов, тогда крыжовника было 8 кустов (16 : 2), а малины – 4 куста (8 : 2). В этом случае кустов смородины будет в 4 раза больше, чем малины (16 : 4 = 4).
Пример 2. Пусть кустов смородины было 12, тогда крыжовника было 6 кустов (12 : 2), а малины – 3 куста (6 : 2). В этом случае кустов смородины тоже будет в 4 раза больше, чем малины (12 : 3 = 4).
Рассматривая конкретные примеры, мы в обоих случаях получили, что смородины в 4 раза больше, чем малины. Случайно ли это? Конечно, нет. Рассмотрим следующую схему, которая моделирует ситуацию, описанную в задаче:
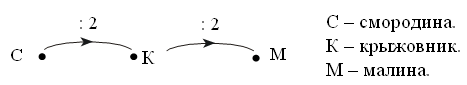
Так как действие двух последовательных «машин»

равносильно действию «машины»,
то
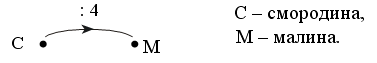
Следовательно, действительно смородины в 4 раза больше, чем малины.

V. Повторение пройденного материала.
1. Работа по учебнику.
Задание № 13 (с. 58).
– Назовите признаки луча.
– Начертите луч 0Х и отметьте на нем точки А (3), В (9), если длина единичного отрезка равна 1 см.
Чертеж:
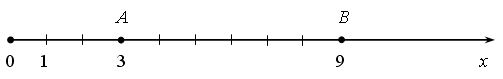
– На каком расстоянии находятся эти точки одна от другой? (9 – 3 = 6 (см).)
– Какая из этих точек находится дальше от начала луча и во сколько раз? (9 : 3 = 3 (раза).)
Задание № 14 (с. 58).
Чертеж:

– Какая фигура является пересечением двух лучей АВ и ВА? (Отрезок.)
2. Работа по карточкам.
Задание № 1.
Выполни рисунок:
а) в одном ряду 2 треугольника, а в другом – на 5 треугольников больше. Запиши выражением, сколько треугольников во втором ряду;
б) в одном ряду 2 треугольника, а в другом – в 5 раз больше. Запиши выражением, сколько треугольников во втором ряду.
Задание № 2.
Выбери выражения, которые соответствуют каждой паре рисунков:
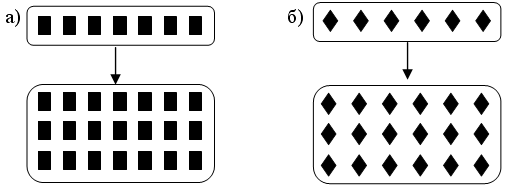
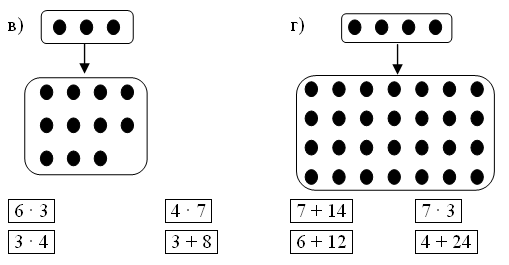
VI. Итог урока.
– Что нового узнали на уроке?
– Назовите правила построения и чтения математических граф.
– Назовите признаки числового луча.
– Что называют единичным отрезком?
Домашнее задание: № 11 (II столбик, учебник).
Урок 92
нахождение нескольких долей числа
Цели: совершенствовать умения решать задачи на нахождение нескольких долей числа; закреплять навыки деления геометрических фигур на доли; развивать логическое мышление и внимание.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Вставьте числа в «окошки», чтобы получились верные равенства:
5 + 7 + = 62 4 + 8 + = 42
8 + 4 + = 92 7 + 4 + = 61
9 + 3 + = 72 6 + 6 + = 32
2. Задачи.
а) 18 малышей построили парами и повели гулять. Сколько пар малышей повели гулять?
б) У Мартышки болит горло. Доктор Айболит дал ей 15 таблеток и велел принимать по одной таблетке в день. На сколько дней хватит таблеток?
3. Выберите фигуру, которую нужно нарисовать.
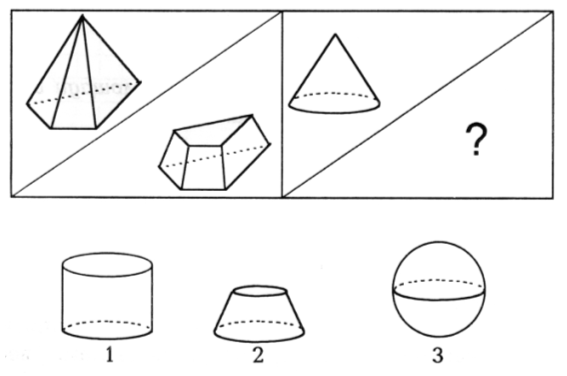
III. Сообщение темы урока.
– Рассмотрите рисунки на доске.
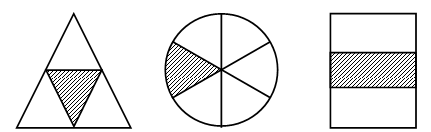
– Как называются данные фигуры?
– Какая часть фигуры закрашена на каждом рисунке?
– Сегодня на уроке будем решать задачи на нахождение нескольких долей числа.
IV. Изучение нового материала.
Справочный материал для учителя
Параллельно с изучением таблицы умножения и соответствующих табличных случаев деления учащиеся учились находить одну долю числа – половину, треть, четвертую часть и т. д. Теперь им предстоит, используя накопленный опыт, научиться находить несколько долей числа или величины.
При рассмотрении материала этой темы целесообразно добиться от учащихся понимания простой истины: если, например, нужно найти третью часть числа, то, деля число на 3, получаем три трети; если находим четверть числа, то, деля число на 4, получаем четыре четверти; если находим пятую часть, то, деля число на 5, получаем пять пятых долей. Соответствующая работа, проведенная учителем в этом направлении сейчас, позволит подготовить усвоение детьми материала следующей темы, где рассматриваются задачи на нахождение числа по нескольким его долям.
* * *
Работа по учебнику.
Учащиеся читают задачи в учебнике (на с. 59–60) и объясняют решение.
– Прочитайте задачи.
– Чем они похожи? Чем отличаются?
– Почему первая задача решается в одно действие?
– Можно ли вторую задачу решить в одно действие?
При необходимости учащиеся выполняют решение данных задач на фишках.
Задание № 1 (с. 60).
– Прочитайте задачу.
– Что известно? Что требуется узнать?
– Составьте рисунок к данной задаче и решите ее.
Запись:
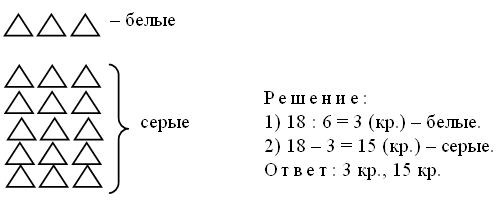
Задание № 2 (с. 60).
– Прочитайте текст. Является ли он задачей? Почему?
– Что вам известно? Что требуется узнать?
– Запишите кратко условие задачи.
Запись:

Решение:
45 : 9 = 5 (р.) – израсходовала.
Ответ: 5 рублей.

V. Повторение пройденного материала.
1. Работа по учебнику.
задание № 9 (с. 61).
– Что значит «увеличь каждое число в 5 раз»?
– Запишите соответствующие примеры.
– Что значит «уменьши числа в 7 раз»?
– Запишите соответствующие примеры.
задание № 11 (с. 62).
– Рассмотрите данный рисунок. Какие фигуры здесь изображены?
– Назовите признаки треугольников.
– В каком из треугольников нарушена закономерность записи чисел?
Закономерность: если числа в треугольниках 1, 2 и 4 расположить в порядке возрастания, то каждое следующее число будет в 2 раза больше предыдущего. Это правило нарушено в треугольнике 3. В этом треугольнике должны быть числа 3, 6 и 12.
2. Работа в печатной тетради № 2.
Задание № 112.
Если сильные учащиеся могут устно выполнить все вычисления, то слабоуспевающим можно разрешить воспользоваться фишками (по аналогии с тем, как это делается при изложении нового материала темы). Например, в случае 3 сначала предложите ученикам пересчитать число бусинок на рисунке и выложить перед собой в ряд столько же фишек (то есть 18). По условию задания надо закрасить восемь девятых бусинок. Значит, сначала надо найти одну девятую числа всех бусинок (то есть разбить все бусинки на 9 равных групп), а затем уже найти восемь девятых (то есть пересчитать число бусинок в 8 группах).
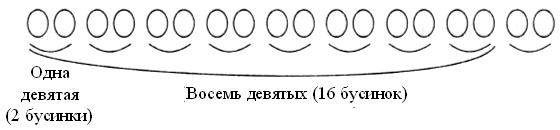
Делаем вывод: надо закрасить шестнадцать бусинок из восемнадцати.
Задание № 113.
Чертежи:
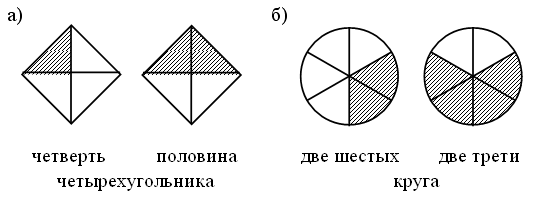
VI. Итог урока.
– Что нового узнали на уроке?
– Назовите признаки треугольника.
– Назовите признаки круга.
Домашнее задание: № 10 (учебник), № 111 (рабочая тетрадь).
Урок 93
нахождение нескольких долей числа
Цели: совершенствовать навыки решения задач на нахождение нескольких долей числа; закреплять навыки нахождения периметра многоугольника; развивать умение анализировать и рассуждать.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Заполните таблицу.
|
Уменьшаемое |
73 |
|
87 |
78 |
|
39 |
|
90 |
|
Вычитаемое |
20 |
50 |
|
|
74 |
|
2 |
|
|
Значение разности |
|
28 |
5 |
6 |
20 |
9 |
47 |
20 |
2. Математический диктант.
– Запишите только ответы на вопросы:
а) Какие двузначные числа делятся на 9?
б) Найдите треть каждого из чисел: 27, 9, 3.
в) Найдите четверть каждого из чисел: 4, 8, 12, 16, 20, 24, 28.
г) Чему равна пятая часть каждого из чисел: 5, 25, 30, 45, 35?
3. Геометрия на спичках.
а) Сколько на чертеже квадратов? Сколько всего многоугольников? Какие они?
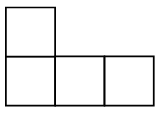
б) Уберите одну палочку так, чтобы осталось 2 квадрата. Найдите три разных решения.
в) Уберите одну палочку так, чтобы осталось 3 квадрата. Найдите два решения и сравните их.
г) Уберите две палочки так, чтобы остался 1 квадрат. Найдите два решения и сравните их.
4. Догадайтесь! Как связаны числа с рисунками?
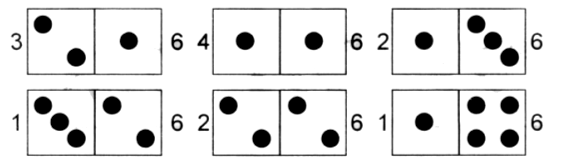
III. Сообщение темы урока.
– Сегодня на уроке мы будем решать задачи на нахождение нескольких долей числа.
IV. Работа по теме урока.
Задание № 3 (с. 60).
– Прочитайте задачу.
– Что известно? Что требуется узнать?
При обдумывании этапов решения такого плана задач удобно использовать не только фишки, но и «машины». Опора на предварительно составленную схему, описывающую этапы решения задачи, помогает учащимся не запутаться в последовательности выполнения арифметических действий при ответе на поставленный вопрос. Рассмотрим, как при этом можно оформить решение.
Запись:
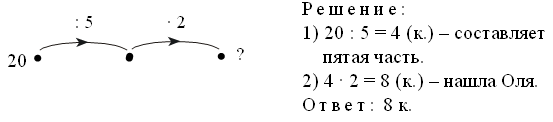
Задание № 4 (с. 60).
Учащиеся читают задание и выполняют следующие записи в тетради:
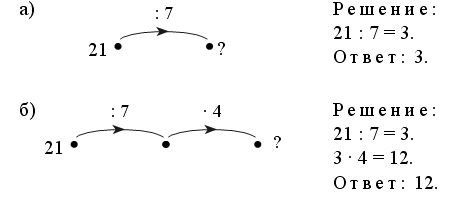
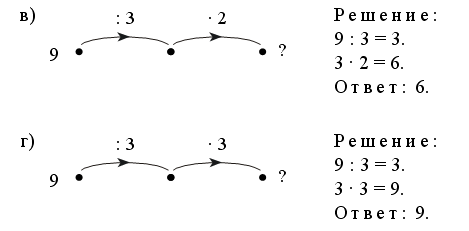
Учитель особое внимание обращает на случай г) данного упражнения.
Схема решения задачи с помощью «машин» наглядно показывает, что три трети числа 9 – это само число 9 (так как деление на 3 и умножение на 3 – это взаимно обратные операции).
Чтобы закрепить этот вывод, учитель дает дополнительные задания.
– Определите, чему равны:
а) пять пятых числа 10 (10);
б) семь седьмых числа 7 (7);
в) шесть шестых числа 12 (12);
г) четыре четвертых любого числа? (Само же число.)

V. Повторение пройденного материала.
1. Работа по учебнику.
задание № 12 (с. 62).
– Рассмотрите рисунок. Как называются данные фигуры? (Многоугольники.)
– Как называется первый многоугольник? (Четырехугольник.)
– Как называется второй многоугольник? (Шестиугольник.)
– Назовите признаки четырехугольника и шестиугольника.
– Что такое периметр?
– Вычислите периметр каждого многоугольника двумя способами.
Решение:
а = 3 см.
Р = 3 + 3 + 3 + 3 = 12 (см).
Р = 3 · 4 = 12 (см).
а = 2 см.
р = 2 + 2 + 2 + 2 + 2 + 2 = 12 (см).
Р = 2 · 6 = 12 (см).
– Какой способ является лучшим? Почему?
– Внесите изменения в данные фигуры так, чтобы решение можно было выполнить только сложением.
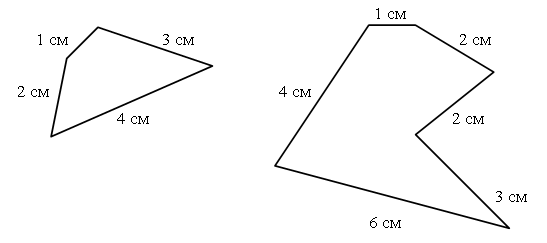
2. Работа в печатной тетради № 2.
Задание № 117.
Перед выполнением задания вспомните с учащимися, что направление движения задается лучом, поэтому, исходя из условия задачи, на чертеже надо изобразить две пары лучей. Причем в случае 1 это два синих луча, которые пересекаются, а в случае 2 это два красных луча, которые не пересекаются.
После таких уточнений учащиеся могут выполнить задание самостоятельно, а затем сделать взаимную проверку.
VI. Итог урока.
– Что нового узнали на уроке?
– Как вычислить периметр многоугольника?
– Назовите признаки числового луча.
Домашнее задание: № 13 (учебник); № 116 (рабочая тетрадь).
Урок 94
нахождение нескольких долей числа
Цели: совершенствовать навыки решения задач на нахождение нескольких долей числа; продолжать формирование умений решать задачи разными способами; закреплять навыки решений задач с величинами «цена», «количество», «стоимость»; развивать логическое мышление.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Поставьте знак «+» или «–».
9 … 4 … 7 = 20 60 … 8 … 40 = 12
10 … 4 … 6 = 20 13 … 30 … 2 = 41
8 … 5 … 70 = 83 80 … 6 … 20 = 94
10 … 3 … 50 = 57 6 … 7 … 40 = 53
2. Задача.
В зоологическом саду живут 15 мартышек. В этом году из трех стран привезли еще по 4 мартышки. Сколько мартышек стало в зоологическом саду?
3. Выберите фигуру, которую нужно нарисовать.
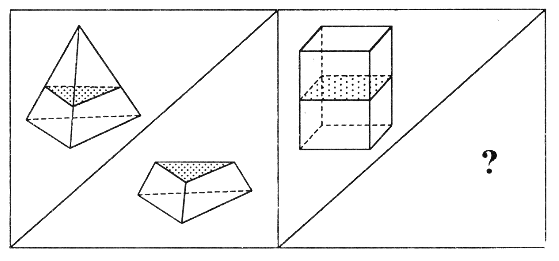
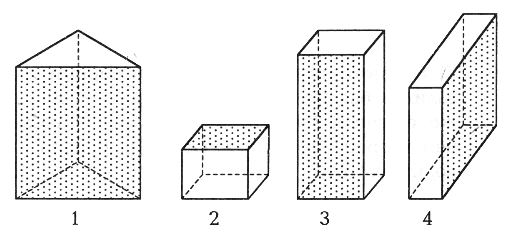
III. Сообщение темы урока.
IV. Работа по теме урока.
Задание № 5 (с. 61).
– Прочитайте текст. Является ли он задачей? Почему?
– Что известно в задаче? Что требуется узнать?
– Составьте к данной задаче схему и решите её.
Запись:

Решение:
1) Сколько детей составляют восьмую часть?
40 : 8 = 5 (чел.).
2) Сколько девочек в классе?
5 · 5 = 25 (чел.).
3) Сколько мальчиков в классе?
40 – 25 = 15 (чел.).
Ответ: 15 человек.
Далее учитель предлагает решить данную задачу другим способом.
– Сколько всего восьмых частей в числе 40? (Восемь.)
– Пять восьмых – это девочки, а сколько тогда восьмых частей приходится на мальчиков? (8 – 5 = 3 (чел.), то есть три восьмых части.)
– решите задачу другим способом.
Запись:
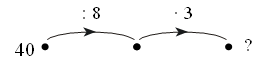
Решение:
1) Сколько детей составляют восьмую часть?
40 : 8 = 5 (чел.).
2) Сколько восьмых частей приходится на мальчиков?
8 – 5 = 3 (чел.).
3) Сколько мальчиков в классе?
5 · 3 = 15 (чел.).
Ответ: 15 человек.
Задание № 6 (с. 61).
Учащиеся рассуждают: «Так как в часе четыре четвертых, а за одну четверть часа катер проходит 20 км, то за четыре четверти он пройдет в 4 раза больше, то есть надо 20 км умножить на 4. Рассуждаем так: 20 – это 2 десятка. 2 десятка умножить на 4 – это 8 десятков, или 80. Следовательно, за 1 час катер пройдет 80 км».

V. Повторение пройденного материала.
1. Работа в печатной тетради № 2.
задание № 114.
Записи на доске:
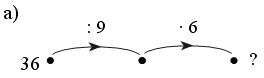
Решение:
36 : 9 = 4 (см).
4 · 6 = 24 (см).
Ответ: 24 см.

Решение:
1 дм = 10 см.
10 : 5 = 2 (см).
2 · 3 = 6 (см).
Ответ: 6 см.
Задание № 119.
– Рассмотрите иллюстрацию. Составьте по ней задачу.
– Заполните таблицу.

Решение:
2 · 4 + 6 = 14 (р.) – стоимость всей покупки.
Ответ: 14 рублей.
2. Работа по учебнику.
Задание № 14 (с. 62).
– Что изображено на рисунке? (Отрезок.)
– Измерьте его длину в сантиметрах. (10 см.)
– Какова длина пятой части отрезка? (10 : 5 = 2 (см).)
– Измерьте длину отрезка в дециметрах. (1 дм.)
– Какую длину будет иметь отрезок, который в 5 раз длиннее данного? (1 · 5 = 5 (дм).)
VI. Итог урока.
– Что нового узнали на уроке?
– Как найти долю от числа?
Домашнее задание: № 118 (рабочая тетрадь).
Урок 95
нахождение нескольких долей числа
Цели: совершенствовать навыки решения задач на нахождение нескольких долей числа; продолжить формирование вычислительных навыков; развивать умение анализировать и обобщать.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Разгадайте правило, по которому составлен первый столбик выражений, и запишите верные равенства:
93 – 3 54 – 2 89 – 7 78 – 5
93 – 30 – – –
39 – 3 – – –
39 – 30 – – –
2. Задача.
В волейбольных соревнованиях принимали участие 8 команд. Сколько человек участвовало в соревнованиях, если в каждой команде 6 основных и 3 запасных игрока? Объясните, что обозначают выражения, составленные по условию данной задачи:
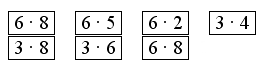 1
1
3. Математический диктант.
Назовите результаты умножения:
3 · 4 9 · 3 6 · 6 8 · 5
6 · 8 5 · 6 3 · 9 7 · 4
4 · 7 7 · 7 4 · 4 8 · 2
5 · 5 9 · 8 7 · 5 2 · 9
8 · 5 4 · 5 9 · 0 8 ·3
4 · 9 6 · 7 0 · 1 7 · 6
9 · 7 8 · 8 6 · 4 4 · 3
5 · 7 3 · 3 5 · 9 9 · 6
III. Сообщение темы урока.
IV. Работа по теме урока.
Задание № 7 (с. 61).
– Рассмотрите рисунок в учебнике. Какие фигуры здесь изображены? (Четырехугольник, треугольник, круг.)
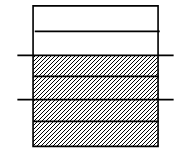
– Назовите признаки четырехугольника.
– Какая часть четырехугольника осталась незакрашенной? (Две шестых.)
– Можно ли утверждать, что закрашено две третьих части этого четырехугольника? (Можно.)
– Докажите.
– Назовите признаки треугольника.
– Какая часть треугольника закрашена? (Одна третья часть.)
– Какая часть треугольника осталась незакрашенной? (Две третьих части.)
– Назовите признаки круга.
– Какая часть круга закрашена? (Одна четвертая часть.)
– Какая часть круга осталась незакрашенной? (Три четвертых части.)
Задание № 8 (с. 61).
– Прочитайте текст. Является ли он задачей? Почему?
– Что известно в задаче? Что требуется узнать?
– Составьте схему и решите эту задачу.
Запись:
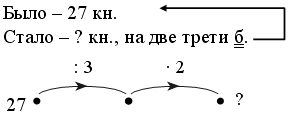
Решение:
1) 27 : 3 = 9 (кн.) – в третьей части.
2) 9 · 2 = 18 (кн.) – стало больше.
3) 27 + 18 = 45 (кн.) – стало.
Ответ: 45 книг.

V. Самостоятельная работа по карточкам.
задание № 1.
– Чем похожи все рисунки?
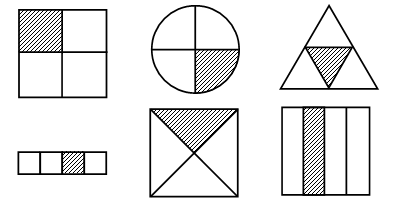
Задание № 2.
![]()
Измерьте отрезок АВ.
Найдите длину десятой части этого отрезка.
Чему равны три десятых этого отрезка?
Задание № 3.
В товарном вагоне 30 т зерна. До обеда выгрузили две третьих зерна. Сколько тонн зерна осталось в вагоне?
Задание № 4.
Нарисуйте в тетради четырехугольник, площадь которого равна 24 клеткам. Закрасьте пять шестых площади прямоугольника.
VI. итог урока.
– Что нового узнали на уроке?
– Как найти несколько долей данного числа или величины?
Урок 96
нахождение нескольких долей числа
Цели: совершенствовать умения решать составные задачи; формировать вычислительные навыки; развивать умение рассуждать и обобщать.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Магические фигуры.
2. Задача.
У мамы было 36 слив. Когда она дала каждому сыну 5 слив, осталась 1 слива. Сколько сыновей?
3. Выберите фигуру, которую нужно нарисовать.
III. Сообщение темы урока.
IV. Работа по теме урока.
задание № 15 (с. 63).
– Назовите признаки отрезка.
– Прочитайте задание. Сколько должно образоваться частей отрезка? (Четыре части.)
– Проверьте свое предположение с помощью чертежа.
Чертеж:
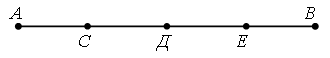
– Сколько всего отрезков на чертеже? (10 отрезков.)
Отрезки: АВ, АС, АД, АЕ, СД, СЕ, СВ, ДЕ, ДВ, ЕВ.
Задание № 16 (с. 63).
– Рассмотрите рисунок. Составьте по этому рисунку задачу.
– Что известно в задаче? Что требуется узнать?
– Заполните таблицу по задаче и решите её.

Решение:
1) 18 : 6 = 3 (л) – в 1 кувшине.
2) 9 : 3 = 3 (к.) – потребуется.
Ответ: 3 к.
Задание № 17 (с. 63).
Это задание важно с точки зрения повторения и закрепления вывода, сформулированного учащимися ранее: чем большую часть числа мы находим, тем меньшее число получаем.
Запись:
а) четверть больше восьмой части числа,
проверка:
24 : 4 = 6,
24 : 8 = 3,
6 больше 3;
б) половина больше девятой части числа,
проверка:
18 2 = 9,
18 : 9 = 2,
9 больше 2.
Задание № 18 (с. 63).
Учащиеся должны сообразить, что, для того чтобы прочесть фразу Ф. Бэкона, надо последовательно «двигаться» в направлении стрелок: «Знание – сила».

V. Повторение пройденного материала.
1. Фронтальная работа.
– Рассмотрите рисунок на доске. Какие фигуры здесь изображены?
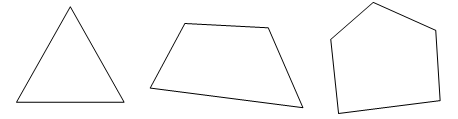
– Назовите признаки треугольника.
– Назовите признаки четырехугольника.
– Назовите признаки пятиугольника.
– По какому правилу изображены геометрические фигуры? (У каждой следующей фигуры на одну сторону, вершину и угол больше, чем у предыдущей, поэтому дальше надо рисовать шестиугольник и семиугольник.)
2. Работа по карточкам.
Задание № 1.
В каждом задании найди правильный ответ и закрась карточку, на которой он записан.
а) В каком числе 4 десятка и 7 единиц?
![]()
б) Какое число меньше, чем 70, на 1?
![]()
в) Найди сумму чисел 8 и 50.
![]()
г) Найди разность чисел 94 и 4.
![]()
д) Найди число, в котором 5 десятков, а единиц на 2 меньше, чем десятков.
![]()
е) Какое число увеличили на 7, если получили 30?
![]()
ж) Какое число уменьшили на 9, если получили 21?
![]()
Задание № 2.
– Начерти прямоугольник. Проведи в нем 2 отрезка так, чтобы на чертеже стало 8 треугольников.
VI. Итог урока.
– Что нового узнали на уроке?
Домашнее задание: № 19 (учебник).
Урок 97
КОНТРОЛЬНАЯ
РАБОТА ПО ТЕМЕ
«РЕШЕНИЕ АРИФМЕТИЧЕСКИХ ЗАДАЧ»
Цели: проверить усвоение понятий «увеличить в…», «уменьшить в…», табличных навыков умножения и деления, сформированность умений выполнять кратное сравнение чисел, решать задачи на нахождение числа, большего или меньшего данного в несколько раз, на нахождение нескольких долей числа и на нахождение числа по нескольким его долям.
I вариант
1. Найди значения выражений:
8 · 7 54 : 6
3 · 6 27 : 3
6 · 4 63 : 9
8 · 3 48 : 8
2. Начерти три отрезка: длина первого 4 см, длина второго – в 3 раза больше длины первого, а длина третьего – в 4 раза меньше длины второго.
3. Маша собрала 8 кг яблок, а Миша – на 16 кг больше, чем Маша. Во сколько раз Миша собрал яблок больше, чем Маша?
4. Бабушка испекла 20 пирожков. Пятая часть всех пирожков была с картошкой, а четвертая часть всех пирожков с капустой. Сколько пирожков было с картошкой? Сколько пирожков было с капустой?
5. Найди число, если его седьмая часть равна:
а) 7; б) 9.
6.* Разгадай правило, по которому записаны числа, и заполни пустые «окошки».
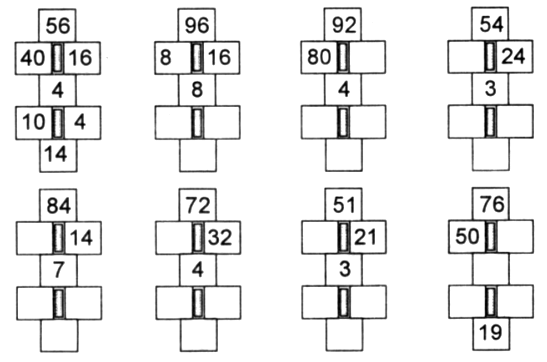
II вариант
1. Найди значения выражений:
7 · 6 72 : 8
5 · 6 54 : 9
9 · 3 63 : 7
8 · 4 36 : 4
2. Начерти три отрезка: длина первого 3 см, длина второго – в 2 раза больше длины первого, а длина третьего – в 3 раза меньше длины второго отрезка.
3. На первой полке 36 книг, а на второй – на 27 книг меньше. Во сколько раз на первой полке книг больше, чем на второй?
4. Учащиеся второго класса взяли в библиотеке 24 книги. Шестая часть всех книг была русские народные сказки. Восьмая часть всех книг – юмористические произведения о детях. Сколько взяли сказок? Сколько взяли юмористических произведений?
5. Найди число, если его девятая часть равна:
а) 9; б) 6.
6.* Разгадай правило, по которому записаны числа, и заполни пустые «окошки».
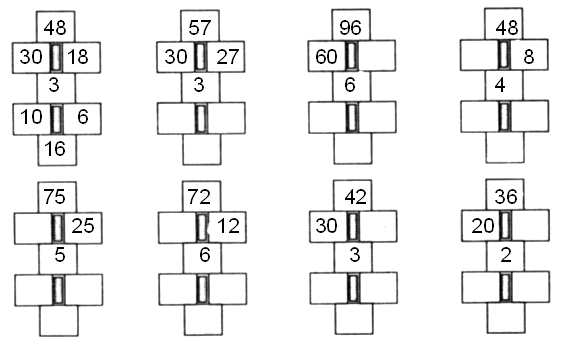
Урок 98
РАБОТА
НАД ОШИБКАМИ.
РЕШЕНИЕ ЗАДАЧ
Цели: провести анализ выполненной контрольной работы; совершенствовать умения решать задачи; развивать внимание и память.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Игра цифр.
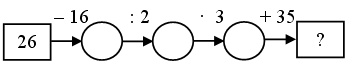
В игре участвуют цифры 1, 2, 3, 4, 5, 6, 7, 8.
Разместите их в кружочках так, чтобы ни одну из цифр нельзя было соединить прямой линией от кружка до кружка – с ее соседками в порядковом ряду. Две цифры уже поставлены на места.
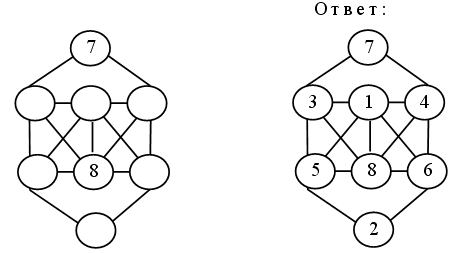
2. Геометрическое задание:
– Какие фигуры изображены на чертеже?

– Назовите признаки четырехугольника.
– Назовите признаки пятиугольника.
– Какие получатся новые фигуры, если стороны АВ и СD продолжить так, чтобы они пересеклись?
3. Закройте «лишнюю» картинку.
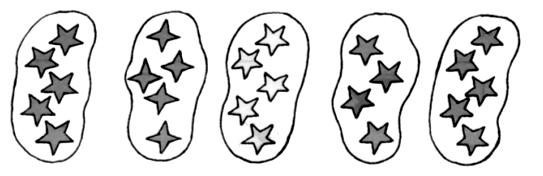
4. Составьте по таблице задачи про птиц, заполняя окошки своими числами. Запишите ответ каждой задачи в третьей строке таблицы.
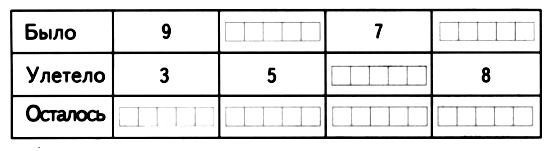
III. Сообщение о результатах выполнения контрольной работы.
IV. Работа над ошибками.

V. Самостоятельная работа по карточкам.
Карточка А
1. В книге 48 страниц. Таня прочитала 30 страниц. Сколько страниц этой книги осталось прочитать Тане?
2. Выбери и закрась кружки с номерами задач, обратных данной. Реши эти задачи.

Карточка В
Около каждой задачи вставь в кружок знак действия, с помощью которого она решается.

Карточка С
Сколько
на чертеже отрезков? ![]()
![]()
Запиши
длину: самого длинного отрезка – ![]() см;
см;
самого короткого отрезка – ![]() см
см
Как узнать, не измеряя, длину третьего отрезка?
VI. Итог урока.
Урок 99
названия
чисел
в записях действий
Цели: ввести названия компонентов арифметических действий; совершенствовать вычислительные навыки; продолжить формирование умений решать составные задачи; развивать внимание и мышление.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Прочитайте условие задачи и обведите её вопрос.
Чтобы угостить друзей в день рождения, Маша купила мороженое – в стаканчиках и рожках. Рожков – на 15 меньше. По дороге домой она отдала 9 рожков встретившимся ей одноклассникам.
– Сколько рожков принесла Маша домой?
– На сколько больше Маша принесла домой стаканчиков, чем рожков?
– На сколько меньше Маша принесла домой стаканчиков, чем рожков?
– Решите задачу.
2. Выберите пары чисел, разность которых равна 32. Запишите верные равенства.
|
72 |
8 |
4 |
39 |
6 |
40 |
30 |
7 |
36 |
2 |
3. Расположите по порядку, используя стрелки.

4. Обведите «лишнюю» фигуру.

III. Сообщение темы урока.
– Какие арифметические действия вам известны? (Сложение, вычитание, умножение, деление.)
– Сегодня на уроке мы узнаем, как называются числа в разных арифметических действиях.
IV. Изучение нового материала.
Работа по учебнику.
Задание № 1 (с. 64).
– Рассмотрите и сравните записи арифметических действий.
Учитель обращает внимание учащихся на то, что, хотя числа, над которыми производятся действия, во всех примерах одинаковы, в каждом из действий они называются по-разному. При этом при сложении и умножении данные числа называются словами, созвучными с названиями действий. Так, при сложении числа называются слагаемыми, а при умножении – множителями.
Названия чисел при вычитании и при делении запомнить труднее. Учащиеся могут пользоваться данной таблицей на первых уроках.
Задание № 2 (с. 64).
– Прочитайте данные примеры.
– Какое действие выполняется в каждом из примеров?
– Прочитайте примеры, используя слова «разность чисел», «сумма чисел», «произведения чисел» и «частное чисел».
Задание № 4 (с. 65).
Учащиеся выполняют записи:
54 : 9 = 6 8 · 7 = 56
97 + 3 = 100 50 – 30 = 20
Задание № 5 (с. 65).
Учащиеся записывают примеры, используя арифметические знаки, и проверяют, верно ли выполнены действия.
45 + 38 = 73 – неверно, так как 45 + 38 = 83.
6 · 7 = 42 – верно.
40 : 8 = 6 – неверно, так как 40 : 8 = 5.
60 – 11 = 59 – неверно, так как 60 – 11 = 49.

V. Повторение пройденного материала.
1. Работа по учебнику.
Задание № 12 (с. 66).
– Что значит выражение «увеличь в 8 раз»?
– Какое действие надо выполнить, если сказано «уменьши на 5»?
Далее учащиеся записывают примеры и находят их значение.
Запись:
(3 + 5) · 8 = 8 · 8 = 64.
(7 + 5) – 5 = 12 – 5 = 7.
(46 – 16) : 6 = 30 : 6 = 5.
Задание № 14 (с. 66).
– Прочитайте текст. Является ли он задачей? Почему?
– Что известно в задаче? Что требуется узнать?
– Запишите кратко условие задачи.
Запись:
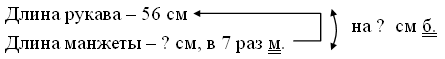
Решение:
1) Чему равна длина манжеты?
56 : 7 = 8 (см).
2) На сколько сантиметров длина рукава больше длины манжета?
56 – 8 = 48 (см).
Ответ: на 48 см больше.
2. Работа в печатной тетради № 2.
Учитель обращает внимание учащихся на правильный выбор терминов.
Задание № 91.
Учащиеся работают самостоятельно и проверку выполняют самостоятельно, соотнеся свою работу с таблицей учебника (с. 68).
3. Работа по карточкам.
Карточка А
Подставь в «окошечко» числа 7, 9, 11, 15, 30.
Вычисли значения суммы.
Образец: 8 + 7 = 15.
![]() 7 9 11 15 30
7 9 11 15 30
Карточка В
Подставь в «окошечко» числа 6, 8, 14, 15, 20. Вычисли значения разности.
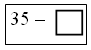 6 8 14 15 20
6 8 14 15 20
VI. Итог урока.
– Что нового узнали на уроке?
– Как называются компоненты сложения? Вычитания? Умножения? Деления?
Домашнее задание: № 3, 13 (I столбик, учебник), № 128 (рабочая тетрадь).
Урок 100
названия
чисел
в записях действий
Цели: учить употреблять названия компонентов сложения, вычитания, умножения и деления при чтении выражений; совершенствовать навыки решения задач с величинами «цена», «количество», «стоимость»; повторить правила построения и чтения математических графов, развивать внимание и мышление.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Задача.
Ира собрала на 12 грибов больше Миши, но 7 её грибов оказались несъедобными. У кого и на сколько больше съедобных грибов?
2. Вычислите неизвестное число:
15 + = 20 + 7 = 30
60 – = 15 – 6 = 13
20 : = 5 · 7 = 42
9 · = 36 : 9 = 7
3. Постройте еще 1 такую же фигуру.
– Как она называется? (Шестиугольник.)
– Назовите признаки шестиугольника.
– Проведите в каждом из них по одному отрезку так, чтобы первый шестиугольник был разделен на 2 четырехугольника, а второй – на 2 пятиугольника.
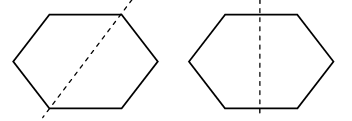
4. Составьте «круговые» примеры:
![]()
III. Сообщение темы урока.
IV. Работа по теме урока.
Задание № 6 (с. 65).
Учащиеся читают задание и выполняют записи:
4 + 27 = 31 6 · 8 = 48
12 – 5 = 7 72 : 9 = 8
Задание № 7 (с. 65).
Это задание направлено на развитие логического мышления учащихся. Выполняя задание, дети приводят доказательство утверждений.
1. Сумма двух чисел может быть равной первому слагаемому, если первое слагаемое – любое число, но при этом второе слагаемое – 0. Учащиеся могут привести следующие примеры:
0 + 0 = 0, 1 + 0 = 1, 17 + 0 = 17 И т. д.
2. Разность чисел может быть равной уменьшаемому, если уменьшаемое – любое число, а вычитаемое – 0. Учащиеся могут привести следующие примеры:
0 – 0 = 0, 32 – 0 = 32, 100 – 0 = 100 И т. д.
3. Разность чисел может быть равной вычитаемому, если уменьшаемое в 2 раза больше вычитаемого. Учащиеся могут привести следующие примеры:
6 – 3 = 3, 18 – 9 = 9, 4 – 2 = 2 И т. д.
Задание № 8 (с. 65).
Произведение двух чисел может быть равно первому множителю, если первый множитель – 0, а второй множитель – любое число или первый множитель – любое число, а второй множитель – 1.
Учащиеся могут привести следующие примеры:
0 · 0 = 0 0 · 9 = 0 5 · 1 = 5
0 · 1 = 0 1 · 1 = 1 12 · 1 = 12 И т. д.
Задание № 9 (с. 65).
Частное чисел может быть равным делимому, если делимое является любым числом, а делитель – 1 или делимое – 0, а делитель – любое число, кроме 0.
Учащиеся могут привести следующие примеры:
1 : 1 = 1 10 : 1 = 10 0 : 3 = 0
7 : 1 = 7 0 : 1 = 0 0 : 11 = 0 И т. д.

V. Повторение пройденного материала.
1. Работа по учебнику.
Задание № 15 (с. 66).
– Прочитайте задачу.
– Что известно? Что требуется узнать?
– Заполните таблицу и решите задачу.

Решение:
1) Сколько стоит ручка?
3 · 6 = 18 (р.).
2) Сколько стоит вся покупка?
3 + 18 = 21 (р.).
Ответ: 21 рубль.
Задание № 16 (с. 66).
– Прочитайте текст. Является ли он задачей?
– Что известно? Что требуется узнать?
– Составьте по данному условию схему.
Запись:
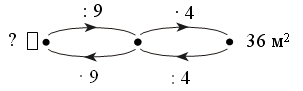
Решение:
1) 36 : 4 = 9 (м2) – составляет девятая часть.
2) 9 · 9 = 81 (м2) – площадь катка.
Ответ: 81 м2.
2. Работа в печатной тетради № 2.
Задание № 123.
– Составьте все возможные примеры на сложение и вычитание с числами 3, 14 и 17.
Учащиеся записывают на доске:
3 + 14 = 17 17 – 3 = 14
14 + 3 = 17 17 – 14 = 3
Затем учащиеся переходят к самостоятельному выполнению задания.
Задание № 126.
Сначала надо построить граф отношения «выше», опираясь на условие задания.
Известно, что сосна выше березы, следовательно, проводим красную стрелку от С к Б. Липа ниже березы (значит, береза выше липы), следовательно, проводим красную стрелку от Б к Л.
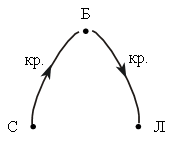
Рассмотрев получившийся граф, учащиеся делают вывод: самое высокое дерево – сосна, а самое низкое – липа.
VI. Итог урока.
– Что нового узнали на уроке?
– Назовите правила построения и чтения математических графов.
– Назовите единицы площади.
Домашнее задание: № 13 (II столбик, учебник); № 120, 121 (рабочая тетрадь).
Урок 101
названия
чисел
в записях действий
Цели: совершенствовать умения решать составные задачи; продолжить формирование навыков строить и читать математические графы; закреплять навыки вычисления периметра любого многоугольника; развивать умение анализировать и сравнивать.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Задача.
В палатку привезли 26 дынь и 42 арбуза, но 9 арбузов разбились. Чего больше можно продать: арбузов или дынь и на сколько?
2. Какое число должно быть записано в последнем окошке?
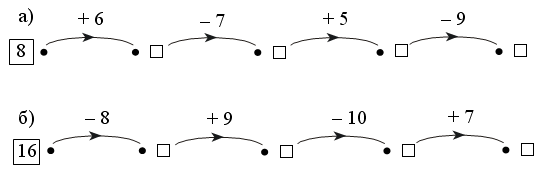
3. Геометрия на спичках.
а) Сколько на чертеже квадратов? Сколько других многоугольников? Сколько всего многоугольников?

б) Уберите одну палочку так, чтобы осталось 3 квадрата.
в) Уберите одну палочку так, чтобы осталось 2 квадрата. Найдите несколько разных решений.
г) Уберите две палочки так, чтобы остался 1 квадрат. Найдите несколько разных решений и сравните их.
д) Уберите две палочки так, чтобы осталось 2 квадрата.
III. Сообщение темы урока.
IV. Работа по теме урока.
Задание № 10 (с. 65).
Обратите внимание учащихся на то, что перебирать все способы представления числа 14 в виде суммы двух слагаемых надо не хаотично, а по определенному правилу. Тогда исключается возможность пропуска того или иного варианта.
Будем, например, брать в качестве первого слагаемого по порядку все числа, начиная с 0, и подбирать второе слагаемое так, чтобы сумма равнялась 14. Тогда возможны следующие варианты:
0 + 14 = 14 5 + 9 = 14 10 + 4 = 14
1 + 13 = 14 6 + 8 = 14 11 + 3 = 14
2 + 12 = 14 7 + 7 = 14 12 + 2 = 14
3 + 11 = 14 8 + 6 = 14 13 + 1 = 14
4 + 10 = 14 9 + 5 = 14 14 + 0 = 14
Задание № 11 (с. 65).
Цель задания – вспомнить с учащимися известные им табличные случаи умножения и свойство умножения на 1, поэтому вполне достаточно, если по ходу работы будут указаны только следующие способы представления числа 24 в виде произведения двух множителей:
3 · 8 = 24 8 · 3 = 24
4 · 6 = 24 6 · 4 = 24
1 · 24 = 24 24 · 1 = 24
Если учащиеся сами не укажут случаи: 2 · 12 = 24 и 12 · 2 = 24, то и не стоит акцентировать на них внимание.

V. Повторение пройденного материала.
1. Работа по учебнику.
Задание № 17 (с. 66).
Решение задачи надо начать с построения графа отношения «дороже». Для этого обозначим буквами цену предметов, о которых идет речь в задаче: К – карандаш, Т – тетрадь, Б – блокнот, Р – ручка, Л – линейка. Известно, что карандаш дороже тетради, следовательно, проводим красную стрелку от К к Т.
Блокнот дешевле тетради (значит, тетрадь дороже блокнота), следовательно, проводим красную стрелку от Т к Б. Блокнот дороже ручки, следовательно, проводим красную стрелку от Б к Р. Линейка дешевле ручки (значит, ручка дороже линейки), следовательно, проводим красную стрелку от Р к Т. Граф построен.
Рассмотрев граф, учащиеся делают вывод, что самый дорогой предмет – карандаш, а самый дешевый – линейка.
Задание № 19 (с. 67).
– Рассмотрите чертеж. Назовите все многоугольники. (Четырехугольник АДЕС, треугольники КМР и АВС, четырехугольник ВДЕС, шестиугольник МВАСРК.)
– Назовите признаки треугольника.
– Назовите признаки четырехугольника и т. д.
– Пересечением каких многоугольников является треугольник АВС? (Треугольник КМР и четырехугольник АДЕС.)
2. Работа в печатной тетради № 2.
Задание № 123.
– Найдите неизвестное число, составив схемы-«машины».
а) + 12 = 61 б) · 9 = 27

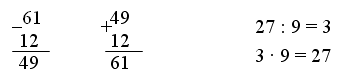
Ответ: 49. Ответ: 3.
3. Работа по карточкам.
Сравните длины сторон треугольника и квадрата. Периметр какого многоугольника больше? Раскрасьте этот многоугольник. Проверьте себя, вычислив периметр каждого многоугольника.
VI. Итог урока.
– Что нового узнали на уроке?
– Назовите признаки треугольника.
– Назовите признаки четырехугольника.
– Как вычислить периметр многоугольника?
Домашнее задание: № 18 (учебник); № 122 (рабочая тетрадь).
Урок 102
числовые выражения
Цели: познакомить учащихся с простейшими выражениями, их названиями (сумма, разность, произведение, частное); учить читать и составлять выражения и вычислять их значение; совершенствовать навыки решения составных задач; развивать умение анализировать и сравнивать.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Задача.
У продавца 28 красных воздушных шариков и 20 жёлтых. На сколько больше у продавца красных шариков, чем жёлтых?
2. Заполните пустые «окошки»:
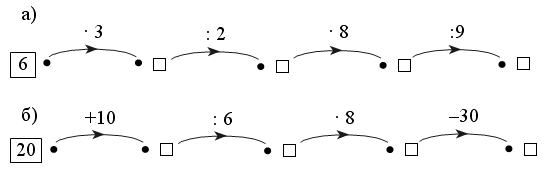
3. Геометрия на спичках.
а) Уберите три палочки так, чтобы осталось 3 квадрата. Найдите три решения и сравните их.

б) Уберите четыре палочки так, чтобы осталось 2 квадрата.
в) Переложите две палочки так, чтобы получилось 2 квадрата.
г) Переложите две палочки так, чтобы получилось 3 квадрата.
д) Переложите две палочки так, чтобы получилось 4 квадрата.
е) Переложите две палочки так, чтобы получилось 5 квадратов.
4. Выберите картинку.
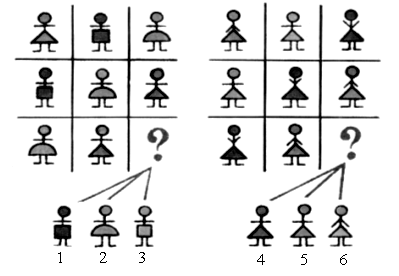
III. Сообщение темы урока.
– Сегодня на уроке мы узнаем, что называют «выражением».
IV. Изучение нового материала.
Учитель проводит подготовительную работу.
На доске записаны два числа: 6 и 3. Учитель ставит между ними знак «+».
– Получилась запись, которую называют выражением.
– Так как это выражение составлено с помощью знака «+», то его называют суммой. Сделайте на доске запись:
![]()
сумма
– Запишите два других числа: 12 и 4. Поставьте между ними знак «–». Получилось выражение, которое называют разностью:
![]()
разность
Следующие два выражения учитель составляет вместе с классом.
– Давайте составим из чисел 8 и 5 и знака умножения выражение, которое назовем произведением. Кто сможет записать произведение чисел 8 и 5 на доске? (Кто-либо из учеников делает запись. Учитель под этим выражением записывает слово произведение.)
![]()
произведение
– Как записать частное 12 и 3? (12 : 3.)
– Запишите под выражением 12 : 3 слово «частное».
![]()
частное
– Если в каждом из этих выражений выполнить действие, то получится число, которое называют значением выражения. (Выпишите снова все выражения одно под другим и выполните действия.)
6 + 3 = 9 8 · 5 = 40
12 – 4 = 8 12 : 3 = 4
– Назовите значение первого (второго, третьего, четвертого) выражения.
– Назовите выражение, значением которого является число 40. (8, 4, 9.)
– Число 9 мы называли суммой чисел 6 и 3, и его значение – число 9. Точно так же разностью называют выражение 12 – 4 и число 8, являющееся его значением; произведением называют выражение 8 · 5 и его значение – число 40; частным – выражение 12 : 34 и его значение – число 4.
Далее учащиеся рассматривают таблицу в учебнике (на с. 68).
– Прочитайте каждое выражение. Назовите их значение.
Справочный материал для учителя
Некоторые дети испытывают затруднения при чтении выражений, так как не всегда знают, как правильно называть числительные в родительном падеже. Поэтому советуем провести необходимую тренировочную работу, предлагая соответствующие задания. Например: «Прочитайте выражения: 35 + 40 (сумма тридцати пяти и сорока), 90 – 23 (разность девяноста и двадцати трех), 0 · 5 (произведение нуля и пятнадцати), 21 : 7 (частное двадцати одного и семи).
Задание № 1 (с. 69).
Используя карточку-помощницу, учащиеся читают числовые выражения:
• сумма чисел сорока шести и восемнадцати;
• произведение чисел девяти и четырех;
• разность чисел сорока восьми и шести и т. д.
Задание № 2 (с. 69).
Учащиеся читают разными способами выражения, используя карточку-помощницу.

V. Повторение пройденного материала.
1. Работа по учебнику.
Задание № 8 (с. 70).
Учащиеся выполняют записи:
7 + 8 = 15 9 · 9 = 81
17 – 9 = 8 48 : 6 = 8
Задание № 9 (с. 71).
– Прочитайте данные выражения.
– Сравните выражения в каждом столбике.
– Чем они похожи? Чем отличаются?
– Выполните действия.
Справочный материал для учителя
Во втором классе при записи сложных числовых выражений, содержащих два и более действий, скобки сохраняются даже в тех случаях, когда они «лишние», например: 18 – (2 · 4), (7 · 5) + (12 : 4), (50 – 30) – 10.
Лишь в третьем классе постепенно будут вводиться правила упрощения выражений; при этом дети научатся определять, в каких случаях скобки в выражении можно опустить, а в каких случаях – нельзя. После этого мы введем правила порядка выполнения действий в выражениях со скобками и без них, и с этого момента выражения будут записываться без «лишних» скобок.
Задание № 10 (с. 71).
– Прочитайте текст. Является ли он задачей? Почему?
– Что известно? Что требуется узнать?
– Запишите кратко условие задачи.
Запись:
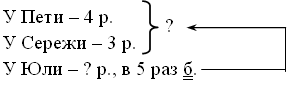
Решение:
1) Сколько денег у Пети и у Сережи вместе?
4 + 3 = 7 (р.).
2) Сколько денег у Юли?
7 · 5 = 35 (р.).
Ответ: 35 рублей.
2. Работа в печатной тетради № 2.
Задание № 130.
Учащиеся должны понимать, что числовые выражения состоят из чисел и связывающих их знаков арифметических действий, поэтому следующие записи не являются выражениями:
![]()
Задание № 132.
Учитель может предложить учащимся пользоваться калькулятором для нахождения значений составленных выражений.
Правильные варианты следующие:
суммы: 26 + 5, 12 + 19, 16 + 15, 3 + 28, 31 + 0.
разность: 38 – 7, 31 – 0.
VI. Итог урока.
– Что нового узнали на уроке?
– Назовите компоненты арифметических действий.
Домашнее задание: № 7 (учебник); № 124, 125 (рабочая тетрадь).
Урок 103
числовые выражения
Цели: учить читать разными способами числовые выражения; совершенствовать вычислительные навыки; повторить правила составления и чтения математических графов; развивать мышление и внимание.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Математический диктант.
Назовите число:
а) половина которого равна: 9, 8, 5;
б) треть которого равна: 9, 6, 7;
в) седьмая часть которого равна: 1, 5, 7;
г) девятая часть которого равна: 9, 8, 6, 2.
2. Из чисел, записанных в домике, наберите число 33. Запишите четыре равенства.
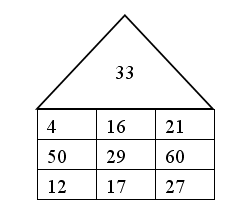
3. Задача.
В первом куске 28 м ситца, во втором – на 10 м больше, чем в первом, а в третьем – на 7 м меньше, чем во втором. Сколько метров ситца в третьем куске?
4. Составьте «круговые» примеры.
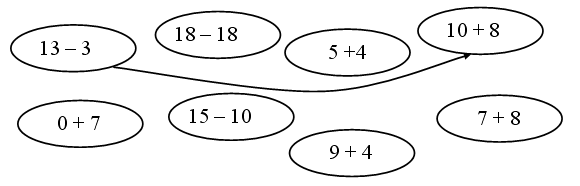
III. Сообщение темы урока.
IV. Работа по теме урока.
Задание № 3 (с. 69).
Учащиеся выполняют записи и находят значения выражений:
36 + 20 = 56 60 – 3 = 57
6 · 8 = 48 21 : 7 = 3
– Составьте свои суммы, значения которых равны 56, 48 и 57.
Учащиеся работают самостоятельно. Взаимопроверка в парах.
Задание № 4 (с. 69).
– Прочитайте данные выражения:
• разность чисел двадцати и двух;
• сумма чисел двадцати и двадцати;
• разность чисел двадцати восьми и восьми;
• произведение чисел четырех и пяти.
– Какие выражения имеют одно и то же значение?
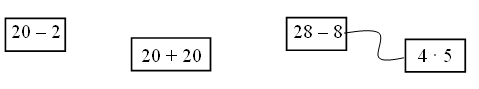
Учащиеся соединяют стрелками выражения.
– Для оставшихся выражений подберите другое выражение, которое имеет соответствующее значение.


V. Повторение пройденного материала.
1. Работа по учебнику.
Задание № 11 (с. 71).
Данное упражнение выполняется с опорой на граф. Учащиеся изображают граф с синими стрелками, то есть граф отношения «меньше». Сначала буквами обозначим число лещей, которые поймали отец, сын и дочь: О – отец, С – сын, Д – дочь.
Так как по условию задачи отец поймал меньше лещей, чем сын, то проведем синюю стрелку от О к С. В то же время отец поймал больше лещей, чем дочь (значит, дочь поймала меньше, чем отец), следовательно, нужно провести синюю стрелку от Д к О. Граф построен.
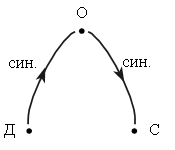
По графу видно, что меньше всего лещей поймала дочь.
Задача № 12 (с. 71).
Учащиеся составляют схемы-«машины» и находят неизвестное число.
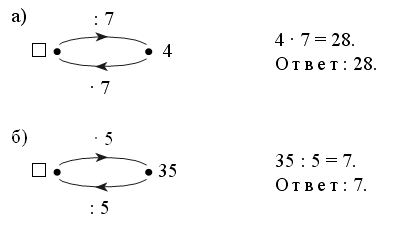
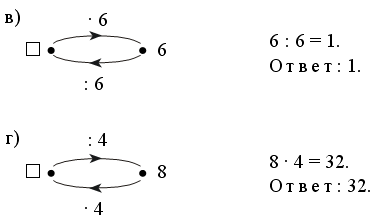
2. Работа в печатной тетради № 2.
Задание № 133.
Это задание является подготовительным к обучению решению уравнений типа: 6 · х = 54 и 35 : у = 7.
Учащиеся могут составить схемы-«машины».
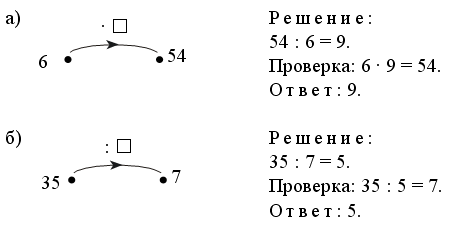
Задание № 134.
– Прочитайте задачу.
– Что известно? Что требуется узнать?
– Составьте краткую запись и схему-«машину» по данному условию.
Запись:
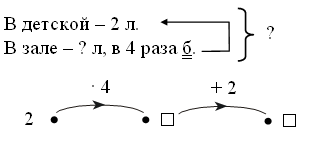
Решение:
1) Сколько лампочек в зале?
2 · 4 = 8 (л.).
2) Сколько лампочек всего?
8 + 2 = 10 (л.).
Ответ: 10 лампочек.
VI. Итог урока.
– Что нового узнали на уроке?
– Назовите правила составления и чтения математических граф.
Домашнее задание: № 13 (учебник); № 131 (рабочая тетрадь).
Урок 104
числовые выражения
Цели: совершенствовать вычислительные навыки; продолжить формирование умений решать составные задачи; рассмотреть различные виды направления движения двух тел; закреплять знания о взаимном расположении геометрических тел; развивать внимание и умение рассуждать.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Математический диктант.
– Две трети числа равны 12. Чему равна одна треть этого числа?
– Две пятых числа равны 16. Чему равна одна пятая этого числа?
– Три четверти числа равны 9. Чему равна одна четверть этого числа?
– Три седьмых числа равны 21. Чему равна одна седьмая часть числа?
– Четыре пятых числа равны 20. Чему равна одна пятая этого числа?
2. Геометрия на спичках.
а) Сколько на чертеже квадратов? Сколько всего многоугольников? Какие это многоугольники?

б) Уберите одну палочку так, чтобы осталось 3 квадрата. Найдите несколько решений и сравните их.
в) Уберите две палочки так, чтобы осталось 3 квадрата. Найдите несколько решений и сравните их.
г) Уберите две палочки так, чтобы остался 1 квадрат.
3. Задача.
У Саши было 26 картинок. Вчера он наклеил в альбом несколько картинок, а сегодня – ещё 6. После этого у него осталось 12 картинок. Сколько картинок Саша наклеил в альбом вчера?
III. Сообщение темы урока.
IV. Работа по теме урока.
Задание № 5 (с. 69–70).
Учащиеся читают задачи. Отмечают, что известно, что требуется узнать. Затем решают каждую задачу, составляя числовое выражение.
Запись:


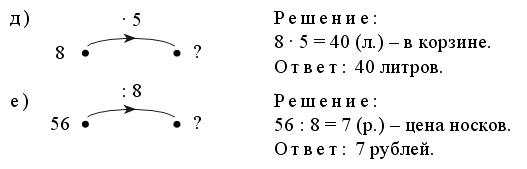
Учитель должен акцентировать внимание учащихся на то, что различных числовых выражений, имеющих значение 8 (0, 1 и 20), существует сколько угодно.
Учащиеся придумывают по заданному значению числового выражения (8, 0, 1, 20) само выражение.
Например:
|
8 2 · 4 = 8 16 – 8 = 8 24 : 3 = 8 20 – 12 = 8 4
+ 4 = 8 |
0 0 · 5 = 0 20 – 20 = 0 0 + 0 = 0 0
: 100 = 0 |
1 1 · 1 = 1 1 + 0 = 1 1 – 0 = 1 1
: 1 = 1 |
20 40 – 20 = 20 10 + 10 = 20 5 · 4 = 20 60
– 40 = 20 |

V. Повторение пройденного материала.
1. Работа по учебнику.
Задание № 15 (с. 71).
Выполняя это задание, учащиеся должны разобраться в терминологии, связанной с направлением движения двух объектов. В дальнейшем это пригодится при решении задач на движение.
Целесообразно решить задачу наглядно, используя модели машинок.
Учитель просит одного из учеников расположить на магнитной доске (фланелеграфе) модели машинок так, чтобы они двигались навстречу друг другу.
Затем спрашивает: «Верно ли, что машины едут в противоположных направлениях?» Одни будут говорить, что верно, а другие – что неверно. Двигая модели машин навстречу друг другу, продемонстрируйте детям, что машины двигаются в противоположных направлениях.

Делаем вывод: когда машины едут навстречу друг другу, они двигаются в противоположных направлениях. Далее попросите расположить модели машин так, чтобы они двигались в одном направлении (одну из машин надо развернуть).

И, наконец, попросите учащихся расположить модели так, чтобы машины двигались в разных направлениях. Например, так:

Можно предложить дополнительные задания. В каких направлениях двигаются машины?
(В противоположных (В одном направлении.)
направлениях.)
в)
(В разных направлениях.)
Задание № 16 (с. 72).
– Рассмотрите иллюстрацию и прочитайте задачу.
– Что известно в задаче? Что требуется узнать?
Повторить условие задачи и наметить план ее решения лучше всего с опорой на иллюстрацию в учебнике. Рассуждать учащиеся должны примерно так:
«Известно, что Петя нашел в 2 раза больше грибов, чем Юра. Значит, Юра нашел в 2 раза меньше грибов, чем Петя. Так как Петя нашел 20 грибов, а Юра в 2 раза меньше, то Юра нашел: 20 : 2 = 10, то есть 10 грибов».
Задание № 17 (с. 72).
Учащиеся составляют схемы-«машины» и решают.
Запись:
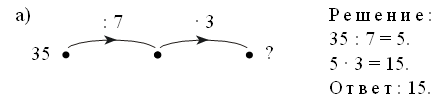


Задача № 18 (с. 72).
– Прочитайте задачу.
– Что известно? Что требуется узнать?
– Составьте схему-«машину» или краткую запись и решите задачу.
Запись:
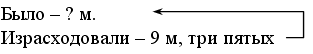
Решение:
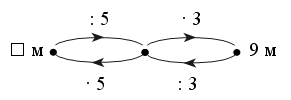
1) Сколько метров составляют пятую часть?
9 : 3 = 3 (м).
2) Сколько метров ткани было?
3 · 5 = 15 (м).
Ответ: 15 м.
2. Работа в печатной тетради № 2.
Задание № 136.
Скорее всего, учащиеся выполнят следующий чертеж:
 (Две
точки пересечения.)
(Две
точки пересечения.)
Дополнительно учитель предлагает учащимся выяснить, сколько точек пересечения имеют окружность и луч на каждом чертеже:
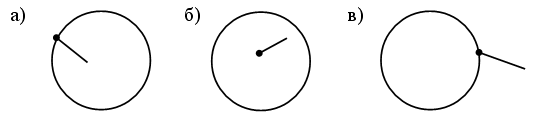
(Две точки (одна точка (одна точка
пересечения.) пересечения.) пересечения.)
VI. Итог урока.
– Что нового узнали на уроке?
– Назовите признаки окружности.
– Назовите признаки луча.
Домашнее задание: № 14 (учебник); № 135 (рабочая тетрадь).
Урок 105
СОСТАВЛЕНИЕ числовыХ выражениЙ
Цели: учить составлять числовые выражения из чисел и знаков действий; совершенствовать умения решать составные задачи; продолжить формирование вычислительных навыков; развивать умение анализировать и делать выводы.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Математический диктант.
а) Назовите число, девятая часть которого равна: 2, 4, 6, 9.
б) Сумма двух чисел равна 20. Назовите несколько пар таких чисел.
в) Произведение двух чисел равно 12. Какие это числа?
2. Геометрия на спичках.
а) Уберите две палочки так, чтобы осталось 2 квадрата. Найдите несколько решений и сравните их.

б) Уберите три палочки так, чтобы остался 1 квадрат.
в) Уберите четыре палочки так, чтобы осталось 2 квадрата.
г) Уберите четыре палочки так, чтобы остался 1 квадрат.
3. Задача.
У Ксюши было 56 рублей. После того как она купила ручку и альбом, у нее осталось 30 р. Сколько стоил альбом, если ручка стоила 7 р.?
4. Поставьте знаки «+» или «–».

III. Сообщение темы урока.
– Сегодня на уроке мы будем составлять числовые выражения, содержащие одну или несколько пар скобок.
IV. Изучение нового материала.
Задание № 1 (с. 73).
– Рассмотрите в учебнике, как составлено выражение :
![]()
Учитель приглашает к доске двоих учеников: один будет исполнять роль Зайца, а другой – Волка. Каждому из них учитель дает заранее подготовленные карточки с такими же записями.
– Сейчас я прочитаю сложное выражение, а вы должны объяснить, как оно составлено. В этом вам помогут Волк и Заяц.
Выражение 9 – (3 + 4) можно прочитать так: «Из числа "девять" вычесть сумму трех и четырех».
– Из чего составлено это выражение? Заяц, покажи карточку с числом. Это первая часть выражения.
– Волк, покажи свою карточку. Что на ней написано? («Три плюс четыре» или «Сумма трех и четырех».)
– Это вторая часть выражения. Каким знаком соединены эти две части? Заяц, покажи карточку со знаком и назови его. (Минус.)
– Я запишу это выражение на доске и выделю в нем две части, вот так:
9 – (3 + 4).
– Как вы думаете, какое действие надо выполнить первым: вычитание или сложение? А почему? (Потому что, прежде чем из 9 вычитать сумму, надо ее вычислить, то есть сложить 3 и 4.) На это указывают скобки.
– Рассмотрим в учебнике следующий рисунок: Волк пригласил Зайку к доске и велел ему выполнить действия, указанные в выражении, то есть найти значение этого выражения. Как Заяц справился с заданием? Прочитайте, что он написал на доске.
А теперь мы будем учиться читать сложные выражения. Назовите в выражении 9 – (3 + 4) первую часть (9), вторую часть (3 + 4). Что представляет собой сложное выражение: сумму или разность? Как это определить? Обычно выражение называют по последнему действию; здесь последним действием выполняется вычитание. Поэтому само выражение называется разностью. Послушайте, как я прочитаю это выражение: «Разность девяти и суммы трех и четырех». А теперь прочитаем текст в рамке (на с. 73).
Сложное выражение может называться суммой, разностью, произведением или частным. Это зависит от того, какое из этих действий выполняется при нахождении значения выражения последним.
Давайте потренируемся составлять сложные выражения и читать их. Оля, подойди к доске. Сейчас мы с Олей составим выражение. Как только я буду произносить слова «сумма», «разность», «произведение» или «частное», Оля будет открывать скобки.
Итак, слушаем. Надо составить выражение из разности... Оля, что ты делаешь? (Открываю скобки.) ...тридцати пяти и двадцати шести... Оля, что ты запишешь? (35 – 26.) Закрывай скобки. Продолжаем: знака «плюс» и частного... (открываем скобки) ...сорока пяти и девяти. Закрываем скобки. Получилась запись: (35 – 26) + (45 : 9). Прочитаем ее. (К разности 35 и 26 прибавить частное 45 и 9.) Прочитаем это выражение по-другому. Сколько частей в этом выражении? (Две: 35 – 26 и 45 : 5.) Какое действие выполняется последним? (Сложение.) Как же называется выражение? (Суммой.) Как его можно прочитать? Я начну, а вы продолжайте: «Сумма...». (Сумма разности тридцати пяти и двадцати шести и частного сорока пяти и девяти.)
Справочный материал для учителя
Автор программы рекомендует использовать скобки уже с 1 класса при записи выражений вида 5 + (2 + 4), (12 – 6) + 5. Хотя обычно в таких записях скобки не пишут, но они четко указывают учащимся порядок действий, и вплоть до изучения в 3 классе специальных правил упрощения выражений «лишние» скобки будут сохраняться.
Если сложное выражение содержит в своем составе одно или несколько простых выражений, соединенных знаками арифметических действий, то рекомендуем научить учащихся при его записи заключать простые выражения в скобки.
Задание № 2 (с. 74).
Цель данного задания – научить составлять числовые выражения в 2–3 действия из частей (чисел, знаков арифметических действий, скобок).
Учащиеся должны понимать, что если при составлении выражения они столкнутся со словами «сумма», «разность», «произведение» и «частное», то нужно использовать скобки.
Когда выражение будет составлено, учитель дополнительно может спросить:
– В каком порядке надо выполнять действия?
– Какое действие последнее?
– Как называется это выражение?
– Чему равно значение выражения?
Запись:
(6 · 4) : 6 = 4.
(56 : 8) – (14 – 9) = 2.
(3 + 6) · (4 + 5) = 81.
(40 – 5) + (24 : 6) = 39.

V. Повторение пройденного материала.
1. Работа по учебнику.
Задание № 7 (с. 74).
Учащиеся читают задание и выполняют схемы-«машины».
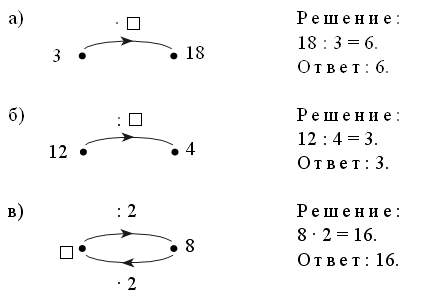
Задание № 10 (с. 75).
– Прочитайте задачу.
– Что известно? Что требуется узнать?
– Запишите кратко условие этой задачи.
Запись:
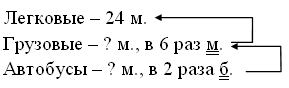
Решение:
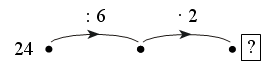
1) Сколько было грузовых машин?
24 : 6 = 4 (м.).
2) Сколько было автобусов?
4 · 2 = 8 (м.).
Ответ: 8 машин.
2. Работа в печатной тетради № 2.
Задание № 140.
Учащиеся впервые сталкиваются с ситуацией, когда по решению надо восстановить текст задачи.
Скорее всего, сопоставляя запись решения с текстом, дети предложат следующую формулировку задачи: «Школьники посадили 4 ряда яблонь по 8 яблонь в каждом ряду и 3 ряда слив по 9 слив в каждом ряду. Сколько всего деревьев посадили школьники?»
Обязательно обратите внимание второклассников на то, что сформулировать задачу можно по-другому, например:
1. Школьники посадили 3 ряда яблонь по 9 яблонь в каждом ряду и 4 ряда слив по 8 слив в каждом ряду. Сколько всего деревьев посадили школьники?
2. Школьники посадили 8 рядов яблонь по 4 яблони в каждом ряду и 9 рядов слив по 3 сливы в каждом ряду. Сколько всего деревьев посадили школьники?
VI. Итог урока.
– Что нового узнали на уроке?
– Как найти неизвестный множитель?
– Как найти неизвестный делитель?
Домашнее задание: № 8 (учебник); № 137 (рабочая тетрадь).
Урок 106
СОСТАВЛЕНИЕ числовыХ выражениЙ
Цели: учить составлять числовые выражения из чисел и знаков действий; совершенствовать вычислительные навыки значений числовых выражений; продолжить формирование умений вычислять площадь прямоугольника; развивать внимание и мышление.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Математический диктант.
– Назовите два числа:
а) разность которых равна 30;
б) частное которых равно 8.
– Первое слагаемое 6, а второе – на 2 больше. Назовите сумму.
– Первое число 12, а второе – на 7 меньше. Назовите сумму этих чисел.
2. Геометрия на спичках.
а) Переложите три палочки так, чтобы стало 3 квадрата.

б) Переложите четыре палочки так, чтобы стало 3 квадрата.
в) Переложите две палочки так, чтобы стало 7 квадратов.
г) Переложите четыре палочки так, чтобы стало 10 квадратов.
3. Задача.
У Саши было 26 картинок. После того как он наклеил несколько картинок в альбом, у него осталось 12 картинок. Сколько картинок Саша наклеил в альбом?
4. Вычислите наиболее лёгким способом.
6 + 7 + 4 + 3 = 4 + 20 + 6 + 50 =
8 + 9 + 2 + 1 = 60 + 6 + 20 + 4 =
4 + 2 + 10 + 8 = 40 + 8 + 30 + 2 =
III. Сообщение темы урока.
IV. Работа по теме урока.
Задание № 3 (с. 74).
– Прочитайте первое выражение.
– Из каких частей состоит это выражение?
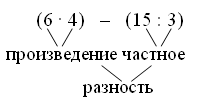
– Из каких частей состоит второе выражение?
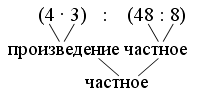
Задание № 4 (с. 74).
– Рассмотрите данные выражения. Чем они похожи? Чем отличаются?
– Какое действие выполняется в каждом выражении последним?
– Как называется каждое выражение?
Если возникнут трудности, учитель на доске может заполнить таблицу.
|
Выражение |
Последнее действие |
Название |
|
(7 · 5) + (21 : 7) |
сложение |
сумма |
|
65 – (5 · 8) |
вычитание |
разность |
|
(64 : 8) · 4 |
умножение |
произведение |
V. Повторение пройденного материала.
1. Работа по учебнику.
Задание № 11 (с. 75).
– Прочитайте задачу.
– Что известно? Что требуется узнать?
– Сколько лет сестре? (8 : 2 = 4 (г.).)
– Замените в тексте слово «старше» словом «моложе».
– Решите новую задачу.
Слабоуспевающим учащимся в помощь можно предложить следующую карточку:
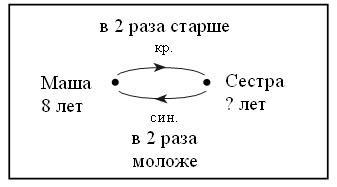
Решение:
8 · 2 = 16 (лет) – сестре.
Ответ: 16 лет.
Задание № 12 (с. 75).
Данное упражнение является подготовительным для введения правила нахождения площади прямоугольника (квадрата).
После построения квадрата попросите учащихся, используя сетку тетради, разбить точками все его стороны на отрезки длиной по 1 см, а затем через отмеченные на сторонах точки мысленно провести горизонтальные и вертикальные линии. В результате фигура разбивается на квадраты площадью 1 см2. Получилось 5 рядов по 5 квадратов в каждом, следовательно, площадь квадрата:
5 · 5 = 25, то есть 25 см2.
В заключение дети, используя палетку, выполняют проверку.
2. Работа в печатной тетради № 2.
Задание № 141.
– Прочитайте текст. Является ли он задачей?
– Рассмотрите выражения и запишите, что они обозначают.
Запись:
(6 · 3) + (3 · 2) – сколько всего детей;
(6 · 3) – (3 · 2) – на сколько девочек меньше, чем мальчиков; (на сколько мальчиков больше, чем девочек);
(6 · 3) : (3 · 2) – во сколько раз мальчиков больше, чем девочек (во сколько раз девочек меньше, чем мальчиков).
Далее учащиеся выполняют вычисления.
Задание № 142.
Учащиеся выполняют схемы-«машины».
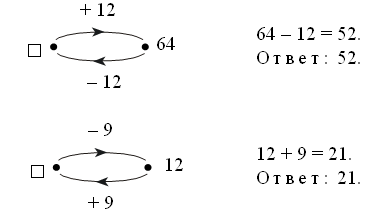
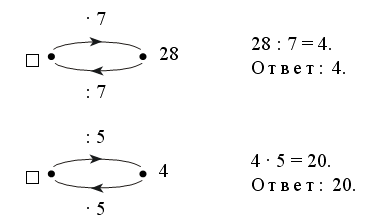
Задание № 143.
Задание рекомендуется выполнять сразу же после упражнения № 142 в рабочей тетради № 2.
Прежде чем учащиеся попытаются сформулировать, например, правило нахождения неизвестного первого слагаемого, вернитесь к примеру + 12 = 64 и организуйте работу так: «Какое неизвестное число действия сложения мы искали? (Первое слагаемое.) Как мы его нашли? (Из 64 вычли 12.) Что такое 64? (Сумма.) Что такое 12? (Второе слагаемое.)».
Делаем вывод: чтобы найти неизвестное первое слагаемое, надо из суммы вычесть второе слагаемое.
Аналогично следует рассуждать и в остальных случаях.
VI. Итог урока.
– Что нового узнали на уроке?
– Назовите единицы измерения площади.
Домашнее задание: № 9 (учебник), № 138 (рабочая тетрадь).
Урок 107
СОСТАВЛЕНИЕ числовыХ выражениЙ
Цели: совершенствовать навыки составления выражений и вычисления их значений; продолжить формирование умений решать составные задачи; развивать внимание и умение рассуждать.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Математический диктант.
а) Число уменьшили на 8 и получили 20. Назовите это число.
б) Число увеличили на 6 и получили 15. Назовите это число.
в) Если число увеличилось в 5 раз, получится 30. Какое это число?
г) Если число уменьшить в 4 раза, получится 8. Какое это число?
2. Геометрия на спичках.
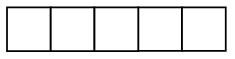
а) Сколько на чертеже квадратов? Сколько других многоугольников? Какие это многоугольники?
б) Уберите одну палочку так, чтобы осталось 3 квадрата. Найдите несколько решений и сравните их.
в) Уберите одну палочку так, чтобы осталось 4 квадрата. Найдите несколько решений и сравните их.
г) Уберите две палочки так, чтобы осталось 4 квадрата.
3. Сравните время, которое показывают часы. По тому же правилу нарисуйте стрелки на последних часах.

III. Сообщение темы урока.
IV. Работа по теме урока.
Задание № 5 (с. 74).
Учащиеся читают задание.
– Из скольких частей состоит выражение?
– Какое действие будет выполняться последним?
– Запишите выражение и вычислите его значение.
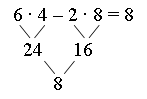
Задание № 6 (с. 74).
– Прочитайте текст. Является ли он задачей?
– Что известно? Что требуется узнать?
– Запишите кратко условие задачи.
Запись:
Было – 25 л. и 14 л.
Израсходовал – 7 л.
Осталось – ? л.
Решение:
1) Сколько листов было?
25 + 14 = 39 (л.).
2) Сколько листов осталось?
39 – 7 = 32 (л.).
Ответ: 32 листа.

V. Повторение пройденного материала.
1. Работа по учебнику.
Задание № 13 (с. 75).
– Рассмотрите чертеж.
– Как называются данные фигуры?
– Чему равна площадь закрашенной части фигуры?
– Сколько клеток в желтой фигуре? (28 клеток.)
– Сколько клеток в синей фигуре? (24 клетки.)
– Сколько клеток образуют 1 см2? (4 клетки.)
– Как вычислить площадь в данном случае?
Запись:
28 : 4 = 7 (см2).
24 : 4 = 6 (см2).
Задание № 14 (с. 75).
Учащиеся составляют схемы-«машины» и отвечают на вопросы задания.
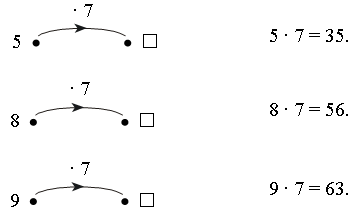
Задание № 15 (с. 75).
Учащиеся работают самостоятельно. Взаимопроверка в парах.
Запись:
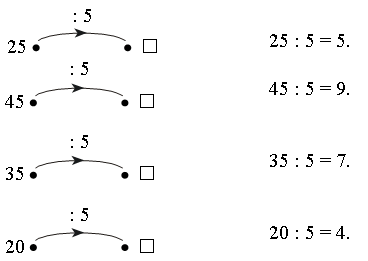
2. Работа по карточкам.
Задание № 1.
Запишите выражения и вычислите их значения.
а) Из числа 90 вычесть сумму чисел 42 и 8.
б) Разность чисел 58 и 50 увеличить на 7.
в) Из числа 39 вычесть разность чисел 17 и 8.
г) Сумму чисел 13 и 7 уменьшить на 9.
д) Из числа 38 вычесть разность чисел 17 и 9.
е) Сумму чисел 7 и 6 уменьшить на 10.
ж) К числу 8 прибавить разность чисел 75 и 70.
з) Разность чисел 13 и 4 увеличить на 20.
Задание № 2.
В вазе было столько же яблок, сколько на тарелке. В вазу положили ещё 5 яблок, и в ней стало 14 яблок. Сколько всего яблок стало на тарелке и в вазе вместе? Найдите выражение для решения задачи и вычислите его значение.

VI. Итог урока.
– Что нового узнали на уроке?
– Назовите компоненты всех арифметических действий.
Домашнее задание: № 139 (рабочая тетрадь).
Урок 108
угол. прямой угол
Цели: познакомить учащихся с понятием «угол»; научить выполнять модель прямого угла; учить определять на чертеже прямой и непрямой угол; совершенствовать вычислительные навыки; развивать внимание и глазомер.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Математический диктант.
– Первое число 6, а второе – в 2 раза меньше.
Назовите:
а) произведение этих чисел;
б) частное этих чисел.
– Одно число 4, а второе – в 2 раза больше.
Назовите:
а) произведение этих чисел;
б) частное этих чисел.
2. Таблица.

а) Не заполняя полностью таблицу числами от 1 до 100, запишите числа, закрытые фигурами.
б) Запишите в таблицу числа: 49, 58, 37, 60, 71, 85.
III. Сообщение темы урока.
– Рассмотрите чертеж на доске:
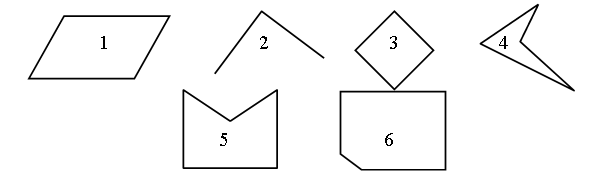
– Какая из данных фигур «лишняя»? (Фигура 2.)
– Как называется эта фигура?
– Сегодня на уроке мы будем строить углы.
IV. Изучение нового материала.
Справочный материал для учителя
С углами учащиеся знакомятся в ходе выполнения практических упражнений. С помощью модели прямого угла, которую легко сделать из куска бумаги, сложив его вчетверо, они учатся находить прямые углы на окружающих предметах, определять, имеет ли прямые углы данный на чертеже многоугольник.
В математике понятие угла часто определяют так: углом называют два луча, имеющих общее начало. В младших классах мы будем пользоваться понятием так называемого плоского угла: плоский угол – это два луча с общим началом и внутренней областью, ограниченной этими лучами.
Представление об угле как о части плоскости позволяет вести работу с опорой на модель, например веер. С его помощью можно проиллюстрировать угол любого вида. При этом, конечно, детям следует сказать о том, что угол как геометрическая фигура имеет стороны, которые являются не отрезками, как у веера, а лучами. Луч – это бесконечная фигура. Поэтому угол – тоже бесконечная фигура; его стороны простираются как угодно далеко.
* * *
– Проведите из точки два луча. Вот так:

– У вас получились фигуры, которые называют углами. Лучи – это стороны угла, точка, из которой проведены лучи, – вершина угла.
Задание № 1 (с. 76).
– Рассмотрите рисунок. На какую фигуру похож раскрытый веер? (на угол.)
– Возьмите веер и с его помощью образуйте такие же по виду углу, как те, которые изображены в учебнике.
– Покажите, используя веер, вершину и стороны каждого угла.
– Покажите вершину угла, стороны угла.
– Вершина – это точка, а стороны – лучи.
С помощью веера учитель показывает острый, тупой и прямой углы. Эти углы изображены на рисунке в учебнике.
– Чтобы построить угол, надо отметить какую-нибудь точку, обозначить ее буквой латинского алфавита и из этой точки провести два луча. Вершина первого угла обозначена буквой А, вершина второго – буквой В.
– Сложите большой лист бумаги. Вот так:
– У вас получился прямой угол. Теперь возьмите маленький лист бумаги и сложите его так же.
– У вас опять получился прямой угол.
– Догадайтесь! Какое высказывание будет верным?
1) Синий угол больше красного.
2) Красный угол больше синего.
3) Синий и красный углы одинаковы.
– Все прямые углы можно наложить так, чтобы их стороны совпали. А стороны угла – лучи.
Учащиеся проверяют наложением.
– Сделайте модель прямого угла с помощью веера.
– Покажите прямые углы на крышке стола и других предметов.
Задание № 2 (с. 76).
– Рассмотрите рисунки. На каком рисунке дороги пересекаются под прямым углом? (Первый рисунок.)

V. Повторение пройденного материала.
1. Работа по учебнику.
Задание № 6 (с. 78).
– Назовите части первого выражения.
– Какое действие выполняется последним? (Деление.)
– Как называется это выражение? (Частное.)
Аналогично анализируется второе выражение.
– Найдите значения выражений.
Запись:

2. Работа в печатной тетради № 2.
Задания № 145, 146.
Сначала учащиеся на глаз определяют прямые углы в многоугольниках и только потом проверяют себя с помощью чертежного угольника.
Учитель должен обратить внимание учащихся на то, что в задании № 145 углы надо выделять дугой (синей – прямые, а красной – непрямые углы).
А в задании № 146 надо выделять синим цветом только вершины прямых углов (то есть соответствующие вершины многоугольников).
3. работа по карточкам.
Задание № 1.
Постройте угол с вершиной в точке А так, чтобы одна его сторона проходила через точку В, а другая – через точку С. Закрасьте углы разным цветом.
Задание № 2.
Постройте острый угол, стороны которого проходят через точки А и В. Закрасьте углы синим цветом.
Задание № 3.
Постройте тупой угол, стороны которого проходят через точки А и В. Закрасьте углы синим цветом.
Задание № 4.
С помощью угольника постройте прямой угол так, чтобы его вершиной была точка А, а одна из сторон проходила через точку В. Закрасьте угол синим цветом.
Задание № 5.
С помощью угольника постройте прямой угол с вершиной в точке А так, чтобы точка С находилась внутри прямого угла.
VI. Итог урока.
– Что нового узнали на уроке?
– Что такое «угол»?
– Как изготовить модель прямого угла?
Домашнее задание: № 7 (учебник); № 144 (рабочая тетрадь).
Урок 109
угол. прямой угол
Цели: познакомить учащихся с понятием «угол»; ввести термины «прямой угол», «непрямой угол»; учить строить прямой угол с помощью модели и чертежного угольника; совершенствовать умения решать задачи; развивать внимание и мышление.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Математический диктант.
– Назовите два таких числа, из которых одно число:
а) на 30 больше другого;
б) на 10 меньше другого;
в) в 8 раз больше другого;
г) в 5 раз меньше другого.
2. Геометрия на спичках.

а) Уберите две палочки так, чтобы осталось 3 квадрата.
б) Уберите две палочки так, чтобы осталось 2 квадрата.
в) Уберите две палочки так, чтобы остался 1 квадрат.
г) Уберите три палочки так, чтобы осталось 4 квадрата.
д) Уберите три палочки так, чтобы осталось 3 квадрата.
3. Не вычисляя значений выражений, найдите и подчеркните верные равенства. Объясните, почему они верны.
3 + 4 + 7 = 3 + 7 + 4
4 + 5 + 6 = 4 + 6 + 5
8 + 40 + 2 = 8 + 2 + 40
20 + 6 + 40 = 20 + 40 + 6
4. Задача.
В зоомагазине в маленькой клетке было 8 попугаев, а в большой – на 7 попугаев больше. Сколько всего попугаев было в этих клетках?
III. Сообщение темы урока.
– Рассмотрите чертеж на доске.
– Сравните фигуры слева и справа. Чем они похожи? Чем отличаются?

– Сегодня продолжим знакомство с геометрической фигурой – углом.
IV. Работа по теме урока.
– Зеленый угол – острый. Если его наложить на прямой угол так, чтобы одна его сторона совпала со стороной прямого угла, то другая его сторона пройдет внутри прямого.
Синий угол – тупой. Если его наложить на прямой угол так, чтобы одна его сторона совпала со стороной прямого угла, то другая его сторона пройдет вне прямого угла. Рассмотрим рисунок. Каким цветом закрашен прямой угол?
– Рассмотрите фигуры, представленные на доске.
– Сколько углов у каждой фигуры? Какие из углов острые, тупые? Проверьте это с помощью угольника.
Задание № 3 (с. 77).
– Определите на глаз, сколько прямых углов на чертеже.
– Проверьте свой ответ, используя чертежный угольник. (3 прямых угла.)
– Назовите вершины прямых углов. (В, Д, К.)
Задание № 4 (с. 77).
– Какое общее название можно дать всем фигурам? (Угол.)
– Определите на глаз, сколько прямых углов.
– Проверьте свой ответ, используя угольник. (Угол под номером 2 является прямым.)

V. Повторение пройденного материала.
1. Работа по учебнику.
Задание № 8 (с. 78).
– Прочитайте задачу.
– Что известно? Что требуется узнать?
– Составьте схему-«машину» и решите задачу.
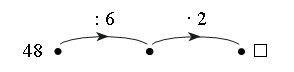
Решение:
1) Сколько яблок в шестой части?
48 : 6 = 8 (кг).
2) Сколько сушеных яблок получится?
8 · 2 = 16 (кг).
Ответ: 16 кг.
Задание № 9 (с. 78).
В каждом задании этого упражнения есть несколько вариантов ответа, поэтому напомните учащимся, что прежде всего надо придумать такое правило перебора вариантов, при котором они не пропустят ни один из возможных ответов.
Во всех случаях удобно перебирать по порядку цифры в разряде единиц и, исходя из условия, находить соответствующую цифру в разряде десятков.
Получим следующие числа:
1) 30, 41, 52, 63, 74, 85, 96;
2) 21, 42, 63, 84;
3) 60, 51, 42, 33, 24, 15.
2. Работа в печатной тетради № 2.
Задание № 147.
Направление задается лучом, поэтому правильно выполнить задание смогут только те учащиеся, которые выделят синим цветом именно луч, а не просто линию, соответствующую средней дорожке.
3. Практическая работа по карточкам.
Задание № 1.
Постройте острый угол с вершиной в точке В так, чтобы точка А была внутри угла.

Задание № 2.
Постройте тупой угол так, чтобы его вершиной была точка А, а одна сторона угла проходила через точку В.
Задание № 3.
С помощью угольника постройте два прямых угла со стороной ОА. Закрасьте их разным цветом.
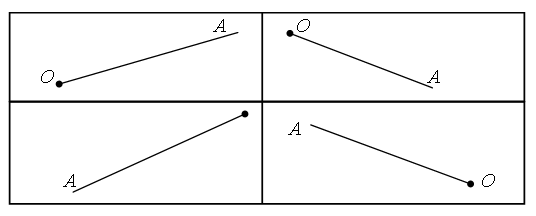
VI. Итог урока.
– Что нового узнали на уроке?
– Как выполнить модель прямого угла?
Домашнее задание: № 11 (учебник); № 148 (рабочая тетрадь).
Урок 110
угол. прямой угол
Цели: продолжить формирование умений строить прямой угол и практическим способом определять прямой угол; совершенствовать вычислительные навыки и умения решать составные задачи; развивать практические умения работы с чертежными инструментами и глазомер.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Математический диктант.
– Назовите сумму, разность, произведение и частное чисел:
а) 9 и 3, б) 8 и 1, в) 0 и 25.
2. Геометрия на спичках.

а) Уберите три палочки так, чтобы осталось 2 квадрата.
б) Уберите три палочки так, чтобы остался 1 квадрат.
в) Уберите три палочки так, чтобы квадратов не осталось.
г) Уберите четыре палочки так, чтобы осталось 3 квадрата.
д) Уберите четыре палочки так, чтобы остался 1 квадрат.
е) Уберите четыре палочки так, чтобы квадратов не осталось.
3. Задача.
В бочке было 20 вёдер воды. Когда из неё взяли для полива огорода несколько вёдер, в бочке осталось 2 ведра воды. Сколько вёдер воды взяли из бочки?
4. Соедините стрелками выражения, которые имеют одинаковое значение.
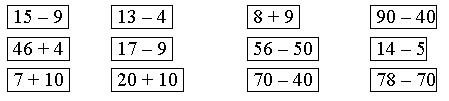
III. Сообщение темы урока.
– Рассмотрите фигуры, представленные на доске.
– Что их объединяет?
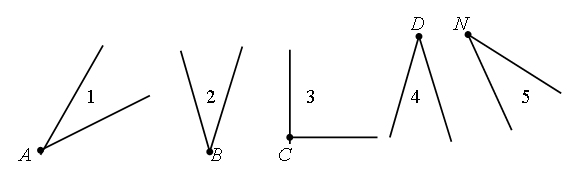
– Какой угол является «лишним»? (Угол 3; так как это прямой угол.)
– Сегодня будем чертить прямые углы и находить прямые углы в окружающих нас предметах.
IV. Работа по теме урока.
1. Работа по учебнику.
Задание № 5 (с. 78).
Чертеж:
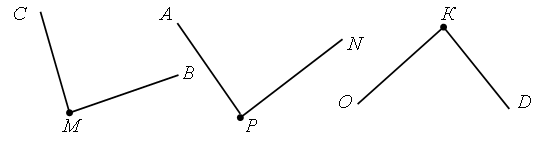
– Назовите вершины построенных углов.
2. Работа по карточкам.
Карточка № 1
С помощью угольника постройте прямой угол так, чтобы одна его сторона проходила через точки А и В.
Закрасьте прямые углы красным цветом.
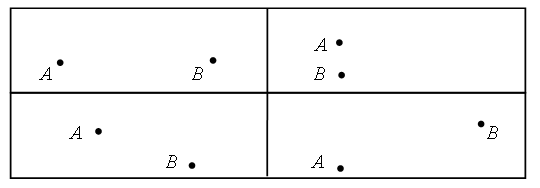
Карточка № 2
С помощью угольника постройте прямой угол так, чтобы одна его сторона проходила через точку А, а другая – через точку В.
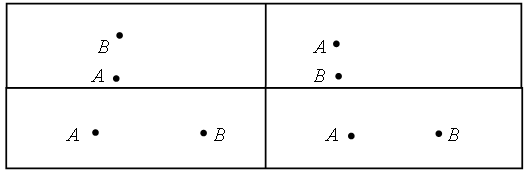
Карточка № 3
С помощью угольника постройте два прямых угла с вершиной в точке А так, чтобы одна сторона каждого угла совпадала:
а) со стороной АС:
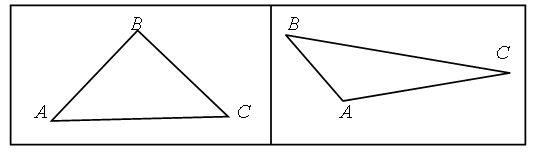
б) со стороной АВ:
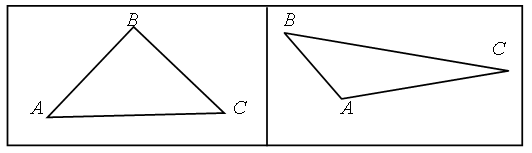

V. Повторение пройденного материала.
1. Работа по учебнику.
Задание № 10 (с. 79).
Учащиеся устно сравнивают арифметические действия и числа в выражениях, их значения.
Вот как примерно должны рассуждать дети:
– Оба выражения 37 + 24 и 37 + 42 являются суммами. Первые слагаемые равны, но в первом выражении второе слагаемое меньше, чем во втором. Следовательно, 37 + 24 меньше 37 + 42.
– 71 + 28 больше 71 – 28, так как сумма двух чисел всегда больше разности этих же чисел.
– (60 + 18) – 2 больше (60 + 15) – 2, так как оба выражения – разности, в которых вычитаемое число – 2, значит, надо сравнить уменьшаемые. Уменьшаемые состоят из суммы двух чисел, где первое слагаемое одинаковое. Теперь сравниваем второе слагаемое: 18 > 15. Следовательно, уменьшаемое в первом выражении больше, чем уменьшаемое во втором. Делаем вывод: первое выражение больше.
Задание № 12 (с. 79).
Учащиеся перед вычислениями вспоминают таблицу соотношений единиц длины:
1 м = 10 дм = 100 см.
Запись:
52 м 48 см + 6 м 20 см = 58 м 68 см.
3 м 8 дм + 15 м 2 дм = 18 м 10 дм = 19 м.
1 м – 6 дм = 10 дм – 6 дм = 4 дм.
1 м – 2 дм 7 см = 10 дм – 2 дм 7 см = 9 дм 10 см – 2 см 7 см = 7 дм 3 см.
2. Работа в печатной тетради № 2.
Задание № 150.
– Прочитайте задачу.
– Что известно? Что требуется узнать?
– Составьте схему-«машину» и решите задачу.
Запись:

Решение:
1) Сколько м2 займут остальные цветы?
18 – 9 = 9 (м2).
2) Сколько м2 займут маки?
9 : 3 = 3 (м2).
Ответ: 3 м2.
– Какую площадь цветника планируется занять гвоздиками?
– Какую – пионами?
– Сравните площади цветника, которые отводятся под розы и под все остальные цветы вместе.
– Какую часть цветника займут розы? (18 : 9 = 2 (ч.).)
– Во сколько раз площадь цветника, отводимая под розы, больше площади, отводимой под пионы?
VI. Итог урока.
– Что нового узнали на уроке?
– Как можно определить прямой угол?
– Назовите единицы площади.
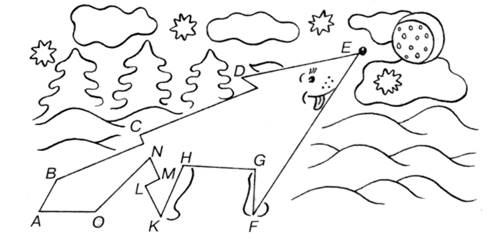
– Отметьте на рисунке прямые углы.
Домашнее задание: № 12 (II столбик, учебник); № 149 (рабочая тетрадь).
Урок 111
ПРЯМОУГОЛЬНИК. КВАДРАТ
Цели: ввести определения «прямоугольник», «квадрат»; учить находить прямоугольники и квадраты среди четырехугольников; совершенствовать вычислительные навыки; развивать внимание и глазомер.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Математический диктант.
– Увеличьте:
а) 20 на 5; в) 6 в 7 раз;
б) 42 на 3; г) 9 в 4 раза.
– Уменьшите:
а) 16 на 9; в) 20 в 4 раза;
б) 56 на 16; г) 40 в 5 раз.
2. Задача.
После того как Алёша полил 16 саженцев, а Никита – 15, им осталось полить 7 саженцев. Сколько всего саженцев им нужно было полить?
3. Геометрия на спичках.
а) Переложите две палочки так, чтобы стало 8 квадратов.
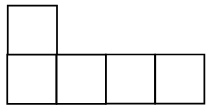
б) Переложите две палочки так, чтобы стало 7 квадратов.
в) Переложите две палочки так, чтобы стало 6 квадратов.
г) Переложите две палочки так, чтобы стало 5 квадратов. Найдите разные решения.
д) Переложите четыре палочки так, чтобы стало 12 квадратов.
е) Переложите четыре палочки так, чтобы стало 11 квадратов.
ж) Переложите четыре палочки так, чтобы стало 10 квадратов.
з) Переложите шесть палочек так, чтобы стало 16 квадратов.
и) Переложите шесть палочек так, чтобы стало 19 квадратов.
к) Переложите шесть палочек так, чтобы стало 15 квадратов.
4. Отметьте на рисунке все прямые углы.
III. Сообщение темы урока.
– Рассмотрите фигуры, представленные на доске.
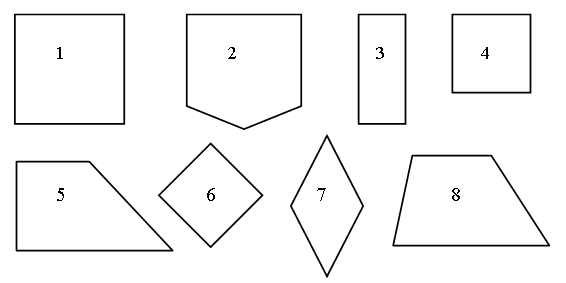
– Какая фигура «лишняя»? (Фигура 2 – пятиугольник.)
– Чем похожи остальные фигуры? (Это все четырехугольники.)
– Назовите четырехугольники, у которых все углы прямые. (Фигуры 1, 3, 4, 6.)
– Сегодня на уроке мы узнаем, как называют четырехугольники, у которых все углы прямые.
IV. Изучение нового материала.
Справочный материал для учителя
В результате соответствующих упражнений учащиеся должны понять, что любой квадрат есть прямоугольник, но не любой прямоугольник является квадратом.
Для того чтобы определить, является ли предъявленная фигура прямоугольником, надо проверить два условия:
1) является ли она четырехугольником;
2) все ли углы прямые.
Если данная фигура не является четырехугольником, то второе условие проверять не нужно, можно сразу сделать вывод.
Для того чтобы определить, является ли данная фигура квадратом, надо проверить также два условия: 1) является ли она прямоугольником, 2) все ли стороны равны по длине.
* * *
1. Работа по учебнику.
Задание 1 (с. 80).
Определения прямоугольника и квадрата вводятся после сравнения этих фигур между собой. Дети рассматривают изображения розовой и зеленой фигур (на с. 80 учебника). На вопрос о том, что общего у этих фигур, дети могут ответить так: обе фигуры – многоугольники (это верно); это четырехугольники (тоже верно). Вероятно, учащиеся обратят внимание на углы этих четырехугольников и даже по виду смогут определить, что в каждом четырехугольнике все углы прямые. Если этого не произойдет, учитель должен предложить второклассникам сравнить углы четырехугольников и определить с помощью модели прямого угла, что все углы в обоих многоугольниках – прямые.
Далее выясняются различия четырехугольников. Возможно, дети назовут некоторые несущественные, непринципиальные различия, например, что фигуры различаются цветом: одна – розовая, а другая – зеленая, что розовая фигура больше по размерам, чем зеленая. Реакция учителя: «Все то, что вы назвали, – правильно, но не это главное». Подведите учащихся к мысли о том, что нужно сравнить в каждой фигуре длины сторон. (Предупреждаем: в данном издании учебника длины сторон не выражаются целым числом сантиметров, поэтому советуем производить сравнение с помощью циркуля.) Итак, в результате сравнения учащиеся выяснят, что в розовом четырехугольнике стороны разной длины, а в зеленом все стороны имеют одну и ту же длину (можно сказать по-другому: длины всех сторон равны).
Подведите итоги: «На рисунке изображены два четырехугольника. У каждого из них все углы прямые. Но у зеленого четырехугольника еще и все стороны имеют одну и ту же длину. Этим он отличается от розового четырехугольника».
Далее прочитайте определение прямоугольника, приведенное в учебнике (на с. 80): «Прямоугольником называется такой четырехугольник, у которого все углы прямые».
– Является ли розовая фигура прямоугольником? (Да, так как это четырехугольник и у него все углы прямые.)
– Является ли зеленая фигура прямоугольником? (Да, так как это четырехугольник и у него все углы прямые.)
– Внимательно посмотрите на зеленый прямоугольник. Вам хорошо знакома эта фигура. Как мы ее назвали?
– Значит, квадрат – это прямоугольник, но особый: у него все стороны равны по длине. Прочитайте в учебнике, какая фигура называется квадратом.
Учащиеся читают определение квадрата (на с. 80).
– Итак, знакомимся: квадрат – это прямоугольник.
2. фронтальная работа с классом по демонстрационным таблицам и индивидуальным карточкам.
Задание 1 (по демонстрационной таблице).
– Рассмотрите таблицу на доске.
– Какие фигуры можно назвать прямоугольниками? Почему?
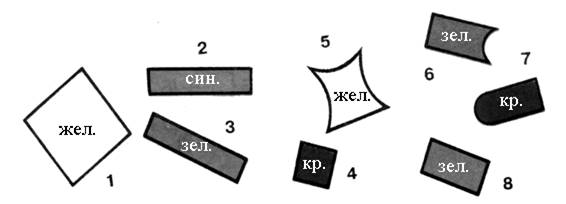
Задание 2 (по карточкам).
– Измерьте длины сторон прямоугольников:
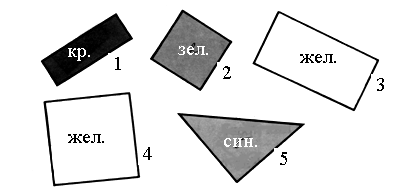
– Назовите прямоугольники, у которых все стороны одинаковой длины. (Фигуры 2, 4.)
– Как называются эти прямоугольники? (Квадраты.)
Задание 2 (по демонстрационной таблице).
– Рассмотрите фигуры на таблице.
– Как называются эти фигуры? (Многоугольники.)
– Посчитайте, сколько углов у каждой фигуры.
– Есть ли среди этих многоугольников прямоугольники?
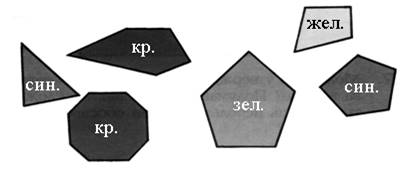

V. Повторение пройденного материала.
1. Работа в печатной тетради № 2.
Задание 151.
При выполнении этих заданий учащиеся должны помнить, что квадрат – это частный случай прямоугольника. Поэтому правильные ответы будут такими:
1) Многоугольники: 1, 2, 3, 4, 5.
2) Четырехугольники: 1, 3, 4.
3) Прямоугольники: 1, 4.
4) Квадраты: 1.
Задание 152.
– Рассмотрите чертеж.

– Сколько на чертеже прямоугольников? (три прямоугольника.)
– Сколько квадратов на чертеже? (один.)
Задание 153.
– Рассмотрите чертеж. На сколько квадратов разбита эта фигура?

– Сколько квадратов вы видите на чертеже?
Решение:
На чертеже дан квадрат, который разбит на 9 квадратов, но можно выделить еще 4 квадрата:
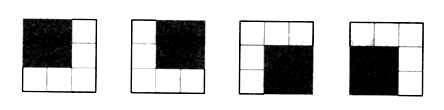
Следовательно, всего на чертеже (1 + 9 + 4) = 14 квадратов.
2. Работа по учебнику.
Задание 6 (с. 81).
Прежде чем учащиеся начнут выполнять вычисления, учитель просит их сравнить выражения и объяснить, чем они отличаются. (Выражения отличаются только порядком выполнения действий.)
Далее учащиеся самостоятельно выполняют вычисления значения каждого числового выражения и сравнивают их.
запись:
а) (96 – 43) – 28 = 53 – 28 = 25;
96 – (43 – 28) = 96 – 15 = 81.
25 не равно 81.
б) 48 – (30 + 8) = 48 – 38 = 10;
(48 – 30) + 8 = 18 + 8 = 26.
10 не равно 26.
в) (24 : 3) · 2 = 8 · 2 = 16;
24 : (3 · 2) = 24 : 6 = 4.
16 не равно 4.
Вывод: значение числового выражения зависит от порядка выполнения в нем действий.
VI. Итог урока.
– Что нового узнали на уроке?
– Назовите признаки прямоугольника.
– Назовите признаки квадрата.
Домашнее задание: № 5 (учебник); № 155 (рабочая тетрадь).
Урок 112
ПРЯМОУГОЛЬНИК. КВАДРАТ
Цели: учить строить прямоугольник и квадрат, находить данные фигуры среди других четырехугольников; совершенствовать умения решать геометрические задачи; развивать умение рассуждать и сравнивать.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Математический диктант.
К числу 20 прибавьте сумму 4 и 5. Из разности 50 и 30 вычтите число 10. К сумме 8 и 7 прибавьте 5. Из числа 100 вычтите сумму 35 и 5. Из суммы 68 и 2 вычтите 30. К разности 99 и 9 прибавьте 10. Из числа 56 вычтите разность 16 и 6.
2. Поставьте знак + или –
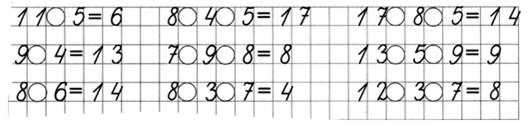
3. Геометрия на спичках.
а) Сколько на чертеже квадратов? Сколько других многоугольников? Какие многоугольники вы нашли на чертеже?

б) Уберите одну палочку так, чтобы осталось 4 квадрата. Найдите несколько решений.
в) Уберите одну палочку так, чтобы осталось 3 квадрата.
г) Уберите две палочки так, чтобы осталось 4 квадрата. Найдите разные решения.
д) Уберите две палочки так, чтобы осталось 3 квадрата.
4. Задача.
Рыболов поймал 7 ершей, а карасей – на 4 больше. Сколько всего ершей и карасей поймал рыболов?
III. Сообщение темы урока.
– Рассмотрите фигуры, представленные на доске.
– Маша назвала первую фигуру прямоугольником, а Миша – квадратом. Кто из них прав?
– Миша назвал вторую фигуру прямоугольником, а Маша – квадратом. Кто из них прав?
– Сегодня на уроке будем выполнять упражнения по определению, нахождению прямоугольников и квадратов.
IV. Работа по теме урока.
1. Работа по учебнику.
Задание 2 (с. 80).
– Рассмотрите рисунки. Какие предметы или их части похожи на прямоугольник?
Учащиеся, скорее всего, назовут следующие предметы: марка, линейка, конверт, салфетка. Но ведь прямоугольниками являются стенки и дно коробки, а также дно подарка. Обратите на это внимание детей.
Задание 3 (с. 81).
– Какую фигуру называют прямоугольником?
– Назовите признаки квадрата.
– Значит, любой квадрат является прямоугольником.
– Сколько прямоугольников на чертеже? (Три прямоугольника: 3, 5, 6.)
– Сколько квадратов на чертеже? (Два квадрата: 5 и 6.)
Задание 4 (с. 81).
– Рассмотрите чертеж. Сколько квадратов на чертеже? (На чертеже 4 больших квадрата и 7 маленьких. Всего 11 квадратов.)
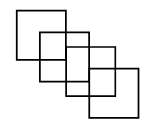
2. Работа в печатной тетради № 2.
Задание 154.
Учащиеся достраивают четырехугольники, используя тетрадную сетку:
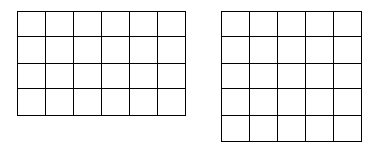

V. Повторение пройденного материала.
1. Работа в печатной тетради № 2.
Задание 156.
Важно, чтобы учащиеся не хаотично выписывали подходящие числа, а действовали по определенному плану.
Например, так:
1. Выписываем все однозначные числа: 4, 6.
2. Выписываем все двузначные числа, у которых цифры в записи одинаковые: 44, 66.
3. Выписываем все двузначные числа, у которых цифры в записи не повторяются: 46, 64.
Ответ: 4, 6, 44, 66, 46, 64.
Задание 158.
Слабоуспевающим учащимся можно разрешить воспользоваться моделью часов. Пусть они сначала поставят стрелки так, чтобы часы показывали 11 ч, а потом повернут стрелки на 2 ч вперед. Затем учащиеся смогут изобразить стрелки на рисунке.
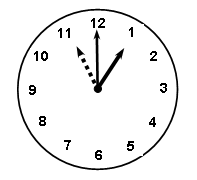
Запись:
Было – 11 ч.
Прошло – 2 ч.
Стало – ? ч.
Решение:
11 + 2 = 13 (ч) – дня.
Ответ: 13 часов.
2. Работа по карточкам.
Карточка 1
Раздели данный прямоугольник на три равных квадрата.

Карточка 2
Выпиши номера четырехугольников, которые называют прямоугольниками.
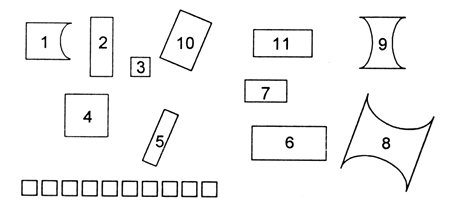
Закрась прямоугольники, которые называют квадратами.
Карточка 3
Проведи луч ОК так, чтобы получился прямой угол, внутри которого проходит луч ОС.
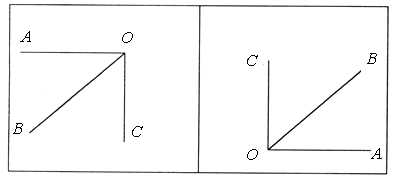
Закрась полученный прямой угол синим цветом.
Карточка 4
Соедини точки так, чтобы получились прямоугольники. Обозначь эти точки буквами.
Карточка 5
Используя данный прямой угол, построй квадрат с помощью циркуля и угольника.
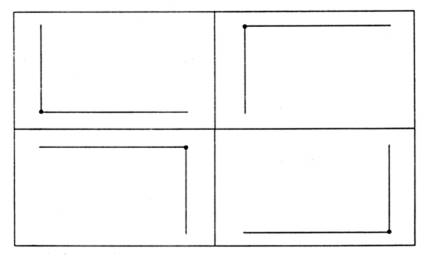
VI. Итог урока.
– Что нового узнали на уроке?
– Назовите признаки прямоугольника.
– Назовите признаки квадрата.
Домашнее задание: № 157 (рабочая тетрадь).
Урок 113
ПРЯМОУГОЛЬНИК. КВАДРАТ
Цели: закреплять и совершенствовать навыки построения прямоугольников и квадратов; продолжить формирование умений решать геометрические задачи; развивать внимание и глазомер.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Математический диктант.
Число 8 умножьте на произведение 2 и 3. Частное 24 и 4 разделите на 3. Произведение 27 и 1 разделите на 9. Произведение 9 и 1 умножьте на 7. Число 48 разделите на произведение 4 и 2. Число 63 разделите на частное 28 и 4.
2. Найдите суммы, складывая числа сначала по строкам, а затем – по столбцам.
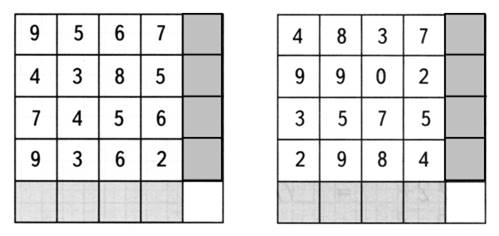
– Проверьте, верно ли выполнены вычисления: числа в каждой таблице подобраны так, что в незакрашенной клетке должна получиться одна и та же сумма независимо от того, как считали.
3. Задача.
Для школьного буфета купили 18 пачек индийского чая и 20 пачек краснодарского. За первую неделю израсходовали 8 пачек. Сколько пачек чая осталось?
III. Сообщение темы урока.
– Рассмотрите рисунок на доске.
– Из каких геометрических фигур выполнен рисунок?
– Назовите признаки четырехугольника.
– Назовите признаки прямоугольника.
– Назовите признаки квадрата.
– Сегодня на уроке продолжим работу по теме «Прямоугольник. Квадрат».
IV. Практическая работа по карточкам.
Карточка 1
Используя данные отрезки, построй прямоугольники.
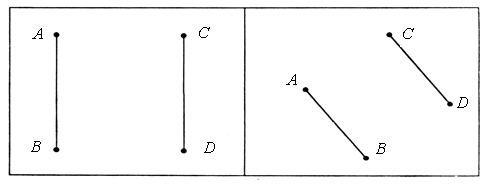
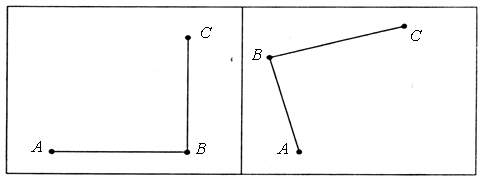
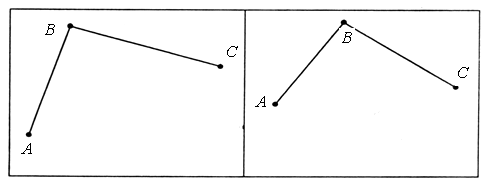
Карточка 2
– Соедини точки так, чтобы получилось два квадрата.
Карточка 3
Проведи в каждой фигуре 2 отрезка так, чтобы получилось 5 треугольников.
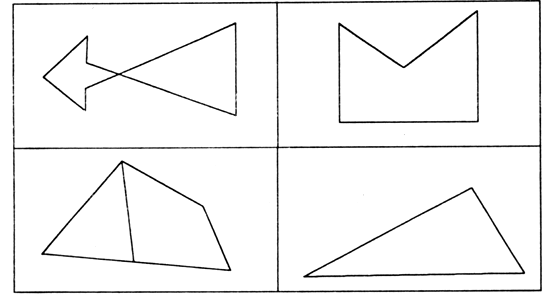
Карточка 4
Проведи в каждой фигуре два отрезка так, чтобы получился прямоугольник, и закрась его.
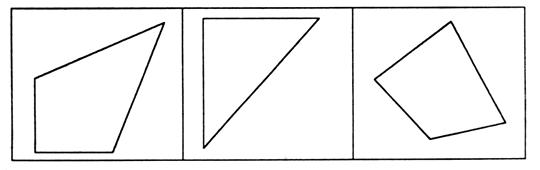
Карточка 5
Проведи в каждой фигуре отрезок так, чтобы получилось:
а) 2 треугольника и 1 четырехугольник:
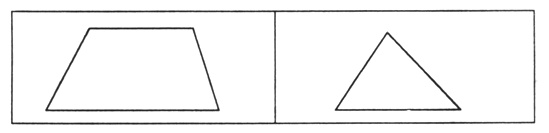
б) 3 четырехугольника:
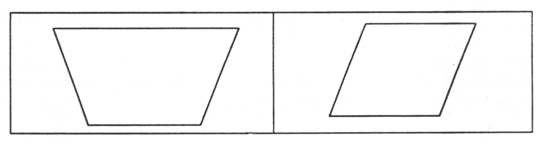
в) 1 треугольник и 2 четырехугольника:
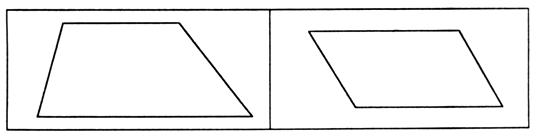

V. Повторение пройденного материала.
1. Работа по учебнику.
Задание 8 (с. 82).
Это задание является логическим.
При ответе на дополнительные вопросы к задаче: «Можно ли утверждать, что этот четырехугольник квадрат? Почему?» – учащиеся учатся выполнять логическую операцию «проведение под определение».
Учащимся известно определение квадрата. Для того чтобы утверждать, что данный четырехугольник является квадратом, надо проверить выполнение двух условий:
1) четырехугольник является прямоугольником;
2) все стороны четырехугольника равны.
Из условия задачи не следует, что четырехугольник является прямоугольником, то есть первое условие может не выполняться, значит, нельзя утверждать, что этот четырехугольник – квадрат (даже несмотря на то что все стороны у него равны, так как имеют одинаковую длину – 7 дм).
2. Работа в печатной тетради № 159.
Слабоуспевающим учащимся для ответа на первый вопрос задачи можно предложить в помощь следующую карточку:
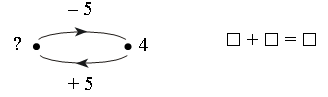
VI. Итог урока.
– Что нового узнали на уроке?
– Назовите признаки прямоугольника.
– Назовите признаки квадрата.
Домашнее задание: № 8 (а, б) в учебнике.
Урок 114
СВОЙСТВА ПРЯМОУГОЛЬНИКА
Цели: познакомить учащихся со свойствами противоположных сторон и диагоналей прямоугольника; совершенствовать умения решать геометрические задачи; продолжить формирование вычислительных умений; развивать умение анализировать и рассуждать.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Соедините геометрическую фигуру с определением.
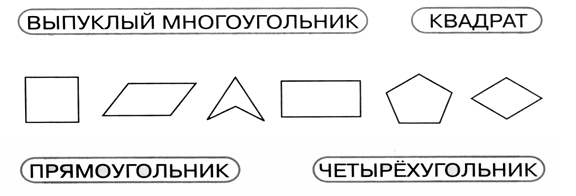
2. Запишите числовые равенства, пользуясь таблицей:
|
Первое слагаемое |
74 |
83 |
67 |
41 |
56 |
32 |
|
Второе слагаемое |
5 |
6 |
2 |
8 |
3 |
7 |
– Чем все эти равенства похожи?
3. Задача.
В пустой бочонок налили сначала 2 кг мёда, а затем на 3 кг больше, чем в первый раз. Масса бочонка вместе с мёдом стала равна 8 кг. Найдите массу пустого бочонка.
III. Сообщение темы урока.
– Рассмотрите фигуры, представленные на доске.
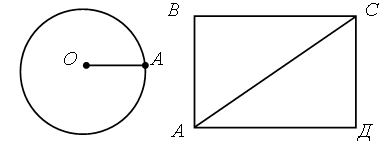
– Какие фигуры здесь изображены?
– Как называется отрезок ОА в окружности?
– Как называется отрезок АС в прямоугольнике?
– Сегодня на уроке мы будем говорить о свойствах прямоугольника.
IV. Изучение нового материала.
Задание № 1 (с. 83).
– Как называется данная фигура?
– Назовите признаки прямоугольника.
– Измерьте длину каждой стороны прямоугольника.
– Какой вывод можно сделать? (В прямоугольнике длины противоположных сторон равны.)
АВ = СД = 3 см.
ВС = АД = 4 см.
Далее учащиеся читают определение в учебнике (на с. 83).
Задание № 2 (с. 83).
– Рассмотрите данный чертеж.
– Назовите диагонали прямоугольника. (отрезки АС и ВД – диагонали.)
– Измерьте длину каждой диагонали прямоугольника.
– Какой вывод можно сделать? (Длины диагоналей прямоугольника равны.) АС = ВД.
Далее учащиеся читают правило в учебнике (на с. 83).
Задание № 3 (с. 84).
Лучше всего выполнить упражнение устно, подробно разбирая каждый пункт задания. При этом просите детей давать подробные и обоснованные ответы.
1. Учащееся могут предложить два общих названия фигур: многоугольник и четырехугольник. Обязательно задайте дополнительный вопрос: «Какое из этих названий точнее?» (Четырехугольник.)
2. У фигур 1 и 2 все углы прямые, а у фигуры 3 нет прямых углов. (Учащиеся проверяют это с помощью чертежного угольника.)
3. Так как фигуры 1 и 2 – четырехугольники, у которых все углы прямые, то их можно назвать прямоугольниками.
4. У фигуры 2, в отличие от фигуры 1, все стороны равны. (Учащиеся проверяют это с помощью циркуля.)
5. Так как фигура 2 – прямоугольник, у которого все стороны равны, то ее можно назвать квадратом.
6. Так как фигура 1 – прямоугольник, то у нее противоположные стороны равны.
7. У фигуры 2 все стороны равны.
В заключение учитель задает дополнительные вопросы:
– Любой ли квадрат является прямоугольником? (Да, любой, так как квадрат по определению – прямоугольник.)
– Любой ли прямоугольник является квадратом? (Нет, не любой прямоугольник является квадратом, а лишь тот, у которого все стороны имеют одну и ту же длину.)

V. Повторение пройденного материала.
1. Работа в печатной тетради № 2.
Задание № 162.
Чертеж:
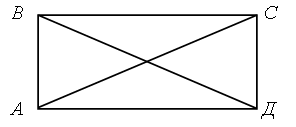
АВ = 2 см
ВС = 4 см
СД = 2 см
АД = 4 см
– Как называется отрезок АС в прямоугольнике АВСД? (Диагональ.)
– Проведите вторую диагональ. (ВД.)
– Что вы знаете о длинах диагоналей прямоугольника?
Задание № 163.
Чертеж к заданию:
Каждый из образовавшихся квадратов составляет половину прямоугольника.
2. Работа по учебнику.
Задание № 10 (с. 85).
Учащиеся составляют схему-«машину».
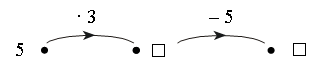
Решение:
1) Чему равно второе число?
5 · 3 = 15.
2) Чему равна разность двух чисел?
15 – 5 = 10.
Ответ: 10.
Задание № 11 (с. 85).

VI. Итог урока.
– Что нового узнали на уроке?
– Назовите свойства прямоугольника.
Домашнее задание: № 8, 9 (учебник); № 160, 161 (рабочая тетрадь).
Урок 115
СВОЙСТВА ПРЯМОУГОЛЬНИКА
Цели: продолжить формирование умений решать геометрические задачи, используя основные свойства прямоугольника; совершенствовать вычислительные навыки; развивать внимание и мышление.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Математический диктант.
а) Число 8 умножьте на 6. Разделите 35 на 7. Сложите 16 и 8. Из 42 вычтите 11.
б) Увеличьте 12 на 8 и из результата вычтите 4. Уменьшите 17 на 7 и к результату прибавьте 50. Увеличьте 9 в 8 раз и к результату прибавьте 8. Уменьшите 42 в 7 раз и результат увеличьте в 48 раз.
2. Задача.
По таблице составьте три задачи и решите их.
|
Было |
15 м. |
? |
18 м. |
|
Уехало |
8 м. |
9 м. |
? |
|
Осталось |
? |
3 м. |
10 м. |
3. Заполните свободные клетки таблицы.
III. Сообщение темы урока.
– Сегодня на уроке будем решать геометрические задачи.
IV. Работа по теме урока.
Задание № 4 (с. 84).
Задание направлено прежде всего на дальнейшее уточнение знаний о диагоналях прямоугольника (квадрата).
В результате выполнения этого упражнения учащиеся должны сделать следующие основные выводы:
1) у прямоугольника, не являющегося квадратом, диагональ не является осью симметрии, а у квадрата диагональ – ось симметрии;
2) у квадрата, так же как и у любого прямоугольника, диагонали равны.
Задание № 5 (с. 84).
Это задание выполняется устно (фронтальная работа).
Задание № 6 (с. 85).
Учащиеся, используя зеркало, проверяют, симметричны ли противоположные вершины квадрата относительно его диагоналей.
Задание № 7 (с. 85).
Задание продолжает серию упражнений, направленных на формирование у учащихся умения выполнять логическую операцию «подведение под определение». Для того чтобы фигура была квадратом, необходимо выполнение двух условий:
1) фигура должна быть прямоугольником;
2) у нее все стороны должны иметь одну и ту же длину.
В данном случае описывается именно такая фигура (прямоугольник, длина каждой стороны которого равна 9 см). Значит, это квадрат.

V. Повторение пройденного материала.
1. Работа по учебнику.
Задание № 13 (с. 86).
Сначала учитель предлагает учащимся выразить данные величины в одних и тех же единицах. Проще всего 1 дм выразить в сантиметрах:
1 дм = 10 см.
– С чего начинают построение отрезка? (Отмечают точку – один из концов отрезка, а затем прикладывают линейку так, чтобы нулевое деление совместилось с отмеченной точкой.)
– Как же выбрать второй конец отрезка, не зная его длину?
Вывод: в качестве второго конца отрезка можно выбрать любую точку между штрихами линейки 10 см и 12 см. Следовательно, можно начертить много различных отрезков.
Учитель должен обратить внимание на тот факт, что только для одного из этих отрезков мы можем указать длину (для отрезка длиной 11 см).
Задание № 14 (с. 86).
– Прочитайте текст. Является ли он задачей?
– Что известно в задаче? Что требуется узнать?
– Запишите условие задачи в таблицу:

Решение:
1) Сколько весят 2 цыплёнка?
4 : 2 = 2 (кг).
2) Сколько весит 1 цыплёнок?
2 : 2 = 1 (кг).
Ответ: 1 кг.
Задание № 15 (с. 86).
– Прочитайте задачу.
– Что известно? Что требуется найти?
– Запишите кратко условие задачи.
Запись:
Было – 20 р. и 15 р.
Сделала – ? букетов по ? роз.

Запишите решение задачи выражением.
Решение:
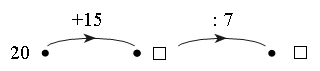
(20 + 15) : 7 = 35 : 7 = 5 (р.) – в 1 букете.
Ответ: 5 роз.
2. Работа в печатной тетради № 2.
Задание № 166.
– Прочитайте задачу.
– Что известно? Что требуется узнать?
– Составьте схему-«машину» и решите задачу.
Запись:
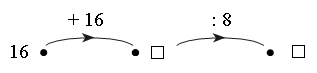
Решение:
1) 16 + 16 = 32 (ф.) – всего.
2) 32 : 8 = 4 (ф.) – осталось.
Ответ: 4 ф.
VI. Итог урока.
– Что нового узнали на уроке?
– Назовите признаки квадрата.
– Назовите признаки прямоугольника.
– Что известно о диагоналях прямоугольника?
– Какие стороны прямоугольника равны?
Домашнее задание: № 164, 165 (рабочая тетрадь).
Урок 116
ПЛОЩАДЬ ПРЯМОУГОЛЬНИКА
Цели: познакомить учащихся с правилом вычисления площади прямоугольника (квадрата); совершенствовать умение решать геометрические задачи; продолжить формирование вычислительных умений; развивать умение обобщать.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Математический диктант.
– Назовите число, которое меньше 30:
а) на 6; б) в 6 раз; в) в 5 раз.
– Какое число больше 9:
а) на 3; б) в 3 раза?
– На какие числа можно разделить каждое из чисел: 12, 9, 8, 10, 18?
2. Задачи.
– Соедините линией кружок с номером задачи и карточки с выражениями для её решения.

3. Геометрия на спичках.
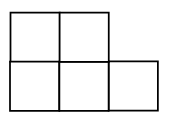
а) Уберите две палочки так, чтобы осталось 2 квадрата.
б) Уберите две палочки так, чтобы остался 1 квадрат.
в) Уберите три палочки так, чтобы осталось 3 квадрата.
г) Уберите три палочки так, чтобы осталось 2 квадрата.
д) Уберите три палочки так, чтобы остался 1 квадрат.
е) Уберите три палочки так, чтобы квадратов не осталось.
ж) Уберите четыре палочки так, чтобы осталось 3 квадрата.
III. Сообщение темы урока.
– Рассмотрите чертежи на доске:
|
|
|
|
|
|
1 см2 |
|
|
1 см2 |
|
|
|
|
|
– Как называются данные фигуры?
– Как быстро вычислить количество клеток в каждой фигуре? (4 · 2 = 8 и 2 · 2 = 4.)
– Как узнать площадь прямоугольника?
– Сегодня на уроке мы узнаем, как вычислить площадь прямоугольника, используя арифметическое действие.
IV. Изучение нового материала.
Справочный материал для учителя
В формулировке правила содержатся термины «длина» и «ширина». По поводу этих терминов сделаем одно разъяснение. Длину прямоугольника обычно связывают с большей его стороной, а ширину – с меньшей. Иногда в упражнениях содержится требование найти площадь прямоугольника, если даны длины сторон, например 4 см и 6 см. В таких случаях учащиеся должны понимать, что для вычисления площади прямоугольника надо перемножить числа 4 и 6. (можно в любом порядке.)
Для квадрата правило нахождения его площади отдельно не формулируется. Выясните у учащихся почему. (Так как квадрат – это прямоугольник, то для вычисления его площади можно пользоваться правилом вычисления площади прямоугольника.)
Выясните также, что надо перемножать при вычислении площади квадрата. (Так как у квадрата длина равна ширине, то для нахождения его площади достаточно перемножить две длины.)
* * *
Задание № 1 (с. 87).
Сначала учитель вводит термины «длина» и «ширина» прямоугольника. (Начертите заранее на доске любой прямоугольник, расположив его произвольно.)
Покажите две смежные стороны этого прямоугольника и назовите большую из них длиной, а меньшую – шириной прямоугольника.
– Измерьте длину и ширину прямоугольника.
– Какова площадь прямоугольника?
– Как найти площадь прямоугольника вычислением?
Учитель знакомит учащихся с правилом в учебнике (на с. 87).
Задание № 2 (с. 87).
Перед выполнением упражнения учитель проводит беседу.
– Как называется первая фигура? (Прямоугольник.)
–Какие измерения необходимо выполнить, чтобы найти площадь прямоугольника? (Нужно измерить длину и ширину.)
– Как называется вторая фигура? (Квадрат.)
– Какие измерения необходимо выполнить, чтобы найти площадь квадрата? (Достаточно измерить длину только одной стороны.)
Далее учащиеся работают самостоятельно.
Запись:
1) 6 · 2 = 12 (см2) – площадь прямоугольника.
2) 3 · 3 = 9 (см2) – площадь квадрата.
Ответ: 12 см2, 9 см2.

V. Повторение пройденного материала.
1. Работа в печатной тетради № 2.
Задание № 169.
Правильный чертеж к заданию следующий:
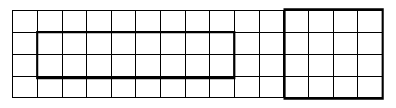
Стороны прямоугольника: 1 см, 4 см.
Сторона квадрата: 2 см.
2. Работа по учебнику.
Задание № 7 (с. 88).
Учащиеся составляют схемы-«машины»:


Задание № 8 (с. 88).
Учащиеся составляют схемы-«машины»:
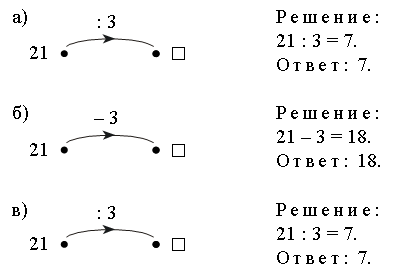
– Задаем вопросы: «Во сколько раз 3 меньше, чем 21?» и «Во сколько раз 21 больше, чем 3?»
VI. Итог урока.
– Что нового узнали на уроке?
– Как вычислить площадь прямоугольника?
– Назовите единицы измерения площади.
Домашнее задание: № 9 (учебник); № 167 (рабочая тетрадь).
Урок 117
ПЛОЩАДЬ ПРЯМОУГОЛЬНИКА
Цели: формировать умения пользоваться правилом вычисления площади прямоугольника (квадрата); совершенствовать умения решать составные задачи разными способами; закреплять знания определений геометрических фигур; развивать внимание и умение анализировать.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Геометрия на спичках.
а) Уберите четыре палочки так, чтобы осталось 2 квадрата.
б) Уберите четыре палочки так, чтобы остался 1 квадрат.
в) Уберите пять палочек так, чтобы осталось 3 квадрата.
г) Переложите две палочки так, чтобы стало 8 квадратов.
д) Переложите две палочки так, чтобы стало 7 квадратов.
е) Переложите две палочки так, чтобы стало 6 квадратов.
2. Поставьте знаки «+» или «–».

3. Задача.
В первый день посадили 20 саженцев, во второй – на 10 саженцев больше, чем в первый, а в третий – на 18 саженцев больше, чем во второй. Сколько саженцев посадили в третий день?
III. Сообщение темы урока.
– Сегодня на уроке будем решать задачи на нахождение площади прямоугольников.
IV. Работа по теме урока.
Задание № 3 (с. 87).
– Как вычислить площадь прямоугольника?
– Что необходимо знать?
Далее учащиеся выполняют вычисления. Запись можно оформить в таблице.
|
|
Длина |
Ширина |
Площадь |
|
I |
5 дм |
3 дм |
Решение: 5 · 3 = 15 (дм2) |
|
II |
9 см |
? на 2 см м. |
1) 9 – 2 = 7 (см) 2) 9 · 7 = 63 (см2) |
|
III |
?, в 2 раза б. |
4 см |
1) 4 · 2 = 8 (см) 2) 8 · 4 = 32 (см2) |
|
IV |
4 дм |
40 см 40 см = 4 дм |
4 · 4 = 16 (дм2) |
Задание № 4 (с. 88).
– Какая фигура изображена на чертеже?
– Что известно по данному чертежу? (Площадь и ширина прямоугольника.)
– Что требуется узнать? (Длину прямоугольника.)
– Запишите условие задачи в таблицу:
|
Длина |
Ширина |
Площадь |
|
? см |
2 см |
16 см2 |
Решение:
16 : 2 = 8 (см) – длина.
Ответ: 8 см.

V. Повторение пройденного материала.
1. Работа по учебнику.
Задание № 11 (с. 89).
– Прочитайте условие задачи.
– Что известно? Что требуется узнать?
– Запишите условие задачи в таблицу:

– Запишите решение задачи разными способами.
Решение:
1-й способ.
1) Сколько дней читали I книгу?
36 : 9 = 4 (дн.).
2) Сколько дней читали II книгу?
45 : 9 = 5 (дн.).
3) Сколько дней читали обе книги?
4 + 5 = 9 (дн.).
2-й способ.
1) Сколько всего страниц в двух книгах?
36 + 45 = 81 (с.).
2) Сколько дней читали обе книги?
81 : 9 = 9 (дн.).
Ответ: 9 дней.
Задание № 12 (с. 89).
– Рассмотрите рисунок. Что вам известно?
– Объясните, что вы узнаете, выполнив действия:
![]() – стоимость двух
карандашей и красок;
– стоимость двух
карандашей и красок;
![]() – на сколько
дороже стоят краски, чем два карандаша (на сколько стоят дешевле два карандаша,
чем краски);
– на сколько
дороже стоят краски, чем два карандаша (на сколько стоят дешевле два карандаша,
чем краски);
![]() – на сколько
дороже стоят краски, чем один карандаш (на сколько дешевле стоит один карандаш,
чем краски);
– на сколько
дороже стоят краски, чем один карандаш (на сколько дешевле стоит один карандаш,
чем краски);
![]() – стоимость
красок и одного карандаша.
– стоимость
красок и одного карандаша.
2. Работа в печатной тетради № 2.
Задание № 171.
Учащиеся работают самостоятельно.
Чертеж:
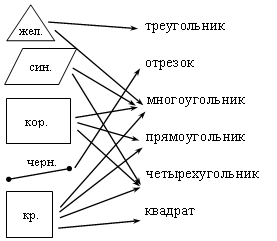
Учитель проводит фронтальную проверку по следующим вопросам:
– Как мы можем назвать желтую фигуру? (Треугольник, многоугольник.)
– Синюю? (Многоугольник, четырехугольник.)
– Коричневую? (Многоугольник, четырехугольник, прямоугольник.)
– Черную? (отрезок.)
– Красную? (Многоугольник, четырехугольник, прямоугольник, квадрат.)
VI. Итог урока.
– Что нового узнали на уроке?
– Как вычислить площадь любого прямоугольника?
Домашнее задание: № 10 (учебник); № 168 (рабочая тетрадь).
Урок 118
ПЛОЩАДЬ ПРЯМОУГОЛЬНИКА
Цели: совершенствовать и закреплять навыки решения геометрических задач на нахождение площади и периметра любых прямоугольников; продолжить формирование умений находить значение выражений с переменными; развивать логическое мышление.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Задача.
Коля поставил на верхнюю полку 18 машинок, а на нижнюю – на 3 машинки меньше. Сколько всего машинок Коля поставил на обе полки?
2. Математический диктант.
– Первое слагаемое 7, второе 9. Назовите сумму.
– Каждое из двух слагаемых равно 8. Чему равна сумма?
– Одно из слагаемых 10, другое – 7. Назовите сумму.
– Сумма двух чисел 12. Одно из них – 5. Назовите другое число.
3. Геометрия на спичках.

а) Переложите две палочки так, чтобы стало 5 квадратов. Найдите разные решения.
б) Переложите четыре палочки так, чтобы стало 12 квадратов.
в) Переложите четыре палочки так, чтобы стало 11 квадратов.
г) Переложите четыре палочки так, чтобы стало 10 квадратов.
д) Переложите шесть палочек так, чтобы стало 16 квадратов.
е) Переложите шесть палочек так, чтобы стало 15 квадратов.
ж) Переложите шесть палочек так, чтобы стало 19 квадратов.
III. Сообщение темы урока.
– Сегодня на уроке будем решать геометрические задачи.
IV. Работа по теме урока.
Задание № 5 (с. 88).
– Как вычислить площадь прямоугольника?
– Что произойдет с площадью прямоугольника, если его длину увеличить в 2 раза, а ширину оставить без изменения? (Площадь увеличится в 2 раза.)
– Заполните таблицу по условию задачи и проверьте свое предположение.

Решение:
1) 3 · 2 = 6 (дм2) – площадь первоначального прямоугольника.
2) 3 · 2 = 6 (дм2) – длина нового прямоугольника.
3) 6 · 2 = 12 (дм2) – площадь нового прямоугольника.
4) 12 : 6 = 2 – во столько раз площадь нового прямоугольника больше площади первоначального прямоугольника.
Вывод: площадь прямоугольника увеличилась в 2 раза.
Задание № 6 (с. 88).
– Прочитайте задачу.
– Что известно в задаче? Что требуется узнать?
– Заполните таблицу по условию задачи.
|
|
Длина стороны квадрата |
Периметр |
Площадь |
|
I |
? см |
16 см |
? см2 |
|
II |
? см |
2 дм = 20 см |
? см2 |
|
III |
? м |
12 м |
? м2 |
|
IV |
? см |
3 дм 6 см = 36 см |
? см2 |
– как узнать длину квадрата, если известен его периметр?
Решение:
1) 16 : 4 = 4 (см) – длина стороны квадрата.
2) 4 · 4 = 16 (см2) – площадь квадрата.
3) 20 : 4 = 5 (см) – длина стороны второго квадрата.
4) 5 · 5 = 25 (см2) – площадь второго квадрата.
5) 12 : 4 = 3 (м) – длина стороны третьего квадрата.
6) 3 · 3 = 9 (м2) – площадь третьего квадрата.
7) 36 : 4 = 9 (см) – длина стороны четвертого квадрата.
8) 9 · 9 = 81 (см2) – площадь четвертого квадрата.
Ответ: 16 см2, 25 см2, 9 м2, 81 см2.

V. Повторение пройденного материала.
1. Работа по учебнику.
Задание № 14 (с. 89).
– Выпишите выражение с переменной и найдите его значение при х = 5, 0, 9.
![]()
а) если х = 5, то (2 · 5) + 3 = 13;
б) если х = 0, то (2 · 0) + 3 = 3;
в) если х = 9, то (2 · 9) + 3 = 21.
Задание № 15 (с. 89).
– Прочитайте задачу.
– Что известно? Что требуется узнать?
– Запишите кратко условие задачи.
Запись:

Решение:
1) Сколько лет брату?
8 · 2 = 16 (л.).
2) Сколько лет сестре?
8 : 2 = 4 (г.).
Ответ: 16 лет, 4 года.
2. Самостоятельная работа по карточкам.
Карточка № 1
Раздели фигуру на части, площадь каждой из которых – 3 см2. Постарайся найти несколько вариантов.
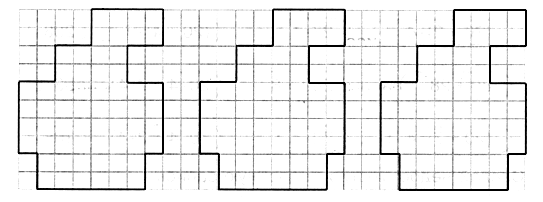
Карточка № 2
Найди площадь фигуры, которую нужно было разделить на части.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найденную площадь впиши в текст задачи.
Карточка № 3
Из красного листа, площадь которого была на 1 дм2 больше площади зелёного листа, вырезали фигуру площадью ________.
Площадь какого листа оказалась после вырезания меньше и на сколько?
Реши полученную задачу.
VI. Итог урока.
– Что нового узнали на уроке?
– Как вычислить площадь прямоугольника? Периметр прямоугольника?
Домашнее задание: № 170, 171 (рабочая тетрадь).
Урок 119
КОНТРОЛЬНАЯ РАБОТА по теме
«ВЫРАЖЕНИЯ»
Цели: проверить сформированность умений решать задачи; усвоение математической терминологии.
Ход урока
I вариант
1. Запиши выражения и найди их значения:
Уменьшаемое 93, вычитаемое 7.
80 уменьшить на 9.
46 увеличить на 8.
Разность чисел 70 и 15.
На сколько число 60 больше, чем число 28?
Произведение чисел 5 и 2.
Во сколько раз 56 больше 8?
Частное чисел 49 и 7.
2. В корзине 6 груш, 8 яблок, а апельсинов на 5 больше, чем груш. Сколько всего фруктов в корзине?
3. Вставь пропущенные числа:
72 : □ + 15 = 24
6 · □ + 30 = 48
42 : □ + 7 = 13
8 · □ – 20 = 22
4. Дорисуй фигуру до прямоугольника, площадь которого равна 21 см2. Вычисли периметр этого прямоугольника, вставив соответствующие числа в «окошки».

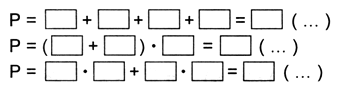
5. Отложи на сторонах прямого угла стороны прямоугольника, периметр которого равен 12 см. Закончи построение каждого прямоугольника и вычисли его периметр и площадь.

II вариант
1. Запиши выражения и найди их значения:
Уменьшаемое 85, вычитаемое 9.
90 уменьшить на 8.
47 увеличить на 5.
Разность чисел 50 и 12.
На сколько число 70 больше, чем число 48?
Произведение чисел 3 и 9.
Во сколько раз 81 больше 9?
Частное чисел 36 и 4.
2. В саду растут 8 берез, 9 сосен, а елей на 4 больше, чем берез. Сколько всего деревьев в саду?
3. Вставь пропущенные числа:
36 : □ + 31 = 40
5 · □ + 62 = 82
48 : □ + 9 = 15
9 · □ – 30 = 42
4. Дострой фигуру до квадрата, площадь которого равна 9 см2. Вычисли его периметр.
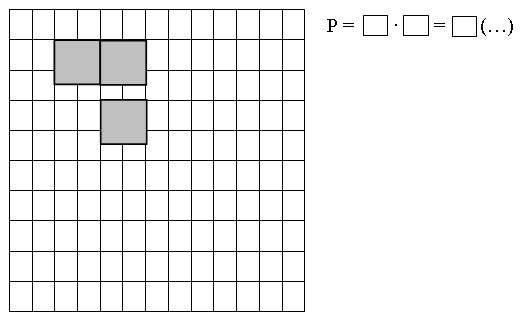
5. Отложи на сторонах прямого угла стороны прямоугольника, периметр которого равен 18 см. Закончи построение каждого прямоугольника и вычисли его периметр и площадь.

Урок 120
РАБОТА НАД ОШИБКАМИ
Цели: провести анализ выполненной контрольной работы; совершенствовать вычислительные навыки; развивать умение рассуждать.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Найдите вырезанную часть таблицы.
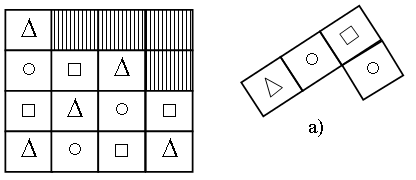
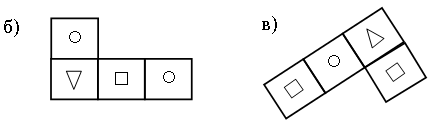
Ответ: б).
2. Игра «Родственные ряды чисел».
– Для каждого набора чисел найдите логическую взаимосвязь между числами первого и второго рядов и исходя из этого определите пропущенные числа.
|
2 |
5 |
|
10 |
12 |
|
7 |
10 |
13 |
15 |
|
|
10 |
12 |
4 |
16 |
|
|
5 |
6 |
|
8 |
4 |
|
14 |
12 |
|
15 |
10 |
|
7 |
5 |
1 |
8 |
|
|
2 |
4 |
6 |
3 |
|
|
10 |
20 |
|
15 |
40 |
3. Сколько треугольников на чертеже?
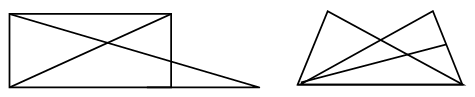
4. Выберите нужную картинку.
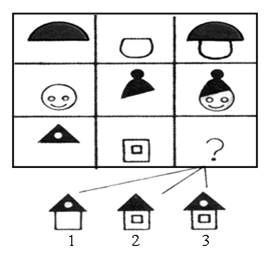
III. Сообщение о результатах выполнения контрольной работы.
IV. Работа над ошибками.

V. Самостоятельная работа по карточкам.
Карточка А
Обведи кружком номера двух задач, обратных задаче 1. Запиши выражение для решения каждой из предложенных задач.
1. После того как Серёжа отдал 5 орехов сестре, у него осталось 10 орехов. Сколько орехов было у Серёжи сначала?
2. У Серёжи было 15 орехов, а у его сестры – 10. Сколько орехов было у Серёжи и у его сестры вместе?
3. У Серёжи было 15 орехов. Он отдал несколько орехов сестре, и у него осталось 10 орехов. Сколько орехов Серёжа отдал сестре?
4. У Серёжи было 15 орехов, а у его сестры – 5. На сколько больше орехов было у Серёжи, чем у его сестры?
5. У Серёжи было 15 орехов. Он отдал 5 орехов сестре. Сколько орехов осталось у Серёжи?
Карточка В
Раскрась. Цвет определи по схеме:
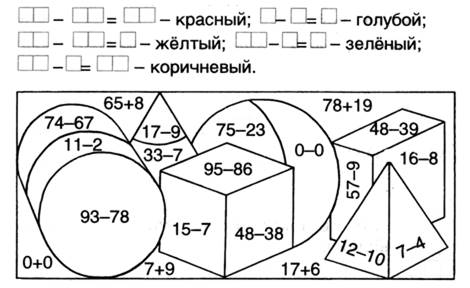
Карточка С
Соедини отрезком каждую пару точек.

1) Сколько всего отрезков получилось?
![]() отрезков
отрезков
2) Найди периметр четырехугольника.
VI. Итог урока.
Урок 121
Повторение по
теме
«СЛОЖЕНИЕ,
ВЫЧИТАние, УМНОЖЕНИЕ
И ДЕЛЕНИЕ ЧИСЕЛ В ПРЕДЕЛАХ 100»
Цели: совершенствовать вычислительные навыки; развивать умение анализировать и рассуждать.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Заполните окошки числами так, чтобы равенства стали верными.
7 + □ + 5 = 15 □□ – 5 – 4 = 6
9 + 3 – □□ = 2 13 – □ + 9 = 16
□ + 4 – 2 = 10 18 – □ – 3 = 7
2. Задача.
На большой кассете записано 12 песен, а на маленькой – на 5 песен меньше, чем на большой. Сколько песен записано на этих двух кассетах вместе?
3. Геометрическое задание.
– Какие фигуры изображены на чертеже?
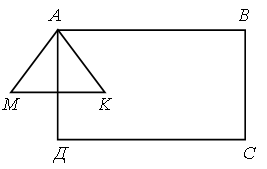
– Какой фигурой является общая часть четырехугольника АВСД и треугольника МАК?
4. Найдите девятый предмет.

III. Сообщение темы урока.
IV. Работа по теме урока.
1. Работа по учебнику.
– Рассмотрите схемы, представленные на доске:
□ + □ □ · □
□ – □ □ : □
– Как называется каждое выражение?
– Назовите компоненты действий сложения, вычитания, умножения и деления.
Далее учащиеся выполняют задания № 1, 2, 3, 4 (с. 90) самостоятельно. Взаимопроверка в парах.
Задания № 9, № 10 (с. 91).
– Что значит «увеличить на несколько единиц»?
– Что значит «увеличить в несколько раз»?
– Что значит «уменьшить на несколько единиц»?
– Что значит «уменьшить в несколько раз»?
Далее задание выполняется фронтально на доске.
Задание № 20, 21, 22 (с. 92).
– Как найти долю от числа? Какое действие надо выполнить?
Задание № 20.
Запись:
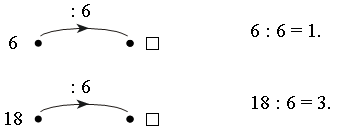
Задание № 21.
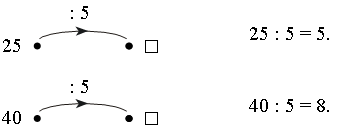
Задание № 22.
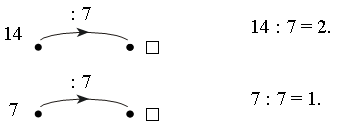
2. Работа в печатной тетради № 2.
Задание № 174.
– Назовите основные правила чтения и построения математических граф.
Запись:
(Учащиеся читают отношения.)
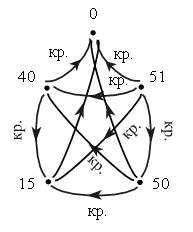
а) • 15 больше 0;
• 40 больше 0;
• 40 больше 15;
• 50 больше 0;
• 50 больше 15;
• 50 больше 40;
• 51 больше 0;
• 51 больше 15;
• 51 больше 40;
• 51 больше 50;
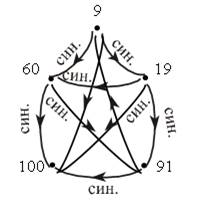
б) • 9 меньше 19;
• 9 меньше 60;
• 9 меньше 91;
• 9 меньше 100;
• 19 меньше 60;
• 19 меньше 91;
• 19 меньше 100;
• 60 меньше 91;
• 60 меньше 100;
• 91 меньше 100.

V. Продолжение работы по теме урока.
1. Фронтальная работа.
Математический кроссворд
По горизонтали:
2. Математическое действие 2 + 3. (Сложение.)
3. Какое математическое действие нужно выполнить, чтобы найти произведение?(Умножение.)
5. Промежуток времени в 24 часа. (Сутки.)
8. Число, которое умножается на другое. (Множитель.)
10. Результат деления. (Частное.)
11. Единица измерения объема жидкости. (Литр.)
По вертикали:
1. Математическое действие. (Деление.)
4. Сумма длин всех сторон. (Периметр.)
6. Прибор для построения окружности. (Циркуль.)
7. Произведение длины на ширину прямоугольника. (Площадь.)
8. Общее название всех фигур. (Многоугольник.)

9. Единица длины. (Метр.)
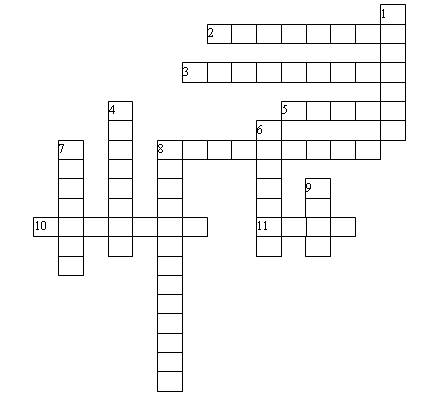
2. Работа в печатной тетради № 2.
задание № 170.
– назовите признаки числового луча.
– Что называют единичным отрезком?
– Что называют координатой точки?
Далее учащиеся выполняют чертеж:

А(62), В(64), С(76), Д(80).
VI. Итог урока.
Домашнее задание: № 23, 24 (учебник); № 173, 175, 178 (рабочая тетрадь).
Урок 122
Повторение по
теме
«АРИФМЕТИЧЕСКИЕ
ЗАДАЧИ»
Цели: совершенствовать умения решать составные задачи, развивать умение анализировать и рассуждать.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Задача.
С первой грядки собрали 11 кг огурцов, со второй – на 9 кг больше, чем с первой, а с третьей – на 4 кг меньше, чем со второй. Сколько килограммов огурцов собрали с третьей грядки?
2. Найдите неверные равенства. Измените в них выражение, записанное справа от знака равенства, так, чтобы равенство стало верным.
16 – 9 = 23 – 6 18 – 9 = 99 – 90
44 + 6 = 100 – 50 37 + 10 = 47 – 10
3. Игра на внимание.
Учащиеся должны запомнить и воспроизвести карточки, не забывая о точках.
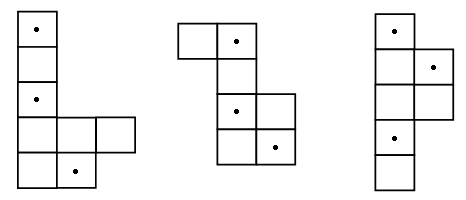
4. Геометрическое задание.
– Сложите фигуру, представленную на доске.
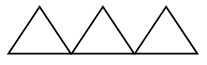
– Сколько треугольников на чертеже?
– Назовите признаки треугольников.
– Переложите 2 палочки так, чтобы получилось 4 равных треугольника.
Решение:
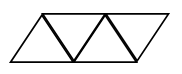
III. Сообщение темы урока.
Математический кроссворд
1. Прямоугольник, у которого все стороны равны. (Квадрат.)
2. Если к значению разности прибавить вычитаемое, то получим… (уменьшаемое).
3. Стороны прямоугольника попарно… (равны).
4. Великий философ, живший в VI веке до нашей эры, его именем названа таблица умножения. (Пифагор.)
5. Чтобы узнать, на сколько одно число больше или меньше другого, надо из большего меньшее … (вычесть).
6. Прямую, у которой есть начало и конец, называют … (отрезок).
7. В выражениях со скобками в первую очередь выполняем действие в… (скобках).
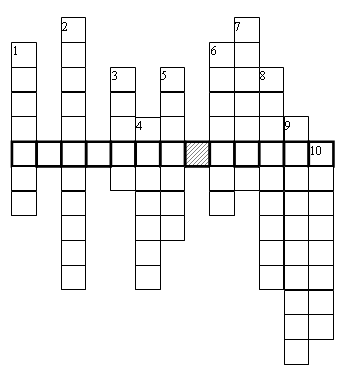
8. Чтобы узнать, во сколько раз одно число больше или меньше другого, надо большее на меньшее… (разделить).
9. Царица наук. (Математика.)
10. Результат деления называют значение … (частного).
Ключевое слово: РЕШЕНИЕ ЗАДАЧ.
iv. Работа по теме урока.
1. Работа по учебнику.
Задание № 1 (с. 98).
– Прочитайте текст. Является ли он задачей?
– Что известно? Что требуется узнать?
– Запишите кратко условие задачи в таблицу и решите эту задачу.
Запись:

Решение:
1) 6 · 3 = 18 (п.) – пришили к 3 курткам.
2) 18 + 8 = 26 (п.) – всего.
Ответ: 26 пуговиц.
Задание № 3 (с. 98).
– Прочитайте текст задачи.
– Что известно? Что требуется узнать?
– Запишите кратко условие задачи и решите ее.
Запись:
Было – 40 л.
Посадили – 2 к. по 9 л.
Осталось – ? л.
Решение:
1) Сколько луковиц посадили?
9 · 2 = 18 (л.).
2) Сколько луковиц осталось?
40 – 18 = 22 (л.).
Ответ: 22 л.
2. Работа в печатной тетради № 2.
Задание № 176.
Чертеж:

Задание № 180.
– Рассмотрите иллюстрации.
– Выразите рост Пети в метрах и сантиметрах. (16 дм = 1 м 60 см.)
– Выразите рост Вани в метрах и сантиметрах. (8 дм = 80 см.)
– Объясните, что обозначают данные выражения.


V. Продолжение работы по теме урока.
1. Работа по учебнику.
Задание № 7 (с. 98).
– Прочитайте текст задачи.
– Что известно? Что требуется узнать?
– запишите условие задачи в таблицу.
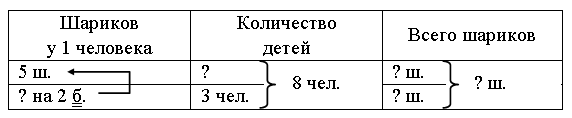
– Запишите решение задачи разными способами.
Решение:
1-й способ.
1) Сколько детей держат по 5 шариков?
8 – 3 = 5 (чел.).
2) Сколько шариков у 5 детей?
5 · 5 = 25 (ш.).
3) Сколько шариков у каждого остального ребенка?
5 + 2 = 7 (ш.).
4) Сколько шариков у трех детей?
7 · 23 = 21 (ш.).
5) Сколько шариков всего?
25 + 21 = 46 (ш.).
2-й способ.
1) Сколько шариков по 5 у всех детей?
5 · 8 = 40 (ш.).
2) Сколько шариков купили еще?
2 · 3 = 6 (ш.).
3) Сколько всего шариков?
40 + 6 = 46 (ш.).
Ответ: 46 шариков.
– Сравните оба способа решения. Какой способ более удобный?
2. Работа в печатной тетради № 2.
Задание № 181.
– Прочитайте условие задачи.
– Что известно? Что требуется узнать?
– Заполните таблицу.
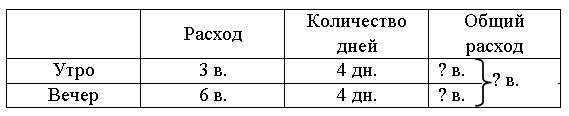
– Решение задачи запишите разными способами.
Запись:
1-й способ.
3 · 4 + 6 · 4 = 36 (в.).
2-й способ.
(3 + 6) · 4 = 36 (в.).
Ответ: 36 в.
VI. Итог урока.
Домашнее задание: № 13, 14 (учебник); № 177, 178 (рабочая тетрадь).
Урок 123
Повторение по
теме
«АРИФМЕТИЧЕСКИЕ
ЗАДАЧИ»
Цели: совершенствовать умения решать составные задачи, составлять задачи по иллюстрации, решать задачи разными способами; развивать логическое мышление и умение рассуждать.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Найдите правило, по которому записаны три числа в каждом прямоугольнике, и запишите в окошки нужные числа.
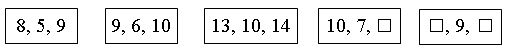
2. Задача.
В первом бочонке 7 кг мёда, а во втором – на 5 кг больше. Сколько килограммов мёда в этих двух бочонках?
– Выберите схематический чертеж, который подходит к задаче. Решите задачу.
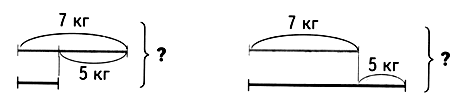
– Каким словом, записанным на карточке, надо заменить одно слово в условии задачи, чтобы новой задаче соответствовал оставшийся схематический чертёж? Выберите эту карточку.
![]()
3. Круговые примеры.
– Узнайте, решив примеры, какую фигуру покажут зрителям ученики на спортивном празднике.
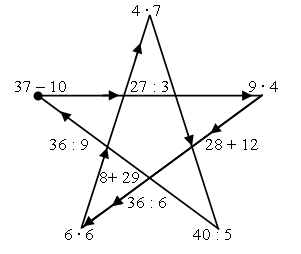
4. геометрическое задание.
– Сколько квадратов на чертеже?

III. Сообщение темы урока.
IV. Работа по теме урока.
1. работа по учебнику.
Задание № 15 (с. 99).
– Прочитайте текст задачи.
– Что известно? Что требуется узнать?
– Запишите условие задачи в таблицу.
|
Цена |
Количество |
Стоимость |
|
? р. |
8 б. |
48 р. |
|
одинаковая |
? б. |
18 р. |
|
одинаковая |
? б. |
36 р. |
|
одинаковая |
? б. |
54 р. |
– Как найти цену? (Стоимость разделить на количество.)
– Как узнать количество купленных билетов? (Стоимость разделить на цену.)
Далее учащиеся самостоятельно записывают решение задачи.
Взаимопроверка в парах.
Задание № 18 (с. 100).
– Прочитайте текст задачи.
– Что известно? Что требуется узнать?
– Заполните таблицу.

Решение:
1) Сколько стоит 1 карандаш?
42 : 7 = 6 (р.).
2) Сколько стоят 3 карандаша?
6 · 3 = 18 (р.).
Ответ: 18 рублей.
– Как узнать стоимость покупки? (Цену надо умножить на количество.)
2. Работа в печатной тетради № 2.
Задание № 183.
– Рассмотрите иллюстрацию. Составьте задачу.
– Что известно? Что требуется узнать?
При необходимости учащиеся используют схему-подсказку.

Задание № 184.
– Составьте задачу по краткой записи.
– Что известно?
– Что требуется узнать?
– Запишите решение с помощью выражения.
Запись:
15 + (15 + 15) = 45 (р.).
Ответ: 45 р.
При затруднениях учитель может использовать карточку-помощницу.
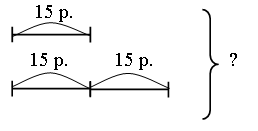

V. Продолжение работы по теме урока.
1. Работа в печатной тетради № 2.
Задание № 182.
– Прочитайте текст. Можно ли его назвать задачей?
– Что известно?
– Поставьте вопрос к условию задачи так, чтобы она решалась делением. (Во сколько раз у Вити марок больше, чем у Миши? Во сколько раз у Миши марок меньше, чем у Вити?)
Решение:
54 : 9 = 6 (раз).
– Объясните, что обозначают выражения:

2. Работа по учебнику.
Задание № 28 (с. 115).
– Прочитайте текст задачи.
– Что известно?
– Что требуется узнать?
– Запишите кратко условие задачи.
Запись:
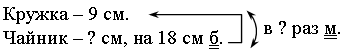
Решение:
1) Какова высота чайника?
18 + 9 = 27 (см).
2) Во сколько раз высота чайника выше высоты кружки?
27 : 9 = 3 (раза).
Ответ: в 3 раза выше.
3. Решение математического кроссворда.
По горизонтали:
3. Период в 100 лет. (Век.)
4. Результат сложения. (Сумма.)
6. Четырехугольник, у которого все углы прямые. (Прямоугольник.)
8. Что получится, если к разности прибавить вычитаемое? (Уменьшаемое.)
9. Результат вычитания. (Разность.)
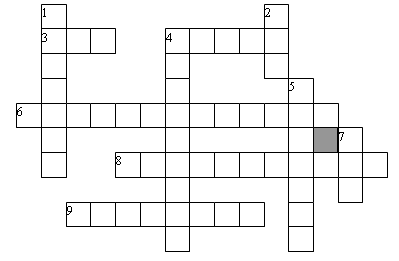
По вертикали:
1. Прямоугольник, у которого все стороны равны. (Квадрат.)
2. Промежуток времени, равный 60 минутам. (Час.)
4. Что получится, если из суммы вычесть слагаемое. (Слагаемое.)
5. Прибор для измерения длины предметов. (Линейка.)
7. Промежуток времени, равный 12 месяцам. (Год.)
VI. Итог урока.
Домашнее задание: № 35, 36 (учебник); № 177 (рабочая тетрадь).
Урок 124
Повторение по
теме
«ФИГУРЫ
И ВЕЛИЧИНЫ»
Цели: совершенствовать умения и навыки решения геометрических задач на нахождение периметра и площади; закреплять знание определений и основных свойств геометрических фигур; развивать пространственное мышление.
Ход урока
I. Организационный момент.
II. Устный счет.
1. Отгадайте загадку.
В сенокос горька,
А в мороз сладка.
Что за ягодка?
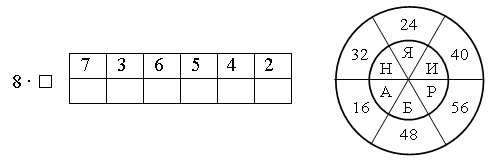
2. Вставьте арифметические знаки так, чтобы равенства были верными.

3. Из каждого столбика выберите «лишнее» число.
6 32 66
18 28 88
24 16 77
22 29 55
30 24 13
4. Сколько треугольников лежит внутри круга, сколько пересекается с кругом, сколько лежит вне круга?
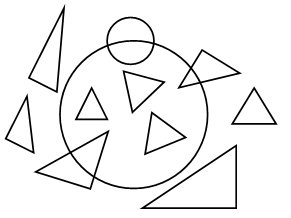
III. Сообщение темы урока.
IV. Работа по теме урока.
Задание № 1 (с. 104) выполняется устно.
На доске можно составить схему:
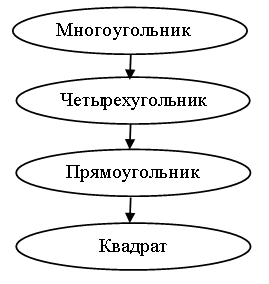
Опираясь на данную схему, учащиеся называют свойства и дают определения.
Задание № 2 (с. 104).
учащиеся выполняют самостоятельно. Взаимопроверка в парах.
Задание № 3 (с. 105).
учащиеся соединяют верные утверждения с геометрической фигурой.
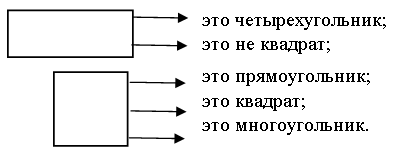
Задание № 4 (с. 105).
Учащиеся определяют верность утверждений.
• Любой квадрат является прямоугольником. (Да.)
• Не любой прямоугольник является квадратом. (Да.)
• Среди четырехугольников есть прямоугольники. (Да.)
• Квадрат – это не прямоугольник. (Нет.)
• Бывают прямоугольники с четырьмя равными сторонами. (Да.)
Задание № 5 (с. 105).
Чертеж:
– Сколько осей симметрии у квадрата? (4 оси симметрии.)

Задание № 8 (с. 106).

– Сколько треугольников на чертеже?
– Сколько четырехугольников на чертеже?

Задание № 9 (с. 106).
Утверждение: «Если два квадрата имеют общую сторону, то эти квадраты равны» – верно.
Учащиеся выполняют построение в тетради и проверяют данное утверждение.
Задание № 10 (с. 106).
– Какая фигура является пересечением (общей частью):
а) квадрата и луча?




Задание № 11 (с. 106).
– Рассмотрите чертежи и назовите отрезки, которые являются диагоналями прямоугольника АВМС.

Ответ: АМ.

Ответ: АМ и ВС.
– Назовите основные свойства прямоугольника.
– Что такое диагональ прямоугольника?
– Назовите свойства диагоналей прямоугольника.
2. Работа в печатной тетради № 2.
Задание № 191.
Учащиеся проводят оси симметрии каждой фигуры:
Чертеж:

– Сколько осей симметрии имеет треугольник? (Три оси симметрии.)
– Почему? (У данного треугольника все стороны равны.)
– Почему текст письма не имеет ни одной оси симметрии?
Задание № 192.
– Назовите признаки окружности.

– Пройдет ли окружность с центром в точке О через каждую красную точку?
Далее учащиеся выполняют построение с помощью циркуля.

V. Продолжение работы по теме урока.
1. Работа по учебнику.
задание № 23 (с. 108).
– Рассмотрите чертеж.

– Чем является отрезок АК для квадрата АВКС? (Диагональю.)
– Чем является отрезок АК для квадрата КАЕМ? (Стороной.)
Задание № 24 (с. 108).
Учащиеся заполняют таблицу:
|
Площадь – 18 см2 |
||||||
|
Длина |
1 |
2 |
3 |
6 |
2 |
18 |
|
Ширина |
18 |
9 |
6 |
3 |
9 |
1 |
Справочный материал для учителя
Измерение площади на Руси
– Мы часто говорили о практическом применении математических знаний в жизни людей. Необходимость заставила человека уже в древности измерять не только длину, расстояние, но и площадь предмета. В обычной жизни площадью мы называем большое, открытое пространство на улице, покрытое асфальтом. Но оказывается, что площадь можно найти и у крышки, и у тетради, у учебника, у пола в классе, у земельного участка. Для измерения площади у русского народа были свои особые мерки: копна, выть, соха, обжа, коробья, веревка, жеребья. Но основными стали десяти и честь. Десятичной называлась поверхность квадрата со стороной 50 сажен (1 сажень = 2,1336 м). Хозяйственная десятина – поверхность прямоугольника со сторонами 30 и 80 сажен.
Сейчас мы не используем этих мер площади. От древних землемеров нам досталось только само слово «площадь».
2. Решение математического кроссворда.

По горизонтали:
1. Значение разности 79 – 9. (Семьдесят.)
2. Мера емкости. (Литр.)
3. Единица длины: 10 см = 1 … (Дециметр.)
4. Число, на которое делят. (Делитель.)
5.
Название фигуры  (Окружность.)
(Окружность.)
По вертикали:
4. Значение выражения 6 : 3. (Два.)
6. Арифметическое действие 3 + 2 = 5. (Сложение.)
7. Арифметическое действие, обратное умножению. (Деление.)
8. Единица длины 100 см = 1 … (Метр.)
9. Число, которое делят. (Делимое.)
10. Название выражения 7 + 3. (Сумма.)
11. Название фигуры  .
(Треугольник.)
.
(Треугольник.)
12. Фигура ![]() .
(Луч.)
.
(Луч.)
13. Название фигуры  (круг.)
(круг.)
VI. Итог урока.
Домашнее задание: № 16, 21 (учебник); № 187, 188, 189 (рабочая тетрадь).
Уроки 125–136 (резервные)
Программой предусмотрены резервные уроки в объеме учебных часов, выделенных на изучение математики, особенно для базисных и сложных тем. Резервные уроки используют для восполнения пробелов в знаниях учащихся или для дополнительного изучения отдельных вопросов, повторения и обобщения учебного материала темы.
Анализ
курса математики по УМК
«Начальная школа ХХI века»
В курсе математики 2 класса получили развитие основные методические идеи и подходы в обучении, которые были заложены в основу построения курса 1 класса. Так, реализация идеи о разностороннем математическом развитии младших школьников позволила ввести в курс новую для начальной школы содержательную линию логико-математических понятий и отношений, объединить многочисленные разрозненные математические сведения, традиционно относящиеся к алгебре, геометрии и другим разделам математики, в несколько цельных содержательных линий: элементы арифметики, величины и их измерение, элементы алгебры, элементы геометрии. Вместе с линией логико-математических понятий получается пять линий содержания обучения, которые в курсе тесно взаимосвязаны.
Эту связь обеспечивает применение нетрадиционных подходов к раскрытию конкретного содержания обучения, применение иной, необычной последовательности рассмотрения учебного материала, оригинальной методики.
Курсы 1 и 2 классов построены на общей научно-методической основе, реализующей принцип комплексного развития личности младшего школьника и позволяющей организовать целенаправленную работу по формированию у учащихся важнейших элементов учебной деятельности.
Важным принципом конструирования курса является дифференциация, которая заключается как в отборе содержания обучения, так и в предъявлении к учащимся разного уровня требований. В программе предлагаются два варианта требований к математической подготовке второклассников. Первый соответствует требованиям «Обязательного минимума содержания начального общего образования» («ученик должен»).
Для учащихся, обладающих более высоким потенциалом математических способностей, программой предусмотрен повышенный уровень требований («ученик может»).
Система упражнений по любой программной теме построена так, что учитель может осуществлять обучение в соответствии с возможностями каждого ребенка.
Во втором варианте требования сгруппированы по видам деятельности: ученик должен уметь называть или различать определенные математические объекты, сравнивать их, моделировать учебную ситуацию, воспроизводить по памяти необходимые для дальнейшего обучения конкретные знания (например таблицу умножения). При этом минимальные и расширенные требования отдельно не выделяются. Рекомендуем учителю иметь в виду оба варианта требований.
В соответствии с учебным планом на изучение математики во 2 классе отводится 136 часов (по 4 урока в неделю).
УМК «Математика» состоит из учебника и двух рабочих тетрадей.
Учебник содержит материал, предназначенный для организации разнообразных видов и форм работы с детьми: устной работы (коллективное обсуждение учебной задачи, устный счет, решение задач без выполнения записей) и письменной работы (запись решения задач, выполнение геометрических построений). Для письменных работ используется обычная тетрадь в клетку.
Учебник построен по тематическому принципу. Это значит, что материал учебника распределен не по урокам, а по темам. Тематический принцип позволяет учителю отказаться от обязательного выполнения на уроке определенного количества упражнений, предоставляет возможность творчески подойти к отбору необходимого материала с учетом особенностей учащихся.
Рубрики «Узнаем новое» и «Вспоминаем пройденное» помогают учащимся и учителю лучше ориентироваться в учебнике. В рубрике «Узнаем новое» изложены необходимые теоретические сведения и система упражнений. Теоретические сведения, как правило, помещены сразу после названия темы и либо представлены в виде связного текста, который ученик должен прочитать и понять, либо даны в проблемном изложении. В редких случаях они даются после нескольких упражнений подготовительного характера.
Упражнения рубрики «Вспоминаем пройденное» не являются простым повторением ранее изученного. Это задания, цель которых – расширение первичных знаний и умений, полученных учащимися после ознакомления с новой темой, а также решение новых видов задач или овладение учащимися новыми способами действий.
Для повышения интереса учащихся к предмету и расширения их кругозора в учебник включен материал из истории математики (рубрика «Путешествие в прошлое»). Читая и анализируя эти тексты, дети знакомятся с историческими событиями и явлениями в области математики, узнают об ученых-математиках. Кроме того, в рубрике «Путешествие в прошлое» приводятся задачи, головоломки, занимательные упражнения.
Методический аппарат учебника разработан с учетом деятельностного подхода к обучению. Например, на страницах учебника (рубрика «Узнаем новое») «активно действуют» два персонажа – Волк и Заяц; они что-то измеряют, чертят, вычисляют. Второклассники должны вникнуть в то, что делают эти персонажи, проверить и оценить способ действия каждого из них, выбрать рациональный. Как правило, способ решения учебной задачи, который предлагает Волк, не самый лучший. Более практично и умно действует Заяц. Нередко учащиеся находят и свой, оригинальный, способ действия. Многие упражнения школьники выполняют, работая в парах.
Материал, представленный в рабочих тетрадях, дополняет содержание учебника упражнениями, способствующими формированию у второклассников необходимых умений и навыков.
В учебник и рабочие тетради включены упражнения занимательного характера, нестандартные задачи, требующие от ученика проявления сообразительности. Эти упражнения и задачи, как и задания повышенной трудности по основному программному материалу, выделены особо.
К некоторым заданиям даются так называемые карточки-помощницы (в системе условных обозначений они именуются как «Подсказка для тебя»). Их цель – помочь, как правило, слабому ученику найти способ решения задачи, выполнить запись по данному образцу, дать возможность вспомнить что-либо из пройденного материала. Иногда такие карточки-помощницы предлагаются и к заданиям повышенной сложности. Обратим внимание на то, что количество упражнений в учебном комплекте умышленно дано с некоторым избытком. Это сделано для того, чтобы обеспечить учителю свободу в подборе упражнений для каждого урока с учетом индивидуальных возможностей учащихся. Если класс сильный и усвоение материала идет быстрым темпом, учитель по своему усмотрению может пропускать более легкие упражнения, зато более тщательно должна вестись работа над упражнениями повышенного уровня сложности.
Ориентироваться в учебнике и рабочих тетрадях учащимся помогают специальные условные обозначения (знаки): «Запомни», «Обрати внимание», «Используй фишки» и др.
Задания для домашней работы специально не выделяются. Учитель подбирает их по своему усмотрению.
ЗАДАНИЯ И ИГРЫ
С ГЕОМЕТРИЧЕСКИМИ ОБЪЕКТАМИ
Начиная с первого класса крайне желательно включать в уроки математики разнообразные задания, позволяющие на наглядном геометрическом материале формировать у детей пространственное воображение, а также основные мыслительные операции.
Ниже мы остановимся на нескольких видах таких заданий, которые ученики воспринимают как увлекательные игры.
1. Задания на построение геометрических фигур.
1) Начертите окружность, проведите диаметр (радиус) и измерьте его.
2) На окружности отмечены точки А, С и В. Какова длина окружности?

3) Сравните радиус и диаметр у одной и той же окружности.
4) Разделите окружность на 2 и 4 равные части.
5) Найдите сумму всех сторон.

6) Какой из отрезков является радиусом окружности: ОА или ОВ?

7) Выполните чертеж.

8) Найдите длину сторон пятиугольника.

9) Какая фигура «лишняя»?

10) Образуйте из букв слова ДРУГ слово, имеющее отношение к окружности. Разрешается заменить одну букву.
Ответ: ДУГА.
11) Выполните построение.

12) Выполните построение.

13) У куба длина ребра 2 см. Какова длина всех ребер куба? Площадь поверхности куба 12 см. Какова площадь одной грани куба?
14) Найдите сумму длин ребер.

15) Найдите высоту фигуры.

16) Найдите сумму узлов основания куба.
17) Постройте внутри куба пирамиду, не меняя основания.
18) Вычислите углы одной грани куба.
19) Найдите угол.

20) Выполните построение.

21) Решите анаграммы и исключите «лишнее» слово:
АДГУ, УДК, ТЕНРЦ, СДАУРИ, АШР.
22) Радиус конуса равен 8 п. Каков диаметр данного конуса?
23) Даны пирамида, конус, шар, куб, цилиндр. Какое из данных тел вам наиболее знакомо? Почему?
24) Площадь основания цилиндра равна 18 см2, площадь боковой поверхности – 3 см2. Какова площадь всей поверхности цилиндра?
25) Найдите углы.

2. Игра «Найди все многоугольники».
Для включения относящихся к этой игре заданий в уроки достаточно сделать на доске соответствующий чертеж. Ниже мы приводим серию постепенно усложняющихся чертежей, выполненных на основе одного и того же треугольника, к каждому из которых предлагается практически одинаковое задание-вопрос: «Сколько на чертеже многоугольников?»
После получения ответа и его проверки можно задавать более конкретные вопросы типа «Какие многоугольники есть на чертеже? Сколько на нем треугольников? Четырехугольников?» и т. д.
Основная цель работы с заданиями – выработка способа поиска ответа не хаотически, а с использованием постепенно формирующейся системы.
Планомерное включение заданий этого вида дает возможность продвигать детей в умении анализировать и синтезировать объекты, рассматривать их с различной точки зрения, соотносить производимые действия и их результаты; продвигает в умении обобщать результаты наблюдений; расширяет математический кругозор; помогает формировать связную грамотную речь, включающую математическую терминологию.
Раскроем основные направления работы с заданиями этого вида на примере первых двух чертежей.
В результате работы с первым чертежом дети должны найти на нем 3 треугольника, однако часто бывает так, что основной большой треугольник теряется, то есть чертеж расчленяется на составные части, а синтезировать из этих частей фигуру ученики еще не могут. В этом случае учитель оказывает помощь, которая может, например, заключаться в том, что чертеж воспроизводится на глазах детей: сначала возникает треугольник, а затем в нем проводится отрезок.
Возможно и использование особого, заготовленного заранее пособия такого вида: из картона вырезается треугольник-основа, на нее сверху накладываются треугольники разного цвета, которые получились при проведении отрезка, и прикрепляются к основе так, чтобы их можно было отогнуть, сверху накладывается бумажный треугольник, на котором воспроизведен чертеж. Этот треугольник тоже должен отгибаться. Если дети не находят решения, верхний треугольник отгибается, и становятся видны 2 треугольника, на которые разделен основной треугольник. Когда эти треугольники тоже отгибаются, появляется нерасчлененный основной треугольник, который и является третьим.

Работа со вторым чертежом строится так же, после чего необходимо рассмотреть оба чертежа вместе, сравнить их друг с другом и установить причину, которая привела к разнице решений (на первом чертеже 3 треугольника, на втором – 2 треугольника и четырехугольник).
Следующий шаг – создание своих чертежей, на которых тоже получается 3 треугольника или 2 треугольника и четырехугольник, а затем общий вывод о том, как в том и другом случае должен располагаться отрезок внутри треугольника (если он соединяет вершину треугольника и любую точку противоположной стороны, получается 3 треугольника, если любые точки двух сторон, которые не являются вершинами, получаем 2 треугольника и четырехугольник).
Развитие этого вида заданий может происходить за счет увеличения числа отрезков, проведенных внутри треугольника, а также за счет использования других многоугольников, имеющих большее число углов.
ЛИТЕРАТУРА
1. Истомина, Н. Б. Наглядная геометрия для 2 класса / Н. Б. Истомина. – М.: Линка-Пресс, 2002.
2. Истомина, Н. Б. Учимся решать комбинаторные задачи / Н. Б. Истомина, Е. П. Виноградова. – Смоленск: Ассоциация XXI век, 2004.
3. Кравченко, В. С. Устные упражнения по математике в 1–3 классах / В. С. Кравченко. – М.: Просвещение, 1979.
4. Рудницкая, В. М. Математика. 2 кл.: учеб. для учащихся общеобразоват. учр.: в 2 ч. / В. М. Рудницкая, Т. В. Юдачева. – М.: Вентана-Граф, 2008.
5. Рудницкая, В. М. Математика: рабочая тетрадь для 2 класса: № 1, 2 / В. М. Рудницкая, Т. В. Юдачева. – М.: Вентана-Граф, 2008.
6. Рудницкая, В. Н. Математика. 2 кл.: методика обучения / В. М. Рудницкая, Т. В. Юдачева. – М.: Вентана-Граф, 2006.
7. Энциклопедический словарь юного математика / сост. Н. П. Ернылев. – М.: Педагогика, 1980.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.