МЕТОДИЧЕСКАЯ РАЗРАБОТКА УРОКА ПО ТЕМЕ

«ВПИСАННЫЕ И ОПИСАННЫЕ ТРЕУГОЛЬНИКИ»

Бычковская Анна Иосифовна,

учитель математики высшей категории,

государственное учреждение образования

 «Ждановичская средняя школа»

Минская область, Минский район, Республика Беларусь

Аннотация: в статье рассматриваются приёмы и методы, используемые при проведении урока обобщения в 9 классе по теме «Вписанные и описанные треугольники»: разгадывание кроссворда, нахождение намеренно сделанных ошибок, решение задач по готовому чертежу.

Ключевые слова: теоретическая разминка, оценочный лист, готовый чертёж, треугольник, вписанная и описанная окружности, соотношение, угол, сторона.

METHODICAL DEVELOPMENT OF A LESSON ON THE TOPIC

"INSCRIBED AND DESCRIBED TRIANGLES"

Bychkovskaya Anna Iosifovna,

Abstract: the article discusses the techniques and methods used in conducting a generalization lesson in the 9th grade on the topic "Inscribed and described triangles": solving a crossword puzzle, finding intentionally made mistakes, solving problems based on a ready-made drawing.

Keywords: theoretical warm-up, evaluation sheet, finished drawing, triangle, inscribed and circumscribed circles, ratio, angle, side.

Тип урока: урок обобщения

Эпиграф урока:

 «Считай несчастным тот день или тот час, в котором, ты не усвоил ничего нового, ничего не прибавил к своему образованию»

                                                                Ян Амос Каменский.

Цель урока:

·       обобщить и систематизировать знания учащихся по теме «Вписанные и описанные треугольники», совершенствовать навыки решения задач по данной теме.

Задачи урока:

·       способствовать развитию умений сравнивать, выявлять закономерности, обобщать.

·       способствовать  созданию  условий для  самоконтроля усвоения знаний и умений.

·       содействовать развитию логического мышления, внимания, речи, повышению познавательной активности детей

·       способствовать воспитанию наблюдательности, самостоятельности, чувства ответственности, повышению уровня мотивации обучения.

Структура урока.

1.     Организационный момент (1 мин.)

2.     Проверка домашнего задания (3 мин)

3.     Теоретическая разминка. (3мин)

4.     Запись основных формул на доске (3 мин)

5.     Разгадывание кроссворда. (3мин)

6.     Нахождение ошибки в теоретических положениях Саши Иванова (5 мин)

7.     Устное решение задач на готовых чертежах (10 мин)

8.     Минутка отдыха (физкультминутка) (1 мин)

9.     Письменное решение задач в тетрадях и на доске. (8 мин)

10. Домашнее задание (2 мин)

11. Подведение итогов, выставление оценок. (3 мин)

12. Рефлексия. (3 мин)

1.     Организационный момент.

Постановка целей:

 Сегодня у нас необычный урок, на нём присутствуют гости, учителя математики нашей школы

Цель нашего с вами урока повторить, обобщить систематизировать свои знания по теме «Вписанные и описанные треугольники»,

совершенствовать навыки решения задач по данной теме.

В процессе решения этих задач мы будем стараться пояснять их решения грамотно и красиво, и этим развивать своё мышление и речь. Также мы будем стараться думать и анализировать, добросовестно выполнять каждое задание.

Эпиграфом сегодняшнего урока мы возьмём слова Яна Амоса Каменского

«Считай несчастным тот день или тот час, в котором, ты не усвоил ничего нового, ничего не прибавил к своему образованию»

Чем же мы будем заниматься на уроке?

·        Проверка домашнего задания

·        Теоретическая разминка.

·        Запись основных формул на доске

·        Разгадывание кроссворда.

·        Нахождение ошибок в теоретических положениях Саши Иванова

·        Устное решение задач на готовых чертежах

·        Минутка отдыха (физкультминутка)

·        Письменное решение задач в тетрадях и на доске.

·        Домашнее задание

·        Подведение итогов, выставление оценок.

Чтобы легче было подвести итоги урока, мы будем использовать оценочные листы, которые у вас на партах.

Инструкция-комментарий по выставлению баллов в оценочный лист.

1.     Домашнее задание.

Ученикам, отвечающим по домашнему заданию у доски, ставится по 3 балла, если нет замечаний, остальным правильно выполнившим домашнее задание – 2 балла

2.     Теоретическая разминка.

За правильный ответ – 1 балл.

3.     За правильный ответ на вопрос кроссворда ученик получает 1 балл.

4.     Нахождение ошибок в теоретических положениях Саши Иванова.

За исправление ошибки – 1 балл.                          

5.     Устное решение задач на готовых чертежах

За полное решение задачи по готовому чертежу –2 балла.

6.     Письменное решение задач в тетрадях и на доске. 

    За решённую задачу ученик получает 2 балла.

Ученик, набравший 14 и более баллов, получает отметку – 10, от 10 до 14 – отметку 9, от 8 до 11 – отметку 8, 7 баллов -  отметка 7, 6 балов - отметка 6  и т.д.

2. Проверка домашнего задания.

Два ученика вызываются к доске для записи и объяснения домашних задач

№1. Найдите радиус окружности вписанной в прямоугольный треугольник с катетами 8 и 15 см.

№2. Один из катетов прямоугольного треугольника равен 12 см. Радиус вписанной в него окружности равен 5 см. Найти периметр треугольника.

После объяснения учащиеся класса задают вопросы отвечающим.

3.Теоретическая разминка

1.     Дайте определение окружности, вписанной в тре­угольник.

2.     Какую из замечательных точек треугольника назы­вают центром вписанной окружности?

3.     Чему равен радиус вписанной окружности?

4.     Дайте определение описанной около треугольника окружности.

5.     Какую из замечательных точек треугольника назы­вают центром описанной окружности?

6.     Чему равен радиус описанной окружности?

7.     Где находится центр окружности, описанной возле прямоугольного треугольника?

8.     Чему равен её радиус?

9.     Как найти радиус вписанной в прямоугольный треугольник окружности, зная гипотенузу и полу­периметр?

10. Как найти радиус описанной возле треугольника ок­ружности, зная сторону и противолежащий угол?

11. Как найти площадь треугольника ( три формулы)

4. Запись основных формул на доске

Произвольный треугольник

         

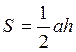
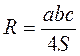
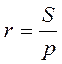
Прямоугольный треугольник

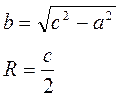             r = c-p

     Равносторонний треугольник

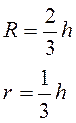    R=2r

1.     Разгадывание кроссворда

1.     Окружность, которая касается всех сторон треугольника.

2.     Где лежит центр вписанной окружности

3.     Что нужно знать для нахождения площади

4.     Окружность, вершины которой лежат на окружности

5.     В каком треугольнике радиус описанной окружности равен половине большей стороны

6.     Где лежит центр описанной окружности около прямоугольного треугольника

7.     Расстояние от центра окружности до любой точки на окружности

 

 

Показывается фотография учёного и сообщается краткая историческая справка.

 

ПИФАГОР

(ок. 570-ок. 500 гг. до н.э.)

 

Письменных документов о Пифагоре Самосском не осталось, а по более поздним свидетельствам трудно вос­становить подлинную картину его жизни и достижений.

 

Рис.1. Пифагор

Известно, что Пифагор покинул свой родной остров Самос в Эгейском море у берегов Малой Азии в знак протеста про­тив тирании правителя и уже в зре­лом возрасте (по преданию в 40 лет) появился в греческом городе Кро­тоне на юге Италии. Пифагор и его последователи - пифагорейцы - обра­зовали тайный союз, игравший не­малую роль в жизни греческих ко­лоний в Италии. Пифагорейцы узна­вали друг друга по звездчатому пя­тиугольнику - пентаграмме.

На учение Пифагора большое влия­ние оказала философия и религия Востока. Он много путешествовал по странам Востока: был в Египте и в Вавилоне. Там Пифагор позна­комился и с восточной математи­кой. Математика стала частью его учения, и важнейшей частью.

Пифагорейцы верили, что в число­вых закономерностях спрятана тай­на мира. Мир чисел жил для пи­фагорейца особой жизнью, числа име­ли свой особый жизненный смысл. Числа, равные сумме своих делите­лей, воспринимались как совершенные (6, 28, 496, 8128); дружественными называли пары чисел, из которых каждое равнялось сумме делителей другого (например, 220 и 284). Пи­фагор впервые разделил числа на четные и нечетные, простые и состав­ные, ввел понятие фигурного числа. В его школе были подробно рассмотрены пифагоровы тройки  натуральных чисел, у которых квадрат одного равнялся сумме квадратов двух других. Пифагору приписывалось высказывание: «Все есть число» К числам он хотел свести весь мир, и математику в частности. Но в самой школе Пифагора было сделано открытие, нарушавшее эту гармонию.

Было доказано, что  не является рациональным числом, т.е. не выражается через натуральные числа.

Естественно, что геометрия Пифагора была подчинена арифметике, это ярко проявилось в теореме носящей его имя и ставшей в  дальнейшем основой применения численных методов в геометрии. По-видимому, пифагорейцы знали правильные тела: тетраэдр, куб и додекаэдр.

Пифагору приписывают систематическое введение доказательств в  геометрию, создание планиметрии прямолинейных фигур, учения о подобии.

С   именем   Пифагора связывают учение об арифметических, геометрических и гармонических пропорциях, средних. [1, с.28]

5.     Нахождение ошибок в теоретических положениях Саши Иванова

 Вариант 1

1. Окружность называется вписанной в треугольник, если её вершины лежат на окружности.

2. Центр окружности вписанной в треугольник лежит на пересечении серединных перпендикуляров

3. В прямоугольном треугольнике

4. Центр окружности описанной около равнобедренного треугольника лежит на середине большей стороны.

5. В равнобедренном треугольнике радиус описанной окружности в 2 раза больше радиуса вписанной окружности.

6.    

Вариант 2

1. Окружность называется описанной около треугольника, если она касается всех сторон окружности.

2. Центр окружности описанной около треугольника лежит на пересечении биссектрис

3.В равнобедренном треугольнике

4. Радиус окружности, описанной около прямоугольного равен половине гипотенузы.

5. 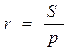           6.  

 

7.Устное решение задач на готовых чертежах [2, с.129]

8. Минутка отдыха (физкультминутка)

Рис.2. Физкультминутка

 

Ученики глазами следят за движением птицы.

 

 

 

 

 

 

1.                             Письменное решение задач в тетрадях и на доске.

Задача 

Равнобедренный треугольник вписан в окружность. Боковая сторона его равна 10 см, а высота – 8 см. Найдите радиус окружности, описанной около этого треугольника. [3, с.56]

10. Домашнее задание

№ 181, 182 (б). Небольшие комментарии для выполнения.

11. Подведение итогов, выставление оценок.

 

Таблица 1

Оценочный лист

Фамилия, имя_________________________		Кол-во баллов
1.	Домашнее задание
2.	Теоретическая разминка Запись основных формул на доске
3.	Разгадывание кроссворда
4.	Нахождение ошибки в теоретических положениях Саши Иванова
5.	Устное решение задач на готовых чертежах
6.	Письменное решение задач в тетрадях и на доске.
7.	Итоговое количество баллов
8.	Отметка за урок

 

12. Рефлексия.

Вопросы учащимся:

1.     Достигли ли мы целей сегодняшнего урока?

2.     Какое задание оказалось для вас самым лёгким?

3.     Какое задание оказалось для вас самым трудным?

4.     Довольны ли вы результатами вашей работы на уроке?

5.     Вернёмся к эпиграфу. «Считай несчастным тот день или тот час, в котором, ты не усвоил ничего нового, ничего не прибавил к своему образованию» Что же прибавил к нашему образованию этот час? Будем ли мы считать его счастливым?

Список литературы.

1.     Энциклопедический словарь юного математика / сост. А. П. Савин. –    М.: Педагогика, 1989.

2.     Казаков, В. В. Геометрия: учеб. пособие для 9-го кл. учреждений, обеспечивающих получение общ. сред. образования, с рус. яз. обучения /               В. В. Казаков. – Минск: Народная асвета, 2019.

3.     Гаврилова, Н.Ф. Поурочные разработки по геометрии: 9 класс, - М. ВАКО, 2022. – 368 с.

А.И. Бычковская, 2024