
Яковлева Татьяна Петровна,
доцент кафедры математики и физики
Камчатского государственного университета
имени Витуса Беринга,
кандидат педагогических наук, доцент,
г. Петропавловск - Камчатский
Зачетная работа по теме «Множества. Математическая логика» (для дисциплин «Математика», «Высшая математика»)
Содержание
Вариант 1
Вариант 2
Вариант 3
Вариант 4
Вариант 5
Вариант 6
Вариант 7
Вариант 8
Список используемой литературы
1. Построить таблицу истинности для двух логических функций:
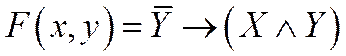
2. Построить таблицу истинности для трех логических функций:
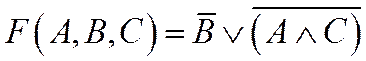
3. По данным промежуткам A и B на числовой прямой определить:
а) ![]()
б) ![]()
в)![]()
г) ![]()
д) ![]()
е)
![]() .
.
|
A |
B |
|
|
(1;7] |
1. Построить таблицу истинности для двух логических функций:
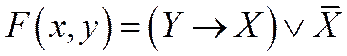
2. Построить таблицу истинности для трех логических функций:
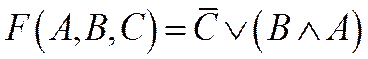
3. По данным промежуткам A и B на числовой прямой определить:
а) ![]()
б) ![]()
в)![]()
г) ![]()
д) ![]()
е)
![]() .
.
|
A |
B |
|
[0;5) |
[1;∞) |
1. Построить таблицу истинности для двух логических функций:
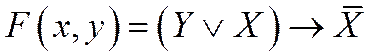
2. Построить таблицу истинности для трех логических функций:
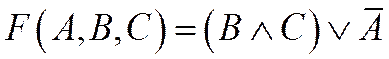
3.
По данным промежуткам A и B на
числовой прямой определить ![]() :
:
а) ![]()
б) ![]()
в)![]()
г) ![]()
д) ![]()
е)
![]() .
.
|
A |
B |
|
[2;∞) |
(1;7] |
1. Построить таблицу истинности для двух логических функций:
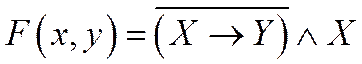
2. Построить таблицу истинности для трех логических функций:
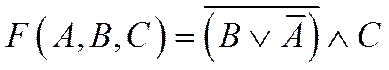
3. По данным промежуткам A и B на числовой прямой определить:
а) ![]()
б) ![]()
в)![]()
г) ![]()
д) ![]()
е)
![]() .
.
|
A |
B |
|
(-6;-3] |
[-5;-1) |
1. Построить таблицу истинности для двух логических функций:
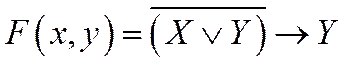
2. Построить таблицу истинности для двух логических функций:
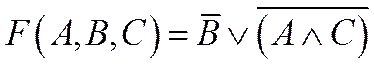
3. По данным промежуткам A и B на числовой прямой определить:
а) ![]()
б) ![]()
в)![]()
г) ![]()
д) ![]()
е)
![]() .
.
|
A |
B |
|
(-∞;1] |
(-2;∞) |
1. Построить таблицу истинности для двух логических функций:
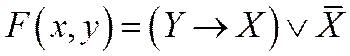
2. Построить таблицу истинности для трех логических функций:
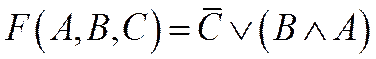
3. По данным промежуткам A и B на числовой прямой определить:
а) ![]()
б) ![]()
в)![]()
г) ![]()
д) ![]()
е)
![]() .
.
|
A |
B |
|
[-6;7] |
(0;10) |
1. Построить таблицу истинности для двух логических функций:
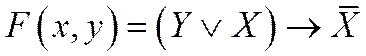
2. Построить таблицу истинности для трех логических функций:
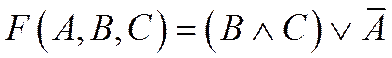
3. По данным промежуткам A и B на числовой прямой определить:
а) ![]()
б) ![]()
в)![]()
г) ![]()
д) ![]()
е)
![]() .
.
|
A |
B |
|
(-6;2] |
[-2;3] |
1. Построить таблицу истинности для двух логических функций:
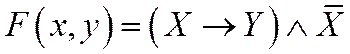
2. Построить таблицу истинности для трех логических функций:
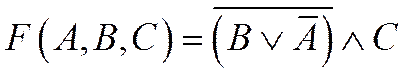
3. По данным промежуткам A и B на числовой прямой определить:
а) ![]()
б) ![]()
в)![]()
г) ![]()
д) ![]()
е)
![]() .
.
|
A |
B |
|
(0;2) |
[1;5) |
1. Баранова Е.С., Васильева Н.В., Федотов В.П. Практическое пособие по высшей математике. Типовые расчеты: Учебное пособие. СПб.: Питер, 2009. – 320 с.
2. Зимина О.В., Кириллов А.И., Сальникова Т.А. Высшая математика / Под ред. А.И. Кириллова. – М.: ФИЗМАТЛИТ, 2005. – 368 с.
3. Индивидуальные задания по высшей математике: учеб. пособие. В 4 ч. Ч. 1. Линейная и векторная алгебра. Аналитическая геометрия. Дифференциальное исчисление функции одной переменной / А.П. Рябушко [и др.]; под общ. ред. А.П. Рябушко. – Минск: Выш. шк., 2011. – 304 с.
4. Соловьев И.А., Шевелев В.В., Червяков А.В., Репин А.Ю. Практическое руководство к решению задач по высшей математике. Линейная алгебра, векторная алгебра, аналитическая геометрия, введение в математический анализ, производная и ее приложения: Учебное пособие. – СПб.: Издательство «Лань», 2007. – 320 с.
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.