Задачи по комбинаторике

Задачи для решения на закрепление нового материала

Задача № 1. Сколькими способами могут быть расставлены 5 участниц финального           

                      забега на 5-ти беговых дорожках? 

Решение: Р₅ = 5!= 1 ∙2 ∙3 ∙4 ∙5  = 120 способов.  

Задача №2. Сколько трехзначных чисел можно составить из цифр 1,2,3, если каждая     

                      цифра входит в изображение числа только один раз?

Решение: Число всех перестановок из трех элементов равно  Р₃=3!, где 3!=1 * 2 * 3=6

            Значит, существует шесть трехзначных чисел, составленных из цифр 1,2,3.

Задача № 3. Сколькими способами четверо юношей могут пригласить четырех из шести               

                       девушек на танец?

Решение: два юноши не могут одновременно пригласить одну и ту же девушку. И         

                  варианты, при которых одни и те же девушки танцуют с разными юношами,       

                  считаются разными, поэтому:     

Задача № 4. Сколько различных трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5,        

                      6, 7, 8, 9  при условии, что в записи числа каждая цифра используется только               

                      один раз?

Решение: В условии задачи предложено подсчитать число всевозможных комбинаций из 

                  трех цифр, взятых из предположенных девяти цифр, причём порядок

                  расположения цифр в комбинации имеет значение (например, числа 132)

                  и 231 различные). Иначе говоря, нужно найти число размещений из девяти        

                  элементов по три.

                  По формуле числа размещений находим:

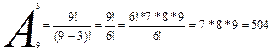                                    Ответ:  504 трехзначных чисел.

Задача №5 Сколькими способами из 7 человек можно выбрать комиссию, состоящую из 3 

                     человек?

Решение: Чтобы рассмотреть все возможные комиссии, нужно рассмотреть все  

                   возможные 3 – элементные подмножества множества, состоящего из  7

                   человек. Искомое число способов равно

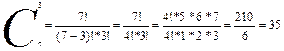
Задача № 6. В соревновании участвуют 12 команд. Сколько существует вариантов  

                       распределения призовых (1, 2, 3) мест?

Решение: А₁₂³ = 12 ∙11 ∙10 = 1320 вариантов распределения призовых мест. Ответ: 1320 вариантов.

Задача № 7.  На соревнованиях по лёгкой атлетике нашу школу представляла команда из  

                       10 спортсменов. Сколькими способами тренер может определить, кто из них  

                        побежит в эстафете 4´100 м на первом, втором, третьем и четвёртом этапах?

Решение: Выбор из 10 по 4 с учётом порядка:  способов.

                                                                                   Ответ: 5040 способов.

Задача № 8. Сколькими способами можно выложить в ряд красный, черный, синий и

                       зеленый шарики?

Решение: На первое место можно поставить любой из четырех шариков (4 способа), на

                  второе – любой из трех оставшихся (3 способа), на третье место – любой из     

                  оставшихся двух (2 способа), на четвертое место – оставшийся последний шар.

                  Всего 4 · 3 · 2 · 1 = 24 способа.

                                              Р₄ = 4! = 1 · 2 · 3 · 4 = 24.                                                                                                                                                                                   Ответ: 24 способа.

Задача № 9. Учащимся  дали список из 10 книг, которые рекомендуется прочитать во

                      время каникул. Сколькими способами ученик может выбрать из них 6 книг?

Решение: Выбор 6 из 10 без учёта порядка:   способов.

Ответ: 210 способов.

Задача № 10. В 9  классе учатся 7 учащихся, в 10  - 9 учащихся, а в 11  - 8 учащихся. Для

                       работы на пришкольном участке надо выделить двух учащихся из 9 класса,

                       трех – из 10,  и одного – из 11 . Сколько существует способов выбора  

                       учащихся для работы на пришкольном участке?

Решение: Выбор из трёх совокупностей без учёта порядка, каждый вариант выбора из

                  первой совокупности (С₇²)  может сочетаться с каждым вариантом выбора из     

                  второй (С₉³)  ) и с каждым вариантом выбора третьей (С₈¹)  по правилу  

                  умножения получаем:

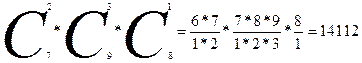
                                                                                                 Ответ: 14 112 способов.

Задача № 11.  Девятиклассники Женя, Сережа, Коля, Наташа и  Оля побежали на  

                         перемене к теннисному столу, за которым уже шла игра. Сколькими

                         способами подбежавшие к столу пятеро девятиклассников могут занять

                         очередь для игры в настольный теннис?

Решение: Первым в очередь мог встать любой девятиклассник, вторым – любой из

                  оставшихся троих, третьим – любой из оставшихся двоих и четвёртым –

                  девятиклассник, подбежавший предпоследним, а пятым – последний. По

                  правилу умножения у пяти  учащихся существует 5· 4×3×2×1=120 способов  

                  занять очередь.