ЗАДАНИЕ ПО ТЕМЕ СИМПЛЕКСНЫЙ МЕТОД РЕШЕНИЯ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

5.5.1. Предприятие производит 3 вида продукции: А₁, А₂, А₃, используя сырье двух видов: В₁ и В₂. Известны затраты сырья i-го вида на единицу изделия j-го вида (),  количество сырья каждого вида  (i=1,2), а так же прибыль, полученная от единицы изделия j-го вида с_j (j=1,2,3).

Сколько изделий каждого вида необходимо произвести, чтобы получить:

1) максимум прибыли;

2) максимум товарной продукции?

3) Решить задачу при дополнительных условиях: предприятие платит за хранение единицы сырья В₁ и В₂ соответственно 0,1 и 0,3 денежных единицы.

4) Решить задачу при условии, что задан план выпуска изделий. При решении учитывать возможность перевыполнения плана.

План =  (200, 100, 250)    

  -------------

Обозначения для вариантов: в таблице приведена матрица затрат: А=(а_ij), справа от таблицы значение b_i (i=1,2) и внизу - с_j (j=1,2,3).

  ========= Решения : =============

  1)  ---- Математическая формулировка задачи:

Найти 

При ограничениях:

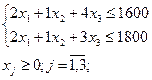
Записываю задачу в каноническом виде, добавив переменные х4 и х5:  

Найти 

При ограничениях:

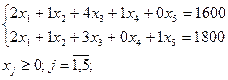
Решение см на листе 5.5.1-1 и 5.5.1-1поиск (решено «Поиском решения»)

  2) максимум товарной продукции

предполагаю – максимум штук (изделий).

Количество штук (изделий) обозначено: х1,х2,х3

Математическая формулировка задачи:

Найти 

При ограничениях:

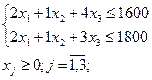
Записываю задачу в каноническом виде, добавив переменные х4 и х5:  

Найти 

При ограничениях:

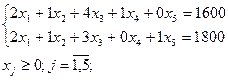
Решение см на листе 5.5.1-2 и 5.5.1-2поиск (решено «Поиском решения»)

 ---------------

3) Решить задачу при дополнительных условиях: предприятие платит за хранение единицы сырья В₁ и В₂ соответственно 0,1 и 0,3 денежных единицы.

(Предполагаю, что ищется максимум прибыли.)

Тогда расход сырья В1 = 2х1+х2+4х3

 --------------

4) Решить задачу при условии, что задан план выпуска изделий. При решении учитывать возможность перевыполнения плана.

План =  (200, 100, 250)    

  -------------

5.5.2. Решить симплекс-методом задачу из п 1.5.1.

Решение выполнено в ЭТ Excel (файл zadaci_glavi5.xls)

  ----------------

5.5.3. Решить симплекс-методом задачу из п 1.5.2.

найти

при ограничениях:

1. Преобразую задачу к каноническому виду, добавляя переменные x3,x4,x5.

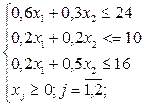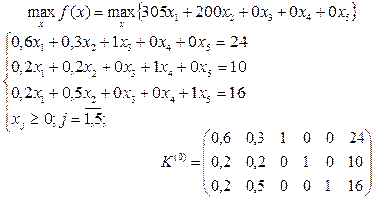Расширенная матрица

системы линейных уравнений является исходной К-матрицей ЗЛП, которая определяет исходный опорный план:

Кроме того,

Решение выполнено в ЭТ Excel (файл tema5-zad.xls)