1. Формат docx. Опубликовано 23.04.2025 в 10:16:50. Автор Кутепова Олеся Александровна

Добавить материал

и получить 10 документов
и свидетельство СМИ

Публикация в СМИ для учителей

Бесплатное участие. Свидетельство СМИ сразу.
Мгновенные 10 документов в портфолио.

Добавить материал

ФОС С, Э .docx

МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ РОСТОВСКОЙ ОБЛАСТИ

ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ РОСТОВСКОЙ ОБЛАСТИ

« ГУКОВСКИЙ СТРОИТЕЛЬНЫЙ ТЕХНИКУМ»

ФОНД ОЦЕНОЧНЫХ СРЕДСТВ

ПО ОБЩЕОБРАЗОВАТЕЛЬНОЙ ДИСЦИПИНЕ «МАТЕМАТИКА»

для специальностей:

08.02.01 «Строительство и эксплуатация зданий и сооружений»

08.02.14 «Эксплуатация и обслуживание многоквартирного дома»

профессии:

15.01.05«Сварщик (ручной и частично механизированной сварки (наплавки)»

08.01.07 «Мастер общестроительных работ»

Гуково

РАССМОТРЕНО

на заседании ПЦК ЕН и МД

«30» августа 2024 г.

Протокол №___ от «30» августа 2024 г.

Председатель ___________

УТВЕРЖДАЮ

Заместитель директора

по УП и МР

__________________

«30» августа 2024 г

Фонд оценочных средств для проведения текущего контроля и промежуточной аттестации в форме письменного экзамена по общеобразовательной дисциплине Математика основной профессиональной образовательной программы (ОПОП) разработан в соответствии с рабочей программой учебной дисциплины Математика (утв. 29.08.23); положением по итоговому контролю учебных достижений обучающихся при реализации федерального государственного образовательного стандарта.

Организация-разработчик: ГБПОУ РО «ГСТ»

Разработчик: Пингина Т.П., преподаватель высшей квалификационной категории

СОДЕРЖАНИЕ

1.	ПАСПОРТ ФОНДА ОЦЕНОЧНЫХ СРЕДСТВ……………….........	4
2.	РЕЗУЛЬТАТЫ ОБУЧЕНИЯ, РЕГЛАМЕНТИРОВАННЫЕ ФГОС ООО С УЧЕТОМ ФГОС СПО…………………………	5
3	ОЦЕНКА ОСВОЕНИЯ УЧЕБНОЙ ДИСЦИПЛИНЫ…………………	15
4	ФОНД ОЦЕНОЧНЫХ СРЕДСТВ ТЕКУЩЕГО КОНТРОЛЯ………..	18
	Входной контроль………………………………………………………….	18
	Вопросы для устных ответов………………………………………………	20
	Практические работы……………………………………………………….	25
	Контрольные работы………………………………………………………..	82
5	ФОНД ОЦЕНОЧНЫХ СРЕДСТВ ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ……………………………………………………………..	96

1. ПАСПОРТ ФОНДА ОЦЕНОЧНЫХ СРЕДСТВ

Фонд оценочных средств предназначен для аттестации обучающихся на соответствие их персональных достижений при освоении программы учебной дисциплины Математика основной профессиональной образовательной программы

Фонд оценочных средств включает оценочные материалы текущего контроля по разделам и темам для объективной оценки качества освоения обучающимися содержания учебной дисциплины и промежуточной аттестации с целью выявления соответствия уровня подготовки обучающихся требованиям ФГОС СПО, а также критерии оценивания, эталоны ответов.

Текущий контроль успеваемости и промежуточная аттестация обеспечивают оперативное управление образовательной деятельностью обучающихся, ее корректировку и выявляют степень соответствия качества образования обучающихся требованиям федерального государственного образовательного стандарта.

Промежуточная аттестация по общеобразовательной дисциплине Математика проводится в форме письменного экзамена.

Объем и распределение часов

Таблица 1

	Содержание обучения	Всего (ч)	В том числе:
	Содержание обучения	Всего (ч)	Практи-ческие работы (ч)	Контроль-ная работа (ч)
1 семестр	Раздел 1. Повторение курса математики основной школы	18	6	2
	Раздел 2. Степени и корни. Степенная функция	14	2	2
	Раздел 3. Показательная функция	14	2	2
	Раздел 4. Логарифмы. Логарифмическая функция	20	6	2
	Раздел 5 Прямые и плоскости в пространстве	36	6	2+2
		102	22	12
2 семестр	Раздел 6. Координаты и векторы	10	2	2
	Раздел 7. Основы тригонометрии. Тригонометрические функции	38	8	2
	Раздел 8. Комплексные числа	8	2	-
	Раздел 9. Производная функции, ее применение	38	8	2
	Раздел 10. Многогранники и тела вращения	8	6	2
	Раздел 11. Первообразная функции, ее применение	12	2	-
	Раздел 12. Множества. Элементы теории графов	8	4	-
	Раздел 13. Элементы комбинаторики, статистики и теории вероятностей	14	6	2
	Раздел 14. Уравнения и неравенства	24	4	2
	Итого за 2 семестр:	186	42	12
	Итого за курс:	288	64	24

2. РЕЗУЛЬТАТЫ ОБУЧЕНИЯ, РЕГЛАМЕНТИРОВАННЫЕ ФГОС ООО С УЧЕТОМ ФГОС СПО

Контроль и оценка результатов освоения общеобразовательной дисциплины раскрываются через дисциплинарные результаты, направленные на формирование общих и профессиональных компетенций по разделам и темам содержания учебного материала.

Таблица 2

Общие компетенции

Планируемые результаты обучения

Личностные и метапредметные результаты

Дисциплинарные(предметные) результаты

ОК 01 Выбирать способы решения задач профессиональной деятельности применительно
к различным контекстам

Трудового воспитания:

- готовность к труду, осознание ценности трудолюбия, интерес к различным сферам профессиональной деятельности, связанным с математикой и её приложениями, умение совершать осознанный выбор будущей профессии и реализовывать собственные жизненные планы, готовность и способность к математическому образованию и самообразованию на протяжении всей жизни, готовность к активному участию в решении практических задач математической направленности;

У обучающегося будут сформированы следующие базовые логические действия как часть познавательных универсальных учебных действий:

-выявлять и характеризовать существенные признаки математических объектов, понятий, отношений между понятиями, формулировать определения понятий, устанавливать существенный признак классификации, основания для обобщения и сравнения, критерии проводимого анализа;

-воспринимать, формулировать и преобразовывать суждения: утвердительные и отрицательные, единичные, частные и общие, условные;

-выявлять математические закономерности, взаимосвязи и противоречия в фактах, данных, наблюдениях и утверждениях, предлагать критерии для выявления закономерностей и противоречий;

-делать выводы с использованием законов логики, дедуктивных и индуктивных умозаключений, умозаключений по аналогии;

проводить самостоятельно доказательства математических утверждений (прямые и от противного), выстраивать аргументацию, приводить примеры и контрпримеры, обосновывать собственные суждения и выводы;

выбирать способ решения учебной задачи (сравнивать несколько вариантов решения, выбирать наиболее подходящий с учётом самостоятельно выделенных критериев).

У обучающегося будут сформированы следующие базовые исследовательские действия как часть познавательных универсальных учебных действий:

-использовать вопросы как исследовательский инструмент познания, формулировать вопросы, фиксирующие противоречие, проблему, устанавливать искомое и данное, формировать гипотезу, аргументировать свою позицию, мнение;

-проводить самостоятельно спланированный эксперимент, исследование по установлению особенностей математического объекта, явления, процесса, выявлению зависимостей между объектами, явлениями, процессами;

-самостоятельно формулировать обобщения и выводы по результатам проведённого наблюдения, исследования, оценивать достоверность полученных результатов, выводов и обобщений;

-прогнозировать возможное развитие процесса, а также выдвигать предположения о его развитии в новых условиях.

-владеть методами доказательств, алгоритмами решения задач; умение формулировать определения, аксиомы и теоремы, применять их, проводить доказательные рассуждения в ходе решения задач;

- уметь оперировать понятиями: степень числа, логарифм числа; умение выполнять вычисление значений и преобразования выражений со степенями и логарифмами, преобразования дробно-рациональных выражений;

- уметь оперировать понятиями: рациональные, иррациональные, показательные, степенные, логарифмические, тригонометрические уравнения и неравенства, их системы;

- уметь оперировать понятиями: функция, непрерывная функция, производная, первообразная, определенный интеграл; уметь находить производные элементарных функций, используя справочные материалы; исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций; строить графики многочленов с использованием аппарата математического анализа; применять производную при решении задач на движение; решать практико-ориентированные задачи на наибольшие и наименьшие значения, на нахождение пути, скорости и ускорения;

- уметь оперировать понятиями: рациональная функция, показательная функция, степенная функция, логарифмическая функция, тригонометрические функции, обратные функции; умение строить графики изученных функций, использовать графики при изучении процессов и зависимостей, при решении задач из других учебных предметов и задач из реальной жизни; выражать формулами зависимости между величинами;

- уметь решать текстовые задачи разных типов (в том числе на проценты, доли и части, на движение, работу, стоимость товаров и услуг, налоги, задачи из области управления личными и семейными финансами); составлять выражения, уравнения, неравенства и их системы по условию задачи, исследовать полученное решение и оценивать правдоподобность результатов;

- уметь оперировать понятиями: среднее арифметическое, медиана, наибольшее и наименьшее значения, размах, дисперсия, стандартное отклонение числового набора; уметь извлекать, интерпретировать информацию, представленную в таблицах, на диаграммах, графиках, отражающую свойства реальных процессов и явлений; представлять информацию с помощью таблиц и диаграмм; исследовать статистические данные, в том числе с применением графических методов и электронных средств;

- уметь оперировать понятиями: случайный опыт и случайное событие, вероятность случайного события; умение вычислять вероятность с использованием графических методов; применять формулы сложения и умножения вероятностей, комбинаторные факты и формулы при решении задач; оценивать вероятности реальных событий; знакомство со случайными величинами; умение приводить примеры проявления закона больших чисел в природных и общественных явлениях;

- уметь оперировать понятиями: точка, прямая, плоскость, пространство, двугранный угол, скрещивающиеся прямые, параллельность и перпендикулярность прямых и плоскостей, угол между прямыми, угол между прямой и плоскостью, угол между плоскостями, расстояние от точки до плоскости, расстояние между прямыми, расстояние между плоскостями; умение использовать при решении задач изученные факты и теоремы планиметрии; умение оценивать размеры объектов окружающего мира;

- уметь оперировать понятиями: многогранник, сечение многогранника, куб, параллелепипед, призма, пирамида, фигура и поверхность вращения, цилиндр, конус, шар, сфера, сечения фигуры вращения, плоскость, касающаяся сферы, цилиндра, конуса, площадь поверхности пирамиды, призмы, конуса, цилиндра, площадь сферы, объем куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара; умение изображать многогранники и поверхности вращения, их сечения от руки, с помощью чертежных инструментов и электронных средств; умение распознавать симметрию в пространстве; умение распознавать правильные многогранники;

- уметь оперировать понятиями: движение в пространстве, подобные фигуры в пространстве; использовать отношение площадей поверхностей и объемов подобных фигур при решении задач;

- уметь вычислять геометрические величины (длина, угол, площадь, объем, площадь поверхности), используя изученные формулы и методы;

- уметь оперировать понятиями: прямоугольная система координат, координаты точки, вектор, координаты вектора, скалярное произведение, угол между векторами, сумма векторов, произведение вектора на число; находить с помощью изученных формул координаты середины отрезка, расстояние между двумя точками;

- уметь выбирать подходящий изученный метод для решения задачи, распознавать математические факты и математические модели в природных и общественных явлениях, в искусстве; умение приводить примеры математических открытий российской и мировой математической науки.

- уметь оперировать понятиями: определение, аксиома, теорема, следствие, свойство, признак, доказательство, равносильные формулировки; умение формулировать обратное и противоположное утверждение, приводить примеры и контрпримеры, использовать метод математической индукции; проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений;

- уметь оперировать понятиями: множество, подмножество, операции над множествами; умение использовать теоретико-множественный аппарат для описания реальных процессов и явлений при решении задач, в том числе из других учебных предметов;

- уметь оперировать понятиями: граф, связный граф, дерево, цикл, граф на плоскости; умение задавать и описывать графы различными способами; использовать графы при решении задач;

- уметь свободно оперировать понятиями: сочетание, перестановка, число сочетаний, число перестановок; бином Ньютона; умение применять комбинаторные факты и рассуждения для решения задач;

-уметь оперировать понятиями: натуральное число, целое число, остаток по модулю, рациональное число, иррациональное число, множества натуральных, целых, рациональных, действительных чисел; умение использовать признаки делимости, наименьший общий делитель и наименьшее общее кратное, алгоритм Евклида при решении задач; знакомство с различными позиционными системами счисления;

- уметь свободно оперировать понятиями: степень с целым показателем, корень натуральной степени, степень с рациональным показателем, степень с действительным (вещественным) показателем, логарифм числа, синус, косинус и тангенс произвольного числа;

- уметь оперировать понятиями: тождество, тождественное преобразование, уравнение, неравенство, система уравнений и неравенств, равносильность уравнений, неравенств и систем, рациональные, иррациональные, показательные, степенные, логарифмические, тригонометрические уравнения, неравенства и системы; умение решать уравнения, неравенства и системы с помощью различных приемов; решать уравнения, неравенства и системы с параметром; применять уравнения, неравенства, их системы для решения математических задач и задач из различных областей науки и реальной жизни;

-уметь свободно оперировать понятиями: график функции, обратная функция, композиция функций, линейная функция, квадратичная функция, степенная функция с целым показателем, тригонометрические функции, обратные тригонометрические функции, показательная и логарифмическая функции; умение строить графики функций, выполнять преобразования графиков функций;

умение использовать графики функций для изучения процессов и зависимостей при решении задач из других учебных предметов и из реальной жизни; выражать формулами зависимости между величинами;

умение свободно оперировать понятиями: четность функции, периодичность функции, ограниченность функции, монотонность функции, экстремум функции, наибольшее и наименьшее значения функции на промежутке; умение проводить исследование функции;

-умение использовать свойства и графики функций для решения уравнений, неравенств и задач с параметрами; изображать на координатной плоскости множества решений уравнений, неравенств и их систем;

- уметь свободно оперировать понятиями: последовательность, арифметическая прогрессия, геометрическая прогрессия, бесконечно убывающая геометрическая прогрессия; умение задавать последовательности, в том числе с помощью рекуррентных формул;

- уметь оперировать понятиями: непрерывность функции, асимптоты графика функции, первая и вторая производная функции, геометрический и физический смысл производной, первообразная, определенный интеграл; умение находить асимптоты графика функции; умение вычислять производные суммы, произведения, частного и композиции функций, находить уравнение касательной к графику функции;

-умение использовать производную для исследования функций, для нахождения наилучшего решения в прикладных, в том числе социально-экономических и физических задачах, для определения скорости и ускорения; находить площади и объемы фигур с помощью интеграла; приводить примеры математического моделирования с помощью дифференциальных уравнений;

- уметь оперировать понятиями: комплексное число, сопряженные комплексные числа, модуль и аргумент комплексного числа, форма записи комплексных чисел (геометрическая, тригонометрическая и алгебраическая); уметь производить арифметические действия с комплексными числами; приводить примеры использования комплексных чисел;

- уметь свободно оперировать понятиями: среднее арифметическое, медиана, наибольшее и наименьшее значения, размах, дисперсия, стандартное отклонение для описания числовых данных; умение исследовать статистические данные, в том числе с применением графических методов и электронных средств; графически исследовать совместные наблюдения с помощью диаграмм рассеивания и линейной регрессии;

- уметь находить вероятности событий с использованием графических методов; применять для решения задач формулы сложения и умножения вероятностей, формулу полной вероятности, формулу Бернулли, комбинаторные факты и формулы; оценивать вероятности реальных событий; умение оперировать понятиями: случайная величина, распределение вероятностей, математическое ожидание, дисперсия и стандартное отклонение случайной величины, функции распределения и плотности равномерного, показательного и нормального распределений; умение использовать свойства изученных распределений для решения задач; знакомство с понятиями: закон больших чисел, методы выборочных исследований; умение приводить примеры проявления закона больших чисел в природных и общественных явлениях;

- уметь свободно оперировать понятиями: точка, прямая, плоскость, пространство, отрезок, луч, плоский угол, двугранный угол, трехгранный угол, пересекающиеся, параллельные и скрещивающиеся прямые, параллельность и перпендикулярность прямых и плоскостей, угол между прямыми, угол между прямой и плоскостью, угол между плоскостями;

- умение использовать при решении задач изученные факты и теоремы планиметрии; умение оценивать размеры объектов в окружающем мире; умение оперировать понятиями: многогранник, сечение многогранника, правильный многогранник, призма, пирамида, фигура и поверхность вращения, цилиндр, конус, шар, сфера, развертка поверхности, сечения конуса и цилиндра, параллельные оси или основанию, сечение шара, плоскость, касающаяся сферы, цилиндра, конуса; умение строить сечение многогранника, изображать многогранники, фигуры и поверхности вращения, их сечения, в том числе с помощью электронных средств; умение применять свойства геометрических фигур, самостоятельно формулировать определения изучаемых фигур, выдвигать гипотезы о свойствах и признаках геометрических фигур, обосновывать или опровергать их;

- умение проводить классификацию фигур по различным признакам, выполнять необходимые дополнительные построения;

- уметь свободно оперировать понятиями: площадь фигуры, объем фигуры, величина угла, расстояние от точки до плоскости, расстояние между прямыми, расстояние между плоскостями, площадь сферы, площадь поверхности пирамиды, призмы, конуса, цилиндра, объем куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара; умение находить отношение объемов подобных фигур;

- уметь свободно оперировать понятиями: движение, параллельный перенос, симметрия на плоскости и в пространстве, поворот, преобразование подобия, подобные фигуры; умение распознавать равные и подобные фигуры, в том числе в природе, искусстве, архитектуре; умение использовать геометрические отношения, находить геометрические величины (длина, угол, площадь, объем) при решении задач из других учебных предметов и из реальной жизни;

- уметь свободно оперировать понятиями: прямоугольная система координат, вектор, координаты точки, координаты вектора, сумма векторов, произведение вектора на число, разложение вектора по базису, скалярное произведение, векторное произведение, угол между векторами; умение использовать векторный и координатный метод для решения геометрических задач и задач других учебных предметов; оперировать понятиями: матрица 2x2 и 3x3, определитель матрицы, геометрический смысл определителя;

- уметь моделировать реальные ситуации на языке математики; составлять выражения, уравнения, неравенства и их системы по условию задачи, исследовать построенные модели с использованием аппарата алгебры, интерпретировать полученный результат; строить математические модели с помощью геометрических понятий и величин, решать связанные с ними практические задачи; составлять вероятностную модель и интерпретировать полученный результат; решать прикладные задачи средствами математического анализа, в том числе социально-экономического и физического характера;

- умение выбирать подходящий метод для решения задачи; понимание значимости математики в изучении природных и общественных процессов и явлений; умение распознавать проявление законов математики в искусстве, умение приводить примеры математических открытий российской и мировой математической науки

ОК 02 Использовать современные средства поиска, анализа и интерпретации информации, и информационные технологии для выполнения задач профессиональной деятельности

Ценности научного познания:

- сформированность мировоззрения, соответствующего современному уровню развития науки и общественной практики, понимание математической науки как сферы человеческой деятельности, этапов её развития и значимости для развития цивилизации, овладение языком математики и математической культурой как средством познания мира, готовность осуществлять проектную и исследовательскую деятельность индивидуально и в группе.

У обучающегося будут сформированы умения работать с информацией как часть познавательных универсальных учебных действий:

-выявлять дефициты информации, данных, необходимых для ответа на вопрос и для решения задачи;

-выбирать информацию из источников различных типов, анализировать, систематизировать и интерпретировать информацию различных видов и форм представления;

-структурировать информацию, представлять её в различных формах, иллюстрировать графически;

-оценивать надёжность информации по самостоятельно сформулированным критериям.

- уметь оперировать понятиями: тождество, тождественное преобразование, уравнение, неравенство, система уравнений и неравенств, равносильность уравнений, неравенств и систем, рациональные, иррациональные, показательные, степенные, логарифмические, тригонометрические уравнения, неравенства и системы; уметь решать уравнения, неравенства и системы с помощью различных приемов; решать уравнения, неравенства и системы с параметром; применять уравнения, неравенства, их системы для решения математических задач и задач из различных областей науки и реальной жизни;

- уметь свободно оперировать понятиями: движение, параллельный перенос, симметрия на плоскости и в пространстве, поворот, преобразование подобия, подобные фигуры; уметь распознавать равные и подобные фигуры, в том числе в природе, искусстве, архитектуре; уметь использовать геометрические отношения, находить геометрические величины (длина, угол, площадь, объем) при решении задач из других учебных предметов и из реальной жизни.

ОК 03 Планировать и реализовывать собственное профессиональное и личностное развитие, предпринимательскую деятельность в профессиональной сфере, использовать знания по финансовой грамотности в различных жизненных ситуациях

Духовно-нравственного воспитания:

-осознание духовных ценностей российского народа, сформированность нравственного сознания, этического поведения, связанного с практическим применением достижений науки и деятельностью учёного, осознание личного вклада в построение устойчивого будущего;

У обучающегося будут сформированы умения самоорганизации как часть регулятивных универсальных учебных действий:

-составлять план, алгоритм решения задачи, выбирать способ решения с учётом имеющихся ресурсов и собственных возможностей, аргументировать и корректировать варианты решений с учётом новой информации.

У обучающегося будут сформированы умения самоконтроля как часть регулятивных универсальных учебных действий:

-владеть навыками познавательной рефлексии как осознания совершаемых действий и мыслительных процессов, их результатов, владеть способами самопроверки, самоконтроля процесса и результата решения математической задачи;

-предвидеть трудности, которые могут возникнуть при решении задачи, вносить коррективы в деятельность на основе новых обстоятельств, данных, найденных ошибок, выявленных трудностей;

-оценивать соответствие результата цели и условиям, объяснять причины достижения или недостижения результатов деятельности, находить ошибку, давать оценку приобретённому опыту.

- уметь оперировать понятиями: многогранник, сечение многогранника, куб, параллелепипед, призма, пирамида, фигура и поверхность вращения, цилиндр, конус, шар, сфера, сечения фигуры вращения, плоскость, касающаяся сферы, цилиндра, конуса, площадь поверхности пирамиды, призмы, конуса, цилиндра, площадь сферы, объем куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара; умение изображать многогранники и поверхности вращения, их сечения от руки, с помощью чертежных инструментов и электронных средств; уметь распознавать симметрию в пространстве; уметь распознавать правильные многогранники;

ОК 04 Эффективно взаимодействовать и работать в коллективе и команде

У обучающегося будут сформированы умения совместной деятельности:

-понимать и использовать преимущества командной и индивидуальной работы при решении учебных задач, принимать цель совместной деятельности, планировать организацию совместной работы, распределять виды работ, договариваться, обсуждать процесс и результат работы, обобщать мнения нескольких людей;

-участвовать в групповых формах работы (обсуждения, обмен мнений, «мозговые штурмы» и иные), выполнять свою часть работы и координировать свои действия с другими членами команды, оценивать качество своего вклада в общий продукт по критериям, сформулированным участниками взаимодействия.

- уметь оперировать понятиями: случайный опыт и случайное событие, вероятность случайного события; уметь вычислять вероятность с использованием графических методов; применять формулы сложения и умножения вероятностей, комбинаторные факты и формулы при решении задач; оценивать вероятности реальных событий; знакомство со случайными величинами; умение приводить примеры проявления закона больших чисел в природных и общественных явлениях;

- уметь свободно оперировать понятиями: график функции, обратная функция, композиция функций, линейная функция, квадратичная функция, степенная функция с целым показателем, тригонометрические функции, обратные тригонометрические функции, показательная и логарифмическая функции; уметь строить графики функций, выполнять преобразования графиков функций;

- уметь использовать графики функций для изучения процессов и зависимостей при решении задач из других учебных предметов и из реальной жизни; выражать формулами зависимости между величинами;

- свободно оперировать понятиями: четность функции, периодичность функции, ограниченность функции, монотонность функции, экстремум функции, наибольшее и наименьшее значения функции на промежутке; уметь проводить исследование функции;

- уметь использовать свойства и графики функций для решения уравнений, неравенств и задач с параметрами; изображать на координатной плоскости множества решений уравнений, неравенств и их систем

ОК 05 Осуществлять устную и письменную коммуникацию на государственном языке Российской Федерации с учетом особенностей социального и культурного контекста

Эстетического воспитания:

- эстетическое отношение к миру, включая эстетику математических закономерностей, объектов, задач, решений, рассуждений, восприимчивость к математическим аспектам различных видов искусства;

У обучающегося будут сформированы умения общения как часть коммуникативных универсальных учебных действий:

-воспринимать и формулировать суждения в соответствии с условиями и целями общения, ясно, точно, грамотно выражать свою точку зрения в устных и письменных текстах, давать пояснения по ходу решения задачи, комментировать полученный результат;

-в ходе обсуждения задавать вопросы по существу обсуждаемой темы, проблемы, решаемой задачи, высказывать идеи, нацеленные на поиск решения, сопоставлять свои суждения с суждениями других участников диалога, обнаруживать различие и сходство позиций, в корректной форме формулировать разногласия, свои возражения;

-представлять результаты решения задачи, эксперимента, исследования, проекта, самостоятельно выбирать формат выступления с учётом задач презентации и особенностей аудитории.-

- уметь оперировать понятиями: среднее арифметическое, медиана, наибольшее и наименьшее значения, размах, дисперсия, стандартное отклонение числового набора; умение извлекать, интерпретировать информацию, представленную в таблицах, на диаграммах, графиках, отражающую свойства реальных процессов и явлений; представлять информацию с помощью таблиц и диаграмм; исследовать статистические данные, в том числе с применением графических методов и электронных средств;

- уметь использовать при решении задач изученные факты и теоремы планиметрии; умение оценивать размеры объектов окружающего мира

ОК 06 Проявлять гражданско-патриотическую позицию, демонстрировать осознанное поведение на основе традиционных общечеловеческих ценностей, в том числе с учетом гармонизации межнациональных и межрелигиозных отношений, применять стандарты антикоррупционного поведения

Гражданского воспитания:

-сформированность гражданской позиции обучающегося как активного и ответственного члена российского общества, представление о математических основах функционирования различных структур, явлений, процедур гражданского общества (выборы, опросы и другое), умение взаимодействовать с социальными институтами в соответствии с их функциями и назначением;

Патриотического воспитания:

- сформированность российской гражданской идентичности, уважения к прошлому и настоящему российской математики, ценностное отношение к достижениям российских математиков и российской математической школы, использование этих достижений в других науках, технологиях, сферах экономики;

-уметь выбирать подходящий изученный метод для решения задачи, распознавать математические факты и математические модели в природных и общественных явлениях, в искусстве; умение приводить примеры математических открытий российской и мировой математической науки.

ОК 07 Содействовать сохранению окружающей среды, ресурсосбережению, применять знания об изменении климата, принципы бережливого производства, эффективно действовать в чрезвычайных ситуациях

Экологического воспитания:

-сформированность экологической культуры, понимание влияния социально-экономических процессов на состояние природной и социальной среды, осознание глобального характера экологических проблем, ориентация на применение математических знаний для решения задач в области окружающей среды, планирование поступков и оценки их возможных последствий для окружающей среды;

- уметь вычислять геометрические величины (длина, угол, площадь, объем, площадь поверхности), используя изученные формулы и методы

ОК 08. Использовать средства физической культуры для сохранения и укрепления здоровья в процессе

профессиональной деятельности и поддержания необходимого уровня физической подготовленности.

Физического воспитания:

-сформированность умения применять математические знания в интересах здорового и безопасного образа жизни, ответственное отношение к своему здоровью (здоровое питание, сбалансированный режим занятий и отдыха, регулярная физическая активность), физическое совершенствование при занятиях спортивно-оздоровительной деятельностью;

Профессиональные компетенции специальности «Строительство и эксплуатация зданий и сооружений»

ПК 1.3. Выполнять несложные расчеты и конструирование строительных конструкций.

ПК 2.3. Проводить оперативный учет объемов выполняемых работ и расхода материальных ресурсов.

ПК 2.4. Осуществлять мероприятия по контролю качества выполняемых работ.

ПК 3.1. Осуществлять оперативное планирование деятельности структурных подразделений при проведении строительно-монтажных работ, текущего содержания и реконструкции строительных объектов.

ПК 4.1. Принимать участие в диагностике технического состояния конструктивных элементов эксплуатируемых зданий.

Профессиональные компетенции специальности «Эксплуатация и обслуживание многоквартирного дома»

ПК 2.3. Подготавливать проектно-сметную документацию на выполнение услуг и работ по эксплуатации, обслуживанию и ремонту общего имущества многоквартирного дома.

ПК 2.5. Проводить оперативный учет и контроль качества выполняемых услуг, работ по эксплуатации, обслуживанию и ремонту общего имущества многоквартирного дома и расхода материальных ресурсов

ПК 2.6. Организовывать и контролировать качество услуг по эксплуатации, обслуживанию и ремонту систем водоснабжения, водоотведения, отопления, внутридомового газового оборудования, электрооборудования, лифтового хозяйства, кондиционирования, вентиляции .

Профессиональные компетенции профессии «Сварщик»

ПК 1.1. Читать чертежи средней сложности и сложных сварных металлоконструкций.

ПК 1.6. Проводить контроль подготовки и сборки элементов конструкции под сварку.

ПК 1.9. Проводить контроль сварных соединений на соответствие геометрическим размерам, требуемым конструкторской и производственно-технологической документации по сварке.

Профессиональные компетенции профессии «Мастер общестроительных работ»

ПК 1.2 Производить общие каменные работы различной сложности.

ПК 1.6. Контролировать качество каменных работ.

ПК 2.5 Осуществлять контроль качества сварочных работ

Распределение типов контрольных заданий при текущем контроле

Таблица 3

	Содержание обучения	Всего к/з (ч)	Практические занятия (каждое занятие 2 часа)	Контрольная работа (ч)
1 семестр	Раздел 1. Повторение курса математики основной школы	8	Практическое занятие 1 «Практико-ориентированные задачи на плоскости» Практическое занятие 2 «Практико- ориентированные задачи на проценты» Практическое занятие 3 «Решение систем уравнений и неравенств»	2
	Раздел 2. Степени и корни. Степенная функция	4	Практическое занятие 4 «Решение иррациональных уравнений»	2
	Раздел 3. Показательная функция	4	Практическое занятие 5 «Решение показательных уравнений и неравенств»	2
	Раздел 4. Логарифмы. Логарифмическая функция	8	Практическое занятие 6 «Преобразования логарифмических выражений» Практическое занятие 7 «Решение логарифмических уравнений и неравенств» Практическое занятие 8 «Применение логарифма»	2
	Раздел 5 Прямые и плоскости в пространстве	8	Практическое занятие 9 «Построение сечений в тетраэдре и параллелепипеде» Практическое занятие 10 «Прямые и плоскости в пространстве» Практическое занятие 11 «Прямые и плоскости в профессиональной деятельности и вокруг нас»	2+2
2 семестр	Раздел 6. Координаты и векторы	4	Практическое занятие 12 «Координатная плоскость. Вычисление расстояний и площадей»	2
	Раздел 7. Основы тригонометрии. Тригонометрические функции	10	Практическое занятие 13 «Вычисление значений тригонометрических функций» Практическое занятие 14 «Преобразования простейших тригонометрических выражений» Практическое занятие 15 «Преобразование графиков тригонометрических функций» Практическое занятие 16 «Использование свойств тригонометрических функций в профессиональных задачах»	2
	Раздел 8. Комплексные числа	2	Практическое занятие 17 «Выполнение расчетов с помощью комплексных чисел. Примеры использования комплексных чисел»	-
	Раздел 9. Производная функции, ее применение	10	Практическое занятие 18 «Техника дифференцирования» Практическое занятие 19 «Физический и геометрический смысл производной в профессиональных и прикладных задачах» Практическое занятие 20 «Построение графика функции» Практическое занятие 21 «Наименьшее и наибольшее значение функции. Нахождение оптимальных результатов в прикладных и профессиональных задачах»	2
	Раздел 10. Многогранники и тела вращения	8	Практическое занятие 22 «Понятие правильного многогранника. Свойства правильных многогранников» Практическое занятие 23 «Симметрия в природе, архитектуре, технике, в быту» Практическое занятие 24 «Использование комбинаций многогранников и тел вращения в практико-ориентированных задачах»	2
	Раздел 11. Первообразная функции, ее применение	2	Практическое занятие 25 «Геометрический смысл определенного интеграла. Формула Ньютона - Лейбница. Решение задач на применение интеграла для вычисления физических величин и площадей»	-
	Раздел 12. Множества. Элементы теории графов	4	Практическое занятие 26 «Операции с множествами. Решение прикладных задач» Практическая работа 27 «Применение графов при решении задач»	-
	Раздел 13. Элементы комбинаторики, статистики и теории вероятностей	8	Практическое занятие 28 «Относительная частота события, свойство ее устойчивости. Статистическое определение вероятности. Оценка вероятности события» Практическое занятие 29 «Вариационный ряд. Полигон частот и гистограмма. Статистические характеристики ряда наблюдаемых данных» Практическое занятие 30 «Первичная обработка статистических данных. Графическое их представление. Нахождение средних характеристик, наблюдаемых данных»	2
	Раздел 14. Уравнения и неравенства	8	Практическое занятие 31 «Общие методы решения уравнений. Уравнения и неравенства с модулем и с параметрами» Практическое занятие 32 «Решение текстовых задач профессионального содержания»	2
	Итого за курс:	88	64	24

3. ОЦЕНКА ОСВОЕНИЯ УЧЕБНОЙ ДИСЦИПЛИНЫ

Перечень оценочных средств

Таблица 4

Формы

оценивания

Общая характеристика формы оценивания

Способ представления

формы оценивания в фонде

оценочных средств

Устный опрос

Цель устного опроса – оценить знания и кругозор обучающегося, умение логически построить ответ,владение монологической и диалогической речью,уровень развития мышления. Обучающая функция уст ного опроса состоит в выявлении вопросов,которые по каким-то причинам оказались недостаточно осмысленными в ходе учебных занятий и при подготовке к зачёту или экзамену, и определении способов коррекции пробелов в знаниях и умениях обучающихся. Устный опрос может осуществляться в различных видах (индивидуальный.

групповой, фронтальный, комбинированный)

Вопросы для

опроса

Практическая работа

Практическая работа - это задание, с помощью которых у обучающихся формируются и развиваются правильные практические действия, четкое и ясное

задание по конкретной предметной области,

требующее однозначно определяемого ответа или

выполнения определенного алгоритма действий.

Варианты заданий

Контрольная

работа

Письменные контрольные работы – одно из средств опроса, которое осуществляется с целью проверки знаний всех обучающихся по данной теме; стимулирования непрерывной систематической работы обучающихся; формирования умений в письменном виде сжато излагать материал.

Различают несколько видов контрольных работ:

обязательные, домашние практические, фронтальные и индивидуальные.

Контрольные работы проводятся, как правило, после завершения изучения темы или раздела (модуля) и содержат задания различных типов и уровней сложности. Во время проверки и оценки контрольных письменных работ проводится анализ результатов выполнения, выявляются типичные ошибки, а также причины их появления.

Варианты заданий

Оценка письменных самостоятельных и контрольных работ

Оценка «5» ставится за работу, выполненную без ошибок и недочетов или имеющую не более одного недочета.

Оценка «4» ставится за работу, выполненную полностью, но при наличии в ней:

а) не более одной негрубой ошибки и одного недочета,

б) или не более двух недочетов.

Оценка «3» ставится в том случае, если обучающийся правильно выполнил не менее половины работы или допустил:

а) не более двух грубых ошибок,

б) или не более одной грубой ошибки и одного недочета,

в) или не более двух-трех негрубых ошибок,

г) или одной негрубой ошибки и трех недочетов,

д) или при отсутствии ошибок, но при наличии 4-5 недочетов.

Оценка «2» ставится, когда число ошибок и недочетов превосходит норму, при которой может быть выставлена оценка «3», или если правильно выполнено менее половины работы.

Оценка устных ответов

Оценка «5» ставится в том случае, если обучающийся:

а) обнаруживает полное понимание сущности рассматриваемых явлений и закономерностей, знание законов и теорий, умеет подтвердить их конкретными примерами, применить в новой ситуации и при выполнении практических заданий;

б) дает точное определение и истолкование основных понятий, законов, теорий, а также правильное определение величин, их единиц;

в) технически грамотно выполняет чертежи, схемы, графики, сопутствующие ответу, правильно записывает формулы, пользуясь принятой системой условных обозначений;

г) при ответе не повторяет дословно текст учебника, а умеет отобрать главное, обнаруживает самостоятельность и аргументированность суждений, умеет установить связь между изучаемым и ранее изученным материалом по курсу, а также с материалом, усвоенным при изучении других смежных дисциплин;

е) умеет делать анализ, обобщения и собственные выводы по данному вопросу;

ж) умеет самостоятельно и рационально работать с учебником, дополнительной литературой и справочниками.

Оценка «4» ставится в том случае, если ответ удовлетворяет названным выше требованиям, но обучающийся:

а) допускает одну негрубую ошибку или не более двух недочетов и может их исправить самостоятельно, или при небольшой помощи преподавателя;

б) не обладает достаточными навыками работы со справочной литературой (например, обучающийся умеет все найти, правильно ориентируется в справочниках, но работает медленно).

Оценка «3» ставится в том случае, если обучающийся правильно понимает сущность рассматриваемых явлений и закономерностей, но при ответе:

а) обнаруживает отдельные пробелы в усвоении существенных вопросов курса, не препятствующие дальнейшему усвоению программного материала;

б) испытывает затруднения в применении знаний, необходимых для решения задач различных типов, при объяснении конкретных явлений на основе теории и законов, или в подтверждении конкретных примеров практического применения теории,

в) отвечает неполно на вопросы преподавателя, или воспроизводит содержание текста, но недостаточно понимает отдельные положения, имеющие важное значение в этом тексте,

г) обнаруживает недостаточное понимание отдельных положений при воспроизведении учебного материала, или отвечает неполно на вопросы, допуская одну-две грубые ошибки.

Оценка «2» ставится в том случае, если обучающийся:

а) не знает и не понимает значительную или основную часть программного материала в пределах поставленных вопросов,

б) или имеет слабо сформулированные и неполные знания и не умеет применять их к решению конкретных вопросов и задач по образцу и к проведению опытов,

в) или при ответе допускает более двух грубых ошибок, которые не может исправить даже при помощи преподавателя.

Оценка практических работ

Оценка «5» ставится в том случае, если обучающийся:

а) выполнил работу в полном объеме с соблюдением необходимой последовательности проведения опытов и измерений, расчетов;

б) в представленном отчете правильно и аккуратно выполнил все записи, таблицы, рисунки, чертежи, графики, вычисления и сделал выводы;

г) правильно ответил на поставленные вопросы;

д) соблюдал требования безопасности труда.

Оценка «4» ставится в том случае, если выполнены требования к оценке 5, но:

было допущено два-три недочета, или не более одной негрубой ошибки и одного недочета.

Оценка «3» ставится, если работа выполнена не полностью, но объем выполненной части таков, что можно сделать выводы, или если в ходе выполнения были допущены следующие ошибки:

а) Записаны не все необходимые формулы,

б) или в отчете были допущены в общей сложности не более двух ошибок (в записях единиц, измерениях, в вычислениях, графиках, таблицах, схемах, анализе погрешностей и т.д.), не принципиального для данной работы характера, не повлиявших на результат выполнения,

г) или работа выполнена не полностью, однако объем выполненной части таков, что позволяет получить правильные результаты и выводы по основным, принципиально важным задачам работы.

Оценка «2» ставится в том случае, если:

а) работа выполнена не полностью, и объем выполненной части работы не позволяет сделать правильные выводы,

б) или в ходе работы и в отчете обнаружились в совокупности все недостатки, отмеченные в требованиях к оценке «3».

Конкретно, для каждой практической работы, обучающимся предлагается шкала оценивания заданий. В каждом задании указано максимальное количество баллов, которое можно получить.

Шкала оценки образовательных достижений

Таблица 6

Результативность: количество набранных баллов	Оценка уровня подготовки (отметка)
(9-10 баллов)	«5»-отлично
(8-8,9 балла)	«4»- хорошо
(7-7,9 баллов)	«3»- удовлетворительно
(менее 7 баллов)	«2»- неудовлетворительно

4. ФОНД ОЦЕНОЧНЫХ СРЕДСТВ ТЕКУЩЕГО КОНТРОЛЯ

Входной контроль 1 курс

Вариант № 1

1. (2 балла) Найти сумму: .

2. (2 балла) Найти частное: .

3. (2 балла) Решить неравенство: 9х-23>15х+1

4. (2 балла) Решить уравнение: х²+2х-8=0.

5. (2 балла) Упростить выражение:

6. (2 балла) Найти число, 10% которого равны 15.

7. (2 балла) Найти неизвестный член пропорции: 2,5 : 1,25=8 : у.

8. (2 балла) Построить график функции: у=2х-3.

9. (2 балла) Найти угол, смежный с углом КМС, если угол КМС равен 40⁰.

10. (2 балла) Вычислить площадь треугольника АВС если АВ=8 см, ВС=6 см, угол АВС=30⁰.

11(2 балла). Диагонали ромба равны 10 см и 24 см. Найти сторону ромба и его площадь.

12. (2 балла) Вычислить длину окружности, радиус которой равен 5 см

Шкала оценки образовательных достижений

Результативность: количество набранных баллов	Оценка уровня подготовки (отметка)
(22-24 балла)	«5»-отлично
(19-21 балл)	«4»- хорошо
(16-18 баллов)	«3»- удовлетворительно
(15 и менее баллов)	«2»- неудовлетворительно

Входной контроль 1 курс

Вариант № 2

1. (2 балла) Найти сумму: .

2. (2 балла) Найти частное: .

3. (2 балла) Решить неравенство: 4+5х 2+7х.

4. (2 балла) Решить уравнение: х²-6х+8=0.

5. (2 балла) Упростить выражение:

6. (2 балла) Найти 20% от 80.

7. (2 балла) Найти неизвестный член пропорции:

8. (2 балла) Построить график функции: у=2х+3.

9. (2 балла) Найти угол, смежный с углом АВС, если угол АВС равен 23⁰.

10. (2 балла) Найти площадь прямоугольного треугольника, если один из катетов равен 6 см, а гипотенуза 10 см.

11.(2 балла). Стороны параллелограмма равны 4 см и 6 см. Острый угол равен 30⁰. Найти площадь параллелограмма.

12. (2 балла) Вычислить длину окружности, радиус которой равен 10 см.

Шкала оценки образовательных достижений

Результативность: количество набранных баллов	Оценка уровня подготовки (отметка)
(22-24 балла)	«5»-отлично
(19-21 балл)	«4»- хорошо
(16-18 баллов)	«3»- удовлетворительно
(15 и менее баллов)	«2»- неудовлетворительно

ВОПРОСЫ ДЛЯ УСТНЫХ ОТВЕТОВ

УО1 Раздел 1: «Повторение курса математики основной школы»

1. Какие числа называются натуральными?

2. Какие числа называются целыми?

3. Дайте определение рациональных чисел.

4. Все ли рациональные числа можно записать в виде конечной десятичной дроби?

5. Какие числа называются действительными?

6. Правила выполнения арифметических действий с обыкновенными дробями

7. Правила выполнения арифметических действий с десятичными дробями.

8. Отношения. Пропорции.

9. Решение текстовых задач арифметическими приемами.

10. Положительные и отрицательные числа.

11. Формулы сокращенного умножения.

12. Какие виды углов вы знаете?

13. Треугольник и его элементы.

14. Площади треугольников.

15. Прямоугольный треугольник. Теорема Пифагора.

16. Четырехугольники. Виды, элементы. Площади.

17. Окружность и круг. Длина окружности и площадь круга.

18. Вписанные и описанные окружности.

УО2 Раздел 2: «Степени и корни. Степенная функция»

1. Дайте определение арифметического корня.

2. Сформулируйте свойства арифметического корня.

3. Дайте определение степени с действительным показателем.

4. Сформулируйте свойства степени с действительным показателем.

5. Сделайте эскизы степенных функций, в зависимости от показателя.

УО3 Раздел 3: «Показательная функция»

1. Какая функция называется показательной?

2. Что является областью определения и множеством значений показательной функции?

3. Является ли показательная функция четной?

4. При каком условии показательная функция является возрастающей?

5. При каком условии показательная функция является убывающей?

6. Как зависит изменение показательной функции от основания?

7. Перечислите свойства функции у = а^х при а>1.

8. Перечислите свойства функции у = а^х при 0<a<1?

УО4 Раздел 4: «Логарифмы. Логарифмическая функция»

1. Дайте определение логарифма.

2. Сформулируйте название действия нахождения логарифма.

3. Запишите основание натурального логарифма.

4. Сформулируйте основное логарифмическое тождество.

5. Сформулируйте теорему о логарифме произведения.

6. Сформулируйте теорему о логарифме частного.

7. Приведите формулу перехода к новому основанию.

8. Какие свойства логарифма используются при выполнении тождественных преобразований?

9. Какой логарифм называется десятичным?

10.Дайте определение логарифмической функции.

11.Сформулируйте определение логарифмического уравнения.

12.Сформулируйте методы решения логарифмических уравнений.

13.Дайте определение логарифмического неравенства.

14.Сформулируйте методы решения логарифмических неравенств.

15.Запишите общий вид логарифмической функции.

16.Как представить число в виде логарифма по основанию a?

17.Изобразите схематично график логарифмической функции.

18.Как определить посторонний корень логарифмического уравнения?

19.Перечислите основные свойства логарифмов a>1, a≠ 1.

20.Обязательно ли при решении логарифмического уравнения находить область существования функций, входящих в уравнение?

21.На что, в первую очередь следует обратить внимание при решении логарифмического неравенства?

УО5 Раздел 5: «Прямые и плоскости в пространстве»

1. Сформулируйте 3 известные аксиомы стереометрии.

2. Как могут располагаться прямые в пространстве?

3. Дайте определение параллельных прямых.

4. Дайте определение скрещивающихся прямых.

5. Сформулируйте признак скрещивающихся прямых.

6. Каковы случаи взаимного расположения прямой и плоскости?

7. Дайте определение параллельности прямой и плоскости.

8. Сформулируйте признак параллельности прямой и плоскости.

9. Каковы случаи взаимного расположения двух плоскостей?

10. Дайте определение параллельности двух плоскостей.

11. Сформулируйте признак параллельности двух плоскостей.

12. Назовите свойства параллельных плоскостей.

13. Дайте определение перпендикулярных прямых в пространстве.

14. Дайте определение перпендикулярности прямой и плоскости.

15. Сформулируйте признак перпендикулярности прямой и плоскости.

16. Дайте определение понятиям «перпендикуляр», «наклонная», «проекция».

17. Сформулируйте теорему о трех перпендикулярах.

18. Как найти угол между прямой и плоскостью.

19. Объясните понятие «двугранный угол».

20. Дайте определение перпендикулярных плоскостей.

21. Сформулируйте признак перпендикулярности двух плоскостей.

22. Запишите формулу для вычисления диагонали прямоугольного параллелепипеда.

УО6 Раздел 6: «Координаты и векторы»

1. Сформулируйте определение вектора.

2. Сформулируйте основные правила действий над векторами.

3. Дайте определение компланарных векторов.

4. Охарактеризуйте прямоугольную декартову систему координат в пространсте.

5. Сформулируйте правила действий над векторами в координатах.

6. Запишите формулу для вычисления длины вектора.

7. Запишите формулу для вычисления скалярного произведения.

8. Запишите формулу для нахождения угла между векторами, заданными координатами.

УО7 Раздел 7: «Основы тригонометрии. Тригонометрические функции»

1. Дайте определение понятий синус, косинус, тангенс и котангенс.

2. Запишите основное тригонометрическое тождество.

3. Проиллюстрируйте знаки тригонометрических функций.

4.Запишите формулы зависимости между синусом косинусом, тангенсом и котангенсом.

5. Запишите формулы двойного угла.

6. Запишите формулы сложения.

7. Запишите формулы приведения.

8. Запишите формулы преобразования суммы и разности в произведение.

9. Формулы для решения простейших тригонометрических уравнений.

10. Как решаются уравнения вида аsinx+вcosx=0?

11. Уравнения какого вида сводятся к квадратным?

12. Приведите алгоритм решения тригонометрического неравенства.

УО8 Раздел 8: «Комплексные числа»

1. Дать определение комплексного числа.

2. Сформулировать определение мнимой единицы.

3. Как найти степень мнимой единицы?

4. Какие комплексные числа называют равными, сопряженными?

5. Записать формулу для нахождения произвольной степени мнимой единицы.

6. Приведите примеры чисто мнимых чисел.

7. Дать определение суммы двух комплексных чисел.

8. Дать определение частного двух комплексных чисел.

9. Как изображаются комплексные числа на координатной плоскости?

10. Дайте определение модуля и аргумента комплексного числа.

11. Запишите формулу для нахождения модуля комплексного числа.

13. Как найти аргумент комплексного числа?

УО9 Раздел 9: «Производная функции и ее применение»

1. Сформулируйте определение производной.

2. Объясните правила нахождения производной.

3. В чём состоит физический смысл производной?

4. В чём состоит геометрический смысл производной?

5. Запишите уравнение касательной.

6. Сформулируйте признак возрастания и убывания функции.

7. Опишите необходимое и достаточное условие экстремума функции.

8. Составьте схему исследования функции для построения графика.

9. Как найти наибольшее и наименьшее значение функции на отрезке?

УО10 Раздел 10: «Многогранники и тела вращения»

1. Какой многогранник называется призмой?

2. Какие виды призм вы знаете?

3. Назовите элементы призмы.

4. Какая призма называется прямой?

5. Какая призма называется правильной?

6. Как называется призма в основании которой лежит четырёхугольник?

7.Напишите формулы для вычисления площади боковой и полной поверхности призмы.

8. Какой многогранник называется пирамидой?

9. Какие виды пирамид вы знаете?

10. Назовите элементы пирамиды.

11. Какая пирамида называется правильной?

12. Назовите свойства правильной пирамиды.

13. Что такое апофема в правильной пирамиде?

14. Какая пирамида называется усечённой? Назовите её элементы.

15. Напишите формулы для вычисления площади боковой и полной поверхности.

16. Какой многогранник называется правильным? Назовите правильные многогранники

1. Какое тело называется цилиндром?

2. Назовите элементы цилиндра.

3. Какие виды сечений в цилиндре вы знаете?

4.Что представляет из себя развертка цилиндра?

5. Напишите формулы для вычисления площади боковой и полной поверхности.

6. Какое тело называется конусом?

7. Назовите элементы конуса.

8. Какие виды сечений в конусе вы знаете?

9.Что представляет из себя развертка конуса?

10. Напишите формулы для вычисления площади боковой и полной поверхности.

11. Какое тело называется сферой?

12. В чём отличие сферы от шара?

13. Назовите элементы сферы и шара.

14. Напишите уравнение сферы.

15. Как может располагаться между собой сфера и плоскость?

16. Напишите формулы для вычисления площади поверхности сферы.

1. Дайте определение понятия площади и объема.

2. Запишите формулу для вычисления объема прямоугольного параллелепипеда.

3. Запишите формулу для вычисления объема куба.

4. Запишите формулу для вычисления объема призмы.

5. Запишите формулу для вычисления объема пирамиды.

6. Запишите формулу для вычисления объема усеченной пирамиды.

7. Запишите формулу для вычисления объема цилиндра.

8. Запишите формулу для вычисления объема конуса.

9. Запишите формулу для вычисления объема шара.

10. Как вычислить объем геометрической фигуры через определенный интеграл.

УО11 Раздел 11: «Первообразная функции и ее применение»

1. Дать определение первообразной.

2. Объясните правила нахождения первообразных.

3. Дать определение неопределенного интеграла.

4. Что такое интегрирование функции?

5. Рассказать правила интегрирования.

6. Перечислить основные свойства неопределенного интеграла.

7. Перечислить методы интегрирования.

8. Дать определение определенного интеграла.

9. Сформулировать основные свойства определенного интеграла

10. Запишите формулу Ньютона – Лейбница для вычисления интеграла.

11. Опишите алгоритм вычисления площади фигуры с помощью интеграла.

УО12 Раздел 12: «Множества. Элементы теории графов»

1. Сформулируйте определение множества.

2. Как можно задать множество?

3. Какие множества называются равными?

4. Какое множество называют пустым?

5. Какое множество является подмножеством другого множества?

6. Какие основные операции выполняются над множествами?

7. Как определяется объединение множеств?

8. Как определяется пересечение множеств?

9. Как определяется разность множеств?

10. Какие бывают множества?

11. Сформулируйте определение графа.

12. Точки графа называются…

13. Линии графа называются…

14. Как называется ребро, имеющее совпадающие начало и конец? 1

15. Ребра называются смежными, если они …

УО13 Раздел 13: «Элементы комбинаторики, статистики и теории вероятностей»

1.Сформулируйте определения понятий: «Размещения», «Перестановки», «Сочетания».

2. Сформулируйте правило включения - исключения.

3. Сформулируйте свойства биноминальных коэффициентов.

4. Проиллюстрируйте треугольник Паскаля.

5. Какое событие называется случайным?

6. Какое событие называется достоверным?

7. Какое событие называется невозможным?

8. Какие события называются противоположными?

9. Какие события называются совместными?

10. Как найти вероятность случайного события?

11. Назовите формулы сложения и умножения вероятностей.

12. Что значит, составить закон распределения случайной величины?

13. Как вычислить математическое ожидание случайной величины?

14. В чем состоит задача математической статистики?

УО13 Раздел 14: «Уравнения и неравенства»

1. Объясните основные приемы решения уравнений.

2. Объясните основные приемы решения систем уравнений.

3. Объясните основные приемы решения неравенств.

4. Объясните основные приемы решения рациональных уравнений и неравенств.

5. Объясните основные приемы решения показательных уравнений и неравенств.

6. Объясните основные приемы решения логарифмических уравнений и неравенств.

7. Объясните основные приемы решения иррациональных уравнений и неравенств.

8. Объясните основные приемы решения тригонометрических уравнений.

ПРАКТИЧЕСКИЕ РАБОТЫ

Практическая работа № 1

по теме «Практико-ориентированные задачи на плоскости»

Цель: Закрепить навыки вычисления площади плоских фигур.

Обеспечение: Задания и методические указания к выполнению работ

Ход работы

Теоретическая часть

1. Записать формулы в рабочую тетрадь

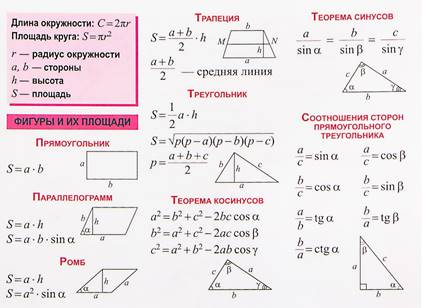
2. Сделайте разбор задач и запишите в рабочую тетрадь.

Задача 1

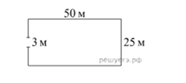Участок земли имеет прямоугольную форму. Стороны прямоугольника равны 25 м и 50 м. Найдите длину забора, которым нужно огородить участок, предусмотрев проезд шириной 3 м. Ответ дайте в метрах.

Решение: Забор представляет собой прямоугольник с отсутствующим кусочком на одной из сторон. Периметр данного прямоугольника без учёта проёма: м. Учитывая длину проёма, получим, что длина забора: м.

Ответ: 147

Задача 2

Масштаб карты такой, что в одном сантиметре 12 км. Чему равно расстояние между городами A и B (в км), если на карте оно составляет 4 см?

Решение: Расстояние между городами равно 4 · 12 = 48 км.

Ответ: 48

Задача 3

Дачный участок имеет форму квадрата, стороны которого равны 30 м. Размеры дома, расположенного на участке и имеющего форму прямоугольника, — 8 м × 5 м. Найдите площадь оставшейся части участка. Ответ дайте в квадратных метрах.

Решение: Площадь квадрата равна квадрату его стороны, поэтому площадь участка равна

30 · 30 = 900 кв. м. Площадь прямоугольника равна произведению его длины на ширину, поэтому площадь дома равна 8 · 5 = 40 кв. м. Тем самым, площадь участка, незанятого домом равна 900 − 40 = 860 кв. м. Ответ: 860.

Практическая часть

1) Выполнить задание в тетради для практических работ

Вариант 1.

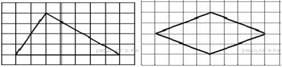1. (4 балла) Найти площадь фигур: 3. 4.

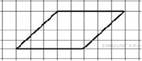
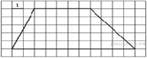
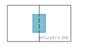2. (2 балла) Два садовода, имеющие прямоугольные участки размерами 20 м на 30 м с общей границей, договорились и сделали общий прямоугольный пруд размером 10 м на 14 м (см. чертёж), причём граница участков проходит точно через центр. Какова площадь (в квадратных метрах) оставшейся части участка каждого садовода?

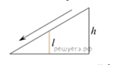
3. (2 балла) Столб подпирает детскую горку посередине. Найдите высоту l этого столба, если высота горки h равна 4,2 м. Ответ дайте в метрах.

4. (2 балла) Сколько потребуется кафельных плиток квадратной формы со стороной 15 см, чтобы облицевать ими стену, имеющую форму прямоугольника со сторонами 3 м и 2,7 м?

5. (2 балла) Пол комнаты , имеющий форму прямоугольника со сторонами 5,5 м и 6 м, нужно покрыть паркетом прямоугольной формы. Длина каждой дощечки паркета равна 30

см, а ширина -5 см. Сколько потребуется таких дощечек для покрытия пола?

Вариант 2.

1. (4 балла) Найти площадь фигур.

2. (2 балла) Дачный участок имеет форму прямоугольника со сторонами 35 м и 20 м. Хозяин планирует обнести его изгородью и отгородить такой же изгородью квадратный участок со стороной 10 м (см. рис.). Найдите суммарную длину изгороди в метрах.

3. (2 балла) От столба к дому натянут провод длиной 15 м, который закреплён на стене дома на высоте 3 м от земли (см. рис.). Найдите высоту столба, если расстояние от дома до столба равно 12 м. Ответ дайте в метрах.

4. (2 балла) Масштаб карты такой, что в одном сантиметре 2,5 км. Чему равно расстояние

между городами A и B (в км), если н а карте оно составляет 12 см?

5. (2 балла) Сколько потребуется кафельных плиток квадратной формы со стороной 15 см, чтобы облицевать ими стену, имеющую форму прямоугольника со сторонами 3 м и 2,7 м?

*****

Шкала оценки образовательных достижений

Результативность: количество набранных баллов	Оценка уровня подготовки (отметка)
(11-12 баллов)	«5»-отлично
(9-10 баллов)	«4»- хорошо
(7-8 баллов)	«3»- удовлетворительно
(менее 7 баллов)	«2»- неудовлетворительно

Практическая работа №2

«Практико- ориентированные задачи на проценты»

Цель: Обобщить и сформировать умения решать задачи на проценты .

Обеспечение: Задания и методические указания к выполнению работ

Ход работы

Теоретическая часть

1) Записать конспект в рабочую тетрадь

Рассмотрим три основных типа задач на проценты.

1)Нахождение процента от числа

Чтобы найти проценты от числа, можно проценты представить в виде десятичной дроби и число умножить на полученную десятичную дробь.

Задача: Предприятие изготовило за квартал 500 насосов, из которых 60 % имели высшую категорию качества. Сколько насосов высшей категории качества изготовило предприятие?

Решение: Найдем 60 % от 500 (общее количество насосов).

60 % = 0,6

500 • 0,6 = 300 насосов высшей категории качества.

Ответ: 300 насосов высшей категории качества.

2)Нахождение числа по его проценту Чтобы найти число по его процентам, можно проценты представить в виде десятичной дроби и данное число разделить на полученную десятичную дробь.

Задача: Ученик прочитал 138 страниц, что составляет 23 % числа всех страниц в книге. Сколько страниц в книге?

Решение:

Итак, нам неизвестно сколько всего страниц в книге. Но мы знаем, что часть, которую прочитал ученик (138 страниц) составляет 23 % от общего количества страниц в книге. Так как 138 стр. – это всего лишь часть, само количество страниц, естественно, будет больше 138. Это поможет нам при проверке.

Проверка: 600 138 (это означает, что 138 является частью 600).

Ответ: 600 (стр.) - общее количество страниц в книге.

2) Сколько процентов одно число составляет от другого.

Чтобы найти сколько процентов одно число составляет от другого можно одно число разделить на другое и полученное произведение умножить на 100.

Задача: Из 200 арбузов 16 оказались незрелыми. Сколько процентов всех арбузов составили незрелые арбузы?

Решение:

16 делим на общее количество арбузов и умножаем на 100 %.

Ответ: 8 % - составляют незрелые арбузы от всех арбузов.

Практическая часть

2)Выполнить задание в тетради для практических работ

Вариант 1.

1. За пропуски занятий студенту уменьшили стипендию на 12%. Сколько ему достанется, если сейчас стипендия 812 рублей?

2. Плата за телефон составляет 340 рублей в месяц. В следующем году она увеличится на 20%. Сколько рублей придётся платить ежемесячно за телефон в следующем году?

3. Грибы при сушке теряют 78% своей массы. Сколько сушеных грибов получится из 100 кг свежих?

4. Какова величина подоходного налога, который составляет 13% от величины заработной платы в 21000 рублей?

5. В декабре телефон стоил 38 тыс. рублей, в сезон цену повысили на 20%, а в мае снизили на 15%, в июле была распродажа со скидкой 30%. Сколько теперь стоит телефон?

Вариант 2

1. В магазине мультиварка продается со скидкой 20% за 4500 рублей. Какова первоначальная цена мультиварки?

2. Плата за телефон составляет 220 рублей в месяц. В следующем году она увеличится на 10%. Сколько рублей придётся платить ежемесячно за телефон в следующем году?

3. Банк начисляет на счёт 15% годовых. Вкладчик положил на счёт 700 рублей. Сколько рублей будет на этом счёте через год, если никаких операций, кроме начисления процентов, со счётом проводиться не будет?

4. Банк начисляет на счёт 12% годовых. Вкладчик положил на счёт 1200 рублей. Сколько рублей будет на этом счёте через год, если никаких операций, кроме начисления процентов, со счётом проводиться не будет?

5.В ноябре планшет стоил 32 тыс. рублей, затем цену повысили на 20%, а в мае снизили на 15%, в июле была распродажа со скидкой 30%. Сколько теперь стоит планшет?

*****

Шкала оценки образовательных достижений

Результативность: количество набранных баллов	Оценка уровня подготовки (отметка)
(5 заданий)	«5»-отлично
(4 задания)	«4»- хорошо
(3 задания)	«3»- удовлетворительно
(2 и менее заданий)	«2»- неудовлетворительно

Практическая работа № 3

по теме «Решение уравнений и неравенств,

систем уравнений и неравенств»

Цель: Закрепить навыки решения уравнений и систем уравнений

Обеспечение: Задания и методические указания к выполнению работ
Ход работы

1. Теоретическая часть

1) Записать конспект в рабочую тетрадь:

Вид уравнения

Формулы

Пример

Линейные

ах=в

х=

а(в+с)=ав+вс

(а+в)((с+d)=ac+ad+bc+bd

2х+1=2(х-3)+8

2x+1=4x-6+8

2х-4х=2-1

-2х=1

х=- 0,5

Ответ: х=-0,5

Квадратные

ах² + вх + с = 0

D=b² - 4ac

Теорема Виета

х² +рх + q = 0

х₁+х₂ = -р, х₁х₂ = q,

Разложение на множители

ах² + вх + с= а(х-х₁)(х-х₂)

х²+6х-7=0

а=1, b=6, c=-7

D=b²-4ac= 6²-4-1(-7)= 36+28=64

Неполные квадратные

ax² + bx = 0

x(ax + b) = 0.

x =0, ax + b =0

x = -

ax² - c = 0

ax² = c

x² =

х=+

5х²-4x=0,

x(5x-4)=0,

x=0 или 5x-4=0, x=5/4=0,8

Ответ: 0;0,8

9x²-36=0,

9а²=36,

а²=4,

а1=2, а2=-2

Ответ: -2; 2

Биквадратные уравнения

ax⁴+bx²+c=0, где a≠0

x²=t,t≥0 at²+bt+c=0, …

х⁴−5x²+6=0

Уравнения, сводящиеся к квадратным

(x² – 2x)² – 2(x² – 2x) – 3 =0

Системы уравнений

1) Метод подстановки

2) Метод сложения

3) Графический метод

Практическая часть

2) Выполнить задание в тетради для практических работ

Вариант 1

Вариант 2

1) 4x-7=2x

2) 4(x+10)=-1

3) x²+8x+15=0

4) 5 x²+20x=0

5) x²-36=0

6) 3x-4(2x-3) <13

7) x²-х- 20≤0

10) Прямоугольный газон обнесен изгородью, длина которой 30 м. Площадь газона 56м². Найдите длины сторон газона.

1) 6x-3=8x

2) 10(x+2)=-7

3) x²+10x+24=0

4) 7 x²-14x=0

5) x²-27=0

6) 8-5(2x-3) >13-6x

7) х²-2x-35≤0

10) Прямоугольный участок земли обнесен забором, длина которого 40 м. Площадь участка 96 м². Найдите длины сторон участка.

*****

Шкала оценки образовательных достижений

Результативность: количество набранных баллов	Оценка уровня подготовки (отметка)
(9-10 заданий)	«5»-отлично
(8 заданий)	«4»- хорошо
(7 заданий)	«3»- удовлетворительно
(6 и менее заданий)	«2»- неудовлетворительно

Практическая работа № 4

по теме: «Решение иррациональных уравнений»

Цель: Отработать навыки решения иррациональных уравнений

Обеспечение: Задания и методические указания к выполнению работ.

Задание: Решите уравнения:

1. Вариант 1 =4

=х

3) х+1=

4) =2

5) +=8.

Вариант 2

=х

3) х+1=

=1.

Вариант 3

=х

3) х+1=

-=2.

Вариант 4

=х

3) =х-2

-=2.

*****

Шкала оценки образовательных достижений

Результативность: количество набранных баллов	Оценка уровня подготовки (отметка)
(5 заданий)	«5»-отлично
(4 задания)	«4»- хорошо
(3 задания)	«3»- удовлетворительно
(2 и менее заданий)	«2»- неудовлетворительно

Практическая работа № 5

по теме: «Решение показательных уравнений и неравенств»

Цель: Отработать навыки решения показательных уравнений и неравенств.

Обеспечение: Задания и методические указания к выполнению работ.

Задание:

*****

Шкала оценки образовательных достижений

Результативность: количество набранных баллов	Оценка уровня подготовки (отметка)
(5-6 заданий)	«5»-отлично
(4 задания)	«4»- хорошо
(3 задания)	«3»- удовлетворительно
(2 и менее заданий)	«2»- неудовлетворительно

Практическая работа № 6

по теме: «Преобразование логарифмических выражений»
Цель:

1) Отработать навыки преобразования логарифмических выражений.

3) Закрепить полученные знания.

Обеспечение: Задания и методические указания к выполнению работ.

Задание:

№ варианта	Вычислить	Вычислить, используя свойства логарифмов.	Вычислить, используя основное логарифмическое тождество.	Вычислить:
1.	log ₃ =	log₆18+ log₆2	7^1+log₇⁵	log₇36-log₇14-3log₇
2.	lg 0,001=	log₅75- log₅3	2 ^2+log₂⁵	log ₅+log₅40-log₅8
3.	log ₃ =	log₁₅9+ log₁₅25	5^log₅^{16 – 1}	2log_1/36- log_1/3400+3log_1/3
4.	log₂ 8 =	log₄8+ log₄2	25 ^{1 – 0,5log}₅¹¹	4log_1/23-log_1/227-2log_1/26
5.	log ₅ 125=	log₆108+ log₆12	10 ^2+lg5	lg0,001-lg10⁵+3lg
6.	log ₁₆ 1=	log₁₆2	6^1+log₆⁵	4log _0,53-log_0,527-2log_0,56
7.	log ₇₌	log₆2+ log₆3		lg0,001+lg10⁴-3lg
8.	lg10=	log₉27	10^lg0,5⁺¹	4log ₅+log₅40-log₅8
9.	log 225=	log₂12- log₂3	5^log₅^{8 – 1}	(log ₇2+ )lg7
10.	log ₃₌	log₁₂16+ log₁₂9	3^log₃¹⁰⁰⁰⁺¹	+

Контрольные вопросы (2 балла):

1. Дайте определение логарифма.

2. Назовите условие существования логарифмов.

3. Сформулируйте свойства логарифмов.

4. Запишите основное логарифмическое тождество.

****

Шкала оценки образовательных достижений:

Результативность: количество набранных баллов	Оценка уровня подготовки (отметка)
(9-10 баллов)	«5»-отлично
(8-8,9 балла)	«4»- хорошо
(7-7,9 баллов)	«3»- удовлетворительно
(менее 7 баллов)	«2»- неудовлетворительно

Практическая работа № 7

по теме: «Решение логарифмических уравнений и неравенств»
Цель: Отработать навыки решения логарифмических уравнений и неравенств.

Обеспечение: Задания и методические указания к выполнению работ.

Задание:

Вариант 1

1) Решить уравнение: log₅(2x-1)=2

2) Решить уравнение: log₃(x+2)+log₃x=1

3) Решить уравнение: ln(x²-6x+9)=ln3+ln(x+3)

4) Решить неравенство: log₃(x-3)≤2

5) Решить неравенство: log ₁_/₃(2-x)>-1

Вариант 2

1) Решить уравнение: log₄(2x-10)=2

2) Решить уравнение: log₂(x-5)+log₂(x+2)=3

3) Решить уравнение: ln(x-2)log₂x= ln(x-2)

4) Решить неравенство: log₂(x-)4≤1

5) Решить неравенство: log ₁_/₅(3-x)>-1

Вариант 3

1) Решить уравнение: log₆(2x-3)=2

2) Решить уравнение: log₃(x-2)+log₃(x+6)=1

3) Решить уравнение: ln(x²-6x+9)=ln3+ln(x+3)

4) Решить неравенство: log₃(x-3)≤2

5) Решить неравенство: log ₁_/₂(6-x)>-1

Вариант 4

1) Решить уравнение: log₄(2x-10)=2

2) Решить уравнение: log₂(3x+1)+log₂(x+2)=3

3) Решить уравнение: ln(x+3)log₃x= ln(x+3)

4) Решить неравенство: log₂(x-4)≤1

5) Решить неравенство: log ₁_/₆(5-x)>-1

*****

Шкала оценки образовательных достижений

Результативность: количество набранных баллов	Оценка уровня подготовки (отметка)
(5 заданий)	«5»-отлично
(4 задания)	«4»- хорошо
(3 задания)	«3»- удовлетворительно
(2 и менее заданий)	«2»- неудовлетворительно

Практическая работа № 8

по теме: «Применение логарифма»

Цель: Познакомиться с математическими фактами и задачами, использующими в своем решении понятие логарифма.

Обеспечение: Задания и методические указания к выполнению работ.

Ход работы

1. Теоретическая часть

Логарифмы находят самое широкое применение во многих областях науки и нашей

жизни, при обработке результатов тестирований в психологии и социологии, в

составлении прогнозов погоды, в экономике, музыке. Очень многие вещи в природе, экономике и других областях описываются при помощи экспоненциальных законов.

Примеры:

* Уровень звукового давления зависит от расстояния до источника звука,

отражения звука и т.д. Наиболее простой вид имеет зависимость уровня давления

от расстояния. Если известен уровень мощности шума Lw, то уровень звукового

давления Lp в дБ на расстоянии r (в метрах) от источника вычисляется так:

Lp =Lw - lgr - 11

Задача 1 Мощность звука холодильного блока равна 78 дБ. Найти уровень звукового

давления на расстоянии 10 м от него.

Решение: (78 - lg10 - 11) дБ = 66 дБ

* Логарифмическая спираль - плоская кривая, описываемая точкой, движущейся по прямой, которая вращается около одной из своих точек О (полюса логарифмической спирали) так, что логарифм расстояния движущейся точки от полюса изменяется

пропорционально углу поворота.

* Золотая спираль (построенная по золотому сечению) применяется во многом, в том числе – и в архитектуре. Законы Золотой спирали всегда использовали и будут использовать для строительства лестниц.

* Применения логарифмической спирали в технике основаны на свойстве этой кривой

пересекать все свои радиусы - векторы под одним и тем же углом. Так, например,

вращающиеся ножи в различных режущих машинах имеют профиль, очерченный

по дуге спирали, благодаря чему угол резания, остается равным и, следовательно, неизменным в силу постоянства угла μ. В зависимости от обрабатываемого материала требуется тот или иной угол резания, что обеспечивается выбором параметра соответствующей спирали. На рис. представлен нож соломорезки.

2. Практическая часть

Заполните таблицу, используя электронные ресурсы.

Применение логарифма в…	Краткое описание	Рисунок

Каждый, верно оформленный пример в таблице оценивается в один балл.

Практическая работа № 9

по теме «Построение сечений».

Цель работы:

1. Научиться строить сечения тетраэдра и параллелепипеда

Оборудование: инструкционный лист с заданием, чертежные принадлежности.

Задание: По данным точкам многогранника построить сечение плоскостью.

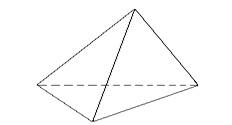Вариант 1

План работы:

Изучить чертеж (выполнение можно начинать с любого)
Перечертить его в тетрадь (с буквенными обозначениями и данными точками)
Выполнить построение.
Заштриховать полученный многоугольник
Записать справа от чертежа «Дано:…, построить…., построение…»
Записать процесс построения.

*****

Критерий оценок:

«5» - Приведена верная последовательность всех шагов выполнения задания. Правильно и аккуратно построены оба сечения. Имеется подробное описание процесса построения.

«4» - Правильно и аккуратно построены оба сечения, но при описании построения одного сечения допущены ошибки.

«3» - Оба сечения поострены неаккуратно или процесс построения не описан или построено и описано только одно сечение.

«2» - Сечения построены неправильно.

2 вариант
3 вариант
4 вариант
5 вариант
6 вариант
7 вариант
8 вариант
9 вариант
10 вариант

Практическая работа № 10

по теме: «Прямые и плоскости в пространстве»

Цель работы: отработать навыки решения задач на прямые и плоскости в пространстве.

Оборудование: инструкционный лист с заданием, чертежные принадлежности.

Ход работы

1. Теоретическая часть

1) Найдите на фото прямые, плоскости.

2) Укажите параллельные, пересекающиеся, скрещивающиеся, перпендикулярные прямые.

3) Найдите на фото прямую, параллельную плоскости; прямую, пересекающую плоскость; прямую, перпендикулярную плоскости.

4) Найдите на фото параллельные плоскости, пересекающиеся плоскости, перпендикулярные плоскости.

5) Приведите свои примеры прямых и плоскостей вокруг нас.

2. Практическая часть:

Решите задачи в тетради (работа в парах)

1. От столба к дому натянут провод длиной 17 м, который закреплён на стене дома на высоте 4 м от земли (см. рис.). Найдите высоту столба, если расстояние от дома до

столба равно 15 м. Ответ дайте в метрах.

2. На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,8 м, если длина его тени равна 1 м, а высота фонаря равна 9 м?

3. На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,8 м, если длина его тени равна 9 м, высота фонаря 5 м?

4. Перила лестницы дачного дома для надёжности укреплены посередине вертикальным столбом. Найдите высоту l этого столба, если наименьшая высота h₁ перил относительно земли равна 1,5 м, а наибольшая h₂ равна 2,5 м. Ответ дайте в метрах.

5. Детская горка укреплена вертикальным столбом, расположенным посередине спуска. Найдите высоту l этого столба, если высота h горки равна 2 метрам. Ответ дайте в метрах.

******

Шкала оценки образовательных достижений

Результативность: количество набранных баллов	Оценка уровня подготовки (отметка)
(9-10 заданий)	«5»-отлично
(8 заданий)	«4»- хорошо
(7 заданий)	«3»- удовлетворительно
(6 и менее заданий)	«2»- неудовлетворительно

Практическая работа № 11

по теме: «Прямые и плоскости в профессиональной деятельности и вокруг нас»

Цель работы: Систематизировать знания о прямые и плоскостях в пространстве.

Оборудование: инструкционный лист с заданием, чертежные принадлежности.

Ход работы

1. Теоретическая часть

Строитель постоянно сталкивается с прямыми и плоскостями в пространстве и ему необходимо знать об их взаимном расположении, также, как и специалисту управляющей компании и, конечно, повару.

Выберите фото, соответствующее вашей специальности и ответьте на вопросы (1 балл):

1) Где вы видите прямые, плоскости?

2) Как они располагаются между собой?

3) Пригодятся ли знания о прямых и плоскостях вам в вашей будущей работе?

2. Практическая часть

Заполните таблицу, используя электронные ресурсы.

Прямые и плоскости в моей будущей профессии	Краткое описание	Рисунок

Каждый, верно оформленный пример в таблице оценивается в один балл.

*****

Шкала оценки образовательных достижений

Результативность: количество набранных баллов	Оценка уровня подготовки (отметка)
(5 заданий)	«5»-отлично
(4 задания)	«4»- хорошо
(3 задания)	«3»- удовлетворительно
(2 и менее заданий)	«2»- неудовлетворительно

Практическая работа № 12

«Координатная плоскость. Вычисление расстояний и площадей»

Цель работы:

1. Отработать навыки построения точек на координатной плоскости в пространстве, вычисление расстояний и площадей.

2. Закрепить теоретические знания.

Обеспечение: Задания и методические указания к выполнению работ.

Задание:

1) (3 балла) Даны точки А(х₁; у₁; z₁), В(х₂; у₂; z₂), С(х₃; у₃; z). Изобразите данный треугольник в декартовой системе координат.

Вариант	1	2	3	4	5	6	7	8	9	10
Зада-ние 1	А(7;-3;3) B(5;7;2) С(1;4;2)	А(4;3;3) B(5;0;2) С(1;4;-2)	А(2;3;3) B(-5;4;2) С(1;-4;2)	А(5;2;3) B(5;1;-2) С(1;-1;2)	А(3;-3;3) B(-2;7;2) С(1;-3;2)	А(2;-3;3) B(5;-4;2) С(-1;4;2)	А(3;3;0) B(5;5;2) С(1;4;2)	А(4;3;3) B(5;7;2) С(1;4;2)	А(3;3;3) B(-5;7;2) С(-6;4;2)	А(0;3;3) B(-2;7;2) С(-6;4;2)

2) (2 балла) Найти длину стороны АВ, треугольника АВС.

3) (2 балла) Вычислить площадь треугольника АВС.

Контрольные вопросы (3 балла):

1. Перечислите координатные оси в пространстве.

2. Запишите формулу для вычисления расстояния между двумя точками в пространстве.

3. Запишите формулу для нахождения площади треугольника.

*****

Шкала оценки образовательных достижений:

Результативность: количество набранных баллов	Оценка уровня подготовки (отметка)
(9-10 баллов)	«5»-отлично
(8-8,9 балла)	«4»- хорошо
(7-7,9 баллов)	«3»- удовлетворительно
(менее 7 баллов)	«2»- неудовлетворительно

Практическая работа № 13

«Вычисление значений тригонометрических функций»

Цель работы:

1. Отработать навыки вычисления значений тригонометрических функций.

2. Закрепить теоретические знания.

Обеспечение:

1.Задания и методические указания к выполнению работ.

Задание:

№	Вычислить, пользуясь таблицей тригонометрических значений (2 балла)	Вычислить cos α или sin α, tg α, sin2α (4 балла)	Вычислить (2 балла)
1.		cos α= , < α <	sin210⁰
2.		cosα=, П< α <	sin225⁰
3.		sin α=, < α <	cos225⁰
4.		sin α= , < α <	cos135⁰.
5.		cos α=, < α <	sin150⁰
6.		sin α= , < α <	cos150⁰
7.		sin α= , < α <	sin120⁰
8.		sin α= , П< α <	sin135⁰
9.		sin α= < α <	cos120⁰
10.		sin α= , < α <	сos210⁰

Контрольные вопросы: (2 балла- по 0,5 за каждый вопрос)

1. Начертите таблицу значений тригонометрических функций с углами 0⁰,30,45⁰,60⁰,90⁰.

2. Запишите основное тригонометрическое тождество.

3. Начертите на единичных окружностях знаки тригонометрических функций.

4. Запишите формулы сложения, приведения.

*****

Шкала оценки образовательных достижений

Результативность: количество набранных баллов	Оценка уровня подготовки (отметка)
(9-10 баллов)	«5»-отлично
(8-8,9 балла)	«4»- хорошо
(7-7,9 баллов)	«3»- удовлетворительно
(менее 7 баллов)	«2»- неудовлетворительно

Практическое занятие № 14

«Преобразования простейших тригонометрических выражений»

Цель работы:

1. Отработать навыки преобразования тригонометрический выражений.

2. Закрепить теоретические знания.

Обеспечение: Задания и методические указания к выполнению работ.

Задание:

№	Вычислить, используя формулы приведения: (2 балла)	Вычислить, используя формулы сложения: (2 балла)	Докажите тождество: (2 балла)	Упростите выражение: (2 балла)
1.	cos (+30⁰)	cos (+30⁰)	=sin2	cos (α-β)+sin(П- α)sin(-β)
2.	sin(- 45⁰)	sin(- 45⁰)	=	sin4 α cos2 α +cos4 α sin2α
3.	sin(-45⁰)	sin(-45⁰)		cos5 α cos2 α +sin5 α sin2α
4.	cos (+60⁰)	cos (+60⁰)	=	cos9 α sin2 α –sin9 α cos2 α
5.	sin(П+45⁰)	sin(П+45⁰)	(1-sin α)* (1+sinα)=cos²α	sin (α+β)+sin(- α)sin(-β)
6.	sin(+45⁰)	sin(+45⁰)	=sin5a	cos7 α cos2 α –sin7 α sin2 α
7.	cos (П-30⁰)	cos (П-30⁰)	(1+cos α)∙(1-cosα)=sin²α	sin (α-β)+sin(- α)sin(-β)
8.	sin(+45⁰)	sin(+45⁰)	(1+sin α)∙(1-sinα)=cos²α	cos5 βcos2 β+sin5βsin2β
9.	cos (П+30⁰)	cos (П+30⁰)	(1-cosα)∙(1+cosα)=sin²α	sin (α-β)-sin(- α)sin(-β)
10.	sin(П-45⁰)	sin(П-45⁰)	=	сos3βcos2β+sin3βsin2β

Контрольные вопросы:(2 балла- по 0,5 за каждый вопрос)

1. Запишите правило для вычисления по формулам приведения.

2. Запишите формулы сложения.

3. Запишите формулы преобразования суммы и разности в произведение.

4. Запишите формулы двойного и половинного угла.

*****

Шкала оценки образовательных достижений

Результативность: количество набранных баллов	Оценка уровня подготовки (отметка)
(9-10 баллов)	«5»-отлично
(8-8,9 балла)	«4»- хорошо
(7-7,9 баллов)	«3»- удовлетворительно
(менее 7 баллов)	«2»- неудовлетворительно

Практическая работа № 15

«Преобразование графиков тригонометрических функций»

Цель работы:

1. Отработать навыки преобразования графиков тригонометрических функций.

2. Закрепить теоретические знания.

Обеспечение: Задания и методические указания к выполнению работ.

Задание: (8 баллов) Построить график функции.

Вариант:

1) у=2cos-1

2) у=3cos1/2 х+1

3) у=2cos1/2 х-1

4) у=1/2 cos3x-5

5) у=5sin1/3 х+1

6) у=2sin1/3 х-2

7) у=3sin1/3 х+4

8) у=1/2sin2x+2

9) у=1/2 cos2x-2

10) у=1/2sin3x+3

Контрольные вопросы:(2 балла- по 0,5 за каждый вопрос)

1. Как построить график функции y=f(x)+a, где a - постоянное число, если вы умеете строить график y=f(x)?

2. Как построить график функции y=к∙f(x), где к - постоянное число, если вы умеете строить график y=f(x)?

3. Как построить график функции y=f(x+b), где b - постоянное число, если вы умеете строить график y=f(x)?

4. Как построить график функции y=f(kx), где k - постоянное число, если вы умеете строить график y=f(x)?

******

Шкала оценки образовательных достижений

Результативность: количество набранных баллов	Оценка уровня подготовки (отметка)
(9-10 баллов)	«5»-отлично
(8-8,9 балла)	«4»- хорошо
(7-7,9 баллов)	«3»- удовлетворительно
(менее 7 баллов)	«2»- неудовлетворительно

Практическая работа № 16

«Использование свойств тригонометрических функций в профессиональных задачах»

Цель работы:

1. Рассмотреть области применения знаний тригонометрии, разобрав ряд практических задач.

Обеспечение: Задания и методические указания к выполнению работ.

Ход работы

Теоретическая часть

Тригонометрические вычисления нашли свое применение почти во всех областях

геометрии, физики и инженерного дела, в армии и навигации, строительстве.

Очень часто в жизни приходится сталкиваться с периодическими процессами, которые повторяются через одинаковые промежутки времени. Эти процессы называются колебательными: биение сердца, дыхательные движения грудной клетки, шаги ног при ходьбе, движение иглы швейной машины, прыжки на батуте, движение качелей, колебание поплавка на воде движение крыльев стрекозы, рессоры вагона и др. Колебательные явления различной физической природы подчиняются общим закономерностям и описываются тригонометрическими функциями. Модель биоритмов и в медицине, и в биологии можно построить с помощью графиков тригонометрических функций.

1. Сделайте разбор задач и запишите в рабочую тетрадь.

Задача 1

У бабушки сломался телевизор со стеклянным экраном и электронно-лучевой трубкой. Решили купить новый, жидкокристаллический. Старый телевизор был 29 дюймов ( ≈ 70см), 29дюймов по диагонали сейчас не делают, возьмем 32( ≈ 80см), пусть бабушка порадуется. Приносим подарок, включаем, а бабушка и говорит: «Ой, маленький какой-то телевизор, мой-то больше был!» Почему бабушка недовольна?

Решение: Старый телевизор:

У нового телевизора отношение сторон приблизительно равно 0,56, то есть α≈29⁰ , а

длины сторон 39 см и 69 см, поэтому он кажется маленьким (сравните высоту).

Чтобы бабушка была довольна, надо было брать с диагональю 40 дюймов ( ≈100см), у

которого стороны 49 см и 87 см. Угол между диагональю и длиной небольшой, но

длины сторон по сравнению со старым телевизором больше.

Задача 2 Расчет материалов на крышу

Расчет кровли в первую очередь начинается с определения угла наклона.

Теоретически он может составлять 11-70 градусов, но больше 45 градусов делать не

стоит. Во время холодных и снежных зим угол наклона 45 градусов позволит избавить кровлю от снежной нагрузки. Также для большого угла наклона кровли необходимо большее количество материала. Следует учитывать, что от вида кровельного покрытия и угла уклона меняется и шаг стропил. Чем больше угол уклона, тем шаг стропил может быть большим.

Чтобы рассчитать приблизительное количество материала и материальных затрат

необходимо выбрать угол уклона и высоту конька или угол уклона и ширину дома.

Ширина дома 10 м, а половина – 5 м.

Если угол уклона нужен больше или меньше, то необходимо изменить либо высоту конька, либо ширину дома во время проектирования. Далее вычислить длину покрытия и, соответственно, площадь крыши и материальные затраты на ее строительство.

Задача 3: Математика в артиллерии

Бомбардировщик на большой скорости – 707 км/ч. – приближается к важному объекту противника. Необходимо поднять в воздух зенитную ракету, скорость которой 1000 км/ч. Под каким углом направить ракету, чтобы она встретилась с самолетом?

Задача 4: Возводим горку во дворе

При постройке горки во дворе тоже потребуется тригонометрия. Для того, чтобы можно было скатываться с горки с безопасной скоростью, надо просчитать оптимальный угол, под которым будет наклонена горка относительно земли, высоту и длину проекции ската.

Если длина двора метров 9м, а угол наклона не более 30 градусов, то высота горки равна:

2. Практическая часть

Заполните таблицу, используя электронные ресурсы.

Применение тригонометрии в…	Краткое описание	Рисунок
Медицина
…
…
…
…

Каждый, верно оформленный пример в таблице оценивается в один балл.

*****

Шкала оценки образовательных достижений

Результативность: количество набранных баллов	Оценка уровня подготовки (отметка)
(5 заданий)	«5»-отлично
(4 задания)	«4»- хорошо
(3 задания)	«3»- удовлетворительно
(2 и менее заданий)	«2»- неудовлетворительно

Практическая работа № 17

«Выполнение расчетов с помощью комплексных чисел.

Примеры использования комплексных чисел»

Цель работы:

1. Отработать навыки выполнения расчетов с помощью комплексных чисел.

2. Найти примеры использования комплексных чисел.

3. Закрепить теоретические знания.

Обеспечение: Задания и методические указания к выполнению работ.

Задание:

1. (6 баллов) Найти сумму, разность, произведение и частное двух комплексных чисел в алгебраической форме.

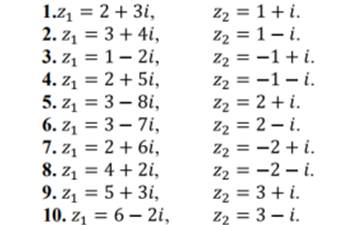
2. (1 балл) Приведите пример использования комплексных чисел.

3. Контрольные вопросы:(3 балла- по 0,5 за каждый вопрос)

1. Что такое комплексное число?

2. Что такое мнимая единица?

3. Что такое действительная часть числа?

4. Что такое мнимая часть числа?

5. Как сравнить два комплексных числа?

6. Какие числа называются сопряженными?

*****

Шкала оценки образовательных достижений

Результативность: количество набранных баллов	Оценка уровня подготовки (отметка)
(9-10 баллов)	«5»-отлично
(8-8,9 балла)	«4»- хорошо
(7-7,9 баллов)	«3»- удовлетворительно
(менее 7 баллов)	«2»- неудовлетворительно

Практическая работа № 18

«Техника дифференцирования»

Цель работы:

1. Отработать навыки вычисления производных.

2. Закрепить теоретические знания.

Обеспечение: Задания и методические указания к выполнению работ.

Задание:

№	Задание № 1 Найти производную функции в точке (2 балла):	Задание № 2 Найти производную (2 балла):	Задание № 3 Найти производную (2 балла):	Задание № 4 Найти производную (2 балла):
1	у=х³-2х+6 х₀=2	у=e^x -2х⁵+lnx	у=х³ ∙cosx	у=
2	у=3х⁴-2х²+4 х₀=-2	у=sinx+11x- e^x	у=х⁴ ∙lnx	у=
3	у=5х³-16х+9 х₀=1	у=log₂x -6х²+172e^x	у=х³ ∙sin x	у=
4	у=10х³-х²+6х х₀=1	у=cosх-10х+lnx	у=х²∙e^x
5	у=5х⁴-6х+10 х₀=-2	у=lnx+3cosx-4e^x	у=e^x∙cos x	у=
6	у=4х³+6х-16 х₀=2	у=e^x- log₃x+4sinx	у=х⁴∙cos x	у=
7	у=3х⁴-5х²+10 х₀=-1	у=sinx-12x+ 5e^x	у=х∙lnx	у=
8	у=4х³-3х+8 х₀=2	у=e^x+32х- log₈x	у=lnx∙sin x
9	у=3х⁴-5х²+6 х₀=1	у=cosx+3e^x+ log₂x	у=2^x∙lnx	у=
10	у=7х⁴+6х-9 х₀=-1	у=3^x-7lnx+6cosx	у=х⁵∙sin x

Контрольные вопросы (2 балла):

1. Дайте определение производной функции.

2. Перечислите основные формулы производных.

3. Перечислите правила нахождения производных.

*****

Шкала оценки образовательных достижений

Результативность: количество набранных баллов	Оценка уровня подготовки (отметка)
(9-10 баллов)	«5»-отлично
(8-8,9 балла)	«4»- хорошо
(7-7,9 баллов)	«3»- удовлетворительно
(менее 7 баллов)	«2»- неудовлетворительно

Практическая работа № 19

по теме: Физический и геометрический смысл производной в профессиональных и прикладных задачах

Цель работы:

1. Отработать навыки решения практических задач на физический и геометрический смысл производной.

2. Закрепить теоретические знания.

Обеспечение: Задания и методические указания к выполнению работ.

Задание:

1. Тело движется по прямой, так что расстояние S от начальной точки изменяется по закону: S=_________(м), где t- время движения в секундах. Через сколько секунд скорость тела будет равна ______ м/с?

2. Тело движется по прямой, так что расстояние S от начальной точки изменяется по закону: S=________ (м), где t- время движения в секундах. Найти скорость тела через ____ секунды после начала движения.

3. Найти угловой коэффициент касательной к графику функции

f(х)=_______, в точке с абсциссой х₀=-5.

4. Дана функция у=________ . Найти координаты точки графика этой функции, в которой угловой коэффициент касательной к нему равен ___.

5. Напишите уравнение касательной к графику функции f (х)=______ в точке с абсциссой х₀=___.

Контрольные вопросы (2 балла):

1. В чем состоит физический смысл производной?

2. В чем суть геометрического смысла производной?

3. Запишите уравнение касательной.

*****

Шкала оценки образовательных достижений

Результативность: количество набранных баллов	Оценка уровня подготовки (отметка)
(9-10 баллов)	«5»-отлично
(8-8,9 балла)	«4»- хорошо
(7-7,9 баллов)	«3»- удовлетворительно
(менее 7 баллов)	«2»- неудовлетворительно

Задания к практической работе № 19

№

Задание № 1

Задание № 2

Задание № 3

Задание № 4

Задание № 5

S=t²+t+4 (м),

v(t)= 15

S=5t²-6t+3(м), t₀=3с.

f(х)=3х²+5х-6, х₀=3

f(х)=3х⁵+7х-16, к=1

у=х³+2х

М(1;3)

S=3t²-2t+1(м),

v(t)= 10

S=2t²+6t-4(м), t₀=1с.

f(х)=5х³+4х-10, х₀=2

f(х)=х²+4х-6, к=2

у=х³+2х

М(-1;2)

S=t²+t+4(м),

v(t)= 13

S=3t²+2t-1(м), t₀=2с.

f(х)=х⁴+12х-5,

х₀= -1

f(х)=3х²+5х-6,

к =3

у=х³+2х

М(-1;3)

S=4t²-6t+4(м),

v(t)= 14

S=9t²-t+4(м), t₀=1с.

f(х)=2х³+4х-7, х₀=2

f(х)=2х³+5х²-2,

к = -1

у=х³+4х

М(0;3)

S=5t²+t-1(м),

v(t)= 21

S=3t²-t+8(м), t₀=2с.

f(х)=5х²+6х-4,

х₀= -3

f(х)=5х³+4х-10, к=2

у=х³+5х

М(1;3)

S=3t²-t+8(м),

v(t)= 17

S=5t²+t-1(м), t₀=3с.

f(х)=3х⁵+7х-16, х₀=1

f(х)=6х²+4х-6, к=2

у=х³-2х

М(1;3)

S=9t²-t+4(м),

v(t)= 17

S=4t²-6t+4(м), t₀=1с.

f(х)=2х³+5х²-2,

х₀= -1

f(х)=2х³+5х²-2,

к= -1

у=х³+2х

М(1;4)

S=3t²+2t-1(м),

v(t)= 14

S=t²+t+4(м), t₀=3с.

f(х)=3х³+8х-11, х₀=3

f(х)=х⁴+12х-5,

к= -1

у=х³+2х

М(1;6)

S=2t²+6t-4(м),

v(t)= 18

S=3t²-2t+1(м), t₀=4с.

f(х)=6х²+4х-6, х₀=2

f(х)=3х⁵+7х-16, к=1

у=х³+12х

М(1;3)

S=5t²-6t+3(м),

v(t)= 4

S=5t²-4t+4(м), t₀=5с.

f(х)=3х⁴+5х²-12, х₀=1

f(х)=2х³+4х-7,

к=2

у=2х³+2х

М(1;3)

Практическая работа № 20

по теме: «Построение графиков функций»

Цель работы:

1. Отработать навыки исследования функции и построения графиков.

2. Закрепить теоретические знания.

Обеспечение: Задания и методические указания к выполнению работ.

Задание:

1. ( 7 баллов) Исследовать функцию и построить ее график.

Вариант:

1. y = . 5. y = . 9. y = . y = . 6. y = . 10. y = .

2. y = . 7. y = .

3. y = . 8. y = .

2. Контрольные вопросы (3 балла):

Запишите алгоритм исследования функции

*****

Шкала оценки образовательных достижений

Результативность: количество набранных баллов	Оценка уровня подготовки (отметка)
(9-10 баллов)	«5»-отлично
(8-8,9 балла)	«4»- хорошо
(7-7,9 баллов)	«3»- удовлетворительно
(менее 7 баллов)	«2»- неудовлетворительно

Практическая работа № 21

по теме: «Наибольшее и наименьшее значение функции. Нахождение оптимальных результатов в прикладных и профессиональных задачах».

Цель работы:

1.Отработать навыки применения производной при решении прикладных задач.

2.Закрепить теоретические знания.

Обеспечение:

1.Задания и методические указания к выполнению работ.

2. Чертежные принадлежности, микрокалькуляторы.

Вариант N (Номер варианта (N) определяется по номеру в журнале)

1. (4 балла) Каким должен быть прямоугольник наибольшей площади, периметр которого равен а.

На основе этих данных составить и решить задачу, связанную со специальностью.

№ варианта	1	2	3	4	5	6	7	8	9	10
а	40	60	100	120	140	160	180	200	210	220

2. (4 балла) Из квадратного листа картона со стороной а нужно сделать открытую сверху коробку прямоугольной формы, вырезав по краям квадраты и загнув образовавшиеся края. Какой должна быть высота коробки, чтобы ее объем был наибольшим?

№ варианта	1	2	3	4	5	6	7	8	9	10
а	30	40	50	60	70	80	90	110	120	130

Контрольные вопросы: (2 балла)

1. Напишите алгоритм исследования функции на экстремум.

*****

Шкала оценки образовательных достижений

Результативность: количество набранных баллов	Оценка уровня подготовки (отметка)
(9-10 баллов)	«5»-отлично
(8-8,9 балла)	«4»- хорошо
(7-7,9 баллов)	«3»- удовлетворительно
(менее 7 баллов)	«2»- неудовлетворительно

Практическая работа № 22

по теме: «Понятие правильного многогранника. Свойства правильных многогранников»

Цель работы: Систематизировать знания по теме: «Правильные многогранники».

Обеспечение: Задания и методические указания к выполнению работ, учебники

Задание: Заполнить таблицу;

Название	тетраэдр	куб	октаэдр	додекаэдр	икосаэдр
чертеж	(образец)
Развертка
Число граней и их форма.	4 грани, правильные треугольники
Число ребер (Р)	6 ребер
Число вершин (В)	4 вершины
Проверьте по т. Эйлера	В+Г-Р= 4+4-6=2	В+Г-Р=	В+Г-Р=	В+Г-Р=	В+Г-Р=
Площадь полной поверхности	S=а²
Объём.	V=

*****

Критерий оценок:

«5» - Заполнена вся таблица. В вычислениях нет ошибок.

«4» - Заполнена вся таблица. В вычислениях имеются ошибки или нет формул некоторых многогранников.

«3» - Таблица заполнена не вся. Неаккуратно сделаны чертежи.

«2» - Таблица не заполнена, Чертежи выполнены плохо.

Практическая работа № 23

по теме: «Симметрия в природе, архитектуре, технике, в быту»

Цель работы: На примерах найти и показать симметрию как основу красоты в природе, архитектуре, технике, быту.

Обеспечение: Задания и методические указания к выполнению работ, чертежные принадлежности.

Ход работы

Теоретическая часть:

С симметрией мы встречаемся буквально на каждом шагу: в природе, технике, искусстве, науке. Понятие симметрии проходит через всю многовековую историю человеческого творчества. Оно встречается уже у истоков человеческого развития. Издавна человек использовал симметрию в архитектуре, в быту. Планируя свое жилое пространство, важно соблюсти некий баланс для комфортного пребывания. Один из инструментов этого баланса – симметрия. На уровне подсознания мы воспринимаем все более-менее симметричное как правильное, безопасное и желанное.

Скорее всего, ваш дом изначально симметричен: комнаты правильной прямоугольной формы, равные промежутки между оконными проемами… Начиная продумывать обстановку, обычно уделяется внимание парным предметам: две прикроватные тумбочки, два кресла около журнального столика, подсвечники на туалетном столике, шторы – многие предметы «зеркалят», уравновешивают друг друга. Если зеркальная расстановка не пришлась вам по вкусу, то предметы можно расположить вокруг условной центральной оси. Например, ставим диван напротив шкафа, а по центру, напротив окна – любимый журнальный столик. Или на примере кухни: справа от варочной панели стоит мультиварка, слева –тостер. В одном углу посудомоечная машина, в другом – мойка. Секрет в том, что даже непарные предметы могут уравновешивать друг друга, если их габариты примерно одинаковы.

Практическая часть:

1) Творческая работа, создай свой узор.

В тетради для практических работ с помощью карандаша и линейки начертите оси симметрии, и изобразите снежинку.

2) Составь план комнаты своей мечты.

*****

Критерий оценок:

«5» - Аккуратно выполнены оба чертежа. Отмечены оси.

«4» - Недостаточно аккуратно выполнены оба чертежа.

«3» - Выполнен только один чертеж.

«2» - Чертеж выполнен неаккуратно или неправильно.

Практическая работа № 24

по теме: «Использование комбинаций многогранников и тел вращения в практико-ориентированных задачах»

Цель работы: Научиться решать задачи на комбинацию тел.

Обеспечение: Задания и методические указания к выполнению работ

Задание:

Вариант 1

1. Вокруг шара описан куб. Ребро куба равно 8 см. Найдите объем шара.

2. (2 балла) Цилиндр описан около шара. Объем шара равен 88. Найдите объем цилиндра.

3. (2 балла) Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объём цилиндра, если объём конуса равен 5.

4. (2 балла) Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем шара равен 28. Найдите объем конуса.

Контрольные вопросы: (2 балла)

1. Запишите формулы для вычисления известных вам многогранников и тел вращения.

Вариант 2

1. (2 балла) Вокруг шара описан куб. радиус шара равен 8 см. Найдите объем куба.

2. (2 балла) Цилиндр описан около шара. Объем шара равен 20. Найдите объем цилиндра.

3. (2 балла) Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объём цилиндра, если объём конуса равен 57.

4. (2 балла) Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объём шара равен 156. Найдите объём конуса.

Контрольные вопросы: (2 балла)

1. Запишите формулы для вычисления известных вам многогранников и тел вращения.

*****

Шкала оценки образовательных достижений

Результативность: количество набранных баллов	Оценка уровня подготовки (отметка)
(9-10 баллов)	«5»-отлично
(8-8,9 балла)	«4»- хорошо
(7-7,9 баллов)	«3»- удовлетворительно
(менее 7 баллов)	«2»- неудовлетворительно

Практическая работа 25

по теме: Геометрический смысл определенного интеграла. Формула Ньютона - Лейбница. Решение задач на применение интеграла для вычисления площадей»

Цель работы:

1. Отработать навыки построения криволинейных трапеций и вычисления их площадей.

2. Способствовать формированию умений и навыков межпредметного характера, связанных с построением и «чтением» чертежей, вычислениями площадей.

Обеспечение: Задания и методические указания к выполнению работ, чертежные принадлежности, микрокалькуляторы

1) у=х-2, у=-х²+4; 2) у=х+2, у= -х²+4; 3) у=х, у=

4) у=2х, у= х²-3; 5) у=2х-3, у=-х²; 6) у=х-1, у= х²-1.

7) у=х+3, у= х²+1; 8) у=х², у= х+2; 9) у=2х-1, у= -х²+2;

10) у=х+4, у= х²+2;

Указание. При выполнении задания воспользоваться алгоритмом:

1) Изобразить фигуру, площадь которой нужно найти. Для этого построить графики данных функций.

2) Найти абсциссы пересечения данных графиков.

3) Составить интеграл для вычисления площади (возможно разность интегралов)

4) Вычислить площадь полученной фигуры, используя формулу Ньютона – Лейбница.

*****

Критерий оценок:

«5» - Приведена верная последовательность всех шагов выполнения задания. График построен аккуратно карандашом и линейкой. В вычислениях нет ошибок.

«4» - Приведена верная последовательность всех шагов выполнения задания. График построен аккуратно, но при вычислении интеграла допущена ошибка.

«3» - График построен, но при составлении интеграла допущена ошибка, в результате чего ответ не верен.

«2» - График не построен, площадь не вычислена.

Практическая работа № 26

по теме: «Операции с множествами. Решение прикладных задач»

Цель работы: Научиться решать прикладные задачи используя понятия «Множества»

Обеспечение: Задания и методические указания к выполнению работ.

Ход работы

Теоретическая часть

1) Записать конспект в рабочую тетрадь:

Понятие множества − одно из первичных в математике. Поэтому очень трудно дать ему какое-либо определение, которое бы не заменяло слово «множество» каким-нибудь равнозначным выражением, например, совокупность, собрание элементов и т.д. Элементы множества − это то, из чего это множество состоит.

Пересечение множеств в теории множеств - это множество, которомупринадлежат те и только те элементы, которые одновременно принадлежат всем данным множествам.

Круги Эйлера - геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Изобретены Леонардом Эйлером. Используется в математике, логике, менеджменте и других прикладных направлениях.

Решение задач с помощью кругов Эйлера

1."Обитаемый остров" и "Стиляги".

Некоторые студенты нашей группы любят ходить в кино. Известно, что 15 ребят смотрели фильм «Обитаемый остров», 11 человек - фильм «Стиляги», из них 6 смотрели и «Обитаемый остров», и «Стиляги». Сколько человек смотрели только фильм «Стиляги»?

Решение:

Чертим два множества таким образом:

6 человек, которые смотрели фильмы «Обитаемый остров» и «Стиляги», помещаем в пересечение множеств.

1. 15 - 6 = 9 - человек, которые смотрели только «Обитаемый остров»,

2. 11- 6 = 5 - человек, которые смотрели только «Стиляги». Получаем:

Ответ: 5 человек.

2. Задача про библиотеки

Каждый из 35 студентов является читателем, по крайней мере, одной из двух

библиотек: техникума ГСТ и городской. Из них 25 человек берут книги в библиотеке ГСТ, 20 в городской.

Сколько студентов:

1. Являются читателями обеих библиотек;

2. Не являются читателями городской библиотеки;

3. Не являются читателями библиотеки ГСТ;

4. Являются читателями только городской библиотеки;

5. Являются читателями только библиотеки ГСТ?

Решение: Чертим два множества: (выполнить самостоятельно)

1) 20+ 25 - 35 = 10 (человек) - являются читателями обеих библиотек. На схеме это общая часть кругов. Мы определили единственную неизвестную нам величину. Теперь, глядя на схему, легко даем ответы на поставленные вопросы.

2) 35 - 20 = 15 (человек) - не являются читателями городской библиотеки,

3) 35 - 25 = 10 (человек) - не являются читателями библиотеки ГСТ,

4) 35- 20 = 10 (человек) - являются читателями только городской библиотеки,

5) 35- 20 = 15 (человек) - являются читателями только библиотеки ГСТ.

Очевидно, что вопросы 2 и 5, а также 3 и 4 - равнозначны и ответы на них

совпадают.

Ответ: 10 человек; 15 человек; 10 человек; 10 человек; 15 человек.

Практическая часть

2) Выполнить задание в тетради для практических работ

1. В детском саду 52 ребенка. Каждый из них любит пирожное или мороженое. Половина детей любит пирожное, а 20 человек - пирожное и мороженое. Сколько детей любит мороженое?

2. В классе 35 учеников. 20 из них занимаются в математическом кружке, 11 — в биологическом, а 1 ничем не занимаются. Сколько ребят занимаются и математикой, и биологией?

3. На фирме работают 67 человек. Из них 47 знают английский язык, 35 -

немецкий язык, а 23 - оба языка. Сколько человек фирмы не знают ни

английского, ни немецкого языков?

4. Из 100 человек 85 знают английский язык, 80 - испанский, 75 - немецкий. Все владеют, по крайней мере, одним иностранным языком. Среди них нет таких, которые знают два иностранных языка, но есть владеющие тремя языками. Сколько человек из этих 100 знают три языка?

5. Из сотрудников фирмы 16 побывали во Франции, 10 - в Италии, 6 - в Англии; в Англии и Италии - 5; в Англии и Франции - 6; во всех трех странах – 5 сотрудников. Сколько человек посетили и Италию, и Францию, если всего в фирме работают 19 человек, и каждый из них побывал хотя бы в одной из названных стран?

*****

Шкала оценки образовательных достижений

Результативность: количество набранных баллов	Оценка уровня подготовки (отметка)
(5 заданий)	«5»-отлично
(4 задания)	«4»- хорошо
(3 задания)	«3»- удовлетворительно
(2 и менее заданий)	«2»- неудовлетворительно

Практическая работа № 27

по теме: «Применение графов при решении задач»

Цель работы: Научиться решать прикладные задачи используя графы.

Обеспечение: Задания и методические указания к выполнению работ.

Ход работы

Теоретическая часть

1) Записать конспект в рабочую тетрадь

Задача 1. Между девятью планетами солнечной системы установлено космическое сообщение. Рейсовые ракеты летают по следующим маршрутам: Земля – Меркурий; Плутон – Венера; Земля – Плутон; Плутон – Меркурий; Меркурий – Венера; Уран – Нептун; Нептун – Сатурн; Сатурн – Юпитер; Юпитер – Марс и Марс – Уран. Можно ли долететь на рейсовых ракетах с Земли до Марса?

Решение. Нарисуем схему условия: планеты изобразим точками, а маршруты ракет – линиями.

Ответ: видно, что долететь с Земли до Марса нельзя.

Задача 2. Между населёнными пунктами A, B, C, D, E, F, G построены дороги, протяжённость которых приведена в таблице. Отсутствие числа в таблице означает, что прямой дороги между пунктами нет. Определите длину кратчайшего пути между пунктами A и G (при условии, что передвигаться можно только по построенным дорогам).

Решение. Для наглядности изобразим граф в виде рисунка (см. рис. 5). Сразу видно, что есть путь из A в G из одного ребра длины 25. Поищем более короткие пути. Поскольку длины всех рёбер положительны, то кратчайший путь не может содержать циклов. Кратчайший путь из A в B имеет длину 5 (это одно ребро), так как любое другое выходящее из A ребро имеет большую длину. Кратчайший путь из A в D имеет длину 12 (тоже одно ребро), так как единственный альтернативный путь A → B → D имеет длину 13. Поэтому кратчайший путь из A в C имеет длину 14 (A → D → C). Из C в G ведут три пути (без циклов): путь C → E → G длины 9, путь C → G длины 10 и путь C → F → G длины 15. Кратчайший из них имеет длину 9. Поэтому

длина кратчайшего «обходного» пути из A в G равна 14 + 9 = 23 < 25. Значит, кратчайший путь из A в G имеет длину 23. Ответ: 23.

Задача 3. На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город М, проходящих через город В?

Решение. Из рисунка видно, что любой путь из А в М проходит через И. По условию задачи мы должны искать только те пути, которые проходят через В. Обозначим число путей через N. Из рисунка видно, что имеется четыре пути из А в В(А → Б → В, А → В, А → Г → В, А → Д → Г → В), три пути из В в И (В → Е → И, В → Ж → И, В → Е → Ж → И) и три пути из И в М (И → К → М, И → М, И → Л → М). Получаем N = 4 · 3 · 3 = 36. Ответ: 36.

Практическая часть

2) Выполнить задание в тетради для практических работ

1 вариант	2 вариант
1) При встрече 4 друзей обменялись рукопожатиями. Сколько всего рукопожатий было сделано?	1) При встрече 6 друзей обменялись рукопожатиями. Сколько всего рукопожатий было сделано?
2) Ориентированный граф G c множеством вершин V = {1, 2, 3, 4, 5, 6} задан списком дуг {(1, 6), (2, 1), (2, 5), (3, 1), (3, 3), (3, 5), (3, 2), (3, 6), (5, 1), (5, 6), (6, 4), (6, 5)}. Построить данный граф.	2) Ориентированный граф G c множеством вершин V = {1, 2, 3, 4, 5, 6} задан списком дуг {(1, 6), (2, 1), (2, 3), (3, 1), (3, 3), (3, 3), (3, 4), (3, 6), (5, 1), (5, 6), (5, 6), (5, 6), (6, 4), (6,6)} Построить данный граф.
3) Граф задан таблицей. Найти длину кратчайшего пути из А в Д.	3) Граф задан таблицей. Найти длину кратчайшего пути из А в Е.
4) Волшебная страна Фарг почти вся состоит из непреодолимых гор и рек. В ней есть шесть городов: А, Б, В, Г, Д и Е. Известно, что из А проложены дороги в Б и Г, из Б — в А, Г и Д, из В — в Г и Е, из Г — в А, Б, В и Д, из Д — в Б и Г, из Е — только в В. Все остальные дороги непроходимы. Нарисуйте карту страны Фарг.
Может ли житель города А попасть в город Д, если ему нельзя проходить через Г?	Может ли житель города А попасть в город Е, если ему нельзя проходить через Г?
5) Построить родословное дерево потомков Владимира Мономаха. Владимир Мономах умер в 1125 г. Он оставил четырёх сыновей: Мстислава (год смерти - 1132), Ярополка (1139), Вячеслава Туровского (1154) и Юрия Долгорукого (1157). После Мстислава остались три сына: Изяслав Волынский (1154), Всеволод Новгородский (1138) и Ростислав Смоленский (1168). У Изяслава Волынского был сын Мстислав (1170), у Мстислава - сын Роман (1205), у Романа - Даниил Галицкий (1264). Ростислав Смоленский имел четырех сыновей: Романа (1180), Рюрика (1215), Давида (1197) и Мстислава Храброго (1180). После Романа Ростиславича остался сын Мстислав Киевский (1224), после Мстислава Храброго - сын Мстислав Удалой (1228). Юрий Долгорукий имел трех сыновей: Андрея Боголюбского (1175), Михаила (1177) и Всеволода (1212). Сыновьями Всеволода были Константин (1217), Юрий (1238) и Ярослав (1246). У Ярослава Всеволодовича было три сына: Александр Невский (1263), Андрей Суздальский (1264) и Ярослав Тверской (1272). Сыновья Александра Невского: Димитрий Переяславский (1294), Андрей Городецкий (1304) и Даниил Московский (1303). У Андрея Суздальского был сын Василий (годы его жизни неизвестны), у Ярослава Тверского - сын Михаил (1318). Глядя на полученное дерево, ответьте на вопрос: сколько поколений князей оно отражает?

*****

Шкала оценки образовательных достижений

Результативность: количество набранных баллов	Оценка уровня подготовки (отметка)
(5 заданий)	«5»-отлично
(4 задания)	«4»- хорошо
(3 задания)	«3»- удовлетворительно
(2 и менее заданий)	«2»- неудовлетворительно

Практическая работа

по теме: «Элементы комбинаторики. Вероятность события».

Цель работы:

1. Отработать навыки решения задач на перестановки, сочетания и размещения;

2. Отработать навыки решения простейших задач по теории вероятностей;

3. Закрепить теоретические знания.

Обеспечение: Задания и методические указания к выполнению работ.

Вариант 1.

Задача 1. (2 балла) Сколькими способами можно разместить на полке 5 книг?

Задача 2. (2 балла) Из 25 человек бригадиру нужно выбрать четверых для определенной работы. Сколькими способами это можно сделать?

Задача 3. (2 балла) Имеется 5 компьютеров и четыре пользователя. Сколькими способами можно рассадить каждого.

Задача 4 (1 балл) Из колоды (36 карт) наудачу выбирают одну карту. Какова вероятность, что она окажется пиковой масти?

Задача 5. (2 балла) Из 8 черных и 5 белых шаров вынимают 2 шара. Какова вероятность того, что шары белые?

Контрольные вопросы (1 балл - по 0,5 б. за каждый вопрос):

1. (1 балл) Сформулируйте определения понятий: «Размещения», «Перестановки», «Сочетания».

2. Сформулируйте определение вероятности события.

*****

Шкала оценки образовательных достижений

Результативность: количество набранных баллов	Оценка уровня подготовки (отметка)
(9-10 баллов)	«5»-отлично
(8-8,9 балла)	«4»- хорошо
(7-7,9 баллов)	«3»- удовлетворительно
(менее 7 баллов)	«2»- неудовлетворительно

Практическая работа

по теме: «Элементы комбинаторики. Вероятность события».

Цель работы:

1.Отработать навыки решения задач на перестановки, сочетания и размещения;

2. Отработать навыки решения простейших задач по теории вероятностей;

3. Закрепить теоретические знания.

Обеспечение: Задания и методические указания к выполнению работ.

Вариант 2.

Задача 1. (2 балла) Сколькими способами можно рассадить взрослых пассажиров в автомобиле, если в нем 3 пассажирских места?

Задача 2. (2 балла) Сколькими способами можно составить команду из 4 человек для соревнований по бегу, если имеется 7 бегунов?

Задача 3. (2 балла) Имеется 10 электронных документов, три из которых нужно поместить в очередь на печать на принтере. Сколькими способами это можно сделать?

Задача 4.(1 балл) Из колоды(36 карт) наудачу выбирают одну карту. Какова вероятность, что это дама?

Задача 5. (2 балла) Из 14 черных и 7 белых шаров вынимают 4 шара. Какова вероятность того, что шары черные?

Контрольные вопросы (1 балл - по 0,5 б. за каждый вопрос):

1. (1 балл) Сформулируйте определения понятий: «Размещения», «Перестановки», «Сочетания».

2. Сформулируйте определение вероятности события.

*****

Шкала оценки образовательных достижений

Результативность: количество набранных баллов	Оценка уровня подготовки (отметка)
(9-10 баллов)	«5»-отлично
(8-8,9 балла)	«4»- хорошо
(7-7,9 баллов)	«3»- удовлетворительно
(менее 7 баллов)	«2»- неудовлетворительно

Практическая работа

по теме: «Элементы комбинаторики. Вероятность события».

Цель работы:

1. Отработать навыки решения задач на перестановки, сочетания и размещения;

2. Отработать навыки решения простейших задач по теории вероятностей;

3. Закрепить теоретические знания.

Обеспечение: Задания и методические указания к выполнению работ.

Вариант 3.

Задача 1 (2 балла) Учащимся необходимо сдать 4 экзамена на протяжении 8 дней. Сколькими способами это можно сделать?

Задача 2. (2 балла) Из 10 учащихся нужно составить группу из 4 для участия в мероприятии. Сколькими способами это можно сделать?

Задача 3. (2 балла) Сколькими способами можно обить 6 стульев тканью, если имеются ткани 6 разных расцветок и все ткани должны быть разного цвета?

Задача 4.(1 балл) Какова вероятность, что преподаватель вызовет вас к доске, если в группе 30 человек?

Задача 5 .(2 балла) Из 10 черных и 5 белых шаров вынимают 3 шара. Какова вероятность того, что шары окажутся белыми?

Контрольные вопросы (1 балл - по 0,5 б. за каждый вопрос):

2. (1 балл) Сформулируйте определения понятий: «Размещения», «Перестановки», «Сочетания».

2. Сформулируйте определение вероятности события.

*****

Шкала оценки образовательных достижений

Результативность: количество набранных баллов	Оценка уровня подготовки (отметка)
(9-10 баллов)	«5»-отлично
(8-8,9 балла)	«4»- хорошо
(7-7,9 баллов)	«3»- удовлетворительно
(менее 7 баллов)	«2»- неудовлетворительно

Практическая работа

по теме: «Элементы комбинаторики. Вероятность события».

Цель работы:

1. Отработать навыки решения задач на перестановки, сочетания и размещения;

2. Отработать навыки решения простейших задач по теории вероятностей;

3. Закрепить теоретические знания.

Обеспечение: Задания и методические указания к выполнению работ.

Вариант 3.

Задача 1. (2 балла) Сколькими способами можно разместить на полке 5 книг?

Задача 2. (2 балла) Сколькими способами можно составить команду из 3 человек для участия в мероприятии, если выбрать нужно из 8 претендентов.

Задача 3. (2 балла) Имеется 4 компьютеров и три пользователя. Сколькими способами можно рассадить каждого?

Задача .4(1 балл) Какова вероятность, что вы победите в соревнованиях, если вместе с вами участвуют 12 человек?

Задача 5 . (2 балла) Из 4 черных и 15 белых шаров вынимают 3 шара. Какова вероятность того, что шары окажутся черными?

Контрольные вопросы (1 балл - по 0,5 б. за каждый вопрос):

3. (1 балл) Сформулируйте определения понятий: «Размещения», «Перестановки», «Сочетания».

2. Сформулируйте определение вероятности события.

*****

Шкала оценки образовательных достижений

Результативность: количество набранных баллов	Оценка уровня подготовки (отметка)
(9-10 баллов)	«5»-отлично
(8-8,9 балла)	«4»- хорошо
(7-7,9 баллов)	«3»- удовлетворительно
(менее 7 баллов)	«2»- неудовлетворительно

Практическая работа

по теме: «Элементы комбинаторики. Вероятность события».

Цель работы:

1. Отработать навыки решения задач на перестановки, сочетания и размещения;

2. Отработать навыки решения простейших задач по теории вероятностей;

3. Закрепить теоретические знания.

Обеспечение: Задания и методические указания к выполнению работ.

Вариант 5

Задача 1. (2 балла) Сколькими способами можно разместить 5 цветочных горшков на подоконнике?

Задача 2. (2 балла) Сколькими способами читатель может выбрать две книжки из шести имеющихся?

Задача 3 (2 балла) Из 9 учащихся нужно составить группу из 3 человек для участия в мероприятии. Сколькими способами это можно сделать?

Задача 4.(1 балл) Из 500 деталей на складе 10 оказались бракованными. Какова вероятность взять исправную деталь?

Задача 5. (2 балла) Из 5 черных и 10 белых шаров вынимают 3 шара. Какова вероятность того, что шары окажутся черными?

Контрольные вопросы (1 балл - по 0,5 б. за каждый вопрос):

1.Сформулируйте определения понятий: «Размещения», «Перестановки», «Сочетания».

2. Сформулируйте определение вероятности события.

*****

Шкала оценки образовательных достижений

Результативность: количество набранных баллов	Оценка уровня подготовки (отметка)
(9-10 баллов)	«5»-отлично
(8-8,9 балла)	«4»- хорошо
(7-7,9 баллов)	«3»- удовлетворительно
(менее 7 баллов)	«2»- неудовлетворительно

Практическая работа

по теме: «Элементы комбинаторики. Вероятность события».

Цель работы:

1. Отработать навыки решения задач на перестановки, сочетания и размещения;

2. Отработать навыки решения простейших задач по теории вероятностей;

3. Закрепить теоретические знания.

Обеспечение: Задания и методические указания к выполнению работ.

Вариант 6

Задача 1. (2 балла) Сколькими способами можно разместить 4 диска на полке?

Задача 2. (2 балла) В классе десять предметов и пять уроков в день. Сколькими способами можно составить расписание на один день?

Задача 3 (2 балла) Сколькими способами можно разложить восемь различных писем по восьми различным конвертам, если в каждый конверт кладется только одно письмо?

Задача 4.(1 балл) Из 800 автомобилей 8 ломаются в течение 1 года эксплуатации. Какова вероятность купить автомобиль, который не поломается в течение 1 года эксплуатации?

Задача 5. (2 балла) Из 7 черных и 13 белых шаров вынимают 4 шара. Какова вероятность того, что шары окажутся белыми?

Контрольные вопросы (1 балл - по 0,5 б. за каждый вопрос):

1. Сформулируйте определения понятий: «Размещения», «Перестановки», «Сочетания».

2. Сформулируйте определение вероятности события.

*****

Шкала оценки образовательных достижений

Результативность: количество набранных баллов	Оценка уровня подготовки (отметка)
(9-10 баллов)	«5»-отлично
(8-8,9 балла)	«4»- хорошо
(7-7,9 баллов)	«3»- удовлетворительно
(менее 7 баллов)	«2»- неудовлетворительно

Практическая работа

по теме: «Элементы комбинаторики. Вероятность события».

Цель работы:

1. Отработать навыки решения задач на перестановки, сочетания и размещения;

2. Отработать навыки решения простейших задач по теории вероятностей;

3. Закрепить теоретические знания.

Обеспечение: Задания и методические указания к выполнению работ.

Вариант 7

Задача 1. (2 балла) Сколькими способами семь книг разных авторов можно расставить на полке в один ряд?

Задача 2. (2 балла) На родительском собрании присутствует 20 человек. Сколько существует различных вариантов состава родительского комитета, если в него должны войти 5 человек?

Задача 3. (2 балла) Имеется 8 электронных документов, три из которых нужно поместить в очередь на печать на принтере. Сколькими способами это можно сделать?

Задача 1.(1 балл). Из 900 автомобилей 9 ломаются в течение 1 года эксплуатации. Какова вероятность купить автомобиль, который не поломается в течение 1 года эксплуатации?

Задача 2. (2 балла) Из 6 черных и 14 белых шаров вынимают 4 шара. Какова вероятность того, что шары окажутся белыми?

Контрольные вопросы (1 балл - по 0,5 б. за каждый вопрос):

1. Сформулируйте определения понятий: «Размещения», «Перестановки», «Сочетания».

2. Сформулируйте определение вероятности события.

*****

Шкала оценки образовательных достижений

Результативность: количество набранных баллов	Оценка уровня подготовки (отметка)
(9-10 баллов)	«5»-отлично
(8-8,9 балла)	«4»- хорошо
(7-7,9 баллов)	«3»- удовлетворительно
(менее 7 баллов)	«2»- неудовлетворительно

Практическая работа

по теме: «Элементы комбинаторики. Вероятность события».

Цель работы:

1. Отработать навыки решения задач на перестановки, сочетания и размещения;

2. Отработать навыки решения простейших задач по теории вероятностей;

3. Закрепить теоретические знания.

Обеспечение: Задания и методические указания к выполнению работ.

Вариант 8

Задача 1. (2 балла) Сколько слов можно образовать из букв слова фрагмент, если слова должны состоять из восьми букв?

Задача 2. (2 балла) Сколькими способами можно разложить 5 различных писем по восьми различным конвертам, если в каждый конверт кладется только одно письмо?

Задача 3. (2 балла) Сколькими способами из восьми человек можно избрать комиссию, состоящую из пяти членов?

Задача 4.(1 балл). Из 900 телевизоров 9 ломаются в течение 1 года эксплуатации. Какова вероятность купить телевизор, который не поломается в течение 1 года эксплуатации?

Задача 5. (2 балла) Из 5 черных и 15 белых шаров вынимают 4 шара. Какова вероятность того, что шары окажутся белыми?

Контрольные вопросы (1 балл - по 0,5 б. за каждый вопрос):

1. Сформулируйте определения понятий: «Размещения», «Перестановки», «Сочетания».

2. Сформулируйте определение вероятности события.

*****

Шкала оценки образовательных достижений

Результативность: количество набранных баллов	Оценка уровня подготовки (отметка)
(9-10 баллов)	«5»-отлично
(8-8,9 балла)	«4»- хорошо
(7-7,9 баллов)	«3»- удовлетворительно
(менее 7 баллов)	«2»- неудовлетворительно

Практическая работа

по теме: «Элементы комбинаторики. Вероятность события».

Цель работы:

1. Отработать навыки решения задач на перестановки, сочетания и размещения;

2. Отработать навыки решения простейших задач по теории вероятностей;

3. Закрепить теоретические знания.

Обеспечение: Задания и методические указания к выполнению работ.

Вариант 9

Задача 1. (2 балла) Сколько чисел можно составить из 4 разных цифр?

Задача 2. (2 балла) На 3 вакантных места по определенной специальности претендуют 7 безработных, состоящих на учете в службе занятости. Сколько возможных комбинаций выбора 3 из 7 безработных?

Задача 3. (2 балла) Сколькими способами можно выбрать 4 делегата на конференцию, если в группе 20 человек?

Задача 4.(1 балл). Из 900 телефонов 9 ломаются в течение 1 года эксплуатации. Какова вероятность купить телефон, который не поломается в течение 1 года эксплуатации?

Задача 5. (2 балла) Из 15 черных и 5 белых шаров вынимают 4 шара. Какова вероятность того, что шары окажутся белыми?

Контрольные вопросы (1 балл - по 0,5 б. за каждый вопрос):

1. Сформулируйте определения понятий: «Размещения», «Перестановки», «Сочетания».

2. Сформулируйте определение вероятности события.

*****

Шкала оценки образовательных достижений

Результативность: количество набранных баллов	Оценка уровня подготовки (отметка)
(9-10 баллов)	«5»-отлично
(8-8,9 балла)	«4»- хорошо
(7-7,9 баллов)	«3»- удовлетворительно
(менее 7 баллов)	«2»- неудовлетворительно

Практическая работа

по теме: «Элементы комбинаторики. Вероятность события».

Цель работы:

1. Отработать навыки решения задач на перестановки, сочетания и размещения;

2. Отработать навыки решения простейших задач по теории вероятностей;

3. Закрепить теоретические знания.

Обеспечение: Задания и методические указания к выполнению работ.

Вариант 10

Задача 1. (2 балла) Сколько чисел можно составить из 4 разных цифр?

Задача 3. (2 балла) Сколькими способами можно выбрать 4 делегата на конференцию, если в группе 20 человек?

Задача 5. (2 балла) Из 15 синих и 5 белых шаров вынимают 4 шара. Какова вероятность того, что шары окажутся синими?

Контрольные вопросы (1 балл - по 0,5 б. за каждый вопрос):

1. Сформулируйте определения понятий: «Размещения», «Перестановки», «Сочетания».

2. Сформулируйте определение вероятности события.

*****

Шкала оценки образовательных достижений

Результативность: количество набранных баллов	Оценка уровня подготовки (отметка)
(9-10 баллов)	«5»-отлично
(8-8,9 балла)	«4»- хорошо
(7-7,9 баллов)	«3»- удовлетворительно
(менее 7 баллов)	«2»- неудовлетворительно

Практическая работа № 29

по теме: «Вариационный ряд. Полигон частот и гистограмма.

Статистические характеристики ряда наблюдаемых данных»

Цель работы:

1. Отработать навыки составления вариационного ряда.

2. Отработать навыки построения полигона частот и гистограммы.

3. Отработать навыки нахождения числовых характеристик случайной величины.

4. Закрепить теоретические знания.

Обеспечение: Задания и методические указания к выполнению работ.

Вариант 1

Задача 1 (4 балла). Для благотворительной лотереи подготовлено 1000 билетов. Из них 4 билетов имеют выигрыш по 500 руб., 10 билетов – по 100 руб. и 100 билетов – по 10 руб., остальные билеты – без выигрыша.

Составить закон распределения случайной величины – размера выигрыша по лотерейному билету. Построить полигон распределения. Найти математическое ожидание и дисперсию данной случайной величины, а также указать интервал ее наиболее ожидаемых значений.

Задача 2 (4 балла). Имеются данные о распределении объемов продаж мобильных телефонов в сетевых салонах связи по ценовым группам:

Цена, тыс. руб.	1-2	2-3	3-4	4-5	5-6	6-7
Доля в объеме продаж (%)	14	23	25	23	8	9

Определить среднюю цену мобильного телефона, продаваемого в сетевых салонах связи, дисперсию, среднее квадратическое отклонение, коэффициент вариации. Построить гистограмму распределения объемов продаж мобильных телефонов по ценовым группам. Сделать выводы.

Контрольные вопросы (2 балла - по 0,5 б. за каждый вопрос)

1. Как построить полигон и гистограмму?

2. Как вычислить числовые характеристики случайной величины?

*****

Шкала оценки образовательных достижений

Результативность: количество набранных баллов	Оценка уровня подготовки (отметка)
(9-10 баллов)	«5»-отлично
(8-8,9 балла)	«4»- хорошо
(7-7,9 баллов)	«3»- удовлетворительно
(менее 7 баллов)	«2»- неудовлетворительно

Практическая работа № 29

по теме: «Вариационный ряд. Полигон частот и гистограмма.

Статистические характеристики ряда наблюдаемых данных»

Цель работы:

5. Отработать навыки составления вариационного ряда.

6. Отработать навыки построения полигона частот и гистограммы.

7. Отработать навыки нахождения числовых характеристик случайной величины.

8. Закрепить теоретические знания.

Обеспечение: Задания и методические указания к выполнению работ.

Вариант 2

Задача 1 (4 балла). Для благотворительной лотереи подготовлено 500 билетов. Из них 2 билета имеют выигрыш по 500 руб., 30 билетов – по 100 руб. и 50 билетов – по 10 руб., остальные билеты – без выигрыша.

Задача 2 (4 балла). Для выяснения возрастных особенностей кадрового состава сотрудников фирмы было произведено выборочное обследование, в результате которого получены следующие данные:

Возраст сотрудников, лет

20-25

25-30

30-35

35-40

40-45

45-50

Старше 50

Число сотрудников

Определить средний возраст сотрудника фирмы, дисперсию, среднее квадратическое отклонение, коэффициент вариации. Построить гистограмму распределения числа сотрудников по интервалам возраста. Сделать выводы.

Контрольные вопросы (2 балла - по 0,5 б. за каждый вопрос)

3. Как построить полигон и гистограмму?

4. Как вычислить числовые характеристики случайной величины?

*****

Шкала оценки образовательных достижений

Результативность: количество набранных баллов	Оценка уровня подготовки (отметка)
(9-10 баллов)	«5»-отлично
(8-8,9 балла)	«4»- хорошо
(7-7,9 баллов)	«3»- удовлетворительно
(менее 7 баллов)	«2»- неудовлетворительно

Практическая работа № 29

по теме: «Вариационный ряд. Полигон частот и гистограмма.

Статистические характеристики ряда наблюдаемых данных»

Цель работы:

1. Отработать навыки составления вариационного ряда.

2. Отработать навыки построения полигона частот и гистограммы.

3. Отработать навыки нахождения числовых характеристик случайной величины.

4. Закрепить теоретические знания.

Обеспечение: Задания и методические указания к выполнению работ.

Вариант 3

Задача 1 (4 балла ) Для благотворительной лотереи подготовлено 1000 билетов. Из них 8 билетов имеют выигрыш по 500 руб., 10 билетов – по 100 руб. и 100 билетов – по 10 руб., остальные билеты – без выигрыша.

Задача 2 (4 балла). Ниже приводятся данные о возрастном составе безработных города, зарегистрированных в службе занятости, в %:

Возраст (лет)	до 20	20-24	25-29	30-49	50-54	55-59	60 и старше
Мужчины	7,7	17,0	11,9	50,9	4,2	5,7	2,6

Найдите средний возраст безработных мужчин, дисперсию, среднее квадратическое отклонение и коэффициент вариации. Постройте гистограмму распределения. Сделайте выводы.

Контрольные вопросы (2 балла)

1. Как построить полигон и гистограмму?

2. Как вычислить числовые характеристики случайной величины?

*****

Шкала оценки образовательных достижений

Результативность: количество набранных баллов	Оценка уровня подготовки (отметка)
(9-10 баллов)	«5»-отлично
(8-8,9 балла)	«4»- хорошо
(7-7,9 баллов)	«3»- удовлетворительно
(менее 7 баллов)	«2»- неудовлетворительно

Практическая работа № 29

по теме: «Вариационный ряд. Полигон частот и гистограмма.

Статистические характеристики ряда наблюдаемых данных»

Цель работы:

1. Отработать навыки составления вариационного ряда.

2. Отработать навыки построения полигона частот и гистограммы.

3. Отработать навыки нахождения числовых характеристик случайной величины.

4. Закрепить теоретические знания.

Обеспечение: Задания и методические указания к выполнению работ.

Вариант 4

Задача 1 (4 балла ) Для благотворительной лотереи подготовлено 500 билетов. Из них 5 билетов имеют выигрыш по 500 руб., 20 билетов – по 100 руб. и 50 билетов – по 10 руб., остальные билеты – без выигрыша.

Возраст (лет)	до 20	20-24	25-29	30-49	50-54	55-59	60 и старше
Женщины	11,2	18,5	11,7	49,5	4,0	3,8	1,3

Найдите средний возраст безработных женщин, дисперсию, среднее квадратическое отклонение и коэффициент вариации. Постройте гистограмму распределения. Сделайте выводы.

Контрольные вопросы (2 балла)

1. Как построить полигон и гистограмму?

2. Как вычислить числовые характеристики случайной величины?

*****

Шкала оценки образовательных достижений

Результативность: количество набранных баллов	Оценка уровня подготовки (отметка)
(9-10 баллов)	«5»-отлично
(8-8,9 балла)	«4»- хорошо
(7-7,9 баллов)	«3»- удовлетворительно
(менее 7 баллов)	«2»- неудовлетворительно

Практическое занятие 30

по теме: «Первичная обработка статистических данных. Графическое их представление. Нахождение средних характеристик, наблюдаемых данных»

Цель работы:

1. Отработать навыки первичной обработки статистических данных.

2. Закрепить теоретические знания.

Обеспечение: Задания и методические указания к выполнению работ.

Задание 1. (4 балла) В течение месяца в магазине регистрировали частоту покупок стирального порошка и собрали следующие данные (x_i): 8, 5, 4, 9, 3, 13, 1, 2, 0, 4, 12, 3, 5, 7, 10, 6, 5, 7, 3, 2, 9, 8, 1, 4, 6, 5, 4, 2, 1, 8.

Проанализируйте полученные данные, для этого постройте вариационный ряд, полигон, определите числовые характеристики. Какие рекомендации Вы дали бы администрации универсама?

Задание 2. (4 балла) Дано распределение фирм города осуществляющих евроремонт по среднесписочному числу рабочих. Найти относительную частоту среднесписочного числа рабочих. Построить гистограмму распределение фирм осуществляющих евроремонт по относительным частотам среднесписочного числа рабочих.

число рабочих	число строительных фирм	относительная частота	накопленная частота
5 -10	12
10 - 15	9
15 - 20	6
25 - 30	3

3. Ответить на контрольные вопросы. (2 балла - по 0,5 б. за каждый вопрос)

1. Задачи математической статистики.

2. Понятие вариационного ряда.

3-4. Определение и формулы для вычисления числовых характеристик вариационного ряда.

*****

Шкала оценки образовательных достижений

Результативность: количество набранных баллов	Оценка уровня подготовки (отметка)
(9-10 баллов)	«5»-отлично
(8-8,9 балла)	«4»- хорошо
(7-7,9 баллов)	«3»- удовлетворительно
(менее 7 баллов)	«2»- неудовлетворительно

Практическое занятие 30

Цель работы:

1. Отработать навыки первичной обработки статистических данных.

2. Закрепить теоретические знания.

Обеспечение: Задания и методические указания к выполнению работ.

Вариант 2

Задание 1. (4 балла) При обследовании 50 членов семей рабочих и служащих установлено следующее количество членов семьи: 5; 3; 2; 1; 4; 6; 3; 7; 9; 1; 3; 2; 5; 6; 8; 2; 5; 2; 3; 6; 8; 3; 4; 4; 5; 6; 5; 4; 7; 5; 6; 4; 8; 7; 4; 5; 7; 8; 6; 5; 7; 5; 6; 6; 7; 3; 4; 6; 5; 4. Проанализируйте полученные данные, для этого постройте вариационный ряд, полигон, определите числовые характеристики. Сделайте выводы.

2. (4 балла) Дано распределение фирм города осуществляющих установку евроокон по среднесписочному числу рабочих. Найти относительную частоту среднесписочного числа рабочих. Построить гистограмму распределение фирм осуществляющих евроремонт по относительным частотам среднесписочного числа рабочих.

число рабочих	число фирм устанавливающие евроокна	относительная частота	накопленная частота
5 -10	8
10 - 15	4
15 - 20	6
25 - 30	2

3.Ответить на контрольные вопросы. (2 балла - по 0,5 б. за каждый вопрос)

1. Задачи математической статистики.

2. Понятие вариационного ряда.

3-4. Определение и формулы для вычисления числовых характеристик вариационного ряда.

*****

Шкала оценки образовательных достижений

Результативность: количество набранных баллов	Оценка уровня подготовки (отметка)
(9-10 баллов)	«5»-отлично
(8-8,9 балла)	«4»- хорошо
(7-7,9 баллов)	«3»- удовлетворительно
(менее 7 баллов)	«2»- неудовлетворительно

Практическое занятие 30

Цель работы:

1. Отработать навыки первичной обработки статистических данных.

2. Закрепить теоретические знания.

Обеспечение: Задания и методические указания к выполнению работ.

Вариант 3

Задание 1. (4 балла) Администрацию универсама интересует оптимальный уровень запасов продуктов в торговом зале, а также среднемесячный объем покупок товаров, которые не являющихся предметом ежедневного потребления в семье (например, таких как сода). Для выяснения этого вопроса менеджер универсама в течение января регистрировал частоту покупок стограммовых пакетиков с содой и собрал следующие данные (x_i): 8, 4, 5, 9, 3, 3, 1, 2, 0, 4, 2, 3, 4, 7, 10, 6, 5, 7, 3, 3, 9, 8, 4, 4, 6, 5, 4, 2, 1, 8.

Постройте вариационный ряд, полигон распределения, определите его числовые характеристики. Какие рекомендации Вы дали бы администрации универсама?

Задание 2. (4 балла) Дано распределение строительных фирм региона по среднесписочному числу рабочих. Найти относительную частоту среднесписочного числа рабочих. Построить гистограмму распределение строительных фирм по относительным частотам среднесписочного числа рабочих.

число рабочих	число строительных фирм	относительная частота	накопленная частота
50 - 100	12
150 - 200	8
250 - 300	15
350 - 400	5

3.Ответить на контрольные вопросы. (2 балла - по 0,5 б. за каждый вопрос)

1. Задачи математической статистики.

2. Понятие вариационного ряда.

3-4. Определение и формулы для вычисления числовых характеристик вариационного ряда.

Практическое занятие 30

Цель работы:

1. Отработать навыки первичной обработки статистических данных.

2. Закрепить теоретические знания.

Обеспечение: Задания и методические указания к выполнению работ.

Вариант 4

Задание 1. (4 балла) При обследовании 50 членов семей рабочих и служащих установлено следующее количество членов семьи: 6; 3; 2; 1; 4; 6; 3; 7; 9; 1; 3; 2; 5; 5; 8; 2; 5; 2; 3; 6; 8; 3; 4; 4; 5; 6; 5; 4; 7; 5; 6; 4; 8; 7; 4; 5; 7; 8; 6; 5; 7; 5; 4; 6; 7; 3; 4; 6; 5; 6. Проанализируйте полученные данные, для этого постройте вариационный ряд, полигон, определите числовые характеристики. Сделайте выводы.

Задание 2 .(4 балла) Дано распределение фирм города осуществляющих евроремонт по среднесписочному числу рабочих. Найти относительную частоту среднесписочного числа рабочих. Построить гистограмму распределение фирм осуществляющих евроремонт по относительным частотам среднесписочного числа рабочих.

число рабочих	число строительных фирм	относительная частота	накопленная частота
5 -10	14
10 - 15	8
15 - 20	6
25 - 30	4

3.Ответить на контрольные вопросы. (2 балла - по 0,5 б. за каждый вопрос)

1. Задачи математической статистики.

2. Понятие вариационного ряда.

3-4. Определение и формулы для вычисления числовых характеристик вариационного ряда.

*****

Шкала оценки образовательных достижений

Результативность: количество набранных баллов	Оценка уровня подготовки (отметка)
(9-10 баллов)	«5»-отлично
(8-8,9 балла)	«4»- хорошо
(7-7,9 баллов)	«3»- удовлетворительно
(менее 7 баллов)	«2»- неудовлетворительно

Практическая работа 31

по теме: «Общие методы решения уравнений.

Уравнения и неравенства с модулем и с параметрами»

Цель работы: Отработать навыки решения уравнений и неравенств.

Обеспечение: Задания и методические указания к выполнению работ.

Вариант 1

Вариант 2

Решить уравнения и неравенства:

1) 3^х-1=;

2) 0,1^2x <10;

3) log₃ (2x+5)=1;

4) log₅(x-4)<3;

5) =4

6)sin (2x – ) = ;

7) 2^3х+2-2^3х-2=30;

8) |х-3|≤1

9)Решить графически: 2^х=х+3

10) Решить уравнение с

параметром а:

2х² + 5х + 3а = 0;

Решить уравнения и неравенства:

1) 4^х-1=;

2) 0,7^2x > 0,49;

3) log₂(x-5)=3;

4) log_1/3(x-4)>-2;

5) =3

6) sin (2x – ) = ;

7) 3^х+1+3 ^х-2=28

8) |х+2|≤4

9) Решить графически: ^х=х-3

10) Решить уравнение с параметром а:

2х² - 5х + 3а = 0;

*****

Шкала оценки образовательных достижений

Результативность: количество набранных баллов	Оценка уровня подготовки (отметка)
(9-10 заданий)	«5»-отлично
(8 заданий)	«4»- хорошо
(6-7)	«3»- удовлетворительно
(менее 6 заданий)	«2»- неудовлетворительно

Практическая работа № 32

по теме: «Решение текстовых задач профессионального содержания»

Цель работы: Отработать навыки решения текстовых задач.

Обеспечение: Задания и методические указания к выполнению работ.

Вариант 1

1.Известь гашеная стоит 22 руб. мешок. Определите, на сколько мешков хватит 300 рублей, если цена повысится на 20%.

2. (1 балл) Определите, сколько банок краски по 3 кг необходимо купить для покраски пола в мастерской площадью 6х9 м², если на 1м² расходуется 300 грамм краски.

3. Длина прямоугольной строительной площадки на 1 м больше его ширины, а диагональ равна 29 м. Найдите площадь площадки.

4. Каменщик с помощником получили за работу 29050р. Каменщик работал 8 дней, а его помощник только 35% этого времени. Дневной заработок Каменщика на 40% больше, чем его помощника. Сколько денег заработал каменщик и сколько его помощник?

5. На строительстве стены первый каменщик работал 5 дней один. Затем к нему присоединился второй, и они вместе закончили работу через 4 дня. Известно, что первому каменщику потребовалось бы на выполнение этой работы на 5 дней больше, чем второму. За сколько дней может построить эту стену первый каменщик, работая один?

Вариант 2

1. Пена монтажная «Ростов» стоит 290 р баллон. Определите, на сколько баллонов хватит 1000 рублей, если цену повысят на 20%.

2. Определите, сколько банок краски по 2 кг необходимо купить для покраски пола в мастерской площадью 6х9 м², если на 1м² расходуется 300 грамм краски.

3. Периметр прямоугольной строительной площадки равен 94 м, а ее диагональ равна 37 м. Найдите площадь данной площадки.

4. Каменщик с помощником получили за работу 39050р. Каменщик работал 7 дней, а его помощник только 35% этого времени. Дневной заработок каменщика на 40% больше, чем его помощника. Сколько денег заработал каменщик и сколько его помощник?

5. На строительстве стены первый каменщик работал 6 дней один. Затем к нему присоединился второй, и они вместе закончили работу через 4 дня. Известно, что первому каменщику потребовалось бы на выполнение этой работы на 5 дней больше, чем второму. За сколько дней может построить эту стену первый каменщик, работая один?

Вариант 3

1. Комплект электродов для сварки стоит 110 руб. Определите, на сколько комплектов хватит 500 рублей, если цена на них повысится на 20%.

2. (1 балл) Определите, сколько банок краски по 3 кг необходимо купить для покраски пола в кабинете площадью 6х9 м², если на 1м² расходуется 300 граммов краски.

3.Раствор для укладки кирпича состоит из цемента, песка и воды. На одно ведро цемента берется 1 ведро воды и два ведра песка, т.е. цемент, вода и песок берутся в отношении 1:1:2 (по объему) . Сколько надо взять ведер воды, песка на 5 ведер цемента?

4. Каменщик с помощником получили за работу 29050р. Каменщик работал 7 дней, а его помощник только 30% этого времени. Дневной заработок каменщика на 40% больше, чем его помощника. Сколько денег заработал каменщик и сколько его помощник?

Вариант 4

1. Проволока омедненная (1 кг) стоит 290 рублей. Определите, на сколько кг хватит 1000 рублей, если цену повысят на 20%.

2. Определите, сколько банок краски по 2 кг необходимо купить для покраски пола в мастерской площадью 6х9 м², если на 1м² расходуется 300 граммов краски.

3. Раствор для укладки кирпича состоит из цемента, песка и воды. На одно ведро цемента берется 1 ведро воды и два ведра песка, т.е. цемент, вода и песок берутся в отношении 1:1:2 (по объему) . Сколько надо взять ведер воды, песка на 4 ведра цемента?

4. Каменщик с помощником получили за работу 29050р. Каменщик работал 8 дней, а его помощник только 25% этого времени. Дневной заработок каменщика на 40% больше, чем его помощника. Сколько денег заработал каменщик и сколько его помощник?

5. На строительстве стены первый каменщик работал 7 дней один. Затем к нему присоединился второй, и они вместе закончили работу через 4 дня. Известно, что первому каменщику потребовалось бы на выполнение этой работы на 5 дней больше, чем второму. За сколько дней может построить эту стену первый каменщик, работая один?

*****

Шкала оценки образовательных достижений

Результативность: количество набранных баллов	Оценка уровня подготовки (отметка)
(5 заданий)	«5»-отлично
(4 задания)	«4»- хорошо
(3 задания)	«3»- удовлетворительно
(менее 3 заданий)	«2»- неудовлетворительно

Контрольная работа

по теме: «Степени и корни. Степенная функция».

Вариант 1

1. Вычислите:

а) б) в)

2. Упростите выражение и найдите его значение:

, при

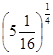3. Вычислите: а); б); в); г); д).

4. Упростите выражение: а) б) в); г).

5. Найдите наибольшее и наименьшее значение функции: у=:

на полуинтервале: (5;16].

Вариант 2

1. Вычислите:

а) б) в)

2. Упростите выражение и найдите его значение:

при

3. Вычислите: а); б); в); г); д).

4. Упростите выражение: а) б) в); г)

5. Найдите наибольшее и наименьшее значение функции: у=:

на полуинтервале: (0;1].

Контрольная работа

по теме: «Показательная функция».

Вариант 1

1. Какая из функций у = , у = , у = , у = х⁵является показательной?

2. Какая из функций ; ; ; является убывающей?

3. Сравнить значение выражений и

4. Решите уравнение: 3^{5х + 1} = 27;

5. Решите уравнение: 3 ∙ 81^х – 10 ∙ 9^х + 3 = 0;

6. Решите неравенство: ()^2х≤;

7. Решите неравенство: 5^{х – 1}+ 5^{х + 1}≤ 26;

8. Решите систему: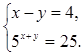

9. Решить графически уравнение = х+ 4

Вариант 2

1. Какая из функций у = , у = , у = , у = не является показательной?

2. Какая из функций ; ; ; является возрастающей?

3. Сравнить значение выражений и

4. Решите уравнение: 11^{4х - 3} = 121;

5. Решите уравнение: 2∙ 9^х – 3∙ 3^х – 9 = 0;

6. Решите неравенство: (0,1)^2х≥ 0,01;

7. Решите неравенство: 4^{х + 1}–4^{х – 1}˃ 120;

8. Решите систему: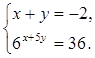

9. Найти точку пересечения графиков у = и у = х+ 4

Контрольная работа

по теме: «Логарифмы. Логарифмическая функция»

Вариант 1

1. Вычислить:

1) 2) 3)

2. Найти область определения функции у = log₃ (x – 13).

3. Решите уравнение: log₅(2x – 1) = 2;

4. Решите уравнение: log₂(x - 2) + log₂ x = 3;

5. Решите неравенство: > -1;

6. Решите систему уравнений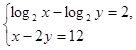

7. Решить графически уравнение: = х-1

Вариант 2

1. Вычислить:

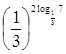1) 2) 3)

2. Найти область определения функции у = lg (x – 5).

3. Решите уравнение: log₄(2x + 3) = 3;

4. Решите уравнение: log₃(x - 8) + log₃ x = 2;

5. Решите неравенство: < 2;

6. Решите систему уравнений: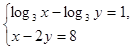

7. Решить графически уравнение: = х-1

Контрольная работа

по теме: «Прямые и плоскости в пространстве»

В заданиях 1–4 укажите правильный ответ.

При выполнении заданий 5–6 запишите ход решения и полученный ответ.

Вариант 1

1. Если две прямые параллельны третьей, то они …

А) скрещиваются между собой;

Б) параллельны между собой;

В) пересекаются между собой;

Г) не параллельны между собой.

2. Прямая и плоскость называются параллельными, если они…

А) имеют одну общую точку;

Б) не имеют общей точки;

В) имеют две общие точки;

Г) имеют три общие точки.

3. Если плоскость проходит через прямую, параллельную другой

плоскости, и пересекает эту плоскость, то линия пересечения плоскостей

А) параллельна данной прямой;

Б) скрещивается с данной прямой

В) не параллельна данной прямой;

Г) параллельна данной плоскости.

4. Если прямая …, то эта прямая перпендикулярна данной плоскости.

А) перпендикулярна каждой из двух скрещивающихся прямых;

Б) перпендикулярна каждой из двух пересекающихся прямых, лежащих в этой плоскости;

В) не перпендикулярна каждой из 2 пересекающихся прямых, лежащих в этой плоскости;

Г) перпендикулярна каждой прямой, лежащей в этой плоскости.

5. Концы отрезка АВ, не пересекающего плоскость, удалены от нее на расстоянии 7,4 м и 2,6 м. Найдите расстояние от середины М отрезка АВ до этой плоскости.

6. Перекладина длиной 8 м своими концами лежит на двух вертикальных

столбах высотой 3 м и 7 м. Каково расстояние между основаниями столбов?

Контрольная работа

по теме: «Прямые и плоскости в пространстве»

В заданиях 1–4 укажите правильный ответ.

При выполнении заданий 5–6 запишите ход решения и полученный ответ.

Вариант 2

1. Если прямая параллельна плоскости, то эта прямая … любой

прямой, лежащей в этой плоскости.

А) параллельна и совпадает с ;

Б) скрещивается;

В) параллельна или скрещивается с;

Г) параллельна.

2. Если прямая параллельна какой-либо прямой, … , то данные

прямая и плоскость параллельны.

А) не лежащей в плоскости;

Б) лежащей в плоскости;

В) не принадлежащей плоскости;

Г) принадлежащей плоскости.

3. Если одна из двух параллельных прямых перпендикулярна

плоскости, то …

А) другая не перпендикулярна этой плоскости;

Б) другая параллельна этой плоскости;

В) другая не пересекает эту плоскость;

Г) и другая перпендикулярна этой плоскости.

4. Если две прямые перпендикулярны плоскости, то они …

А) пересекаются;

Б) скрещиваются;

В) не параллельны;

Г) параллельны.

5. Точка А лежит в плоскости, точка В на расстоянии 12,5 см от этой

плоскости. Найдите расстояние от середины отрезка АВ до плоскости.

6. Какой длины нужно взять перекладину, чтобы ее можно было положить

концами на две вертикальные опоры высотой 4 м и 8 м, поставленные на

расстоянии 3 м одна от другой?

Контрольная работа за 1 семестр

Вариант 1

1. Цемент фасованный «Ростов» стоит 170 руб. Определите, на сколько мешков хватит 1500 рублей, если цена повысится на 20%.

2. Определите, сколько банок краски по 3 кг необходимо купить для покраски пола в мастерской площадью 6х9 м², если на 1м² расходуется 300 грамм краски.

3. Определите, какие из перечисленных точек принадлежат графику функции у (х) =7х-1. А (1; 1); В (0; 1); С (2; 13); Д (3; 5).

4. Вычислите значение выражения .

5. Решите уравнение 5^2х+4 = 125^2х.

6. Вычислите значение выражения lg4 + lg25 – lоg₄16 + lоg₅1.

7. Решите уравнение log₃ (4х +1)= 2.

8. Определите взаимное расположение прямых:

KN и LK;

KN и LM;

PS и LM; если LP=PN, MS=SN

Рис.1

9. Через вершину К прямоугольного треугольника КМN с прямым углом М проведена прямая КА. Доказать, что АМN прямоугольный.

10. Вычислите диагональ куба, если его ребро равно 2 .

Вариант 2

1. Доска обрезная «Ростов» стоит 290 р штука. Определите, на сколько досок хватит 1500 рублей, если цену повысят на 20%.

3. Определите, какие из перечисленных точек принадлежат графику функции у (х) =4х-1. А (1; 1); В (0; 1); С (2; 7); Д (3; 5).

4. Вычислите значение выражения 3.

5. Решите уравнение 5^6х+4 = 25^2х.

6. Вычислите значение выражения lg2 + lg5 – lоg₃81 + lоg₅1.

7. Решите уравнение log₂(7х +1)=3.

8. Определите взаимное расположение прямых:

АД и СА;

АД и ВС;

МN и АС; если АМ=МД, СN=NД

Рис.1

9. Из точки К проведен перпендикуляр КА к плоскости прямоугольника АВСД. Доказать, что КВС прямоугольный.

10. Вычислите диагональ параллелепипеда, если его измерения равны:

6; 5; 2.

Контрольная работа

по теме: «Координаты и векторы»

Вариант 1

1. Дан параллелепипед АВСДА₁В₁С₁Д₁. Выполнить указанные действия:

а) АА₁+Д ₁С₁+СВ; б) ДД₁-А ₁Д₁.

2. Даны векторы и .

Найти координаты вектора 3 -2.

3. Вычислить координаты вектора и его длину, если А (4;-4; 0)

В(-3;5;-3)

4. Найти косинус угла между векторами:

Вариант 2

1. Дан параллелепипед АВСДА₁В₁С₁Д₁. Выполнить указанные действия:

а) АД+А ₁В₁+ВС; б) СД-Д ₁Д.

2. Даны векторы

Найти координаты вектора 2 -3.

3. Вычислить координаты вектора и его длину, если А (7; 2;-1), В(1;4;-2)

4. Найти косинус угла между векторами:

Контрольная работа

по теме: «Координаты и векторы»

№ варианта

Дан параллелепипед АВСДА₁В₁С₁Д₁. Найти:

Даны векторы и Найти координаты вектора 3 -2

Вычислить координаты вектора и его длину.

Найти косинус угла между векторами

cos( ; )=

а) АА₁+Д ₁С₁+СВ;

б) ДД₁-А ₁Д₁.

А (-6; 4;1)

В(8;-1;4)

а) СС₁+В ₁А₁+Д ₁Д;

б) ВС-Д ₁С₁.

А (4;-4; 0)

В(-3;5;-3)

а) АД+А ₁В₁+ВС;

б) СД-Д ₁Д.

А (-2; 4; 3)

В(1;4;-1)

а) СД+С ₁В₁+ВА;

б) В ₁С₁-Д ₁С₁.

А (5; -4; 2)

В(1;-1;10)

а)

А ₁В₁+ВС+Д₁Д+СД₁;

б) АВ-СС₁.

А (6; 4;-2)

В(3;-1; 0)

а) ВС+В ₁А₁+С ₁В₁;

б) АВ-С ₁В₁.

А (7; 2;-1)

В(1;4;-2)

а) АВ+А ₁Д₁+СД;

б) СС₁-В ₁С₁.

А (1;-4; 2)

В(-3;7;-3)

а)Д ₁А₁+ДС+В ₁В;

б) ВА-С ₁В₁.

А (7;-9; -5)

В(2;-1;-6)

а) СВ+В ₁А₁+АД;

б) АА₁-С ₁Д₁.

А (-5; 4; 2)

В(-3;9;6)

10.

а) А ₁Д₁+АВ+ДА;

б) ДС-В ₁С₁.

А (-7; 5; 2)

В(-3;8; 1)

Контрольная работа

по теме: «Тригонометрические уравнения и неравенства»

варианта

Решить уравнение:

Найдите все корни уравнения принадлежащие отрезку [0;2П].

Решить уравнение, сведя его к квадратному:

Решить однородное уравнение:

Решить уравнение,

разложив его на множители:

Решить

неравенство:

sin 4x=0

sin =

2sin² x-3sinx+1=0.

cosx+sinx=0

cos² x=sinxcosx

cоsx<-

cos =0

sin4x=

cos² x+6sinx-6=0

cosx+sinx=0

cos² x+sinxcosx=0

Sinx>

sin(2x-)=

tg5x=

2cos² x-cosx-1=0.

4cosx-2sinx=0

sinxcosx=cos² x

соsx≥-

sin =0

cos2x=

2sin² x+7cosx+2=0

cosx-sinx=0

sin² x- sinxcosx=0

sinx≤-

сos4x=0.

sin5x=

2cos² x-3cosx+1=0.

3cosx+sinx=0

sinxcosx=cos² x

sinx≤ -

sin 9x=1

cos=

2sin² x+5cosx-4=0

cosx-sinx=0

sinxcosx+cos² x=0

cоsx<

сos6x=-1.

tg =

4sin² x+4cosx+5=0

3cosx+2sinx=0

cos² x-sinxcosx=0

Sinx>-

sin =1

cos4x=

2cos² x+cosx-6=0.

cosx+sinx=0

sinxcosx=sin² x

sinx≤

sin10x=-1

tgx=-

2sin² x+3cosx=0

2cosx-5sinx=0

sin² x+sinxcosx=0

соsx≥

10.

cos =-1

sin2x=

tg² x-3tgx-4=0

cosx-sinx=0

sinxcosx=sin² x

sinx≤

Шкала оценки образовательных достижений

Результативность: количество решенных заданий	Оценка уровня подготовки (отметка)
5-6 заданий	«5»-отлично
4 задания	«4»- хорошо
3 задания	«3»- удовлетворительно
менее 3 заданий	«2»- неудовлетворительно

Контрольная работа

по теме: «Производная функции, ее применение».

Вариант № 1

1. Тело движется по прямой, так что расстояние S от начальной точки изменяется по закону:S=3t+t²(м), где t- время движения в секундах. Найти скорость тела через 3 секунды после начала движения.

2. Найти производные:

а) у=х lnx б) в) у=sin(3x-1)

3. Найти угловой коэффициент касательной к графику функции

f(х)=3х²+5х-6, в точке с абсциссой х ₀ =-3.

4. Найти значение производной функции у=3⁵^x^-3 в точке х=

5. Напишите уравнение касательной к графику функции f (х)=х²-3х в точке с абсциссой х₀=3 .

6. Найдите точки экстремума функции: ;

7. (2 балла) Найти наибольшее и наименьшее значение функции у=2х³+3х²-12х-1 на отрезке [-1; 2]

Шкала оценки образовательных достижений

Результативность: количество набранных баллов	Оценка уровня подготовки (отметка)
(9-10 баллов)	«5»-отлично
(8-8,9 балла)	«4»- хорошо
(7-7,9 баллов)	«3»- удовлетворительно
(менее 7 баллов)	«2»- неудовлетворительно

Контрольная работа

по теме: «Производная функции, ее применение».

Вариант № 2

1. Тело движется по прямой, так что расстояние S от начальной точки изменяется по закону:S=12t+3t²(м), где t- время движения в секундах. Найти скорость тела через 3 секунды после начала движения.

2. Найти производные:

а) у=e^x ∙sinx б) у= в) у=сos(5x+3)

3. Дана функция у=5-4х-2х² . Найти координаты точки графика этой функции, в которой угловой коэффициент касательной к нему равен 4.

4. Найти значение производной функции у=e⁷^x^-2 в точке х=

5. Напишите уравнение касательной к графику функции f (х)=х²+2х в точке с абсциссой х₀=-2 .

6. Найдите точки экстремума функции: ;

7. (2 балла) Найти наибольшее и наименьшее значение функции у=2х³-6х²+2 на отрезке [-2; 1]

Шкала оценки образовательных достижений

Результативность: количество набранных баллов	Оценка уровня подготовки (отметка)
(9-10 баллов)	«5»-отлично
(8-8,9 балла)	«4»- хорошо
(7-7,9 баллов)	«3»- удовлетворительно
(менее 7 баллов)	«2»- неудовлетворительно

Контрольная работа

по теме: Многогранники и тела вращения

Вариант 1

1. Дан прямой параллелепипед. Стороны основания равны 4 см и 6 см и образуют угол 30⁰. Высота параллелепипеда равна 10 см. Найти площадь полной поверхности и объем параллелепипеда.

2. Сторона основания правильной треугольной пирамиды равна 6 см. Боковое ребро равно Найти площадь полной поверхности и объем пирамиды.

3. Осевым сечением цилиндра является квадрат, диагональ которого равна 6 см. Найти площадь поверхности и объем цилиндра.

4. Найти площадь полной поверхности и объем тела, полученного при вращении прямоугольного треугольника с катетом 4 см и противолежащим углом 30⁰вокруг большего катета.

5. Сумма площадей поверхностей двух шаров радиуса 5 см равна площади поверхности некоторого большого шара. Каков объем этого шара?

Вариант 2

1. Основанием прямой призмы является прямоугольный треугольник, у которого катеты равны 8см и 6 см. Боковое ребро равно 4 см. Найти площадь полной поверхности и объем призмы.

2. Сторона основания правильной треугольной пирамиды равна 12 см. Высота равна 1 см. Найти площадь поверхности и объем пирамиды.

3. Высота конуса равна 10 см, а угол при вершине осевого сечения равен 120⁰. Найти площадь полной поверхности и объем конуса.

4. Найти площадь полной поверхности и объем тела, полученного при вращении прямоугольника со сторонами 6 см и 12 см вокруг прямой, которая проходит через середины его больших сторон.

5. Два металлических шарика, радиусы которых равны 1 см и 3 см сплавлены в один шар. Найти площадь поверхности этого шара.

Контрольная работа

по теме: Элементы комбинаторики, статистики и теории вероятностей

Вариант 1

1. Вычислите .

2. Имеется 10 электронных документов, три из которых нужно поместить в очередь на печать на принтере. Сколькими способами это можно сделать?

3. Какова вероятность, что ребенок родится 7 числа?

4. Для благотворительной лотереи подготовлено 1000 билетов. Из них 10 билетов имеют выигрыш по 500 руб., 45 билетов – по 100 руб. и 150 билетов – по 10 руб., остальные билеты – без выигрыша.

Составить закон распределения случайной величины – размера выигрыша по лотерейному билету. Найти математическое ожидание и дисперсию данной случайной величины, а также указать интервал ее наиболее ожидаемых значений.

5. Измерение времени выполнения работы разными рабочими (в минутах) представлено выборкой: 93,97, 96,97, 95, 98, 99, 95, 96, 97. Проанализируйте полученные данные, для этого постройте вариационный ряд, полигон, определите числовые характеристики.

Вариант 2

1. Вычислить: .

2. Сколькими способами из 20 обучающихся группы можно выбрать четырех для участия в праздничном концерте?

3. Какова вероятность, что ребенок родится в мае?

4. Для благотворительной лотереи подготовлено 1000 билетов. Из них 8 билетов имеют выигрыш по 500 руб., 10 билетов – по 100 руб. и 100 билетов – по 10 руб., остальные билеты – без выигрыша. Составить закон распределения случайной величины – размера выигрыша по лотерейному билету. Найти математическое ожидание и дисперсию данной случайной величины, а также указать интервал ее наиболее ожидаемых значений.

5. Менеджер фирмы в течение месяца регистрировал частоту заказов в день и собрал следующие данные (x_i): 8, 14, 4, 9, 3, 13, 1, 2, 0, 4, 12, 3, 5, 7, 10, 6, 5, 7, 3, 2, 9, 8, 1, 4, 6, 5, 4, 2, 11, 8. Проанализируйте полученные данные, для этого постройте вариационный ряд, полигон, определите числовые характеристики.

КОНТРОЛЬНАЯ РАБОТА

Вариант 1

1. (2 балла) Решите неравенство:

2. (2 балла) Решите уравнение: ;

3. (2 балла) Решите уравнение: ;

4. (2 балла) Решите уравнение: sin2x=1;

5. (2 балла) Тело движется по прямой так, что расстояние S от него до некоторой точки А изменяется по закону (м), где t - время движения в секундах. Найдите скорость тела через 3 с после начала движения.

6.(3 балла) Найдите точки экстремума функции:

7. (2 балла) Найдите первообразную функции, график которой проходит через точку (0;3).

8. (2 балла) Для оклейки стен в ванной комнате нужно приобрести керамическую плитку. Ширина комнаты 2 м, длина 1,9 м, высота 2,5 м (окон нет). Ширина двери равна 0,75 м, высота 2 м. Цена плитки 300 руб. за 1 м². Определите стоимость плитки, если стены решено оклеить полностью, от пола до потолка.

9.(2 балла) Найти площадь полной поверхности тела, полученного при вращении прямоугольного треугольника с катетом 3 см и противолежащим углом 30⁰ вокруг большего катета.

*****

Шкала оценки образовательных достижений

Результативность: количество набранных баллов	Оценка уровня подготовки (отметка)
(9-10 баллов)	«5»-отлично
(8-8,9 балла)	«4»- хорошо
(7-7,9 баллов)	«3»- удовлетворительно
(менее 7 баллов)	«2»- неудовлетворительно

КОНТРОЛЬНАЯ РАБОТА

Вариант 2

1. (2 балла) Решите неравенство:

2. (2 балла) Решите уравнение: ;

3. (2 балла) Решите уравнение: ;

4. (2 балла) Решите уравнение: cos2x=1;

5. (2 балла) Найдите точки экстремума функции: ;

7. (2 балла) Найдите первообразную функции, график которой проходит через точку (-2;-5).

8. (2 балла) Для оклейки стен в ванной комнате нужно приобрести керамическую плитку. Ширина комнаты 2 м, длина 1,8 м, высота 2,4 м (окон нет). Ширина двери равна 0,75 м, высота 2 м. Цена плитки 350 руб. за 1 м². Определите стоимость плитки, если стены решено оклеить полностью, от пола до потолка.

9. (2 балла) Найти площадь полной поверхности тела, полученного при вращении прямоугольника со сторонами 4 см и 10 см вокруг оси симметрии, параллельной большей стороне.

*****

Шкала оценки образовательных достижений

Результативность: количество набранных баллов	Оценка уровня подготовки (отметка)
(9-10 баллов)	«5»-отлично
(8-8,9 балла)	«4»- хорошо
(7-7,9 баллов)	«3»- удовлетворительно
(менее 7 баллов)	«2»- неудовлетворительно

3.Фонд оценочных средств для проведения промежуточной аттестации

ПАКЕТ ЭКЗАМЕНАТОРА

3.1 Общие положения

Экзамен по математике при реализации основной профессиональной образовательной программы НПО/СПО по профессиям/специальностям с получением среднего (полного) общего образования является обязательным и проводится в письменной форме.

Содержание экзаменационных материалов отвечает требованиям к уровню подготовки выпускников, которые предусмотрены государственным стандартом среднего (полного) общего образования по соответствующей общеобразовательной дисциплине и зафиксированы в рабочей программе учебной дисциплины «Математика» для профессий начального профессионального образования и специальностей среднего профессионального образования.

Экзаменационные материалы сформированы из двух частей: обязательной, включающей задания минимально обязательного уровня, и дополнительной – с более сложными заданиями.

В экзаменационную работу включены задания, выполнение которых свидетельствует о наличии общематематических навыков, необходимых человеку в современном обществе. Эти задания должны проверять базовые вычислительные и логические умения и навыки, умения анализировать информацию, представленную в графиках, ориентироваться в простейших геометрических конструкциях и др.

Оценка результатов выполнения экзаменационной работы осуществляется согласно критериям, которые дополняют экзаменационные материалы.

Результаты экзамена признаются удовлетворительными, если обучающийся при выполнении экзаменационной работы получил оценку не ниже удовлетворительной (3).

Экзаменационная работа сопровождается инструкцией для обучающихся по ее выполнению.

Государственное бюджетное образовательное учреждение

Ростовской области

Гуковский строительный техникум

Согласовано

на заседании ПЦК ЕН и МД

« » 202 г.

Председатель ПЦК:

______________________

Утверждаю

Замдиректора по УП и МР:

_____________________

« » мая 202 г.

ЭКЗАМЕНАЦИОННАЯ РАБОТА

по дисциплине «Математика»

специальность СПО: 08.02.01 «Строительство и эксплуатация зданий и сооружений»

Курс I семестр 2 Преподаватель: Пингина Т.П.

Вариант 1

Критерии оценки выполнения работы

Оценка	Число баллов, необходимое для получения оценки
«3» (удовлетворительно)	9–14
«4» (хорошо)	15–20 (не менее одного задания из дополнительной части)
«5» (отлично)	21–30 (не менее двух заданий из дополнительной части)

При выполнении всех заданий запишите ход решения и полученный ответ

Обязательная часть

1.(1 балл) Цемент фасованный «Ростов» стоит 170 руб. Определите, на сколько мешков хватит 1000 рублей, если цена повысится на 20%.

3. (1 балл) Определите, какие из перечисленных точек принадлежат графику функции у (х) =7х-1. А (1; 1); В (0; 1); С (2; 13); Д (3; 5).

4. (1 балл) Вычислите значение выражения .

5. (1 балл) Найдите значение cosα, если известно, что sinα=0,8 и α II четверти.

6. (1 балл) Решите уравнение 5^2х+4 = 125^2х.

7.(1 балл) Вычислите значение выражения lg4 + lg25 – lоg₄16 + lоg₅1.

8. (1 балл) Решите уравнение log₃ (4х +1)= 2.

9. (1 балл) Определите, какой из приведенных графиков соответствует нечетной функции.

Используя график функции у = f() (см. рис.),

определите и запишите ответ:

10. (1 балл) наименьшее значения функции;

11. (1 балл) промежутки возрастания функции;

12. (1 балл) при каких значениях f() 0.

13. (1 балл) От крыши дома, высотой 12 м к столбу, высота которого 4 м натянут кабель. Определите длину кабеля, если расстояние между домом и столбом 6 м.

14. (1 балл) Тело движется по закону: S(t)= t²–7t+10. Определите, в какой момент времени скорость будет равна 5.

15. (1 балл) На 3 вакантных места по определенной специальности претендуют 7 безработных, состоящих на учете в службе занятости. Сколько возможных комбинаций выбора 3 из 7 безработных?

16. (1 балл) Вычислить длину вектора , если А (5; -4;1) В(-2;3;4)

17. (1 балл) На экзамене 40 билетов. Коля не выучил 4 из них. Найдите вероятность того, что ему попадётся выученный билет.

18. (1 балл) Прямоугольный треугольник с катетами 6 см и 8 см вращается вокруг меньшего катета. Найдите площадь боковой поверхности получившегося тела.

Дополнительная часть.

19.(3 балла) Найдите наибольшее значение функции f(x)=2x³ + 3x² – 36x на отрезке [-4;3].

20.(3 балла) Боковое ребро правильной треугольной пирамиды образует с высотой пирамиды угол 45 градусов. Найдите объём пирамиды, если сторона основания равна 6см.

21.(3 балла) Решить систему уравнений: 2^х+у= 32,

3^3у-х=27.

22.(3 балла) Решите уравнение 2sinx∙cosx – cosx=0, укажите корни, принадлежащие отрезку [0;П].

Государственное бюджетное образовательное учреждение Ростовской области

Гуковский строительный техникум

Согласовано

на заседании ПЦК ЕН и МД

« » 20 г.

Председатель ПЦК:

______________________

Утверждаю

Замдиректора по УП и МР:

_____________________

« » мая 20 г.

ЭКЗАМЕНАЦИОННАЯ РАБОТА

по дисциплине «Математика»

специальность СПО: 08.02.01 «Строительство и эксплуатация зданий и сооружений»

Курс I семестр 2 Преподаватель: Пингина Т.П.

Вариант 2

Критерии оценки выполнения работы

Оценка	Число баллов, необходимое для получения оценки
«3» (удовлетворительно)	9–14
«4» (хорошо)	15–20 (не менее одного задания из дополнительной части)
«5» (отлично)	21–30 (не менее двух заданий из дополнительной части)

При выполнении всех заданий запишите ход решения и полученный ответ

Обязательная часть

1.(1 балл) Доска обрезная «Ростов» стоит 290 р штука. Определите, на сколько досок хватит 1000 рублей, если цену повысят на 20%.

2.(1 балл) Определите, сколько банок краски по 2 кг необходимо купить для покраски пола в мастерской площадью 6х9 м², если на 1м² расходуется 300 грамм краски.

3. (1 балл) Определите, какие из перечисленных точек принадлежат графику функции у (х) =4х-1. А (1; 1); В (0; 1); С (2; 7); Д (3; 5).

4. (1 балл) Вычислите значение выражения 3.

5.(1 балл) Найдите значение cosα, если известно, что sinα=-0,8 и α III четверти.

6.(1 балл) Решите уравнение 5^6х+4 = 25^2х.

7.(1 балл) Вычислите значение выражения lg4 + lg25 – lоg₃81 + lоg₅1.

8. (1 балл) Решите уравнение log₃(4х +1)=2.

9. (1 балл) Определите, какой из приведенных графиков соответствует четной функции.

Используя график функции у = f() (см. рис.),

определите и запишите ответ:

10. (1 балл) наименьшее значения функции;

11. (1 балл) промежутки возрастания функции;

12. (1 балл) при каких значениях f() 0.

13.(1 балл) От крыши дома, высотой 8 м к столбу, высота которого 2 м натянут кабель. Определите длину кабеля, если расстояние между домом и столбом 8 м.

14.(1 балл) Тело движется по закону: S(t)= t²+4t+7. Определите, в какой момент времени скорость будет равна 6.

15. (1 балл) Из 12 учащихся нужно составить группу из 4 для участия в мероприятии. Сколькими способами это можно сделать?

16. (1 балл) Вычислить длину вектора , если А (3; 4;2) В(2;5;-1)

17. (1 балл) Из колоды (36 карт) наудачу выбирают одну карту. Какова вероятность, что она окажется пиковой масти?

18. (1 балл) Прямоугольник со сторонами 6 см и 8 см вращается вокруг оси симметрии, параллельной большей стороне. Найдите площадь боковой поверхности получившегося тела.

Дополнительная часть.

19.(3 балла) Найдите наибольшее значение функции f(x)=2x³ + 3x² – 36x на отрезке [-2;1].

20.(3 балла) Боковое ребро правильной треугольной пирамиды образует с плоскостью основания пирамиды угол 45 градусов. Найдите объём пирамиды, если сторона основания равна 4см.

21.(3 балла) Решить систему уравнений)

22. (3 балла) Решите уравнение sinx cosx = sin²x, укажите корни, принадлежащие отрезку [ ]

Эталон экзамен Вариант 1

Критерии оценки выполнения работы

Оценка	Число баллов, необходимое для получения оценки
«3» (удовлетворительно)	9–14
«4» (хорошо)	15–20 (не менее одного задания из дополнительной части)
«5» (отлично)	21–30 (не менее двух заданий из дополнительной части)

Обязательная часть ( каждое задание оценивается 1 балл)

1) 170∙1,2=204 (руб) – новая цена мешка цемента

1000: 204=4,9 т.е 4 мешка Ответ: 4

2) 9∙6=54 (м²) – площадь пола

54∙300=16200(г)=16,2(кг) – понадобится краски

16,2: 3=5,4 те. 6 банок краски нужно Ответ: 6

3) у(х)=7х-1

А(1;1) 1=7∙1-1 1 – точка графику не принадлежит

В(0;1) 1=7∙0-1 1 – точка графику не принадлежит

С(2;13) 13=7∙2-1 13=13– точка графику принадлежит

Д(3;5) 5=7∙1-1 5 – точка графику не принадлежит Ответ. С(2;13)

4) =(3²)^3/2+(4³)^2/3+10=3³+4²+10=27+16+10=53

5) cos=+, т.к. во второй четверти, то cos <0, cos=-= - 0.6;

6) 5^2х+4 = 125^2х5^2х+4 = ((5)³) ^2х 2х+4=6х -4х=-4 х=1 Ответ: 1

7) lg4 + lg25 – lоg₄16 + lоg₅1= lg100 – 2+0=2-2+0=0 Ответ: 0

8) log₃(4х +1 )=2 4х+1=9 4х=8 х=2 Ответ: 2

9) 3

10) -2,5

11) [3;6]

12) [1;5]

13) 12-4=8 6²+8²=100 длина кабеля 10 Ответ:10

14) v(t)=s′(t)=2t-7 v(t)=5 2t-7=5 t=6 Ответ: 6

15) ==5∙7=35 Ответ: 35

16){-2-5;3+4;4-1}{-7;7;3 }

17) n=40, m=36 0,9 Ответ: 0,9

18) r=8, h=6 S=2πrh=2π∙8∙6=96π Ответ:96π

Дополнительная часть (каждое задание оценивается 3 балла)

19) . f(-4)= 2∙(-4)³ + 3∙(-4)² - 36∙(-4) = 128

f(3)= 2∙3³ + 3∙3² - 36∙3 = -27

f¹(х)=6х² + 6х –36; 6х² + 6х –36=0; х² + х –6=0; х₁=-3; х₂=2;

f(3)= 2∙3³ + 3∙3² - 36∙3 = -27

f(-3)= 2∙(-3)³ + 3∙(-3)² - 36∙(-3 )= 27

f(2)= 2∙2³ + 3∙2² - 36∙2 = -44

наибольшее значение функции 128

20).

V=1/3S_oh АВ=6 см ОSC=45⁰

S_o= =9 cм² ОС=R===2

Т.к. ОSC=45⁰, то ОС=ОS

V= ∙ 9 ∙ =18 (cм³)

21)

1) 5-у=3у-3, 4у=8, у=2

2) х=5-2=3 (3;2)

22) 2sinxсosx-cos x=0

cos x(2sinx- 1)=0

cos x=0 2sinx- 1=0

x=+ πn n sinx= 0,5

х = (-1)ⁿarcsin 0,5 + πn n

х = (-1)ⁿ + πn n

Найдем корни, принадлежащие отрезку[0

n=0 x= [-π, х=[0,

n=1 x=- [0, х

Ответ: а) x=+ πn, х = (-1)ⁿ + πn n, б) , - .

Эталон экзамен Вариант 2

Критерии оценки выполнения работы

Оценка	Число баллов, необходимое для получения оценки
«3» (удовлетворительно)	9–14
«4» (хорошо)	15–20 (не менее одного задания из дополнительной части)
«5» (отлично)	21–30 (не менее двух заданий из дополнительной части)

Обязательная часть ( каждое задание оценивается 1 балл)

1) 290∙1,2=348 (руб) – новая цена доски (1 шт)

1000: 348=2,87, т.е 2 шт Ответ: 2

2) 6∙9=54 (м²) – площадь пола

54∙300=16200 (г)=16,2(кг) – понадобится краски

16,2: 2=8,1 банок краски нужно Ответ: 9

3) у(х)=4х-1

А(1;1) 1=4∙1-1 1 – точка графику не принадлежит

В(0;1) 1=4∙0-1 1– точка графику не принадлежит

С(2;7) 9=4∙2-1 7=7– точка графику принадлежит

Д(3;5) 5=4∙3-1 5 – точка графику не принадлежит Ответ. С(2;7)

4) =(6²)^3/2+(3³)^2/3+11=6³+3²+11=216+9+11=236

5) cos=+, т.к. в третьей четверти, то cos <0, cos=-= - 0.6;

6) 5^6х+4 = 25^2х5^6х+4 = ((5)²) ^2х 6х+4=4х 2х=-4 х=-2 Ответ: -2

7) lg4 + lg25- lоg₄81 + lоg₅1= lg100 –3+0=2-3+0=-1 Ответ: -1

8) log₃ (4х +1 )=2 4х+1=9 4х=8 х=2 Ответ: 2

9) 1

10) -2,5

11) [-3,5,-1] и [2,4]

12) [1;3,5]

13) 8-2=6 6²+8²=100 длина кабеля 10 Ответ: 10

14) v(t)=s′(t)=2t+4 v(х)=6 2х+4=6 х=1 Ответ: 1

15) == Ответ: 495

16){2-3;5-4;-1-2}{-1;1;-3 }

17) n=36,m=9 Ответ: 0,25

18) r=3, h=8 S=2πrh=2π∙8∙3=48π Ответ:48π

Дополнительная часть (каждое задание оценивается 3 балла)

19) . f(x)=2x³ + 3x² – 36x

f(-2)= 2∙(-2)³ + 3∙(-2)² - 36∙(-2) = 68

f(1)= 2∙(1)³ + 3∙(1)² - 36∙(1) = -31

f¹(х)=6х² + 6х –36; 6х² + 6х –36=0; х² + х –6=0; х₁=-3; х₂=2;

х₁=-3, х₂=2 не принадлежат промежутку [-2;1].

Наибольшее значение функции 68 Ответ: 68

20) V=1/3S_oh АВ=4 см ОСS=45⁰

S_o= =4 cм² ОС=R==

Т.к. ОSC=45⁰, то ОС=ОS

V= ∙ 4 ∙ = (cм³)

21)

1) 4x+2y=4+y 4x+y=4 y=4-4x

2) 2y-3x=-3 2(4-4x)-4x=-3 8-8x-3x=-3 -11x=-11 x=1

y=4-4∙1=0

Ответ: (1;0)

22. sinxсosx = sin²x x[ ]

sinxсosx - sin²x = 0,

sinx (сosx – sinx) = 0,

sinx = 0, сosx – sinx = 0,

х = πn, n - tgx = 0,

tgx =

х = + πn, n .

Найдем корни, [ ]

n=0 х=[,

n=1 х=π [, x=- [, х

n= -1 х= - [,

Ответ: а)х = πn, n, х = + πn, n,

б) , π, - , -

Скачано с www.znanio.ru

Ньютона; умение применять комбинаторные факты и рассуждения для решения задач; -уметь оперировать понятиями: натуральное число, целое число, остаток по модулю, рациональное число, иррациональное число, множества…

(вещественным) показателем, логарифм числа, синус, косинус и тангенс произвольного числа; - уметь оперировать понятиями: тождество, тождественное преобразование, уравнение, неравенство, система уравнений и неравенств, равносильность уравнений,…

Бернулли, комбинаторные факты и формулы; оценивать вероятности реальных событий; умение оперировать понятиями: случайная величина, распределение вероятностей, математическое ожидание, дисперсия и стандартное отклонение случайной величины, функции…

ОК 02 Использовать современные средства поиска, анализа и интерпретации информации, и информационные технологии для выполнения задач профессиональной деятельности

ОК 04 Эффективно взаимодействовать и работать в коллективе и команде

ОК 06 Проявлять гражданско-патриотическую позицию, демонстрировать осознанное поведение на основе традиционных общечеловеческих ценностей, в том числе с учетом гармонизации межнациональных и межрелигиозных отношений, применять стандарты…

Профессиональные компетенции специальности «Строительство и эксплуатация зданий и сооружений»

Распределение типов контрольных заданий при текущем контроле

Оценка письменных самостоятельных и контрольных работ

Оценка «2» ставится в том случае, если обучающийся: а) не знает и не понимает значительную или основную часть программного материала в пределах поставленных вопросов, б)…

Какой логарифм называется десятичным? 10

Какой многогранник называется пирамидой? 9

Тем самым, площадь участка, незанятого домом равна 900 − 40 = 860 кв

Практическая работа №2 «Практико- ориентированные задачи на проценты»

Чтобы найти сколько процентов одно число составляет от другого можно одно число разделить на другое и полученное произведение умножить на 100

Практическая работа № 3 по теме «Решение уравнений и неравенств, систем уравнений и неравенств»

Практическая работа № 4 по теме: «Решение иррациональных уравнений»

Практическая работа № 5 по теме: «Решение показательных уравнений и неравенств»

Практическая работа № 6 по теме: «Преобразование логарифмических выражений»

Практическая работа № 7 по теме: «Решение логарифмических уравнений и неравенств»

Практическая работа № 8 по теме: «Применение логарифма»

Практическая работа № 9 по теме «Построение сечений»

2 вариант 3 вариант 4 вариант 5 вариант 6 вариант 7 вариант 8 вариант 9 вариант 10 вариант

Практическая работа № 10 по теме: «Прямые и плоскости в пространстве»

Практическая работа № 12 «Координатная плоскость

Практическая работа № 13 «Вычисление значений тригонометрических функций»

Практическое занятие № 14 «Преобразования простейших тригонометрических выражений»

Практическая работа № 15 «Преобразование графиков тригонометрических функций»

Практическая работа № 16 «Использование свойств тригонометрических функций в профессиональных задачах»

Практическая работа № 17 «Выполнение расчетов с помощью комплексных чисел

Практическая работа № 18 «Техника дифференцирования»

Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.

Посмотрите также