11. Прямая и Обратная Методические указания к уроку. Вариант 2

Методические указания к уроку

тема "Прямая пропорциональная зависимость. Обратная пропорциональная зависимость "

Цели обучения 6.1.1.2 понимать, какие величины являются прямо пропорциональными, приводить примеры, решать задачи;

6.1.1.3 понимать, какие величины являются обратно пропорциональными, приводить примеры, решать задачи;

6.5.1.1 распознавать и решать задачи, в которых величины связаны прямой и обратной пропорциональностями

Организационный момент. Мотивация к учебной деятельности. Беседа.

Предложим ответить на вопросы:

1.      Что такое пропорция?

2.      Сформулируйте основное свойство пропорции.

3.      Какие перестановки членов пропорции снова приводят к верным пропорциям?

4.      Составьте три новые верные пропорции из пропорции: 5:15=4:12.

5.      Дано отношение 5:15. Продолжите заполнение таблицы, чтобы получить верные пропорции:

Введем термин "зависимость".

Устное обсуждение (поиск решения)

Показать презентацию слайд 2.

1.  За 2 кг овощей заплатили 1000 тенге. Сколько стоят 4 кг овощей?  6 кг? 8 кг? Заполните таблицу.

При увеличении количества товара в n раз, стоимость товара также увеличилась в n   раз.

2. Два трактора вспахали поле за 6 дней. За сколько дней вспашут это поле 4 трактора, если будут работать с той же производительностью?

При увеличении количества тракторов в 2 раза, количество дней уменьшится в 2 раза.

Учащиеся могут сами дать ответ на вопрос: все ли величины, окружающие нас, являются прямо пропорциональными (то есть увеличение (уменьшение) одной из величин влечет за собой увеличение (уменьшение) другой величины во столько же раз).

Показать презентацию слайд 3. Обращаем внимание на примеры где величины не имеют прямой зависимости и делаем вывод: в этих примерах две величины такие, что увеличение одной в несколько раз влечет за собой уменьшение другой величины в то же количество раз и наоборот - такие величины будем называть обратно пропорциональными. (Можно предложить учащимся попробовать привести другие примеры прямо и обратно пропорциональных величин из повседневной жизни.)

Предложить ученикам определить тему и цели урока.

Вывод определений.

Определение 1. Две величины называют прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая тоже увеличивается (уменьшается) во столько же раз.

Определение 2. Две величины называют обратно пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая уменьшается (увеличивается) во столько же раз.

Устные упражнения для закрепления представления о пропорциональной зависимости величин: Приложение 1.

Приложение 1 (устно)

Какие из следующих величин являются прямо пропорциональными, а какие обратно пропорциональными:

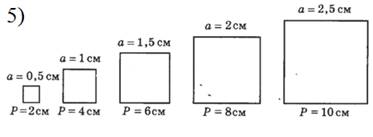
1.      периметр квадрата и длина его стороны;

2.      длина и ширина прямоугольника при постоянной площади:

3.      площадь прямоугольника и его длина при постоянной ширине;

4.      скорость поезда и время для преодоления им заданного расстояния;

5.      количество буханок и их масса при постоянной массе одной буханки хлеба;

6.      количество пакетов и масса одного пакета при расфасовке 10 кг муки;

7.      длина провода и его стоимость;

8.      длина ребра куба и его объем?

9.      площадь квадрата и длина его стороны;

10.  масса тела и его объем;

П- прямая пропорциональность;

О - обратная пропорциональность.

Ключ к заданию:

Работа с классом. Решение практических задач.

Кроме понимания содержания понятия прямо и обратно пропорциональные величины, учащиеся должны научиться решать задачи составлением пропорции.

Надо объяснить учащимся, что задачи, которые решаются на прямую пропорциональную зависимость на этом уроке, похожи на те, что решали в теме «Нахождение дроби и процентов от числа и числа по его дроби и процентам» . Но теперь мы учимся решать эти задачи, составляя пропорции.

Для закрепления и оценки уровня умения применять свойства пропорциональной зависимости величин, предварительно решить несколько задач из учебника, применяя образцы.

Работа в парах. Взаимное обучение.

Создать пары с разным уровнем обучаемости. Предложить ученикам процесс взаимного обучения при решении практических задач: объяснять решение задачи своему напарнику при возникновении вопроса по той или иной задаче, т.е. ученики выполняют задания индивидуально, но имеют возможность обсудить непонятные вопросы с напарником.

Задачи на прямую и обратную пропорциональные зависимости в отдельных блоках, для закрепления навыков решения типовых задач.

Приложение 2

(Количество задач определяет учитель в зависимости от уровня класса).

При решении задач на зависимости запись краткого условия задачи делаем в виде таблицы, обозначив за x неизвестное и расставив стрелки, которые указывают направление от меньшей величины к большей величине.

При прямой пропорциональной зависимости стрелки в одном направлении, при обратной пропорциональной зависимости в разном направлении.

Прямая пропорциональная зависимость.

Образец оформления решения:

Задача. За 3,2 кг конфет заплатили 1152 тенге. Сколько надо заплатить за 1,5 кг конфет?

Решение:

Зависимость между количеством конфет и стоимостью покупки прямо пропорциональные величины, так как при покупке конфет в несколько раз больше стоимость покупки увеличится во столько же раз.

Запишем кратко условие задачи в виде таблицы, обозначив за x стоимость (в тенге)
1,5 кг конфет.

Условно обозначим такую зависимость одинаково направленными стрелками.

Запишем пропорцию:

Найдем неизвестный член пропорции: .

Ответ: 540 тенге.

Реши задачи на прямую пропорциональную зависимость составлением краткого условия и пропорции.

1. Стальной шарик объемом 5 см³ имеет массу 39 г. Какую массу имеет шарик объемом 2,5 см³, сделанная из той же стали?

2. Из 100 кг семян льна получается 37 кг масла. Сколько масла получится из 250 кг таких семян?

Ключ к заданию:

Обратная пропорциональная зависимость

Образец оформления решения:

Задача. Для строительства стадиона 5 бульдозеров расчистили участок по 210 мин. За какое время 7 бульдозеров расчистят эту область?

Решение:

Зависимость между количеством бульдозеров и временем расчистки обратно пропорциональные величины, так как при увеличении количества бульдозеров в несколько раз больше, время расчистки уменьшится во столько же раз. Составим таблицу, поставим стрелки: поскольку величины являются обратно пропорциональными, стрелки ставим в противоположных направлениях, поэтому и отношение будем брать в противоположных направлениях:

Запишем пропорцию:

Найдем неизвестный член пропорции: .

Ответ: 150 минут.

Реши задачи на обратную пропорциональную зависимость составлением краткого условия и пропорции.

1. Два прямоугольника имеют одинаковую площадь. Длина одного прямоугольника 8 м, а ширина 4,5 м. Найдите длину второго прямоугольника, если его ширина равна 2 м.

2. В книге 448 страниц, на каждой странице 41 строка, в каждой строке в среднем 54 буквы. На скольких страницах может быть перепечатана эта книжка, если на странице будет 48 строк и в каждой строке 42 буквы.

Ключ к заданию:

Самопроверка задания по ключу.

Групповая работа. Повторение теоретического материала.

Деление на группы произвольное.

Раздать группам конверт с набором пронумерованных карточек, на каждом из которых написана задача. Предложить учащимся, определить вид зависимости величин. В первый столбик записать номера карточек с задачами на прямую пропорциональную зависимость. Во второй столбик - на обратную пропорциональную зависимость. В третий столбик номера задач где нет зависимости величин.

Приложение 3

Определить вид зависимости величин. В первый столбик записать номера карточек с задачами на прямую пропорциональную зависимость. Во второй столбик - на обратную пропорциональную зависимость. В третий столбик номера задач где нет зависимости величин.

7) Изменение температуры воздуха в течение суток

8) Из 30 кг свежих слив получают 10,5 кг сушеных. Сколько надо взять свежих слив, чтобы получить 14,7 кг сушеных слив?

 9) Для перевозки груза машине грузоподъемностью 6 т надо сделать 10 рейсов. Сколько надо сделать рейсов автомобилю, грузоподъемность на 2 т меньше, чтобы перевезти тот же груз?

10) Верблюд в течение одного часа выдерживает груз массой 200 кг. В течение какого времени он выдержит груз массой 2 т? (Величины не являются пропорциональными)

11) Для изготовления 10 деталей требуется 3,2 кг металла. Сколько металла нужно взять, чтобы изготовить 12 таких деталей?

12) Из 2,5 кг семечек изготавливают 1,8 кг чистого семени. Сколько нужно подсолнечника, чтобы получить 4,2 кг чистого семя?

13) Девять рабочих выполняют некоторое задание за 14 часов. За какое время выполнят это задание три рабочие, если будут работать с той же производительностью труда?

14) Таблица роста ребенка

15) Расстояние между двумя посёлками равно 240 км. Определи, за какое время можно доехать из одного посёлка в другой, если скорость 20км/ч увеличить в 2 раза, 3 раза, в 4 раза? Заполни таблицу.

Во время выполнения этих заданий стоит обратить внимание учащихся на то, что для поиска правильного ответа можно воспользоваться таким методом: представить, что одна из величин увеличилась в какое-то количество раз (например, в 2 раза), а затем проверить или на интуитивном уровне, или используя изученные ранее формулы и соотношения, как изменилась другая величина.

Провести проверку задания по ключу устно.

Для определения понимания зависимостей учащимися и закрепления темы урока организовать Игровой момент.

Приложение 4

Примите участие в игре!

Представьте себе, что на Земле произошла путаница и для процессов, описываемых прямой пропорциональностью, используют обратную пропорциональность и наоборот.

Тогда бы мы говорили:

- Чем больше покупаем конфет, тем .... (меньше платим денег).

Придумайте свои подобные перепутанные выводы (2-3) описываемых прямой пропорциональностью, используют обратную пропорциональность и допишите.

.

Приложение 4

Примите участие в игре!

Представьте себе, что на Земле произошла путаница и для процессов, описываемых прямой пропорциональностью, используют обратную пропорциональность и наоборот.

Тогда бы мы говорили:

- Чем дольше горит свеча, тем... (она становится длиннее и т. д.)

Придумайте свои подобные перепутанные выводы (2-3)  описываемых обратной пропорциональностью, используют прямую пропорциональность и допишите.

Каждая группа представляет по 2-3 примера. Оцениваем совместно.

Беседа. Рефлексия.

- Что узнал, чему научился?

- Что осталось непонятным?

- Над чем необходимо поработать?

- Как прошёл процесс взаимного обучения?

- Какой этап урока понравился больше всего?

Домашнее задание.

Знать ...№№.

На уроке предусмотрена дифференциация в виде работы в однородных группах (одного уровня обучаемости). Ученики самостоятельно выбирают уровень сложности заданий. Предусмотрена В ходе коллективной деятельности при решении задач устно оценивается умение применять определение зависимостей; самопроверка по ключу, в ходе которой ученики оценивают умение применять зависимости величин.         Запланированы виды деятельности на уроке, способствующие передвижению учащихся по классу. Следить за осанкой учащихся.