13. Прямая Методические указания к уроку. Вариант 2

Методические указания к уроку

тема "Прямая пропорциональная зависимость. Обратная пропорциональная зависимость "

Цели обучения:

 6.1.1.2 понимать, какие величины являются прямо пропорциональными, приводить примеры, решать задачи;

6.1.1.3 понимать, какие величины являются обратно пропорциональными, приводить примеры, решать задачи;

6.5.1.1 распознавать и решать задачи, в которых величины связаны прямой и обратной пропорциональностями

Организационный момент. Мотивация к учебной деятельности. Беседа. совместно определить тему и цели урока/ЦО в процессе повторения темы "Пропорция" и упражнений на простые пропорции: Приложение 1.

Приложение 1

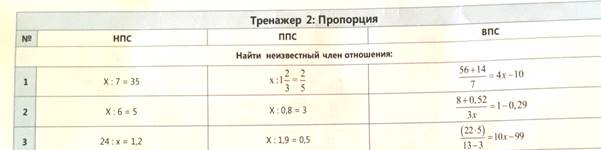
Предложить ученикам определить тему и цели урока.

 Индивидуальная работа. Решение практических задач.

Кроме понимания содержания понятия прямо и обратно пропорциональные величины, учащиеся должны научиться решать задачи составлением пропорции. Проверка остаточной информации. Задачи на прямую и обратную пропорциональные зависимости в отдельных блоках, для закрепления навыков решения типовых задач.

Приложение 2

Реши задачи на прямую пропорциональную зависимость составлением краткого условия и пропорции.

1. В 80 кг картофеля содержится 14 кг крахмала. Сколько картофеля надо взять, чтобы получить 35 кг крахмала?

Решение:

Зависимость между количеством картофеля и содержанием крахмала прямо пропорциональные величины, поэтому если взять картофель в несколько раз больше, то крахмал увеличится во столько же раз.

Запишем кратко условие задачи в виде таблицы, обозначив за x картофель (в кг) в котором содержится 35 кг крахмала.

Запишем пропорцию: ;         

Найдем неизвестный член пропорции: .

Ответ: 200 кг картофеля.

2. На пошив 30 одинаковых костюмов пошло 99,6 м ткани. Сколько таких же костюмов получится из 149,4 м ткани?

Решение:

Запишем пропорцию: ;         

Найдем неизвестный член пропорции: .

Ответ: 45 костюмов получится.

3. На некотором участке железнодорожного пути старые рельсы длиной 6 м решили заменить новыми длиной 9 м. Сколько нужно новых рельсов, чтобы заменить 720 старых?

Ключ к заданию:

Обратная пропорциональная зависимость

Реши задачи на обратную пропорциональную зависимость составлением краткого условия и пропорции.

1. Для перевозки груза потребовалось 24 автомобили грузоподъемностью 7,5 т. Сколько потребуется автомобилей грузоподъемностью 4,5 т, чтобы перевезти тот же груз?

Решение:

Зависимость между количеством автомобилей и грузоподъемностью обратно пропорциональные величины, так как при уменьшении грузоподъемности автомобилей в несколько раз меньше, количество автомобилей увеличится во столько же раз. Составим таблицу, поставим стрелки: поскольку величины являются обратно пропорциональными, стрелки ставим в противоположных направлениях, поэтому и отношение будем брать в противоположных направлениях:

Запишем пропорцию:

Найдем неизвестный член пропорции: .

Ответ: 40 автомобилей.

2. Трое маляров могут закончить работу за 5 дней. Для ускорения работы им дали еще 2-х маляров. За какое время они закончат работу, если все маляры работают с одинаковой производительностью?

Решение:

Составим таблицу, поставим стрелки: поскольку величины являются обратно пропорциональными, стрелки ставим в противоположных направлениях, поэтому и отношение будем брать в противоположных направлениях:

Запишем пропорцию:

Найдем неизвестный член пропорции: .

Ответ: 3 дня.

3. 8 одинаковых труб заполняют бассейн за 25 минут. За сколько минут заполнят бассейн 10 таких труб?

Ключ к заданию:

Провести проверку задания по ключу устно.

Работа в парах. Взаимное обучение.

Создать пары с разным уровнем обучаемости. Прежде чем приступят к решению задач, учащимся можно показать видео: для обобщения опыта и знаний по данной теме.

Предложить ученикам процесс взаимного обучения при решении практических задач: объяснять решение задачи своему напарнику при возникновении вопроса по той или иной задаче, т.е. ученики выполняют задания индивидуально, но имеют возможность обсудить непонятные вопросы с напарником. Решить  типовые задачи с учебного пособия на прямую и обратную пропорциональные зависимости.

Работа в группе. Контроль усвоения практических навыков  Предложите задачи из Приложения 3. Объединить учащихся в группы по 4 - 6 учеников, по выбранному сезонам дат рождения, задания у всех групп одинаковые. Каждая группа выбирает по 2 задачи на прямую и обратную пропорциональные зависимости. Предоставить достаточно времени для выполнения задания.

Приложение 3

1.      За 1,6 ч мальчик прошел 6,4 км. При той же скорости за 2,8 ч мальчик пройдет:

А. 11,2 км.

В. 10,8 км.

С. 11,8 км.

D. 10,2 км.

Е. 12,2 км.

2.      Со 125 гусей получают 4 кг пуха. С 875 гусей можно получить:

А. 24 кг.

В. 32 кг.

С. 18 кг.

D. 28 кг.

Е. 36 кг.

3.      Бригада из 8 рабочих выполняет производственное задание за 12 дней. Если число рабочих сократить до 6, то бригада выполнит задание:

А. за 16 дней.

В. за 14 дней.

С. за 6 дней.

D. за 18 дней.

Е. за 15 дней.

4.      Бригада из 8 рабочих выполняет производственное задание за 12 дней. Работая с той же производительностью, это задание за 8 дней выполнят:

А. 18 рабочих.

В. 15 рабочих.

С. 16 рабочих.

D. 10 рабочих.

Е. 12 рабочих.

5.      Токарь изготовил за смену 644 детали, что составило 184% задания. Сверх задания токарь изготовил:

А. 288 детали.

В. 294 детали.

С. 272 детали.

D. 296 детали.

Е. 284 детали.

Взаимопроверка задания по ключу в группах.

Подвести итог после решения этих задач:

Беседа. Рефлексия.

- Что узнал, чему научился?

- Что осталось непонятным?

- Над чем необходимо поработать?

- Как прошёл процесс взаимного обучения?

- Какой этап урока понравился больше всего?

Домашнее задание.

Знать ...№№.

Дифференциация выражена в подборе заданий, в ожидаемом результате от конкретного ученика, в оказании индивидуальной поддержки учащемуся, в подборе учебного материала и ресурсов с учетом индивидуальных способностей учащихся. Более способным учащимся предлагаются задания более высокого уровня.      Предусмотрена самопроверка по ключу, в ходе которой ученики оценивают умение применять формулы.

В ходе коллективной деятельности при решении задач устно оценивается вычислительные навыки учащихся, умение адаптировать теоретические знания к практическим заданиям. Запланированы виды деятельности на уроке, способствующие передвижению учащихся по классу. При использовании ИКТ применять правила ТБ. Следить за осанкой учащихся.

Литература:

Вассерман Ф.Я. Учебное пособие для учащихся Математика 6 класс, БиС, Алматы 2014

Интернет ресурсы:

http://www.mathematics-repetition.com/tag/nayti-krayniy-tchlen-proportsii

https://www.mathopolis.com/questions/course.php