
Описанная около четырехугольника, правильного многоугольника окружность.
Повторяем теорию.
 Окружность называется описанной около четырехугольника, если все вершины
четырехугольника лежат на окружности.
Окружность называется описанной около четырехугольника, если все вершины
четырехугольника лежат на окружности.
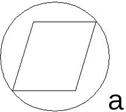
Около четырехугольника не всегда можно описать окружность. Например, нельзя описать окружность около ромба, не являющегося квадратом (рис. а).
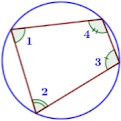 В любом вписанном
четырехугольнике сумма противоположных углов равна 180°.
В любом вписанном
четырехугольнике сумма противоположных углов равна 180°.
∠ 1 + ∠ 3 = ∠ 2 + ∠ 4 = 180°
Обратное утверждение: если сумма противоположных углов четырехугольника равна 180°, то около него можно описать окружность.
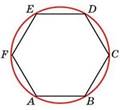 Около любого правильного многоугольника можно описать
окружность, и притом только
одну
Около любого правильного многоугольника можно описать
окружность, и притом только
одну
AB = BC = CD = DE =EF = FA
Центр окружности, описанной около правильного многоугольника, совпадает с центром окружности, вписанной в тот же многоугольник.
Эта точка называется центром правильного многоугольника.
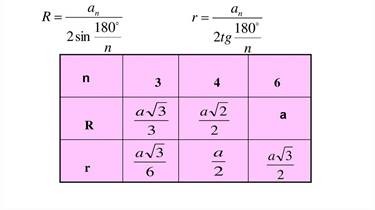 Формулы радиусов описанной и вписанной окружностей для правильных n- угольников.
Формулы радиусов описанной и вписанной окружностей для правильных n- угольников.
Проверяем себя.
Т1. Вставьте пропущенное слово:
а) Если все вершины многоугольника лежат на окружности, то окружность называется около многоугольника.
б) Около четырехугольника можно описать окружность.
в) В любом вписанном четырехугольнике сумма углов равна 180°.
г) Окружность можно описать около трапеции.
Ответ: а) описанной; б) не всегда; в) противоположных; г) равнобедренной.
Т2.Выберите верное утверждение
а) Радиус окружности, описанной около правильного шестиугольника, равен половине его стороны.
б) В любом вписанном четырехугольнике сумма противоположных углов равна 180°.
в) Окружность называется описанной около многоугольника, когда окружность пересекает все стороны этого многоугольника.
г) Окружность называется описанной около многоугольника, когда центры многоугольника и окружности совпадают.
Ответ: б).
Т3.Выберите верное утверждение
а) Около ромба можно описать окружность.
б) Сторона правильного четырехугольника равна радиусу описанной около него окружности.
в) Любой прямоугольник можно вписать в окружность.
г) Радиус окружности, описанной около правильного шестиугольника, равен половине его стороны.
Ответ: в).
Решаем задачи.
1.
![]() а) Около квадрата описана
окружность. Найдите радиус
окружности, если сторона
квадрата равна 12√2.
а) Около квадрата описана
окружность. Найдите радиус
окружности, если сторона
квадрата равна 12√2.
Ответ: 12
![]() б) Около квадрата описана
окружность. Найдите радиус окружности, если сторона
квадрата равна 8√2.
б) Около квадрата описана
окружность. Найдите радиус окружности, если сторона
квадрата равна 8√2.
Ответ: 8
![]() в) Около квадрата описана
окружность. Найдите радиус окружности, если сторона
квадрата равна 3√2.
в) Около квадрата описана
окружность. Найдите радиус окружности, если сторона
квадрата равна 3√2.
Ответ: 3
2. ![]() а) Найдите радиус окружности, описанной около правильного шестиугольника, если радиус окружности, вписанной
в этот шестиугольник равен 3,5√3.
а) Найдите радиус окружности, описанной около правильного шестиугольника, если радиус окружности, вписанной
в этот шестиугольник равен 3,5√3.
Ответ: 7
![]() б) Найдите радиус окружности, описанной около правильного шестиугольника, если радиус окружности, вписанной
в этот шестиугольник равен 6√3.
б) Найдите радиус окружности, описанной около правильного шестиугольника, если радиус окружности, вписанной
в этот шестиугольник равен 6√3.
Ответ: 12
![]() в) Найдите радиус окружности, описанной около правильного шестиугольника, если радиус окружности, вписанной
в этот шестиугольник равен 8√3.
в) Найдите радиус окружности, описанной около правильного шестиугольника, если радиус окружности, вписанной
в этот шестиугольник равен 8√3.
Ответ: 16.
3. а) Большая диагональ правильного шестиугольника, вписанного в окружность, равна 6. Найдите радиус этой окружности.
Ответ: 3
б) Большая диагональ правильного шестиугольника, вписанного в окружность, равна 5. Найдите радиус этой окружности.
Ответ: 2.5
в) Большая диагональ правильного шестиугольника, вписанного в окружность, равна 12. Найдите радиус этой окружности.
Ответ: 6.
4. а) Найдите диагональ прямоугольника, вписанного в окружность, радиус которой равен 5.
Ответ: 10
б) Найдите диагональ прямоугольника, вписанного в окружность, радиус которой равен 7.
Ответ: 14
в) Найдите диагональ прямоугольника, вписанного в окружность, радиус которой равен 15.
Ответ: 30.
5. а) Боковая сторона равнобедренной трапеции равна её меньшему основанию, угол при основании равен 60°, большее основание равно 12. Найдите радиус описанной окружности этой трапеции.
Ответ: 6
б) Боковая сторона равнобедренной трапеции равна её меньшему основанию, угол при основании равен 60°, большее основание равно 18. Найдите радиус описанной окружности этой трапеции.
Ответ: 9
в) Боковая сторона равнобедренной трапеции равна её меньшему основанию, угол при основании равен 60°, большее основание равно 22. Найдите радиус описанной окружности этой трапеции.
Ответ: 11.
6. а) Около параллелограмма, одна из диагоналей которого равна 7 см, описана окружность. Найдите вторую диагональ параллелограмма.
Ответ: 7
б) Около параллелограмма, одна из диагоналей которого равна 9 см, описана окружность. Найдите вторую диагональ параллелограмма.
Ответ: 9
в) Около параллелограмма, одна из диагоналей которого равна 17 см, описана окружность. Найдите вторую диагональ параллелограмма.
Ответ: 17
7. а) Найдите сторону прямоугольника, вписанного в окружность радиуса 10, если она стягивает дугу 60°.
Ответ: 10
б) Найдите сторону прямоугольника, вписанного в окружность радиуса 14, если она стягивает дугу 60°.
Ответ: 14
в) Найдите сторону прямоугольника, вписанного в окружность радиуса 23, если она стягивает дугу 60°.
Ответ: 23
Задачи с развернутым ответом.
1. Около трапеции описана окружность. Периметр трапеции равен 60, средняя линия равна 25. Найдите длину боковой стороны трапеции.
Ответ:5
2. Периметр правильного шестиугольника равен 108. Найдите диаметр описанной окружности.
Ответ: 36
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.