2212

Тренировочные тесты для подготовки к ОГЭ по геометрии

Вариант 1

1. 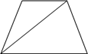Ос­но­ва­ния рав­но­бед­рен­ной тра­пе­ции равны 50 и 104, бо­ко­вая сто­ро­на 45. Най­ди­те длину диа­го­на­ли тра­пе­ции.

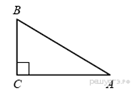
2. В тре­уголь­ни­ке    угол    пря­мой,  . Най­ди­те  .

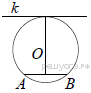
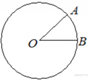
3.  Ра­ди­ус окруж­но­сти с цен­тром в точке O равен 85, длина хорды AB равна 102 (см. ри­су­нок). Най­ди­те рас­сто­я­ние от хорды AB до па­рал­лель­ной ей ка­са­тель­ной k.

4. 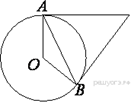Ка­са­тель­ные в точ­ках A и B к окруж­но­сти с цен­тром O пе­ре­се­ка­ют­ся под углом 24°. Най­ди­те угол ABO. Ответ дайте в гра­ду­сах.

5. Пе­ри­метр квад­ра­та равен 160. Най­ди­те пло­щадь квад­ра­та.

6. В тре­уголь­ни­ке одна из сто­рон равна 10, дру­гая равна , а угол между ними равен 45°. Най­ди­те пло­щадь тре­уголь­ни­ка.

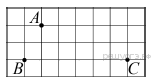
7. На клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1см x 1см от­ме­че­ны точки А, В и С. Най­ди­те рас­сто­я­ние от точки А до пря­мой ВС. Ответ вы­ра­зи­те в сан­ти­мет­рах.

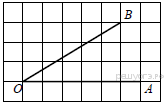
8.  Най­ди­те тан­генс угла AOB, изоб­ражённого на ри­сун­ке.

9. Какое из сле­ду­ю­щих утвер­жде­ний верно?

1. Все углы ромба равны.

2. Если сто­ро­ны од­но­го четырёхуголь­ни­ка со­от­вет­ствен­но равны сто­ро­нам дру­го­го четырёхуголь­ни­ка, то такие четырёхуголь­ни­ки равны.

3. Через любую точку, ле­жа­щую вне окруж­но­сти, можно про­ве­сти две ка­са­тель­ные к этой окруж­но­сти.

10. Ука­жи­те но­ме­ра вер­ных утвер­жде­ний.

 

1) Если при пе­ре­се­че­нии двух пря­мых тре­тьей пря­мой со­от­вет­ствен­ные углы равны 37°, то эти две пря­мые па­рал­лель­ны.

2) Через любые три точки про­хо­дит не более одной пря­мой.

3) Сумма вер­ти­каль­ных углов равна 180°.

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их но­ме­ра в по­ряд­ке воз­рас­та­ния.

 

 

 

 

 

Вариант 2

1. В вы­пук­лом четырёхуголь­ни­ке  из­вест­но, что , , , . Най­ди­те угол . Ответ дайте в гра­ду­сах.

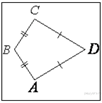
2. Один угол па­рал­ле­ло­грам­ма в два раза боль­ше дру­го­го. Най­ди­те мень­ший угол. Ответ дайте в гра­ду­сах.

3. 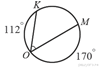Най­ди­те  ∠KOM, если гра­дус­ные меры дуг  KO  и  OM  равны 112° и 170° со­от­вет­ствен­но.

4. 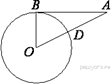От­ре­зок AB = 40 ка­са­ет­ся окруж­но­сти ра­ди­у­са 75 с цен­тром O в точке B. Окруж­ность пе­ре­се­ка­ет от­ре­зок AO в точке D. Най­ди­те AD.

5. В ромбе сто­ро­на равна 10, одна из диа­го­на­лей — , а угол, ле­жа­щий на­про­тив этой диа­го­на­ли, равен 150°. Най­ди­те пло­щадь ромба.

6. В тре­уголь­ни­ке одна из сто­рон равна 10, дру­гая равна , а угол между ними равен 60°. Най­ди­те пло­щадь тре­уголь­ни­ка.

7. Най­ди­те тан­генс угла .

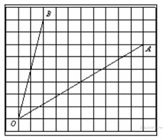
8. 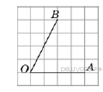Най­ди­те тан­генс угла AOB, изоб­ра­жен­но­го на ри­сун­ке.

 

9. Какие из сле­ду­ю­щих утвер­жде­ний верны?

1) Если пло­ща­ди фигур равны, то равны и сами фи­гу­ры.

2) Пло­щадь тра­пе­ции равна про­из­ве­де­нию суммы ос­но­ва­ний на вы­со­ту.

3) Если две сто­ро­ны тре­уголь­ни­ка равны 4 и 5, а угол между ними равен 30°, то пло­щадь этого тре­уголь­ни­ка равна 10.

4) Если две смеж­ные сто­ро­ны па­рал­ле­ло­грам­ма равны 4 и 5, а угол между ними равен 30°, то пло­щадь этого па­рал­ле­ло­грам­ма равна 10.

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их но­ме­ра в по­ряд­ке воз­рас­та­ния.

10. Какое из сле­ду­ю­щих утвер­жде­ний верно?

1) Пло­щадь па­рал­ле­ло­грам­ма равна по­ло­ви­не про­из­ве­де­ния его диа­го­на­лей.

2) Сумма углов пря­мо­уголь­но­го тре­уголь­ни­ка равна 90 гра­ду­сам.

3) Бис­сек­три­сы тре­уголь­ни­ка пе­ре­се­ка­ют­ся в цен­тре впи­сан­ной в него окруж­но­сти.

Вариант3

1. Диа­го­наль пря­мо­уголь­ни­ка об­ра­зу­ет угол 51° с одной из его сто­рон. Най­ди­те ост­рый угол между диа­го­на­ля­ми этого пря­мо­уголь­ни­ка. Ответ дайте в гра­ду­сах.

2. Пло­щадь пря­мо­уголь­но­го тре­уголь­ни­ка равна  Один из ост­рых углов равен 30°. Най­ди­те длину ка­те­та, ле­жа­ще­го на­про­тив этого угла.

3.

В тре­уголь­ни­ке ABC угол C равен 90°, AC = 30 , BC =  Най­ди­те ра­ди­ус окруж­но­сти, опи­сан­ной около этого тре­уголь­ни­ка.

4. 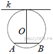Ра­ди­ус окруж­но­сти с цен­тром в точке O равен 85, длина хорды AB равна 102 (см. ри­су­нок). Най­ди­те рас­сто­я­ние от хорды AB до па­рал­лель­ной ей ка­са­тель­ной k.

5. В ромбе сто­ро­на равна 10, одна из диа­го­на­лей — , а угол, из ко­то­ро­го вы­хо­дит эта диа­го­наль, равен 45°. Най­ди­те пло­щадь ромба, де­лен­ную на 

6. Тан­генс остро­го угла пря­мо­уголь­ной тра­пе­ции равен . Най­ди­те её бóльшее ос­но­ва­ние, если мень­шее ос­но­ва­ние равно вы­со­те и равно 14.

7. На клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1см ✕ 1см от­ме­че­ны точки A, B иC. Най­ди­те рас­сто­я­ние от точки A до се­ре­ди­ны от­рез­ка BC . Ответ вы­ра­зи­те в сан­ти­мет­рах.

8. 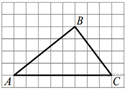На клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1x1 изоб­ражён тре­уголь­ник ABC. Най­ди­те длину его вы­со­ты, опу­щен­ной на сто­ро­ну AC.

9. Какие из сле­ду­ю­щих утвер­жде­ний верны?

1) Пло­щадь мно­го­уголь­ни­ка, опи­сан­но­го около окруж­но­сти, равна про­из­ве­де­нию его пе­ри­мет­ра на ра­ди­ус впи­сан­ной окруж­но­сти.

2) Если диа­го­на­ли ромба равна 3 и 4, то его пло­щадь равна 6.

3) Пло­щадь тра­пе­ции мень­ше про­из­ве­де­ния суммы ос­но­ва­ний на вы­со­ту.

4) Пло­щадь пря­мо­уголь­но­го тре­уголь­ни­ка мень­ше про­из­ве­де­ния его ка­те­тов.

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их но­ме­ра в по­ряд­ке воз­рас­та­ния.

10. Ука­жи­те но­ме­ра вер­ных утвер­жде­ний.

1) Если угол равен 47°, то смеж­ный с ним равен 153°.

2) Если две пря­мые пер­пен­ди­ку­ляр­ны тре­тьей пря­мой, то эти две пря­мые па­рал­лель­ны.

3) Через любую точку про­хо­дит ровно одна пря­мая.

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их но­ме­ра в по­ряд­ке воз­рас­та­ния.

 

 

 

 

 

Вариант 4

1. Два угла впи­сан­но­го в окруж­ность че­ты­рех­уголь­ни­ка равны 82° и 58°. Най­ди­те боль­ший из остав­ших­ся углов. Ответ дайте в гра­ду­сах.

2. 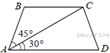Най­ди­те боль­ший угол рав­но­бед­рен­ной тра­пе­ции ABCD, если диа­го­наль AC об­ра­зу­ет с ос­но­ва­ни­ем AD и бо­ко­вой сто­ро­ной AB углы, рав­ные 30° и 45° со­от­вет­ствен­но.

3. 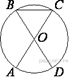AC и BD — диа­мет­ры окруж­но­сти с цен­тром O. Угол ACB равен 79°. Най­ди­те угол AOD. Ответ дайте в гра­ду­сах.

4. 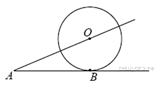К окруж­но­сти с цен­тром в точке О про­ве­де­ны ка­са­тель­наяAB и се­ку­щая AO. Най­ди­те ра­ди­ус окруж­но­сти, если AB = 12 см,AO = 13 см.

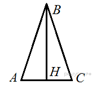
5. В рав­но­бед­рен­ном тре­уголь­ни­ке  . Най­ди­те  , если вы­со­та  .

6. 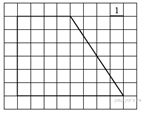Най­ди­те пло­щадь тра­пе­ции, изоб­ражённой на ри­сун­ке.

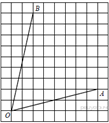7. Най­ди­те тан­генс угла AOB.

8. 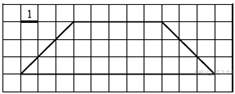Най­ди­те пло­щадь тра­пе­ции, изоб­ражённой на ри­сун­ке.

9. Какое из сле­ду­ю­щих утвер­жде­ний верно?

1) Все рав­но­бед­рен­ные тре­уголь­ни­ки по­доб­ны.

2) Су­ще­ству­ет пря­мо­уголь­ник, диа­го­на­ли ко­то­ро­го вза­им­но пер­пен­ди­ку­ляр­ны.

3) Сумма углов пря­мо­уголь­но­го тре­уголь­ни­ка равна 90 гра­ду­сам.

10. Ука­жи­те но­ме­ра вер­ных утвер­жде­ний.

1) Если три сто­ро­ны од­но­го тре­уголь­ни­ка про­пор­ци­о­наль­ны трём сто­ро­нам дру­го­го тре­уголь­ни­ка, то тре­уголь­ни­ки по­доб­ны.

2) Сумма смеж­ных углов равна 180°.

3) Любая вы­со­та рав­но­бед­рен­но­го тре­уголь­ни­ка яв­ля­ет­ся его бис­сек­три­сой.

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их но­ме­ра в по­ряд­ке воз­рас­та­ния.

 

Вариант 5

1. 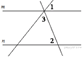Пря­мые m и n па­рал­лель­ны. Най­ди­те ∠3, если ∠1 = 22°, ∠2 = 72°. Ответ дайте в гра­ду­сах.

2. 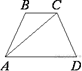В тра­пе­ции ABCD AB = CD, AC = AD и ∠ABC = 95°. Най­ди­те уголCAD. Ответ дайте в гра­ду­сах.

3. На окруж­но­сти с цен­тром в точке  от­ме­че­ны точки  и  так, что . Длина мень­шей дуги  равна 50. Най­ди­те длину боль­шей дуги .

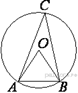
4.  Тре­уголь­ник ABC впи­сан в окруж­ность с цен­тром в точке O. Най­ди­те гра­дус­ную меру угла C тре­уголь­ни­ка ABC, если угол AOB равен 27°.

5. 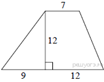Най­ди­те пло­щадь тра­пе­ции, изоб­ражённой на ри­сун­ке.

6. 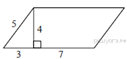Най­ди­те пло­щадь па­рал­ле­ло­грам­ма, изоб­ражённого на ри­сун­ке.

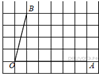7. Най­ди­те тан­генс угла AOB, изоб­ражённого на ри­сун­ке.

8.

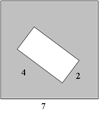
Из квад­ра­та вы­ре­за­ли пря­мо­уголь­ник (см. ри­су­нок). Най­ди­те пло­щадь по­лу­чив­шей­ся фи­гу­ры.

9. Какие из сле­ду­ю­щих утвер­жде­ний верны?

1) Если две сто­ро­ны од­но­го тре­уголь­ни­ка со­от­вет­ствен­но равны двум сто­ро­нам дру­го­го тре­уголь­ни­ка, то такие тре­уголь­ни­ки равны.

2) Сред­няя линия тра­пе­ции па­рал­лель­на её ос­но­ва­ни­ям.

3) Длина ги­по­те­ну­зы пря­мо­уголь­но­го тре­уголь­ни­ка мень­ше суммы длин его ка­те­тов.

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их но­ме­ра в по­ряд­ке воз­рас­та­ния.

10. Какие из сле­ду­ю­щих утвер­жде­ний верны?

1) Окруж­ность имеет бес­ко­неч­но много цен­тров сим­мет­рии.

2) Пря­мая не имеет осей сим­мет­рии.

3) Пра­виль­ный пя­ти­уголь­ник имеет пять осей сим­мет­рии.

4) Квад­рат не имеет цен­тра сим­мет­рии.

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их но­ме­ра в по­ряд­ке воз­рас­та­ния.

Вариант 6

1. 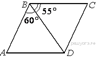Диа­го­наль BD па­рал­ле­ло­грам­ма ABCD об­ра­зу­ет с его сто­ро­на­ми углы, рав­ные 60° и 55°. Най­ди­те мень­ший угол па­рал­ле­ло­грам­ма.

2. 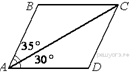Диа­го­наль AC па­рал­ле­ло­грам­ма ABCD об­ра­зу­ет с его сто­ро­на­ми углы, рав­ные 35° и 30°. Най­ди­те боль­ший угол па­рал­ле­ло­грам­ма.

3. 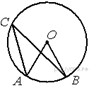Точка О — центр окруж­но­сти, ∠ACB = 24° (см. ри­су­нок). Най­ди­те ве­ли­чи­ну угла AOB (в гра­ду­сах).

4. Бо­ко­вая сто­ро­на рав­но­бед­рен­но­го тре­уголь­ни­ка равна 4. Угол при вер­ши­не, про­ти­во­ле­жа­щий ос­но­ва­нию, равен 120°. Най­ди­те диа­метр окруж­но­сти, опи­сан­ной около этого тре­уголь­ни­ка.

5. Пе­ри­метр ромба равен 24, а тан­генс од­но­го из углов равен . Най­ди­те пло­щадь ромба.

6. Най­ди­те пло­щадь пря­мо­уголь­ни­ка, если его пе­ри­метр равен 102, а от­но­ше­ние со­сед­них сто­рон равно 2:15.

7. На клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1см x 1см от­ме­че­ны точкиА, В и С. Най­ди­те рас­сто­я­ние от точки А до се­ре­ди­ны от­рез­ка ВС. Ответ вы­ра­зи­те в сан­ти­мет­рах.

8. Най­ди­те пло­щадь тра­пе­ции, изоб­ражённой на ри­сун­ке.

За­да­ние 12 № 340867

9. Какие из сле­ду­ю­щих утвер­жде­ний верны?

1) Если пло­ща­ди фигур равны, то равны и сами фи­гу­ры.

2) Пло­щадь тра­пе­ции равна про­из­ве­де­нию суммы ос­но­ва­ний на вы­со­ту.

3) Если две сто­ро­ны тре­уголь­ни­ка равны 4 и 5, а угол между ними равен 30°, то пло­щадь этого тре­уголь­ни­ка равна 10.

4) Если две смеж­ные сто­ро­ны па­рал­ле­ло­грам­ма равны 4 и 5, а угол между ними равен 30°, то пло­щадь этого па­рал­ле­ло­грам­ма равна 10.

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их но­ме­ра в по­ряд­ке воз­рас­та­ния.

10. Какое из сле­ду­ю­щих утвер­жде­ний верно?

1) Если два угла од­но­го тре­уголь­ни­ка равны двум углам дру­го­го тре­уголь­ни­ка, то такие тре­уголь­ни­ки по­доб­ны.

2) Диа­го­на­ли ромба равны.

3) Тан­генс лю­бо­го остро­го угла мень­ше еди­ни­цы.

 

 

 

Вариант 7

1. В тре­уголь­ни­ке ABC BM — ме­ди­а­на и BH – вы­со­та. Из­вест­но, что AC = 216, HC = 54 и ∠ACB = 40°. Най­ди­те угол AMB. Ответ дайте в гра­ду­сах.

2. Ос­но­ва­ния тра­пе­ции равны 4 и 10. Най­ди­те боль­ший из от­рез­ков, на ко­то­рые делит сред­нюю линию этой тра­пе­ции одна из её диа­го­на­лей.

3. AC и BD — диа­мет­ры окруж­но­сти с цен­тром O. Угол ACB равен 79°. Най­ди­те угол AOD. Ответ дайте в гра­ду­сах.

 

4. Тре­уголь­ник ABC впи­сан в окруж­ность с цен­тром в точке O. Най­ди­те гра­дус­ную меру угла C тре­уголь­ни­ка ABC, если угол AOB равен 48°.

5. В пря­мо­уголь­ном тре­уголь­ни­ке ги­по­те­ну­за равна 70, а один из ост­рых углов равен 45°. Най­ди­те пло­щадь тре­уголь­ни­ка.

6. В рав­но­бед­рен­ном тре­уголь­ни­ке бо­ко­вая сто­ро­на равна 10, ос­но­ва­ние — , а угол, ле­жа­щий на­про­тив ос­но­ва­ния, равен 135°. Най­ди­те пло­щадь тре­уголь­ни­ка, де­лен­ную на 

7. Най­ди­те тан­генс угла AOB, изоб­ра­жен­но­го на ри­сун­ке.

8. На ри­сун­ке изоб­ра­жен ромб  . Ис­поль­зуя ри­су­нок, най­ди­те  .

9. Ука­жи­те но­ме­ра вер­ных утвер­жде­ний.

1) Если три сто­ро­ны од­но­го тре­уголь­ни­ка про­пор­ци­о­наль­ны трём сто­ро­нам дру­го­го тре­уголь­ни­ка, то тре­уголь­ни­ки по­доб­ны.

2) Сумма смеж­ных углов равна 180°.

3) Любая вы­со­та рав­но­бед­рен­но­го тре­уголь­ни­ка яв­ля­ет­ся его бис­сек­три­сой.

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их но­ме­ра в по­ряд­ке воз­рас­та­ния.

10. Какое из сле­ду­ю­щих утвер­жде­ний верно?

1. Пло­щадь квад­ра­та равна про­из­ве­де­нию двух его смеж­ных сто­рон.

2. Диа­го­наль тра­пе­ции делит её на два рав­ных тре­уголь­ни­ка.

3. Если две сто­ро­ны од­но­го тре­уголь­ни­ка со­от­вет­ствен­но равны двум сто­ро­нам дру­го­го тре­уголь­ни­ка, то такие тре­уголь­ни­ки равны.

 

 

Вариант 8

1. Точка H яв­ля­ет­ся ос­но­ва­ни­ем вы­со­ты, про­ведённой из вер­ши­ны пря­мо­го угла B тре­уголь­ни­каABC к ги­по­те­ну­зе AC. Най­ди­те AB, если AH = 6, AC = 24.

2. Углы, от­ме­чен­ные на ри­сун­ке одной дугой, равны. Най­ди­те угол  . Ответ дайте в гра­ду­сах.

3. Цен­траль­ный угол AOB равен 60°. Най­ди­те длину хорды AB, на ко­то­рую он опи­ра­ет­ся, если ра­ди­ус окруж­но­сти равен 5.

4. К окруж­но­сти с цен­тром в точке О про­ве­де­ны ка­са­тель­наяAB и се­ку­щая AO. Най­ди­те ра­ди­ус окруж­но­сти, если AB = 12 см,AO = 13 см.

5. Най­ди­те пло­щадь кру­го­во­го сек­то­ра, если длина огра­ни­чи­ва­ю­щей его дуги равна 6π, а угол сек­то­ра равен 120°. В от­ве­те ука­жи­те пло­щадь, де­лен­ную на π.

6. В ромбе сто­ро­на равна 10, одна из диа­го­на­лей — , а угол, из ко­то­ро­го вы­хо­дит эта диа­го­наль, равен 45°. Най­ди­те пло­щадь ромба, де­лен­ную на 

7. На клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1x1 изоб­ра­жен пря­мо­уголь­ный тре­уголь­ник. Най­ди­те длину его боль­ше­го ка­те­та.

8. На клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1х1 от­ме­че­ны три точки: ,  и . Най­ди­те рас­сто­я­ние от точки  до се­ре­ди­ны от­рез­ка .

9. Какое из сле­ду­ю­щих утвер­жде­ний верно?

1) Точка пе­ре­се­че­ния двух окруж­но­стей рав­но­уда­ле­на от цен­тров этих окруж­но­стей.

2) В па­рал­ле­ло­грам­ме есть два рав­ных угла.

3) Пло­щадь пря­мо­уголь­но­го тре­уголь­ни­ка равна про­из­ве­де­нию длин его ка­те­тов.

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их но­ме­ра в по­ряд­ке воз­рас­та­ния.

10. Ука­жи­те но­ме­ра вер­ных утвер­жде­ний.

1) Если угол ост­рый, то смеж­ный с ним угол также яв­ля­ет­ся ост­рым.

2) Диа­го­на­ли квад­ра­та вза­им­но пер­пен­ди­ку­ляр­ны.

3) В плос­ко­сти все точки, рав­но­удалённые от за­дан­ной точки, лежат на одной окруж­но­сти.

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их но­ме­ра в по­ряд­ке воз­рас­та­ния.

 

 

Вариант 9

1. В тра­пе­цию, сумма длин бо­ко­вых сто­рон ко­то­рой равна 24, впи­са­на окруж­ность. Най­ди­те длину сред­ней линии тра­пе­ции.

2. В тре­уголь­ни­ке    угол    пря­мой,  . Най­ди­те  .

3.  Ра­ди­ус OB окруж­но­сти с цен­тром в точке O пе­ре­се­ка­ет хорду ACв точке D и пер­пен­ди­ку­ля­рен ей. Най­ди­те длину хорды AC, если BD = 1 см, а ра­ди­ус окруж­но­сти равен 5 см.

4. От­рез­ки AC и BD — диа­мет­ры окруж­но­сти с цен­тром O. Угол ACB равен 23°. Най­ди­те угол AOD. Ответ дайте в гра­ду­сах.

5. Вы­со­та BH па­рал­ле­ло­грам­ма ABCD делит его сто­ро­ну AD на от­рез­ки AH = 1 и HD = 28. Диа­го­наль па­рал­ле­ло­грам­ма BD равна 53. Най­ди­те пло­щадь па­рал­ле­ло­грам­ма.

6. Пло­щадь па­рал­ле­ло­грам­ма ABCD равна 5. Точка E — се­ре­ди­на сто­ро­ны AD. Най­ди­те пло­щадь тра­пе­ции AECB.

7. Най­ди­те тан­генс угла AOB, изоб­ра­жен­но­го на ри­сун­ке.

8. Най­ди­те тан­генс угла С тре­уголь­ни­ка ABC , изоб­ражённого на ри­сун­ке.

9. Какие из сле­ду­ю­щих утвер­жде­ний верны?

1) Если в па­рал­ле­ло­грам­ме диа­го­на­ли равны, то этот па­рал­ле­ло­грамм — пря­мо­уголь­ник.

2) Если диа­го­на­ли па­рал­ле­ло­грам­ма делят его углы по­по­лам, то этот па­рал­ле­ло­грамм — ромб.

3) Если один из углов, при­ле­жа­щих к сто­ро­не па­рал­ле­ло­грам­ма, равен 50°, то дру­гой угол, при­ле­жа­щий к той же сто­ро­не, равен 50°.

4) Если сумма трех углов вы­пук­ло­го че­ты­рех­уголь­ни­ка равна 200°, то его чет­вер­тый угол равен 160°.

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их но­ме­ра в по­ряд­ке воз­рас­та­ния.

10. Какие из сле­ду­ю­щих утвер­жде­ний верны?

1) Через любые три точки про­хо­дит не более одной окруж­но­сти.

2) Если рас­сто­я­ние между цен­тра­ми двух окруж­но­стей боль­ше суммы их диа­мет­ров, то эти окруж­но­сти не имеют общих точек.

3) Если ра­ди­у­сы двух окруж­но­стей равны 3 и 5, а рас­сто­я­ние между их цен­тра­ми равно 1, то эти окруж­но­сти пе­ре­се­ка­ют­ся.

4) Если дуга окруж­но­сти со­став­ля­ет 80°, то впи­сан­ный угол, опи­ра­ю­щий­ся на эту дугу окруж­но­сти, равен 40°.

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их но­ме­ра в по­ряд­ке воз­рас­та­ния.

Вариант 10

 

1. Най­ди­те угол  ABC  рав­но­бед­рен­ной тра­пе­ции  ABCD, если диа­го­наль  AC  об­ра­зу­ет с ос­но­ва­ни­ем  AD и бо­ко­вой сто­ро­ной  CD  углы, рав­ные 30° и 80° со­от­вет­ствен­но.

2. Четырёхуголь­ник ABCD впи­сан в окруж­ность. Угол ABC равен 136°, угол CAD равен 82°. Най­ди­те угол ABD. Ответ дайте в гра­ду­сах.

3. На окруж­но­сти по раз­ные сто­ро­ны от диа­мет­ра AB взяты точки M иN. Из­вест­но, что ∠NBA = 38°. Най­ди­те угол NMB. Ответ дайте в гра­ду­сах.

4. Цен­траль­ный угол AOB опи­ра­ет­ся на хорду АВ так, что угол ОАВравен 60° . Най­ди­те длину хорды АВ, если ра­ди­ус окруж­но­сти равен 8.

5. В ромбе сто­ро­на равна 10, одна из диа­го­на­лей — , а угол, из ко­то­ро­го вы­хо­дит эта диа­го­наль, равен 30°. Най­ди­те пло­щадь ромба.

6. Най­ди­те пло­щадь па­рал­ле­ло­грам­ма, изоб­ражённого на ри­сун­ке.

7. На клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1х1 изоб­ражён па­рал­ле­ло­грамм. Най­ди­те его пло­щадь.

 

8. Пло­щадь одной клет­ки равна 1. Най­ди­те пло­щадь фи­гу­ры, изоб­ражённой на ри­сун­ке.

9. Какие из сле­ду­ю­щих утвер­жде­ний верны?

1.Рас­сто­я­ние от точки, ле­жа­щей на окруж­но­сти, до цен­тра окруж­но­сти равно ра­ди­у­су.

2.Пло­щадь тра­пе­ции равна про­из­ве­де­нию ос­но­ва­ния тра­пе­ции на вы­со­ту.

3.Тре­уголь­ни­ка со сто­ро­на­ми 1, 2, 4 не су­ще­ству­ет.

10. Какое из сле­ду­ю­щих утвер­жде­ний верно?

1. Пло­щадь квад­ра­та равна про­из­ве­де­нию двух его смеж­ных сто­рон.

2. Диа­го­наль тра­пе­ции делит её на два рав­ных тре­уголь­ни­ка.

3. Если две сто­ро­ны од­но­го тре­уголь­ни­ка со­от­вет­ствен­но равны двум сто­ро­нам дру­го­го тре­уголь­ни­ка, то такие тре­уголь­ни­ки равны.

 

 

 

Вариант 11

1. На пря­мой AB взята точка M. Луч MD — бис­сек­три­са угла CMB. Из­вест­но, что ∠DMC = 44°. Най­ди­те угол CMA. Ответ дайте в гра­ду­сах.

2. Тан­генс остро­го угла пря­мо­уголь­ной тра­пе­ции равен 2. Най­ди­те её боль­шее ос­но­ва­ние, если мень­шее ос­но­ва­ние равно вы­со­те и равно 78.

3. Окруж­ность с цен­тром в точке O опи­са­на около рав­но­бед­рен­но­го тре­уголь­ни­ка ABC, в ко­то­ром AB = BC и ∠ABC = 177°. Най­ди­те ве­ли­чи­ну углаBOC. Ответ дайте в гра­ду­сах.

4. На окруж­но­сти с цен­тром в точке  от­ме­че­ны точки  и  так, что . Длина мень­шей дуги  равна 50. Най­ди­те длину боль­шей дуги .

5. Пло­щадь па­рал­ле­ло­грам­ма  равна 12. Точка  - се­ре­ди­на сто­ро­ны . Най­ди­те пло­щадь тра­пе­ции .

6. Ос­но­ва­ния тра­пе­ции равны 18 и 12, одна из бо­ко­вых сто­рон равна , а угол между ней и одним из ос­но­ва­ний равен 135°. Най­ди­те пло­щадь тра­пе­ции.

7. Най­ди­те пло­щадь тра­пе­ции, изоб­ражённой на ри­сун­ке.

 

8. Най­ди­те тан­генс угла AOB.

9. Какие из сле­ду­ю­щих утвер­жде­ний верны?

1) Через любые три точки про­хо­дит не более одной окруж­но­сти.

2) Если рас­сто­я­ние между цен­тра­ми двух окруж­но­стей боль­ше суммы их диа­мет­ров, то эти окруж­но­сти не имеют общих точек.

3) Если ра­ди­у­сы двух окруж­но­стей равны 3 и 5, а рас­сто­я­ние между их цен­тра­ми равно 1, то эти окруж­но­сти пе­ре­се­ка­ют­ся.

4) Если дуга окруж­но­сти со­став­ля­ет 80°, то впи­сан­ный угол, опи­ра­ю­щий­ся на эту дугу окруж­но­сти, равен 40°.

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их но­ме­ра в по­ряд­ке воз­рас­та­ния.

10. Какое из сле­ду­ю­щих утвер­жде­ний верно?

1. Все­гда один из двух смеж­ных углов ост­рый, а дру­гой тупой.

2. Пло­щадь квад­ра­та равна про­из­ве­де­нию двух его смеж­ных сто­рон.

3. Все хорды одной окруж­но­сти равны между собой.

 

 

 

Вариант 12

1. Ос­но­ва­ния рав­но­бед­рен­ной тра­пе­ции равны 50 и 104, бо­ко­вая сто­ро­на 45. Най­ди­те длину диа­го­на­ли тра­пе­ции.

2. Най­ди­те угол  ABC  рав­но­бед­рен­ной тра­пе­ции  ABCD, если диа­го­наль  AC  об­ра­зу­ет с ос­но­ва­ни­ем  AD  и бо­ко­вой сто­ро­ной  CD  углы, рав­ные 20° и 100° со­от­вет­ствен­но.

3. В угол C ве­ли­чи­ной 79° впи­са­на окруж­ность, ко­то­рая ка­са­ет­ся сто­рон угла в точ­ках A и B. Най­ди­те угол AOB. Ответ дайте в гра­ду­сах.

4. В окруж­но­сти с цен­тром O AC и BD — диа­мет­ры. Цен­траль­ный уголAOD равен 130°. Най­ди­те впи­сан­ный угол ACB. Ответ дайте в гра­ду­сах.

5. В пря­мо­уголь­ни­ке одна сто­ро­на равна 10, дру­гая сто­ро­на равна 12. Най­ди­те пло­щадь пря­мо­уголь­ни­ка.

6. В тра­пе­ции ABCD AD = 3, BC = 1, а её пло­щадь равна 12. Най­ди­те пло­щадь тре­уголь­ни­ка ABC.

7. Най­ди­те тан­генс угла    тре­уголь­ни­ка  , изоб­ражённого на ри­сун­ке.

8. На ри­сун­ке изоб­ра­же­на тра­пе­ция  . Ис­поль­зуя ри­су­нок, най­ди­те  .

9. Ука­жи­те но­ме­ра вер­ных утвер­жде­ний.

1) Бис­сек­три­са рав­но­бед­рен­но­го тре­уголь­ни­ка, про­ведённая из вер­ши­ны, про­ти­во­ле­жа­щей ос­но­ва­нию, делит ос­но­ва­ние на две рав­ные части.

2) В любом пря­мо­уголь­ни­ке диа­го­на­ли вза­им­но пер­пен­ди­ку­ляр­ны.

3) Для точки, ле­жа­щей на окруж­но­сти, рас­сто­я­ние до цен­тра окруж­но­сти равно ра­ди­у­су.

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их но­ме­ра в по­ряд­ке воз­рас­та­ния.

10. Какие из сле­ду­ю­щих утвер­жде­ний верны?

1) Один из углов тре­уголь­ни­ка все­гда не пре­вы­ша­ет 60 гра­ду­сов.

2) Диа­го­на­ли тра­пе­ции пе­ре­се­ка­ют­ся и де­лят­ся точ­кой пе­ре­се­че­ния по­по­лам.

3) Все диа­мет­ры окруж­но­сти равны между собой.

 

 

Вариант 13

1. Пря­мые m и n па­рал­лель­ны. Най­ди­те ∠3, если ∠1= 37°, ∠2 = 77° . Ответ дайте в гра­ду­сах.

2. В рав­но­бед­рен­ном тре­уголь­ни­ке ABC с ос­но­ва­ни­ем AC внеш­ний угол при вер­ши­не C равен 123°. Най­ди­те ве­ли­чи­ну угла ВАС. Ответ дайте в гра­ду­сах.

 

3. Ка­са­тель­ные в точ­ках A и B к окруж­но­сти с цен­тром O пе­ре­се­ка­ют­ся под углом 72°. Най­ди­те угол ABO. Ответ дайте в гра­ду­сах.

 

4. Окруж­ность с цен­тром в точке O опи­са­на около рав­но­бед­рен­но­го тре­уголь­ни­ка ABC, в ко­то­ром AB = BC и ∠ABC = 177°. Най­ди­те ве­ли­чи­ну углаBOC. Ответ дайте в гра­ду­сах.

5. В тра­пе­ции ABCD из­вест­но, что AD=4, BC=1, а её пло­щадь равна 35. Най­ди­те пло­щадь тре­уголь­ни­ка ABC.

6. В пря­мо­уголь­ном тре­уголь­ни­ке один из ка­те­тов равен 10, ост­рый угол, при­ле­жа­щий к нему, равен 60°, а ги­по­те­ну­за равна 20. Най­ди­те пло­щадь тре­уголь­ни­ка, делённую на .

7. На ри­сун­ке изоб­ра­жен ромб  . Ис­поль­зуя ри­су­нок, най­ди­те  .

8. Най­ди­те тан­генс угла    тре­уголь­ни­ка  , изоб­ражённого на ри­сун­ке.

9. Ука­жи­те но­ме­ра вер­ных утвер­жде­ний.

1) Су­ще­ству­ет квад­рат, ко­то­рый не яв­ля­ет­ся пря­мо­уголь­ни­ком.

2) Если два угла тре­уголь­ни­ка равны, то равны и про­ти­во­ле­жа­щие им сто­ро­ны.

3) Внут­рен­ние на­крест ле­жа­щие углы, об­ра­зо­ван­ные двумя па­рал­лель­ны­ми пря­мы­ми и се­ку­щей, равны.

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их но­ме­ра в по­ряд­ке воз­рас­та­ния.

10. Какие из сле­ду­ю­щих утвер­жде­ний верны?

1) Пра­виль­ный ше­сти­уголь­ник имеет шесть осей сим­мет­рии.

2) Пря­мая не имеет осей сим­мет­рии.

3) Цен­тром сим­мет­рии ромба яв­ля­ет­ся точка пе­ре­се­че­ния его диа­го­на­лей.

4) Рав­но­бед­рен­ный тре­уголь­ник имеет три оси сим­мет­рии.

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их но­ме­ра в по­ряд­ке воз­рас­та­ния.

 

 

 

Вариант 14

1. Тан­генс остро­го угла пря­мо­уголь­ной тра­пе­ции равен   Най­ди­те её боль­шее ос­но­ва­ние, если мень­шее ос­но­ва­ние равно вы­со­те и равно 15.

2. Диа­го­наль пря­мо­уголь­ни­ка об­ра­зу­ет угол 51° с одной из его сто­рон. Най­ди­те ост­рый угол между диа­го­на­ля­ми этого пря­мо­уголь­ни­ка. Ответ дайте в гра­ду­сах.

3. AC и BD — диа­мет­ры окруж­но­сти с цен­тром O. Угол ACB равен 79°. Най­ди­те угол AOD. Ответ дайте в гра­ду­сах.

4. Тре­уголь­ник ABC впи­сан в окруж­ность с цен­тром в точке O. Най­ди­те гра­дус­ную меру угла C тре­уголь­ни­ка ABC, если угол AOB равен 115°.

5. Сред­няя линия тра­пе­ции равна 11, а мень­ше ос­но­ва­ние равно 5. Най­ди­те боль­шее ос­но­ва­ние тра­пе­ции.

6. Из квад­ра­та вы­ре­за­ли пря­мо­уголь­ник (см. ри­су­нок). Най­ди­те пло­щадь по­лу­чив­шей­ся фи­гу­ры.

7. Най­ди­те тан­генс угла AOB, изоб­ра­жен­но­го на ри­сун­ке.

8. На ри­сун­ке изоб­ра­жен ромб . Ис­поль­зуя ри­су­нок, най­ди­те .

9. Какое из сле­ду­ю­щих утвер­жде­ний верно?

1) Пло­щадь па­рал­ле­ло­грам­ма равна по­ло­ви­не про­из­ве­де­ния его диа­го­на­лей.

2) Сумма углов пря­мо­уголь­но­го тре­уголь­ни­ка равна 90 гра­ду­сам.

3) Бис­сек­три­сы тре­уголь­ни­ка пе­ре­се­ка­ют­ся в цен­тре впи­сан­ной в него окруж­но­сти.

10. Ука­жи­те но­ме­ра вер­ных утвер­жде­ний.

1) Любые три пря­мые имеют не более одной общей точки.

2) Если угол равен 120°, то смеж­ный с ним равен 120°.

3) Если рас­сто­я­ние от точки до пря­мой боль­ше 3, то и длина любой на­клон­ной, про­ведённой из дан­ной точки к пря­мой, боль­ше 3.

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их но­ме­ра в по­ряд­ке воз­рас­та­ния.

 

 

Вариант 15

1. Точка D на сто­ро­не AB тре­уголь­ни­ка ABC вы­бра­на так, что AD = AC. Из­вест­но, что ∠CAB = 80° и ∠ACB=59∘. Най­ди­те угол DCB. Ответ дайте в гра­ду­сах.

2.

В па­рал­ле­ло­грам­ме ABCD про­ве­де­на диа­го­наль AC. УголDAC равен 47°, а угол CAB равен 11°. Най­ди­те боль­ший угол па­рал­ле­ло­грам­ма ABCD. Ответ дайте в гра­ду­сах.

3. Най­ди­те ∠KOM, если из­вест­но, что гра­дус­ная мера дуги MN равна 124°, а гра­дус­ная мера дуги KN равна 180°.

4. Ка­са­тель­ные в точ­ках  и  к окруж­но­сти с цен­тром в точке  пе­ре­се­ка­ют­ся под углом 82°. Най­ди­те угол . Ответ дайте в гра­ду­сах.

5. Вы­со­та рав­но­бед­рен­ной тра­пе­ции, про­ведённая из вер­ши­ны C, делит ос­но­ва­ние AD на от­рез­ки дли­ной 1 и 5. Най­ди­те длину ос­но­ва­нияBC.

6. Сто­ро­на ромба равна 50, а диа­го­наль равна 80. Най­ди­те пло­щадь ромба.

7. Най­ди­те тан­генс угла AOB, изоб­ра­жен­но­го на ри­сун­ке.

8. Най­ди­те тан­генс угла В тре­уголь­ни­ка ABC, изоб­ражённого на ри­сун­ке.

9. Какое из сле­ду­ю­щих утвер­жде­ний верно?

1) Внеш­ний угол тре­уголь­ни­ка равен сумме его внут­рен­них углов.

2) Диа­го­на­ли ромба точ­кой пе­ре­се­че­ния де­лят­ся по­по­лам.

3) Ка­са­тель­ная к окруж­но­сти па­рал­лель­на ра­ди­у­су, про­ведённому в точку ка­са­ния.

10. Ука­жи­те но­ме­ра вер­ных утвер­жде­ний.

1) Су­ще­ству­ет квад­рат, ко­то­рый не яв­ля­ет­ся пря­мо­уголь­ни­ком.

2) Если два угла тре­уголь­ни­ка равны, то равны и про­ти­во­ле­жа­щие им сто­ро­ны.

3) Внут­рен­ние на­крест ле­жа­щие углы, об­ра­зо­ван­ные двумя па­рал­лель­ны­ми пря­мы­ми и се­ку­щей, равны.

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их но­ме­ра в по­ряд­ке воз­рас­та­ния.

 

Ответы:

вариант	1	2	3	4	5	6	7	8	9	10
1	85	20	153	156	1600	50	2	0,8	3	12
2	78	60	39	10	50	75	1	2	4	3
3	78	38	17,5	153	50	49	4	4	234	2
4	122	105	22	5	12	36	2	24	2	12
5	86	10	400	13,5	168	40	4	41	23	3
6	65	115	48	8	12	270	5	24	4	1
7	140	5	22	24	1225	25	2	0,5	12	13
8	12	40	5	5	27	50	7	3	2	23
9	12	20	6	134	1305	3,75	2	1	124	124
10	110	54	52	8	50	20	18	20,5	13	1
11	92	117	3	400	9	60	40	2	124	2
12	85	60	101	25	120	3	1,5	0,8	13	13
13	66	57	36	3	7	50	0,75	0,75	3	13
14	33	78	22	57,5	17	28	2	0,75	3	3
15	9	122	56	41	4	2400	2	3,5	2	3

 

Скачано с www.znanio.ru