Поделиться
МА_5.61-62 Степень числа.pdf
Краткий
способ записиСумму нескольких одинаковых слагаемых можно представить в виде произведения.
7+7+7+7+7
= 7・5
Произведение нескольких одинаковых множителей можно представить в виде степени числа .
 |
Запишем Представьте в виде степени
1. 6・6・6 =
2. 5・5・5・5・5=
3. 7・7・7・7・7=
4. 73・73 =
5. a・a・a・a・a・a・a=
6. (x+1)・(x+1)・(x+1)・(x+1)・(x+1) =
|
(x+1)4 3 12 6・6・6 5・5・5 6・6・6・6・6・6 12・12・12 4・a |
a・a・a・a a4 |
63 53 36 5 3 (x+1)・(x+1)・(x+1)・(x+1) 4・(x+1) 1212 312 66 |
СтепеньСтепень числа a с показателем n записывается как
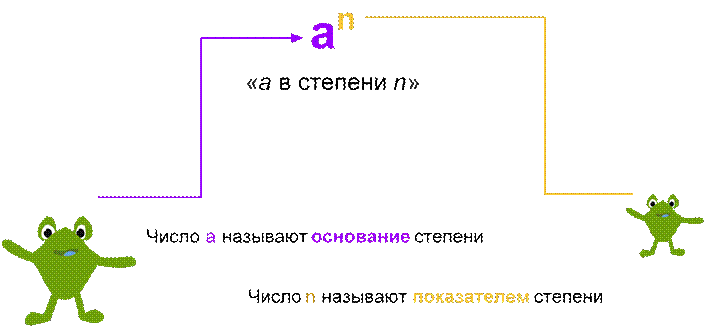
Прочитайте выражения. Назовите основание и показатель степеней.
основание
степени показатель степени
 |
75 129 е8
Квадрат и кубНекоторые степени имеют свои названия.
м2
«метр квадратный» см3
«сантиметр
кубический»
26 23 22 43
s3 32 24
k3
|
1) 21= 2) 22= 3) 23= 4) 24= 5) 25= 6) 31= |
1) 52= 2) 62= 3) 73= 4) 32・5= 5) 32 + 5= |
7) 32=
8) 33=
9) 34=
Порядок действий
 |
 |
||
1) 5+42=
2) (5+4)2=
3) 52+42=
Составьте числовое выражение и найдите его значение:
1) сумма куба числа 5 и квадрата числа 8;
2) разность квадратов чисел 6 и 2;
3) квадрат разности чисел 6 и 2;
4) разность куба числа 3 и квадрата числа 5.
Кто быстрее и правильнее?
252
: (242 +72) 152
: (132 -124)
1) 5・105+4・104+ 3・103+2・102+1・10=
2) 5・108+4・106+ 3・103+2・102+1・10=
3) 2 345 =
4) 50 706 =
Найдите значение выражения:
1) 16 - с3, если с = 2:
2) х3 - х2, если х = 10:
3) (х2 - у2) : (х - у), если х = 4, у = 2:
1) y・y =9
2) y2 = 9
3) x・x =25
4) x2 = 25
5) n2= 169
6) n3= 512
1) Сумма двух чисел 549. Одно из них в 8 раз больше другого. Найдите эти числа.
2) 3x+5x+96 = 1568
3) 63 - (25+p)= 26
4) 62- 52=
Домашнее задание
❏ Выполняем работу над ошибками по см/р
❏ Читаем п. 16 «Степень»
❏ №№ 657 (1 строка), 658 (а),667(2).
❏ Доп. стр 124 прочитать заметку про Колмогорова А.Н.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
