8 класс. ФОП. Пропорциональные отрезки.

ФИ_____________________

Пропорциональные отрезки.

ФИ_____________________

Пропорциональные отрезки.

 

 

 

ФИ_____________________

Пропорциональные отрезки.

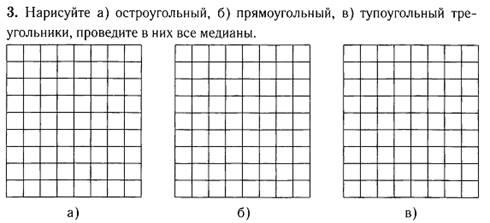
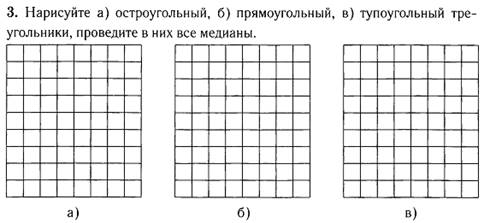
ФИ_____________________

Пропорциональные отрезки.

 

 

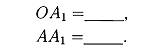
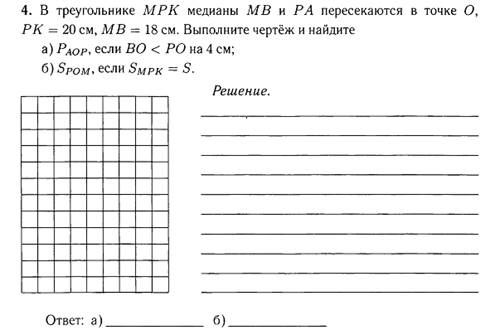
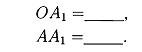
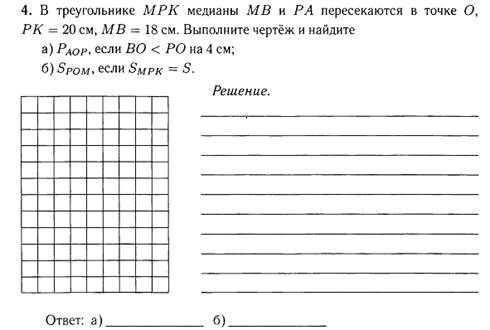
ФИ_____________________

Пропорциональные отрезки.

ФИ_____________________

Пропорциональные отрезки.

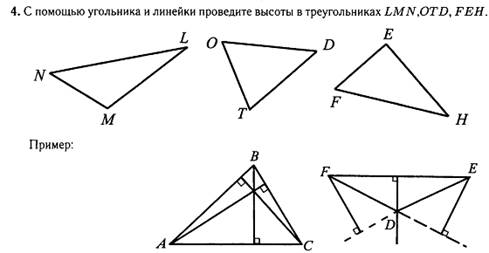
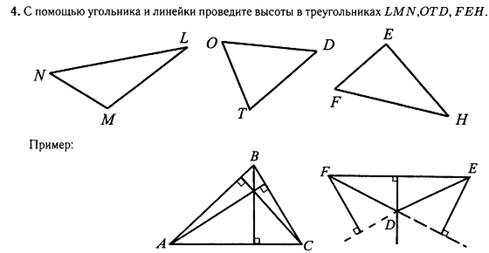
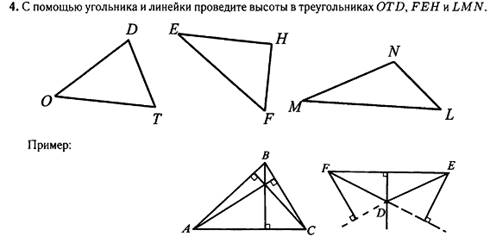
Подпишите длины! Проверьте соотношение

∆LMN =____________ ∆OTD =_____________ ∆FEH =___________

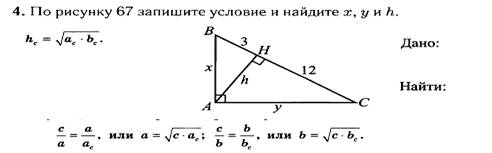
РЕШЕНИЕ:__________________________________________________

Подпишите длины! Проверьте соотношение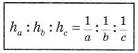

∆LMN =____________ ∆OTD =_____________ ∆FEH =___________

РЕШЕНИЕ:__________________________________________________

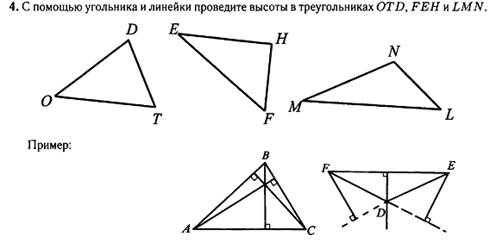
Подпишите длины! Проверьте соотношение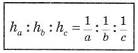

∆ OTD =____________ ∆ FEH =_____________ ∆ LMN =___________

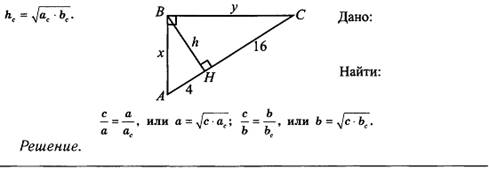
Подпишите длины! Проверьте соотношение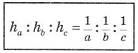

∆ OTD =____________ ∆ FEH =_____________ ∆ LMN =___________

ФИ_____________________

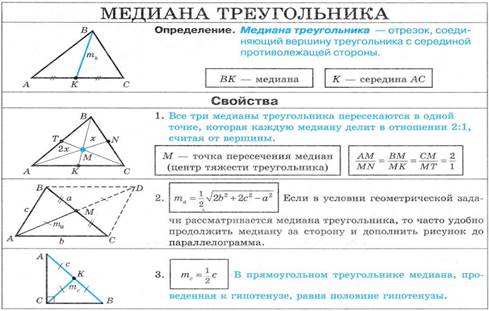
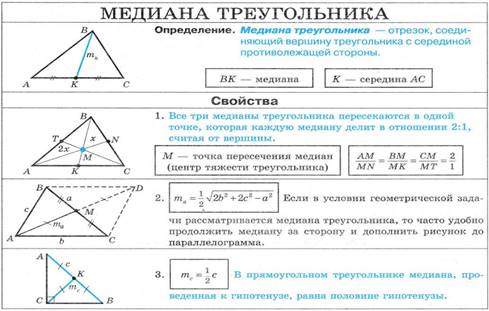
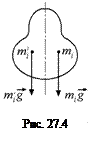
Центр масс в треугольнике.

Утверждение. Если однородное плоское тело имеет ось симметрии, центр тяжести находится на этой оси.

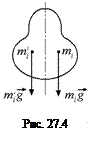Действительно, для всякой точечной массы m_i, расположенной справа от оси симметрии, найдется такая же точечная масса , расположенная симметрично относительно первой (рис. 27.4). При этом сумма моментов сил .

Поскольку  все тело можно представить разбитым на подобные пары точек, то суммарный момент сил тяжести относительно любой точки, лежащей на оси симметрии равен нулю, а значит, на этой оси находится и центр тяжести тела. Отсюда следует важный вывод: если тело имеет несколько осей симметрии, то центр тяжести лежит на пересечении этих осей (рис. 27.5).

Рис. 27.5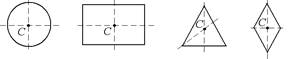 

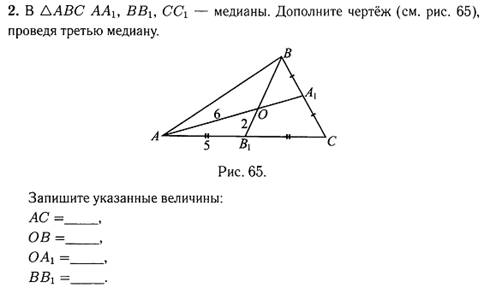
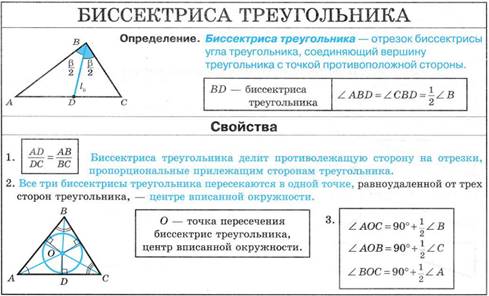
ВЫВОД: все три биссектрисы треугольника ______________________

____________________и являются_______________________________.

ФИ_____________________

Центр масс в треугольнике.

Утверждение. Если однородное плоское тело имеет ось симметрии, центр тяжести находится на этой оси.

Действительно, для всякой точечной массы m_i, расположенной справа от оси симметрии, найдется такая же точечная масса , расположенная симметрично относительно первой (рис. 27.4). При этом сумма моментов сил .

Поскольку  все тело можно представить разбитым на подобные пары точек, то суммарный момент сил тяжести относительно любой точки, лежащей на оси симметрии равен нулю, а значит, на этой оси находится и центр тяжести тела. Отсюда следует важный вывод: если тело имеет несколько осей симметрии, то центр тяжести лежит на пересечении этих осей (рис. 27.5).

Рис. 27.5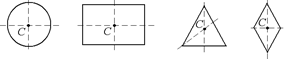 

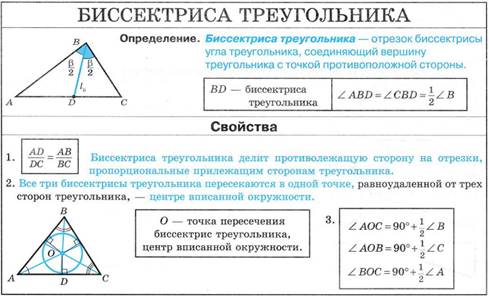
ВЫВОД: все три биссектрисы треугольника ______________________

____________________и являются_______________________________.

.

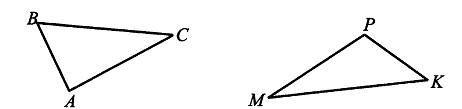
Подпишите длины! Проверьте соотношение

__________________________________________________

=

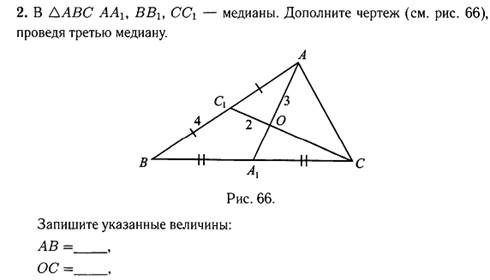
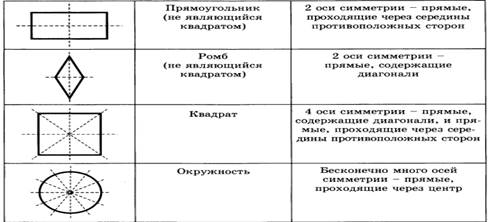
2. Заполните таблицу.

Фигура	Чертеж	Количество и расположение осей симметрии	Расположение центра симметрии
Равносторонний треугольник
Прямоугольник
Окружность

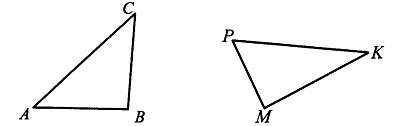
Подпишите длины! Проверьте соотношение

__________________________________________________

А=__________

2. Заполните таблицу.

Фигура	Чертеж	Количество и расположение осей симметрии	Расположение центра симметрии
Равнобедренный треугольник
Квадрат
Окружность

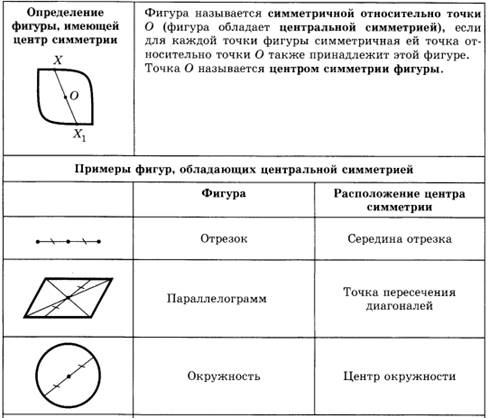
Сколько осей симметрии имеет фигура рис 1-3? Сколько центров симметрии имеет фигура рис 2,3?

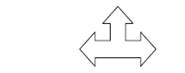
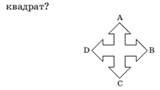
            Рис. 1                                     рис.2.                         рис.3.