
Поурочные разработки по Алгебре и началам анализа 11 класс к УМК А. Г. Мордковича - 2011 год
Показательная функция, ее свойства и график - Показательная и логарифмическая функции
Цель: рассмотреть показательную функцию, ее свойства и график.
Ход уроков
I. Сообщение темы и цели уроков
II. Изучение нового материала
Ранее было определено понятие степени числа с целым и рациональным показателями. Определим теперь степень числа с иррациональным показателем, и тогда степень числа будет определена для произвольного действительного показателя.
Пример 1
Обсудим,
что понимается под числом ![]() Число
r = √2 является иррациональным числом и может быть представлено в виде
бесконечной десятичной дроби:
Число
r = √2 является иррациональным числом и может быть представлено в виде
бесконечной десятичной дроби: ![]() где
а1 и а2, а3, а4, ..., аn,
... - цифры целой и дробной части числа соответственно.
где
а1 и а2, а3, а4, ..., аn,
... - цифры целой и дробной части числа соответственно.
Очевидно,
что ![]() где
где ![]() -
рациональное приближение числа r с избытком. Например, для r = √2 эти
приближения равны (соответственно, для одной, двух, трех и т. д. значащих
цифр): rn: 1; 1,4; 1,41; 1,414; 1,4142; 1,41421; r'n: 2;
1,5; 1,42; 1,415; 1,4143; 1,41422;
-
рациональное приближение числа r с избытком. Например, для r = √2 эти
приближения равны (соответственно, для одной, двух, трех и т. д. значащих
цифр): rn: 1; 1,4; 1,41; 1,414; 1,4142; 1,41421; r'n: 2;
1,5; 1,42; 1,415; 1,4143; 1,41422;
Для
n значащих цифр разница между приближением r’n с избытком и
приближением rn с недостатком число r составляет величину ![]() и
уменьшается с увеличением числа значащих цифр. Это позволяет оценить
иррациональное число r сколь угодно точно рациональными числами rn,
r’n.
и
уменьшается с увеличением числа значащих цифр. Это позволяет оценить
иррациональное число r сколь угодно точно рациональными числами rn,
r’n.
Так
как понятие степени с рациональным показателем было уже введено, то число 3r удовлетворяет
неравенству: ![]()
![]()
С
увеличением n число 3r может быть оценено сколь угодно точно
числами ![]() При
больших п можно считать, что
При
больших п можно считать, что ![]() что
и считается степенью числа с иррациональным показателем.
что
и считается степенью числа с иррациональным показателем.
Дадим точное определение степени с иррациональным показателем (заметим, что в школьном курсе это определение не приводится, но при учебе в вузе требуется).
Определение 1. Степенью a’ положительного числа a(a > 0) с иррациональным показателем r называется предел числовой последовательности степеней этого числа с рациональными показателями rn или r'n, являющимися n-значными приближениями числа r по недостатку или избытку:
![]()
После введенного определения степень числа с произвольным действительным показателем определена.
Пример 2
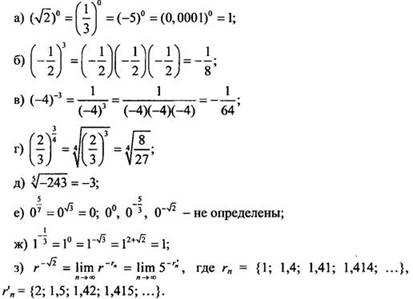
Теперь можно ввести понятие показательной функции.
Определение 2. Функция, заданная формулой у = ax (где a > 0, а ≠ 1, х - любое действительное число), называется показательной функцией с основанием а.
Составив таблицу значений показательной функции для различных значений аргумента, легко построить график такой функции. Приведем подобную таблицу и график функции у = 2х.
|
x |
-2 |
-1 |
0 |
1 |
2 |
|
y |
1/4 |
1/2 |
1 |
2 |
4 |
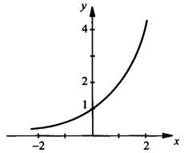
Перечислим основные свойства показательной функции.
1) Область определения - множество действительных чисел (-∞; +∞).
2) Определенной четности не имеет.
3) Монотонность: при 0 < a < 1 функция убывающая, при a > 1 функция возрастающая.
4) Функция ограничена снизу и не ограничена сверху.
5) Функция ни наименьшего, ни наибольшего значений не имеет.
6) Функция непрерывна.
7) Область значений - множество всех положительных чисел (0; +∞).
8) Выпукла вниз.
На рисунках приведены графики функций у = ax.
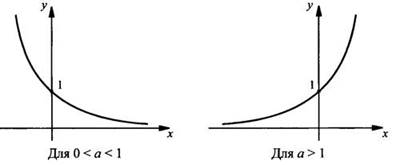
Отметим, что показательную функцию у = ax, а также ее график называют экспонентой. Прямая у = 0 (т. е. ось абсцисс) является горизонтальной асимптотой графика функции у = ax (т. е. для 0 < a < 1 х → +∞ и для a > 1 у → 0 при х → -∞). Для всех а график функции у = ax пересекает ось ординат в точке (0; 1).
Рассмотренные свойства показательной функции позволяют решать значительный круг задач.
Пример 3
Сравним
числа ![]()
Второе
число запишем в виде степени с основанием 2 и получим: ![]() Сначала
сравним показатели степеней. Так как √5 ≈ 2,2, то -3√5 <
-5,6. Функция у = 2х является возрастающей. Поэтому большему
значению аргумента соответствует большее значение функции. Тогда имеем:
Сначала
сравним показатели степеней. Так как √5 ≈ 2,2, то -3√5 <
-5,6. Функция у = 2х является возрастающей. Поэтому большему
значению аргумента соответствует большее значение функции. Тогда имеем: ![]() или
или ![]() т.
е. второе число больше.
т.
е. второе число больше.
Пример 4
Сравним
числа х и у, если верно неравенство ![]()
Используя
свойство степеней, запишем первое число в виде ![]() Тогда
данное неравенство имеет вид: (0,6)х > (0,6)y.
Так как функция (0,6)x убывающая, то показатели степеней
связаны неравенством противоположного знака, т. е. х < у.
Тогда
данное неравенство имеет вид: (0,6)х > (0,6)y.
Так как функция (0,6)x убывающая, то показатели степеней
связаны неравенством противоположного знака, т. е. х < у.
Пример 5
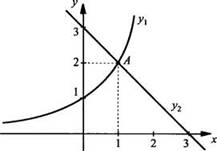
Графически решим уравнение 2х = 3 - х.
Построим графики показательной функции у1 = 2х и линейной функции у2 = 3 - х. Видно, что графики этих функций пересекаются в одной точке А, абсцисса которой х = 1 является решением данного уравнения (что легко проверяется подстановкой).
Пример 6
Построим график функции у = |2х - 2|.
Сначала построим график функции у = 2х - 2. Он получается смещением графика функции y = 2х на 2 единицы вниз.
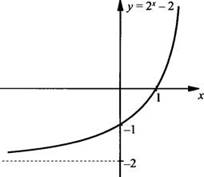
Затем построим график функции у = |2Х - 2|.
Для этого сохраняем часть предыдущего графика, для которой у ≥ 0. Ту часть графика, для которой у < 0, отражаем вверх относительно оси абсцисс.
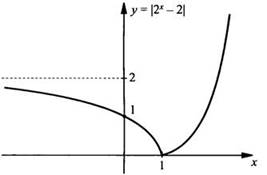
Пример 7
Построим
график функции ![]()
Данная
функция является сложной ![]() где
аргумент
где
аргумент ![]() является
функцией переменной х. Поэтому сначала построим график функции z(x), например
используя производную. Учтем, что функция нечетная и ее график проходит через
начало координат. Теперь перейдем к построению основного графика y(х).
является
функцией переменной х. Поэтому сначала построим график функции z(x), например
используя производную. Учтем, что функция нечетная и ее график проходит через
начало координат. Теперь перейдем к построению основного графика y(х).
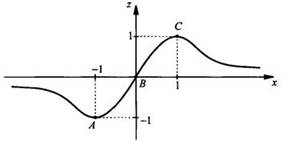
Как
видно из графика, при x → ∞ z → 0 и ![]() Поэтому
график функции y(x) имеет горизонтальную асимптоту у = 1. Рассмотрим также
точку минимума А (для которой х = -1 и z = -1), тогда
Поэтому
график функции y(x) имеет горизонтальную асимптоту у = 1. Рассмотрим также
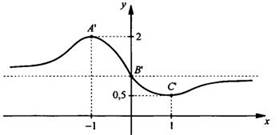
точку минимума А (для которой х = -1 и z = -1), тогда ![]() Строим
точку А' с координатами х = -1 и у = 2. Учтем точку В с координатами х = 0 и z
= 0, тогда
Строим
точку А' с координатами х = -1 и у = 2. Учтем точку В с координатами х = 0 и z
= 0, тогда ![]() Строим
точку В' с координатами х = 0 и у = 1. И наконец, рассмотрим точку С (для
которой х = 1 и z = 1), тогда
Строим
точку В' с координатами х = 0 и у = 1. И наконец, рассмотрим точку С (для
которой х = 1 и z = 1), тогда ![]() Построим
точку С с координатами х = 1 и у = 0,5. После изложенного строим окончательный
график функции у(х).
Построим
точку С с координатами х = 1 и у = 0,5. После изложенного строим окончательный
график функции у(х).
Отметим, что рассмотренные примеры основывались на свойствах показательных функций у = ax, в первую очередь на свойстве монотонности. Сформулируем это свойство в виде, полезном при решении уравнений и неравенств.
Теорема 1. Равенство at = aS справедливо только при t = S.
Теорема 2. Если a > 1, то неравенство at > aS справедливо только при t > S, неравенство at < aS - только при t < S. Другими словами, неравенство at v aS выполнено, если аргументы функций tи S связаны неравенством того же знака t v S.
Теорема 3. Если 0 < a < 1, то неравенство at > aS справедливо только при t < S, неравенство at < aS - только при t > S. Другими словами, неравенство at v aS выполнено, если аргументыфункций t и S связаны неравенством противоположного знакаt ^ S.
Разумеется, t и S могут быть и числами, и некоторыми функциями, зависящими от х.
Пример 8
Решим
неравенство ![]()
Так как основание показательной функции a = 1/3 удовлетворяет условию 0 < а < 1, то по теореме 3 аргументы функций связаны неравенством противоположного знака: х3 - х2 + 4 ≤ 4х. Решим это кубическое неравенство методом интервалов. Запишем его в виде: х3 - х2 - 4х + 4 ≤ 0, или х2(х - 1) - 4(х - 1) ≤ 0, или (х – 1)(x2 - 4) ≤ 0, или (х – 1)(x – 2)(x + 2) ≤ 0. Решение этого неравенства х ∈ (-∞; -2] U [1; 2].
![]()
На следующих уроках более детально будет рассмотрено решение показательных уравнений и неравенств.
Заметим, что показательные функции часто используются как математические модели реальных ситуаций в различных областях науки и отраслях техники.
III. Контрольные вопросы
1. Поясните понятие степени с иррациональным показателем.
2. Дайте определение показательной функции.
3. Приведите графики показательной функции.
4. Перечислите основные свойства показательной функции (фронтальный опрос).
5. Теоремы о показательных уравнениях и неравенствах (фронтальный опрос).
IV. Задание на уроках
§ 39, № 3 (а, 6); 10 (б, г); 11; 14; 19 (а); 20 (в, г); 22 (а, б); 24 (в); 26; 29 (а); 30 (б); 31 (а, б); 36; 41 (в, г); 42 (а, г).
V. Задание на дом
§ 39, № 3 (в, г); 10 (а, в); 15; 19 (б); 20 (а, б); 22 (в, г); 24 (а); 27; 29 (б); 30 (в); 31 (в, г); 37; 41 (а, б); 42 (б, в).
VI. Творческие задания
Постройте график функции, уравнения или неравенства:
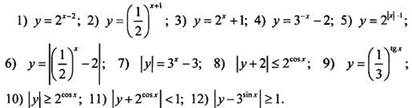
Указание: используйте способы преобразования графиков функций и определение модуля.
VII. Подведение итогов уроков
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.