Алгебра

Поурочные разработки по Алгебре и началам анализа 11 класс к УМК А. Г. Мордковича - 2011 год

Логарифмические уравнения - Показательная и логарифмическая функции

Цели: систематизировать логарифмические уравнения; рассмотреть способы их решения.

Ход уроков

I. Сообщение темы и цели уроков

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (письменный опрос).

Вариант 1

1. Докажите теорему о логарифме произведения двух чисел.

2. Вычислите: 

3. Постройте график функции у = log₂(4x).

Вариант 2

1. Докажите теорему о логарифме частного двух чисел.

2. Вычислите: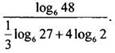 

3. Постройте график функции 

III. Изучение нового материала

Логарифмические уравнения

Логарифмическим уравнением называют уравнение, в котором неизвестная входит только в аргументы логарифмических функций при некоторых постоянных основаниях.

Пример 1

а) Уравнение  логарифмическое.

б) Уравнение  не является логарифмическим.

Так как логарифмическая функция log_a х монотонна и ее область значений (-∞; ∞), то простейшее логарифмическое уравнение log_a x = b имеет единственный корень. Именно к видуlog_a x = bнадо сводить более сложные уравнения. Типы и способы решения логарифмических уравнений схожи с показательными уравнениями.

1. Простейшие уравнения

Пример 2

Решим уравнение 

По определению логарифма получаем уравнение:  или 2x² – 2x - 1 = 3, или х² - х - 2 = 0. Корни этого квадратного уравнения x₁ = -1 и х₂ = 2 также являются решениями данного логарифмического уравнения.

Пример 3

Решим уравнение  Несмотря на громоздкость этого уравнения, оно тоже относится к простейшим. Используя определение логарифма, получаем:  или  Вновь используем определение логарифма. Имеем:  откуда  Еще раз применяя определение логарифма, находим 

Особенностью логарифмических уравнений (в отличие от показательных) является появление посторонних решений. Это связано с расширением ОДЗ уравнения в ходе его преобразований. Поэтому полученные корни необходимо проверять подстановкой или следить за изменением ОДЗ.

Пример 4

Рассмотрим уравнение 

Его ОДЗ задается неравенствами  Решая эту систему неравенств, получаем: 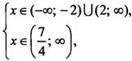 откуда х ∈ (2; ∞). Так как в данном уравнении равны логарифмы двух величин, то равны и сами величины. Получаем квадратное уравнение: х² - 4 = 4х - 7 или x² – 4x + 3 = 0. Очевидно, ОДЗ этого уравнения х ∈ (-∞; ∞), т. е. произошло расширение ОДЗ по сравнению с первоначальным уравнением. Корни квадратного уравнения x₁ = 1 и х₂ = 3. Однако в ОДЗ исходного уравнения попадает только число х = 3, которое и является его решением. Корень х = 1 является посторонним и возник при расширении ОДЗ.

2. Уравнения, решаемые их преобразованиями

Во многих случаях при решении логарифмического уравнения его необходимо преобразовать, используя основные свойства логарифмов.

Пример 5

Решим уравнение 

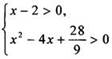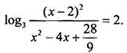ОДЗ уравнения определяется условиями  (решать эту систему неравенств не будем). Сведем данное уравнение к простейшему. Запишем уравнение в виде:  или  По определению логарифма получаем: 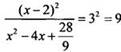 или х² - 4х + 3 = 0. Корни этого квадратного уравнения х₁ = 1 и х₂ = 3. В ОДЗ данного уравнения входит только решение х = 3.

Пример 6

Решим уравнение 

ОДЗ уравнения задается условиями  откуда х ∈ (11; ∞). Запишем уравнение в виде:  или  или  По определению логарифма получаем квадратное уравнение: х² - 13х + 22 = 36 или х² - 13х - 14 = 0. Корни этого уравнения х₁ = 14 и х₂ = -1 (не входит в ОДЗ).

3. Уравнения, решаемые разложением на множители

Пример 7

Решим уравнение  Перенесем все члены уравнения в левую часть, сгруппируем их и разложим эту часть на множители. Получаем:  или  или  или  Произведение множителей равно нулю, если один из них равен нулю, а остальные множители имеют смысл. Получаем два уравнения:

а)  тогда log₂(3x² - 5) = 2 и 3х² - 5 = 4, откуда х² = 3 и х = ±√3. Однако при x = -√3 второй множитель не имеет смысла.

б)  тогда  и х - 1 = 1 и х = 2. Для этого значения х первый множитель определен.

Итак, данное уравнение имеет два корня: x₁ = √3 и х₂ = 2.

4. Уравнения, решаемые с помощью замены неизвестной

Этот способ широко используется при решении любых типов уравнений.

Пример 8

Решим уравнение 

Сделаем замену у = log₂(2x - 1). Тогда получаем квадратное уравнение у² + у - 2 = 0. Заметим, что ОДЗ исходного уравнения устанавливать нет необходимости, так как если уравнение у² + у - 2 = 0 имеет решения (его корни у₁ = -2, у₂ = 1), то это означает, что log₂(2x - 1) существует, т. е. 2х - 1 > 0.

Таким образом, приходим к совокупности уравнений  или 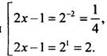 Отсюда: 

В случае однородных уравнений приходится вводить две новые переменные.

Пример 9

Решим уравнение 

ОДЗ уравнения задается условиями  откуда х > 10/3. Введем две новые переменные:  и получим однородное уравнение: a² = 3ab - 2b² или a² -3ab + 2b² = 0. Решения этого уравнения а = b и а = 2b. Вернемся к старой переменной. Получаем два уравнения:

а)  тогда 10 - 3х = 4 - х, откуда х = 3 (входит в ОДЗ).

б)  или log₂(10 - 3x) = log₂(4 - x)², тогда 10 - 3х = (4 - х)² или 0 = х² - 5х + 6, откуда x₁ = 3 и х₂ = 2 (оба корня входят в ОДЗ).

Итак, данное уравнение имеет два решения: х = 3 и х = 2.

5. Уравнения, решаемые с помощью его специфики

Встречаются задачи, решение которых основано на свойствах входящих в них функций.

Пример 10

Решим уравнение 

Исследуем монотонность функций, входящих в уравнение. Функция у₁= log₂x возрастающая, функция  убывающая. Очевидно, если данное уравнение имеет корень, то он единственный. Далее этот корень надо подобрать (угадать). Подбором находим х = 4.

В ряде случаев встречаются уравнения, содержащие логарифмы неизвестных, но не являющиеся логарифмическими. Тогда используются специальные приемы, суть которых станет понятна из примеров.

Пример 11

Решим уравнение 

Найдем логарифм по основанию 3 от обеих частей данного уравнения и используем свойства логарифмов. Получаем:  или  или  или  Введем новую неизвестную у = log₃ х и получим квадратное уравнение: 1 + у = 2у² или 0 = 2у² - у - 1. Его корни у₁ = 1 и у₂ = -1/2. Вернемся к старой неизвестной х. Имеем два уравнения: log₃ х = 1 (корень x₁ = 3¹ = 3) и log₃ х = -1/2 (тогда ).

Пример 12

Решим уравнение 

Используя основное логарифмическое тождество, запишем основание степени в виде  Тогда данное уравнение имеет вид:  или  или  Получаем:  и log₅ x = 4, откуда х = 5⁴ = 625.

6. Уравнения, решаемые графически

При решении уравнений и исследовании их корней часто используется графический способ.

Пример 13

Определим число корней уравнения  и найдем меньший из них.

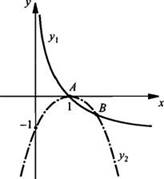
Запишем уравнение в виде  и построим графики функций  (сплошная линия) и у₂ = -(х - 1)² (штрихпунктирная линия). Видно, что графики этих функций пересекаются в двух точках А и В. Следовательно, уравнение имеет два решения. Абсцисса точки А меньше абсциссы точки В. Поэтому меньший корень уравнения х = 1.

Системы логарифмических уравнений

При решении систем логарифмических уравнений используются те же приемы, что и при решении отдельных уравнений. Поэтому остановимся только на некоторых способах решения систем уравнений.

1. Сведение к системе алгебраических уравнений

Пример 14

Решим систему уравнений  Заменим эту систему системой линейных уравнений:  Сложив уравнения, найдем 8х = 27 или х = 27/8. Тогда из первого уравнения найдем  Итак, решение системы 

Во многих случаях перед тем как свести систему к системе алгебраических уравнений приходится выполнить тождественные преобразования уравнений системы.

Пример 15

Решим систему уравнений 

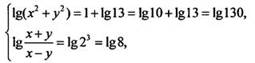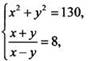Запишем систему в виде  или  или  решая которую найдем:  причем второе решение не удовлетворяет ОДЗ второго исходного уравнения (т. е. не является решением).

2. Подстановка неизвестного из одного из уравнений

Очень распространенный способ решения систем уравнений, при котором одно из неизвестных выражается через другое из наиболее простого уравнения и подставляется в другое. Полученное уравнение одной неизвестной затем решается.

Пример 16

Решим систему уравнений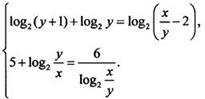 

Решим сначала второе уравнение системы, сделав замену  или z² - 5z + 6 = 0, корни которого z₁ = 2, z₂ = 3. Отсюда получаем:  или  или х = 4у и х = 8у.

Обратимся теперь к первому уравнению системы, которое можно записать в виде  В случае  имеем: у² + у - 2 = 0, т. е. у₁ = 1, у₂ = -2 (не удовлетворяет ОДЗ) и x₁ = 4. В случае x/y = 8 получаем: у² + у - 6 = 0, т. е. у₃ = 2, у₄ = -3 (не удовлетворяет ОДЗ) и х₃ = 16. Итак, решения системы: (4; 1); (16; 2).

3. Замена переменных

Замена переменных является одним из наиболее распространенных способов решения уравнений, неравенств, систем уравнений.

Пример 17

Решим систему уравнений 

Введем новые переменные  Тогда имеем систему алгебраических симметричных уравнений  Такая система имеет решения (-1; 2) и (2; -1).

Вернемся к старым неизвестным х, у и получим две простейшие системы.

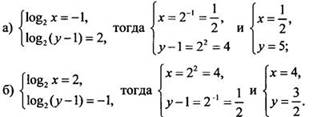
Итак, данная система имеет два решения 

IV. Задание на уроках

§ 44, № 2 (а); 4 (в); 7 (б); 8 (г); 10 (а); 12 (б); 13 (а, б); 14 (а); 15 (б); 16 (а, б); 18 (а); 19 (б); 20 (а); 21 (б); 22 (а).

V. Задание на дом

§ 44, № 2 (г); 4 (б); 7 (г); 8 (б); 10 (б); 12 (а); 13 (в, г); 14 (б); 15 (а); 16 (в, г); 18 (б); 19 (а); 20 (б); 21 (а); 22 (б).

VI. Подведение итогов уроков