Алгебра. 8 класс. свойства степени с натуральным показателем.

Тема: «Свойства степени с натуральным показателем»

 

Ход урока

I.      Организационный момент:

 

Постановка целей и задач урока

Здравствуйте, ребята! Сегодня на уроке мы повторим, обобщим и приведем в систему изученный материал. Ваша задача показать свои знания свойств степени с натуральным показателем и умение применять их при выполнении различных заданий.

 

 

 

II.     Актуализация опорных знаний. Систематизация теоретического материала.

 

Начнем мы урок с повторения свойств степени, с натуральным показателем

 

- К доске вызываются 4 ученика.

Вы должны выполнить задание, выбрать карточку с числом, равным показателю, получившейся   в ответе степени. На обороте карточки – буква, ее запишите, рядом с соответствующим примером.

 

1 карточка                    2  карточка                              3  карточка         4карточка

1.  С⁵∙С³                         5. С¹⁴.С⁸                                 9.С⁴ .С⁵  . С                13.(С⁴ )⁴                    

2.  С⁸: С⁶                        6.С⁷:С⁴                                 10.С¹⁶ .С⁸               14.С²⁰:С³

3.  (С⁴)³                           7. (С⁴)³ ∙С                              11. (С³)⁵                15.С⁵.С⁹:С³

4.  С⁵ ∙С³ : С³                  8.С².С³.С                              12.С⁸:С⁶:С     

(Слайд 2)      

 

Пока ребята у доски выполняют задание, мы с вами вспомним некоторые теоретические вопросы по данной теме. Поднимайте руку и отвечайте на вопрос.

 

 

-Теоретический опрос:

· Сформулируйте определение степени числа  с натуральным показателем.

· Из чего состоит степень?

· О чем говорит основание степени?

· О чем говорит показатель степени?

· Сформулируйте правила умножения, деления степеней с одинаковыми основаниями, правило возведения степени в степень; правило возведения в степень произведения, дроби.

· Что можно сказать о квадратах противоположных чисел?

· Что можно сказать о кубах противоположных чисел?

· -Степень положительного числа  есть число …

· -Степень отрицательного числа с  нечётным показателем  есть число …

· -Степень отрицательного числа с  чётным показателем  есть число …(Слайд 5)

Молодцы!

А теперь посмотрим, что же получилось у ребят. Если все выполнено  правильно ,то должно получиться  МИХАИЛ  ЛОМОНОСОВ

Спасибо ребята, садитесь!

Это М.В.Ломоносову  принадлежат слова

 «Пусть кто – нибудь  попробует вычеркнуть из математики степени, и он увидит, что без них далеко не уедешь». М.В.Ломоносов

Первый крупный русский учёный-естествоиспытатель. Яркий пример «универсального человека» : энциклопедист, физик и химик. учёный-энциклопедист, основатель Московского университета.

 

Сейчас поработаем парами. Запишите в тетради примеры со слайда. И выполните задания.

 

 

 -  Используя  правила, сравните с нулём значения выражения.

 

             (-5) ⁴ ;

         

             -5 ⁴;

       

          -5² +25;

      

            (-3) ⁵;

 

      (-3) ⁴ + (-81);    

 

     - (3 ∙ 4)²;              

 

       (-3,5) ³· 0;                   

 

Давайте проверим (каждая пара называет ответ на одну строчку задания, другие пары проверяют, соглашаются или нет, дискуссируют).

 

Ребята давайте рассмотрим пример (записывает на доске):

5³/5³ т.е. число делим само на себя, и результатом такого деления будет 1.

Но, с другой стороны, воспользуемся свойством степени: 5³/5³=5^3-3=5⁰

Что, тогда получается: Ребята делают вывод, что любое число в нулевой степени, есть 1.

 

- Дайте определение степени с нулевым показателем?

 

Закончите запись   

                                             а ^п • а ^k = ……. ;        а ^п : а ^k = ……. , a0, n>k;

                                      (a bc)ⁿ = ……. ;         (aⁿ) ^k = ………

 

          -  Из этих свойств вытекают правила действий со степенями.  Сформулируйте эти правило самостоятельно.

Формулируют САМИ правила в соответствии со свойствами степеней. Обсуждают.

1)  Проверка заданий по карточкам

Запишите ответ в виде степени с основанием  С  и вы узнаете фамилию и имя великого французского математика, который первым ввел понятие степени числа.

Угадайте фамилию ученого математика.

		1.	С14∙ С8
1.	С5∙С3	2.	С7 : С5
2.	С8: С6	3.	(С4)3 ∙С
3.	(С4)3	4.	С4∙ С5∙ С0
4.	С5 ∙С3 : С6	5.	С16 : С8
		6.	(С3)5

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Ответ: РЕНЕ ДЕКАРТ

Р

Ш

М

Ю

К

Н

А

Т

Е

Д

С8

С5

С1

С40

С13

С12

С9

С15

С2

С22

 

 

 

 

На каком уроке мы с вами познакомились с этим ученым?

На геометрии.

Что изобрел Рене Декарт?

Прямоугольную систему координат!

Вот теперь мы свстретились с ним и на алгебре!!!

 

 

 

 

 

 

Декарт Рене (1596-1650) — французский философ, математик, физик и физиолог. Декарту принадлежит заслуга создания современных систем обозначений: он ввел знаки переменных величин (x, y, z...), коэффициентов (a, b, c...), обозначение степеней (a², x^-1...).

 

III. Основная часть.

                                      

2)    Представьте в виде степени выражения.   (Выполняют самостоятельно в тетрадях) 

 

 

 

 

 

 

                                                                                                                  

 

 

 

 

 

 

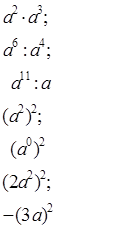  - Проверим.

      Каждый ученик проверяет работу соседа, используя  

 

3)     - Ученик, выполняя преобразования выражений, допустил ошибки. Исправьте ошибки и объясните, какие определения, свойства и правила не знает ученик.  

 

          5 • 5 • 5 • 5 = 4 ⁵;                     2 ³ • 2 ⁷ = 4 ¹⁰;

          7¹ = 1;                                     2 ³⁰ : 2 ¹⁰ = 2 ³;

          4 ⁰ = 4;                                   (2х) ³ = 2х ³;

          2 ³ • 2 ⁷  = 2 ²¹;                        (а ³) ² = а ⁵.

 

 

 

4)    -  Подумайте, чем можно заменить  ?  

 

             х⁵ •   = х¹⁷;                 

             : k ⁴ = k ¹¹;                

                                  

           7 ¹² •  = 7 ¹⁹;              

                               

 

5)Самостоятельная работа(по группам:а)-1 ряд,б)-2 ряд,в)-3 ряд)

 

   1)  Выполните возведение в степень:

          

 

 

  2)  Представьте выражение в виде степени с указанным показателем: 

      

 

  

  в) 0,0016х²⁰у²⁴ =(…)⁴   

 

3) Представьте выражение в виде степени:                                   

 

 

 

6) (слайд24)

 Сравните, не выполняя вычислений. Найдите верные неравенства. Из соответствующих им букв составьте фамилию архитектора, по проекту которого в 1825 году было построено здание Большого театра в Москве:

 

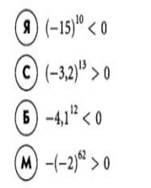
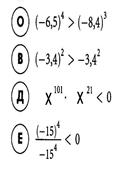
Бове. По проектам этого известного архитектора также были построены здания Манежа и Триумфальные ворота, создан проект Александровского сада.

7)  Выполните умножение (по групам :2 парты-1 групп)(слайд26)

1. о,2а²в⁴ .0,3ав

2. -а⁴в⁹ . (-ав) .44а²в⁴   

Дополнительные задания.  Выполните преобразования. Используя найденные ответы, запишите в таблицах два высказывания Козьмы Пруткова(по рядам)

-Проверка (слайд 28)

 

IV:  Подведение итогов, оценивание, выставление отметок.

  

 Рефлексия (3 мин).()

Ученикам выдаются заранее приготовленные листочки с незаконченными высказываниями, которые нужно закончить относительно данного урока.

1. Я умею …

2. Я понял…

3. Мне было интересно ….

4.Для меня сложно ….., потому что

V. Домашнее задание

№1

-  Подумайте, чем можно заменить  ?  

 

             n ¹⁵:  = n ⁵;                        

             b ² •  • b ⁸ = b ²⁴;

                                          

           5 ¹² • 5 ³ = 5 ¹⁹;                   

                                       

         

 

 

                                  

 

Скачано с www.znanio.ru