алгебра и начало анализа

Разработка открытого урока

по алгебре:

«Разложение многочлена на множители способом группировки»

7 «Г» класс

Сеит-Нафе С.Н.

Ноябрь 2014

Тема: «Разложение многочлена на множители способом группировки»

Цель урока:

·                          Научить применять на практике   различные способы разложения многочлена на множители;

·                          развивать навыки теоретического мышления при помощи различных приемов; различных способов разложения;

·                          развивать умение работать в парах.

Ход  урока:

I.                  Организационный момент. Создание коллаборативной среды.

Прием «Дружеское пожелание»

Здравствуйте ребята и уважаемые гости. Сегодня у нас урок  закрепления материала по теме «Разложение многочлена на множители способом группировки». Девиз нашего урока «Мало иметь хороший ум, главное – хорошо его применять».  Сегодня нам как раз нужно как можно более эффективно применять свойства нашего ума при решении примеров и заданий.

II.               Проверка домашней работы.

№259

1)  (ах+ау)+(вх+ву)=(х+у)(a+b)

2)( ах-ау)+( вх-ву) =(x-y)(a+b)

3)(а²+ав)+(ас+вс)=(a+b)(a+c)

4)( ах+ау)+(6х+6у)=(x+y)(a+6)

5)(1-х)+(в-вх)=(1-x)(1+b)

III.Актуализация опорных знаний учащихся

Устная работа. (3мин)

1) x² *x;   2) –2aba;       3) m⁵:m²=m³;  4) –bca*bca²;  5)(2n²)³=8n⁶ ;  6)f⁵*f^-5;

7)2014*36-2014*34=2014*2=4028 

IV.В тетрадях запишем число и тему урока «Разложение многочлена на множители способом группировки»

1.Графический тест  (теоретический материал).

1.     Одночленом называют сумму числовых и буквенных множителей. ––

2.     Буквенный множитель одночлена, записанного в стандартном виде, называют коэффициентом одночлена. ––

3.     Сумма показателей степеней всех букв входящих в одночлен называется степенью одночлена.

4.     Одинаковые или отличающиеся друг от друга только коэффициентами члены многочлена называются  подобными членами.

5.     Многочлен, в котором отсутствуют подобные члены и каждый из них одночлен стандартного вида называется многочленом стандартного вида.

6.     В результате умножения многочлена на одночлен получается одночлен. ––

7.     Чтобы раскрыть скобки, перед которыми стоит знак “+”, скобки надо опустить, сохранив знак каждого члена, который был заключен в скобки.

8.     Когда раскрываем скобки, перед которыми стоит знак “-”, скобки опускаем, и знаки членов, которые были заключены в скобки, меняют на противоположные.

Ответ:- -^ ^ ^ - ^ ^

Выставите себе оценки:       

  «5» - ошибок нет      «4» - две ошибки      «3» - четыре ошибки      «2» - больше четырех ошибок.

 V. Работа в группах.(10 мин) Объединяются в группы по 4 человека. С каждой группы по одному ученику выходят к доске и решают примеры. Остальные учащиеся решают примеры на местах, записывая решение в тетрадь.

 Разложите на множители (ответы к заданиям закодированы).

1.        ax + 2a + 3x + 6

2.        5z (x + y) – x – y

3.        x (a + y) + ay + y²

4.        10ay – 5cy + 2ax – cx

5.        x² – 2x – xy + 2y

6.        6cy + 15cx + 4 ay + 10ax

Ответы:

Историческая справка.( выступление ученицы)

Таинственный и знаменитый лист Мебиуса (иногда говорят лента Мебиуса) придумал в 1858 году немецкий геометр Август Фердинанд Мебиус (1790–1868), ученик “короля математиков” Гаусса. Мебиус был первоначально астрономом, как Гаусс и многие другие из тех, кому математика обязана своим развитием. В те времена занятия математикой не встречали поддержки, а астрономия давала достаточно денег, чтобы не думать о них, и оставляла время для собственных размышлений. И Мебиус стал одним из крупнейших геометров XIX века. В возрасте 68 лет ему удалось открытие односторонних поверхностей, одна из которых – лист Мебиуса.

VI. Физ минутка.

VII. Игровой момент.  Пазлы «Тарсия»

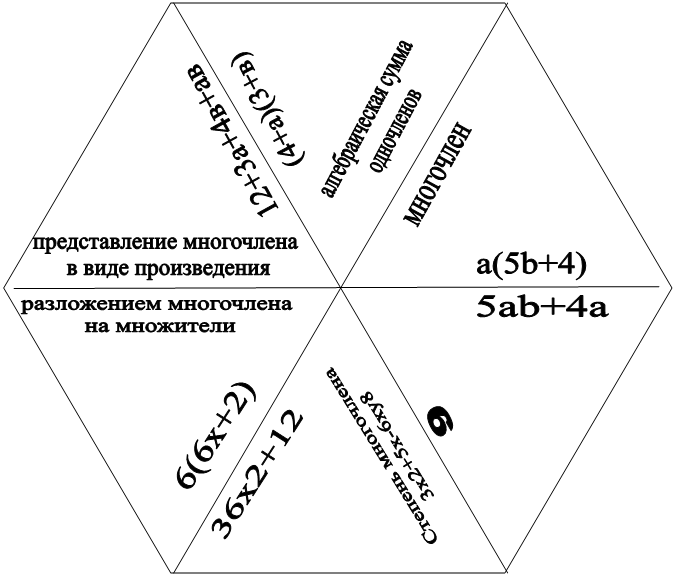
VIII. Задание на дом №260(3,4), №259(6,7) , провести эксперимент с листом Мебиуса

IХ. Подведение итога. Рефлексия.  «Светофор»

Отрабатывали, какую тему?

Сколько способов разложения мы с вами выучили?

С помощью сигнальных карточек оцените свои знания:

Красный-

Желтый-

Зеленый-

Оценочный лист

Ф.И.____________________________________________класс______дата_____________