алгебра и начало анализа

Применение формулы разности квадратов
при решении различных задач

Цели: закрепить изученный материал; выполнить более сложные задания на применение формулы разности квадратов; подготовить учащихся к контрольной работе.

Ход урока

I. Устная работа.

Какие из следующих многочленов можно разложить на множители? Если возможно, сделайте это.

а) а² – 49;                          г) х² + 4х – 4;                ж) 16х² – 8х + 1;

б) х² + ;                           д)  + n²;                    з)  – y²;

в) х² – 2х + 1;                     е) х² + 3х + 9;

II. Формирование умений и навыков.

Все задания можно разбить на две группы. В 1-ю группу войдут задания на применение формулы разности квадратов. А во 2-ю группу – задания на все известные учащимся формулы сокращенного умножения, чтобы подготовить их к контрольной работе.

1-я группа

1. № 894.

Решение:

(Записи лучше вести подробно, Скобки, перед которыми стоят знаки «минус» (–) и «плюс» (+), открывать не сразу.)

а)

б)
= (8 – b – 1) (8 + b + 1) = (7 – b) (9 + b);

в)
= (4a – 7) (4a + 1);

г)
= (5 – a – 7) (5 + a + 7) = (–a – 2) (a + 12) = – (a + 2) (a + 12).

2. № 897 (а, б).

Решение:

а) (x – 2y)) =
= (2x + y – x + 2y) (2x + y + x – 2y) = (x + 3y) (3x – y);

б)
= (a + b – b – c) (a + b + b + c) = (a – c) (a + 2b + c).

3. № 898.

Решение:

Разложим на множители данное выражение:

Поскольку один из множителей произведения 7 (2п + 7) делится на 7, то и всё произведение делится на 7.

2-я группа

1. Упростите выражение.

а)                             г) (3a + 4) (4 – 3a) – a (5 – 9a);

б)                     д)

в)                        е) y (4 – y) – 2 (y + 3) (y – 3).

2. Решите уравнение.

а)

б)

Некоторым сильным учащимся дополнительно можно предложить выполнить задания на карточках.

Карточка 1

1. Вычислите наиболее рациональным способом.

.

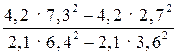2. Решите уравнение  x³ + 2x² – 4x – 8 = 0.

3. Докажите, что разность квадратов двух последовательных целых чисел равна сумме этих чисел.

Карточка 2

1. Вычислите наиболее рациональным способом.

.

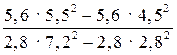2. Решите уравнение  x³ + 5x² – 25x – 125 = 0.

3. Докажите, что разность квадратов двух последовательных чётных чисел равна удвоенной сумме этих чисел.

Решение заданий на карточках

Карточка 1

1.

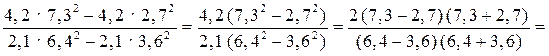
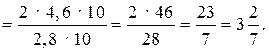
2. x³ + 2x² – 4x – 8 = 0.

   (x³ + 2x²) – (4x + 8) = 0;

    x² (x + 2) – 4 (x + 2) = 0;

   (x + 2) (x² – 4) = 0;

   (x + 2) (x – 2) (x + 2) = 0;

    х + 2 = 0    или    х – 2 = 0;

    х = –2        или    х = 2.

Ответ: –2; 2.

3. Обозначим два последовательных целых числа за п и п + 1. Согласно условию задачи нужно доказать следующее тождество:

Преобразуем левую часть равенства:

Доказано.

Карточка 2

1.

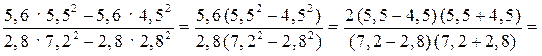
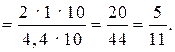
2. x³ + 5x² – 25x – 125 = 0.

   (x³ + 5x²) – (25x + 125) = 0;

    x² (x + 5) – 25 (x + 5) = 0;

   (x + 5) (x² – 25) = 0;

   (x + 5) (x – 5) (x + 5) = 0;

    х + 5 = 0    или    х – 5 = 0;

    х = –5        или    х = 5.

Ответ: –5; 5.

3. Пусть 2п и 2п + 2 – два последовательных чётных числа. Найдем разность их квадратов.

Найдем удвоенную сумму чисел 2п и 2п + 2:

2 (2n + 2n + 2) = 2 (4n + 2).

Получили одинаковые выражения, то есть утверждение доказано.

III. Итоги урока.

– Назовите известные вам формулы сокращенного умножения.

– Когда  эти  формулы  применяются  слева  направо,  а  когда  справа налево?

– Всегда ли можно разложить на множители разность квадратов двух выражений?

– Когда можно разложить на множители трёхчлен?

Домашнее задание: № 896; № 897 (в, г); № 899; № 975 (б, г, е, з).