Алгебра и начало анализа

Тема «Среднее арифметическое, размах и мода ряда чисел.»

                                             

 

Цели урока :

-закрепление приобретенных по теме знаний и умений находить среднее арифметическое,

размах и моду ряда чисел;

-развитие устной и письменной речи учащихся ;потребности читать математическую

литературу;

-воспитание организованности , дисциплинированности, ответственности за свой

труд.

Ход урока

1.Организационный момент.

Учитель.  Вы познакомились с такими простейшими статистическими характеристиками как среднее арифметическое, размах и мода.

Ваша задача на этом уроке: применить полученные  теоретические знания и практические навыки  при выполнении соответствующих заданий.

2.Актуализация

 

Устная работа.

Дидактическая игра «Светофор»

Учащиеся работают с помощью сигнальных карточек:

красная- «нет»

желтая- «не знаю»

зеленая- «да»

Теоретический тест.

 

    1.Среднее арифметическое ряда чисел-это частное от деления суммы этих чисел на число слагаемых?  (Да)

     2. Среднее арифметическое ряда чисел может не совпадать ни с одним из этих чисел ? (Да)

     3. Можно определить среднюю урожайность зерновых и бахчевых культур в фермерском

хозяйстве ?  ( Нет)

     4. Можно определить средний суточный удой молока от одной коровы на ферме ?  (Да)

     5. Размахом ряда чисел называется сумма наибольшего и наименьшего из этих чисел. (Нет)

     6. Любой ряд чисел имеет моду ?  (Нет)

     7. Ряд чисел может иметь только одну моду ?  (Нет)

     8. Мода не совпадает ни с одним из чисел ряда ?  (Нет)

 

3.Закрепление  изученного  материала.

 

 

 №7.11.

В   таблице показано число деталей, изготовленных за сме­ну рабочими одной бригады:

№ п/п	Фамилия	Число деталей	№ п/п	Фамилия	Число деталей
1 2 3 4 5  6	Иванов Лазарев  Ильин Бережной Егоров Петров	38  42  36  45 48 45	7  8  9 10 11	Семенов Лукин Андреев Попов  Сурков	45  42 40 47 39

Для представленного в таблице ряда чисел найдите среднее арифметическое, размах и моду. Каков смысл каждого из этих показателей?

Решение.

.  Среднее арифметическое данного ряда чисел прибли­женно равно 42, размах ряда равен 48 — 36 = 12, мода равна 45. Значит, в среднем рабочие бригады вырабатывали по 42 дета­ли, наибольшее различие в выработке равно 12 деталям, чаще всего встречается выработка, равная 45 деталям.

 

  №7.12.  На соревнованиях по фигурному катанию судьи поставили спортсмену следующие оценки:

5,2, 5,4, 5,5, 5,4, 5,1, 5,1, 5,4, 5,5, 5,3.

Для полученного ряда чисел найдите среднее арифметиче­ское, размах и моду. Что характеризует каждый из этих по­казателей?

Решение.

  Среднее арифметическое равно 5,3, размах ряда равен 0,4, мода равна 5,4. Значит, средняя оценка, полученная спортс­меном, составляет 5,3 балла, наибольшее колебание в оценках отдельных судей равно 0,4 балла, преимущественной является оценка 5,4.

 

   №7.14.  В фермерском хозяйстве отведены под пшеницу три участ­ка, площади которых равны

12 га, 8 га и 6 га. Средняя уро­жайность на первом участке составляет 18 ц с 1 га, на вто­ром— 19 ц с 1 га, на третьем — 23 ц с 1 га. Чему равна средняя урожайность пшеницы в этом хозяйстве?

   Решение.

  Всего было собрано 18 • 12 + 19 • 8 + 23 • 6 ц. Общая площадь трех участков равна

  12 +8 + 6 га.  Средняя урожайность равна

18 • 12 + 19 • 8 + 23 • 6 , т.е . 506      ,что примерно 19,5 ц/га.

12 + 8 + 6                               26

 

  №7.17.  В таблице записаны результаты ежедневного измерения на метеостанции в полдень температуры воздуха (в градусах Цельсия) в течение первой декады марта:

Число месяца	1	2	3	4	5	6	7	8	9	10
Температура, °С	_2	-1	-3	0	1	2	2	3	4	3

Найдите среднюю температуру в полдень в эту декаду. Со­ставьте таблицу отклонений от средней температуры возду­ха в полдень в каждый из дней декады.

Решение.

. Средняя температура воздуха в полдень в эту декаду  равна Т°, где   Т :

                   -2-1-3+0+1+2+2+3+4+3   , или 0,9     

                                                                                       ₁₀                            

Отклонение равно t° — Т°, где t" — температура в данный день, Т° — средняя температура.

 

Таблица отклонений приведена ниже.

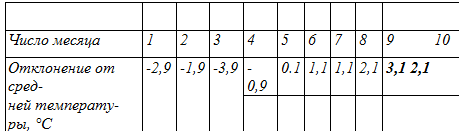
   №7.37(устно)  

   Сколько чисел в ряду, если его медианой служит:

а) пятнадцатый член; б) среднее арифметическое семнадца­того и восемнадцатого членов?

Решение.

  а) Если упорядочить данный ряд чисел, то до члена с номером n = 15 в полученном ряду будет находиться 14 членов. Так как 15-й член является медианой, то после него тоже на­ходится 14 членов. Всего в ряду 14 + 1 + 14, т. е. 29 членов.

б) Если упорядочить данный ряд чисел, то до 17-го члена в полученном ряду находится 16 членов. Так как 17-й и 18-й чле­ны расположены в упорядоченном ряду чисел посередине, то после 18-го члена также находится еще 16 членов. Всего в ря­ду 16 + 2 + 16, т. е. 34 члена.

 

  Для более подготовленных учащихся дополнительное задание.

 

     №7.36. 

 Среднее арифметическое некоторого ряда данных, состоя­щего из 10 чисел, равно 7.

К этому ряду приписали числа 17 и 18. Чему равно среднее арифметическое нового ряда чисел?

     Решение.

  Сумма членов данного ряда равна 7 • 10, т. е. равна 70. После того как к ряду данных приписали числа 17 и 18, сум­ма членов ряда стала равна 70 + 17 + 18 = 105. Всего в ряду ока­залось 12 членов. Значит, среднее арифметическое стало равно  105/12=8,75.

 

 

 

4.Самостоятельная работа

Вариант 1.

1.Определение  моды.

2. №7.2.  Найдите среднее арифметическое, размах и моду ряда чисел:

      б)  21, 18,5, 25,3, 18,5, 17,9;

 

Вариант 2.

1.Определение размаха.

2.№7.2.  Найдите среднее арифметическое, размах и моду ряда чисел:

     в)  67,1, 68,2, 67,1, 70,4, 68,2;

 

5.Подведение итогов.

Учитель.

1.  Что называется средним арифметическим ряда чисел? Может ли среднее арифметическое ряда чисел не совпадать ни с од­ним из этих чисел?

2.  Что называется размахом ряда чисел?

3.  Что называется модой ряда чисел? Любой ли ряд чисел имеет моду? Может ли ряд чисел иметь более одной моды? Может ли мода ряда чисел не совпадать ни с одним из этих чисел?

 

6.Домашнее задание.

    №7.3.

      Найдите среднее арифметическое, размах и моду ряда чисел:

     в)  61, 64, 64, 83, 61, 71, 70;

     г)  -4, -6, 0, 4, 0, 6, 8, -12.

   Решение.

 №7.3.   в) Среднее арифметическое приближенно равно 67,1 Размах ряда равен 12. Ряд имеет две моды: 61 и 64.

 

 

 

   №7.13.

    В аттестате о среднем образовании у четырех друзей — вы­пускников школы — оказались следующие оценки:

Ильин: 4, 4, 5, 5, 4, 4, 4, 5, 5, 5, 4, 4, 5, 4, 4;

 Семенов: 3, 4, 3, 3, 3, 3, 4, 3, 3, 3, 3, 4, 4, 5, 4;

Попов: 5, 5, 5, 5, 5, 4, 4, 5, 5, 5, 5, 5, 4, 4, 4;

Романов: 3, 3, 4, 4, 4, 4, 4, 3, 4, 4, 4, 5, 3, 4, 4.

С каким средним баллом окончил школу каждый из этих выпускников? Укажите наиболее типичную для каждого из них оценку в аттестате. Какие статистические характерис­тики вы использовали при ответе?

Решение.

       Средний балл равен среднему арифметическому, наибо­лее типичная оценка равна моде.

 Для Ильина средний балл равен  5*6+4*9

                                                                15      , что приближенно равно 4,4;  наиболее типичной является оценка 4.

Для Семенова средний балл равен  5+4*5+3*9

                                                                   15         , что приближенно равно 3,5; наиболее типична оценка 3.

. Для Попова средний балл равен  5*10+4*5

                                                                15         , что приближенно равно 4,7;

 

наиболее типична оценка 5.

 Для Романова средний балл равен  5+4*10+3*4

                                                                     15          . что приближенно равно 3,8;

 наиболее типична оценка 4.