

АЛГЕБРА
В ТАБЛИЦАХ

АВТОРЫ—СОСТАВИТЕЛИ:
Л.И.Звавич, А.Р.Рязановский [
8-е издание, стереотипное
ирофа
Москва 2004
УДК 371.672.8:512(083.4)
ББК 22.14я2
А45
Алгебра в таблицах. 7—11 кл.: Справочное по-
А45 собиё/Авт.-еост. Л. И. Звавич, А. Р. Рязановский. — 8-е изд., стереотип. — М.: Дрофа, 2004. — 96 с: ил.
18ВК 5—7107—8105—3
Пособие содержит таблицы по всем наиболее важным разделам школьного курса арифметики, алгебры, начал анализа. В таблицах кратко изложена теория по каждой теме, приведены основные формулы, графики и примеры решения типовых задач. В конце книги помещен предметный указатель.
Пособие будет полезно учащимся 7—11 классов, абитуриентам, студентам, учителям и родителям.
УДК 371.672.8:512(083.4)
![]() ББК
22.14я2 Учебное издание
ББК
22.14я2 Учебное издание
АЛГЕБРА В ТАБЛИЦАХ
7—11 классы
Справочное пособие
Авторы-составители:
Звавич Леонид Исаакович
Рязановский Андрей Рафаилович
Редактор М. Г. Циновская. Оформление А В. Кузнецов
Компьютерная верстка О. А Молочное, С. А. Белых
Технический редактор Н. И. Герасимова Корректор Г. И. Мосякина
Санитарно-эпидемиологическое заключение
N1» 77.99.02.953.Д.006315.08.03 от 28.08.2003.
Подписано к печати 05.02.04. Формат 84х1081/аг.
Бумага типографская. Гарнитура «Школьная». Печать офсетная. Усл. -печ. л. 5,04. Тираж 16 000 экз. Заказ № 1437. ООО «Дрофа». 127018, Москва, Сущевский вал, 49.
По вопросам приобретения продукции издательства «Дрофа» обращаться по адресу: 127018, Москва, Сущевский вал, 49.
Тел.;Д095) 795-05-50, 795-05-51. Факс: (095) 795-05-52.
От авторов
Тематические таблицы по всем наиболее важным разделам школьного курса арифметики, алгебры, начал анализа предназначены для школьников от седьмого до одиннадцатого классов. В каждой таблице кратко изложена теория конкретного вопроса (определения, теоремы, следствия, формулы); приводятся рисунки, графики, а также примеры решения наиболее принципиальных задач.
Таблицы помогут систематизировать знания, быстро и полно повторить основные моменты той или иной темы, с помощью предметного указателя найти нужные сведения. Таблицы можно разрезать и наклеить на плотную бумагу, оставив оборот чистым для пометок и добавлений (для такой операции надо иметь два экземпляра книги).
Ученик может:
— при подготовке к ответу или к контрольной работе прочитать и обдумать соответствующую таблицу, посмотреть предметный указатель;
— при решении задач по данной теме использовать соответствующую таблицу в качестве справочника;
— после уроков по данной теме самому внести в таблицу (на чистый оборот) добавления и изменения, отметить неизученные в классе вопросы;
— при итоговом повторении материала прежде всего просмотреть таблицы;
— устроить себе или своему товарищу зачет по таблице или предметному указателю;
— использовать таблицу как план ответа на устном экзамене или зачете.
Учитель может:
— использовать таблицы при подготовке к уроку;
— при объяснении нового материала подавать таблицы через кодоскоп (вывешивать на доске увеличенную таблицу), а еще лучше — положить книгу перед каждым учеником;
— проводить письменный или устный опрос по материалам таблиц или предметного указателя;
Абитуриент может: внимательно прочитав каждую таблицу •от корки до корки», уяснить, всем ли материалом он владеет в должной мере; при недостатке времени таблицы могут быть основным источником тематического повторения при подготовке к письменному экзамену. Если вас ждет и устный экзамен, то материал таблиц должен быть вашим лоцманом при чтении учебников. Родители ученика могут игпольэовать таблицу:
— для проверки знаний своего ребенка по той или иной теме:
— для проверки своих собственных знаний по школьной математике и для их расширения.
Таблицы могут быть использованы также будущими учителями, репетиторами, членами предметных комиссий институтов, студентами.
Авторы надеются что таблицы принесут пользу всем, кто будет использовать их в своих занятиях по математике.
Авторы выражают благодарность Борису Петровичу Пнгареву, внимательно прочитавшему таблицы и сделавшему ряд ценных аамечпний.
Таблица 1. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
Множество натуральных чисел Натуральные числа 1; 2; 3...
Множество целых чисел
|
2, |
N |
Целые числа состоят из натуральных, нуля и чисел, противоположных натуральным. |
|
0 |
||
|
|
||
|
|
2 |
Рациональные числа представимы как где р — целое, а д — натуральное. Nс2с^ |
|
|
Множество действительных чисел
|
К |
« |
Действительвые числа — это бесконечные десятичные дроби. Рациональные числа — бесконечные периодические дроби. Период не может состоять иа одних девяток. Если период состоит иа одних нулей, дробь может считаться конечной десятичной дробью. Множество иррациональных чисел. Иррациональные числа — бесконечные непериодические десятичные дроби. |
|
3 |
3 б N. 3 е 2, -6 е N. -6 Ё 2,0,26 е К 0,25 « 2,0,25 е Я, 0,25 е Й.
Делимость целых неотрицательных чисел Число о делится на число Ь, если существует с, такое, что а — Ьс. а\Ь; Ь — делитель а; а — кратноеЬ.
I
Таблица 1. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
Ноль делится на любое натуральное число.
Любое число делится на единицу.
Любое число делится само на себя.
|
Бели а > 0 и а ] 6, то а » 6.
Бели а ; (Ьс), то а | Ь, а ; с и |
Бели а Бели а . Бели а |
6 и Ь; а, то а — 6. & и А * О, то ой • ЬА. с и Ь • с, то (от + 6л); |
|
с. |
Если а |
с и (а + е) ; с. то Ь; с. |
с.
Деление с остатком Для любых двух натуральных чисел а и о найдутся такие целые неотрицательные д и г, что о — Ь • д + г, О < г < о.
Если г - О, то а \ Ь. Число г называется остатком от деления а на в.
Признаки делимости
|
Число делится на два, если ото последняя цифра делитс на два. |
я на 2 |
|
Число делится на пять, если его последняя цифра делит ся на пять. |
на 5 |
|
Число делится на четыре, если число, составленное из двух его последних цифр, делится на четыре. |
•а 4 |
|
Число делится на двадцать пять, если число, составленное из двух его последних цифр, делится на двадцать пять. |
на 25 |
|
Число делится на три, если сумма его цифр делится на |
три. на 3 |
|
Число делится на девять, если сумма его цифр делится на девять. |
на 9 |
|
Число делится на одиннадцать, если алгебраическая сумма его цифр Од - О] + а% — а8 + ... + (—1)" ~ 1ап _ г делится на одиннадцать. |
на 11 |
в
Таблица 1. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
Десятичная запись п-значного натурального числа:
Ля-1ал-г-°2о1°0 "
- аЛ.х - 10""1 + а„_а • 10""а + ... + вд • 102 + ах • 101 + о<,; а, — цифры числа, о„_|*0, пе №.
|
НОК (о; Ь) |
Наименьшее положительное из общих кратных чисел вив называется наименьшим общим крат ным этих чисел. НОК (15; 10) - 30 |
|
НОД (о; о) |
Наибольший из общих делителей чисел авЬ называется наибольшим общим делителем этих чисел. НОД (15; 10) - 5 |
НОК (в; Ь) • НОД (с; о) - а • о
![]() Числа оно
называются взаимно простыли, если НОД (а; в) - 1.
Числа оно
называются взаимно простыли, если НОД (а; в) - 1.
Натуральное число р называется простым, если оно имеет ровно два различных делителя (единицу и само это число).
2; 3; б; 7; 11; 18; 17; 19; 23... — простые числа
Свойства простых чисел
Любое натуральное число либо делится на простое, либо взаимно просто с ним.
Произведение натуральных чисел делится на простое число тогда и только тогда, когда хотя бы одно ив них делится иа его простое число.
Простых чисел бесконечно много (нет самого большого простого числа).
Если натуральное число не делится ни на одно простое, квадрат которого не превосходит это натуральное число, то оно само простое.
Любое простое число р (р > 3) предстааимо в виде р — б« ± 1, А е N.
Каноническое разложение натурального числа п (п > 1):
п 1 А г д в
~ Р1* • Р* • Рв* — Р* • Л — простое, р, < р, + ! н О < щ «= N.
120 - 23 • 81 • б1
1
Таблица 2. МОДУЛЬ
-о, с<0
|
Основные свойства модуля |
Геометрическая |
|
14 >0 \-а\ = \а\ |
интерпретация модуля |
|
|а-Ь1-|Ь-а] |
Бели точка А на числовой оси имеет координату а, то рас |
|
| а |-И ^ | а ± Ь ] « | а | + |б| |
стояние от А до 0 равно |а|. |
Расстояние между точками А (а) и Б (о) на прямой равно |о — о].
Уравнения с модулем
|
|
\х-Ь\-а |
\Г(х)\-\8(х)} |
|М*>1-**<*) |
|
|
а < 0 решений нет |
а < 0 решений нет |
|
равносильно объединению уравнений Л*) - В[х) /(*) - -е(х) |
равносильно системе уравнений Г Я») - «I) 1л*>--л*) К!») > 0 |
|
« - 0 х = 0 |
а = о я: - 6 |
|||
|
[- |
а > 0 Г л = 6 - а I. я: - Ь + а |
|||
Неравенства с модулем
|
|х - в] < а |
|* - в] > а |
|М*)1< ей |
|
|
решений нет |
хе Я |
равносильно системе: |
равносильно объединению: Г(х)>е(х) Пх)<-8{х) |
|
а > 0 6 - а < х < <Ь + а |
а > 0 х*5&-аили х>Ь + а |
Неравенство |/ <х)| > |# (х)| равносильно неравенству ^(х) > ^(х) или неравенству (х) - 4? (х)) (/ (х) + р (х)) > 0.
Таблица 2. МОДУЛЬ
Примеры
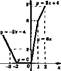 Раскрытие
модулей «по промежуткам* у - |г + 2] + 3 И
- 2 \х - 11
Раскрытие
модулей «по промежуткам* у - |г + 2] + 3 И
- 2 \х - 11
-2 О 1 х
х « -2. у = + 2) - Зх + 2 (ж -1) - -2х - 4
- 2 < х < 0 . и = * + 2-Зх+2(ж 1)-0 0 < х « 1 , у - а : + 2 + Зд: + 2<х-1)-6а: х > 1, 0 = х + 2 + Зх-2(х 1) - 2х + 4
Решить уравнение 8х2 - б|х] - 8 - О.
Заметим, что \х\3 — х2; введем обозначение |х| — *.
3(2 - Б* - 8 - 0.
8
|х] ™ —1, решений нет.
. , 8 8 8
| * | - д : * 1 - - д . * В = з -
Ответ: х1 - - | ; х2 - | -
Построить график функции р — 1а; х • {сов л).
Данная функция периодическая, период 7 — 2л. Построим график на каждом промежутке внакопостоянствв косинуса.
Приоовх > 0 хе у - вш л;
/к Зп"\ при С08 X <" О X 6= I -; — I, у —В1П X.
Таблица 3. ДЕЙСТВИЯ С МНОГОЧЛЕНАМИ 3
Сложение многочленов; (а2 + аЬ - Ь) + (За2 - 2аЬ + Ь) - 4а2 - аЬ.
Вычитание многочленов:
(2а - Ь ) - (За + Ь) - (2а - Ь) + (-За - Ь) - -а - 26.
Умножение многочленов:
(а + ЗЬ)(а - Ь) - а2 - аЬ + ЗаЬ - ВЬ2 - а2 + 2а& - ЗЬ2,
Формулы сокращенного умножения
|
квадрат суммы |
(с + *) 2 - о + 2аЬ + о |
|
квадрат разности |
(а - о 2 - 2ао + Ь2 |
|
куб суммы |
(о + о)3 - о3 + За2Ь + Зае2 + о3 |
|
куб разности |
(а - а3 - За2г + ЗоЬ2 -Ь 3 |
|
разность квадратов |
а2 - (а + Ь) (о - Ь) |
|
разность кубов |
а3 -о3> - (о - Ь) (о2 + оЬ + ь2) |
|
сумма кубов |
а3 + Ь3 - (о + о) (а2 - о* + о2) |
Бином Ньютона: (а + Ь)п -
- ал + С1 ап " 1 Ь + С2 ал " V + ... + С* ап " *Ь* + ... + Ьл
с п с С 9 п п п - к п " ' п 2 ' « (п - Л)! *! п € N. п > 1 (01 - 1; 1! - 1; п! - 1 • 2 ... • п).
Треугольник Паскаля 1
• 1 1
1 2 1
1 3 3 1
Таблица 3. ДЕЙСТВИЯ С МНОГОЧЛЕНАМИ
|
Вынесение общего множителя за скобку |
2аЪ + 14а2 + 2а - 2а (Ь + 7а + 1); За2&3 - 1ба8Ь - За2Ь (Ь2 - ба). |
|
Метод группировки |
аЪ-\-ас-Ъ-с^а{Ь-\-с)- - (Ь + с) - (Ь + с) (а - 1). |
|
Использование формул сокращенного умножения |
а2 + 4аЬ + 4&2 - (а + 2Ь)2; а4 + 4 - а4 + 4а2 + 4 - 4а2 « - (а2 + 2)2 - (2а)2 * - (а2 - 2а + 2) (а2 + 2а + 2). |
|
Дополнительные формулы |
(а11 - 1) - -(а-1)(а п - 1 + ап-2 + ... + а + 1); (а2т + 1 + ! ) « - (а + 1) (а2т - а2"1 ~1 + ... - а + 1). |
Многочлены от одной переменной
Общий вид: / (х) - апхп + ап _ ^ " *+ + аххх + а0, п — степень многочлена, а1 — коэффициенты, ап — старший коэффициент, ап Ф О.
Если ап = 1, то многочлен называется приведенным.
Вх4 - х3 + 2х2 - б — многочлен 4-й степени с коэффициентами: а4 — 3; а3 — -1; а2 — 2; аг — О; а0 — -5.
Квадратный трехчлен — многочлен второй степени ах2 + Ъх + с {а*О),
а — первый коэффициент, Ь — второй коэффициент, с — свободный член.
Деление многочленов
Теорема о делении с остатком Деление «уголком»
Р(х) « М(х) • 0(х) + Щх), где
Р(х) — делимое^ М(х) — делитель,
Таблица 3. ДЕЙСТВИЯ С МНОГОЧЛЕНАМИ
![]()
Деление многочлен* /(ж) ша двучлен ж —
|
Теорема Безу. Остаток от деления многочлена на двучлен ж - о равен значению этого |
Схема Горнера. Разделить многочлен Я*) - ж3-* Ьх2 - 3 не (ж - б) |
||||
|
многочлена при ж — а, т. е. К — /( |
а). Ь2 |
||||
|
К*) - (ж - а) • (Цх) + Па) |
Ъ\ -ь1 Б + а *>с 5 + о. Е 5 + До Я - 1 (Б) - 247 «3 "а «1 а0 |
||||
|
б |
1 |
5 |
0 |
-3 |
|
|
1 |
10 |
60 |
247 |
||
|
ь2 *1 Ьо Я |
|||||
Корнем многочлена называется такое число х0, при котором значение многочлена равно нулю Ц (жд) — 0).
Целые корни многочлена с целыми коэффициентами являются делителями его свободного члена.
Пример.
х8 + 5ж2 + 2ж - 8 = О
Целые корни можно искать только среди чисел -1; 1; 2; -2; 4; -4; 8; -8.
Ответ: х — 1; ж - -2; ж - -4 — корни.
Таблица 4. КВАДРАТНЫЕ КОРНИ
|
Определение арифметического корня с2 - о |
.Дб - 4, т.к. 4 > 0, 42 - 16; ^26 * 7, т-к. 72 * 25; ,/26 / 6, т.к. -6 < 0; ./^8 ке определен. |
Д"86 - 0,6; ЛЯОО - 70; Д Ш -0,01; 2 < & < 3; 0,8 < ,/оТв <• 0,0. |
|
|
Тождестве |
Основные свойства |
||
|
(л/а)2 - о , а ? 0 ^ - И, а е Л |
& • 7ь - -1аЪ Га Га |
Л~В - № • № Га М <ь № |
|
Сравнения, связанные с квадратными корнями Если а > 6 > 0, то & > *[Ь.
& + „/& > ч/о + 6Если о>1,тои>л/«и-^а > } .
Если 0 < о < 1 , т о в < И 0 < ^ < 1.
|
Вынесение из-под корня |
Внесение под корень |
|
|
л/о2 о - |а| • 7Ь, о > 0 |
Ол/& — |
-л/в2*, если о<0, |
|
|
в»0 |
*/а2о, если а^0 |
|
763 - 79~7 =3^7; |
Б- Л = -/з б2 - ^75; -2,/7 = А/28; |
|
|
^ёь5 + ,/Б =&7б + ,/&; Лзс* 1 ^ - -с/3 + ^ . |
(^5 - 2) • л/9 + 4,/Б - |
|
|
- Ж,/! - 2)2 (9 + 4.Д) - 1; |
||
|
{./З -2) • & + 4^3 - |
||
|
|
||
11
Таблицам КВАДРАТНЫЕ КОРНИ
Иррациональность в знаменателе
2^ 2Л
7§
5(73 + 1) 5(л/3 + 1) 6(73 + 1)
|
7§ - 1 (7§ - 1)(73 + 1) |
3 - 1 2 |
|
Сравнение среднего геометрического (пропорционального) двух чисел и их среднего арифмети |
Построение 4п (п ^ ЛГ) на числовой прямой |
 ческого
ческого
> 4аЪ ,а>0;Ъ>0.
0х х ЛЛ 2 8Ло
( ^ Г Т Т ) 2 - ( ^ ) 2 + 1 2
Примеры
Найти х2 и упростить выражение х - 73 - 272 - ^З + 2л/2 Заметим, что х < О, т. к. 3 - 272 < 3 + 2^2. х- -2 3 - 2^2 - 2 7 9 - 8 + 3 + 272 = 6 - 2 = 4. Значит, X = -2.
Ответ: х2 = 4; 73 - 272 - 7з + 272 - -2.
г- ТЗЗ - 1
![]() Сравнить
числа 72 + 1 и ^ •
Сравнить
числа 72 + 1 и ^ •
|
• Запишем: |
72+1 |
? |
7§3 - 1 2 |
|
|
272 +2 |
? |
7§3 - 1 |
|
|
7§ + з |
? |
Тзз |
Так как сравниваемые числа положительны, то можно
Таблица 5. КОРНИ НАТУРАЛЬНОЙ СТЕПЕНИ
Определение арифмети
|
ческого корня натуральной степени из неотрицательного числа а п 4а-Ь Ь>0 п а |
У27 - 3; У09 0000001 - ОД; Л024 - 4; 2 < «/О < 3; б УЗ - 3; . 0,2 < б,/0,00036 <0,3. 3 70,008 - 0,2; Если а < О, то 2п~1/а = - 2п~\Га. |
|
Извлечение корня нечетной степени из отрицательного числа |
*/3 --2; Ч/^Ш - -6/243 - -3; |
- 2)8 - -8л/(2 - 73) з - -(2 - 7з) - 7з - 2.
Корень четной степени из отрицательного числа не определен.
|
Тождества |
Основные свойства |
|
Если 1/а существует, то (п7а)п = а. 2п/~2п га |а|, а € Я |
п п п Ч/а 4а- Л - 7аЬ; п (*/аУ>-п№; |
|
а, а € Л |
1^ - птл/а; п^а - п*./? |
Если а > Ь ^ 0, то Ч/а > 1/6.
Сравнения, связанные 1/а + 1/6 > Ч/а~ТЪ. с корнями
Если а > 1, то Ч/а > 1 и Ч/а < а.
Таблица 5. КОРНИ НАТУРАЛЬНОЙ СТЕПЕНИ
|
|
8- */2 - \1в*-2 - *Д62; |
|
Внесение под корень |
-2-У5 --в^2*~8 --«/192; (1 - Л ) " *Л --^{1 -Л* 2: (1- Я)-У2 - ^ 1 - Л)* 2. |
|
Иррациональность В знаменателе |
3 8 4 ^ 3 4 ^ *л~ 2 2 : 2 2 (У9 - УЗ + 1) УЗ + 1 3 - 1 - *Л - Уз + 1. |
|
|
Ш : Л - 6Л? : вЛ? - \ЙЗ - |
|
Действия с корнями различных показате лей |
е 3 Л 'Л'Л- Л 22 2 - 41? - 2. |
|
Сравнить АЛ ияЛ. *л -ч/? -чя». № -'?/? -ч/П. Так как 125 > 81. то 12Л25 > 4/81 и т > ш. |
|
|
Среднее геометрическое и среднее арифметическое неотрицательных чисел |
П + /1_ + + Л »/«, О * - * , < „ Равенство достигается в\ — од —... ** а„- |
16
Таблица 6. СТЕПЕНИ. СТЕПЕННАЯ ФУНКЦИЯ. ФУНКЦИЯ у ="Л
|
Степень с натуральным показателем |
а1-а а" - а о-у— а, , п е №, о е Я |
||
|
Степень с целым показателем |
о°-1. «*0 а" пе»; |
В"2- |; (-1,2)° = 1; /-гу3 /б-*8 126
Ы " 8 - |
|
|
Степень с рациональным показателем для неотрицательного числа а |
в" - т е г, п е N Если т < 0, то о> 0 Если т > 0, то а ? |
2 § 8й - я/9; О 6 -0; в . 2 1 26 - «/гб - 126; 0. (0,04)2=Ж04=0.2; 1 (-27)3 не определе |
|
|
|
на. |
||
|
Понятие о степени с иррациональным показателен |
3я < 3" < 84 (0.3)2 < {0.31*^ < (0.3}' 88.1 < 8" < Зз.2 (0.8)1'5 < (0,8)"^ < (0,8)м 8з,м <ая<8з.1В (0,8)1И2< (0,8)*^ <(0,8)1-*1 (Я-8.1415—) (,/2 -1.4142...) |
||
|
Степень с действительным показателем |
г>0 а Г е Л ' { а>0 " { о»0 |
||
|
Свойства степеней |
о* - аг = оР + г (ор)г - о?г (!Г-ат аг • Ьг - {аЬУ аг:Ъг- ^ |
||
2 Зак 1437 17
Таблица 6. СТЕПЕНИ. СТЕПЕННАЯ ФУНКЦИЯ
|
Свойства степеней, связанные с неравенствами |
а > Ь > 0 г > 0 а > Ь > 0 1 г<0 1 |
>а >Ь г |
р > г 1 * а>1 ] 0<а<1 |
р >=*а |
г >а <а |
![]()
![]() Ум
Ум
у-х»
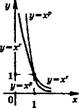
Графики степенной функции
У - х г ,
г е К О < р < г < 1 1 < р < г р < г < 0
Жу) = [0; +°°);
|
1 {/ - * 2 |
|
|
!/ 1 0 |
, У ~ •/*
1 * |
||
|
у -Ух 1 3 У- Ж |
|
|
У -I1 |
г 1 ^ |
1 |
|
|
|
|
1 . |
0 1 х о -1 |
1 ** |
||
|
I / - 2п+Ух |
» 1 |
У - |
у |
2 +1 у - " Л ' \ ш |
||
|
0 |
1 |
т N х |
0 1 ~х -1 |
|||
- [0; +со); возрастает на [0; +оо).
Щу) = [0; +со); Е{у) - [0; +оо); возрастает на [0; +оо).
Щу) - (0; +оо); Е(у) - (О; +оо); убывает на (0; +оо).
Таблица 7. ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ ШКОЛЬНОГО КУРСА
|
Линейная функция у - ах + Ь |
График — у - ах + Ь (о < 0) |
• прямая у - ах + Ь (а > 0) / у - Ь ( а - О ) |
|
Щ)) - Я. |
||
|
При а — О Е(у) — {о} (постоянная), все точки — точки экстремума. При а * 0 Е(у) - К. |
||
|
При а > 0 возрастает на В. При а < 0 убывает на Л. Экстремумов нет. |
/о |
|
|
Функция у — кх — прямая пропорциональность (к > 0). Нечетная функция. |
"Ау-М 1 У - * 2 * * ! - *В а « 2 - 1к р |
|
Квадратичная функция у — ах2 + Ьх + с (а * 0)
|
Щу) - Д. |
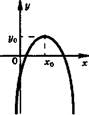
Вид графика — парабола. Координаты вершины параболы: * о - - ^ ; у о - у ( * о ) - Ось симметрии х — х0. При а < 0 2/д — наибольшее значение. При а > 0 {/о — наименьшее значение. |
||
|
При а > 0 убывает на ( -со; х0] и возрастает на [де0; + ° ° ) , 0 дс0 — ~ 2о т о ч к а минимума, Уо - У(*о) минимум. Е(у) - [у0; +°°). |
|||
|
При а < 0 возрастает на (-со; х0] и убывает на [аг0; + ° ° ) , Ь лг0 •= ~2д\ — точка максимума, Уо ~ У(*о) — максимум. Е(у) - (-со; у0]. |
|||
|
У = ах2 »{ \ 0 |
|
||
Четная функция
Таблица 7. ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ ШКОЛЬНОГО КУРСА
|
Б - Ь2 - Аас > О |
И - Ь2 - 4ас - О |
О — Ьг - 4ас < О |
|
Два корня Хх и дс2; график пересекает ось Ох в двух точках. |
Один корень х0; график касается оси Ох. |
Нет корней; график лежит по одну сторону от оси Ох. |
![]()
[у
![]()
0
2/о
 п
п
ах + Ь
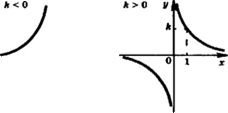
Дробно-линейная функция и = ; (ай - Ьс * 0)
Вид графика — гипербола у - , где к - (Ьс - «и*)/сЛ
Функция у = - (й * О). Вертикальная асимптота х — О, горизонтальная у — О.
 -
(-со;
0)
и
(0;
+оо), Е(у) - (-со;
0)
и
(О;
+оо). Два промежутка монотонности (-со; 0) и (О;
+оо); при к < 0 функция на каждом из них возрастает, при к
> О на каждом убывает.
-
(-со;
0)
и
(0;
+оо), Е(у) - (-со;
0)
и
(О;
+оо). Два промежутка монотонности (-со; 0) и (О;
+оо); при к < 0 функция на каждом из них возрастает, при к
> О на каждом убывает.
Экстремумов нет.
Нечетная функция. обратная пропорциональность
Таблица 7. ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ ШКОЛЬНОГО КУРСА
Примеры дробно-линейных функций
|
8х - 2 У - з + - ! - - х - 1 х - 1 |
2х - 1 " ~ х + 1 |
|
6 - 2х У 1 + " 2х - 3 " - 2 х - 3 |
|||
|
х * \ ; у * 3 ; у | |
ж * -1; у * 2; у - - - |
|
8/2 **3/2;1,*-1; |
|||
|
3 |
|
Л 1 |
2 |
|
У 0 |
» 1 \ з/2\а х |
|
|
-110 |
Г |
х |
|
|
|
Функция у — 4х
|
Щу) = [0; +оо) = Е(у). |
У 1 |
|
|
|
|
|
Возрастает на !)({/). Экстремумов нет. Четностью и нечетностью не обладает. |
2 |
|
|
у = Л |
|
|
|
|
1 |
|||
|
у = 1 и* |
1 |
|
|
|
|
|
0 |
1 |
|
4 |
X |
Функция у — \[х
Щу) = ( -со; +СО) - Е(у).
|
|
У 2 - I 1 |
|
|
У - 34х |
|
|
П |
|
|
1 - |
||
|
|
|
0 1 |
|
|
8 х |
|
— |
—""-г |
|
|
|
|
Возрастает на Щу).
Экстремумов нет.
Нечетная функция.
1
У =
21
Таблица 7. ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ ШКОЛЬНОГО КУРСА
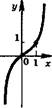
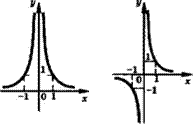
Степенная функция у — хп У - пх' л - 1
п ш О; у - 1; - (-оо; 0) и (0; + с о ) ; Е(у) - {1}.
|
п > 0, натуральное |
п < 0, целое |
|
п — четное - п — нечетное т у ) я т у ) = Д Е(у) = [0;+со) |
п — четное п — нечетное щу) - (-со; 0) и (0; +оо) ОД) = (0; + о о ) Е(1/) = (-ОО;0)и и (О; +оо) |
![]() 1 х
1 х
|
Четная функция |
Нечетная Четная функция функция п — не целое число |
Нечетная функция |
|
п > 1 |
0 < п < 1 |
л < 0 |
ГЦу) - [0; + о о ) = Е(у) ту) = (0; +°°) = Е(у)
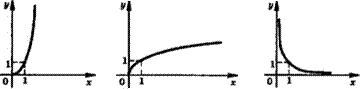
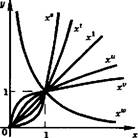 и><0<V<и<1<^<8
и><0<V<и<1<^<8
Сравнение графиков степенных функций Таблица 7. ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ ШКОЛЬНОГО КУРСА
|
Показательная функция у - а* (а > 0; а * 1) у' — а* • 1п а |
Логарифмическая функция у-1оеах{а>0;а*1)у'-х Ыа |
||||
|
О(и) - Я; - (0; + о о ) ; один промежуток монотонности; экстремумов нет. |
Щу) - (0; +оо); Е(у) - Я; один промежуток монотонности; экстремумов нет. |
||||
|
а > 1 У а 0 |
возрастает на Я 1 х |
а > 1 в< 0 |
>зрастает на Щу) |
||
|
0 < а < 1 0 |
убывает на Я V - . 1 х |
0 < а < У 0 |
1 убывает на Щу) |
||
е - 2,718281828450046... » 2,7 — основание натурального логарифма (1о%ех — 1п х).
|
(е*)' - ех |
|
|
С Ш . г - 1 |
|||
|
\<г\ с*\ |
\ 0 й< с < |
1 °/ 1 1 < а < Ь |
** |
У |
а* |
|
|
0 |
|
а<Ь<1<с<й |
||||
23
Таблица 7. ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ ШКОЛЬНОГО КУРСА
Тригонометрические функции
|
|
у — В1П X |
у — сое X |
|
|
ту) |
Я |
Я |
( - | +лА; | + яА) л е г |
|
Е(у) |
1-й ч |
[-1; 1] |
я |
|
Бесконечное множест во промежутков монотонности |
Убывает на [| + 2пк; ^ + 2пк]; возрастает на [-|+27Л;^ + 2пя]. |
Убывает на [2пк; л + 2яА]; возрастает на [-я + 2пк; 2пк]. |
Возрастает на каждом промежутке непрерывности (-^ + пк; \ + яА). |
|
Точки минимума |
х = -\ + 2я« |
х - я + 2пк |
нет |
|
Точки максимума |
х - \ + 2пк |
х = 2пк |
нет |
|
Минимумы |
-1 |
-1 |
нет |
|
Максимумы |
1 |
1 |
нет |
|
Нули |
х = пк |
х = ^ + кк |
х — пк |
|
Промежутки знакопос- тоянства (У>0) |
(2лА; я + 2пк) |
(-\ + 2пк; ?+2лА) |
(пк; \ + яА) |
|
Промежутки знакопос- тоянства (У<0) |
(-я + 2пк; 2пк) |
(|[+2лА;^+2яя) |
( | + яА; я + пк) |
|
Период |
2л |
2л |
я |
|
Четность |
Нечетная 8Ш (~х) — -8Н1 X |
Четная соз ( - х ) — С08 X |
Нечетная |
|
Асимптоты |
нет |
нет |
Вертикальные х = ^ + яА |
|
Производная |
сое X |
-8Ш X |
1/С082Х |
Таблица 7. ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ ШКОЛЬНОГО КУРСА
У — 81П X у — СОВ X
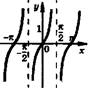 У
У
Графики .-я/2
Обратные тригонометрические функции
|
|
у = агсзт х |
у — агссоз х |
у = агс*е х |
|
||||
|
|
[-1; 1] |
[-1; 1] |
К |
|
||||
|
Е{у) |
Г-- - -1 |
[0;к] |
(--• -) к 2 ' 2 ' |
|
||||
|
Монотонность |
Возрастает на Щу) |
Убывает на Щу) |
Возрастает на Щу) |
|
||||
|
Четность |
Нечетная |
— |
Нечетная |
|
||||
|
Производная |
1 |
1 |
1 |
|
||||
|
Л-х2 (х * ±1) |
(х * ±1) |
1 + * 2 |
|
|||||
|
Графики |
У я 2 -1 |
]\ / 1 |
У К |
я л \ |
У я 2 |
|
|
|
|
\[ |
0 1 "х я ~2 |
я ~2 |
0 |
" |
||||
|
-1 0 |
1 х |
|||||||
Таблица 8. ОСНОВНЫЕ ПРИЕМЫ ПРЕОБРАЗОВАНИЯ ГРАФИКОВ
|
|
|
У, |
|
||
|
Г(х + а) |
Перенос графика у — /(х) на вектор р(-а; 0). |
/о |
У - 4х г I 1 1 т |
||
|
-2-1 |
1 2 4 х р(-2; 0) |
||||
|
|
|
У |
|
||
|
Г(х) + Ь |
Перенос графика у — /(х) на вектор р (0; о). |
1 |
|
||
|
0 -1 |
*\ х Р(0; -1) |
||||
|
|
|
У |
|
||
|
-№ |
Симметрия относительно оси абсцисс. |
1 |
у - Л |
||
|
0 |
у - -Л |
||||
|
/(-*) |
Симметрия относительно оси ординат. |
г- * У - 4-х |
т г у - 4х |
||
|
< |
) 1 ~х |
||||
|
1/<*)1 |
Часть графика в верхней полуплоскости и на оси абсцисс без изменения, а вместо части графика в нижней полуплоскости строим симметричную ей относительно оси Ох. |
|
1, = |дг2-1| |
||
|
-1 |
V - у? - 1 |
||||
Таблица 8. ПРЕОБРАЗОВАНИЯ ГРАФИКОВ
Часть графика в правой полуплоскости и на оси ординат без изменения, а вместо части в левой полуплоскости строим симметричную правой относительно оси
Оу.
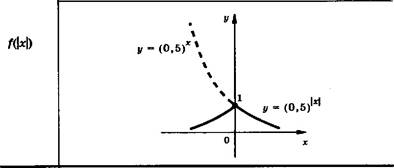
При к > 1 сжатие к точке (0; 0) вдоль оси абсцисс в к раз; при 0 < к < 1 растяжение от точки (0; 0) вдоль оси абсцисс в 1/к раз.
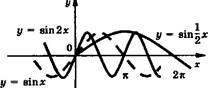 Г(кх)
Г(кх)
(к > 0)
При к > 1 растяжение от точки (0; 0) вдоль оси ординат в к раз; при 0 < к < 1 сжатие к точке (0; 0) вдоль оси ординат в 1/к раз.
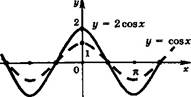 Щх)
Щх)
(к > 0)
27
Таблица 9. ГРАФИК УРАВНЕНИЯ С ДВУМЯ ПЕРЕМЕННЫМИ
|
ах + Ьу = с |
Прямая линия. |
X |
\ . |
||
|
0 |
\ * |
||||
|
|
|
У |
|
||
|
(х - о)2 + (у - Ь)2 = В2 |
Окружность с центром (а; Ь) радиуса Н. |
( |
У |
||
|
|
)У * • |
||||
|
/ 2 2 у=^а -х |
Полуокружность с центром (0; 0) радиуса а. |
АУ{ |
|
||
|
-а 0 |
а х |
||||
|
у = ах2 + Ьх + с |
Парабола вида у — ах2; при а > 0 ветви вверх, при а < 0 ветви вниз; вершина Ь = *о -2^'^о = !/(*о)- |
!/(*о) |
1 |
||
|
0 |
х0 х |
||||
|
* = сну2 + Ьу + с |
Парабола вида х — ау2; при а > 0 ветви вправо, при а < 0 ветви влево; вершина Ь Уо " ~2а\ • х0 = ^Уо)- |
У, Уо |
С |
||
|
0 |
|
||||
Таблица 9. ГРАФИК УРАВНЕНИЯ С ДВУМЯ ПЕРЕМЕННЫМИ
|
(х - а)({/ - о) - к к *0 |
Гипербола к вида у - - ; асимптоты х = а; |
|
И" > * > 0 |
|
Н + Ы - 1 |
Квадрат |
|
|
|
\х-а\ 1 \у-Ь\ т п т > 0, п > 0 |
Ромб |
1 а 0 |
|
|
М-Ы - 1 |
«Перекресток» |
>У |
к 1 |
Если дан график зависимости Р(х; у) = О, то график зависимости
Р(х — а; у — Ь) = 0 можно получить переносом всех точек на вектор р(а; о); график Р (|дг|; у) = 0 можно получить, оставив часть графика в правой полуплоскости и на оси ординат без изменения, а вместо части в левой полуплоскости построить линию, симметричную
правой относительно оси Оу;
график Р (х; \у\) = 0 можно получить, оставив часть графика в верхней полуплоскости и на оси абсцисс без изменения, а вместо части в нижней полуплоскости построить линию, симметричную верхней части графика относительно оси Ох.
29
Таблица 10. КВАДРАТНЫЙ ТРЕХЧЛЕН
Квадратный трехчлен ах2 + Ьх + с — это многочлен второй степени; а * О — первый коэффициент; Ь — второй коэффициент; с — свободный член.
( Ъ Л 2 Ь -4ас
2
Выделение полного квадрата: ах + Ьх + с а\х + ^1 4а
График функции ^(дг) — ах + Ьх + с — парабола; координаты вер-
62-4ас .О
шины
х0 =
, у0 -
Р(х0) ^
4а'
Б — Ь2 - Аас — дискриминант квадратного трехчлена.
Корин квадратного трехчлена
Квадратный трехчлен не имеет корней и сохраняет знак
1><0 первого коэффициента при всех значениях х: а • Р(х) > 0.
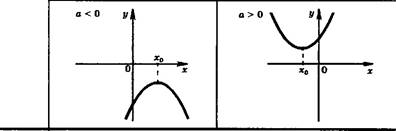
Квадратный трехчлен имеет один корень (два равных
0 - 0 корня) х - х0- - ~
У функции Щх) два промежутка знакопостоянства, на каждом из которых она сохраняет знак первого коэффициента: аЩх) >0(х* *0).
Парабола касается оси абсцисс в своей вершине.
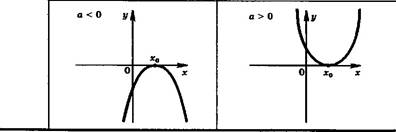
Таблица 10. КВАДРАТНЫЙ ТРЕХЧЛЕН
Квадратный трехчлен имеет два корня: С > 0
-ь-4Ъ - ь + 4р
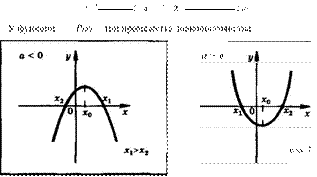
Теорема Виета
Если квадратный трехчлен ах + Ьх + с (квадратное уравнение ах2 + Ьх + с — 0) имеет корни х1 и х2 (т.е. И ^ 0), то
Ь с
Для приведенного (о — 1) квадратного уравнения х2 + рх + д — 0
Обратная теорема: Если числа 11 и <2 таковы, что *1 + 1% = — - и
*1 ' *2 " д > то о н и являются корнями квадратного трехчлена ах2 + Ьх + с (квадратного уравнения ах2 + Ьх + с = 0).
Пример. Квадратное уравнение х2 - (б + Л )х + 5 Л "0 имеет корни х — б; х — Л'.
Разложение квадратного трехчлена на линейные множители
|
О < 0 |
Квадратный трехчлен на линейные множители не раскладывается. |
|
1)>0 |
ах2 + Ьх + с = а(х - х ^ х - х2) |
|
О = 0 |
ах2 + Ьх + с = а1хА" - ^ 1 Ь Л 2 |
31
Таблица 10. КВАДРАТНЫЙ ТРЕХЧЛЕН
Составление квадратного трехчлена с корнями 1х и *2
Существует бесконечно много квадратных трехчленов с корня ми <1 и 1г; они имеют вид
а(дг2 - (*! + *2)л: + 1Х • 12),
среди них один приведенный:
х2 - («1 + 12)х + *! • 12.
Пример. Приведенный квадратный трехчлен с корнями 2 и 8. х2 - 10* + 16,
так как 2 + 8 = 10, 2 • 8 = 16.
Корни квадратного трехчлена ах* + Ьх + с
|
положительны, если |
отрицательны, если |
||
|
|
с х, • х0 — — > 0 |
|
с хл • д:9 — — >0 1 2 о |
|
|
Ь л * 1 + * 2 " - • а - > 0 |
|
Ь л
|
|
|
2) = 0 2 -4ас>0 |
|
И = Ь2-4ас^0 |
|
одного знака, если |
разных знаков, если |
||
|
|
с 1 г а И = Ь 2 -4ас»0 |
х о - < 0 1 *2 ~ • |
|
Таблица 11. ПРОГРЕССИИ
Последовательность — функция натурального аргумента.
|
Задание последова |
а„ = Г(п), п е ЛГ |
|
тельности формулой |
ап = п2 + п + 41 |
|
общего члена |
а, ' 43; а2 = 47; аз ™ 53; ... |
|
Задание последовательности рекур |
Дано: аг; а2; ...; а„ _ ] |
|
рентным соотноше нием |
а = а а п Л°п - Г. п - 2> -•: 1) |
Числа Фибоначчи: 1; 1; 2; 3; 5; 8; 13; 21; 34; ... . (аг - а2 = 1; а„ + 2 - + ап + 1)
Формула общего члена: а„ — ^ ( ( ^ ~ ^ ^ ) ~ ( " 2*^) }
Свойства: ах + а3 + аь + ... + а2п + 1 - а2п + 2; а2 + а4 + а6 + ... + а2п - а2п + г - 1.
Арифметической прогрессией называется последовательность, заданная рекуррентным соотношением: ап + 1 — ап + Л, п & N [ау — первый член прогрессии, а" — разность прогрессии).
Геометрической прогрессией называется последовательность, заданная рекуррентным соотношением: Ь„ + , — Ьп - д (Ь>1 * 0 — первый член прогрессии; д }* О — знаменатель прогрессии).
|
|
Арифметическая (-?-) |
Геометрическая ( ^ ) |
|
Допустимые значения |
а, и а" любые |
Ьх и д не равны нулю |
|
Формула общего члена |
а„ = аг + (п - 1) • Л |
Ь „ ^ й 1 д п - 1 |
|
Характеристическое свойство |
а п + 1 + а „ - 1 2 |
Ь Ъ п -г 1 ' °п - 1 ~ п ьп*о |
|
Формула суммы п первых членов |
а, +ап Я„ - 2 ' п - 2а1+[п-1)ё 2 |
д - 1, 5„ - п • Ьх |
3 Зак. 1437 33
Таблица 11. ПРОГРЕССИИ
|
|
- 6. (п * т) 71- т |
ьп - о " " т Ь п + 1~ ®п + 1 ~ ®п |
|
|
Другие формулы |
«п + 1 ~ |
•ьп ~ Ь2 " °п - 1 ~ |
|
|
|
*1 + ~ °2 + ап - 1 ~ о* + ап - к + 1 |
-ьк " Ьп - к + 1 |
Бесконечно убывающая геометрическая прогрессия (О < |д| < 1)
Ит
д - 0, 8 - Нт 8_ - .
П - » о о П - > о о 1 ~ 9
Формула суммы:
1-9
|
Примеры |
|
|
|
0 47 37 0,(37) - 0,37 + 0,0037 + ... - - а _'0 01 - 90 ({>! - 0,37; д 0,01) |
|
|
|
0,02 0,6(2) - 0,6 + 0,02 + 0,002 + : . . - | + 1-0,1 (Ьг - 0,02; 9 - 0,1) |
1 - 2 |
2 47 90 " 90 |
Суммирование
п(п + 1) 1 + 2 + 3 + 4 + ... + п
12 + 22 + 32 + 42 + . . . + п 2 - " ( П + 1>(2ге + 1 ) о
!3 + 23 + дЗ + 43 + _ + „3 . "V + I)2
4
Примеры
Если а„ арифметическая прогрессия, то
1 1
+ - * - + - ± - + . . . + •' 8 » 4 о,п а и п + 1 а1 ап + 1
Все натуральные числа, дающие при делении на 7 в остатке б, имеют вид ап - 7(п - 1) + б - 7п - 2, п е # .
34
Таблица 12. ТРИГОНОМЕТРИЧЕСКАЯ ОКРУЖНОСТЬ
Тригонометрической (единичной) ок
I четверть:
ружностью называется окружность с центром в начале координат, радиуса 1. Точки 0 + 2ка < к | + 2кк. единичной окружности можно поставить II четверть:
в соответствие действительным числам.
Числу О ставится в соответствие точка 5 + 2я*<*<я + 2яя.
|
/ 11 |
I/ Vе |
|
\ 0 111 V |
11 х IV |
Р0{1; 0), а каждому числу г ставится в соответствие точка Р(, полученная поворотом точки Р0(1; 0) на угол I* вокруг начала координат (если I > 0, то поворот осуществляется против часовой стрелки, если I < 0 — по часовой стрелке). Таким образом, каждому действительному числу I соответствует единствен III четверть:
ная точка на единичной окружности 8я
к + 2я* < * + 2пк.
Рг, а каждой точке Р4 — бесконечное множество действительных чисел вида IV четверть: г + 2яА, * е г . 8я
•7Г + 2я* < * < 2л + 2я*. Длина дуги РоР( - * (0 < * < 2я). Связь градусной и радианной мер:
а е а - я • (радиан); х (радиан) - ^ 18о) . Две точки, симметричные относительно
|
оси абсцисс |
оси ординат |
начала координат |
|||
|
у |
|\ 1 1 х |
V |
• * |
У / \ / \ | |
ч 1 х |
|
V 0 а-±Л + те 2 |
У . 2пт, |
\ 0 а -
(-1)"< |
+ Я П , |
0 V а - 1 + яА к е 2 |
1 \ /1 » |
86
Таблица 12. ТРИГОНОМЕТРИЧЕСКАЯ ОКРУЖНОСТЬ
Вершины правильного п-угольника, вписанного в единичную окружность (одна из вершин Р{).
"4
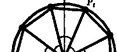
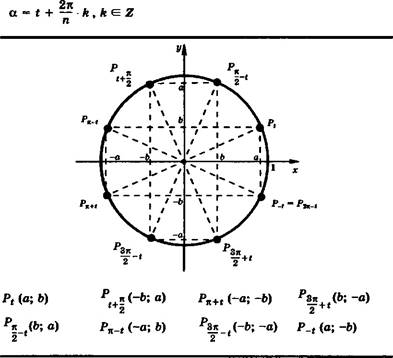
Таблица 13. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
|
Косинусом числа * называется абсцисса точки Рг единичной окружности, а синусом — ордината этой точки. |
Тангенсом числа * называется отношение 81П * к соз * (сое * * 0). зш( Б С08* |
|
|
|
х-1 |
|
N (с1г«; 1) |
1 |
|
|
|
|
У- 1 |
|
|
|
1 х М (1; 18 «) |
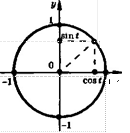 Ось тангенсов — прямая х — 1.
Ось тангенсов — прямая х — 1.
Котангенсом числа I называется отношение сое I к вт *.
Р,(со8(; 8Ш()
СОБ Ф
с1е * - -г—; (вт г * 0)
6
81П1 * '
Ось котангенсов — прямая у = 1.
|
Основные формулы вт2 г + соа2 * •= 1, (6 в. 1 = 1 + я 6 2 « * с о е * * * ! * - * СОЗ* 6 81П* |
Дополнительные формулы 1 + 1В2* = —^5-2, » , * * = + я т , т б 2 2 соз * 1 + с*в^* - — 2 " , 1 * п к . к ^ 2 8Ш * 1в * • с*е * = 1, * * % ' е 2 |
Формулы приведения преобразуют тригонометрические функ-
я а я а К а п а Зл а Зл , ав Т ИГ0Н
ции чисел д ~ > 2 ' ~ * ' У ~ ' У Р °-
метрические функции числа а 6 К. (Удобно считать а углом первой четверти.)
|
* |
л - а |
л + а |
л 2 |
л 2 + а |
Зл а У " |
Зл у + « |
|
СОЗ * |
-сов а |
-сое а |
81П а |
-вт а |
-вт а |
81П О |
|
зш * |
8ш а |
-вт а |
сов а |
соз а |
-сов а |
-сое а |
|
* * < |
-*8 а |
*8 а |
с1в а |
-с*8 а |
с*? а |
-с1е а |
37
Таблица 13. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
|
Периодичность |
Четность |
|
|
СОВ (* + 2П) — СОВ 1 Тсоа - 2л |
|
соз (-а) — сое а |
|
8Ш (* + 2п) — 81П 1 |
с*е С + я) - с*§ е |
Вт (-а) = -вш а *е (-а) = -*е а |
Значения тригонометрических функций некоторых углов
|
а, рад |
0 |
л/6 |
л/4 |
л/3 |
л/2 |
л |
Зл/2 |
|
о а |
0° |
30° |
45° |
60° |
90° |
180° |
270° |
|
вш а |
0 |
1 2 |
1 Л |
Л 2 |
1 |
0 |
-1 |
|
сое а |
1 |
7з 2 |
1 Л |
1 2 |
0 |
-1 |
0 |
|
ЪВ а |
0 |
1 7з |
1 |
7з |
не опр. |
0 |
не опр. |
|
с*е а |
не опр. |
л |
1 |
1 7з |
0 |
не опр. |
0 |
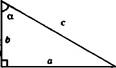
Тригонометрические функции в прямоугольном треугольнике а о , а Ь вш а = - сов а = - 4е а = г с4е а — -
Приближеные значения тригонометрических функций некоторых углов
|
а" |
5' |
10" |
20" |
30' |
40" |
50" |
60" |
70' |
80" |
85" |
|
|
8ш а •=> |
0,09 |
0,17 |
0,34 |
0,50 |
0,64 |
0,77 |
0,87 |
0,94 |
0,98 |
1,00 |
» соз а |
|
чТ « - |
0,09 |
0.18 |
0,36 |
0,58 |
0.84 |
1,19 |
1,73 |
2,75 |
5,67 |
11,43 |
« с*в а |
|
|
85' |
80" |
70" |
60" |
50" |
40" |
30' |
20' |
Ю- |
5" |
а* |
Для малых положительных чисел вш а =• о и (к а » а.
38
Таблица 13. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
Знаки тригонометрических функций по четвертям
|
вт а |
сов а |
1% а и с1% а |
|||
|
Ц / + |
+ \ |
у, |
+\ |
V |
+ \ |
|
\ — |
0 у х |
\ — |
0 \ * х |
V + |
о у" |
Способы нахождения значений тригонометрических функций числа (угла) а
|
по формулам |
по вспомогательному треугольнику |
|
|
сое а — -0,6; II четверть |
1б а — 3; III четверть |
|
|
|ет а| - 71-сов2а - Л-0,36 -0,8 вт а > 0 => вш а - 0,8 вта 4 1 е а = с о з а * 3 1 3 с4еБ а — г— — 4 - т *е« |
1 зш а сов а с*б а |
3 < 0 => вт а — - - = 7!о < 0 => сое а — — ТГо |
|
5 с1# а — - ^2 ; IV четверть |
> 0 => вш а — 0,1; I четверть с1е а - | |
|
|
1 1 + с 4, * 2 I 6 9 . 2 " * « " 1 4 4 вт а (ил а ) " Л вт а < 0 => вт а — ^ |сова|- Л - 8 Ш а - ^1-1739 - ^ 5 соз а > 0 =* сое а = 13 1 12 |
1 соз а *6 а с*в а |
799 > 0 =» сов а — - ^ о " ; К 799 > 0 => с*е а - 799 |
а " б
39
Таблица 13. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
|
Формулы сложения |
Формулы двойного угла |
|
С08 (X + у) - С08 X СОВ у - 81П X 8Н1 у |
С08 2Х — С082Х - 81П2Х |
|
С08 (х - у) = СОЗ X С08 у + 81П X 8Ш У |
сов 2х — 2 сов2х - 1 |
|
81П (X + у) — 81П X С08 у + С08 X 8Ш у 81П (X - у) = 81П X С08 у - СОЗ X 81П у 1-*?х4еу 2 к яп л + лп п е „ у * 2 + ! * + У * 2 ' *6 (* у) - — = * - , х * 5 + яп; я я „ У * 2 + яп; х - у # ^ +яп,11б2 |
сое 2х = 1 - 2 вт2х вш 2х = 2 81П х • соз X 1-4? х х * | + як , * 6 2 |
|
Формулы понижения степени |
Дополнительные формулы |
|
9 1 соз х = ^ (1 + сов 2х) |
1 + соз 2х = 2 соз2х |
|
81П2Х = | (1 - соз 2х) |
1 - сое 2х — 2 8Н12Х |
|
(8Н1 X + С08 X)2 — 1 + 81П 2х |
1 . „ 81П х • сое х — 2 8Ш 2х |
|
Формулы половинного угла |
Универсальная подстановка |
|
1 X . /1 + С08Х |со8 |= 2 Л 2 1 . х, /1 — СОЗХ 1 8 1 П 2 | _ ^ 2 |
'-«41) соз
х = '••41) |
|
X 81ПХ 1 - СОЗХ ё 2 " 1 + 0О8Х ~ 8И1Х ' х * пк, к е 2 |
•*© 81П X = х * я + 2пк, * Е 2 |
40
Формулы преобразования суммы в произведение
сов х + сов у - 2 сое ^ • сое —2^
„ . х + у х - у
С08 X - СОЗ У — -2 81П — ^ • 81П ^
_ . х + у х - у
81П X + 81П У — 2 81П ^ " 0 0 8 ~ 2
_ . х - у х + у
81П X - 81П у — 2 81П ^ " с о 8 —2
|
8т(х + и) |
. 81П(Х-{/) |
|
у СОВ х - соз у |
сое х • сов у |
|
8Ш(у+х) |
, . 81П(у-Х) |
|
с1г х + с1е у - - 1 — у . |
с*е х - с** у - - — у . |
|
в * " 81П X • 81П у |
Б е " 8111 X • 81П у |
произведения в сумму
сое х • сов у = | (сов (х — у) + соз (х + у))
81П X • 8Ш у — | (СОЗ (X — у) - СОЗ (х + у))
8Ш X • СОЗ у — | (ВШ (X + у) + 81П (X - у)) Формула дополнительного угла
I 2 2 а
а сов х + Ь вш х = V*» +Ь • сов (х - а), где соз а ГТ—2
+Ь
Таблица 14. ЛОГАРИФМЫ
Логарифмом положительного числа а по положительному и не равному единице основанию Ь называется показатель степени, в который надо возвести число Ь, чтобы получить а. \о^ь о. — с (а > О; Ь > О; Ь * 1) тогда и только тогда, когда Ъс — а
Основное логарифмическое тождество: Ь — а.
Примеры
|
51овв7-7 |
211**0'7=0,7 |
8 2 =(2) -(2 ' ) -3 3 -27 |
|
1ое2 8 - 3, так как 23 - 8 8 1с#д 27 -1,6, так как 92 - 27 |
1ок-0,2б 16 "* ~2, так как 0.25-2 - 16 1о82б 7б - 0,26, так как 2б0,26 - Л |
|
1°вв не определен, так как -7 < 0;
1°8"(-2) не определен, так как -2 < 0, -8 < 0;
1о&1 27 не определен, так как не выполнено условие 6*1.
Логарифмы по основанию 10 называются десятичными логарифмами: 1ое"ю а = \$ а.
Примеры.
1е 100 -.2; 1в 0,0001 - -4; 1& 100000000 - 8; 3 < 1$ 2166 < 4; - К 0,56 < 0.
|
а |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
ч? а » |
0,30 |
0,48 |
0,60 |
0,70 |
0,78 |
0,85 |
0,90 |
0,95 |
Логарифмы по основанию е называются натуральными логарифмами: 1оее а = 1п а. е = 2,718281828459045... иррациональное число; е = 2,7.
|
а |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
100 |
1000 |
|
1п а = |
0,69 |
1,10 |
1,39 |
1,61 |
1,79 |
1,95 |
2,08 |
2,20 |
2,30 |
4,61 |
6,91 |
42
Таблица 14. ЛОГАРИФМЫ
|
1<ОД1 1ов0 а код ат = т 1°еа \ -1 1ое а — — 1 . 1ое т а - — п п |
|
|
а |
т а т |
|
Основные соотношения Логарифм произведения: |
Дополнительные соотношения |
|
код (аЪ) - код а + 1оес Ь. Логарифм частного: код (а/Ь) - код а - \оес Ь. Логарифм степени: 1овс а* — к код а. Переход к новому основанию: код а код а код о Примеры 5108в5 =5,08в6 = 6 . |
код Ь код а 1оеп о _ 1оИт 0 код о код с " 1овт с код Ь • 1оет с - 1овт Ь • код с 1°8„ Ь . 1с«п а а = 6 |
^юбб 49 • 1ое7 25 - 71ое7 49 1оВб 25 - Л~2 - 2.
Сравнить: 4 и 6
Так как 6 = 4 и код 7 > 1обз 6, то 4 > 6
Сравнение логарифмов
Если О < а < 1 и 0 < хг < х2, то 1о%а хг > код х2.
(знак неравенства меняется)
Если а > 1 и 0<дс 1 < х2, то код хг < код х2
(знак неравенства не меняется)
|
Если 1 < а < Ь Если 0 < а < Ь < 1 Если 1 < а < Ь Если 0 < а < Ь < 1 |
и х > 1, то и х > 1, то и 0 < х < 1, то и 0 < х < 1, то |
код х > код х. код х > код х. 1о%а х < код х. код х < код х. |
43
Таблица 14. ЛОГАРИФМЫ
\о%ь а > 0 тогда и только тогда, когда положительные числа а и о лежат «по одну сторону от единицы*: а > 0 ;Ь>Ои(о- 1)(Ь - 1 ) > О.
1о%ь а < О тогда и только тогда, когда положительные числа а и о лежат «по разные стороны от единицы»: а > 0 ;о>Ои(а- 1ХЬ - 1) < О.
Примеры
|
1ое0,7 °«2 < 1оео.7 0,11 |
1ое6 2 < 1ое6 11 |
1ое5 7 > 1о88 7 |
|
1о 7 1о ео,2 > ео,8 7 |
1ое4 5 < 1ое3 5 < 1ое3 6 => 1ое4 5 < 1овз 6 |
|
Сравнить 1ое;4 15 и 717 . Так как 1ое4 15 < 4, а Д7 > 4, то 1ое4 15 < 717 .
Сравнить 1о^з 4 и 1ов;4 5.
|
/ способ. 1оез 4 |
? |
1ов;4 5 |
|
1оед 4 - 1 |
? |
1ое4 5 - 1 |
|
1ое3 | 4 5 Так как 5 > т , то о 4 4 , 5 , 5 т. е. 1оц3 4 > 1ов4 5. |
? |
1о б 4 | |
II способ. Рассмотрим функцию /(х) = \о%х (х + 1) — *П ^* * при х > 1.
1п х _ 1п(х + 1)
х + 1 х х 1п х - (х + 1) 1п (х + 1)
< 0
(1пх) х(х + 1 ) ( 1 п х ) при х > 1.
Значит, 1оЕз 4 > 1ое;4 б, так как функция /(х) убывает.
Таблица 15. УРАВНЕНИЯ
Корнем уравнения называется значение переменной, при подстановке которого в уравнение получается верное равенство. Примеры х3 + х — 0 — один корень: х — О.
(х2 + х - 12) • л/лТ+З = 0 — два корня: х - -3, х = 3. вт (ях) = 0 — бесконечное число корней 1 ^ 2 . х2 + 2х + 1 - (х + I)2 — верно при всех х е Д. х2 — х2 + 1 — нет корней (пустое множество корней 0 ) . Два уравнения называются равносильными, если множества их корней совпадают.
![]()
Примеры
|
х2 - х + 2 |
и |
х2 - х - 2 - 0 |
равносильны. |
|
х4 + 2 = -16 |
и |
81П ЗХ = 2 |
равносильны. |
|
Тх - 2х - 6 |
и |
х = (2х -б) 2 |
неравносильны. |
![]()
Неравносильные преобразования могут привести к:

|
х2 + х-1 |
4х-3 |
правильное решение: |х2 + х-1 = 4х-3 |
|
х-1 |
х-1 |
|
|
х2 + х - 1 = 4 х - 3 |
1х*1 |
|
|
х2 - Зх + 2 - 0 х — 1 и х — 2 «Посторонний» корень х — 1. |
Гх2-Зх + 2 - 0 \х*1 Ответ: х — 2. |
|
45
Таблица 15. УРАВНЕНИЯ
Методы решения уравнений
Разложение на множители
Произведение нескольких множителей равно нулю, если хотя бы один из них ноль, а остальные при этом существуют.
х - 1
х - 1
(х - IX*2 - 4) • 4х - О <=> х - ±2 х — 2 Ответ: 0; 1; 2. х - О х - 0
х>0
Замена переменной
(х + I) 4 + х2 = 1 - 2х <=> (х + I) 4 + (х2 + 2х + 1) - 2 «=>
|
\1 - (х + 1) 2 »0 2 1* + *-2 - 0 |
г - 1 * - -2 |
» * = 1 <=> |
х - -2 х - О |
*>0
Использование монотонности
2х + 5* = 29. Функция /(х) - 2* + 5* возрастает; /(2) - 29 =» х = 2 — единственный корень.
Сравнение обеих частей по величине
ЯП7 х - СОЗ22 X - 1 <=> 8Ш7 X " 1 + С0822 X, 9Ш X < 1 , , 22 _ ,
1 + соз х > 1
81П X — " 1 Г а и м - 1
С0822 X = 0 I СОЗХ — О <=> х - 2 + 2лп, пег
Использование однородности
3(х + 8)2 - 4(х + 8)(х2 + 2х + 2) + (х2 + 2х + 2)2 = 0.
Пусть х + 8 - а; х2 + 2х + 2 - Ь. Тогда За2 - 4аЬ + о2 = О,
2Ь+Ь ь о
а1> 2 = д ; а - о или а — д •
|
х + 8 - = х 2 + 2х + 2 |
Зх + 24 - х2 + 2х + 2 |
|
|
х2 + х - 6 = 0 |
х2 - х - 22 - 0 |
Ответ: -3; 2; |
|
хх - -3; х2 - 2 |
*8. 4 - 2 |
1-,/89 1 +,/89 2 ' 2 |
46
Таблица 15. УРАВНЕНИЯ
Линейные уравнения
(приводимые к виду ах — Ь)
|
а*0 |
а = Ь - 0 |
|
|
один корень |
бесконечное |
а = 0, о * 0 |
|
_ Ь |
множество корней |
решений нет |
|
а |
х е к |
|
Квадратные уравнения
(приводимые к виду ах2 + Ьх + с = 0 (а * 0))
Равносильными преобразованиями уравнение приводится к виду
( Ь у Ь - 4 о с „
=
^дс
+ г— • Наличие корней зависит от
знака выражения:
Б — Ь - Аас (дискриминант квадратного уравнения).
|
Б<0 корней нет |
0 = 0 ь х = _ один корень 2а |
Б > 0 два корня -ь - 4Ъ -ь + 4Ъ х 2а ' * 2а |
|||
|
а > о ^ |
1 |
а > 0 > |
ч / У
|
о > 0 » |
х о / |
|
0 |
* 0 * |
0 |
|
|
|
Частные формулы для решения квадратных уравнений
|
Приведенное квадратное уравнение х2 + рх + д - 0 (а - 1) |
Квадратное уравнение с четным вторым коэффициентом ах2 + 2кх + с - 0 (Ь = 2й) |
|
Если Б > 0, -Р ± л/О *1. 2 - 2 если О — 0, х — • |
О* = к2 - ас (О* - | О) _ -А ± л/о*
Если
О > 0, дс1? 2 -
а |
Неполное квадратное уравнение
|
ах2 + с - 0 (о - 0) |
аде2 + б* = 0 (с = 0) |
а*2 = 0 |
|
Если ас > 0, решений нет; если ас < 0, х <- ~ |
дс(ах + Ь) = 0 два корня: Ь х — 0, х = -- . а |
один корень х - 0 |
47
Таблица 15. УРАВНЕНИЯ
Алгебраические уравнения высших степеней
(приводимые к виду Дх) ~ О, где /(х) — многочлен степени выше 2)
Разложение на множители Подстановка
2*^ - х + 2 - О (биквадратное уравнение) х2(х - 2) - (х - 2) - О х4 - Зх2 + 2 = 0; х2 - I
(х- 2Х*2-1) = 0=>х = 2;х-±1 - 3* + 2 -
1; г - 2 х - ± 1 ; х = ±.У2
|
Применение схемы Горнера х8 - 4х2 + х + 6 = О |
Использование монотонности х3 + х - б-Уб = О 3 |
|
1 |
-4 |
1 |
6 |
|
1 |
-5 |
6 |
0 |
|
1 |
-3 |
0 |
|
|
1 |
0 |
|
X + X бл/б
-1 => х - -1 Функция ^(х) — х3 + х возрас
2 => X = 2 тает на В; Р(4Ъ) = 6ТЕ =>
3 =» х = 3 х = -Уб — единственный корень.
|
Возвратное уравнение 2х4 - 5х3 + 6х2 - 5х + 2 - О Так как х = 0 не является корнем, можно делить на х2. с О 2х2 - бх + 6 - - + 4 = 0 . X 2 ' X 2(х2 + ^ ) - 6 ( , + 1) + в-0. Подстановка: у = х + - ; г / 2 - 2 - х 2 + Л 2(у2 - 2) - 5«/ + 6 = О 2у2 - 5у + 2 - О |
Использование однородности Зх2 + 4х(х2 + Зх + 4) + (х2 + + Зх + 4)2 = О Пусть у = х2 + Зх + 4. Тогда Зх2 + 4х{/ + у* - 0. 3_| Решаем относительно х: 1 х = -у;х = -д{/. Следовательно, х - - х 2 - З х - 4 Зх = -х2 - Зх - 4 Ответ: -2; -3 ±„/б. |
|
Уравнение л//(х) = #(х) равносильно системе: /(х) = ц\х) 8(х)>0 |
Уравнение Л(х) = 40{х) равносильно системе: / ( * ) = е(х) /(х)>0 (или 8(х)>0) |
Неравенства в системах, как правило, проверяют, а не решают.
48
Таблица 15. УРАВНЕНИЯ
Иррациональные уравнения
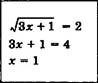 Простейшие
л/1
- 2х = -5 корней нет
Простейшие
л/1
- 2х = -5 корней нет
Возведение обеих частей уравнения Замена переменной в степень
|
4бх + 6 + л/Зх + 4 = 2 с* 5х + 6>0; Зх + 4>0 5х + 6 + Зх + 4 + <=> + 2л/(5х + 6)(Зх + 4) - 4 5л; + 6^0 -/(5х + 6)(Зх + 4) = -4х - 3 |
42 -х = Зх + 8 Пусть у - л/2 -х 0. Тогда х - 2 - у2 и у - 3(2 - у2) + 8 о У^О Зу2 + у - 14 = 0 <=> у = 2 <=> 42-х 2 <=> |
о х = -2
5х + 6>0; - 4 х - 3 > 0
(5х + 6)(3х + 4) = (-4х - З)2 о х = -1
Уравнения, связанные со степенной функцией
_ 2/3 . 1 / 8 с „
5х + х -6 = 0
Г х>0
I у — х ^0
5у2 + у - 6 = 0 =* =>у = 1;у = - | < 0
х1/3 = 1 => х - 1
б8*/? + 37х - 6 = 0
3
у = 7х е й
5у2 + у - 6 = 0
8 З
7х - 1, у = л/х - •
Г§"\3 216
\Ъ) 125
216 Ответ: х = 1; х = 125
2 4
8 3 . X X = 4 х » 0
2+4
3 3 . х = 4
х2 = 4 х = ±2
Ответ:
х - 2 .
49
Показательные уравнения
Решение простейших показательных уравнений основано на монотонности показательной функции у = ах ( а> 0, а * 1, Щу) = Я,
Е(у) - (0; +°о)).
Простейшее показательное уравнение ах — Ь при Ь > 0 имеет единственное решение, записывающееся в общем виде х — 1о&а о.
При Ь < 0 решений нет.
|
6х = 36 |
2 * = 1 |
100* = 10 |
10* = 3 |
е* = 2 |
625* = -25 |
|
х - 1оя6 36 |
** 8 |
* - 1оеюо ю |
* = 1вЗ |
х = 1п2 |
решений |
|
* « 2 |
*=1ое2(1/8) х - -3 |
х - 0,5 |
|
|
нет |
Уравнения вида а"*> — аЛ*' равносильны уравнению /(х) — е(х).
Методы решения показательных уравнений
|
Приведение |
Логарифмирование |
||
|
к одному основанию |
обеих частей уравнения |
||
|
5* • 0,2 - 1252 |
61/х .2* =12 |
||
|
Зх 1 |
Логарифмируем по основанию 2: |
||
|
5* • Б-1"- б 2 • б 2 |
^ 1о&2 6 + х = 1об2 12 о |
||
|
Зх + 1 |
о 1 + 1ое2 3 + х2 = (2 + 1ое2 3)х дс2 - (2 + 1ов2 3)х + (1 + 1ог2 3) - 0 Ответ: х — 1; х - 1 + 1ое2 3. |
||
|
В * " 1 - 6 2 Зх + 1 |
|||
|
2 :=> х = -3 |
|||
|
Выкесекие |
Составление отношения |
Замена переменной |
|
|
за скобку |
4* + 3* _ 1 - 4* " 1 + 3* + 2 |
25* + 5* + 1 - 6 - 0 |
|
|
7х + 7х + г = 350 7*(1 + 72) = 350 7 * = ^ - 22 = 7 1 + 7 х = 1 |
4* - 4* - 1 = 3* + 2 _ з* - 1 4* - г(4 - 1) - 3* " ЧЗ3 - 1) 4* - 1 • 3 = 3* " 1 • 26 4*"1 26 (4\х ~1 26 |
5* = у > 0 у2 + Ъу - 6 = 0 у - 1; у - -6 < 0 5* - 1 =» х = 0 |
|
|
3 х-1 " 3 ^ 3 26 дс = 1ое4 3" + 1 3 |
|||
Таблица 15. УРАВНЕНИЯ
•Завуалированное » Использование Использование обратное число однородности монотонности
{Л - 2 У + (Л +2)*- 18 3 • 16* - 12* - 4 • 9* 2* + б* - 29
(Л ~ 2)(Л + 2) - Делим на 9* > О: Пх)возрастает на - 2* + б* В.
- 6 - 4 - 1
Г(2) - 29 =»
Пусть (Л ~ 2)* - у > О х — 2 — единст
венный корень.
У + ^ - 1 8 = > 1 / - 9 ± 4 7 5
( Л - 2 У - 9 - 4 Л -
Пусть ^| ^ - у > О =*
-(Л - 2 ) 2 = > х - 2
З у 2 - у - 4 - 0 = >
(Л - 2 ) * - 9 + 4,/5 -
4
-(л/б +2) 2 -(7б -2)_2=> у - д ; у - - к о = > х - - 2
* 4
Ответ: 2; -2. (1) = > 1
3 * "
Логарифмические уравнения
Решение простейших логарифмических уравнений основано на монотонности логарифмической функции у — \о&а х (а > 0; а # 1; Жу) - (0; +оо); Е{у) - В).
Типы простейших логарифмических уравнений 1) 1оца х = Ь при всех допустимых а имеет единственное решение
2) 1ов0 (/(х)) — Ь равносильно уравнению /*(х) — а".
3) 1ов0 (/(*)) — в(х) равносильно уравнению /*(х) — а***).
Л*) " **(*) 4) 1оя;в (Ах)) — 1о80 (в*(х)) равносильно системе Л*)>0
« • ( * ) > о
Причем любую из двух последних строк можно (и, как правило, нужно) опустить.
В логарифмических уравнениях, как правило, совершенно не обязательно находить области существования функций, входящих в уравнение. Достаточно проверить, какие из полученных корней уравнения системы удовлетворяют неравенствам в системе.
51
Уравнения, сводящиеся к типу 4
\о%2 (х2 + х - 2) = 1 + 1ов2 х <=> 1ов2 (х2 + х - 2) - 1ов2 (2х) <=>
2 х - -1
х + х - 2 2х 2 = 0 2 х - X х = 2 ° * "
2х>0
х>0 х>0
Потенцирование уравнений, сводящихся к типу 4
Замена переменной
(1е10-1ех)2 + 1ех = 7 у - 1? х => (1 - у)2 + у - 7 =э
' = 3 , ч?ж = 3
1у = -2 1« х - -2 Ответ: х - 1000; х 0, 01.
1об1 (х + 1) + 1ов3 ^ ) - 2 - 21061 (х2) »
<=> 1о§х(х + 1) - = 1оегд - иэвлО* ) <=>
|
х>0 |
|
|
|
. 2(х + 1) |
. 1 о |
|
|
I х х>0 |
з 9х2 |
|
|
|
-Д1 |
- з |
|
2(х + 1) 1 — 9х 2 |
о х — |
|
3 8 3 3
Уравнение с неизвестным в основании логарифма
1о%х б - 3 <=>
х>0 х*1
X — б о х - з/б
Ответ: У
1ое{-х) 26 = -2
х2*1 х<0
1ое г х = 0,5 о х>0 х*-1
2 0,5 (-хГ2 = 25
(X ) = X х<0 х>0 х*-1
х*1 Г х>0 2 = _1_
Х*-1 1 х*1 * 25
1*1 = *
Ответ: х е (0; 1) и (1; + о о ) . Ответ: х — - г .
о
Таблица 15. УРАВНЕНИЯ
Тригонометрические уравнения
|
|
81П х — а |
|
С08 х = а |
||
|
Н>1 |
1 |
М>1 |
|
||
|
решений нет |
у 1 я-агс8т
а Ж |
•^^н-сат а |
решений нет |
V |
, . а гс сое а 1 Л х 1 - |
|
\ 0 |
11 х |
\ 0 |
а \ 11 х "-агссоа а |
||
|
|
х = (-1)лагсвт а + пп. |
|
х = ± агссов а + 2лп, пег |
||
При |а| < 1: л При |а| < 1: я л 2
~2 < агсзт а< ^ 2 О < агссоа а < я
сов( агссов а) = а
81п(агсзт о) = а агссоз (-а) —
агссоа а = я - агссов а агсзт (-а) =
= -агсзт а агсвт а + агссоа а = ^
|
= а |
= а |
|||||||
|
|
\ 1 ^агс |
|
1 |
а |
||||
|
|
\( агсс1е о |
|||||||
|
1 0 |
( |
|
1 0 |
• \ |
||||
|
1 \^ |
г |
11 X *- |
\ • п+агсс1в <»^^^ |
' I » 1\ X |
||||
|
х = агс*^ а + лп, п б 2 |
X = агсс1& а + лп, п е 2 |
|||||||
|
При любом а: п л 2 < агс*еа < г> *В (агс*е а) = а агс*е (-а) = = -вгсЬе а |
а |
0 |
1 •Уз |
1 |
|
При любом а: 0 < агсс1е; а < л с1& (агсс1& а) = а агсс1§ (-а) = — л - агсс4е; о. |
||
|
|
0 |
я 6 |
4 |
я 3 |
||||
|
агсс1е о |
я 2 |
я 3 |
л 4 |
л 6 |
||||
|
агсц* о + агссге а = 2 |
||||||||
53
Частные решения
|
8 Ш 1 У г |
|
8Н1 |
х - 1 |
с о е |
|
С08 |
. с - 1 1 Л . |
|
|
N х -= Я П , п е г |
У
|
л * = 2 п е г |
и " + 2яп, |
N л = * 2 п е г |
V' пп. ' V |
N х - 2го п е г |
1, |
|
|
81П ( / ( х ) ) - а |
соз ( / ( х ) ) - а |
Ч (Л*)) - а |
||||||
|
при |а| < 1: / ( х ) — а г е н т а + 2лл / * ( х ) — я - а г с в т а + + 2яп п е г |
при |а| < 1: / ( х ) — ± в г с с о з а + 2лп п е г |
при в с е х а: / ( х ) - агс1# а + ял п е г |
||||||
Методы решения тригонометрических уравнения
Тригонометрические уравнения, приводимые к уравнениям от одной тригонометрической функции одной переменной, решаются (как правило) подстановкой.
|
ВШ2 х + 4со8 х - 2,75 1 - соз2 х + 4сов х - 2,75 сов х — I; И < 1 I2 - 41 + 1,75 - О * - | > 1 х - ±д + 2лл, п е г |
1е; * + Зс<# х - 4 ч Т * + ^ - 4 <«х - I I2 - 4* + 3 - О * - 1; * - 3 л . X — 7 + Я П 4 |
п, А е г |
|
х - агс*е 3 + пк |
||
соз х + соз 4х = 0,25
0,5(1 + соз 2х) + 2со82 2х - 1 = 0,25 сое 2х = ы; |и| ^ 1
4и2 + и - 1,5 - 0
1 3 и : и =
" 2 -4
1 3 я
х - ±« а г с с о 8 (~2) + яп; х - ±= + яп, п
Таблица 15. УРАВНЕНИЯ
Однородные тригонометрические уравнения и уравнения, сводящиеся к ним
|
2вш х • сое х - сое2 х — 0 СОВ Х(281П X - С08 х) - 0 |
5зт2 х + вт х • сое х - 2С082 х - 2 бет2 х + вш х • сое х - 2сов2 X - |
|
с о в х - 0 = > х « 5 + ял, п е г |
- 2сов2 х + 2вш2 х |
|
См |
Звт2 х + вш х • сов х - 4соз2 х -0 |
|
2вш х - сое х — 0 Корни уравнения соз х — 0 не |
сов х * 0. Делим на соз2 х: о |
|
удовлетворяют этому уравнению. |
3*а^ х + * в * - 4 = 0 = > |
|
Делим на сое х * 0: |
*вх-1; Ь в х - - ^ |
|
2*? х - 1 - 0 |
о |
|
«-*"! х - агс1^2 + яп, п е г |
я 4 х = ^ + кп\ х - -агс*Вд + яЛ; п , * е г |
Разложение на множители
72 81П X • С08 X - 2 — С08 X -2^2 81П X ^ 81П х • соз х - сое х — 2 + 2 л/2 81П X — 0 соз х(72 вт х - 1) - 2(1 - 72 вт х) - 0
(72 вт х - 1)(сов х + 2) = 0
72втх - 1 = 0
. созх + 2 - 0
1
81П X = - =
72 х = (-1)" • 5 + яп;
п е г сое х = -2, корней нет.
Уравнения, решаемые на основе условия равенства тригонометрических функций вт /(х) = 81П <р(х) СОЗ Л*) = с°8 ф(х) *е Л*) = * е ф(*)
/(х) = ф(х) + 2яА Дх) = <р(х) + 2яп Нх) = ф(х) + яп
/(х) г, - я - г ф(х) + 2лп Лх) = -ф(х) + г, г 2яА \
п е к е ф(*) * + я/
п е я е п е г, /. е г
55
Уравнения с обратными тригонометрическими функциям л
|
агент х — а |
агесоа х — а |
агсге х — а |
агсс1е; дс — а |
|
71 К ~2<а*2 X = 81П а |
0 $ а < л ж = сое а |
л л - - < а < = 2 2 дс = 1е а |
0 < а < л дс = с1в а |
|
71 ТС а < - ^ или а> 2 решений нет |
а < 0 или а > л решений нет |
л • . я а % - 2 или а > 2 решений нет |
а < 0 или а > л решений нет |
Уравнения с параметрами
2х + 3 .
Решить уравнение —х - а —
= 0 для каждого значения а.
Г2х + 3 - О
Данное уравнение равносильно системе
| * - а*О
ДС — —; х*а.
Ответ: при а * х = - « ц , при а = р е ш е н и й нет.
Найти все такие значения р, для которых один из корней уравнения х2 — Зрх + 2р2 — О равен 1, и для каждого такого значения р найти остальные корни.
Для того чтобы один из корней уравнения был равен 1, необходимо и достаточно, чтобы I2 - Зр • 1 + 2р2 = 0, т. е. 2р2 - Зр + 1 — О,
1
=
Р1 " 1. Р2 2 *
При р = 1 х2 - Зх + 2 - О, X! - 1, х2 = 2;
1 2 3 . 1 Л , 1
+ 1 2 = при р = 2 * ~ 2 * 2 " * * " * * 2 "
Ответ: прир — 1 и прир — |- Прир — 1 х2 — 2; прир — | х2 — |.
Таблица 15. УРАВНЕНИЯ
Уравнения с параметрами (продолжение)
При каких значениях а уравнение 4* - (а + 2) 2х + 2а = О имеет а) хотя бы одно решение; б) ровно одно решение; в) более одного решения? Сделаем замену 2х = I, г2 - (а + 2) • г + 2а = 0, 1г = а, 12 - 2.
2х "= 2, х = 1 при любом а.
2х — а, при а < О решений нет; при а > О х = 1ов2 а.
Заметим, что при а = 2 х = 1 совпадает с первым корнем. Ответ: а) при всех значениях а; б) при о ( О и о = 2; в) при
0 < а < 2 и о > 2 .
При каких значениях Ь уравнения вш2 х - (3 + Ь) вт х + ЗЬ — О и х2 — о равносильны?
Если первое уравнение имеет решение х0, то оно имеет и бесконечно много решений вида х0 + 2кк, т. е. не может быть равносильно уравнению х2 — Ь, имеющему не более двух решений.
Уравнения равносильны, если они оба не имеют решений.
Уравнение х2 = Ь при Ъ < 0 не имеет решений, второе уравнение
Г81П х = Ь
равносильно объединению не имеющему решений
1.8т х = 3,
при Ь < -1 или Ь > 1. Таким образом, оба уравнения не имеют решений, т. е. равносильны при Ь < -1.
Ответ: при о < -1.
Найти все значения р, при которых сумма действительных корней уравнения х2 - рх + 3 — 0 меньше пяти.
При Б > 0 хх + х2 = р.
Гр<5 ГР< Гр< 5
(-оо;-2.УЗ]и[2Л;5). 12 > О
Ответ: р е (-«э; -2./3] и [2-ТЗ; 5)
57
Таблица 15. УРАВНЕНИЯ
Уравнения с параметрами (продолжение)
При каких значениях т уравнения х2 + Зх - т - О и тх2 + х + 3 - О имеют общий корень? Для каждого такого значения т найти этот корень.
Пусть I — общий корень уравнений. Составим систему двух уравнений с двумя неизвестными (* и т ) :
и + 3* -' ° т - О Ш* + 3) - т (1(1 + 3) - т
[т12+ « + 3 - 0 *(* + 3) - т Г т - 0
и = -1
+ 3
2 * * 1 2
Ь + 3 - - т * 1т - -тг I
При т — О \-оК л *"* * " общий корень ж — -3;
[х + 3 - 0 при *; - -1 т = (-1М-1 + 3) - -2. Где2 + Зх + 2 - О
^ общий корень х — -1.
1-2х + х + 3 - О
Ответ: при т — -2 х — -1; при т — 0 х — -3.
Найти все пары действительных чисел а и Ь, при которых уравнение |х - 1| + |х + 3| = ах + Ь имеет бесконечное множество решений.
-2х - 2 при х<-3
|х - 1| + |х + 3| = 4 при -3 < х < 1
2х + 2 при х > 1
Уравнение имеет бесконечное множество решений, если ах + Ь тождественно равно -2х - 2, т. е. а — -2; Ь — -2.
Аналогично ох + о тождественно равно 4, т. е. а — 0; Ь — 4. Аналогично а - 2; Ь - 2. Ответ: (-2; -2); (0; 4); (2; 2).
При каких значениях т уравнение х2 - тх + 1—0 имеет два корня, расстояние между которыми на числовой оси равно 2?
Уравнение имеет два различных корня, если Т> > 0, т. е. т — 4 > 0. Расстояние между корнями на числовой оси равно 1*1 ~ *г1 = т. - 4Ъ т + Щ = 70.
Г т - 4>0 Г т - 5 - 272
Имеем систему
• / 2 - 4 = 2 [ т = -272 Ответ: т - 2 7 2 , т =- 272.
58
Таблица 16. МЕТОДЫ РЕШЕНИЯ СИСТЕМ УРАВНЕНИЙ
Метод подстановки
|
х + Ьу = 6 х2 + Зу = 4 |
6 - х У = х2 + 3 |
6 - х 5х2 - Зх - 2 - О |
|
6 - х |
|
|
6 2 б 1 |
о |
![]() Г 2
х » - -
Г 2
х » - -
32
[У " К
Гх = 1
\у - 1
2 32
Ответ: ( - ^ ; (1; 1).
[2х + у = я у = я - 2х
[сов(Зх - 2у) = 0,5 соз(Зх - 2я + 4х) = 0,5
2яА
х = -5- +21 + 7
19я 4лА
сов7х = 0,5 21 7
у = я - 2х я 2яп п, *ег
"21 + 7
23я 4яп
21 7
_ /'я 2лА 19я 4яАЛ
0 т в е т + ; Ч 2 1 — Т Г ~ " Т >
Л__я_ 2яп 23я _ 4пп\
{ 21 + 7 ; 21 7 / п ' А е г -
59
Таблица 16. МЕТОДЫ РЕШЕНИЯ СИСТЕМ УРАВНЕНИЙ
Метод алгебраического сложения
|
5х + 2у = 9 умножим на 3 7х - Зу — 1 умножим на 2 |
15* + 6у = 27 уравнения 14х - 6у = 2 |
|29х = 2 9 Гх - 1
** [7х - Зу - 1 [у = 2
Ответ: (1; 2).
сое дс соз у — 0,75 сложим уравнения системы
{ зш дс бш у — 0,25 вычтем уравнения системы
Г сов дссоз у + атх вш у = 1 [сов(х - у) — 1
[соз хсоз у - зтх вш у = 0,5 [соз(х + у) — 0,{
х - у = 2лА
К
х + у + 2яп
х — у = 2кк
л л <=>
х + у = ±5 + 2лл
3 х - у = 2лА
* + У - ~5 + 2 л п
Ответ: (^ + п(п + А); ^ + л(п - А)); ( - | + л(л + А); - | + л(п - А)), л, А е 2.
Таблица 16. МЕТОДЫ РЕШЕНИЯ СИСТЕМ УРАВНЕНИЙ
Дополнительные методы
|
Применение теоремы Виета Гх + у - б |
Симметрические системы |
|
|
|
замена |
|
|
[х-у - 4 |
\х2 + у2 - Зху = -1 |
х + у - р |
|
х,у — корни уравнения: а2 - Ьа + 4 - 0. а - 1; а = 4. |
1х + у - ху - 1 г 2 Г(У - 2?) - За = -1 |
ху - 9 |
|
|
||
|
Ответ: (1; 4); (4; 1). |
1р - 9 - 1 |
|
![]() Сведение
к объединению более простых систем х2 -
5ху + 4у2 = О (х-у)(х-4у) = О
Сведение
к объединению более простых систем х2 -
5ху + 4у2 = О (х-у)(х-4у) = О
Зх2 - 2у = 8 Зх - 2у = 8
х - у = О Зх" - 2у - 8 х -4у =
(2)
Зх2-2у - 8
Г* - У (2; 2)
Ш 2
1зх -2х-8 = О " ("4/3; -4/3)
|х = 4у (1 + ./385 1 + ./385Л (1 -,/385 1 -./385^
<2М 2 0 « ( " й - : — ^ ; —48 1;
2
24у -у-4
Использование однородности
2 2
Умножим
первое уравнение на (-3), {Зх -ху + у = 5 второе
— на 5 и сложим. х2 + 2у2 - 3
![]() 15 - 4х2 +
Зху + 7у2 « О
15 - 4х2 +
Зху + 7у2 « О
[ - 9х2 + Зху - Зу2 х2 + 2у2 = 3
|
Гу + * - О 1.x2 + 2у2 - 3 |
г(1; -1) и-1.1) |
1бх2 + 10у2 = 15
|
|
и+ 2у = 3 |
(_ТЛ 4^3 ^ .1 ^ ; " Ч |
|
Ответ: (1;-1); <-!;!); |
) ; ( - 1 * |
) . |
![]() (у + х)(7у-4х) - О
(у + х)(7у-4х) - О
2 + 2у2 = 3 Г7у-7у2 - 4х = О [ 9 • 9 )
61
Таблица 17. НЕРАВЕНСТВА
|
Строгие неравенства |
Нестрогие неравенства |
|
Число о > Ь (а больше о), если разность (а - Ь) положительное число. Если а < Ь, то Ь > а. В этом случае разность (а — Ь) отрицательное число. |
а< о |
Свойства числовых неравенств
|
а, Ь — любые числа |
а,Ь — положительные числа |
|
Если а > 6 и о > с, тоа>с (свойство транзитивности). Если а > Ь, то о + с > Ь + с (с е Я). Если а > Ь и с положительное число, то ас > Ьс. Если а > Ъ и с отрицательное число, то ас < Ьс. Если о>Ьис>с1,тоо + с>Ь + А |
. . 1 1 Если о > о > 0, то - < г • а о Если а > о > 0 и с > а * > 0 , то ас > Ьй. Если а > о > 0 и »л«=ЛГ, то ат > Ьт. Если а > о > 0 и те Л, то "Та > "То. |
Двойное неравенство (а < 6 < с)
Сложение двойных неравенств а ^ о < с, р< т < д => а + р<г'>+т<с + д
Умножение двойных неравенств с положительными членами
0< а < Ь <с; 0 < р < т < д =* ар < Ьт < сд
Методы доказательства неравенств
Составление разности (если разность двух чисел положительна, то уменьшаемое больше вычитаемого).
Метод использования известных неравенств.
Метод усиления (использование транзитивности).
Использование монотонности функции, применение производной.
Пример. Доказать неравенство: ех > 1 + х при х > 0. Рассмотрим функцию /(х) - е* - 1 - х. /"(х) - ех - 1 > 0 при х > 0. Следовательно, /(х) возрастает на [0; +«э). Но /(0) - 0. Значит, /Чх) > 0 при х > 0. При х — 0 неравенство обращается в равенство. Итак, ех - 1 - х > 0, то есть ех > 1 + х при х > 0.
Таблица 17. НЕРАВЕНСТВА
Сравнение средних величин положительных чисел
(а > Ь > О, а4 > 0, п е ЛГ)
|
Среднее арифметическое |
двух чисел а+Ь 2 |
п чисел а1+а2 + ...+ап п |
|
Среднее геометрическое |
двух чисел ТаБ |
п чисел Фг « 2 — ап |
|
|
двух чисел |
п чисел |
|
Среднее гармоническое |
2аЬ 2 |
п |
|
а+Ь 1 1 а о |
1 . 1 1 — + — + ... + — а а а 1 2 п |
|
|
Среднее квадратичное |
двух чисел |
п чисел |
|
/ 2 ^ ь2 4 2 |
/ 2 2 2 К+а2 + ... + а„ V /1 |
. /а2 + о2 ^ а + Ь ъ Г - ъ 2
а Ь
(верно и для п чисел)
Линейные неравенства
(приводимыек виду ах > Ь; ах> Ь; ах < о; ах ^ Ь)
|
3 • х > -6 |
- 5 x ^ 1 |
0 • х < 2 |
0 • х > 8 |
|
х > -2 |
1 |
|
|
|
х е (-5 !; + ° о ) |
X е ( - 0 0 ; -1' |
х с К |
х б ( 0 ) |
(ТВ - 77)х>(7б - 77) х < 1, так как 7б - 77 < О х <= (-оо; 1)
63
Таблица 17. НЕРАВЕНСТВА
Квадратные неравенства
(приводимые к виду ах2 + Ьх + с > О, ах2 + Ьх + с < О, а > 0)
Для решения квадратного неравенства вычислим дискриминант О — Ь2 - 4ас и определим корни квадратного трехчлена.
|
Неравенство |
в < 0 |
с - 0 |
в > 0 |
|
|
V У |
|
|
|
X |
|
|
|
|
ах2 + Ьх + о 0 |
х е к |
* е (-оо; х0) и и (х0; +оо) |
х е (-оо; Х 1 ) и и (х2; +оо) |
|
ах2 + Ьх + с < 0 |
решений нет |
решений нет |
дс е дс2) |
Простейшие иррациональные неравенства
|
|
*[х < а |
4х > а |
|
а < 0 |
решений нет |
дс > 0 с* дс е [0; +°°) |
|
а = 0 |
решений нет |
дс > О <=* х е (О; +оо) |
а > 0 о < х < а2, х е [0; а2) дс> а2 <=> дс е (а2; +°°)
|
Жх~) < е(х) |
Жх] > е{х) |
Жх~) > ЛКх~) |
|
|
равносильно системе |
равносильно объеди нению систем |
равносильно системе |
|
|
8(х) > 0
Пх) > 0 |
|
' Ых ) < 0 \Нх) > 0 г*(*) > о \Пх)>е2(х) |
Шх)>Щх) \в(х) > 0 |
Простейшие показательные неравенства
|
|
а* < т |
а* > т |
аЛ*> < т |
|
|
т < 0; а > 0, а Ф 1 |
нет решений |
х е к |
нет решений |
|
|
т > 0; а > 1 |
дс < \о%ат |
х > к>е0»п |
Лх) < \о%ат |
/*(х) > \о%ат |
|
т > 0 ; 0 < а < 1 |
х > 1оеат |
* < 1огат |
/(х) > 1оеа/ге |
/(х) < 1ое;0т |
|
а««) > «*<*> |
при а > 1 равносильно неравенству /(дс) > я(х) при 0 < а < 1 равносильно неравенству /(х) < #(х) |
|||
Таблица 17. НЕРАВЕНСТВА
Простейшие логарифмические неравенства
|
в е я |
1оеа* < т |
1о%ах > т |
1о&,Л*) < т |
|
||
|
а > 1 |
Г т 1 х < а 1х>0 |
х > ат |
\Пх)<ат |
/(х) > ат |
||
|
0 < а < 1 |
х > ат |
С т 1х<а \х>0 |
Цх) > ат |
{/(*)< ат [Кх)>0 |
||
|
\о%а1(х) < 1ое;а$(х) |
1о (х)0(х) 8я(*)Л*) < 1овя |
|
||||
|
при а > 1 при 0 < о < 1 равносильно равносильно системе системе (У(*)<*(*) Г(х)>е(х) 1Л*)>0 *(х)>0 |
равносильно объединению систем неравенств: Я(х)>0 Я(х)>1 Н(х)<1 Нх) <е(х) и /(х)>0 |
|
||||
е ( х ) > о
Примеры простейших тригонометрических неравенств
|
8 Ш х < -1,3 |
В Ш х > -1,3 |
8И1 х < 71.3 |
81П х > 71,3 |
||
|
решений нет, -1 < вш х ^ 1 |
х е В |
х е В, так как вш х < 1 < ТПЗ |
решений нет |
||
|
81П X < -0,6 |
в т х > -0,5 |
||||
|
У |
|
У |
|
||
|
( 0 |
\1 х |
0 |
| 1 |
||
|
V -0,5 6 |
1 |
1 6 7л\^ 1 6 х _ - 1 |
• — / л 1 Т 6 |
||
— у л х 6 ^2лп - ; 2яп - ^ I 2пп - ^; -р- + 2лп I
пен г
66
Таблица 17. НЕРАВЕНСТВА
|
81П X < ~2 |
81П х> ~2~ |
||
|
2 тс »( ЗУ 2 |
7тс |
У 2я 3/ 2 |
|
|
V 0 |
|
\ 0 |
У1 * |
/"„ 2л 7л „ Л ( л 2л л
хе1 2лп + -д-; -д- + 2лп I I 2яп + д; -д- + 2лп I п е 2 п е г
|
соз х < -З0,7 |
сов х < 1п 3 |
л СОВ X > -д |
соз х > е0,2 |
|
решений нет |
х е к , так как сое дс < 1 < 1п 3 |
х е В, так как соз х ^ —1 > -д |
решений нет, так как е0,2 > 1 |
соз х < —~2~ сое х < 0,5
|
|
|
* б ( 2 я п + 5р ^ + 2яп) х е ^2яп + д ; -д- + 2лп I л е г п е г
соз х > 0 соз х > 0,7
|
|
У |
^~~Ч^ агссов 0,7 Л |
|
\ |
0 |
0,7|11 * ^^^-агссов 0,7 |
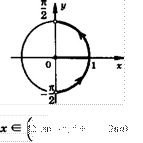 х
е (2лп - агссов 0,7;
х
е (2лп - агссов 0,7;
п е г агссов 0,7 + 2лп) п е г
Таблица 17. НЕРАВЕНСТВА
7з I? х < -2~1
|
|
|
^лп - ~ яп - агс*в;
с1# ж > 1
|
|
|
^лп; ^ + лл^, л е й
х е ^ л л - ^ ; ^ + я п ^ , л 6 2
Более сложные примеры решения тригонометрических неравенств М г ) < «
![]() Зл
Зл
г - 2 х - т
соз * < О
* е ^2ял + ^; у + 2лл)
п
о . Зл Зя
+ < <
2лл 2 Т " 2 ~
, 7 л 1Бл , _ _ лл + ^ < х < -^г + яп, п е г
67
Таблица 17. НЕРАВЕНСТВА
|
81П X > СОВ X |
; з |
|
|||
|
У: |
^ в т * — СОВ X |
У |
, к |
Л |
|
|
|
|
т \ ш \ |
/ |
|
|
|
4 |
• ' л 0 и ** |
V / % / |
ч° \ А — Л \ 3 |
1 -Л |
х |
2лп + 7 ^4 х С Щ4 + 2яп, _ Г*е*^Тз лег
я л п „
[л п ~ 3' з яп > ге *
бсов ж - соз х - 1 < О
Пусть у — соз дс. Тогда
Гбу2-у - 1<0
1 1
< { / <
"8 2 •д < соз х < ^
![]() ас е ^2яп - агссов (-|); 2лл - агссов |-) и
ас е ^2яп - агссов (-|); 2лл - агссов |-) и
и ^2лп + агссоз |; 2яп + агссоз (-| ))
ИЛИ х е ^2лп - агссоз (-|); 2лп - Ц-) и
и (| + 2лл; агссоз (-|) + 2лп), пег
Таблица 17. НЕРАВЕНСТВА
МП X - 81П 2х ^ О
вшх ( 1 - 2 соз ж) < О
![]() Используем метод интервалов на тригонометрической
окружности, считая х е [0; 2л). Р(х)
•= 8ШХ (1 - 2 С08*)
Используем метод интервалов на тригонометрической
окружности, считая х е [0; 2л). Р(х)
•= 8ШХ (1 - 2 С08*)
л 5я
Р(х) = 0 => х = 0; л;
3' 3
х е |^2лп + ^; л + 2лп^ ^
и[^2лп + ^р 2я + 2лп|, л е 2
Примеры неравенств с обратными тригонометрическими функциями
|
агссов х < -5 решений нет, так. как 0 ^ агссоз х ^ л |
аггсов дг > -4 ж 6= [-1; 1] |
л агссов ж < д х 6 (0,5; 1] |
агссоз х > 1 дс 6 [-1; сов 1) |
|
агсвт х < л х 6= [-1; 1] |
агсвт дс < -1,7 решений нет, |
^ л агсвт х < -г 6 |
агсвт х > 0 * еЕ (0; 1] |
|
|
так как л _ я ~2 ^ агсзт х < ^ |
х 6 [-1; -0,5] |
|
|
атсЬц х < 2 г е я , так как л агс л ~2 < *6 ж < 2 |
агс1е; д: > 5 решений нет |
агс*е д: ^ * е (-°°;*е^] |
агс*б * < 0 X е ( - 0 0 ; 0] |
69
Таблица 17. НЕРАВЕНСТВА
Метод интервалов (промежутков)
Методом интервалов решают неравенства, приведенные к виду Р(х) > О или Р(х) < О, (Р(х) > О или Р{х) < 0).
Метод основан на том, что непрерывная на промежутке функция может менять знак только в тех точках, где ее значение равно нулю (но может и не менять).
Алгоритм применения метода
Найдем ЩР(х)) и промежутки, на которых Р(х) непрерывна.
Найдем нули функции Р(х) — значения х, при которых Р(х) — 0.
Нанесем на числовую ось найденные промежутки и нули. Определим интервалы знакопостоянства и в каждом из них поставим найденный подсчетом или рассуждением знак. Выпишем ответ. Примеры
х(х - 4)(х + 5)2 > 0
Рассмотрим функцию Р(х) — х(х - 4)(х + б)2.
ЩР) - К, функция непрерывна на К.
Р(х) - 0 в точках х - 0; х - 4; х = -5. _ ^ ^ Р(-6) > 0; Р(-1) > 0; Р(1) < 0; .Р(5) > 0. + 1 + 1 ~ Ответ: (-оо ; -б) и (-5; 0) и (4; оо). -Б О 4 х(х - 4)(х + б)2 ^ 0 при х € Е {-5} и [0; 4].
х(х + 2 ) . „, . х(х + 2)
![]() — < 0 . Рассмотрим функцию Р(х)
«•
— < 0 . Рассмотрим функцию Р(х)
«• ![]() . х -
5 х - 5
. х -
5 х - 5
И(Р)~ (-оо; 5) и (5; со).
Р(х) - Ов точках х = 0; х = -2. .
Р(-3) < 0; Р(-1) > 0; Р(1) < 0; *-(6) > 0. + Г - ^ о + ,
Ответ: (-со ; -2] и [0; 5). -2 0 5
л/Зх +1 > 2х. Приведем неравенство к виду: ,/Зх + 1 - 2х > 0.
Р(х) = л/Зх + 1 - 2х.
ЩР) = [ ~ | I +°°)- Найдем нули этой функции.
![]() ,
, ![]() Гх > 0
Гх > 0
,/Зх + 1 - 2х - 0 <=> ^ . 2 13х + 1 - 4х
*"(х) - 0 при х - 1. Рф) > 0; Д б ) < 0.
Ответ: Г-|; 1.\
Таблица 18. НЕРАВЕНСТВА
С ДВУМЯ ПЕРЕМЕННЫМИ
ах + Ъу + с>Оиах + Ъу + с<0 — полуплоскости (а2 + Ь2 * 0)
![]() граница — прямая ах + Ьу + с — 0 ах*
+ Ъх + с>уи ах2 +
Ьх + с<у ау2 +
Ьу
+ О ж и ау2 + + с < дс граница — парабола оде2 +
Ьх + с - 0
граница — прямая ах + Ьу + с — 0 ах*
+ Ъх + с>уи ах2 +
Ьх + с<у ау2 +
Ьу
+ О ж и ау2 + + с < дс граница — парабола оде2 +
Ьх + с - 0
_ «Ц/2 + 01/ + С < X
![]() ау2 +
Ьу + с
ау2 +
Ьу + с
' / / С
граница — парабола ау2 + Ьу + с — д;
(* - *о)(У - Уо) > * и (дс - дс0)(у - у0) < * (* * 0)
граница — гипербола
![]() (дс - х0)(у - у0)
-
к
(дс - х0)(у - у0)
-
к
(две ветви)
( * - *о) (» - Уо) - *
71
Таблица 18. НЕРАВЕНСТВА С ДВУМЯ ПЕРЕМЕННЫМИ
(* - *0)(у ~ Уо) > 0 и (х- х0)(у - уа) < О (я - О)
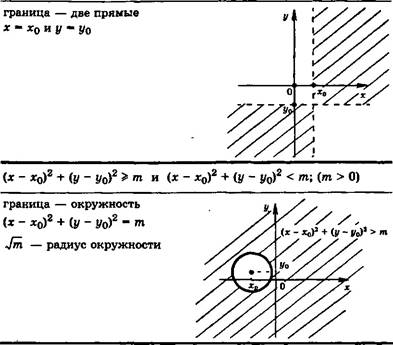
Таблица 19. ДИФФЕРЕНЦИРОВАНИЕ
Производной функции / в точке Хо называется предел отношения приращения функции Д/ = /(х0 + Дх) - Цх0) к приращению аргумен-
= ит Г(х0+Ах) -/(*„)
та Дх при стремлении Дх к нулю, 7*'(*о)
Д*-»0 Дх
Операция нахождения производной функции называется дифференцированием .
Необходимое условие дифференцируемости функции
Для того чтобы функция / была дифференцируема (имела производную) в точке х0, необходимо (но недостаточно), чтобы она была непрерывна в этой точке (т.е. Д/*(х) - /(х) - /*(х0) -» 0).
Примеры нахождения производной функции /* по определению
|
/(*) ~ х2 х0 = 2 |
(2+Дх) 2 -2 2 _ Ит 4Дх + Дх2 Г ( 2 ) = 11га Дж-»0 Дх Дл-»0 Дх - Ит (4 + Дх) = 4 Дх-»0 з/хо+Дх-з/^ 7*'(*о) = 11т |
|
|
Г(х) - 3,/х х 0 * 0 |
Дл:-»0 Дх (х0 + Дх) - х0 = Нт д*-*о 2 0 + Дх)х0 + ф^Ах '(з/(х0 + Дх) + з/(х |
3 Й |
, 8 1 п (х0 + Дх) - з т х 0
/
(х0)
= Ь т — ![]()
/(х) = вт х д*->о Дх х„ея „ . Дх ( Л*Л
2 з т — • соз! х 0 + I
= Нт СОЗХд
Ддс-+0 Дх
цт 1-2-гДх|(-2+Дх) -8 .
л^-н-х2 д*->о Дх
х0 = -2 = цт ( 2 - Д х ) ( - 2 + Ах) 2 -8 _ _12
Д* -> о Дх
Таблица 19. ДИФФЕРЕНЦИРОВАНИЕ
Пример непрерывной, не дифференцируемой в точке х0 функции Дх) - |х - 2| П2). Ит К- + *«>-21-о _ Цт !дг! ж0-2 д*-»о А* д*->оД*
предел не существует, /'(2) не существует.
3/(1 + Ах)-1-0 _ , . т ^
Я*) - 8 л ^ 3 Т Д*-»0 Дх д*->о Ах
х 0 » 1 = Нт °о, ^'(1) не существует.
Вторая производная Производные высших порядков
/"<*) - (Г(х)У ^ ( х ) - ^ » " 1 ^ ) ) '
(ЛУ -8/2У
(гТх)
(СОВ X ) " — (-81П X ) ' — - С О З X 3 -5/2
= = Х —
8
Производная
|
Табличное дифференцирование |
сложной функции (/("(*)))' = Пи) • и'(х) |
|
(с)' - О, е е Я (константа) (ж)' - 1, Л Е К (х")'-пх п _ 1 , Л б Д , 1 Ё 4 ; и л и -п е ЛГ, х * 0; или (сое х)' — -81П X , х е я ( В Ш X ) ' — СОв X , Х Е Л (** х)' • 1 2 ' х * ^ + я*, * 6 2 СОВ X (с18 х)' . 2 ,х*лк,кег В1П X (1п * ) ' = " , х е (0; +оо) (10в0х)' - , X 6 (0; +«=, (ехУ - <?, 1 Е В |
(ц")' - пи" - 1 • и'* (сое и)' — -вт и • и' (вш и)' — сов и • и' Не и)' - - \ - • и' сов и (с*г - - 2 вш и (1 п и)'7 = - • и' * и (1ое•а«)' а ' и • 1па (еи)' = еи • и' (ац)' - а" • 1п а • и' |
|
х — а*1п |
и = н(х) |
( а ) ' а, х е к
Таблица 19. ДИФФЕРЕНЦИРОВАНИЕ
Производная обратной функции
Функции у - /(х) и у - <р(х) /(а) - Ь <=> а - <р(о) взаимообратны.
/'(а) • Ф'(Ь) - 1
(вгсзш г ) ' х е (-1; 1) (агсзш ы)' ••
1 1
(агссоз х)' = - 2 * е ( - 1 ; П (агссоз и)'
УГ^ '
1 1
(агс*8 * ) ' (агс*§ и)' -
1+х' 1 + и
(агсс1(Г, х)' — -- (агсс1# ы)' - --
1 +х' 1+и
Основные формулы Следствия из основных формул
(и + V)' = и' + ь' (и - у)' - и' - и'
(и • V)' — и' • V + и • и' (с • и)' - с • и'
(иУ и' у - и -у'
© ' " 7
Примеры
вш Тх
(соз Тх)' = -81П ./х • (л/х)' —
((2х2 - х + I)10)' - 10 • (2х2 - х + 1)в • (2х2 - х + 1)' - 10 • (2х2 - х + I)9 • (4х - 1).
|
Физический смысл производной |
Геометрический смысл производной |
|
Пусть з = з ( 0 — зависимость пути от времени, тогда: V = 0 ( 0 - в ' ( 0 Скорость — производная пути по времени. - а = о ( 0 - 1 / ( 0 = з " ( 0 Ускорение — производная скорости по времени (вторая производная пути по времени). |
Касательной к графику функции Дх) в точке х0 называется прямая, задаваемая уравнением: У - Г(х0) + Г(х0) • (х - х„) Г ( * 0 ) = ч? Окас ~ *кас Значение производной функции в точке равно угловому коэффициенту касательной к графику функции в этой точке. |
Таблица 19. ДИФФЕРЕНЦИРОВАНИЕ
Касательная к графику функции
Уравнение касательной (не вертикальной) к графику функции У " Л*) в точке графика с абсциссой х0:
У - Г(х0) + Г(*о) • (х - х„)
Если функция /(х) не имеет производной в точке х0, но непрерывна в этой точке, то у графика функции в этой точке либо вообще нет касательной, либо есть вертикальная касательная. у — \х\ не имеет касательной в точке графика с абсциссой х = 0.
у — \[х имеет в точке графика с абсциссой х = 0 вертикальную касательную *<=0.
Примеры решения задач на составление уравнения касательной
Составить уравнение касательной к кривой у — х8 - х2 в точке графика с абсциссой х0 ~ 1.
Координаты точки касания Хд = 1; у о — I3 - I2 = 0. и' = 3х2-2х => Акас = у'(1) - 1.
Уравнение касательной: у = 0 + 1 - ( х - 1 ) => у = х — 1
Составить уравнение касательной к кривой Дх) = (х2 + 6х + 3)/2, не пересекающей прямую у — 2х + 5.
Так как касательная не пересекает прямую у — 2х + 5, значит, она параллельна касательной. Следовательно, Л(*о) = 2. Но /'(х) = х + 3. Отсюда х0 + 3 — 2 и х0 — -1. Ордината точки касания у0 равна
((-I)2 + 6 • (-1) + 3)/2 = -1. Координаты точки касания (-1; -1). Уравнение касательной у = -1 + 2(х + 1 ) или у " 2х + 1
Составить уравнение касательной к кривой у — х3, проходящей через точку -1 ^. Пусть (х0; у$) — точка касания. Тогда у0 = х3,;
2 3 2
Акас = Зх0. Уравнение касательной у — х„ + Зх0(х - х0). Точка
-1^ лежит на касательной. Поэтому -1 — Хр + Зх2, ^| - х0^ =>
=> 2х„ - х„ - 1 - 0 => х0 - 1 => у0 - 1.
Уравнение касательной у •* 1 + 3(х - 1) или у — Зх - 2
Таблица 19. ДИФФЕРЕНЦИРОВАНИЕ
Исследование функции при помощи производной
|
Монотонность функции |
VI |
1 1 |
^ 1 1 1 |
|
|
|
Теорема Лагранжа Если Дх) непрерывна на [а; 0] и дифференцируема на (а; 6), то существует с е (а; о) такое, что Да) - ЛЬ) = Г(с) • (а - в ) . |
|||||
|
0 |
а |
с Ь |
|||
(Заметим, что таких точек с на (а; о) может быть и более одной.)
Для исследования функции Цх)на монотонность можно исследовать ее производную на знакопостоянство.
|
Если / " ( * ) > 0 на (а; В), то Дх) возрастает на (а; о). Если Дх) непрерывна на [а; в ] , то Дх) возрастает на [а; о]. |
Если / " ( * ) < 0 на (а; В), то Дх) убывает на (а; в ) . Если Дх) непрерывна на [а; в ] , то Дх) убывает на [а; 6]. |
|
Дх) - х2 - 6х + 1; /'(ж) - 2х - 6 > 0 при х > 3 => Дх) возрастает на [3; + ° о ) . |
Дх) - 7 ^ ; / ' ( * ) = — р = < 0 при х < 0 =* 2Т - Х Дх) убывает на (-°°; 0]. |
|
Если Дх) возрастает и диффиренцируема на [а; в ] , то /"(х) > 0. |
Если Дх) убывает и дифференцируема на [а; В], то /"(х) < 0. |
Критические точки функции
Внутренние точки области определения функции, в которых производная равна нулю или не существует, называются критическими точками функции.
|
|
|
|
У |
||
|
У |
1 \ |
|
1 |
1 I |
|
|
1 0 |
|
0 |
|
*0 |
0 \ х |
|
Г(х0) = ( У, |
/'(* 0 ) = 0 • |
/'(*о) - 0 |
|||
|
х0 — крит. точка; |
х0 - крит. точка; |
хо - крит . точка; |
|||
|
Л*о) ~ /шах- |
Л*0) - /щш- |
Дх0) не является экстремумом. |
|||
Таблица 19. ДИФФЕРЕНЦИРОВАНИЕ
Критические точки (примеры)
|
Л(*о) не существует; х0 - крит. точка; /(х0) не является экстремумом. |
Г(*о) не существует; Нет критических х0 - крит. точка; точек; х0 — 0 не является /(*о) = / щ и т внутренней точкой области определения. |
|||||||||||
|
|
|
|
|||||||||
|
Нет критических точек; х0 — точка разрыва. |
/'(х) — О при всех х е (-3; 4); П-В), /'(4) не существуют; все х е [-3; 4] критические точки. Экстремумы |
/'(*о) не существует; х0 — крит. точка; Ихо) — / л и п * |
||||||||||
|
х0 е !)(/) — точка максимума Лх), если существует 6 > 0 такое, что при х 6 (х0 - 8, х0 + 8) Лх0) > /(X) |
х0 е !)(/) — точка минимума /(х), если существует 8 > 0 такое, что при х е (х0 - 8, х0 + 8) /(х0) < /(X) |
|||||||||||
|
Точки максимума и минимума < |
гункции называются ее точками |
|||||||||||
экстремума, а значения в них — экстремумами (максимумами или минимумами).
|
Г(*о) - о при х < х0 /'(ж) > О при х > х0 /'(х) < О |
Пх0) - О при х < х0 /'(х) < О при х > х0 Нх) > О |
У гаах
Таблица 19. ДИФФЕРЕНЦИРОВАНИЕ
Примеры критических точек различных функций
1) У ~ Н; *о ~ 0; У'(0) не существует; у(0) - 0 — минимум.
2) у - х2; х0 - 0; у'(0) - 0; у(0) - 0 — минимум.
В) у х ; х0 — 0; у'(0) "= 0; экстремумов нет.
4) у — 2х - |х|; х0 = 0; у'(0) — не существует; экстремумов нет.
![]()
Примеры исследования функций на монотонность

на [1; + ° о ) ; Дх) убывает на [-1; 1].
![]()
X X
|
/'(*) - 0 при х = 1; Дх) возрастает на (—°о; 0) и на [1; +оо); Дх) убывает на (0; 1]. Дх) - х4 - х3; |
разрыв шш |
|
|
/"(*) - 4х3 - Зх2 - х2(4х - 3); Дх) возрастает на ^|; +°°); Дх) убывает на (-со; ^. |
Г(х) 0 0 0 4 Л*) |
© |
|
Д х ) - х + \;Пх)=1- \ ; |
П*) © - , . © 0 0 1 © |
|
|
х
|
я*) ^ х*' |
|
|
Дх) возрастает на (-°°; -1] и
|
шах раз- ш!п рыв |
|
на [1; +со);
Дх) убывает на [-1; 0) и на (0; 1].
Таблица 20. ИССЛЕДОВАНИЕ ФУНКЦИЙ
Область определения функции — множество значений х, при которых функция определена.
|
Дх) х + 1 |
Я * > - * - 1 Щ Г ) - { х \ х * 1 } |
Г(х)-*Л-х 1КГ)-{х\х4 1) |
|
|
|
№ - 1е х + \е (-х) |
||
|
/ ( х ) - -У2х-х2 -1 В(Г) - {1} |
|||
Область значений функции Е(Т) — множество значений, которые может принимать Дх) при х 6 Щ$)- (Все значения а, при которых уравнение Дх) — а имеет решения.)
|
Дх) - х3 - Зх Е(Г) = Я |
Дх) = 1 + ^ X Е(Г) = {у\у* 1} |
Дх) - г Н х - х2 Е(Г) - {У 1 У « 1} |
|||
|
Дх) - 1 + -/4х - х2 - 4 Я(Я = {1} |
Дх) = в ш х + сое X |
||||
|
Четность |
Нечетность |
||||
|
Д-х) - Дх), х 6 С(Л |
Д-х) - -Дх), х е ЩГ) |
||||
|
График четнс метричен отнс динат. У ж' / -х 0 |
>й функции симюительно оси ор- х х \ |
График нечетн метричен отнс координат. У -X |
ой функции сим- сительно начала |
||
|
* ж 1 ж т. . Ж |
0 * * |
||||
|
Примеры четных функций Дх) - х4 - 21х2 *(х) - 6х + б"1 ф(х) - VI - х + 3л/1 + х |
Примеры нечетных функций п(х) - х3 - 20х х х и(х) - 5 - б" о(х) - VI - х - 4\ + X |
||||
Дх) — вт х - сов х не обладает четностью или нечетностью.
80
Таблица 20. ИССЛЕДОВАНИЕ ФУНКЦИЙ
Периодичность
Дх - «) - Г(х + I) - Дх), х е ЩГ), * * 0 Число 4 называется периодом функции, а наименьшее положительное значение I основным периодом функции (Г).
|
|
— 8Н1 АХ |
« х ) - сое 2ях |
|
Дх) - 17 |
|
т |
2л л - 4 = 2 |
2л Г = 2л 1 |
Дх) - 2 • л Т = - Зя 1/3 |
г е (0; + о о ) основного периода нет |
/(х) — х + вш х; Дх) = сов(х2) — непериодические функции.
/ (х) - вш х - сов х. Т - 2я
![]() График периодической функции состоит из повторяющихся
фрагментов на отрезке длины Т; на любом таком отрезке периодическая
функция принимает все свои значения.
График периодической функции состоит из повторяющихся
фрагментов на отрезке длины Т; на любом таком отрезке периодическая
функция принимает все свои значения.
Корень (нуль) функции —
значение аргумента, при котором значение функции равно нулю.
|
Дх) = 4х - \ |
Дх) - х • Л -х |
Дх) - (1 + х) • Тх |
|
|
.1 корни: х = ±^ |
корни: х - 0; х - 1 |
корень: х = 0 |
|
|
Дх) — 81П х + соз X я „ корни: х — -- + ли, п е г |
|
Дх) - - А — 81П X корней нет |
|
Промежуток зиакопостояиства — промежуток, на котором все значения функции положительны (или отрицательны), а на любом его расширении нет.
Примеры
Дх) - Зх2 + 5х - 8; Дх) < 0 при х 6 ( - - ; ^ ;
Дх) > 0 при х 6 ( - с о ; - | ) о (1; + о о ) .
Дх) —х-2; два промежутка зиакопостояиства (-со; 0) и (0; +°°), на обоих функция положительна.
Таблица 20. ИССЛЕДОВАНИЕ ФУНКЦИЙ
Монотонность
|
Функция Дх) называется возрастающей на промежутке /, если для любых хх и х2 из это |
Функция Дх) называется убывающей на промежутке I, если для любых хг и х2 из этого про |
|
го промежутка *1 > *2 =» Д*1> > Д*2)- Промежуток / называется промежутком возрастания функции /(ж), если на этом промежутке функция возрастает, а на любом его расширении нет. |
межутка х 2 =» {(х\) < Дх2). \ > х Промежуток / называется промежутком убывания функции Дх), если на этом промежутке функция убывает, а на любом его расширении нет. |
Промежутки возрастания и убывания называются промежутками монотонности функции.

5 г 5 Л
Г ' ( х ) > 0 при х > ; Дх) возрастает на промежутке I — ^; +°о 1; /'(х) < 0 при х < - | ; Дх) убывает на промежутке ^-°°; - | ] -
Дх) — — д в а промежутка монотонности (-°°; 0) и (0; +°°);
х на обоих функция возрастает.
Дх) — Зх + 4 возрастает на К, один промежуток монотонности (-ОО; + 0 0 ) .
Дх) « Зх2 + 6х - 8; Пх) = 6(х + 1) - 0 при х - - 1 ;
Г(-2) < 0 =» Дх) убывает на (-оо ; -1];
/'<0) > 0 => Дх) возрастает на [-1; +°°); Хд = -1 — точка минимума; Д-1) = -11 — минимум.
Дх) — х — экстремумов нет.
82
Таблица 20. ИССЛЕДОВАНИЕ ФУНКЦИЙ
Исследование функции при помощи производной.
Построение графика
Найдите ГНУ).
Найдите производную, критические точки, исследуйте знаки производной.
Найдите промежутки монотонности, точки экстремума, определите вид точек экстремума. Найдите экстремумы функции.
Исследуйте функцию на четность, нечетность, периодичность (периодическую функцию лучше исследовать на промежутке длины Г).
•Набросайте» эскиз графика.
Найдите « ( / ) .
Найдите несколько значений функции (по крайней мере по одному в каждом промежутке монотонности).
По возможности
Исследуйте поведение функции на концах области определения и в точках разрывов.
Найдите горизонтальные и вертикальные асимптоты.
Найдите корни и промежутки энакопостоянства функции.
Постройте график функции
![]() Пример:
у - -5
Пример:
у - -5 .
х + 1 Ш - в.
, 1 (х2 + 1)-лс 2х 1-х2
У ™ 2 2 " 2 2
(* + 1 ) ( 1 + х " )
у' существует при агЕЙ; у' - 0 при х — ±1.
Упип " !/(-!) " ~ \ ; Ушах " » Ш " | • Функция нечетная: у(-х) - -у(х). ВД-[-|; |].
Нт
у — 11т — — Нт — 0.
х
у — 0 — горизонтальная асимптота; вертикальных асимптот нет. у — 0 при х - 0 (корень), у > 0 при х > 0; у < 0 при х < 0.
Таблица 2 1 . НАХОЖДЕНИЕ НАИБОЛЬШЕГО И НАИМЕНЬШЕГО ЗНАЧЕНИЙ ФУНКЦИИ НА ПРОМЕЖУТКЕ
Наибольшим (наименьшим) значением функции Дх) на / называется такое число М ( т ) , что существует х0 6 I такое, что Д*о) " м (Д*о) = т)> М > Дх) (т < Дх)) для всех х из /.
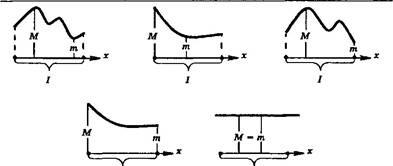
/
Наибольшее и наименьшее значения непрерывная на / функция может принимать либо на концах промежутка (если это числа), либо в критических точках, лежащих внутри промежутка.
Алгоритм нахождения наибольшего и наименьшего на [а; Ь] значений функции, непрерывной на [а; о].
1) Найдите Да) и До) — значения функции на концах промежутка.
2) Найдите критические точки функции внутри промежутка
(т.е. на (а; о)).
3) Найдите значения функции в критических точках.
4) Из всех найденных значений выберите наибольшее и наименьшее; они и будут наибольшим и наименьшим значением функции на [а; Ь].
Пример
Дх) = 8х2 - х4, х е [-1; 3]. Д-1) = 7; ДЗ) = -9;
/'(*) = 16х - 4х3 = 4х(4 - х2) - 0 => х - 0; х - 2; х = -2 <2 [-1; 3]. ДО) - 0; Д2) - 16. тах {7; -9; 0; 16} = 16 = Ф тах Дх) = 16;
[-1; 81
т т {7; -9; 0; 16} - -9 => т т /(*) = -9.
Ч
84
Таблица 21. НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЯ
Пример
Если непрерывная функция имеет на промежутке / единственную точку экстремума и этот экстремум максимум (минимум), то в этой точке достигается наибольшее (наименьшее) значение функции.
Дх) - вш х + 73 • сое х, х 6 [0; л].
ДО) - 7§ ; Дл) - - 7§ ; /'(х) - соз х - 7§ зш х; /"(*) = 0 при сое х = 73 вт х => 4# х = => х = ^ + ля е [0; л] при я — 0. шах Ддс) - /[ |[ ] = вш ^ + л/3 сое н = 2;
|в!«1 У.Ь^ О О пип Дх) = Дл) - -7з г м ф е „
6
Задача
В полукруг радиуса В вписать прямоугольник наибольшей площади так, чтобы одна его сторона лежала на диаметре полукруга, А о у и а две вершины — на дуге полукруга.
Обозначим стороны прямоугольника АВ = х, АО — 2у.
I 2 2
Тогда его площадь 8 — 2ху. Заметив, что у = </К - х , получим
5 - 2х-'Ы - х2 - 2 • л/й2*2 - х4, х е (0; Л).
Исследуем на максимум функцию Дх) = К2х2 - х4 при х е (0; Л).
/"(ж) - 2В2х - 4х3 - 2х(Д2 - 2х2). / ' ( * ) = 0 при х -
(так как х е (0; В)).
Следовательно, при х = площадь прямо- а » »
72 Их) к
угольника наибольшая. Л
Ответ. Прямоугольник имеет наибольшую
В г
площадь, если его стороны х = -^,2у — В^2.
85
Таблица 22. ПЕРВООБРАЗНАЯ И НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Функция Р(х) называется первообразной функции Дж) на промежутке /, если для всех ж из этого промежутка Р'(х) - /(ж).
Если ^(ж) одна из первообразных функции /(ж) на /, то любая первообразная функции Дж) на этом промежутке имеет вид Р(х) + С, где С е д .
Множество всех первообразных функции Дж) называется неопределенным интегралом и обозначается Г/(ж)а'ж.
|У(х)а*х - Р(х) + С, где ^(ж) — любая первообразная /(ж), а С 6 Я.
Свойства первообразных
Первообразная /'(ж) равна Дж) + С.
Если первообразная /(ж) равна Р(х), то первообразная ОД равна Р#).
Е с л и первообразная /(ж) равна Р(х), то первообразная яДж) равна кР(х).
Пусть первообразная /х(ж) равна ^(х), первообразная /гС*) равна Р^х), тогда первообразная ^(ж) + равна ^(ж) + ^ ( х ) .
Пусть первообразная /(ж) равна ^(ж), тогда первообразная ДАж + р) равна ^ .Р(«ж + р).
Для того чтобы доказать, что функция Р(х) является первообразной функции /(ж) на промежутке /, нужно показать, что для всех ж из этого промежутка Р'{х) "• /(ж) (т.е. воспользоваться определением).
Задачи
Доказать, что функция Л(*) "* 2 8Ш 2ж + ж является первообразной для функции Дж) — 1 + соз 2ж на В.
Р'(х) = | соз 2ж - 2 + 1 = 1 + соз 2ж = /(ж).
Полученное равенство верно для всех действительных значений ж.
Найти первообразную функции /(ж) — Зж2 - 1, график которой проходит через точку М(1; -1).
Любая первообразная функции /(ж) — Зж2 - 1 имеет вид Р(х) — ж3 - ж + С. График искомой первообразной пройдет через точку М(1; -1), если Р(\) - -1, т. е. I8 - 1 + С - -1 => С - -1. Ответ. Р(х) — ж8 - ж - 1.
86
Таблица 22. ПЕРВООБРАЗНАЯ
Найти первообразную функции /(дс) - сов2 ^.
Преобразуем /(дс) — сов2 ^ | (1 + сое дс) - | + | сое дс.
Первообразная суммы равна сумме первообразных. Следовательно, первообразная Р{х) - | х + | вш х + С, где С — произвольная постоянная.
Найти неопределенный интеграл Зж - сое х их. |вн1 Зж • соз х Лх — | ^{вт. 4дс + вш 2дс) а*ж - | • • соз 4дс + ' * • ( - ! ) - о о в 2 х ] - - | , ц сов 4дс - ^ соз 2дс + С.
Найти первообразную для функции /(ж) < 2 4 ж - 1
Преобразуем /(ж) - „
4ж2 _ ! 2^2* - 1 2ж + 1)
Следовательно, первообразная «р
Щх) - | ( | 1п|2ж - 1| - | 1п|2ж + 1|) - \ 1п 2ж - 1 + С.
2ж + 1
Таблица первообразных
|
/(*) |
2?(ж) |
Промежуток / |
|
А |
Ах + С |
В |
|
п ж" (а * -1) |
а + 1 х , + с а + 1 |
а е №, * 6 Я; -а е л г , ж е (-оо; 0) и (0; +°о); а е 2, ж е (0; +со) |
|
1 ж |
1п |ж| + С |
(-со; 0) и л и (0; +со) |
|
е* |
е* + С |
В |
|
а* |
X г - + с |
В |
|
С 0 8 Ж |
ша ж + С 8 1 П |
В |
|
вш ж |
-соз ж + С |
В |
|
1 2 сов ж |
*?дс + С |
( - 5 + л й ; § + « * ) , * е 2 |
|
1 . 2 8 1 П Ж |
-сЬе ж + С |
(яА; я + яА), А е г |
87
Таблица 23. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
Если функция Дх) непрерывна на промежутке / числовой оси, содержащем точки х - а м х - Ь , то разность значений Рф) - Р{а) (где Р(х) — первообразная /(х) на /) называется определенным интегралом от функции /(х) от а до 6:
\Г(х)ах -Рф)-Р(а).
Определенный интеграл есть число.
Основные свойства
Дх)йХ - -|/(х)йх
ь
с Ь
Дх)о*х - ^Д*)о*х + ^?^x)йx, если а, о и с — любые точки про
межутка / непрерывности Дх)
АДх)йх - к - |Дх)о*ж
ь в
Таблица 23. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
Дополнительные свойства
Если /(х) четная, то ^ Л*)а"х - 2 • ^(х)с*ж.
Если Т(Х) нечетная, то Г {{х)а"х — 0.
|
Лримеры |
|
|
|
Ч |
4 |
|
|
1 |
1 |
,!т18/В +1ЫН/2.1* ,4„ *,2-1,+ |
|
2 В |
а + 4 |
|
|
г ах 1 е аг 8 2 Ь * ^ З х + 4) 1 8 Г-1) + 4 Зх + 4 - I |
1 I I м 1/1 11 7 3 *!, ~ 8Ц0 ^ ~ 90 |
|
О Г 0 . 5 " ^ - 1 0 ; Ь | 1 +50- ^ - ™ + * »
] * 1п 2,Б]0 1п 0.5|0 1п 2,Б 1п 2
86
Таблица 23. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
Площадь криволинейной трапеции
![]() Фигура, ограниченная прямыми у — 0; х — а; х
— Ь и графиком непрерывной и неотрицательной на [а; о] функции /(ж),
называется криволинейной трапецией. Площадь криь
Фигура, ограниченная прямыми у — 0; х — а; х
— Ь и графиком непрерывной и неотрицательной на [а; о] функции /(ж),
называется криволинейной трапецией. Площадь криь
волинейной трапеции 5 — ^(л^ах Ь х
Вычисление площадей
|
Пх т )<^ X / Я 1х) 1 1 (/А' а с Ь * х ь ь |
а Ь _ |
|
|
Их) 6 |
|
|
|
8 - \Пх)ёх - \8(х)йх |
8 - -|7(*)о*х |
|
|
^ л |
а |
|
а с
![]()
![]() Г(х)
> е(х) на [а, Ь]
Г(х)
> е(х) на [а, Ь]
8 - |м*)-в-(*))о*х
|
1 1 «<*) : |
I 1в | | 11 • | , а!!с " * > |
|
|
|
а с Ь с а |
|||
|
с « - |(/(*)-*(*))а-* + а |
|||
|
Ь +^Г2(.х)-е(х))ах |
е |
||
|
с |
Г |
||
90
Таблица 23. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ПРИЛОЖЕНИЯ
Вычисление объемов тел вращении
|
Криволинейная трапеция (вокруг оси Ох) |
У |
ш |
|
|
Ь У ох " * ГА*)*** о |
|
|
0 |
а |
Ь х |
||||
|
Конус |
У л |
0 |
ъ |
г х |
0 2 81*^ Я 1о 3 |
|
|
Шар |
У г 0 |
,
|
X |
Л 2 2 2 Уш-тс |(7я -х)йдг - -л л - 2тс|(Д2 - х 2 ) ^ - 0 |
||
Путь, пройденный материальной точкой за время *2 ~ '1 (*2 > '1) при прямолинейном движении со скоростью и(0. равен:
8- Ги(*)Л.
Предметный указатель
Арифметическая прогрессия . . . 33
Арифметический корень 13
Бесконечно убывающая геометри
ческая прогрессия 34 Бином Ньютона 10
Вершина параболы (координаты) 19
Взаимно простые числа 7 Возвратное уравнение 48
Вторая производная 74
Выделение полного квадрата. . . 30
Вычитание многочленов 10
![]() Геометрическая
прогрессия. . . . 33 Геометрическая интерпретация модуля 8
Геометрическая
прогрессия. . . . 33 Геометрическая интерпретация модуля 8
Геометрический смысл производной 75
Гипербола 20
График уравнения с двумя переменными 28
Двойные неравенства 62
Действительные числа б
Действия с квадратными корнями 13
Действия с корнями 15, 16 Деление многочленов 11
Делитель 5
Десятичная запись натурального числа 6
Десятичные логарифмы 42
Дискриминант 30, 47
Дифференцирование (формулы) 75
Дифференцируемость в точке . . 73 Доказательство неравенств (методы) ![]() 62
62
Дробно-линейная функция . . . . 20 Задание последовательностей . . 33 Замена переменной в уравне
нии 46 Знаки корней квадратного
трехчлена 30, 31
— тригонометрических функ
ций 39
Значения тригонометрических
функций 38
Интеграл 86—91
![]() Иррациональность
в знаменателе 14
Иррациональность
в знаменателе 14
Иррациональные числа 5
— неравенства 64
— уравнения 49
92
Исследование функции
на монотонность 77, 79
![]() с помощью произ
с помощью произ
водной 77, 83
Каноническое разложение нату
рального числа 7 Касательная 76
Квадратичная функция 19 Квадратные неравенства 64
— уравнения 47
Квадратный корень 13
— трехчлен 30
Коэффициенты многочлена. . . .11
Корень многочлена 12
— нечетной степени 15
— функции 81
![]() —
уравнения 45 Косинус числа 37
—
уравнения 45 Косинус числа 37
Котангенс числа 37
Кратное 5
Криволинейная трапеция 90 Критические точки функ
ции 77, 78
Линейная функция 19
Линейные неравенства 63
— уравнения 47 Логарифм 42
Логарифмическая функция.... 23
Логарифмические неравенства. .65
— уравнения 51
Логарифмов сравнение 43
Логарифмы (действия с ними). .43
— (таблица значений) 42
Метод интервалов
(в неравенствах) 70
Методы построения графи
ков 26, 27
— разложения на множители . .11
— решения уравнений 46
— доказательства неравенств . . 62 — решения систем уравнений . . 59 Многочлены от одной переменной 11
Модуль действительного числа 8
Модуль (раскрытие модуля) . . 9
![]() Монотонность
функции 82
Монотонность
функции 82
Наибольшее и наименьшее
значения функции 84
Наибольший общий делитель . . 7 Наименьшее общее кратное. . . . 7
Натуральные числа 5
![]() логарифмы 42
логарифмы 42
Нахождение производных
по определению 73
Неопределенный интеграл . . . . 86 Неполные квадратные уравнения 47
Неравенства с модулем 8
— с двумя переменными . . 71, 72
— с обратными тригонометриче
скими функциями 69
Неравносильные преобразования 45
Нестрогие неравенства 62
Нули функции 81
Обратная пропорциональность. . 20 Обратные тригонометрические
функции 25
Однородные уравне
ния 46, 48, 51, 55
Определенного интеграла
(нахождение) 89
Определенный интеграл 88
Основное логарифмическое
![]() тождество 42
Остаток 6
Ось
котангенсов (ось тангенсов) 37
тождество 42
Остаток 6
Ось
котангенсов (ось тангенсов) 37
Первообразная 86
Перевод периодической дроби
В обыкновенную 34
Периодичность тригонометриче
ских функций 38
Площадь и интеграл 90
Показательные неравенства ... 64
— уравнения 50
Показательная функция 23
Последовательность (числовая) 33 Построение отрезка длины л/п ,
#1 е ЛГ 14
![]() — графика (производная)
83 —
графиков (методы) 26, 27 Приведенное квадратное
уравнение 47
— графика (производная)
83 —
графиков (методы) 26, 27 Приведенное квадратное
уравнение 47
Приведенный квадратный
трехчлен 32
— многочлен 11
Признаки делимости на 2, 4, 5,
9, 11, 25 6
Приложения определенного
интеграла 90, 91
Производная обратной функции 75
— сложной функции 74
— функции 73
Производные высших порядков 74
Промежутки знакопостоянства . 81
— монотонности 82
Простые числа 7
Прямая пропорциональность. . .19
Равносильные преобразования. . 45
— уравнения 45
Радианная мера 35
Разложение квадратного трех
члена на множители 31 Расположение графика квадра
тичной функции 20 Рациональные числа 5
Рекуррентное задание последовательности 33 Свойства делимости 6
— квадратных корней 13
— логарифмов 43 — модуля 8
— обратных тригонометрических функций 25
— определенного интеграла . . . 88
![]() —
первообразной 86
—
первообразной 86
— простых чисел 7
— степеней .17
функций 24
— числовых неравенств 62
Симметрические системы уравнений 61 Синус числа 37
Системы уравнений 59—61
Сложение двойных неравенств . 62
— многочленов 10
Составление квадратного трех
члена по корням 32
Сравнение квадратных кор
ней 13
— корней 15
— средних величин 63
Среднее геометрическое 16
— арифметическое 16
Старший коэффициент много
члена 11 Степень 17
Степени многочлена 11 Степенная функция 18, 22
Суммирование 34 Схема Горнера 12
Таблица первообразных 87
— производных 74
Тангенс числа 37
93
Теорема Безу 12
— Виета 31
— Лагранжа 77
Точки экстремума (минимума,
максимума) 78
Треугольник Паскаля 10
Тригонометрическая окруж
ность 35
Тригонометрические неравенства 65
![]() —
соотношения 37, 40 в прямоугольном треугольнике 38
—
соотношения 37, 40 в прямоугольном треугольнике 38
— уравнения 53
— функции 24
Угловой коэффициент касательной 75
Умножение многочленов 10
Универсальная подстановка . . . 40
Уравнения высших степеней. . .48
— с модулем 8
— со степенной функцией . . . . 49
— (методы решений) 46 — с обратными тригономет
рическими функциями 56
— с параметрами 56—58
Факториал 10
Фибоначчи (числа) 33
Физический смысл производ
ной 75
Формула общего члена после
довательности 33
Формулы двойного угла 40 — дифференцирования 75 — дополнительного угла 41
— корней квадратного уравнения 47
— понижения степени 40
— приведения 37
![]() —
сокращенного умножения... 10 Целые корни многочлена 12
—
сокращенного умножения... 10 Целые корни многочлена 12
— числа 5
Четность тригонометрических
функций 38
Числовые неравенства 62
Экстремумы 78
ПРИЛОЖЕНИЕ
Простые числа от 2 до 997
|
2 |
3 |
5 |
7 |
11 |
13 |
17 |
19 |
23 |
29 |
31 |
37 |
41 |
43 |
|
47 |
63 |
59 |
61 |
67 |
71 |
73 |
79 |
83 |
89 |
97 |
101 |
103 |
107 |
|
109 |
113 |
127 |
131 |
137 |
139 |
149 |
161 |
167 |
163 |
167 |
173 |
179 |
181 |
|
191 |
193 |
197 |
199 |
211 |
223 |
227 |
229 |
233 |
239 |
241 |
251 |
257 |
263 |
|
269 |
271 |
277 |
281 |
283 |
293 |
307 |
311 |
313 |
317 |
331 |
337 |
347 |
349 |
|
353 |
369 |
367 |
373 |
379 |
383 |
389 |
397 |
401 |
409 |
419 |
421 |
431 |
433 |
|
439 |
443 |
449 |
457 |
461 |
463 |
467 |
479 |
487 |
491 |
499 |
503 |
509 |
521 |
|
523 |
541 |
547 |
657 |
663 |
569 |
571 |
577 |
587 |
593 |
599 |
601 |
607 |
613 |
|
617 |
619 |
631 |
641 |
643 |
647 |
653 |
659 |
661 |
673 |
677 |
683 |
691 |
701 |
|
709 |
719 |
727 |
733 |
739 |
743 |
751 |
757 |
761 |
769 |
773 |
787 |
797 |
809 |
|
811 |
821 |
823 |
827 |
829 |
839 |
853 |
867 |
859 |
863 |
877 |
881 |
883 |
887 |
|
907 |
911 |
919 |
929 |
937 |
941 |
947 |
953 |
967 |
971 |
977 |
983 |
991 |
997 |
94
Квадраты натуральных чисел от 11 до 99
|
•гт |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1 |
121 |
144 |
169 |
196 |
225 |
256 |
289 |
324 |
361 |
|
2 |
441 |
484 |
529 |
576 |
625 |
676 |
729 |
784 |
841 |
|
3 |
961 |
1024 |
1089 |
1156 |
1225 |
1296 |
1369 |
1444 |
1521 |
|
4 |
1681 |
1764 |
1849 |
1936 |
2025 |
2116 |
2209 |
2304 |
2401 |
|
5 |
2601 |
2704 |
2809 |
2916 |
3025 |
3136 |
3249 |
3364 |
3481 |
|
6 |
3721 |
3844 |
3969 |
4096 |
4225 |
4356 |
4489 |
4624 |
4761 |
|
7 |
5041 |
5184 |
5329 |
5476 |
5625 |
5776 |
5929 |
6084 |
6241 |
|
8 |
6561 |
6724 |
6889 |
7056 |
7225 |
7396 |
7569 |
7744 |
7921 |
|
9 |
8281 |
8464 |
8649 |
8836 |
9025 |
9216 |
9409 |
9604 |
9801 |
Факториалы и степени
|
п |
п\ |
2п |
3" |
5" |
|
0 |
1 |
1 |
1 |
1 |
|
1 |
1 |
2 |
3 |
5 |
|
2 |
2 |
4 |
9 |
25 |
|
3 |
6 |
8 |
27 |
125 |
|
4 |
24 |
16 |
81 |
625 |
|
5 |
120 |
32 |
243 |
3125 |
|
6 |
720 |
64 |
729 |
15625 |
|
7 |
5040 |
128 |
2187 |
78125 |
|
8 |
40320 |
256 |
6561 |
390625 |
|
9 |
362880 |
512 |
19683 |
1953125 |
|
10 |
3628800 |
1024 |
59049 |
9765625 |
СОДЕРЖАНИЕ
![]() Таблица
6.
Таблица
6.
Таблица 8.
8 4
92
Приложение 94
15ВМ 5 - 7 1 0 7 - 8 1 0 5 - 3

9 М 7 8 5 7 1 0 " 7 8 1 0 5 0
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.