Алгебраические свойства геометрических фигур

АЛГЕБРА ГЕОМЕТРИЧЕСКОЙ ФИГУРЫ ПРЯМОУГОЛЬНИК.

Павлюк Никита Александрович

Ученик 9 класса школы лицей номер 8 г. Павлодар

Титченко Анжелика Петровна

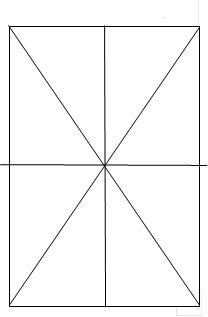
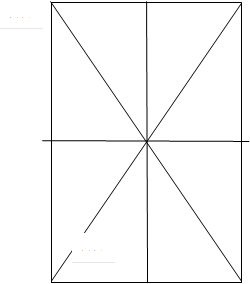
Работа посвящена алгебраическим свойства прямоугольника первого уровня абстракции, как одной из геометрических фигур плоскости. Геометрические свойства этой фигуры хорошо известны из математического курса средней общеобразовательной школы, где также отражены метрические особенности этой фигуры. Наша цель-через симметрию [1] этой фигуры охарактеризовать теоретико-алгебраические свойства, которые выразятся через абстрактный алгебраический объект полезный для развития абстрактного логико-математического мышления ученика. Каждое предложение любого социального языка представляет собой законченную мысль. Мысль структурируется понятиями, символами и смыслом, где отражаются абстрактные свойства понятий. Понятия, суждения и умозаключения ̶ форма абстрактного мышления, восходящие к конкретному объекту. Наш объект для изучения – прямоугольник (см. рис.1).

Вершины этого прямоугольника пронумеруем натуральными числами – , и прямоугольник будем самосовмещать не меняя ориентации плоскости (оставляя плоскость, привязанную к плоскости листа). Ясно, что первое самосовмещение  прямоугольника произойдет, когда мы оставим его на листе и запишем эту неподвижную симметрию как , то есть каждая вершина прямоугольника перешла в себя (нулевой поворот вокруг точки О)

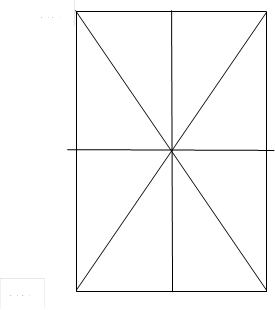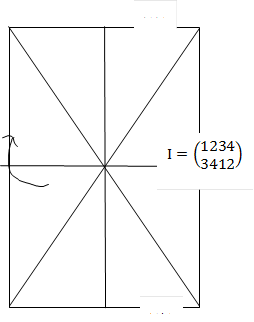
Выражение ,единичная подстановка четырех символов множества , или отражение множества на себя. Следующая симметрия просматривается при повороте прямоугольника вокруг центра симметрии точки О на 180⁰  по часовой стрелке. При этой симметрии произойдет самосовмещение прямоугольника с собой по правилу  . Прямоугольника окажется в следующем положении (рис.2). В скобках отмечено прежнее положение вершин, то есть исходное положение. I

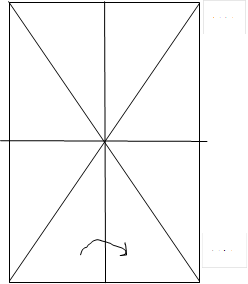
Далее, замечаем, что прямоугольник можно совместить с собой отражая его по центральным  линиям , которые в нем взаимно перпендикулярны. Это обстоятельство облегчит совмещение в (1) с (4) при отражении от боковой центральной линии (2)(1) (рис. 3 а), а при отражении от диагонали (1)(3) - вершин (2)(4). Таким образом симметрия , симметрия . Других самосовмещений прямоугольника нет.

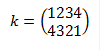
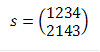
Что произойдет, если мы будем последовательно выполнять симметрии одна за другой? Например, i и i т.е.  и .  Проследим ,  Результат: . По этой схеме мы получим, что . Осуществим оставшиеся произведения симметрий и поместим результаты в таблицу.

Анализируя таблицу 1 выявим алгебраические свойства множества  с отражением последовательного выполнения симметрий (умножение симметрий) .

1.Умножение двух симметрий дает в произведении симметрию. То есть умножение симметрий замкнуто (не выходит за пределы четырех симметрий). Это свойство следует из того, что каждая симметрия прямоугольника имеет порядок два, то есть  . Таким образом, для любого элемента из множества симметрий прямоугольника , если  и , если . Таким образом,

 .                                                          (1)

2. Множество V с бинарной (двухместной) операцией обладает сочетательным свойством, то есть    

,

                                               (2)

3 В множестве симметрии прямоугольника существует нейтральная симметрия е, которая оставляет на месте при умножении любую другую (в том числе и е) симметрию, таким образом

(3) 4.Во множестве симметрий прямоугольника для любой симметрии x существует такая симметрия , что  (см. таблицу 1). Таким образом,

                                                 (4)

5.Умножение симметрии прямоугольника коммутативно. Расположение симметрии симметрично относительно главной диагонали (слева-направо-вниз), то есть

                                                       (5)

Чтобы убедиться в этом достаточно перебрать по три элемента из множества V и найти их произведение в различных сочетаниях по два.

Формулами (1),(2),(3),(4) определяется алгебраическая система, которая называется группой [2]. Рассмотренная нами группа  - группа прямоугольника является коммутативной на её элементах выполняется формула (5).

ЛИТЕРАТУРА

1.Тарасов Л. В. Этот удивительно симметричный мир: Пособие для учащихся. — М.: Просвещение, 1982. — 176 с.

2.Фрид Э.  Элементарное введение в абстрактную алгебру. Пер. с венгер. Ю.А. Данилова. –М.: Мир, 1979. –260 с.