Алгебралық бөлшектің негізгі қасиеті

Алгебра пәні бойынша 7 сынып оқушысының өзіндік жұмысының жоспары

IV тоқсан

Сабақтың номері :    84

Сабақтың тақырыбы: Алгебралық бөлшектің негізгі қасиеті

Мақсаты: 1. Алгебралық бөлшектің  негізгі қасиетін қолдану;

2. Алгебралық бөлшекті қысқартуды үйрену;

 3. Теңбе-теңдік және теңбе-тең түрлендіру ережелерін білу.

Конспект

Оқулық Алгебра 7 Алматы «Атамұра» 2017 авторы Ә.Н. Шыныбеков  6.1.2

Бөлшектің негізгі қасиеті:

Егер бөлшектің алымын да, бөлімін де нөлге тең емес өрнекке көбейтсе,онда берілген бөлшекке тең бөлшек

шығады.

Бөлшектің негізгі қасиетін қолдану арқылы шығарылатын есептердің  түрі – бөлшектерді қысқарту.

Анықтама: Құрамындағы барлық айнымалылардың мүмкін мәндері жиынында ақиқат болатын теңдікті теңбе-теңдік деп атайды. Өрнекті оған теңбе-тең өрнекпен алмастыруды теңбе-тең түрлендіру деп атайды.

 Егер бөлшектің алымының (немесе бөлімінің) таңбасын өзгертсек, онда бөлшектің де таңбасы өзгереді.

Бейнеүзінді: https://www.youtube.com/watch?v=1SXYt9k3ybc

Мысал:

1.       Бөлшекті алдымен қысқартып алып, мәнін табыңдар:

1)

Шешімі:    Алымын қысқаша көбейту формула қолдану арқылы, ал бөлімін ортақ көбейткішті жақша сыртына шығару арқылы көбейткіштерге жіктеп алып бөлшекті қысқартамыз   

Шешімі:

2.      Теңбе-теңдікті  дәлелдеңдер:    

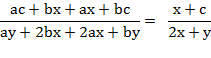
Шешімі:Теңдіктің сол жағын топтау арқылы көбейткіштерге жіктеп түрлендіреміз

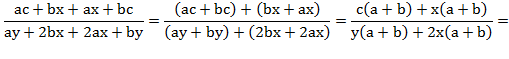
Тапсырма:

№1  Бөлшекті қысқартыңдар:

1).     

2).

3).   

4).  

№2    Бөлшекті қысқартыңдар:

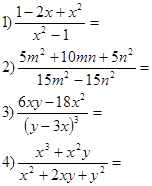
Әзірлеуші: Альмаганбетова Ж.К. №178 лицейдің математика пәні мұғалімі. Алматы қаласы Білім басқармасының Қалалық білім берудегі жаңа технологиялардың ғылыми-әдістемелік орталығының қолдауымен ұсынылып отыр.

Скачано с www.znanio.ru