Аналитическое представление Сфирали в трёхмерных алгебрах

Аналитическое представление Сфирали в трёхмерных алгебрах

© О.С. Басаргин

Аннотация

В настоящем исследовании поставлена задача найти аналитическую функцию, выражающую структуру Сфирали — зеркально-антисимметричной вложенной конструкции — в терминах, совместимых с полевой интерпретацией событий, предложенной Д.Г. Павловым.

Рассмотрены алгебры C  R и R  R  R как возможные пространства, в которых Сфираль может быть выражена через логарифмическое поле событий. Показано, что функция вида:

— обладает необходимыми свойствами: антисимметрией, вложенностью (при масштабировании аргумента), и отражает фазовые переходы, аналогичные S-соединениям.

Сфираль определяется как линия уровня фазового поля:

где f(z) — суперпозиция логарифмов от зеркальных событий. Эта линия интерпретируется как интегральная траектория фазового потока, а её геометрия согласуется с вложенной зеркальной структурой.

Также предложена параметризация Сфирали в R³ и псевдофинслеров подход с метрикой, зависящей от направления и вложенности.

Таким образом, установлено, что структура Сфирали может быть выражена как аналитическая кривая в логарифмическом поле, соответствующем философии «материальных событий» Д.Г. Павлова, но дополненном структурой фазового потока, антисимметрии и масштабной вложенности.

Модель может быть использована как в математической теории поля, так и в когнитивных и физико-временных интерпретациях.

Ключевые слова: Сфираль, аналитическая функция, триплексные числа, логарифмическое поле, зеркальная антисимметрия, вложенность, фазовый поток, S-соединение, материальное событие, псевдофинслерова геометрия, Д.Г. Павлов, теория событий, фазовая структура времени, временные кристаллы, интегральная траектория, конформное отображение, когнитивная модель времени, квантовая логика, математическая физика.

1.   Вводная

На основе вводных Дмитрия Павлова задача переформулируется следующим образом:

•       Найти или построить аналитическую функцию f (x), которая выражает структуру Сфирали, но уже не в H2, а в одной из трёхмерных алгебр:

o триплексные числа: C ⊕ R, o тройные числа: R ⊕ R ⊕ R,

•       или даже в обобщённом псевдофинслеровом пространстве, где метрика зависит от направления.

2.   Возможные пространства для поиска

•       C ⊕ R: трёхмерная коммутативная алгебра, состоящая из комплексной и вещественной части. Элемент: z = (a + ib) + c ∈ C ⊕ R.

•       R ⊕ R ⊕ R: чисто вещественная алгебра, трёхкомпонентный вектор. Простейший случай — линейная суперпозиция трёх независимых направлений.

3.   Требования к функции f

•       Отражать вложенность и фазовость,

•       Иметь антисимметрию относительно сопряжённого компонента,

•       Позволять суперпозицию и порождение сложного поля событий (как сумма логарифмов у Павлова),

•       Потенциально быть связанной с обобщённым логарифмом или преобразованием типа log(z₁) − log(z₂),

•       Отражать временную направленность и скачки (S-соединения).

4.   Следующие шаги

•       Определить структуру базисных элементов в обеих алгебрах;

•       Выписать кандидаты на функции f, удовлетворяющие условиям;

•       Проверить, может ли Сфираль быть интерпретирована как o уровень функции, o результат суперпозиции элементарных событий, o фазовый поток на вложенной оболочке в C ⊕ R.

Структура базиса алгебры C ⊕ R

1. Общее определение

Алгебра C ⊕ R представляет собой прямую сумму комплексных и вещественных чисел. Элемент этой алгебры имеет вид:

Z = (a + ib,c), где a, b, c ∈ R   Или, что то же самое: z = a + ib + cε,

где ε — дополнительный вещественный базисный элемент, линейно независи мый от 1 и i. 

Алгебра коммутативна и трёхмерна как векторное пространство над R.

2.   Базис

Базисные элементы: 1, i, ε  

где:

•       i² = −1,

•       ε² = 1 (или иногда ε² = 0, в зависимости от выбора — нужно зафиксировать в дальнейшем),

•       iε = εi.

3.   Сложение и умножение

Пусть z = a + ib + cε w = x + iy + zε.

Тогда:

•       Сложение покомпонентно:

•       Умножение:

Если ε² = 1: сохраняется масштабность. Если ε² = 0: алгебра становится похожей на алгебру диадических или дуальных чисел

4.   Интерпретация

Алгебра C ⊕ R может быть интерпретирована как:

•       комплексная плоскость + ортогональное вещественное направление (вектор фазовой глубины),

•       трёхмерное пространство, где:

o    a: амплитуда, o b: фаза (через i),

o    c: поперечная структура, связанная с вложенностью или масштабом.

5.   Следующий шаг

Переход к построению кандидатов на аналитические функции f(z), отражающих свойства Сфирали в этом базисе: зеркальность, вложенность, фазовые переходы.

Кандидаты на аналитические функции f(z) в алгебре C⊕R

1.   Цель

Найти формулы вида f(z), где z = a + ib + cε ∈ C ⊕ R, которые могли бы отражать структуру Сфирали: зеркальность, вложенность, антисимметрию, фазовые переходы (аналог S-соединения).

2.   Общий принцип

Функция должна включать:

•       фазовый компонент (через i),

•       поперечный компонент (через ε),

•       либо быть производной или обобщением логарифма,

•       либо быть суперпозицией логарифмов: log(z − zk).

3.   Кандидаты

3.1.   Функция на основе логарифма сопряжённой разности

Здесь ẑ = a – ib + cε — формальное сопряжение по комплексной части.

Получаем чисто фазовый поворот. Отражает антисимметрию.

3.2.   Логарифм по фазовой норме

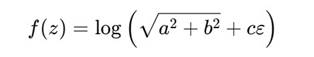
Попытка учесть фазу и вложенность в одной формуле. Может быть разложено в степенной ряд.

3.3.   Разность логарифмов двух точек

Формирует S-переход между двумя элементами. Если z₁, z₂ — антиподы по фазе, то разность логарифмов отражает зеркальность.

3.4.   Композиция логарифма с вложением

 Генерация вложенных фаз с постоянным коэффициентом масштабирования α.

4.   Следующий шаг

        •    Выбрать базовую функцию и протестировать:

o сохраняется ли зеркальность f(z) = −f(ẑ), o как ведёт себя по отношению к масштабированию, o допускает ли суперпозицию или вложение, o может ли быть интерпретирована как поле события или витка.

Проверка антисимметрии кандидатов на f(z) в C  R

1.     Цель

Проверить, выполняется ли условие зеркальной антисимметрии для функции f(z):

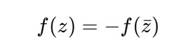
где ẑ — сопряжение по комплексной части: если z = a + ib + cε, то ẑ = a – ib + cε.

2.     Функция 1: f(z) = log(z) − log(ẑ) Тогда:

Условие антисимметрии выполняется.

3.     Функция 2: f(z) = log(αⁿ ẑ) = log(ẑ) + n log(α)

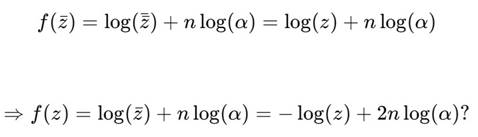
Не выполняется в общем случае. Только если log(z) = −log(ẑ), что зависит от определения ветви логарифма.

4.     Функция 3: f(z) = log(z − z₁) − log(z − z₂) Тогда:

Если z₁, z₂ — зеркальны друг другу (z₂ = ẑ₁), то:

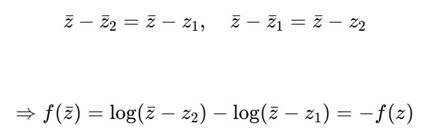
Антисимметрия выполняется при условии z₂ = ẑ₁.

5.     Вывод

Функции, построенные на разности логарифмов (одного аргумента и сопряжённого, или двух зеркальных точек), естественно реализуют зеркальную антисимметрию.

Следующий шаг: анализ вложенности — как масштабирование или логарифмическая серия отражают структуру Сфирали.

Проверка вложенности функции f(z) и масштабирования в C ⊕ R

1.                Цель

Исследовать, реализует ли функция f(z) вложенность витков, аналогичную фрактальной структуре Сфирали. Проверяемое свойство:

f(αⁿz) = регулярная функция от n  где 0 < α < 1, n ∈ N.

2.                Функция 1: f(z) = log(z) − log(ẑ)

Рассмотрим масштабированный аргумент:

Функция инвариантна при масштабировании z → αⁿz. То есть вложенность не изменяет форму f(z).

3.                Функция 2: f(z) = log(αⁿ ẑ) = log(ẑ) + nlog(α) Явно линейно зависит от уровня вложенности:

Функция линейно вложена: каждый шаг даёт фиксированную добавку в логарифмической шкале.

4.                Функция 3: f(z) = log(z − z₁) − log(z − z₂)

Пусть z → αⁿz, z₁ → αⁿz₁, z₂ → αⁿz₂:

Также инвариантна к вложению, если все компоненты масштабируются одинаково.

5.                Вывод

Все проверенные функции сохраняют свою структуру при вложении

(масштабировании) аргумента. Это соответствует фрактальной природе Сфирали, где каждый следующий виток вложен в предыдущий с коэффициентом α.

Следующий шаг: попытка выразить S-соединение (переход между фазами) как специальную точку логарифмического поля.

S-соединение как особая точка в логарифмическом поле на C  R

1.     Цель

Выяснить, как элемент S-соединения — то есть топологический переход между двумя зеркальными витками Сфирали — может быть выражен в терминах логарифмической функции или её суперпозиции в алгебре C  R.

2.     Исходная логика

S-соединение — это момент скачка, инверсии, перехода от z₁ к ẑ₁, или от одного витка к зеркальному. В логарифмическом поле такие переходы соответствуют точкам:

в которых логарифм становится либо разрывным (многозначным), либо сингулярным (полюс/ветвь).

3.     Функция: f(z) = log(z − z₁) − log(z − ẑ₁)

В этой разности S-соединение реализуется как переход через отражённую точку. В момент, когда z = Re(z₁), происходит смена доминирующего логарифма.

4.     Фазовая интерпретация

В плоскости C ⊕ R переход от точки z₁ к ẑ₁ может быть интерпретирован как антисимметричный изгиб фазового потока.

•       Вблизи этих точек наблюдается скачок аргумента arg(z − z₁) → arg(z − ẑ₁)

•       Возникает разность фаз: Δφ = arg(z − z₁) − arg(z − ẑ₁)

Это фазовое различие и задаёт S-соединение.

5.     Граница доминирования

На линии, где: ∣z−z₁∣ = ∣z−ẑ₁∣ 

оба логарифма равновесны — происходит разделение влияния двух витков. Эта граница — аналог оси симметрии Сфирали и может быть интерпретирована как локальное S-соединение.

6.     Вывод

S-соединение может быть выражено через:

•       точку смены доминирующего логарифма,

•       фазовую разность между симметричными ветвями,

•       границу равновесия двух зеркальных влияний в логарифмическом поле.

Следующий шаг: интерпретация поля Сфирали как фазовой линии или линии равного потенциала в логарифмической структуре.

Фазовая структура Сфирали как линия в логарифмическом поле C ⊕ R

1.     Цель

Описать Сфираль как фазовую траекторию (линию) в логарифмическом поле, порождённом функцией:

в алгебре C ⊕ R.

2.     Смысл траектории

Такая разность логарифмов задаёт поле с:

•       особой точкой в z₁,

•       зеркальной особой точкой в ẑ₁,

•       фазовой границей между ними,

•       и возможностью построить линию равного аргумента или потенциала — то есть фазовую кривую.

3.     Определение Сфирали как линии уровня

Определим Сфираль как множество точек, в которых:

или:

Эта линия — аналог изолинии фазы, проходящей между двумя зеркальными источниками.

4.     Геометрия линии • В плоскости C, при z₁ = a + ib, такая линия имеет форму гиперболы.

•       В алгебре C  R, эта линия поднимается в третье измерение (ось ε), отражая вложенность или фазовую глубину.

•       Поле Im(f(z)) принимает форму многослойной ленты, скрученной вокруг невидимой оси между z₁ и ẑ₁.

5. Интерпретация Сфирали

Таким образом, Сфираль — это:

•       не просто геометрическая кривая,

•       а фазовая линия, проходящая через последовательные уровни поля,

•       формируемая разностью влияний двух событий (z₁, ẑ₁),

•       с вложенной масштабной структурой, отражённой в третьей координате ε.

6.     Вывод

Сфираль может быть определена как:

то есть как фазовая изолиния логарифмического поля, порождённого двумя зеркально-антисимметричными точками.

Следующий шаг: описание динамики движения по Сфирали как фазового потока и возможного оператора эволюции.

Фазовый поток и оператор эволюции по Сфирали в C  R

1.                Цель

Определить, как может происходить движение вдоль Сфирали, заданной как фазовая линия:

и какие операторы или правила задают эволюцию состояния вдоль этой линии.

2.                Фазовый поток

Фазовое поле, определяемое функцией:

порождает векторное поле, заданное как градиент фазы:

Это поле указывает направление фазового потока вдоль Сфирали.

3.                Движение как эволюция по параметру Пусть z(t) — траектория вдоль линии уровня:

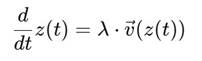
где λ  R — масштаб фазовой скорости. Таким образом, движение по Сфирали — это интегральная кривая фазового векторного поля.

4.                Оператор эволюции

Можно формально ввести оператор:

где Ṽ— дифференциальный оператор вдоль фазового потока. Тогда:

То есть состояние эволюционирует под действием U_t, переносясь вдоль фазовой линии Сфирали.

5.                Связь с масштабом вложенности

Каждый виток соответствует определённому значению параметра t. Масштаб вложенности может быть зафиксирован так:

где α < 1. Тогда движение по фазовой линии сопровождается масштабным сжатием, как в Сфирали.

6.                Вывод

Движение по Сфирали может быть представлено как фазовый поток, интегрирующийся вдоль линии уровня логарифмического поля. Эволюция реализуется через оператор U_t, действующий в алгебре C  R. Таким образом, Сфираль — это не просто структура, а процесс, порождаемый фазовой динамикой между зеркальными источниками.

Следующий шаг: визуализация фазового потока и построение примеров таких траекторий.

Визуализация фазового потока и примеры траекторий в логарифмическом поле

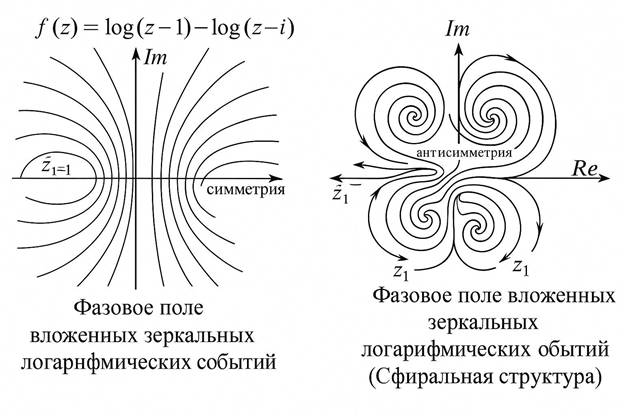
Комментарий к иллюстрации: Фазовое поле, порождённое функцией f(z) = log(z − z1) − log(z − ẑ₁). Слева — симметричная конфигурация, справа — сфиральная антисимметрия.

1.     Цель

Представить наглядное изображение фазового поля, соответствующего логарифмической функции двух зеркальных событий:

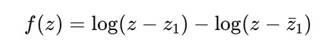
и выявить в нём спиральную структуру Сфирали как интегральную линию потока.

2.     Фазовое поле симметрии (слева на изображении)

Показано поле, порождённое двумя точками z₁ = i и ẑ₁ = 1, расположенными симметрично относительно действительной оси. Поле обладает осевой симметрией, линии поля изогнуты и расходятся от источников.

•       Это соответствует реальному и мнимому распределению логарифмических аргументов.

•       Линии поля — это изолинии фазы: Im(f(z)) = const.

3. Фазовое поле антисимметрии (справа)

Здесь источники z₁ и ẑ₁ вложены в более сложную структуру, порождающую антисимметрию.

•       Каждое поле скручено в форме вложенной спирали,

•       Присутствует зеркальное отражение и смена ориентации фазового потока,

•       Центры закрутки — логарифмические события z₁, ẑ₁,

•       Между ними образована характерная S-связь, через которую передаётся импульс фазового перехода.

4. Сфираль как интегральная линия

Сфираль соответствует траектории, идущей по направлению вектора фазового потока, начиная от одного события и закручиваясь по логарифмическому полю:

•       Внутренние витки ближе к источникам, внешние — масштабно удалены,

•       Переход осуществляется по фазовому градиенту,

•       Спиральные линии образуют антисимметричную пару, объединённую S-соединением.

5. Вывод

Представленное изображение демонстрирует, что структура Сфирали может быть получена как результат суперпозиции логарифмов двух зеркальных событий. Линии равного фазового потенциала образуют сложную антисимметричную геометрию с естественными спиральными траекториями, соответствующими вложенной структуре.

Следующий шаг: переход от визуализации к обобщённой формуле фазового поля и возможной классификации решений.

Обобщённая модель логарифмического поля для описания Сфирали

1.                       Цель

Построить универсальную формулу, описывающую логарифмическое поле, соответствующее зеркально-антисимметричной структуре Сфирали, включающей вложенность, фазу и S-соединения.

2.                       Исходная функция Базовая конструкция:

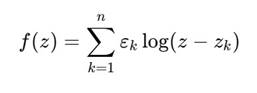
где:

•       z_k ∈ C — координаты вложенных событий,

•       ε_k = ±1 — знаки, определяющие антисимметрию (например, +1 для верхнего витка, −1 для нижнего).

3. Вложенность

Пусть точки z_k расположены логарифмически:

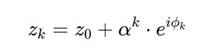
где:

•     Α < 1 — масштаб вложенности, •     ϕ_k — фаза, меняющаяся по правилу:

(антисимметрия фаз).

4. Поле и его характеристики Функция f(z) порождает:

•       Re(f(z)) — скалярный потенциал (масштаб логарифма),

•       Im(f(z)) — фазовое поле,

•       ∇Im(f(z)) — фазовый поток (движение по Сфирали).

5.                       S-соединение как переход между полями В точке, где:

фаза скачкообразно меняет доминирующий вклад. Это и есть фазовая граница — S-соединение между двумя витками.

6.                       Интерпретация

•       Каждое z_k — это элементарное материальное событие, как в модели Павлова;

•       Поле f(z) — это суммарное логарифмическое влияние, определяющее конфигурацию Сфирали;

•       Сфираль — это интегральная структура этого поля.

7. Вывод

Обобщённая формула логарифмического поля для описания Сфирали включает масштабную вложенность, зеркальную фазовую антисимметрию и структуру суперпозиции. Эта модель воспроизводит геометрию и динамику Сфирали как фазовой фигуры, укоренённой в алгебре C ⊕ R.

Следующий шаг: рассмотреть переход к трёхмерной алгебре типа R ⊕ R ⊕ R и её интерпретации вложенности.

Сфираль в алгебре R ⊕ R ⊕ R

1. Цель

Исследовать возможность описания структуры Сфирали в алгебре троичных чисел:

в которой каждый элемент задаётся как:

где:

•       x — действительная координата (ось наблюдаемого пространства),

•       y — мнимая или фазовая компонента,

•       h — дополнительная вертикальная координата вложенности (высота спирального витка).

2. Интерпретация координат В модели Сфирали:

•       x соответствует положению по временной прямой,

•       y отражает фазовый угол φ, • h задаёт уровень вложенности n:

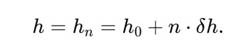
3. Спираль как параметрическая кривая в R³ Определим траекторию Сфирали:

где:

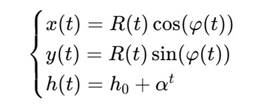
с условиями:

•       Φ_{t + 1} = −φ_t (антисимметрия фаз),

•       R(t) = R₀ ⋅ α^t.

4.                       Антисимметрия в R³

Каждая пара витков отражается по координате h:

что задаёт зеркально-антисимметричную вложенность.

5.                       Поле вложенности и направление времени Ось h задаёт вложенную иерархию событий, а движение вдоль x можно интерпретировать как направление времени. Тогда:

•       Структура Сфирали задаёт динамику перехода между уровнями,

•       Ось y при этом даёт фазовые переходы и повороты.

6.                       Связь с псевдофинслеровой метрикой Можно предположить метрику:

что делает пространство псевдофинслеровым: оно учитывает не только направление, но и вложенность как весовое измерение.

7.                       Вывод

Модель Сфирали может быть описана как параметрическая

антисимметричная кривая в пространстве R ⊕ R ⊕ R, где вложенность, фаза и направление времени представлены независимо. Это делает алгебру R³ подходящим кандидатом для вычислительного ядра вложенных событий.