АНАЛИЗ ИНФОРМАЦИОННЫХ МОДЕЛЕЙ ПРИ ИЗУЧЕНИИ КУРСА «ИНФОРМАТИКА И ИКТ»

Современная  школьная  информатика  –  это дисциплина,  направленная  на  формирование широкого спектра  предметных и метапредметных образовательных  результатов,  отвечающая требованиям  времени  и  непрерывно изменяющаяся  в  соответствии  с  этими требованиями.

Согласно Государственному  образовательному  стандарту  среднего  общего образования предметные результаты освоения учебного предмета «Информатика и ИКТ»  должны  быть  ориентированы  на  изучение  системы  базовых  знаний, отражающих вклад информатики в формирование  современной  научной картины мира, роль информационных процессов в обществе, биологических и  технических  системах,  овладение умениями  применять,  анализировать, преобразовывать  информационные  модели  реальных  объектов  и  процессов, используя  ИКТ,  в  том  числе  при изучении  других  школьных  дисциплин, освоении  информационных  технологий,  необходимых  как  в  самом образовательном процессе, так и в их повседневной и будущей жизни [1].

С информационным моделированием учащиеся начинают знакомиться ещё в 6 классе, где они осваивают сущность понятий «модель», «информационная модель», учатся различать информационные модели, приводить их примеры. Знакомятся с правилами построения табличных моделей, схем, графов, деревьев. С каждым последующим классом данная тема усложняется. Так, в 9 классе при изучении темы «Моделирование и формализация», учащиеся знакомятся с компьютерным моделированием при создании баз данных, учатся строить и интерпретировать различные информационные модели.

Усвоение данной темы позволит развить логическое мышление учащихся, научиться структурировать данные, познакомиться со способами организации хранилищ данных и поиска информации в них, методами построения информационных моделей сложных систем в различных предметных областях.

Модель - очень широкое понятие, включающее в себя множество способов представления изучаемой реальности [2]. Различают модели материальные (натурные) и информационные. Материальные модели – это реальные предметы, в уменьшенном или увеличенном виде, воспроизводящие внешний вид, структуру или поведение объекта моделирования. Информационные модели – это совокупность информации об объекте, описывающая свойства и состояние объекта, процесса или явления, а также связи и отношения с окружающим миром.

Еще более сложную картину представляют информационные модели.

Представляю Вашему вниманию следующую классификацию информационных моделей.

рассмотрим примеры решения задач, которые требуют знания информационных моделей (таблиц, диаграмм, графиков). Определим особенности нахождения кратчайшего пути между некоторыми пунктами с помощью графов и по графу научимся определять количество путей.

 Начало теории графов все единодушно относят к 1736 г. , когда Л. Эйлер решил популярную в то время задачу о кенигсбергских мостах. Однако этот результат более ста лет оставался единственным результатом теории графов. Лишь в середине XIX века инженер- электрик Г. Кирхгоф разработал теорию деревьев для исследования электрических цепей, а математик А. Кэли в связи с описанием строения углеводородов решил перечислительные задачи для трех типов деревьев. Родившись при решении головоломок и занимательных игр (задачи о шахматном коне, о ферзях, « кругосветное путешествие », задачи о свадьбах и гаремах и т. п.), теория графов стала в настоящее время простым, доступным и мощным средством решения вопросов, относящихся к широкому кругу проблем [7].

Графы буквально вездесущи. В виде графов можно, например, интерпретировать схемы дорог и электрические цепи, географические карты и молекулы химических соединений, связи между людьми и группами людей.

Рассмотрим примеры решения некоторых задач по моделированию.

При решении задач данного вида используется перебор вариантов, выбор лучшего по определенному признаку. Особых знаний, кроме умения перебирать варианты (не пропустив ни одного) здесь, как правило, не требуется. Полезно знать, что такое граф и как он описывается в виде таблицы, хотя, как правило, все необходимые объяснения даны в формулировке задания. Чаще всего используется взвешенный граф, где с каждым ребром связано некоторое число (вес), оно может обозначать, например, расстояние между городами или стоимость перевозки. Рассмотрим граф (рисунок слева), в котором 5 вершин (A, B, C, D и E); он описывается таблицей, расположенной в центре; в ней, например, число 5 на пересечении строки В и столбца С означает, что, во-первых, есть ребро, соединяющее В и С, и во-вторых, вес этого ребра равен 5; пустая клетка на пересечении строки А и столбца В означает, что ребра из А в В нет [7].

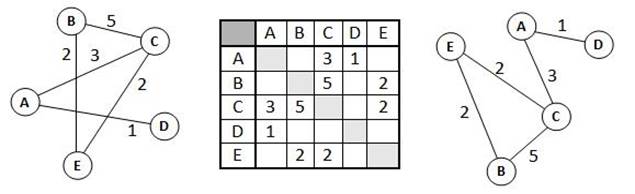
Обратите внимание, что граф по заданной таблице, которая еще называется весовой матрицей, может быть нарисован по-разному; например, той же таблице соответствует граф, показанный на рисунке справа от нее. В приведенном примере матрица симметрична относительно главной диагонали; это может означать, например, что стоимости перевозки из В в С и обратно равны (это не всегда так). Желательно научиться быстро и правильно строить граф по весовой матрице и наоборот.

Задача 1. Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.) 

       Определите длину кратчайшего пути между пунктами A и F (при условии, что передвигаться можно только по построенным дорогам) [6].

Решение:

Для решения этой задачи лучше построить взвешенный граф.

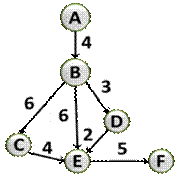
Используя данный граф с помощью перебора легко перечислить все возможные пути между пунктами A и F.

1-й способ: ABCEF – длина пути 4+6+4+5=19

2-й способ: ABEF– длина пути 4+6+5=15

3-й способ: ABDEF – длина пути 4+3+2+5=14

Выберем кратчайший путь. Это путь ABDEF длинной 14.

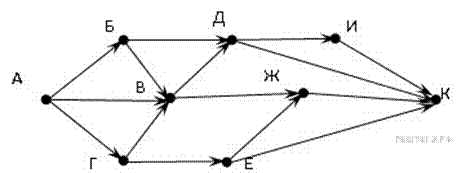
Задача. На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К? [6]

Решение:

Начнем считать количество путей с конца маршрута – с города К. N_X — количество различных путей из города А в город X, N — общее число путей.

В "К" можно приехать из И, Ж, или Е, поэтому:

N = N_К = N_И + N_Д + N _Ж + N _Е (1) 

Аналогично:

N_И = N_Д;

N_Д = N_Б + N_В;

N_Ж = N_В + N_Е;

N_Е = N_Г.

Добавим еще вершины:

N_Б = N_А = 1 ;

N_В = N_Б + N_А + N_Г = 1 + 1 + 1 = 3;

N_Г = N_А = 1;

Преобразуем первые вершины с учетом значений вторых:

N_И = N_Д = 4;

N_Д = N_Б + N_В = 1 + 3 = 4;

N_Ж = N_В + N_Е = 3 + 1 = 4;

N_Е = N_Г = 1.

Подставим в формулу (1):

N = N_К = 4 + 4 + 4 + 1 = 13.

Психологическая готовность ребенка к жизни в информационном обществе должна формироваться с первых лет обучения в школе. Это связано с необходимостью владения компьютерной грамотностью. Более важной задачей является формирование у обучающихся навыков абстрактного мышления, умение логически рассуждать, анализировать. Задачи компьютерного моделирования учат школьников не только выполнять вычисления, использовать математические формулы и логику, но и дают возможность самостоятельно исследовать законы и явления из разных научных областей, сравнивать и давать анализ объектам.

Список литературы:

1.        Государственный образовательный стандарт среднего общего образования (утвержден приказом № 679 от 30.07.2018 года);

2.                 Гусева Е.Н. Имитационное моделирование как среда компьютерной визуализации знаний/ В книге: Новые информационные технологии в образовании/ Материалы VII международной научно-практической конференции. Российский государственный профессионально-педагогический университет. 2014. С. 395-399.

3.        Донецкий Республиканский Институт Дополнительного Педагогического Образования - / [Электронный ресурс]. – Режим доступа: URL:   https://www.donippo.org

4.        Информатика  и  ИКТ.  Базовый  уровень.  10-11  класс:  методическое  пособие/  Семакин   И.Г., Хеннер Е.К.-2-е изд.-М.: Бином. Лаборатория знаний, 2011

5.        Информатика.  Задачник-практикум  в  2  т.  Под  ред.  И.Г. Семакина, Е.К.  Хеннера. –  М.:  Лаборатория базовых знаний, 2011.

6.        Сайт министерства образования и науки Донецкой Народной Республики - / [Электронный ресурс]. - Режим доступа: URL:   http://mondnr.ru

7.        Сухан И. В., Иванисова О. В., Кравченко Г. Г. Элементы теории графов в курсе дискретной математики // Педагогика высшей школы. — 2016. — №3. — С. 44-47. — / [Электронный ресурс]. – Режим доступа: URL: https://moluch.ru/th/3/archive/43/1176/ (дата обращения: 08.04.2019).

8.        Теория и методика обучения информатике - / [Электронный ресурс]. – Режим доступа: URL: https://sites.google.com/site/methteachinfo/home

Скачано с www.znanio.ru