
Тема: «Графы. Решение алгоритмических задач, связанных с анализом графов»
Класс 11
Тип урока: урок систематизации и обобщения знаний и умений.
Цель урока: показать учащимся многообразие практических задач, решаемых с помощью графа, изучить разные способы решения задач.
Задачи:
Образовательные:
● систематизировать и расширить представления учащихся о графах;
● продолжить формирование познавательного интереса к информатике.
Развивающие:
● развивать познавательные процессы (внимание, восприятие, мышление);
● развивать эмоциональную сферу;
● развивать коммуникативные умения;
● развивать мыслительные процессы (анализ, синтез, классификация и другие).
Воспитательные:
● воспитывать умение слушать;
● воспитывать умение работать в парах.
Формы работы: фронтальная, парная, индивидуальная.
Материалы к уроку: презентация, интерактивная доска, компьютер, учебник.
План урока:
I. Организационный момент (1 мин.)
II. Актуализация знаний (10 мин.)
III. Изложение нового материала (10 мин.)
IV. Физминутка (1 мин)
V. Закрепление (15 мин)
VI. Итог урока (1 мин.)
VII. Д\З (1 мин.)
VIII.Рефлексия (1 мин.)
Ход урока:
I. Организационный момент. Приветствует учащихся, проверяет их готовность к уроку.
- Сегодня вы пройдете очередной шаг по дороге знаний, и я с радостью помогу вам сделать этот шаг.
II. Актуализация знаний. Что мы на прошлом уроке изучали?
Фронтальный опрос:
Что такое модель? Приведите примеры.
Что такое моделирование? Какие виды моделей бывают?
Что такое натурная (материальная) модель? Приведите примеры.
Что такое информационная модель? Приведите примеры
Виды информационных моделей?
Что такое компьютерная модель? Приведите примеры
Что такое компьютерная моделирование? Перечислите основные этапы компьютерного моделирования.
Какие возможности даёт компьютерное моделирование?
III. Изложение нового материала
Перед вами задача ОГЭ по информатике.
На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж и К. По каждой дороге можно двигаться только в одном направлении, указанном
стрелкой. Сколько существует различных путей из города А в город К?
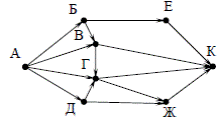
Что вы можете пояснить по решению данной задачи? Учащиеся обсуждают решение.
Решение:
АБЕК, АБВК, АБВГК, АБВГЖК
АВК, АВГК, АВГЖК,
АГК, АГЖК,
АДЖК, АДГК, АДГЖК
Ответ: 12
Между населенными пунктами А, В, С, D, Е построены дороги, протяженность которых (в километрах) приведена в таблице: Определите длину кратчайшего пути между пунктами А и E. Передвигаться можно только по дорогам, протяженность которых указана в таблице.
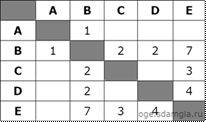
Определите длину кратчайшего пути между пунктами А и E. Передвигаться можно только по дорогам, протяженность которых указана в таблице.
Построим граф, соответствующий таблице и обозначим на графе длины существующих дорог:
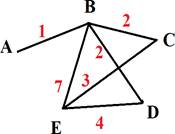
Запишем все возможные дороги из А в Е и вычислим их длину: ABE – 1+7=8
ABCE – 1+2+3=6
ABDE – 1+2+4=7
Ответ: 6
Теперь давайте сформулируем тему урока, а также чем мы будем заниматься на нем:
Повторим…
Изучим…
Узнаем…
Графы используют во всех отраслях нашей жизни. Знание основ теории графов необходимо в управлении производством, бизнесе, при построении путей транспортировки и доставки, решении задач.
Графы используют в связи с развитием теории вероятности, математической логики и информационных технологий.
Граф — это конечная совокупность вершин, некоторые из которых соединены ребрами, т.е. это совокупность точек, называемых вершинами, и линий, соединяющих некоторые из вершин, называемых ребрами или дугами в зависимости от вида графа.
Примеры:
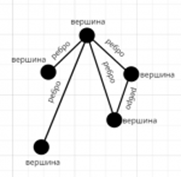
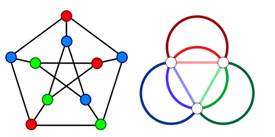
Мультиграф — это граф, у которого пара вершин соединены несколькими ребрами. А такие ребра, которые соединяют одну и ту же пару вершин, называют кратными. Две различные вершины графа, соединенные ребром, называются смежными.
Ребро не всегда соединяет разные вершины.
Петля — это ребро, которое соединяет вершину саму с собой.
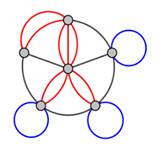
Рис. 1
На рисунке 1 изображен мультиграф со смежными ребрами (выделены черным цветом), кратными ребрами (выделены красным) и петлями (выделены синим).
Степенью вершины называют количество ребер, выходящих из одной вершины. Для петли ребро выходит из вершины дважды. Обозначать степень вершины, а будем как γ(а).
Пример:
На рисунке 2 изображен граф с 7 вершинами.
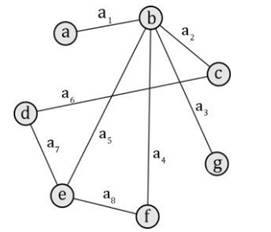
Рис. 2
Составим список степеней вершин этого графа: γ(a)=1,γ(b)=5,γ(c)=2,γ(d)=2,γ(e)=3,γ(f)=2,γ(g)=1.
Свойства графов:
1. В любом графе есть, по крайней мере, две вершины, имеющие одинаковую степень.
2. Для любого графа количество вершин нечетной степени всегда будет четное.
3. Сумма степеней всех вершин графа равна удвоенному числу его ребер.
Когда мы разобрались с определениями, мы можем переходить к разбору задания. Всего у 1 задачи есть 3 типа: Неоднозначное и однозначное соотнесение таблицы с графом и задачи на алгоритм Декстера. Алгоритм Дейкстры — алгоритм на графах, который находит кратчайшие пути от одной из вершин графа до всех остальных. Алгоритм широко применяется в программировании и технологиях.
Кардинальных различий между ними нет, лишь то, что в “Неоднозначных” не всегда можно точно определить полное соответствие между вершинами графа и их значением в таблице. Но в этих задачах это не требуется. Также в таблице смежности не указаны вершины, а их названия заменены на цифры. Обычно нам нужно найти соответствие между заданной вершиной и цифрой или длину ребра между двумя вершинами (если вместо звездочек стоят числа, соответствующие длине дороги).
Главная идея решения этой задачи заключается в том, что нужно найти одну или несколько вершин, которые чем-то отличаются от других. Они могут отличаться степенью или степенями смежных с ними вершин. И уже для этих вершин мы можем сделать некоторые выводы и от них строить соответствие между таблицей и графом.
Алгоритм решения:
1. Нужно у каждой вершины рядом записать ее степень
2. Разбить все вершины на группы по их степени
3. Установить соответствие между группой вершин и номерами вершин в таблице, которые им соответствуют. Если есть вершины со степенью, которая не повторяется у других вершин, то можно установить однозначное соответствие для этой вершины.
4. Разбить в одной группе на подгруппы по степени смежных с ними вершин
5. Проанализировать полученную информацию.
Рассмотрим пример «Представление графа таблицей смежности»:
На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о дорогах между населенными пунктами (звездочка означает, что дорога между соответствующими городами есть).
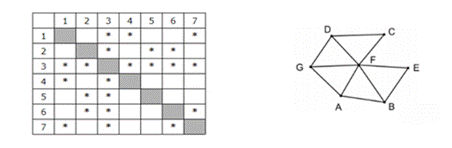
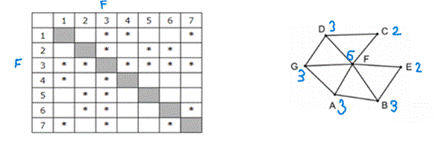
Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите номера населенных пунктов A и G в таблице. В ответе запишите числа в порядке возрастания без разделителей.
В этой задаче нам необходимо определить под какими номерами записаны вершины A и G, причем нам не необязательно определять точное соответствие, достаточно найти два номера.
Начнем решать, пройдемся по пунктам нашего алгоритма
1. A – 3, B – 3, C –2, D – 3, E – 2, F – 6, G –3.
2. У нас получилось 3 группы. F-6 вершин, C и E – 2 вершины и A, B, D, G – 3 вершины.
3. Мы можем заключить, что вершине F соответствует номер 3, C и E — 4 и 5, а A, B, D и G — 1, 2, 6 и 7.
4. Заметим, что некоторые вершины графа симметричны C – E, D – B, G – A, также заметим, что группу степени 3 можно разбить на 2 подгруппы, те у которых смежные вершины имеют степень 3, 3, 6 и 3, 2, 6, вершины первой подгруппы - A, G, а вершины второй подгруппы - D, B.
5. Начнем анализировать информацию, вершины 4,5 (C, E) связаны с вершинами 3, 1, 2, мы знаем, что F-3, значит 1, 2 соответствуют B, D. Значит вершинам A и G соответствуют вершины 6 и 7.
Пример 1.2:
Рассмотрим еще одну задачу, в ней вместо звездочек нам даны числа, обозначающие длину ребер между вершин. Нам нужно найти сумму длин ребер Б - Д и В - Е.
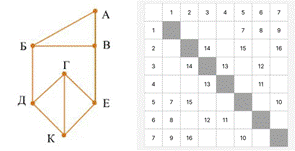
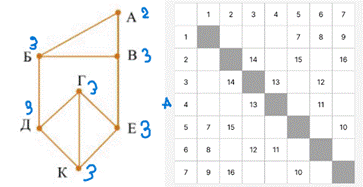
Воспользуемся нашим алгоритмом
1. А - 2, Б - 3, В - 3, Г - 3, Д - 3, Е - 3, К - 3.
2. Здесь у нас получается всего две группы А - 2 вершины и Б, В, Г, Д, Е, К - 2 вершины.
3. Мы можем понять, что вершине А соответствует номер 4 из таблицы.
4. В группе Б, В, Г, Д, Е, К можем выделить подгруппу Б, В у них смежные вершины имеют степень 2, 3, 3, в то время как у всех остальных смежные вершины имеют степень 3, 3, 3.
5. Начнем анализировать информацию. Вершина А соединена с вершинами Б, В, а судя по таблице 4 вершина соединена с 3 и 6 вершиной, значит вершинам Б, В соответствуют вершины 3, 6. Рассмотрим вершины 3, 6, они соединены с вершинами 2, 4, 6 и 1, 3, 4 соответственно. Можем сделать вывод, что вершинам Д, Е соответствуют номера 1, 2. Тогда ребрам Б - Д и В - Е соответствуют ребра 3 – 2, 6 – 1. Их длина равна 14 и 8, а их сумма равна 22.
IV. Физминутка. Упражнение для глаз
V. Закрепление
К доске выходит ученик. Решает следующее задание
На рисунке схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о протяжённости каждой из этих дорог (в километрах).
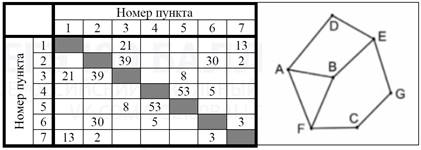
Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. В таблице в левом столбце указаны номера пунктов, откуда совершается движение, в первой строке – куда. Определите, какова сумма протяженностей дорог из пункта А в пункт D и из пункта G в пункт С. В ответ запишите целое число.
Работа в парах.
Вариант№2
Задание №1 На рисунке слева изображена схема дорог Н-ского района, в таблице звёздочкой обозначено наличие дороги из одного населённого пункта в другой. Отсутствие звёздочки означает, что такой дороги нет. Определите, какие номера населённых пунктов в таблице могут соответствовать населённым пунктам В и Е на схеме. В ответе запишите эти два номера в возрастающем порядке без пробелов и знаков препинания.
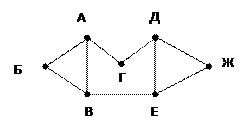 |
1 2 3 4 5 6 7 1 * * 2 * * * 3 * * 4 * * * 5 * * 6 * * * 7 * * *
Задание №2. На рисунке схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о протяжённости каждой из этих дорог (в километрах).
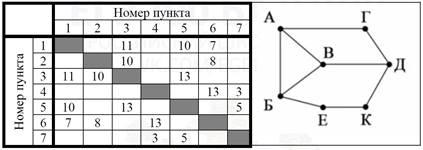
Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите сумму длин дорог между пунктом А и пунктом Б, и между пунктом Е и пунктом К. В ответе запишите целое число.
Вариант№2
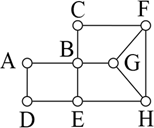
Задание №1 На рисунке справа схема дорог Н-ского района изображена в виде графа, в таблице звёздочками обозначено наличие дорог. Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными
обозначениями на графе. Найдите номера пунктов F и H. В качестве ответа запишите найденные номера в порядке убывания без разделителей.
 |
|||
 |
|||
Задание №2 На рисунке схема дорог Н-ского района изображена в виде графа, в таблице содержатся сведения о протяжённости каждой из этих дорог (в километрах).
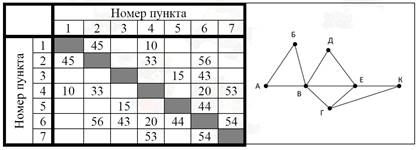
Так как таблицу и схему рисовали независимо друг от друга, то нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Определите, какова длина дороги из пункта Г в пункт Е. В ответе запишите целое число.
VI. Итог урока. Теперь давайте вспомним задачи урока, которые мы сформулировали в начале урока:
Повторим…
Достиг ли урок своих целей?
Все ли задачи были выполнены в ходе урока?
VII. Д\З. Параграф 11 стр. 148-158. Выполнить задание на стр.159 №2
VIII.Рефлексия
Сегодня я узнал….
Было трудно…
Я выполнил задание…
Теперь я могу….
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.