Поделиться
ПРОГРЕССИИ.docx
АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ
Последовательность (
), каждый член которой, начиная со
второго, равен предыдущему члену, сложенному с одним и тем же числом.
an = kn + b - арифметическая прогрессия
an+1 = an + d - условие (d - const)
d = an+1 - an (d - разность арифметической прогрессии)
an = a1 + d ·(n - 1) - формула n - го члена арифм. прогрессии
Sn = 
=
·n - сумма n первых членов
- свойство
ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ
Последовательность (
) отличных от нуля чисел, каждый
член которой, начиная со второго, равен предыдущему члену, умноженному
на одно и то же число.
bn+1 = b·q и bn ≠ 0 - условие
q = 
(q - знаменатель
геометрической прогрессии)
bn = 
- формула n - го члена геометр.
прогрессии
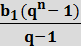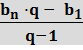Sn = 
= 
·n =
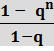- сумма n первых
членов
S = 
,
- сумма n первых членов
убывающей бесконечной геометрической прогрессии
- свойство
АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ
Последовательность (
), каждый член которой, начиная со
второго, равен предыдущему члену, сложенному с одним и тем же числом.
an = kn + b - арифметическая прогрессия
an+1 = an + d - условие (d - const)
d = an+1 - an (d - разность арифметической прогрессии)
an = a1 + d ·(n - 1) - формула n - го члена арифм. прогрессии
Sn = 
= 
·n - сумма n первых членов
- свойство
ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ
Последовательность (
) отличных от нуля чисел, каждый
член которой, начиная со второго, равен предыдущему члену, умноженному
на одно и то же число.
bn+1 = b·q и bn ≠ 0 - условие
q = 
(q - знаменатель
геометрической прогрессии)
bn = 
- формула n - го члена
геометр. прогрессии
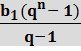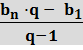Sn = 
= 
·n =
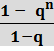- сумма n первых
членов
S = 
, 
- сумма n первых членов
убывающей бесконечной геометрической прогрессии
- свойство
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
