
Задачи оптимизации в Excel
Автоматизированное решение общей задачи линейного
программирования
ЗАДАНИЕ.
Фирма N, имеющая филиалы (k), производит продукцию. Каждый филиал фирмы выпускает четыре вида продукции из пяти (i=1-5). Данные, характеризующие производство филиалов bki, приведены в табл.1.
Таблица 1
Максимальный объем выпуска, bki, в тн
|
Номер филиала (К) |
|
Вид продукции (i ) |
|
||
|
i=1 |
i =2 |
i=3 |
i=4 |
i=5 |
|
|
2 |
3,6 |
4,2 |
|
3,4 |
1,7 |
Филиалы фирмы закупают сырье, из которого производят продукцию, у семи АО ( j =1-7). Выход готового продукта из 1 тонны сырья aij показан в табл.2.
Таблица 2
Выход (из 1тн сырья) готового продукта, aij
|
Номер АО (j) |
|
Вид продукции (i ) |
|
||
|
i=1 |
i =2 |
i=3 |
i=4 |
i=5 |
|
|
1 |
0,2 (* |
0,2 (* |
0,1 (* |
0,1 (* |
0,1 (* |
|
2 |
0,1 |
0,2 |
0,15 |
0,15 |
0,1 |
|
3 |
0,15 |
0,15 |
0,1 |
0,2 |
0,1 |
|
4 |
0,2 |
0,1 |
0,25 |
0,1 |
0,1 |
|
5 |
0,25 |
0,1 |
0,1 |
0,15 |
0,1 |
|
6 |
0,1 |
0,2 |
0,15 |
0,2 |
0,1 |
|
7 |
0,3 |
0,1 |
0,1 |
0,1 |
0,1 |
*) Остальная доля сырья идет в отход.
Прибыль филиалов фирмы при закупке 1тн сырья у разных АО, Сkj , показана в табл.3.
Таблица 3
Прибыль филиалов, ckj, в тыс.руб/тн сырья
|
№ филиала (к) |
|
|
Номер АО (j) |
|
|
||
|
|
j=1 |
j=2 |
j=3 |
j=4 |
j=5 |
j=6 |
j=7 |
|
|
30 |
40 |
55 |
40 |
60 |
50 |
30 |
В разделе 1 работы требуется:
1.1.Определить количество закупаемого заданным филиалом фирмы сырья у каждого АО, (xj), максимизируя прибыль филиала. Далее, студент формулирует экономико-математическую модель общей задачи линейного программирования (ОЗЛП).
1.2.С помощью полученных в результате реализации модели отчетов сделать рекомендации филиалу фирмы по расширению программы выпуска ассортимента продукции.
РЕШЕНИЕ.
Решение.
1. Составляем модель задачи в Excel.
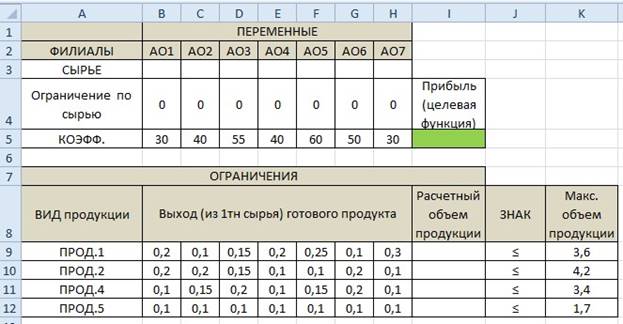
Рассчитываем прибыль
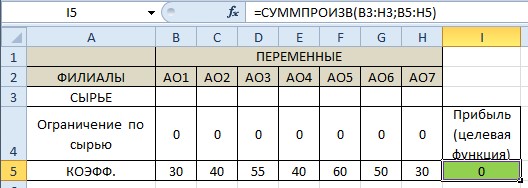
и вектор расчетного объема продукции.
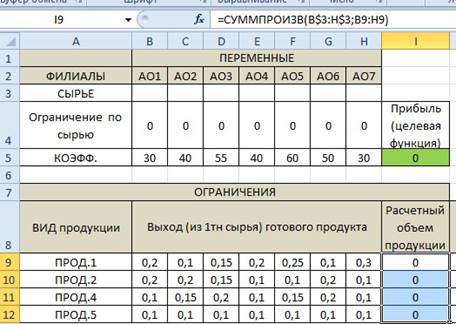
Настраиваем «Поиск
решения».
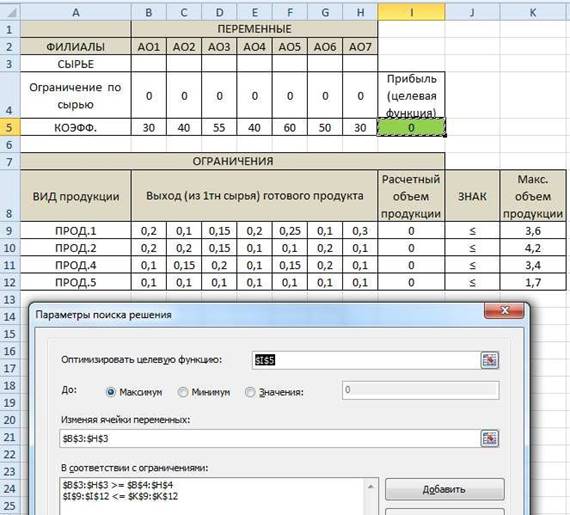
Получаем решение.
|
|
ПЕРЕМЕННЫЕ |
|
|
|
||||||
|
ФИЛИАЛЫ |
АО1 |
АО2 |
АО3 |
АО4 |
АО5 |
АО6 |
АО7 |
|
|
|
|
СЫРЬЕ |
0 |
0 |
6,5 |
0 |
10,5 |
0 |
0 |
|
|
|
|
Ограничение по сырью |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
Прибыль (целевая функция) |
|
|
|
КОЭФФ. |
30 |
40 |
55 |
40 |
60 |
50 |
30 |
987,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ОГРАНИЧЕНИЯ |
|
|
|||||||
|
ВИД продукции |
Выход (из 1тн сырья) готового продукта |
Расчетный объем продукции |
ЗНАК |
Макс. объем продукции |
||||||
|
ПРОД.1 |
0,2 |
0,1 |
0,15 |
0,2 |
0,25 |
0,1 |
0,3 |
3,6 |
≤ |
3,6 |
|
ПРОД.2 |
0,2 |
0,2 |
0,15 |
0,1 |
0,1 |
0,2 |
0,1 |
2,025 |
≤ |
4,2 |
|
ПРОД.4 |
0,1 |
0,15 |
0,2 |
0,1 |
0,15 |
0,2 |
0,1 |
2,875 |
≤ |
3,4 |
|
ПРОД.5 |
0,1 |
0,1 |
0,1 |
0,1 |
0,1 |
0,1 |
0,1 |
1,7 |
≤ |
1,7 |
Следовательно, филиалу предприятия выгодно закупать сырьё только у акционерных обществ АОЗ и АО5 в количестве 6,5 и 10,5 тонн. При этом максимум прибыли предприятия составит 987,5 тыс. рублей и будут произведены следующие объемы продукции: предприятие 1 – 3,6 т, предприятие 2 – 2,025 т, предприятие 3 – 2,875 т, предприятие – 1,7т.
2. Анализируем отчет по устойчивости.
Ограничения
|
|
Окончательное |
Тень |
Ограничение |
Допустимое Допустимое |
|
|
Ячейка |
Имя Значение |
Цена |
Правая сторона |
Увеличение Уменьшение |
|
|
$I$9 |
ПРОД.1 Расчетный объем продукции 3,6 |
50 |
3,6 |
0,65 |
1,05 |
|
$I$10 |
ПРОД.2 Расчетный объем продукции 2,025 |
0 |
4,2 |
1E+30 |
2,175 |
|
$I$11 |
ПРОД.4 Расчетный объем продукции 2,875 |
0 |
3,4 |
1E+30 |
0,525 |
|
$I$12 |
ПРОД.5 Расчетный объем продукции 1,7 |
475 |
1,7 |
0,190909091 |
0,26 |
Ищем продукты, у которых теневая цена не равна 0.
Это 1 и 5 продукты – это дефицитные продукты их производство следует расширять.
При увеличении производства продукта 1 на 1 тонну прибыль вырастет на 50 тыс. руб., при увеличении производства продукта 5 на 1 тонну прибыль вырастет на 475 тыс. руб. Продукт 5 – наиболее ценен.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.