Авторская программа " Математика в сказках"

МУНИЦИПАЛЬНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ АВТОНОМНОЕ УЧРЕЖДЕНИЕ

СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 12

ГОРОДСКОГО ОКРУГА ГОРОД НЕФТЕКАМСК

РЕСПУБЛИКИ БАШКОРТОСТАН

ПРОГРАММА

ДОПОЛНИТЕЛЬНОГО ОБРАЗОВАНИЯ ПО МАТЕМАТИКЕ

«МАТЕМАТИКА В СКАЗКАХ»

(срок реализации программы – 1 учебный год, возраст детей – 5-6 класс)

                                                                                 Автор-составитель программы:

                                                                                 Разетдинова Эльвира Ахнафовна,

                                                                                 учитель математики МОАУ СОШ № 12

Нефтекамск-2017

I. ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

Актуальность программы обусловлена тем, что сокращение количества часов, отведенных в программах, приводит к тому, что многие вопросы, сформулированные в стандартах по математике, остаются  недостаточно проработанными.  В связи с трудностью предмета многие дети теряют интерес к математике. Следовательно, возникает необходимость привлечь внимание тех обучающихся, которым интересна математика и ее приложения, а также тех обучающихся, которым математика и ее приложения кажутся скучными и неинтересными. Поэтому все большую роль в обучении играют самостоятельность и познавательная активность обучающихся.

Сказочная основа курса выбрана не случайно и заключает в себе самостоятельную воспитательную функцию. Волшебная  сила сказок известна с давних  пор. До нас дошло немало  сказочных повествований, отражающих  многовековой опыт предшествующих  поколений и до сих пор питающих наши умы, чувства и воображение. Уже давно было замечено, что сказка наравне с развлекательным характером носит воспитательное, познавательное, чувственное и эстетическое значение. Мудрость, поданная в простой и ясной сказочной форме, учит детей думать, находить решения проблем, развивает воображение и интуицию, позволяет накапливать опыт.

Наши предки  знали все эти достоинства  сказок и использовали их в  качестве самого эффективного  средства общения с детьми. Сказка  – универсальный язык, способный  в доступной форме донести  до ребенка нужную информацию. Психологи тоже оценили благотворное влияние сказки на психику ребенка. Вы наверно и сами не раз замечали, что лучшим средством успокоения или воздействия на своего малыша всё чаще становится вовремя придуманная и рассказанная история.

Современные  психологи используют рассказывание сказок, проигрывание сказочных сюжетов, как своеобразную терапию. С помощью метода сказкотерапии они раскрывают душу ребенка, налаживают с ним контакт, упорядочивают внутренний мир, помогают преодолеть проблемы и изменить поведение; либо просто развивают ребенка и обогащают его знания. Сказка является учебником духовных и жизненных знаний.

В процессе слушания, придумывания и обсуждения сказки у ребенка развиваются необходимые для эффективного существования фантазия, творчество. Он усваивает основные механизмы поиска и принятия решений.

Новизна программы:

Ÿ  усвоение математических понятий и развитие творческих способностей детей посредством сказок;

Ÿ  разработка программы дополнительного образования, которая связывает математику с жизнью, с декоративно-прикладным искусством;

Ÿ  научное обоснование влияния внеклассной работы на развитие самостоятельности, познавательной активности, творческих способностей обучающихся, освоение ими новых способов познавательной деятельности.

Данный курс интегрирован с такими школьными предметами как литература, русский язык. Казалось бы, сказка и математика – понятия несовместимые: яркий сказочный образ и сухая абстрактная мысль. Но сказочные задачи усиливают интерес к математике. Когда обучающиеся слышат чарующее слово «сказка», их глаза зажигаются особенным светом, они полны счастья. Это ли не активизация познавательной деятельности! Это очень важно для обучающихся 5-6 классов.

Цель программы:

Ÿ  сформировать у обучающихся  готовность и способность самостоятельно, творчески осваивать и совершенствовать новые способы познавательной деятельности.

Задачи программы:

Ÿ  обеспечить развитие исследовательских навыков и умений обучающихся;

Ÿ  способствовать развитию самостоятельности и творчества;

Ÿ  развивать критическое мышление;

Ÿ  формировать навыки работы в группе, развивать способности при помощи информационно-коммуникационных технологий;

Ÿ  учить самостоятельно искать, анализировать, отбирать необходимую информацию;

Ÿ  экспериментально проверить влияние внеклассной работы по математике на развитие самостоятельности и творческих способностей обучающихся;

Ÿ  формировать и развивать интерес к математике через решение задач с использованием сказок.

Методы и приемы обучения:

На этапе предъявления нового материала:

Ÿ  ситуативность;

Ÿ  объяснение;

Ÿ  слушание и повторение.

На этапе тренировки:

Ÿ  чтение материала;

Ÿ  проверка и работа над ошибками.

На этапе практической работы:

Ÿ  презентация, обсуждение;

Ÿ  письменная работа в виде написания сказки.

Основные принципы отбора и структурирования материала: обучение основывается на принципах сознательности и активности, наглядности, систематичности и последовательности, прочности, научности, доступности, связи теории с практикой. На основе указанных принципов подбирается материал для подготовки школьников по вопросам, включенным в программу с целью познания и изучения.

Оценивание в ходе занятий проводится в нестандартной форме: за особые достижения (правильное решение, оригинальное решение…) выдаются сказочные деньги «Сказики». По результатам изучения курса полученные «деньги» можно обменять на призы (книги по математике, энциклопедии).

Программа дополнительного образования  предназначена для обучающихся 5-6 классов, заинтересованных в углубленном изучении математики и для организации кружковой работы в рамках дополнительного образования детей. Программа рассчитана на 34 часа. Периодичность занятий – 1 раз в неделю в течение 1 учебного года.

Ожидаемые результаты:

Ÿ  развитие общеучебных умений, навыков и способов познавательной деятельности обучающихся;

Ÿ  повышение уровня математического развития обучающихся в результате углубления их знаний по основному курсу;

Ÿ  формирование интереса обучающихся к математике в ходе получения ими дополнительной информации;

Ÿ  удовлетворение познавательных интересов обучающихся по обозначенной теме.

II. УЧЕБНО-ТЕМАТИЧЕСКИЙ ПЛАН

III. СОДЕРЖАНИЕ ПРОГРАММЫ

Тема № 1 (1час)

Вводное занятие

1.     Основные вопросы.

     Развитие творческих способностей детей в написании сказок.

2.     Требования к знаниям и умениям.

    Обучающиеся должны:

знать: формы и методы написания математических сказок

уметь: применять методы и идеи математики в практической жизни, приобщить знания к научно- исследовательской деятельности

Самостоятельная работа.

Вспомнить стилистические приемы и шаги написания сказок

3.     Тематика практических работ.

    Черновики первых сказок

Тема № 2 (5 часов)

Натуральные числа

4.     Основные вопросы.

Систематизировать и обобщить сведения о натуральных числах: об их сравнении, сложении и вычитании, умножении и делении.

5.     Требования к знаниям и умениям.

Обучающиеся должны:

знать: законы сложения и умножения, свойство вычитания, правило порядка действий;

уметь: вычислять значения числовых выражений, применяя правило порядка действий, решать задачи «на части», на нахождение двух чисел по их сумме и разности.

6.     Самостоятельная работа.

Создание собственной сказки по заданной теме – написание черновика сказки, работа над ошибками, художественно-эстетическое оформление сказки (создание иллюстраций к сказке, работа на компьютере).

7.     Тематика практических работ.

Сказка по теме «Натуральные числа».

Тема № 3 (5 часов)

Положительные и отрицательные числа

1.     Основные вопросы.

Выработать прочные навыки арифметических действий с положительными и отрицательными числами.

2.     Требования к знаниям и умениям.

Обучающиеся должны:

знать: правила сложения отрицательных чисел, сложения чисел с разными знаками, вычитания рациональных чисел, определение рационального числа, свойства рациональных чисел, правила умножения и деления положительных и  отрицательных чисел;

уметь: применять на практике алгоритмы сложения и вычитания положительных и отрицательных чисел как дробных, так и целых.

3.     Самостоятельная работа.

Создание собственной сказки по заданной теме – написание черновика сказки, работа над ошибками, художественно-эстетическое оформление сказки (создание иллюстраций к сказке, работа на компьютере).

4.     Тематика практических работ.

Сказка по теме «Положительные и отрицательные числа».

Тема № 4 (5 часов)

Координатная плоскость

1.     Основные вопросы.

Развитие творческих способностей, логического мышления, углубление знаний, полученных на уроке, и расширение общего кругозора ребенка в процессе живого и забавного рассмотрения различных практических задач и вопросов, развитие творческих способностей учащихся при построении точек на координатной плоскости.

2.     Требования к знаниям и умениям.

Обучающиеся должны:

знать: понятие «координатная плоскость», понятие «координаты точки»;

уметь: отмечать на координатной плоскости точку с заданными координатами, находить координаты изображенной точки, определять месторасположение точки по ее координатам.

3.     Самостоятельная работа.

Создание собственной сказки по заданной теме – написание черновика сказки, работа над ошибками, художественно-эстетическое оформление сказки (создание иллюстраций к сказке, работа на компьютере).

4.     Тематика практических работ.

Сказка по теме «Координатная плоскость».

Тема № 5 (5 часов)

Обыкновенные и десятичные дроби

1.     Основные вопросы.

Выработать прочные навыки арифметических действий с  дробями и решений основных задач на дроби.

2.     Требования к знаниям и умениям.

Обучающиеся должны:

знать: определение дроби и основное свойство дроби, законы сложения и умножения дробей;

уметь: решать задачи на нахождение части числа и числа по его части, решать задачи на совместную работу, выполнять все действия с десятичными и обыкновенными дробями.

3.     Самостоятельная работа.

Создание собственной сказки по заданной теме – написание черновика сказки, работа над ошибками, художественно-эстетическое оформление сказки (создание иллюстраций к сказке, работа на компьютере).

4.     Тематика практических работ.

Сказка по теме «Обыкновенные и десятичные дроби».

Тема № 6 (5 часов)

Геометрические фигуры

1.     Основные вопросы.

Расширить сведения о геометрических фигурах и рассмотреть некоторые свойства.

Требования к знаниям и умениям.

Обучающиеся должны:

знать: отличие круга от окружности, прямоугольника от квадрата.

уметь: пользоваться языком геометрии для описания предметов окружающего мира, решать задачи с примене­нием формул.

2.     Самостоятельная работа.

Создание собственной сказки по заданной теме – написание черновика сказки, работа над ошибками, художественно-эстетическое оформление сказки (создание иллюстраций к сказке, работа на компьютере).

3.     Тематика практических работ.

Сказка по теме «Геометрические фигуры».

Тема № 7 (5 часов)

Делимость натуральных чисел

1.                 Основные вопросы.

Расширение и углубление теоретического материала, изученного на уроках математики, а также развитие умений применять полученные знания к решению нестандартных задач, формированию определенной культуры работы над задачей.

2.     Требования к знаниям и умениям.

Обучающиеся должны:

знать: свойства и признаки делимости натуральных чисел, определения НОД и НОК;

уметь: доказывать основные свойства и признаки делимости чисел, находить НОД и НОК, проводить простейшие умозаключения, обосновывая свои действия ссылками на определения и правила данной темы.

3.     Самостоятельная работа.

Создание собственной сказки по заданной теме – написание черновика сказки, работа над ошибками, художественно-эстетическое оформление сказки (создание иллюстраций к сказке, работа на компьютере).

4.     Тематика практических работ.

Сказка по теме «Делимость натуральных чисел».

Тема № 8 (3 часа)

Проценты

1.     Основные вопросы.

Систематизация, обобщение и углубление знаний, полученных школьниками при изучении темы «Проценты» в школьном курсе, усвоение обучающимися практической значимости этого понятия в различных сферах деятельности человека.

2.     Требования к знаниям и умениям.

Обучающиеся должны:

знать: содержательный смысл термина «процент», как социального способа выражения доли величины, широту применения процентных вычислений в жизни;

уметь: решать основные задачи на проценты, применять формулу сложных процентов, производить прикидку и оценку результатов вычислений соотносить процент с соответствующей дробью (особенно в некоторых социальных случаях).

3.     Самостоятельная работа.

Создание собственной сказки по заданной теме – написание черновика сказки, работа над ошибками, художественно-эстетическое оформление сказки (создание иллюстраций к сказке, работа на компьютере).

4.     Тематика практических работ.

Сказка по теме «Проценты».

Тема № 9 (1 час)

Итоговое занятие

 1.Основные вопросы.

   Систематизация, обобщение знаний.

2.Требования к знаниям и умениям.

   Обучающиеся должны:

   знать:

   приемы и методы написания математических сказок

   уметь:

   написать математические  сказки на различные  темы с иллюстрациями

3.Самостоятельная работа.

   Рефлексия

4.Подведение итогов.

IV. МЕТОДИЧЕСКОЕ ОБЕПЕЧЕНИЕ ПРОГРАММЫ ДОПОЛНИТЕЛЬНОГО ОБРАЗОВАНИЯ

1. Методы работы:

-       словесный;

-       метод наглядности;

-       практический;

-       объяснительно-иллюстративный;

-       эвристический или частично-поисковый.

2.Основные приемы:

-       рассказ;

-       беседа;

-       объяснение;

-       дискуссия.

3. Основные формы работы:

-       групповая;

-       парная;

-       фронтальная;

-       индивидуальная.

4. Организация учебно-воспитательного процесса:

-       взаимное сотрудничество учителя и ученика, ученика и учителя, учеников между собой.

5. Дидактические материалы:

-       литература по занимательной математике;

-       интернет-ресурсы

6. Техническое оснащение занятий:

-       школьные канцелярские принадлежности, набор цифр, набор геометрических фигур, предметные картинки, демонстрационный счётный материал;

-       компьютер, ноутбук, интерактивная доска, проектор;

-       игры и игрушки.

7. Формы  подведения итогов

-       защита готовых сказок, рисунков, презентаций;

-       рефлексия самими учащимися;

-       награждение самых активных, самых способных, «самых-самых кружковцев».

ПРИЛОЖЕНИЕ 1

ВВОДНОЕ ЗАНЯТИЕ

Цель: ознакомить с методикой написания сказок.

Ход занятия:

I.  Организационный момент.

II. Методика написания математических сказок.

Как написать сказку? С чего начать?

Придумайте персонажей для своей сказки: добрых и злых, главных героев и второстепенных. Продумайте их особенности, "изюминку". В сказке нет полутонов: мир делится на чёрное и белое, хорошее и плохое. И главный герой  однозначно должен вызывать симпатию.  А героем может стать кто и что угодно – здесь открывается полный простор для фантазии. Вспомните ваши первые сказки: "Колобок", "Курочка Ряба", "Репка". Персонажи могут быть и позатейливее, как  в современном сказочном творчестве. Можете сотворить своего авторского, ни на кого не похожего героя! Собственно именно с его определения, некоторой характеристики начинается завязка сказки. Кто, где, когда жил – можно следовать этой схеме.

И вдруг… Спокойные ноты сменяются на интригующие: случается некое неожиданное событие, с которого для главного героя начинаются яркие, невероятные приключения, с чудесами, превращениями, волшебными предметами! Этому повествованию посвящена основная часть сказки.

Для того, чтобы правильно написать сказку, пользуйтесь стилистическими приёмами: троекратными повторами, преувеличениями, противопоставлениями  и, конечно, украшающими определениями. Это создаёт традиционную сказочную атмосферу и позволяет охарактеризовать героев.

Точка напряжения. В любой сказке рано или поздно происходит самый напряжённый момент – кульминация, когда добро и зло непосредственно сталкиваются или когда герою предстоит самое серьёзное испытание. Но что бы ни выпало на его долю – добро неизменно побеждает зло. Это, пожалуй, самый важный сказочный закон. Об этом говорится в развязке. Вы можете и не ставить окончательную точку в своей сказке (открытый финал), дать порассуждать  каждому, чем она может закончиться. А может, у вашей сказки будет продолжение?

Итак, для того, чтобы написать сказку, нужно сделать пять шагов:

1.     Найти хорошую идею.

2.     Обыграть идею в действии (чудесное происшествие).

3.     Взвесить идею.

4.     Украсить сказку.

5.     Развернуть сказку.

После краткой теоретической подготовки можно приступать непосредственно к написанию сказки. Начнется это действие с вопросов к себе:

1.     Какими мыслями я хочу поделиться с читателями с помощью своей сказки? Что донести до человека в иносказательной, сказочной форме?

2.     Запишите возрастную категорию, которой предназначается сказка.

3.     Третья запись в вашей тетрадке: жанр сказки. В каком из жанров вашу идею будет легче всего и интересней всего воплотить, объяснить.

4.     Сюжет. Подумайте, каким образом в рамках выбранного жанра можно вашу идею проиллюстрировать. Составьте «костяк» сюжета – примерный план, еще без четких действующих лиц, имен и пр.

5.     Какие герои необходимы в вашем сюжете? (Не берите слишком много героев). Составьте список.

6.     Проработайте образ каждого героя: как его зовут, как он выглядит, во что одет, какова его родословная, его черты характера, привычки, особенности поведения.

7.     Теперь, когда основа у вас есть, можете приступать к написанию сказки. В этом процессе вы можете менять и черты героев, и усложнять или упрощать сюжет, добавлять в него какие-то новые хитросплетения. Если вам только это будет нужно.

Когда сказка написана – перечитайте ее, убедитесь в том, что язык вашей сказки – живой, яркий и грамотный, лексика вашей сказки подходит для выбранной вами целевой возрастной группы, смысл – понятен, идея – читается. Оставьте сказку на какое-то время в покое. Через несколько дней вернитесь и перечитайте – не стоит ли что-то исправить, все ли интересно и внятно написано. Если да – то предложите прочесть новое творение вашим друзьям, прислушайтесь и к их советам.

Таким образом, человеку, решившему написать сказку, следует ее хорошенько продумать, записать грамотным, красивым языком и затем  «отшлифовать» текст, добиться точности, понятности, стилистического совершенства. Желаю вам удачи!

III. Предложить примеры сказок на различные темы.

ПРИЛОЖЕНИЕ 2

Тема № 1 (5 часов)

Натуральные числа

Занятие № 1. Слушаем

Ход занятия:

1. Актуализация знаний

Вопросы:

Ÿ  Какие числа мы называем натуральными?

Ÿ  Какие действия применяют для натуральных чисел?

Ÿ  Как образуются двух-трехзначные числа, свойство ноля?

2. Предъявление сказки «Появление ноля»

Шестерка поливала цветы и так была поглощена этим занятием, что вздрогнула, услышав незнакомый голос: «Скажите, пожалуйста, где живут цифры»?

Цифра Шесть повернулась и увидела симпатичное овальное существо.

— Меня послала к вам царица Математики, — объяснило овальное существо. — Ведь это вы написали ей письмо с просьбой о помощи?

— Да, мы просили ее научить нас считать большие числа. В прошлом году, к примеру, у меня расцвело множество астр, но я не смогла посчитать их. Мы все грустим, когда не можем что-то посчитать, — объяснила Шестерка.

— Не волнуйтесь, я вам помогу! — утешило Шестерку овальное существо.

— Скорее сюда. К нам прибыла самая большая цифра на свете! — закричала взволнованная Шестерка.

Все сразу собрались вокруг гостя.

— Меня зовут Ноль, — вежливо представился он цифрам.

— О, какой круглый! — восхитилась Троечка.

— А какие числа ты, можешь считать? — спросила Девятка, которую больше всего волновал этот вопрос.

— Я вообще ничего посчитать не могу, — со вздохом ответил гость.

— Даже одно дерево не можешь посчитать? — растерянно спросила Единица.

— Ничего не могу, — еще раз подтвердил Ноль.

Цифры не знали, что и думать. Наконец, мудрая Девятка решила:

— Тут скрыта какая-то тайна. Не зря же царица Математики послала его к нам. Давайте построим ему домик в нашем городе, а пока пусть живет у всех по очереди. Начнем с тебя, Единица. Веди гостя отдохнуть с дороги.

— Ой, воробьи прилетели, — воскликнула Пятерка, — надо скорее их считать.

— Сегодня их ровно десять, — хором сказали Единица с Ноликом, которые в это время проходили мимо стайки воробьев.

— Как вам удалось так быстро посчитать всех птиц? — удивилась Пятерка.

— Не знаем, как это получилось, — снова хором заговорили Единица и Нолик. — Но как только мы встали рядом, мы стали десяткой.

Все цифры оглянулись, услышав такую поразительную новость.

— Удивительно, — проговорила Девятка, — если Ноль встает рядом с цифрой, он увеличивает ее в десять раз. Это надо проверить.

В этот момент Пятерка прошептала что-то Единичке, та послушно отпустила Ноль. Пятерка тут же пристроилась рядом с ним и весело рассмеялась:

— Вот я и проверила! Какая я стала большая: не просто Пять, а целых пять десятков, ровно пятьдесят. Вот это да!!!

Цифры разволновались, каждой хотелось постоять рядом с Ноликом и узнать свои новые возможности. Двойка подняла Нолика под облака и превратилась в двадцать. Тройка угостила его печеньем и превратилась в число тридцать. Четверка обсудила с Ноликом, какой ему построить домик. Конечно, при этом она стала числом сорок. Но Девятка, увидев, что Нолик чуть не падает от усталости, сказала строгим голосом:

— Веди, Единичка, гостя домой, он уже еле живой. Единичка гордо удалилась под руку с гостем. Все остальные цифры тоже разошлись по домам, завидуя счастливице Единице.

3. Вопросы и задания к сказке:

Ÿ  Чем характер Ноля отличается от характера остальных цифр?

Ÿ  Как меняется характер Ноля, когда он образует десятки с другими цифрами?

Ÿ  Как вы думаете, какой домик цифры построят для Ноля?

Ÿ  В какое время года на улице чаще всего бывает ноль градусов?

Ÿ  Когда говорят «ноль часов», и почему этот час не обозначен на часах?

Ÿ  Что значит выражение «полный ноль»? Может ли кто-то быть полным нолем?

4. Сценка «Кому нужен ноль?»

Дети делятся на группы по три человека. Один из них — Ноль, остальные — две любые цифры. В сценке дети должны придумать причину, зачем им необходимо превратиться в десятки, и уговорить Ноль встать рядом с ними. Ноль встает рядом с тем, чьи аргументы кажутся ему наиболее убедительными.

5. Рисунок «Портрет Нолика»

Дети вытягивают карточки, на которых написаны разные настроения, например: мечтательный, радостный, грустный. Дети должны нарисовать портрет Ноля, когда он веселый, мечтательный, грустный, сердитый и т.д.

6. Игра «Кто с нулем встречается»

Один из детей — Ноль. Остальные вытягивают карточки с разными цифрами от единицы до девяти. Ноль говорит: «Кто с Нолем встречается, в десятки превращается. Саша и Таня выходите». Два человека, которых назвал Ноль, поднимают кверху свои карточки с цифрами. Ноль должен быстро назвать два двухзначных числа, которые получатся, если к цифрам, изображенным на карточках, добавить ноль.

7. Написание черновика сказки (возможно задание на дом)

Занятие № 2. Показываем

Ход занятия:

1. Прослушивание предложенных вариантов создания сказки.

2. Первичное ознакомление со сказкой.

3. Исправление и работа над ошибками.

4. Написание черновика сказки.

Занятие № 3. Читаем

Ход занятия:

1. Прослушивание созданных материалов.

2. Дополнение яркими, красочными элементами.

3. Подготовка и оформление сказки на компьютере.

Занятие № 4. Рисуем

Ход занятия:

1. Рисунки к сказкам (предложить готовый вариант  или творческая фантазия обучающихся), например:

Занятие № 5. Защита работ

Ход занятия:

Обучающиеся представляют созданные ими сказки. Оценивание проводится в нестандартной форме: за особые достижения (правильное решение, оригинальное решение…) выдаются сказочные деньги «Сказики».

Примеры созданных сказок:

«НОЧНОЙ СПОР»

Однажды, когда вечер давным-давно кончился, а утро еще не началось, на школьной доске приключилась следующая история. Так как дежурные забыли стереть доску, на ней остались примеры, которые дети решали на уроке.

Среди ночной тишины раздался голос: «В математике я самый главный знак», - сказал Знак Плюс. «В мире все прибавляется: и люди, и деньги, и весной трава».

«А вот и нетушки», - сказал Знак Минус. - «В мире все уменьшается: весной снег, и талая вода, и деньги».

«Кто это так там выступает?» - спросил Знак Умножения. - «В мире все умножается: и весенние всходы, и весеннее тепло, и летние ягоды».

«А вот и нет», - сказал Знак Деления. - «В мире все делится: и радость, и конфеты, и урожай каждого года».

«Долго я вас всех слушал и должен сказать, что все вы здесь неправы», - сказал Знак Равенства. - «В мире все поровну: и прибавление, и убыток. Мир держится на законе равенства: если где-то убудет, то в другом месте обязательно прибудет».

КАК ЧИСЛА НАШЛИ ЗНАКИ И НАУЧИЛИСЬ ДЕЛАТЬ ПРИМЕРЫ

В одном городе чисел жили-были три друга, числа Три, Пять и Восемь. Как-то раз, когда они веселились на солнышке, числу Три пришла в голову идея, что можно построить пример. Он предложил это друзьям, и они начали думать, как это сделать. Числа становились по-разному, менялись местами, но так и не смогли ничего сделать.

Но вот Пять поняла, что не хватает знаков  «+» и «-», и друзья отправились искать помощь в страну знаков. Шли они шли и повстречали знак «-». Вежливо поздоровавшись, числа спросили, не знает ли он, есть ли где еще другие знаки. Минус ответил, что знает, и повел их к Плюсу. Друзья познакомились и с Плюсом и пригласили Плюс и Минус в город чисел. Там им очень понравилось.

Числа рассказали знакам, что задумали построить пример, но у них ничего не вышло, и спросили, не могут ли знаки им помочь. Знаки с радостью согласились и сказали, что это очень легко. Друзья  начали, играя, строить примеры: 5+3+8, 8-5-3, 8-5+3 и многие другие.

Знаки остались жить в городе чисел, в домиках, которые им помогли построить Три, Пять и Восемь. И они жили-поживали и примеры сочиняли.

ПРИЛОЖЕНИЕ 3

Тема № 2 (5 часов)

Положительные и отрицательные числа

Занятие № 1. Слушаем

Ход занятия:

1. Предъявление сказки «Фаворит царицы арифметики»

В стране Математике жили два злейших врага: Положительный и  Отрицательный знаки.

Борьба между ними шла с самого рождения, и им было все равно, что они братья. Они боролись друг с другом как вода с огнем, как свет с тьмой, Когда один пел, другой хранил молчание. Они были отражениями друг друга. Знаете, каково это драться с самим собой, правая рука против левой, палец против пальца? Они  боролись за прекрасную царицу Арифметику.

И, наконец, настал день выбора фаворита. Зал математического поединка был богато убран.  Вокруг стояли цилиндры с цветами, а на стенах висели ковры с изображениями графиков. Царица Арифметика восседала на троне, наблюдала за происходящим. Кроме чисел поединок помогал вести знак Равно. Ибо он был главным судьей и следил за правильностью решения примера. И вот салют из цветных точек оповестил о начале состязаний. В первом туре победил знак Плюс, так как решение было таким:

6 +(– 2) = 4

Во втором туре победил тоже он. Потому что выражение было таким:

7 + 6= 13

В третий раз было так:

- 3 + (-10) = -13

И победил знак Минус.              

И догадаться, что в четвертом туре победил снова Минус, было совсем не сложно, так как выражение было такое:

-5 + 2 = -3

И честный знак Равно заключил, что у них ничья. И тогда царица Арифметика решила, что из этих двух знаков никто не станет ее фаворитом, а им станет правдолюбивый знак Равно.

И вот так знак Равно стал фаворитом царицы Арифметики и ему доставались все почести.

А Плюс и Минус так и продолжали бороться между собой, потому что были похожи, но были совершенно разными.

2. Вопросы и задания к сказке:

Ÿ  Чем характер положительного числа отличается от характера отрицательного числа?

Ÿ  Назовите положительные и отрицательные черты характера людей.

Ÿ  Укажите  положительные стороны учебы в школе.

Ÿ  Укажите отрицательные стороны незнаний…

3. Сценка «Красивая мозаика»

          Ребята, я хотела показать вам красивую мозаику, но, когда я шла к вам на урок,  нечаянно её рассыпала, поэтому хочу попросить вас собрать мозаику заново. Но для этого вам нужно каждому выполнить задание, которое написано на обратной стороне составной части мозаики, и приложить эту часть к нужной ячейке на плакате: ответ на ячейке должен совпасть с ответом на задание (учитель раздает ученикам части мозаики, на обратной стороне которых написаны задания).

           Разрезаем плакат на прямоугольники, количество которых соответствует  количеству учеников в классе. На обратной стороне плаката (там, где нет изображения) пишем задачи разного содержания, на доске вывешиваем ватман такого же размера как плакат. На нем написаны ответы. Дети решают задачи или примеры, а затем прикрепляют свои задачи к соответствующим ответам на доске, картинкой вверх. Если все задания решили правильно, то и плакат примет исходное изображение.

4. Портреты положительных, отрицательных чисел

Дети вытягивают карточки, на которых написаны разные настроения, например: мечтательный, радостный, грустный. Дети должны нарисовать портреты чисел, когда они веселые, мечтательные, грустные, сердитые и т.д.

5. Игра «Кто больше, кто меньше?»

В одном государстве – Множестве – жили положительные и отрицательные числа. Извечный был между ними спор – кто из них больше, кто меньше. Однажды король этой страны Ноль решил раз и навсегда навести в своем государстве порядок. Он собрал все числа и, повернувшись к ним лицом, сказал: «Встаньте справа от меня все положительные числа, а слева – отрицательные и разберитесь по росту». Получилась длинная-длинная цепочка – прямая чисел. Теперь каждое число видело, что есть число больше его и меньше. Эту прямую назвали числовой прямой, где меньшее число расположено левее, а большее – правее. Числа расставляются по своим местам.

6. Проверка усвоения учебного материала

Вопросы:

Ÿ  Какое число больше: положительное или отрицательное?

Ÿ  Как читается правило сравнения отрицательных чисел?

Ÿ  Какое из чисел больше: отрицательное или ноль; положительное или ноль?

Ÿ  Как сравнить числа с помощью координатной прямой?

Ÿ  Число а изменилось на число в. Как изменилось число а, если в – положительное; если в – отрицательное.

7. Написание черновика сказки (возможно задание на дом)

ПРИЛОЖЕНИЕ 4

Тема № 3 (5 часов)

Координатная  плоскость

Занятие № 1. Слушаем

Ход занятия:

1. Предъявление сказки «Чудесный сон»

Однажды на уроке математики Незнайка заснул, и приснился ему сон, что его друзья-коротышки  собрались в космическое путешествие. Незнайка решил полететь вместе со своими друзьями в математический городок на этом транспорте:

1(0;8), 2(-2;4), 3(-2;-3), 4(- 4;-5), 5(-4;-9), 6(-2;-9), 7(-2;-7), 8(-1;-7), 9(-1;-9), 10(1;-9), 11(1;-7), 12(2;-7), 13(2;-9), 14(4;-9), 15(4;-5), 16(2;-3), 17(2;4), 18(0;8) (ракета)

И вот перед ними ворота  математического городка. На воротах кодовый замок, который можно открыть только верным построением семи точек на координатной плоскости. Точки О(-7;2), К(-3;4), Ы(1;4), Т(-5;3), Р(-1;5), О(5;2), Т(3;3). Ворота открылись, и они  попали в сказочный инопланетный парк, в котором свободно гуляют разные сказочные звери:

Незнайке так понравилось гулять по парку, что он даже в ладоши захлопал и … проснулся. Оказывается, он на уроке математики и пришло время открыть дневник и записать домашнее задание.

2. Вопросы и задания к сказке:

·        В какую страну и каким образом попали Незнайка и его друзья?

·        По какому правилу были выстроены точки на координатной плоскости?

3. Сценка «Запутанные точки»

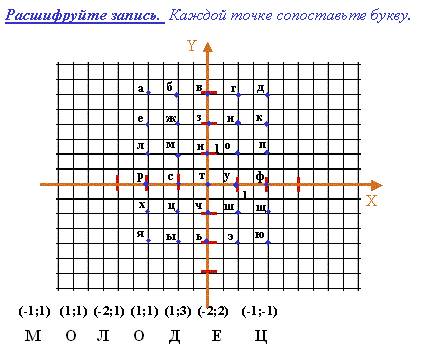
На координатной плоскости каждой точке поставлена в соответствие буква русского алфавита. Под плоскостью записаны координаты точек (своеобразный шифр слова). Необходимо расшифровать запись. Проверить задание можно простым нажатием на «мышку». На экране появится слово.

4. Игра «Корабли»

Можно играть всем классом (если компьютер один) или каждый обучающийся самостоятельно (если занятие проходит в компьютерном классе).

«По океану катились длинные волны. Они сменяли одна другую… Ничто не предвещало беду. Но вдруг на горизонте появились странные корабли. Это были пираты. Чтобы наш корабль не попал в руки пиратов, необходимо узнать координаты нахождения пиратских судов. Определяйте координаты по порядку, начиная с первого».

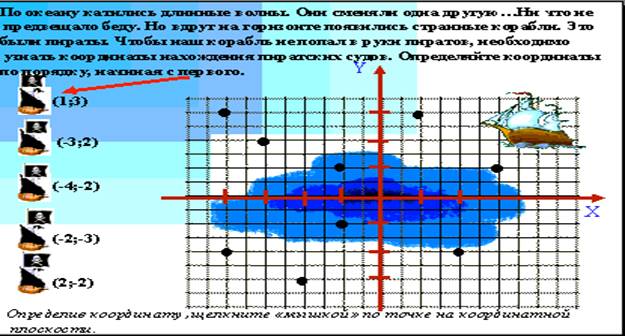
Игра заключается в следующем. В левой части экрана расположены координаты пиратских кораблей. В правой – координатная плоскость с множеством точек (вражеские корабли). Задача состоит в том, чтобы правильно указать местоположение корабля. При нажатии курсором на правильно выбранную точку вы услышите взрыв, и точка исчезнет. Таким образом, вы переходите к поиску следующего корабля. Если ошиблись, то появляется слайд «Будь внимательней», который отсылает на предыдущий слайд, чтобы исправить ошибку. Игра считается законченной, если не осталось ни одного корабля пиратов.

5. Проверка усвоения учебного материала

Вопросы:

·        Что называют координатной плоскостью?

·        Какую координатную прямую называют осью абсцисс?

·        Какую координатную прямую называют осью ординат?

·        Как построить на координатной плоскости точки по заданным координатами?

7. Написание черновика сказки (возможно задание на дом)

ПРИЛОЖЕНИЕ 5

Тема № 4 (5 часов)

Обыкновенные и десятичные дроби

Занятие № 1. Слушаем

Ход занятия:

1. Актуализация знаний

·        Сформулируйте правила сложения и вычитания дробей с разными знаменателями.

·        Сформулируйте правила сложения и вычитания смешанных чисел.

·        Как умножить дробь на число, дробь на дробь?

·        Как разделить дробь на число, дробь на дробь?

·        Сформулируйте основное свойство дроби.

·        Как найти часть от числа и число по заданной его части?

2. Предъявление сказки «Опытная запятая и нуль»

Жили-были Нуль и Опытная запятая, жили не тужили. Как-то отправились они в очередное путешествие. Идут-идут, много ли мало ли никто не знает. И вот подошли они к лесу. Вошли в лес и видят: на пеньке сидят два числа 9,3 и 100 и плачут. Подошли к ним Нуль и Запятая и спрашивают:

- Почему вы плачете?

Отвечает число 9,3:

- Как же не плакать. Шло я по лесу и встретило число 100. И решили мы перемножиться. Где-то я слышало, что для этого надо переместить запятую, но как это сделать – я не знаю. Да и моя запятая не хочет никуда двигаться, раскапризничалась!

Запятая оправдывается:

- Во-первых, я сегодня приболела, а во-вторых, я неопытная запятая, я на практике. А число 9,3 не дает мне покоя, ему всё куда-то прыгай.

- Ну, хорошо, - сказала Опытная запятая, - я тебя научу. Так вот, Запятая, смотри. Сколько нулей у числа 100?

- Два.

- Поэтому ты на два знака вправо скачешь. Понятно? (9,3 х 100 = 930)

- Кажется, да! Получилось 930.

- Молодец!

- Дорогой Нуль, если число 100 не против, подойди к нему справа, умножим получившуюся 1000 на 9,3, - попросила Опытная Запятая.

- Опять прыгать! - испугалась Запятая.

- Да, ты должна научиться. 9,3 х 1000 = 9300

- Ладно. Прыгаю на три знака вправо. Вот что получилось – 9300. Спасибо за учёбу, Старая Запятая.

Отправились наши путешественники дальше. Повстречались им два числа: 13,768 и 100, которые спорили.

- Ну, а вы что кричите?

- Ах, я считаю, что я слишком велико, - сказало число 13,768, - я захотело быть поменьше, например, в 100 раз, и попросило об этом число 100. Но ничего у нас не получилось, так как моя запятая на уроке математики много болтала и всё прослушала. Вот теперь и спорим.

Опытная Запятая стала разъяснять.

- Сколько нулей в числе 100?

- Два.

- Какое действие будем выполнять?

- Деление.

- Вот слушай теперь. Прыгай на два знака влево.

И запрыгала запятая на два знака влево, и получилось число 0,13768, которое в 100 раз меньше числа 13,768.

А Нуль с Опытной Запятой вернулись домой весёлые и счастливые. Стали жить по-прежнему.

А запятые, которых они учили, приходили к ним в гости, рассказывали о своих делах. Из их рассказов узнали, что практику они закончили на "5" и стали опытными запятыми, которые знают, как себя вести при умножении и делении с разрядными единицами.

3. Вопросы и задания к сказке:

·        Как умножить числа на 10,100,1000 и т.д…

·        Как разделить числа на 10,100,1000 и т.д…

·        Какие изменения происходят при умножении и деление чисел на 10,100,1000 и т.д…

4. Сценка «Хотелось бы побольше!»

Выходят Пятачок, Мартышка, Кролик.

Пятачок:

-Погодите, погодите! Я не совсем понимаю, как можно единицу разделить на доли? Вот если бы это был пирог – тогда другое дело.

Кролик:

- Ну, смотри! Вот представь себе, что был 1 пирог. И этот пирог разрезали на 7 равных долей. А потом тебе дали сразу 5 долей. Это означает, что тебе повезло – ты получил 5/7 пирога.

Мартышка:

- Или вот, смотри! Разделили банан на 5 долей и дали мне 3 доли. Получается, что я съела 3/5 банана. Хотелось бы, конечно, побольше!

5. Рисунок «Настроение десятичных и обыкновенных дробей»

Дети вытягивают карточки, на которых написаны разные настроения, например: мечтательный, радостный, грустный. Дети должны нарисовать портрет чисел, когда они веселые, мечтательные, грустные, сердитые и т.д.

6. Игра «Дробная схватка»

На листочках записаны дроби 1/1, 1/2, 2/2, 1/3, 2/3, 3/3, 1/4, 2/4, 3/4, 4/4, 1/5, 2/5, 3/5, 4/5, 5/5, 1/6, 2/6, 3/6, 4/6, 5/6, 6/6, 1/8, 2/8, 3/8, 4/8, 5/8, 6/8, 7/8, 8/8, 1/9, 2/9, 3/9, 4/9, 5/9, 6/9, 7/9, 8/9, 9/9, 1/10, 2/10, 3/10, 4/10, 5/10, 6/10, 7/10, 8/10, 9/10, 10/10, 1/12, 2/12, 3/12, 4/12, 5/12, 6/12, 7/12, 8/12, 9/12, 10/12, 11/12, 12/12.

Учитель перемешивает листочки и кладет их в две стопки так, чтобы сторона с дробями была снизу. Ученики по очереди открывают верхние листочки и сравнивают выпавшие дроби. Ученик, на чьем листочке дробь оказалась большей, забирает обе карточки. Если выпали равные дроби, начинается "дробная схватка": каждый ученик выкладывает в ряд три листочка лицевой стороной вниз, а четвертый листочек – лицевой стороной вверх. Тот ученик, на чьем листочке выпадает большая дробь, забирает все восемь листочков и листочки, с которых началась схватка. Когда игра закончилась, ученики подсчитывают количество выигранных листочков. Побеждает тот ученик, у которого листочков оказалось больше.

7. Написание черновика сказки (возможно задание на дом).

ПРИЛОЖЕНИЕ 6

Тема № 4 (5 часов)

Геометрические фигуры

Занятие № 1. Слушаем

Ход занятия:

1. Актуализация знаний

Вопросы:

·        Назовите элементы квадрата и прямоугольника.

·        Чем отличается круг от окружности?

2. Предъявление сказки «Квадрат и Квадраталина»

В некотором царстве, в некотором государстве жил был король Прямоугольник. Было у него два сына: старший – Прямоугольник, младший – Квадрат.

Дети взрослели, но король Прямоугольник больше любил старшего сына. Отец считал, что старший сын похож на него больше.

Время шло, дети, наконец, выросли пора им жениться. Говорит отец: «Дорогой сынок, Прямоугольник, твоя жена будет Прямая линия. С ней у вас хорошая пара получится».

«Ну, а ты, сын Квадрат, найдешь жену за тридевять земель в тридевятом королевстве, заключена в самой высокой башне самая красивая и умная принцесса Квадраталина, охраняет её змей Горыныч. Ждет давно она спасителя».

Отправился Квадрат на верную гибель: принцессу искать. Сын Прямоугольник спрашивает у отца: «Почему у Квадрата самая красивая принцесса?»

Отец Прямоугольник отвечает: «Понимаешь, сынок, скоро я состарюсь и умру, а королевством править должен один король – ты».

- Почему? А куда Квадрат денется?

- Убьет его Змей Горыныч.

- А если он спасет принцессу? Ведь ты же, отец, знаешь приказ: «Кто спасет принцессу Квадраталину, тот и будет королем».

- Не придет он, не волнуйся.

Обрадовался Прямоугольник-сын, стал жить счастливо с молодой женой.

А в это время отрубил голову Квадрат Змею Горынычу и спас принцессу Квадраталину, посадил на своего коня и повез ее в королевство Прямоугольника.

Узнал об этом люд честной и радуется. Узнали об этом король и его старший сын. Испугались они, что он их прогонит, да и перед народом стыдно стало.

Вышли они навстречу молодым: Квадрату и Квадратилине. А те обнялись и при этом образовали прямоугольник. Подумал король: «Они вдвоем очень похожи на меня». Посмотрел на любимого сына Прямоугольника, его жена Прямая линия прижалась к нему так, что он разделился на два квадрата. И понял царь, что оба сына похожи на него. «Извините, дорогие мои сыновья, что я хотел разлучить вас. Живите мирно. Пусть у вас появятся дети, хоть квадраты, хоть прямоугольники. Мы все – одна семья!»

И жила эта семья, состоящая из прямоугольников и квадратов, долго и счастливо.

3. Вопросы и задания к сказке:

·        Почему Царь не взлюбил сына Квадрата?

·        Чем отличается квадрат от прямоугольника?

·        Каким образом можно получить прямоугольник из двух квадратов?

4. Сценка «Два брата»

 Автор: Жили-были два брата: Треугольник и Квадрат. Старший – квадратный, добродушный, приятный. Младший – треугольный, вечно недовольный. Стал расспрашивать Квадрат.

Квадрат: Почему ты злишься, брат?

Автор: Тот кричит ему.

Треугольник: Смотри, ты полней меня и шире. У меня углов лишь три, у тебя же их четыре.

Автор: Но Квадрат ответил.

Квадрат: Брат! Я же старше, я – Квадрат.

Автор: И сказал ещё нежней.

Квадрат: Неизвестно, кто нужней!

Автор: Но настала ночь, и к брату, натыкаясь на столы, младший лезет воровато срезать старшему углы.

(Треугольник подходит к Квадрату и ножницами срезает у бумажного квадрата все четыре угла, а шапочку его отбрасывает в сторону)

Автор: Уходя, сказал.

Треугольник: Приятных я тебе желаю снов! Спать ложился – был Квадратом, а проснёшься без углов.

Автор: Но на утро младший брат страшной мести был не рад. Стало скучно квадрату. Отправился он путешествовать. Ходил, ходил Квадрат по свету, стало тяготить его одиночество: не с кем побеседовать и потрудиться в хорошей и дружной компании. Ведь весело и легко бывает только с друзьями. И решил квадрат поискать родственников… “Если встречу родственника, то сразу его узнаю,– думал Квадрат, – ведь он должен быть похож на меня”.

Однажды встречает он на пути такую фигуру.

Пригляделся Квадрат к ней и увидел что-то знакомое.

“Как тебя зовут?” – спрашивает.

–  Прямоугольник.

– А мы не родственники с тобой?

– Да,– говорит Прямоугольник. –  У нас есть признаки, по которым мы похожи, значит, мы близкие родственники и у нас может быть одна фамилия.

5. Рисунок «Настроение геометрических фигур»

Дети вытягивают карточки, на которых написаны разные настроения, например: мечтательный, радостный, грустный. Дети должны нарисовать портрет чисел, когда они веселые, мечтательные, грустные, сердитые и т.д.

6. Игра «Скорее в круг!»

В середине площадки чертят круг диаметром 1-2 метра (в зависимости от числа играющих). Выбирают водящего, который становится в круг. Остальные игроки располагаются за кругом. Они становятся на равном расстоянии друг от друга и чертят вокруг себя небольшие кружки диаметром в 0,5 метра. Перед началом игры все участники входят в большой круг. Один из них подкидывает мяч вверх (и немного в сторону), а остальные, кроме водящего, разбегаются по своим кружкам.

Водящий, как только мяч коснулся земли, старается ударом руки закатить мяч в центральный круг. Однако стоящие в кругах мешают ему сделать это, также отгоняя мяч руками. При этом они имеют право выбегать из своих кругов и отбегать от них. Но вместе с тем игроки зорко следят за тем, чтобы водящий не занял их место в кружке. В противном случае игрок, оставшийся без круга, становится новым водящим. Если водящему удалось закатить мяч в круг или прокатить его через круг, игра начинается снова. При этом учитель назначает нового водящего.

7. Написание черновика сказки (возможно задание на дом)

ПРИЛОЖЕНИЕ 7

Тема № 6 (5 часов)

Делимость натуральных чисел

Занятие № 1. Слушаем

Ход занятия:

1. Предъявление «Сказки про то, как появились квадраты простых чисел»

Ходила как-то цифра 3 и скучала: «Почему я не составное число? Ведь у составных чисел больше двух делителей!» И стало ей обидно. Тут она встретила Умножение. Пожаловалась она Умножению. Умножение и говорит: «Не плачь, пошли к Квадрату числа! Он что-нибудь придумает». Пришли они к нему и все рассказали. Квадрат им отвечает: «Могу поставить три в квадрат». Троечка подумала и согласилась. Поставил Квадрат число Три в квадрат, и стала она Девять. И появился у неё третий делитель. А вскоре и другие простые числа захотели стать  «составными». Вот так и появились  квадраты простых чисел: два в квадрате равно четыре, три в квадрате равно девять,  пять в квадрате равно двадцать пять … , и все эти числа стали иметь три делителя.

2. Вопросы и задания к сказке:

·        Сколько делителей имеет простое число?

·        Сколько делителей имеет составное число?

·        Число 1 – составное число или простое?

3. Сценка “В гостях у числа 28”

Число 28: “Сегодня я пригласила в гости своих друзей – моих делителей, младше, чем я. Пора их встречать.”

Стук в дверь. Заходит 1, за ней 2, 4, 7, 14.

- Что-то вас немного, друзья мои. Мне хочется, что гостей было много. Прошу вас, приведите своих меньших делителей.

Все засуетились. Стали искать своих делителей. Оказалось, что все они здесь.

Единица: “Уважаемое число 28, гостей больше не будет. Они все здесь. Но не расстраивайтесь, число 28, мы приготовили тебе замечательный подарок. Пусть это будет для тебя сюрпризом”.

Входят четыре плюса и встают между делителями.

Единица: “А вот и сюрприз. Сложи нас!”

Число 28 восклицает, что получилось оно же само: “Вот здорово, так то же я!” Единица: “Теперь ты не просто число, а совершенное число”.

Все хлопают в ладоши, поздравляют число 28.

Число 28: “Благодарю вас, друзья мои!»

4. Рисунок «Настроение геометрических фигур»

Дети вытягивают карточки, на которых написаны разные настроения, например: мечтательный, радостный, грустный. Дети должны нарисовать портрет чисел, когда они веселые, мечтательные, грустные, сердитые и т.д.

5. Игра «Скорее вставай»

Перед участниками разложены билеты с примерами на формулировку признаков делимости. Первый игрок берет билет с вопросом, если он ответил правильно, то имеет право на следующий билет, если неверно, то ход передается следующему игроку. В случае верного решения участник зарабатывает 1 балл.

6. Проверка усвоения учебного материала

Вопросы

·        Какие числа называются натуральными?  

·        Что называется делителем натурального числа? Приведите примеры. 

·        Что называется кратным натурального числа? Приведите примеры.  

·        Сформулируйте признак делимости на 3, на 9, на 5, на 2, на 1 и т.д.  

·        Для чего нужны признаки делимости?

7. Написание черновика сказки (возможно задание на дом)

ПРИЛОЖЕНИЕ 8

Тема № 7 (3 часа)

Проценты

Занятие № 1. Слушаем

Ход занятия:

1. Актуализация знаний

Вопросы:

·        Что называется процентом? Замени проценты десятичной и обыкновенной дробью: 1%, 2%, 5%, 10%, 20%, 25%, 50%, 75%, 100%.

·        Как выразить число в процентах?

·        Как выразить проценты десятичной дробью?

·        Как найти несколько процентов числа?

·        Как найти число по его процентам?

·        Как найти процентное отношение двух чисел?

2. Предъявление «Сказки о хитром и жадном короле»

Один хитрый и жадный король созвал как-то свою гвардию и торжественно заявил:

- Гвардейцы! Вы славно служите мне! Я решил вас наградить и повысить каждому месячное жалованье на 20%!

- Ура! – закричали гвардейцы.

- Но, – сказал король, – только на один месяц. А потом я его уменьшу на те же самые  20%. Согласны?

- А чего же не согласиться? – удивились гвардейцы. – Пусть хоть на один месяц!

Так и было решено. Прошел месяц, все были довольны.

- Вот здорово! – говорил старый гвардеец друзьям. – Раньше я получал 10 долларов в месяц, а в этом месяце получил 12 долларов!

Прошел еще месяц. И получил старый гвардеец жалованья только 9 долларов 60 центов.

- Как же так? – заволновался он. – Ведь если сначала на 20% увеличить жалованье, а потом его уменьшить на те же самые 20%, то оно же должно остаться прежним!

- Вовсе нет, - объяснил мудрый звездочет. – Повышение твоего жалованья составляло 20% от 10 долларов, т. е. 2 доллара, а понижение составляло 20% от 12 долларов, т. е. 2,4 доллара.

Погрустили гвардейцы, но делать нечего – ведь сами согласились. И вот решили они обхитрить короля. Пошли они к королю и сказали:

- Ваше Величество! Вы, конечно, были правы, когда говорили, что повысить жалованье на 20% и понизить его потом на те же 20% – это одно и то же. И если это одно и то же, то давайте сделаем еще раз, но только наоборот. Давайте сделаем так: Вы сначала понизите нам жалованье на 20%, а потом увеличите его на те же 20%.

- Ну что ж, – ответил король, – ваша просьба логична; пусть будет по-вашему!

3. Вопросы и задания к сказке:

·        Останется ли товар по своей цене, если его увеличить на 1%, а потом уменьшить на 1%?

·        Как происходит изменение в стоимости товара?

4. Сценка “Как разрешили спор”

Две подружки 0,5 и 1/2 вдруг повздорили: я больше, я лучше. Собрали консилиум. Пришли дроби: и обыкновенные, и десятичные, пригласили царицу Математику.

- Я лучше, потому что я – десятичная, а ты – обыкновенная.

- Нет, я лучше.

- Мой знаменатель – десять, а твой – только два.

- А у меня есть волшебная палочка, а у тебя только запятая.

И тут царица Математика разрешила их спор:

- Вы, красавицы-дроби, обе одинаковы, потому что ½ = 1 : 2 = 0,5. Вы сестрички-близнецы.

5. Рисунок «Настроение геометрических фигур»

Дети вытягивают карточки, на которых написаны разные настроения, например: мечтательный, радостный, грустный. Дети должны нарисовать портрет чисел, когда они веселые, мечтательные, грустные, сердитые и т.д.

6. Игра «Кто быстрее?»

         Участники должны перечислить по очереди различные области применения процентов. В случае, если команда не отвечает, то право ответа переходит к следующей команде. Каждый  правильный ответ приносит команде 1 балл. Также 2 балла присуждаются дополнительно за дисциплину.

Задание: Перечислите сферы применения процентов в нашей жизни.

7. Написание черновика сказки (возможно задание на дом)

ПРИЛОЖЕНИЕ 9

ИТОГОВОЕ ЗАНЯТИЕ

Цель: подвести итоги проделанной за учебный год работы.

Ход занятия:

I.  Организационный момент.

II. Рефлексия обучающихся.

     Продолжи предложения:

Ÿ  я узнал…

Ÿ  было интересно…

Ÿ  было трудно…

Ÿ  я выполнял задания…

Ÿ  я понял, что…

Ÿ  теперь я могу…

Ÿ  я почувствовал, что…

Ÿ  я приобрел…

Ÿ  я научился…

Ÿ  у меня получилось …

Ÿ  я смог…

Ÿ  я попробую…

Ÿ  меня удивило…

Ÿ  урок дал мне для жизни…

Ÿ  мне захотелось…

III. Подведение итогов.

      Награждение самых активных, самых способных, «самых-самых кружковцев».

V. СПИСОК ЛИТЕРАТУРЫ

Основная литература:

1.     Занимательная математика на уроках и внеклассных мероприятиях. 5-8 классы / Ю. В. Щербакова. – М.: Глобус, 2009.

2.     Математика. 5-8 классы: игровые технологии на уроках / И. Б. Ремчукова. – Волгоград: Учитель, 2008.

3.     Нестандартные уроки математики (5-9 классы) / Н. А. Курдюмова. – М.: Школьная пресса, 2009.

4.     Математические кружки в школе. 5-8 классы / А. В. Фарков. – 3-е изд. – М.: Айрис-пресс, 2009.

5.     Сказки и подсказки (задачи для математического кружка)/ Е.Г.Козлова. – М.: МЦНМО, 2010. – 165 с.  КомКнига, 2005. – 208 с.

6.     Газета “Математика”, 2005-2009 г.г.

Дополнительная литература:

1.     Шейнина О.С., Соловьева Г.М. Математика: Занятия школьного кружка. 5-6 кл. – М.: НЦ ЭНАС, 2008.

2.     Внеклассная работа по математике в 5-6 классах / А. С. Чесноков и др. Под ред. С. И. Шварцбурда.  – М.: Просвещение, 2007.

3.     Внеклассная работа по математике. 5-11 классы / А. В. Фарков. – 2-е изд. – М.: Айрис-пресс, 2007. – 288 с.

4.     Развитие логического мышления школьников. Занимательные задачи в русских сказках: кн. для учителей и родителей/  Е.А.Аксенова. – М.: Гуманитарн. изд. центр ВЛАДОС, 2007. – 124 с.: ил.

Информационно-компьютерная поддержка учебного процесса:

1.  CD-диск «1С: Репетитор. Математика» (КиМ);

2.   Интернет-ресурсы:

-       Педагогическая мастерская, уроки в Интернет:  http://teacher.fio.ru , http://uztest.ru/adv

-       Новые технологии в образовании: http://edu.secna.ru/main/

-       Путеводитель «В мире науки» для школьников:  http://www.uic.ssu.samara.ru/~nauka/

-       Мегаэнциклопедия Кирилла и Мефодия: http://mega.km.ru

-       Скачано с www.znanio.ru