Aylantirish, ustma-ust qo‘yish

Aylantirish, ustma-ust qo‘yish (jipslashtirish) usullari va ular yordamida masalalar echish bo‘yicha tushunchalar

156,a–rasmda umumiy vaziyatdagi Q tekislikni Q_N gorizontal izi atrofida aylantirib, H tekislikka jipslashtirish ko‘rsatilgan. Tekislikning gorizontal izi aylanish o‘qi sifatida qabul qilingani uchun uning vaziyati o‘zgarmaydi. Bu tekislikni H tekislikka jipslashtirish uchun mazkur tekislikka tegishli biror nuqtaning H tekislikka jipslashtirish kifoya. Bunday nuqta sifatida tekislikning frontal iziga tegishli B(B′,B″) nuqtani olish mumkin. Bu nuqta orqali Q_N ga perpendikulyar M gorizontal proyeksiyalovchi tekislik o‘tkaziladi. B nuqta O′B_o=R radiusli yoy bo‘yicha M_N iz bilan kesishguncha aylantiriladi. Natijada, hosil bo‘lgan B′₁ nuqta bilan Q_x ni o‘zaro tutashtirsak, Q tekislikni H tekislikka jipslashtirilgan vaziyatiga ega bo‘lamiz. Tekislikni bunday jipslashtirganda unga tegishli geometrik shakllar H tekislikka jipslashib, haqiqiy o‘lchamlarida proyeksiyalanadi.

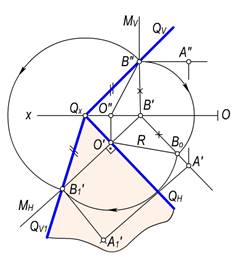
a)                                                               b)

156-rasm.

156,a–rasmdan shuni aniqlash mumkinki, Q tekislikni Q_N izi atrofida aylantirib, uni H tekislikka jipslashtirishda Q_V iziga tegishli Q_xB₁ kesma o‘zining haqiqiy o‘lchamiga teng bo‘lgani uchun Q_xB″=Q_xB′₁ bo‘ladi. Demak, chizmada Q(Q_N, Q_V) tekislikni H tekislikka jipslashtirish uchun uning Q_V izida tanlab olingan B ≡ B″ nuqtani va Q_X markazdan Q_x B″ radius bilan yoy chizib, M tekislikning M_N izi bilan kesishgan B₁ nuqta aniqlanadi. So‘ngra B₁ va Q_X nuqtalardan tekislikning Q_V1 izi o‘tkaziladi.

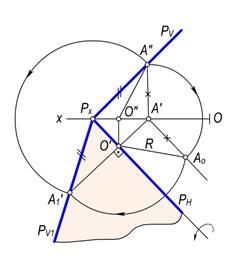
Chizmada P(P_N, P_V) tekislikni P_N izi atrofida aylantirib, H tekislikka jipslashtirish uchun aylantirish radiusining haqiqiy o‘lchamini aniqlash zarur bo‘lsin (156,b–rasm). Ma’lumki, aylantirish radiusi tekislikning aylanish o‘qiga perpendikulyar bo‘ladi. To‘g‘ri burchakning proyeksiyalanish xususiyatiga ko‘ra, tekislikning P_V izida olingan A(A′, A″) nuqtaning A′ proyeksiyasidan tekislikning P_N iziga perpendikulyar o‘tkaziladi va O′ hamda O″ nuqtalarni topamiz. Chizmada hosil bo‘lgan O′A′ va O″A″ aylantirish radiusining proyeksiyalari, O′A₀ esa uning haqiqiy o‘lchami bo‘ladi.

Xuddi shuningdek P(P_H, P_V) tekislikni V tekislikka ham jipslashtirish mumkin (157–rasm). Buning uchun berilgan P tekislikning P_H gorizontal izida ixtiyoriy A nuqta tanlab, uning aylantirish radiusi P_X A′ aniqlanadi va tekislikning P_N izini P_V izi atrofida aylantirib, tekislikka jipslashtiriladi. Chizmadan ko‘rinib turibdiki, P tekislikni P_N izi atrofida aylantirilganda P_xA′ kesma P_xA″₁ ga teng bo‘ladi. 

Umumiy vaziyatda berilgan tekislikka tegishli geometrik shaklning haqiqiy o‘lchamini aniqlash uchun uning xarakterli nuqtalarini proyeksiyalar tekisligiga jipslashtirish yo‘li bilan aniqlanadi. Masalan, Q(Q_N, Q_V) tekislikka tegishli ∆ABC(A′B′C′, A″B″C″) ning (158–rasm) haqiqiy o‘lchami uning A, B va C nuqtalarini V tekislikka jipslashtirish yo‘li bilan aniqlanadi.

Tekislikning jipslashgan holati berilgan bo‘lsa, uning dastlabki vaziyatini tiklash mumkin. Tekislikning dastlabki vaziyatini aniqlash natijasida tekislikka tegishli bo‘lgan shakllarning ham proyeksiyalarini aniqlash mumkin.

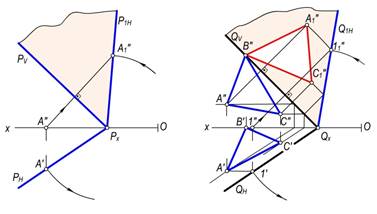
157-rasm.                               158-rasm.

Masalan, P tekislikning H tekislikka jipslashtirilgan vaziyati P_H, P_V, P_1V izlari va shu tekislikka tegishli O₁ markaz va R radiusli aylana berilgan bo‘lsin (159–rasm).

Bu aylananing P tekislikdagi proyeksiyalarini yasash uchun aylana markazidan tekislikning h′₁ gorizontali o‘tkaziladi va 1′₁ nuqta aniqlanadi. Bu nuqtadan tekislikning P_N iziga perpendikulyar o‘tkazib, Ox proyeksiyalar o‘qiga tegishli 1′ nuqta topiladi. Bu nuqtadan h′₁ ning h′ proyeksiyasi o‘tkaziladi. So‘ngra P_x markazdan P_x1′₁ radius bilan o‘tkazilgan yoyning 1′ dan Ox o‘qiga o‘tkazilgan perpendikulyar bilan kesishgan 1″ nuqtasi topiladi. Bu nuqtadan h′₁ ning h″ proyeksiyasini o‘tkaziladi. So‘ngra 1″ va P_x nuqtalar tutashtirilib, tekislikning P_V izi hosil qilinadi. Aylana markazining proyeksiyalarini yasash uchun O′₁ dan P_N ga perpendikulyar o‘tkazib, h′ bilan kesishgan O′ nuqtani va h″ da O″ nuqta topiladi. Shuningdek, bu gorizontalda joylashgan aylananing A′₁ va B′₁ nuqtalarining A′, A″ va B′, B″ proyeksiyalari aniqlanadi.

Tekislikning f′₁ frontalini aylananing markazi O′₁ dan P_1V ga parallel qilib o‘tkazilib, aylananing E′₁ va F′₁ nuqtalarning E′, E″ va F′, F″ proyeksiyalari yasaladi.[1]

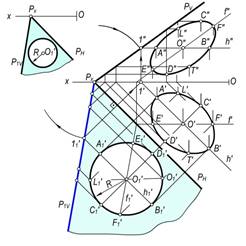
159-rasm. 

Xuddi shu tarzda aylananing L′₁ va T′₁, C′₁ va D′₁ nuqtalarning proyeksiyalari tekislikning gorizontallari yordamida aniqlanadi. Bu nuqtalarning bir nomli proyeksiyalarini mos ravishda o‘zaro tutashtirsak, aylananing gorizontal va frontal proyeksiyalari – ellipslar hosil bo‘ladi.

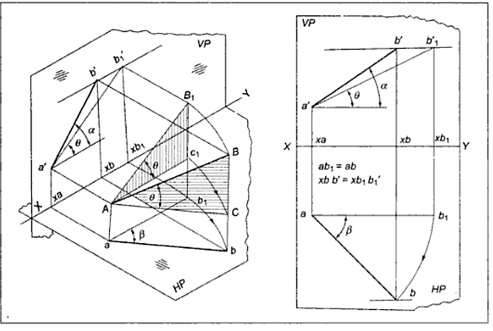
Agar AB kesma har ikkala proyeksiyalar tekisligigadan biriga aylantirib proyeksiyalansa chizmadagi ko’rinishda (fazoviy holati va epyurasi) bo’ladi. [2]

Скачано с www.znanio.ru